1. Giới thiệu
Trong dữ liệu tài chính, giá cổ phiếu ở thời điểm t không chỉ phụ thuộc vào dữ liệu hôm trước, mà có khả năng bị ảnh hưởng mạnh mẽ theo từng giai đoạn. Vì vậy, nhu cầu đặt ra là phải có một kiến trúc có khả năng quan sát toàn bộ chuỗi giúp mô hình nhận diện đúng các tín hiệu dài hạn quan trọng thay vì bị chi phối bởi những biến động nhiễu ngắn hạn. Tính cấp thiết của đề tài còn xuất phát từ thực tế rằng thị trường đang trở nên khó lường hơn. Giá cổ phiếu phản ứng gần như tức thì với thông tin, khiến việc dự báo thủ công trở nên kém hiệu quả. Trong bối cảnh đó, các mô hình dự báo chuỗi thời gian hiện đại không chỉ hỗ trợ nhà đầu tư ra quyết định nhanh chóng hơn mà còn mang lại lợi thế cạnh tranh đáng kể. Đồng thời, nhu cầu nghiên cứu và thực thi các mô hình dự báo minh bạch, có khả năng mở rộng và phù hợp với điều kiện dữ liệu thực tế cũng ngày càng tăng cao.
Bài viết này được xây dựng với mục tiêu giới thiệu và triển khai các mô hình dự báo chuỗi thời gian phổ biến trong phân tích giá cổ phiếu, đồng thời trình bày cách ứng dụng chúng trong dự đoán giá cổ phiếu FPT.
2. Cơ sở lý thuyết
Dự báo chuỗi thời gian trong bối cảnh dữ liệu tài chính đòi hỏi cách tiếp cận linh hoạt, có khả năng mô hình hóa mối quan hệ phi tuyến, bắt được tính phụ thuộc theo thời gian và hạn chế nhiễu trong tín hiệu. Do đó, bài viết tập trung vào ba nhóm phương pháp tiêu biểu, đại diện cho ba hướng tiếp cận khác nhau trong học máy và xử lý chuỗi thời gian.
Đầu tiên, các mô hình theo kiến trúc MLP (Multilayer Perceptron) được xem như nền tảng của học sâu, cho phép mô phỏng các quan hệ phi tuyến giữa các biến đầu vào và đầu ra. Tiếp theo là nhóm mô hình RNN (Recurrent Neural Network) và các biến thể, vốn được thiết kế đặc biệt để học thông tin phụ thuộc theo thời gian – một thành phần cốt lõi trong dữ liệu chuỗi thời gian. Cuối cùng, bộ lọc Savitzky–Golay được sử dụng như một kỹ thuật xử lý tín hiệu nhằm làm mượt dữ liệu và giảm nhiễu trước khi đưa vào mô hình, giúp tăng độ ổn định trong quá trình dự báo.
2.1. Kiến trúc MLP
Những mô hình Transformer có khả năng giải quyết những vấn đề liên quan đến phụ thuộc dài hạn của dữ liệu tài chính. Tuy nhiên, độ phức tạp của các mô hình Transformer không những dễ overfit với loại dữ liệu nhiều nhiễu như tài chính mà còn tốn kém và không khả thi trong thời gian thật.
Trong bối cảnh đó, nhóm mô hình tuyến tính và phi tuyến dựa trên cơ chế tách thành phần hoặc ánh xạ thẳng đang ngày càng được quan tâm nhờ tính đơn giản, tốc độ nhanh và hiệu quả cao với dữ liệu có cấu trúc rõ ràng. Ba mô hình tiêu biểu trong hướng tiếp cận này gồm Linear, DLinear và NLinear.
2.1.1. Mô hình Linear
Mô hình Linear sử dụng phép ánh xạ tuyến tính trực tiếp từ không gian đầu vào sang đầu ra. Đây là mô hình đơn giản nhất, giả định rằng chuỗi thời gian có mối quan hệ tuyến tính ổn định và có thể dự báo bằng cách kết hợp có trọng số của các quan sát gần nhất.
Dựa trên giả định rằng giá trị tương lai có thể được suy ra từ tổ hợp tuyến tính của các quan sát ở quá khứ, với một chuỗi thời gian $x_t$, nhiệm vụ của mô hình là ước tính giá trị tại bước tiếp theo $\hat{x}_{t+1}$ thông qua hàm tuyến tính:
$$ \hat{x}_{t+1} = \mathbb{w}^T \mathbb{x}_t + b $$
Trong đó:
- $\mathbb{x}_t = [x_t,x_{t-1},...,x_{t-L+1},]$ là cửa sổ đầu vào gồm L quan sát gần nhất
- $\mathbb{w}$ là vector trọng số
- $b$ là bias
Mục tiêu của mô hình là tìm $\mathbb{w}$ và $b$ sao cho hàm mất mát đạt giá trị nhỏ nhất:
$$ L = \frac{1}{N}\sum_{i=1}^N(\hat{x_i}-x_i)^2 $$
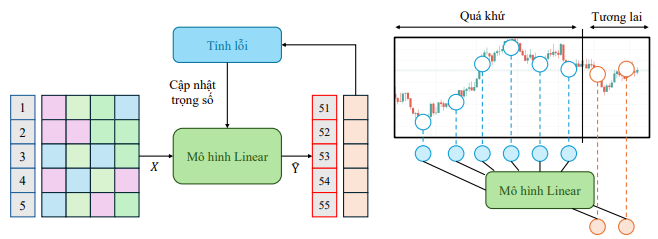
Hình 1: Quy trình huấn luyện Linear Model
Mô hình Linear chỉ học được những mối quan hệ tuyến tính nên có nhiều hạn chế trong bối cạnh dữ liệu biến động mạnh và có tính phi tuyến cao. Tuy nhiên, với số lượng tham số ít, tốc độ huấn luyện nhanh và khả năng khái quát tốt trong các chuỗi có sự phụ thuộc đơn giản, mô hình Linear thưởng được sử dụng như một baseline giúp đánh giá hiệu quả của các mô hình phức tạp hơn.
2.1.2. Mô hình DLinear
DLinear là mô hình có thể cải thiện những hạn chế của mô hình Linear truyền thống trong dự báo chuỗi thời gian. Ý tưởng của DLinear xuất phát từ quan sát thực nghiệm rằng phần lớn chuỗi thời gian thực tế—đặc biệt là dữ liệu kinh tế và tài chính—có thể được biểu diễn bởi hai thành phần chính:
- Xu hướng (Trend): biến động chậm, phản ánh quỹ đạo dài hạn.
- Mùa vụ hoặc dao động (Seasonal/Residual): thay đổi nhanh, mang tính lặp lại hoặc nhiễu ngắn hạn.
Thay vì ánh xạ trực tiếp toàn bộ chuỗi vào một lớp Linear duy nhất, DLinear tách chuỗi đầu vào thành hai phần, sau đó áp dụng mô hình tuyến tính độc lập cho từng thành phần.
Với chuỗi thời gian $\hat{x}$, DLinear thực hiện phân rã:
$$ x_t = x_t^{(trend)} + x_t^{(seasonal)} $$
Trong đó:
- $x_t^{(trend)}$ được tạo ra bằng cách làm mượt chuỗi thời gian $x_t$ (ví dụ bằng Moving Average)
- $x_t^{(seasonal)} = x_t^{(trend)} - x_t$
Mỗi thành phần trên được đưa vào một mô hình Linear riêng biệt:
$$ \hat{x}_{t+1}^{(trend)} = \mathbb{w}_1^T \mathbb{x}_t^{(trend)} + b_1 \\ \hat{x}_{t+1}^{(seasonal)} = \mathbb{w}_2^T \mathbb{x}_t^{(seasonal)} + b_2 $$
Dự báo cuối cùng sẽ được kết hợp từ 2 thành phần dự đoán trend và seasonal/residual:
$$ \hat{x}_{t+1} = \hat{x}_{t+1}^{(trend)} + \hat{x}_{t+1}^{(seasonal)} $$
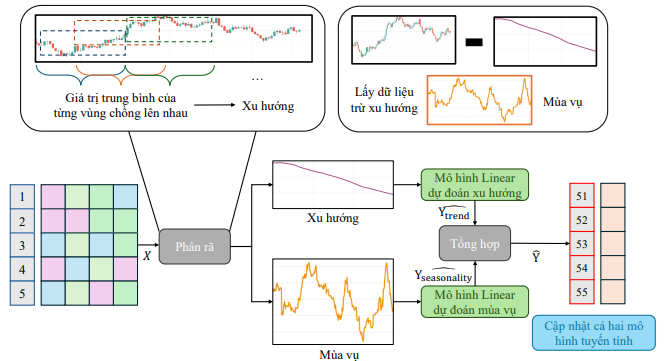
Hình 2: Quy trình huấn luyện DLinear Model
Mô hình DLinear tận dụng cấu trúc tự nhiên của chuỗi thời gian và ổn định hơn mô hình tuyến tính truyền thông, đặc biệt trong chuỗi có xu hướng rõ hoặc dao động mạnh, và vẫn giữ được ưu điểm về tốc độ tính toán và bộ nhớ của các mô hình tuyến tính.
2.1.3. Mô hình NLinear
NLinear là một mở rộng của mô hình Linear truyền thống, được thiết kế nhằm khắc phục hạn chế lớn nhất của Linear và DLinear là việc không thể mô hình hóa các quan hệ phi tuyến trong chuỗi thời gian.
NLinear sử dụng một phép biến đổi phi tuyến lên dữ liệu đầu vào trước khi đưa vào lớp Linear. Cách tiếp cận này cho phép mô hình thể hiện các quan hệ phức tạp hơn mà Linear không nắm bắt được, trong khi vẫn giữ được tính đơn giản của kiến trúc tuyến tính.
$$ \mathbb{z}_t = g(\mathbb{x}_t) $$
Một số phép biến đổi phi tuyến mà mô hình NLinear có thể áp dụng là dịch chuyển theo mean, dịch chuyển theo median, chuẩn hóa theo min-max hoặc dịch chuyển theo giá trị đầu/cuối. Các biến đổi này giúp mô hình giảm ảnh hưởng của giá trị tuyệt đối, nhấn mạnh biến động tương đối và học cấu trúc phi tuyến mà Linear thuần không thể học được.
Dữ liệu đã biến đổi được đưa qua một lớp Linear:
$$ \hat{x}_{t+1} = \mathbb{x}^T\mathbb{z}_t + b $$
Sau đó kết quả $\hat{x}_{t+1}$ được chuyển ngược về không gian ban đầu.
Tóm lại, NLinear nắm bắt tốt hơn các quan hệ phi tuyến, chi phí tính toán thấp (tương đương Linear) và hiệu quả tốt đối với các chuỗi nhiễu cao và biến động nhanh.
2.1.4. Mô hình TimeMixer
TimeMixer ra đời như một kiến trúc vừa giữ được ưu điểm của mô hình tuyến tính về tốc độ và chi phí vừa có thể mô hình hóa các quan hệ phi tuyến và phụ thuộc dài hạn. TimeMixer là mô hình hóa chuỗi thời gian bằng cách trộn (mix) thông tin theo thời gian thông qua các phép biến đổi phi tuyến và thích nghi, thay vì dựa hoàn toàn vào ánh xạ tuyến tính hoặc self-attention (chi phí tính toán cao). Thay vì chỉ dựa vào phép tuyến tính, TimeMixer bổ sung các phép trộn phi tuyến và cơ chế khuếch đại các tương tác phức tạp giữa những điểm dữ liệu xa nhau.
Kiến trúc TimeMixer bao gồm ba thành phần nền tảng được thiết kế theo pipeline nhất quán, tối ưu cho các đặc trưng của dữ liệu chuỗi thời gian:
- Temporal Decomposition — tách tín hiệu thành Trend và Seasonal.
- Multi-Scale Temporal Mixing — pha trộn tín hiệu trên nhiều thang thời gian khác nhau, giúp mô hình học được xu hướng cục bộ và quan hệ dài hạn của dữ liệu.
- Progressive Learning Mechanisms — cơ chế học tiến dần để ổn định hoá quá trình huấn luyện.
Temporal Decomposition
Tương tự DLinear, để giảm độ phức tạp của tín hiện đầu vào, TimeMixer bắt đầu bằng bước phân rã tín hiệu thành Trend và Seasonal. Các thành phần phân rã này sẽ được đưa vào một mạng phi tuyến như Tanh hoặc ReLU để mô hình học các mối quan hệ phi tuyến.
Hàm Tanh có thể được lựa chọn để làm mượt thành phần Trend. Hàm Tanh là một hàm có đạo hàm bậc một 1 liên tục và các đạo hàm bậc cao cũng mượt nên tạo ra các ưu điểm như biến đổi đầu ra mượt mà theo một cách không gây đứt gãy hay ổn định hơn khi mô hình cần học cấu trúc nền, chu kỳ dài, hoặc các tín hiệu có độ biến thiên nhỏ qua thời gian.
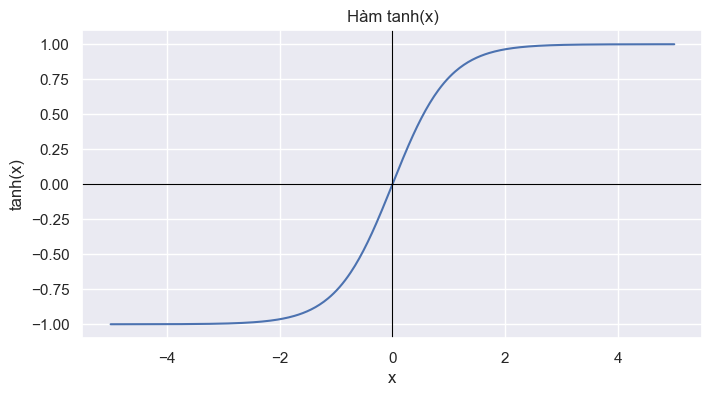
Hình 3: Đồ thị hàm Tanh
Trong khi đó, hàm ReLU tạo ra đặc tính phi tuyến sắc nét — phù hợp mô hình hóa dao động và biến động mạnh ở thành phần Seasonal. ReLU không mượt và không có đạo hàm tại 0. Do đó, ReLU tạo ra đường gãy tại 0, các biến đổi nhanh và mạnh, khả năng kích hoạt thưa (chỉ giữ lại tín hiệu quan trọng). ReLU bắt được kiểu biến động này tốt hơn Tanh vì không bị nén biên độ, dễ tạo ra pattern ngắt quãng và phản ứng nhạy với sự thay đổi đột ngột của tín hiệu
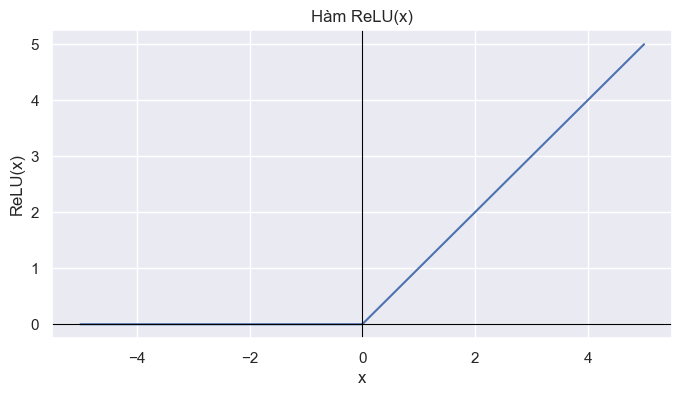
Hình 4: Đồ thị hàm ReLU
Multi-Scale Temporal Mixing
Chuỗi thời gian thực tế thường có tính đa tần (multi-frequency), có chứa:
- Thành phần biến thiên nhanh: dao động cục bộ, nhiễu, sự kiện đột ngột
- Thành phần biến thiên trung bình: chu kì ngày-tuần, giai đoạn tăng giảm ngắn
- Thành phần biến thiên dài hạn: xu hướng dài hạn, hành vi ổn định theo thời gian
Bộ lọc đơn tần không thể nắm bắt toàn bộ thành phần này. TimeMixer vì vậy tổ chức kiến trúc dựa trên đa tầng, đa độ phân giải, khai thác một tập các lớp trộn thời gian theo nhiều scale khác nhau.
Với mỗi scale $s$, TimeMixer tạo ra một ánh xạ đặc trưng thông qua một mixer block tuyến tính mở rộng:
$$ h_s = MLP_s(x_s) $$
Trong đó:
- $x_s$ là chuỗi đầu vào được downsample theo scale $s$ (ví dụ: scale 1 = full resolution, scale 2 = cách 2 điểm, scale 4 = cách 4 điểm,...)
- $MLP_s$ là MLP xử lý scale $s$
- $h_s$ là vector đặc trưng mô tả tần số đặc trưng của scale $s$
TimeMixer không chỉ ghép các scale lại — nó học trọng số tối ưu cho từng scale. Sau khi thu được các đặc trưng theo nhiều scale, TimeMixer áp dụng cơ chế Scale Attention để xác định trọng số mức độ quan trọng của từng scale (học trọng số của từng scale):
$$ α_s = Softmax(W ⋅ [h_1;h_2;...;h_k]) $$
Trong đó:
- $[h_1;h_2;...;h_k]$ là vector chứa thông tin đa tần từ mọi scale
- Ma trận $W$ biến đổi vector đó sang không gian mới
- $\alpha_s$ là độ quan trọng (attention weight) của scale $s$
Biểu diễn đa tần cuối cùng sau khi trộn $H$ là đặc trưng tổng hợp của chuỗi bằng tổng có trọng dố các đặc trưng từng scale.
$$ H = \sum_{s=1}^k \alpha_s h_s $$
Progressive Learning: PRU và LRU
Để giảm hiện tượng bất ổn trong quá trình học, TimeMixer sử dụng hai cơ chế học tiến dần:
Progressive Representation Update (PRU): Biểu diễn được cập nhật theo từng bước nhỏ nhằm tránh việc mô hình thay đổi đột ngột, giúp gradient ổn định và giảm nhiễu trong quá trình học.
Learnable Residual Update (LRU): Thay vì sử dụng residual truyền thống $y=x+F(x)$, LRU cho phép mô hình kiểm soát mức độ “giữ lại” hay “biến đổi” của tín hiệu, giúp giảm sai lệch và tránh hiện tượng khuếch đại lỗi trong dự báo dài hạn. Residual được điều chỉnh bởi hai hệ số học được:
$$ y=\alpha x + \beta F(x) $$
Kết luận
TimeMixer là một kiến trúc hiệu quả, được thiết kế phù hợp với đặc trưng tự nhiên của chuỗi thời gian nhờ khả năng phân rã tín hiệu có cấu trúc, trộn đa tần linh hoạt, và học tiến dần ổn định.
2.2. Kiến trúc RNN
RNN là lớp mô hình học sâu được thiết kế để xử lý dữ liệu có tính chuỗi, trong đó đầu ra tại thời điểm $t$ phụ thuộc không chỉ vào đầu vào mà còn vào trạng thái trước đó. RNN nắm bắt quan hệ tuần tự, nhưng mô hình này bộc lộ hai hạn chế cơ bản là Gradient vanishing/exploding khiến việc học quan hệ dài hạn trở nên khó khăn và thiếu sức mạnh mô hình hóa các cấu trúc thời gian phức tạp.
Long Short-Term Memory (LSTM) được xem là cải tiến lớn của RNN, giải quyết vấn đề khó học quan hệ dài hạn thông qua việc giới thiệu một bộ nhớ dài hạn và các cổng tuyến tính điều chỉnh dòng thông tin.
2.2.1. Mô hình xLSTM
Do mỗi cổng trong LSTM (input, forget, output) đều là ánh xạ tuyến tính kèm với Sigmoid, nghĩa là độ phi tuyến thấp,không đủ sức biểu diễn các cấu trúc dao động phức tạp, khó mô hình hóa xu hướng + mùa vụ + mối quan hệ có đa tần số. Trong bối cảnh đó, xLSTM ra đời với ý tưởng cốt lõi là thay cổng tuyến tính (linear gate) bằng cổng phi tuyến (deep nonlinear gate), kết hợp chuẩn hóa (normalization) và skip-connection kiểm soát giúp tăng khả năng mô hình hóa mà vẫn giữ đặc tính tuần tự của LSTM.
Deep Gating Mechanism
Thay vì sử dụng cổng tuyến tính, xLSTM sử dụng cổng thông qua lớp MLP sâu. Nhờ đó, mô hình có thể học quan hệ phi tuyến mạnh, tương tác phức tạp giữa trạng thái và tín hiệu mới, và đặc tính đa tần.
xLSTM nâng cấp biểu diễn từ “tuyến tính nông” lên “phi tuyến nhiều tầng”.
Gated Residual Connection
Thay vì residual đơn giản:
$$ y_t = F(x_t) + x_t $$
xLSTM sử dụng:
$$ y_t = \alpha_t F(x_t) + (1-\alpha_t) x_t $$
Trong đó $\alpha_t$ là một cổng điều khiển học được, giúp mô hình tránh khuyếch đại lỗi và điều chỉnh mức độ giữ lại thông tin.
2.2.2. Mô hình xLSTMTime
Đặc điểm chung của LSTM và xLSTM là trạng thái phụ thuộc tuần tự vào trạng thái trước, hàm cập nhật phi tuyến không có ràng buộc ổn định, và rất khó kiểm soát khuếch đại/làm suy biến tín hiệu trong chuỗi dài. Do đó, chỉ cần một sai số nhỏ cũng có thể bị khuếch đại theo thời gian, đặc biệt trong dự báo nhiều bước.
xLSTMTime được thiết kế để khắc phục vấn đề ổn định dài hạn mà LSTM và xLSTM vẫn chưa giải quyết triệt để.
Ý tưởng của xLSTMTime là sự kết hợp của Linear Recurrent Dynamics, Time-Modulated Gating và Multi-Scale Temporal Mixing.
Linear Recurrent Dynamics
Linear Recurrent Units (LRU) là một lớp RNN mới, được thiết kế để giữ lại bộ nhớ dài hạn ổn định, tránh exploding/vanishing, và có thể học chuỗi rất dài.
xLSTMTime tích hợp LRU với ràng buộc ổn định:
$$ h_t = Ah_{t-1} + Bx_t $$
Trong đó ma trận $A$ có mô-đun eigenvalue ≤ 1, nghĩa là bán kính phổ của A nhỏ hơn 1 giúp hệ thống tuyến tính ổn định.
Time-Modulated Gating
Mặc dù LRU có ưu điểm là ổn định và nhớ rất dài hạn nhưng LRU không biết "thời điểm nào" thông tin là quan trọng. xLSTMTime sử dụng time gate giải quyết điều đó, giúp kiểm soát độ dài bộ nhớ được dùng tại mỗi thời điểm, học tính chu kì, và giảm nhiễu.
$$ h_t = g_t ⊙ h_t^{LRU} $$
Trong đó:
- $h_t^{LRU}$ là bộ nhớ dài hạn ổn định do LRU sinh ra như đã đề cập ở trên
- $g_t$ là gate phụ thuộc thời gian (time-modulated gating)
Multi-Scale Temporal Mixing
xLSTMTime bổ sung phép trộn nhiều tần số, giúp mô hình học được xu hướng cục bộ và quan hệ dài hạn của dữ liệu. Cơ chế này tương tự ý tưởng TimeMixer đề cập ở mục 2.1.4 nhưng giữ nền tảng RNN.
Kết luận
xLSTMTime kết hợp bộ nhớ dài hạn của LRU với cơ chế gating theo thời gian để học chu kỳ và biến động, giúp mô hình vừa ổn định khi học chuỗi rất dài, vừa linh hoạt trước các biến động theo thời gian.
2.3. Phương pháp Savitzky–Golay Filter
Savitzky–Golay Filter (SG Filter) là kỹ thuật lọc tín hiệu dựa trên xấp xỉ đa thức cục bộ (local polynomial regression). Khác với Moving Average truyền thống thực hiện trung bình trượt đơn giản, SG Filter sử dụng cửa sổ trượt để khớp một đa thức bậc thấp với các điểm dữ liệu, sau đó lấy giá trị đa thức tại điểm trung tâm làm giá trị đã được làm mượt.
SG Filter bảo toàn cấu trúc hình thái của chuỗi thời gian: giữ lại các đỉnh, đáy và biên độ dao động tự nhiên, đồng thời loại bỏ nhiễu ngắn hạn mà vẫn bảo tồn xu hướng dài hạn. Nhờ nền tảng hồi quy đa thức, phương pháp này có khả năng xử lý tín hiệu phi tuyến nhẹ và cho phép tính đạo hàm bậc cao để phân tích tốc độ biến động. Những đặc tính này làm SG Filter đặc biệt phù hợp cho bước hậu xử lý dự báo giá cổ phiếu, nơi các mô hình học sâu thường tạo ra chuỗi dự đoán có dao động mạnh và nhiễu ngẫu nhiên.
Về mặt toán học, tại mỗi vị trí $t$, bộ lọc chọn cửa sổ gồm $w$ điểm và ước lượng các hệ số đa thức bậc $d$ sao cho tổng bình phương sai số đạt cực tiểu. Để đảm bảo tính không gây lệch pha (zero-phase smoothing), kích thước cửa sổ ww
w phải là số lẻ:
$$ w = 2m + 1 $$
Điều kiện này tạo cấu trúc đối xứng với các điểm trong cửa sổ được gán vị trí tương đối:
$$ \{−m,−(m−1),…,−1,0,1,…,m−1,m\} $$
Trong đó vị trí 0 là điểm trung tâm. Cấu trúc đối xứng này đảm bảo hệ số lọc cũng đối xứng, loại bỏ hiện tượng dịch pha. Ngược lại, nếu $w$ là số chẵn, ma trận thiết kế trở nên bất đối xứng, dẫn đến dịch pha không mong muốn trong tín hiệu đã lọc. Do đó, việc chọn window_length là số lẻ là yêu cầu toán học xuất phát từ bản chất xấp xỉ đa thức đối xứng của Savitzky–Golay filter.
3. Phương pháp thực hiện
3.1. Quy trình thực hiện
-
Chuẩn bị và Tiền xử lý Dữ liệu (Data Preparation and Preprocessing)
1.1. Thu thập và khởi tạo dữ liệu
1.2. Sắp xếp và biến đổi dữ liệu
-
Sắp xếp dữ liệu theo thời gian.
-
Tạo tính toán giá trị log của giá cổ phiếu: Cột
close_logđược tạo ra bằng cách áp dụng hàm logarit tự nhiên lên giá đóng cửa của cổ phiếuclose, giúp làm giảm độ biến động và phù hợp hơn với mô hình dự đoán.
1.3. Phân chia dữ liệu theo thời gian
Dữ liệu được phân chia theo đúng thứ tự thời gian, gồm:
-
Tập huấn luyện (70%)
-
Tập kiểm tra (15%)
-
Tập kiểm thử (15%)
Trong khi các tập kiểm tra và kiểm thử giữ nguyên cấu trúc thời gian, tập huấn luyện được shuffle ngẫu nhiên để tăng tính đa dạng của batch và cải thiện khả năng học của mô hình.
-
-
Thiết lập Môi trường và Cấu hình Mô hình (Environment Setup and Model Configuration)
2.1. Cố định tính ngẫu nhiên
Để đảm bảo kết quả có thể tái lập, các seed ngẫu nhiên của PyTorch, NumPy, Python và CUDA đều được cố định. Điều này giúp giảm sai khác giữa các lần huấn luyện.
2.2. Thiết lập siêu tham số
Các siêu tham số quan trọng được cấu hình, gồm:
-
Độ dài chuỗi đầu vào:
INPUT_LEN -
Độ dài chuỗi đầu ra:
OUTPUT_LEN -
Số epoch huấn luyện tối đa
-
Learning rate
-
Batch size
Các tham số này được điều chỉnh phù hợp với từng mô hình và mục tiêu dự báo ngắn hạn hoặc dài hạn.
2.3. Xây dựng kiến trúc mô hình
Hệ thống triển khai nhiều kiến trúc hiện đại, bao gồm:
-
LinearModel – Hồi quy tuyến tính cơ bản.
-
NLinearModel – Tuyến tính có chuẩn hóa đầu vào.
-
DLinearModel – Tuyến tính có tách thành phần xu hướng – mùa vụ.
-
xLSTMModel – LSTM mở rộng với exponential gating.
-
xLSTMTimeModel – LSTM với time-attention giúp mô hình hóa phụ thuộc động theo thời gian.
-
TimeMixerModel – Mô hình phân rã xu hướng–mùa vụ và trộn đa tỷ lệ (multi-scale mixing).
-
-
Huấn luyện và Đánh giá Mô hình (Model Training and Evaluation)
3.1. Quy trình huấn luyện với Early Stopping
Quá trình huấn luyện sử dụng:
-
Hàm mất mát: MSELoss
-
Bộ tối ưu: Adam
Các mô hình được huấn luyện qua nhiều epoch, đồng thời áp dụng Early Stopping để dừng huấn luyện khi không còn cải thiện trên tập kiểm tra, giúp tránh overfitting.
3.2. Đánh giá và lựa chọn mô hình tốt nhất
Sau khi huấn luyện, mô hình được đánh giá trên tập kiểm thử để đo lường sai số. Mô hình có hiệu suất tốt nhất (Sai số thấp nhất và ổn định nhất) được chọn làm mô hình cuối cùng phục vụ dự đoán.
-
-
Dự đoán và Làm mượt Kết quả (Prediction and Smoothing)
4.1. Quy trình dự đoán
Dữ liệu đầu vào là chuỗi giá trị
close_logmới nhất. Mô hình dự báo các giá trị log trong tương lai. Sau đó, kết quả được chuyển lại sang miền giá thực bằng hàm mũ. Điều này cho phép mô hình làm việc trên tín hiệu ổn định nhưng vẫn dự báo đúng giá trị thực tế.4.2. Làm mượt với Savitzky–Golay Filter
Để giảm nhiễu trong chuỗi dự đoán và cải thiện tính mượt, mô hình áp dụng bộ lọc Savitzky–Golay, vốn sử dụng hồi quy đa thức cục bộ để làm mượt mà không làm biến dạng cấu trúc tín hiệu. Điều này giúp đường dự báo ổn định, tránh dao động không tự nhiên do nhiễu mô hình.
3.2. Mô tả tập dữ liệu
Mục tiêu bài toán: Xây dựng mô hình dự đoán giá cổ phiếu FPT theo chuỗi 100 ngày liên tiếp dựa vào các đặc trưng trong quá khứ.
Tập dữ liệu bao gồm dữ liệu liên quan đến cổ phiếu FPT từ 08/03/2020 tới 10/03/2025, bao gồm 1149 dòng và 7 cột. Trong đó:
time: Ngày diễn ra phiên giao dịch, định dạng YYYY-MM-DDopen: Giá mở cửa trong ngàyhigh: Giá cao nhất trong ngàylow: Giá thấp nhất trong ngàyclose: Giá đóng cửa trong ngàyvolume: Khối lượng giao dịch trong ngàysymbol: Mã cổ phiếu (ticker)
Những dữ liệu về giá đều có đơn vị là nghìn đồng.
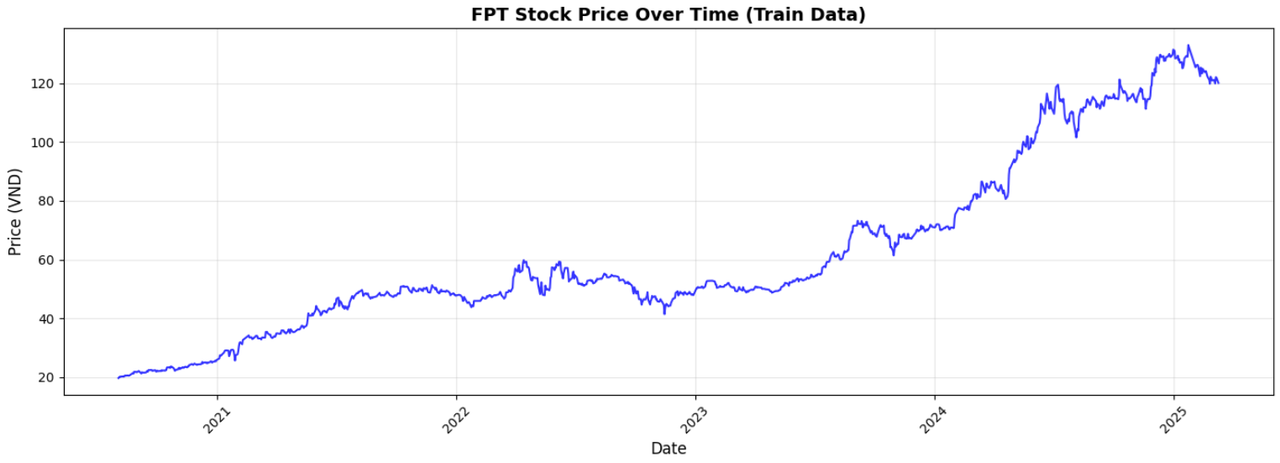
Hình 5: Giá đóng cửa cổ phiếu FPT theo thời gian
Từ biểu đồ giá đóng cửa cổ phiếu FPT từ tháng 3/2020 đến tháng 3/2025 trên tập dữ liệu huấn luyện có thể dễ dàng nhìn thấy xu hướng tăng trong dài hạn (5 năm). Tốc độ tăng giá bắt đầu tăng rất nhanh trong năm 2024. Trong 5 năm quan sát, xuất hiện khá nhiều sự điều chỉnh về giá trong ngắn hạn.
4. Kết quả
Trong bài toán dự báo chuỗi thời gian, nhóm đã lựa chọn phương pháp Direct Forecasting - học trực tiếp mối quan hệ giữa 400 ngày quá khứ và 100 ngày kế tiếp thay vì Recursive để tránh sai số tích lũy và tối ưu hiệu quả tính toán.
Dữ liệu giá cổ phiếu có tính phi tuyến, nhiễu mạnh, khó ổn định. Việc thêm hàng loạt đặc trưng như MA, RSI, lag features… đôi khi dẫn đến quá khớp hay gây nhiễu thông tin gốc. Sẽ khả quan hơn nếu áp dụng thêm các cổ phiếu cùng ngành, hay VN-index, tuy nhiên, điều này nằm ngoài phạm vi bài toán. Chính vì thế, nhóm chỉ dựa trên đặc trưng giá đóng cửa FPT.
Mô hình Linear cơ bản đóng vai trò như baseline nhưng bị giới hạn trong việc nắm bắt quan hệ phi tuyến và các cấu trúc tiềm ẩn của chuỗi thời gian tài chính. Do đó, nhiều mô hình hiện đại đã được phát triển để tách, làm mượt, khuếch đại tín hiệu quan trọng trong chuỗi thời gian, giúp mạng học hiệu quả hơn.
Các mô hình bằng thư viện PyTorch, trong đó mỗi mô hình được hiện thực hóa theo đúng cơ chế xử lý đặc trưng của nó. Các bước tiền xử lý như chuẩn hóa theo giá trị cuối, tách xu hướng – mùa vụ, trộn đa thang thời gian hay kết hợp LSTM với attention đều được tích hợp trực tiếp trong hàm forward, giúp mô hình vận hành thống nhất giữa giai đoạn huấn luyện và suy luận. Cách triển khai này giữ cho kiến trúc rõ ràng, dễ mở rộng, đồng thời tối ưu hiệu quả dự báo trên chuỗi giá tài chính.
# ===== MODELS =====
class LinearModel(nn.Module):
def __init__(self, input_len, output_len):
super(LinearModel, self).__init__()
self.input_len = input_len
self.output_len = output_len
self.linear = nn.Linear(input_len, output_len)
def forward(self, x):
return self.linear(x)
class NLinearModel(nn.Module):
def __init__(self, input_len, output_len):
super(NLinearModel, self).__init__()
self.input_len = input_len
self.output_len = output_len
self.linear = nn.Linear(input_len, output_len)
def forward(self, x):
last_value = x[:, -1:].detach()
x_norm = x - last_value
output_norm = self.linear(x_norm)
output = output_norm + last_value
return output
class DLinearModel(nn.Module):
def __init__(self, input_len, output_len, kernel_size):
super(DLinearModel, self).__init__()
self.input_len = input_len
self.output_len = output_len
self.kernel_size = kernel_size
self.linear_trend = nn.Linear(input_len, output_len)
self.linear_seasonal = nn.Linear(input_len, output_len)
def forward(self, x):
trend = self._moving_average(x, self.kernel_size)
seasonal = x - trend
trend_output = self.linear_trend(trend)
seasonal_output = self.linear_seasonal(seasonal)
output = trend_output + seasonal_output
return output
def _moving_average(self, x, kernel_size):
batch_size, seq_len = x.shape
pad_size = (kernel_size - 1) // 2
x_padded = torch.cat([
x[:, 0:1].repeat(1, pad_size),
x,
x[:, -1:].repeat(1, pad_size)
], dim=1)
x_unfolded = x_padded.unfold(dimension=1, size=kernel_size, step=1)
trend = x_unfolded.mean(dim=-1)
return trend
class xLSTMModel(nn.Module):
def __init__(self, input_len, output_len, hidden_size=128, num_layers=3, dropout=0.2):
super(xLSTMModel, self).__init__()
self.input_len = input_len
self.output_len = output_len
self.hidden_size = hidden_size
self.num_layers = num_layers
# LSTM layers
self.lstm = nn.LSTM(
input_size=1,
hidden_size=hidden_size,
num_layers=num_layers,
dropout=dropout if num_layers > 1 else 0,
batch_first=True
)
# Exponential gating layer
self.exp_gate = nn.Sequential(
nn.Linear(hidden_size, hidden_size),
nn.Tanh(),
nn.Linear(hidden_size, hidden_size),
nn.Sigmoid()
)
# Output projection
self.fc = nn.Linear(hidden_size, output_len)
def forward(self, x):
# x shape: [batch, seq_len]
batch_size = x.size(0)
x = x.unsqueeze(-1) # [batch, seq_len, 1]
# LSTM forward
lstm_out, (h_n, c_n) = self.lstm(x)
# Take last hidden state
last_hidden = h_n[-1] # [batch, hidden_size]
# Apply exponential gating
gate = self.exp_gate(last_hidden)
gated_hidden = last_hidden * gate
# Project to output
output = self.fc(gated_hidden) # [batch, output_len]
return output
class xLSTMTimeModel(nn.Module):
def __init__(self, input_len, output_len, hidden_size=128, num_layers=2,
n_heads=4, dropout=0.2):
super(xLSTMTimeModel, self).__init__()
self.input_len = input_len
self.output_len = output_len
self.hidden_size = hidden_size
# Positional encoding
self.pos_encoding = nn.Parameter(torch.randn(1, input_len, hidden_size))
# Input projection
self.input_proj = nn.Linear(1, hidden_size)
# xLSTM layers
self.lstm = nn.LSTM(
input_size=hidden_size,
hidden_size=hidden_size,
num_layers=num_layers,
dropout=dropout if num_layers > 1 else 0,
batch_first=True
)
# Temporal attention
self.temporal_attention = nn.MultiheadAttention(
embed_dim=hidden_size,
num_heads=n_heads,
dropout=dropout,
batch_first=True
)
# Exponential gating
self.exp_gate = nn.Sequential(
nn.Linear(hidden_size, hidden_size),
nn.Tanh(),
nn.Linear(hidden_size, hidden_size),
nn.Sigmoid()
)
# Output layers
self.layer_norm = nn.LayerNorm(hidden_size)
self.fc = nn.Linear(hidden_size, output_len)
def forward(self, x):
# x shape: [batch, seq_len]
batch_size = x.size(0)
x = x.unsqueeze(-1) # [batch, seq_len, 1]
# Project input and add positional encoding
x = self.input_proj(x) # [batch, seq_len, hidden_size]
x = x + self.pos_encoding
# LSTM forward
lstm_out, (h_n, c_n) = self.lstm(x)
# Temporal attention
attn_out, _ = self.temporal_attention(lstm_out, lstm_out, lstm_out)
# Combine LSTM and attention outputs
combined = lstm_out + attn_out
combined = self.layer_norm(combined)
# Take last hidden state
last_hidden = combined[:, -1, :] # [batch, hidden_size]
# Apply exponential gating
gate = self.exp_gate(last_hidden)
gated_hidden = last_hidden * gate
# Project to output
output = self.fc(gated_hidden) # [batch, output_len]
return output
class TimeMixerModel(nn.Module):
def __init__(self, input_len, output_len, hidden_size=128, n_scales=2, kernel_size=25):
super(TimeMixerModel, self).__init__()
self.input_len = input_len
self.output_len = output_len
self.hidden_size = hidden_size
self.n_scales = n_scales
self.kernel_size = kernel_size
# Multi-scale mixing layers
self.scale_mixers = nn.ModuleList([
nn.Sequential(
nn.Linear(input_len, hidden_size),
nn.ReLU(),
nn.Dropout(0.1),
nn.Linear(hidden_size, hidden_size)
) for _ in range(n_scales)
])
# Trend extraction
self.trend_extractor = nn.Sequential(
nn.Linear(input_len, hidden_size),
nn.Tanh()
)
# Seasonal extraction
self.seasonal_extractor = nn.Sequential(
nn.Linear(input_len, hidden_size),
nn.ReLU()
)
# Scale-wise attention
self.scale_attention = nn.Sequential(
nn.Linear(hidden_size * n_scales, hidden_size),
nn.Tanh(),
nn.Linear(hidden_size, n_scales),
nn.Softmax(dim=-1)
)
# Fusion layers
self.fusion = nn.Sequential(
nn.Linear(hidden_size * 2, hidden_size),
nn.ReLU(),
nn.Dropout(0.1),
nn.Linear(hidden_size, output_len)
)
def _moving_average(self, x, kernel_size):
"""Extract trend using moving average"""
batch_size, seq_len = x.shape
pad_size = (kernel_size - 1) // 2
x_padded = torch.cat([
x[:, 0:1].repeat(1, pad_size),
x,
x[:, -1:].repeat(1, pad_size)
], dim=1)
x_unfolded = x_padded.unfold(dimension=1, size=kernel_size, step=1)
trend = x_unfolded.mean(dim=-1)
return trend
def forward(self, x):
# x shape: [batch, seq_len]
batch_size = x.size(0)
# Decomposition
trend = self._moving_average(x, self.kernel_size)
seasonal = x - trend
# Extract trend and seasonal features
trend_feat = self.trend_extractor(trend) # [batch, hidden_size]
seasonal_feat = self.seasonal_extractor(seasonal) # [batch, hidden_size]
# Multi-scale mixing
scale_outputs = []
for i, mixer in enumerate(self.scale_mixers):
# Downsample input for different scales
if i == 0:
scale_input = x
else:
scale_factor = 2 ** i
if x.size(1) >= scale_factor:
scale_input = x[:, ::scale_factor]
# Pad if necessary
if scale_input.size(1) < self.input_len:
pad_size = self.input_len - scale_input.size(1)
scale_input = torch.cat([
scale_input,
scale_input[:, -1:].repeat(1, pad_size)
], dim=1)
else:
scale_input = x
scale_out = mixer(scale_input)
scale_outputs.append(scale_out)
# Concatenate all scale outputs
all_scales = torch.stack(scale_outputs, dim=1) # [batch, n_scales, hidden_size]
# Scale attention
scale_concat = all_scales.view(batch_size, -1) # [batch, n_scales * hidden_size]
scale_weights = self.scale_attention(scale_concat) # [batch, n_scales]
scale_weights = scale_weights.unsqueeze(-1) # [batch, n_scales, 1]
# Weighted sum of scales
mixed_scales = (all_scales * scale_weights).sum(dim=1) # [batch, hidden_size]
# Combine all features
combined = torch.cat([trend_feat + seasonal_feat, mixed_scales], dim=-1)
# Final projection
output = self.fusion(combined) # [batch, output_len]
return output
Kết hợp thêm cơ chế Early Stopping để tránh overfitting vào trong quá trình huấn luyện. Ở mỗi epoch, mô hình được tối ưu trên tập huấn luyện và sau đó đánh giá trên tập validation. Nếu loss trên validation không cải thiện sau một số vòng nhất định, quá trình train sẽ dừng sớm và mô hình tốt nhất (checkpoint có val loss thấp nhất) được giữ lại. Cuối cùng, hàm evaluate_model thực hiện kiểm tra mô hình trên tập test độc lập và trả về MSE để đánh giá khách quan hiệu quả dự đoán.
def train_model_with_early_stopping(model, train_loader, val_loader, model_name,
num_epochs=100, patience=10, lr=0.001):
"""Training với early stopping và lưu best checkpoint"""
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = model.to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
best_val_loss = float('inf')
best_model_state = None
patience_counter = 0
train_losses = []
val_losses = []
print(f"\n===== Training {model_name} =====")
for epoch in range(num_epochs):
# Training phase
model.train()
epoch_train_loss = 0.0
for batch_x, batch_y in train_loader:
batch_x, batch_y = batch_x.to(device), batch_y.to(device)
optimizer.zero_grad()
outputs = model(batch_x)
loss = criterion(outputs, batch_y)
loss.backward()
optimizer.step()
epoch_train_loss += loss.item()
avg_train_loss = epoch_train_loss / len(train_loader)
train_losses.append(avg_train_loss)
# Validation phase
model.eval()
epoch_val_loss = 0.0
with torch.no_grad():
for batch_x, batch_y in val_loader:
batch_x, batch_y = batch_x.to(device), batch_y.to(device)
outputs = model(batch_x)
loss = criterion(outputs, batch_y)
epoch_val_loss += loss.item()
avg_val_loss = epoch_val_loss / len(val_loader) if len(val_loader) > 0 else float('inf')
val_losses.append(avg_val_loss)
# Save best model
if avg_val_loss < best_val_loss:
best_val_loss = avg_val_loss
best_model_state = copy.deepcopy(model.state_dict())
patience_counter = 0
else:
patience_counter += 1
if (epoch + 1) % 5 == 0:
print(f"Epoch [{epoch+1}/{num_epochs}] - "
f"Train Loss: {avg_train_loss:.6f}, "
f"Val Loss: {avg_val_loss:.6f}, "
f"Best Val: {best_val_loss:.6f}")
# Early stopping
if patience_counter >= patience:
print(f"Early stopping triggered at epoch {epoch+1}")
break
# Load best model state
model.load_state_dict(best_model_state)
print(f"Training completed! Best validation loss: {best_val_loss:.6f}")
return model, train_losses, val_losses, best_val_loss
Kết quả thực nghiệm dựa trên các mô hình cho thấy sự ưu việt của các mô hình lai (Hybrid) so với các mô hình hồi quy thuần túy (Recurrent). Bảng dưới đây tóm tắt kết quả huấn luyện tốt nhất:
| Mô hình | Best Val Loss (MSE) | Test Loss (MSE) | Đánh giá |
|---|---|---|---|
| LinearModel | 0.070546 | 0.111316 | Hiệu suất trung bình, mô hình cơ sở. |
| NLinearModel | 0.108246 | 0.087593 | Test Loss thấp nhất, nhưng Val Loss cao gấp đôi TimeMixer. |
| DLinearModel | 0.088248 | 0.142963 | Kém hơn Linear thường do tách xu hướng chưa tối ưu |
| xLSTM | 0.046855 | 0.197729 | Có dấu hiệu Overfitting (Val thấp, Test cao). |
| xLSTMTime | 0.125901 | 0.487573 | Hiệu suất kém nhất, sai số rất lớn trên tập Test. |
| TimeMixer | 0.044842 | 0.101230 | Best Fit. Val Loss thấp nhất và Test Loss ổn định. |
Bảng 1. Kết quả huấn luyện mô hình
Nhận xét:
- TimeMixer được lựa chọn làm mô hình chính thức nhờ đạt Validation Loss thấp nhất (0.0448). Mặc dù NLinear có kết quả Test tốt hơn một chút (0.0875), nhưng TimeMixer thể hiện khả năng tổng quát hóa (generalization) tốt hơn hẳn trên tập Validation, giảm thiểu rủi ro học tủ dữ liệu (data leakage) khi triển khai thực tế.
- Các mô hình họ LSTM (xLSTM, xLSTMTime) cho thấy sự không phù hợp với bộ dữ liệu này khi mức sai số (MSE) trên tập Test vọt lên tới 0.19 - 0.48, cao gấp nhiều lần so với nhóm Linear.
Sau khi chọn TimeMixer và dự đoán giá đóng cửa 100 ngày kế tiếp, nhóm áp dụng bộ lọc Savitzky–Golay để làm mượt kết quả. Phương pháp này giữ lại hình dạng tổng thể của xu hướng nhưng loại bỏ nhiễu dao động nhỏ, nhờ đó đường dự báo trở nên ổn định và dễ diễn giải hơn. Bộ lọc được cấu hình với cửa sổ trượt 9 điểm và đa thức bậc 2 — đủ nhỏ để không làm méo xu hướng nhưng vẫn giảm nhiễu hiệu quả.
from scipy.signal import savgol_filter
# Apply Savitzky-Golay filter
window_length = 9 # Must be odd number (9% of 100 days)
polyorder = 2 # Polynomial order
predictions_close_smooth = savgol_filter(
predictions_close,
window_length=window_length,
polyorder=polyorder
)
print(f"\n===== SMOOTHING APPLIED =====")
print(f"Window length: {window_length}")
print(f"Polynomial order: {polyorder}")
print(f"Raw predictions (first 10): {predictions_close[:10]}")
print(f"Smoothed predictions (first 10): {predictions_close_smooth[:10]}")
# Use smoothed predictions for final output
predictions_close_final = predictions_close_smooth
prediction_ids = list(range(1, TOTAL_PREDICT_DAYS + 1))
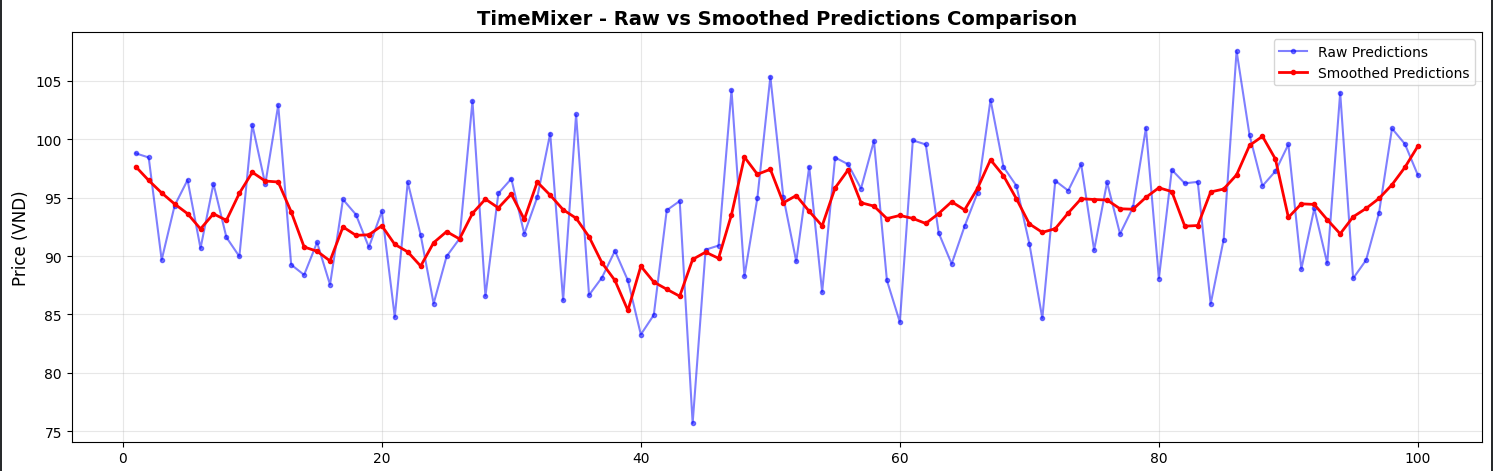
Hình 6: Biểu đồ so sánh dự báo trước và sau khi làm mượt
Nhìn vào hình ảnh trên, bạn có thể thấy sự đối lập rõ rệt:
-
Đường màu xanh (Raw Predictions): Đại diện cho dự báo thô của mô hình. Các điểm dữ liệu dao động với biên độ rất lớn và thiếu ổn định. Ví dụ, chỉ trong 10 ngày đầu, giá có lúc nhảy từ 98.78 xuống 89.66 rồi lại bật ngược lên 96.50. Một biến động gần 10% trong thời gian ngắn như vậy là thiếu thực tế đối với một cổ phiếu vốn hóa lớn và ổn định như FPT.
-
Đường màu đỏ (Smoothed Predictions): Sau khi áp dụng bộ lọc, đường dự báo trở nên mượt mà hơn, phản ánh đúng quán tính và xu hướng vận động của giá. Giá trị được điều chỉnh về dải biên độ hợp lý (từ 97.64 $\rightarrow$ 96.46 $\rightarrow$ 95.40), loại bỏ các cú "nhảy gap" bất thường mà vẫn giữ được hướng đi chính của thị trường.
Dựa trên biểu đồ dự báo (Smoothed Predictions), xu hướng giá đóng cửa cổ phiếu FPT được chia thành 3 pha như dự đoán:
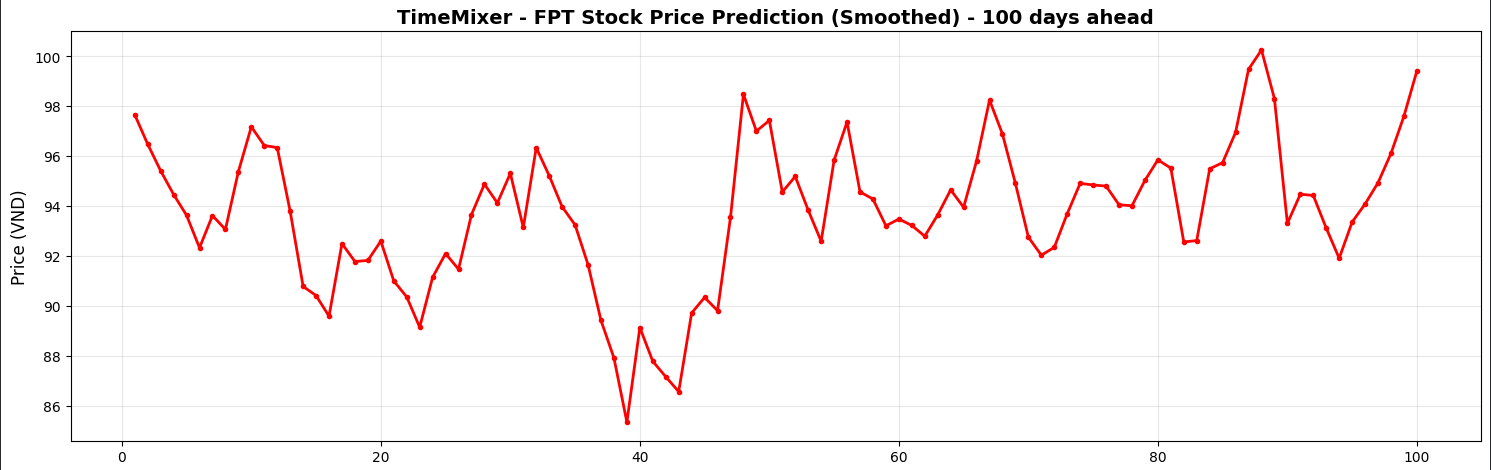
Hình 7: Kịch bản dự báo 100 ngày kế tiếp
Pha 1: Điều chỉnh (Ngày 0 - 40)
- Mô hình dự báo áp lực chốt lời ngắn hạn. Giá từ vùng đỉnh ngắn hạn ~97.600 VND sẽ bước vào nhịp điều chỉnh giảm.
- Đáy của đợt điều chỉnh dự kiến rơi vào khoảng ngày thứ 38-40, với mức giá thấp nhất tiệm cận vùng 85.500 - 86.000 VND. Đây là vùng hỗ trợ tiềm năng để tích lũy.
Pha 2: Hồi phục & Tích lũy (Ngày 40 - 85)
- Sau khi tạo đáy, giá cổ phiếu có xu hướng hồi phục theo mô hình răng cưa (sideway up).
- Giá dao động trong biên độ 92.000 - 96.000 VND, cho thấy sự giằng co giữa phe mua và bán trước khi xác nhận xu hướng mới.
Pha 3: Tăng trưởng (Ngày 85 - 100)
- Giai đoạn cuối của chu kỳ dự báo cho thấy động lực tăng giá mạnh mẽ trở lại.
- Giá phá vỡ nền tích lũy cũ, hướng tới việc chinh phục lại mốc đỉnh cũ và thiết lập mức cao mới. Giá trị dự báo tại ngày thứ 100 đạt mức ~99.400 VND.
5. Kết luận
Nhóm đã thành công trong việc ứng dụng các kiến trúc Deep Learning vào bài toán dự báo chuỗi thời gian tài chính, khắc phục được những thách thức về độ nhiễu cao và tính bất định của giá cổ phiếu FPT. Mục tiêu xây dựng một hệ thống dự báo không chỉ chính xác về mặt số học mà còn hợp lý về mặt xu hướng thị trường đã được hiện thực hóa thông qua việc sàng lọc mô hình nghiêm ngặt và áp dụng kỹ thuật hậu xử lý tín hiệu.
-
Nhóm đã thực nghiệm và so sánh hiệu quả của 6 mô hình khác nhau, bao gồm các biến thể Linear hiện đại: NLinear, DLinear và các mạng nơ-ron phức tạp: xLSTM, TimeMixer. Sự vượt trội của các mô hình lai (Hybrid) có khả năng xử lý đa khung thời gian so với các mô hình hồi quy thuần túy truyền thống trên tập dữ liệu này.
-
TimeMixer được xác định là mô hình hiệu quả nhất với Validation Loss thấp nhất (0.0448). TimeMixer thể hiện sự cân bằng tốt nhất giữa khả năng nội suy và ngoại suy, chứng minh khả năng tổng quát hóa mạnh mẽ nhờ cơ chế trộn (mixing) các đặc trưng từ nhiều tỷ lệ thời gian khác nhau.
-
Việc áp dụng bộ lọc Savitzky-Golay đóng vai trò then chốt trong việc chuyển đổi các dự báo thô nhiều nhiễu động thành các đường xu hướng mượt mà với
window length = 9,polynomial order = 2nhằm loại bỏ các biến động bất thường (noise) nhưng vẫn giữ lại cấu trúc xu hướng chính, làm tăng tính khả thi và độ tin cậy của kết quả khi áp dụng vào thực tế. -
Hệ thống đã đưa ra bức tranh dự báo định lượng cho 100 ngày tới với kịch bản rõ ràng:
- Điều chỉnh: Nhịp điều chỉnh ngắn hạn về vùng 86.000 VND để hấp thụ áp lực bán.
- Tích lũy: Giai đoạn đi ngang và tích lũy động lượng.
- Bứt phá: Tăng trưởng mạnh mẽ trở lại vùng đỉnh cũ, hướng tới mức giá mục tiêu ~99.400 VND vào cuối chu kỳ dự báo.
Chưa có bình luận nào. Hãy là người đầu tiên!