1. Giới thiệu
Multilayer Perceptron (MLP) là bước khởi đầu để hiểu cơ chế hoạt động của mạng nơ-ron sâu, từ đó mở rộng sang các kiến trúc phức tạp hơn như CNN hay Transformer. MLP bắt nguồn từ ý tưởng hồi quy tuyến tính, đồng thời bổ sung nhiều tầng ẩn cùng hàm kích hoạt phi tuyến để học các quan hệ phức tạp hơn. Logistic Regression dùng sigmoid cho phân loại nhị phân hay Softmax Regression cho phân loại đa lớp là những trường hợp đặc biệt của một perceptron đơn tầng. MLP tổng quát hóa ý tưởng này bằng cách xếp chồng nhiều tầng perceptron cùng hàm kích hoạt phi tuyến, từ đó mở rộng khả năng mô hình hóa sang không gian đặc trưng đa chiều và quan hệ phi tuyến phức tạp.
2. Cơ sở lý thuyết
2.1. Khái niệm
MLP là một kiến trúc mạng nơ-ron nhân tạo thuộc nhóm feedforward neural networks, gồm ba thành phần chính: Input layer, hidden layer, output layer. Các tầng này được kết nối đầy đủ, trong đó mỗi perceptron thực hiện phép tính tuyến tính giữa trọng số và dữ liệu đầu vào, sau đó áp dụng một hàm kích hoạt phi tuyến như sigmoid, tanh hoặc ReLU để tăng khả năng biểu diễn. Trong đó
- Input layer: nhận dữ liệu gốc của bài toán
- Hidden layer: nơi các perceptron kết hợp tuyến tính và áp dụng hàm kích hoạt để trích xuất, biến đổi đặc trưng
- Output layer: nhận đầu vào từ hidden layer cuối và sinh ra dự đoán $\hat{y}$.
Với dữ liệu có nhiều đặc trưng phi tuyến, hàm kích hoạt ReLU và các biến thể được ưu tiên vì khả năng hội tụ nhanh và hiệu quả tính toán. Sigmoid/tanh có đạo hàm nhỏ khi đầu vào lớn, khiến gradient giảm dần qua nhiều tầng, dễ dấn đến vanishing gradient. ReLU có đạo hàm luôn bằng 1 trên miền dương, nên gradient không bị suy giảm. Điều này giữ cho quá trình lan truyền ngược ổn định, giúp mô hình cập nhật trọng số đều đặn và nhanh chóng đạt nghiệm tốt. Ngoài ra, tại bước lan truyền ngược, đạo hàm của ReLU là 1 nếu đầu vào dương, 0 nếu âm. Trong khi sigmoid/tanh phải lưu và tính toán các giá trị phi tuyến phức tạp, vừa tốn bộ nhớ, vừa chậm hơn. Trong đó, tính chất các hàm như sau:
- Hàm Sigmoid:
$$ \text{sigmoid}(x) = \frac{1}{1 + e^{-x}} $$
$$ \text{sigmoid}'(x) = \text{sigmoid}(x) \cdot \left(1 - \text{sigmoid}(x)\right) $$

Hình 1. Hàm Sigmoid
- Hàm Tanh:
$$ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{2}{1 + e^{-2x}} - 1 = 1 - \frac{2}{e^{2x} + 1} $$
$$ \tanh'(x) = 1 - \tanh^2(x) $$

Hình 2. Hàm Tanh
- Hàm ReLU:
$$ \text{ReLU}(x) = \begin{cases} 0 & \text{nếu } x \leq 0 \\ x & \text{nếu } x > 0 \end{cases} $$
$$ \text{ReLU'}(x) = \begin{cases} 0 & \text{nếu } x \leq 0 \\ 1 & \text{nếu } x > 0 \end{cases} $$

Hình 3. Hàm ReLU
Quá trình huấn luyện MLP diễn ra qua hai giai đoạn: lan truyền thuận và lan truyền ngược. Trong lan truyền thuận, dữ liệu đầu vào được biến đổi qua các tầng để tạo ra đầu ra dự đoán. Sai số giữa đầu ra dự đoán và giá trị thực được đo lường bằng hàm mất mát. Tiếp đó, lan truyền ngược sử dụng thuật toán tối ưu (Stochastic Gradient Descent, Adam) để cập nhật trọng số, nhằm giảm thiểu sai số và cải thiện hiệu năng mô hình.
2.2. Cơ chế hoạt động

Hình 4. Quy trình tổng quát huấn luyện mô hình MLP trong bài toán hồi quy
Quy trình huấn luyện MLP mô tả như sau:
- Khởi tạo tham số ban đầu
- Khởi tạo trọng số và bias cho từng lớp:
- $\mathbf{W}^{(1)}, \mathbf{b}^{(1)}$ cho lớp ẩn
- $\mathbf{W}^{(2)}, \mathbf{b}^{(2)}$ cho lớp đầu ra
- Quy ước:
- $\mathbf{a}^{(0)} = \mathbf{x}$ (đầu vào)
- Lớp 1 là lớp ẩn, lớp 2 là lớp đầu ra
- Với mỗi mẫu dữ liệu $(\mathbf{x}_i, y_i)$ trong tập huấn luyện, thực hiện:
-
Lan truyền thuận
- Tính đầu ra lớp ẩn:
$$ \mathbf{z}_i^{(1)} = \mathbf{W}^{(1)} \mathbf{a}_i^{(0)} + \mathbf{b}^{(1)} $$
$$ \mathbf{a}_i^{(1)} = \text{ReLU}(\mathbf{z}_i^{(1)}) $$ - Tính đầu ra lớp cuối:
$$ \mathbf{z}_i^{(2)} = \mathbf{W}^{(2)} \mathbf{a}_i^{(1)} + \mathbf{b}^{(2)} $$
$$ \hat{y}_i = \mathbf{a}_i^{(2)} = \mathbf{z}_i^{(2)} \quad \text{(đầu ra tuyến tính)} $$
- Tính đầu ra lớp ẩn:
-
Tính hàm mất mát
$$ L_i(\hat{y}_i, y_i) = (\hat{y}_i - y_i)^2 $$ -
Lan truyền ngược
-
Gradient tại lớp đầu ra:
$$ \delta_i^{(2)} = \frac{\partial L_i}{\partial \mathbf{z}_i^{(2)}} = 2(\hat{y}_i - y_i) $$
$$ \frac{\partial L_i}{\partial \mathbf{W}^{(2)}} = \delta_i^{(2)} (\mathbf{a}_i^{(1)})^\top $$
$$ \frac{\partial L_i}{\partial \mathbf{b}^{(2)}} = \delta_i^{(2)} $$ -
Truyền lỗi về lớp ẩn:
$$ \delta_i^{(1)} = (\mathbf{W}^{(2)})^\top \delta_i^{(2)} \odot \text{ReLU}'(\mathbf{z}_i^{(1)}) $$Trong đó:
$$ \text{ReLU}'(\mathbf{z}_i^{(1)}) = \begin{cases} 1, & \text{nếu } \mathbf{z}_i^{(1)} > 0 \\ 0, & \text{nếu } \mathbf{z}_i^{(1)} \leq 0 \end{cases} $$ -
Gradient tại lớp ẩn:
$$ \frac{\partial L_i}{\partial \mathbf{W}^{(1)}} = \delta_i^{(1)} (\mathbf{a}_i^{(0)})^\top $$
$$ \frac{\partial L_i}{\partial \mathbf{b}^{(1)}} = \delta_i^{(1)} $$
-
-
Cập nhật tham số
- Với $\eta > 0$ là learning rate:
$$ \theta^{(t+1)} = \theta^{(t)} - \eta \cdot \frac{\partial L_i}{\partial \theta^{(t)}} $$ - Với $\theta \in \{ \mathbf{W}^{(1)}, \mathbf{b}^{(1)}, \mathbf{W}^{(2)}, \mathbf{b}^{(2)} \}$
- Với $\eta > 0$ là learning rate:
Sau khi đi qua toàn bộ các mẫu, ta hoàn thành một epoch huấn luyện. Tiếp tục lặp lại cho đến khi hàm mất mát hội tụ hoặc đạt số epoch mong muốn.
3. MLP cho dữ liệu ảnh
3.1. Bối cảnh
Khi chúng ta nhìn vào một bức ảnh chụp chiếc giày hay cái áo, não bộ ngay lập tức nhận thông tin từ đặc điểm hình dạng, màu sắc và nhận diện vật thể ngay lập tức.
Đối với máy tính thì khác, máy tính nhìn nhận một bức ảnh dưới dạng một cấu trúc ma trận gồm những giá trị số thực được biểu diễn tương ứng với các điểm ảnh (pixel). Các điểm pixel này chính là đặc điểm giúp cho máy tính nhận diện vật thể.
-
Với ảnh xám (Grayscale): Máy tính nhìn thấy một ma trận 2 chiều (chiều rộng x chiều cao). Mỗi giá trị thường chạy từ 0 (đen tuyệt đối) đến 255 (trắng tuyệt đối).
-
Với ảnh màu (RGB): Bức ảnh là một khối đa chiều, gồm 3 lớp ma trận chồng lên nhau tương ứng với 3 kênh màu: Red (Đỏ) - Green (Xanh lá) - Blue (Xanh dương).

Hình 5. Ví dụ chữ số viết tay ‘6’ trong MNIST dataset – Ảnh grayscale 28×28 (bên trái) và ma trận pixel (bên phải)
Trong các bài học trước, chúng ta đã làm quen với Softmax Regression. Về bản chất, Softmax Regression là một mô hình tuyến tính. Nó hoạt động dựa trên phương trình:
$$
z = wx + b
$$
Sau đó đưa qua hàm Softmax để tính xác suất:
$$
\sigma(z) = \frac{1}{1 + e^{-z}}
$$
Các đặc trưng ảnh có mối quan hệ phi tuyến phức tạp với nhãn, vị trí của các pixel, hình dạng đối tượng, ..., tất cả đều là các quan hệ phi tuyến mà mô hình tuyến tính chỉ có một mặt phẳng siêu phẳng (hyperlane) như Softmax Regression không thể nắm bắt được. Hơn nữa, Softmax Regression xử lý từng pixel như một đặc trưng độc lập, hoàn toàn bỏ qua cấu trúc không gian của ảnh. Đây là hạn chế cơ bản của mọi mô hình tuyến tính khi làm việc với dữ liệu có cấu trúc phức tạp.
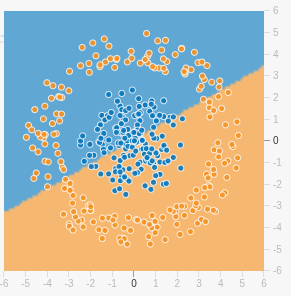
Hình 6. Hạn chế của Softmax Regression khi không thể phân loại chính xác dạng dữ liệu phi tuyến tính
Ông bà chúng ta có câu: "Một cây làm chẳng nên non, ba cây chụm lại nên hòn núi cao". Nếu chỉ với số lượng tham số hiện tại của Softmax Regression không thể học được đặc trưng phi tuyến tính phức tạp thì ta sẽ gia tăng nó lên bằng các lớp ẩn (hidden layers), giúp cho mô hình có thể học được các đặc trưng phi tuyến tính phức tạp tốt hơn. Đây cũng chính là động lực để chuyển từ Softmax Regression (chỉ có input và output) sang Multilayer Perceptron (có thêm các hidden layers).
3.2. Thực nghiệm
Chúng ta sử dụng bộ dữ liệu Fashion để thử nghiệm và đánh giá cho hai mô hình Softmax Regression và Multilayer Perceptron, vì đây là một bộ dữ liệu chuẩn được sử dụng rộng rãi để kiểm tra hiệu suất của các thuật toán phân loại hình ảnh cơ bản.
Fashion MNIST là một bộ sưu tập khổng lồ gồm 70.000 hình ảnh các mặt hàng thời trang và phụ kiện. Cụ thể:
- Định dạng: Ảnh xám (Grayscale images)
- Độ phân giải: $28 \times 28$ pixels
- Số lượng: 60,000 mẫu huấn luyện và 10,000 mẫu kiểm thử

Hình 7. Ví dụ các lớp trong Fashion-MNIST
Chúng ta sẽ sử dụng thư viện Pytorch làm thư viện chính. PyTorch là một thư viện mã nguồn mở (open-source) dựa trên Python, nó được thiết kế để cung cấp một nền tảng linh hoạt và hiệu quả cho việc xây dựng và huấn luyện các mô hình học sâu.
Chuẩn bị dữ liệu
Bước đầu tiên của bất kỳ pipeline huấn luyện mô hình Supervised Learning nào cũng là chuẩn bị dữ liệu.
from torchvision import datasets, transforms
transform = transforms.Compose([
transforms.ToTensor()
])
train_dataset = datasets.FashionMNIST(
root='./data', train=True, download=True, transform=transform)
test_dataset = datasets.FashionMNIST(
root='./data', train=False, download=True, transform=transform)
Giải thích:
-
transforms.ToTensor(): Chuyển ảnh PIL [0–255] uint8 sang dạng dữ liệu tensor float trong khoảng [0.0, 1.0] và đổi channel thành (C, H, W).
-
train_dataset = datasets.FashionMNIST(...): Tạo một đối tượng tập dữ liệu (Dataset object) cho dữ liệu huấn luyện. Đơn giản hơn, mỗi mẫu trong train_dataset là một tuple
(image, label). -
root='./data': Chỉ định thư mục nơi tập dữ liệu sẽ được lưu trữ. Nếu thư mục chưa tồn tại, nó sẽ được tạo.
-
train=True: Xác định rằng chúng ta đang tải xuống/sử dụng tập huấn luyện (training set) của FashionMNIST (60,000 mẫu).
-
download=True: Nếu dữ liệu chưa có trong thư mục ./data, PyTorch sẽ tự động tải xuống từ nguồn.
-
test_dataset = datasets.FashionMNIST(...): Tương tự, tạo một đối tượng tập dữ liệu cho tập kiểm tra (test set) bằng cách đặt train=False (10,000 mẫu).
Trong thực tế, chúng ta hiếm khi đưa toàn bộ dữ liệu huấn luyện (60,000 bức ảnh) vào mô hình cùng một lúc. Điều này không chỉ làm tràn bộ nhớ mà còn khiến việc tính toán gradient trở nên chậm chạp và kém hiệu quả. Vì vậy chúng ta sẽ chia dữ liệu thành các gói nhỏ (mini-batches).
from torch.utils.data import DataLoader
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=128, shuffle=False)
Ở đây, DataLoader đóng vai trò là một "người vận chuyển", nó giúp chúng ta gom 128 ảnh thành một khối để xử lý song song (batching). shuffle giúp xáo trộn dữ liệu, làm thay đổi thứ tự của dữ liệu ban đầu, đảm bảo mô hình không học vẹt theo thứ tự xuất hiện của các nhãn lớp, từ đó giúp thuật toán tối ưu hội tụ tốt hơn.
Thiết kế mô hình
Ở phần này, chúng ta sẽ thiết kế hai mô hình Softmax Regression và Multilayer Perceptron bằng Pytorch.
Softmax Regression
Như đã đề cập ở phần mở đầu, đây là dạng đơn giản nhất của mạng nơ-ron: không có lớp ẩn (hidden layer).
class SoftmaxRegression(nn.Module):
def __init__(self, input_size=28*28, num_classes=10):
super().__init__()
self.linear = nn.Linear(input_size, num_classes)
def forward(self, x):
x = x.view(x.size(0), -1)
return self.linear(x)
Mã nguồn trên khai báo một lớp SoftmaxRegression, lớp này sẽ khởi tạo một thuộc tính self.linear nhận vào một vector đặc trưng kích thước 784 tương ứng ảnh $28 \times 28$ sau khi được flatten và trả về 10 giá trị logit tương ứng với 10 lớp mục tiêu. Trong biếủ diễn toán học, có thể hiểu self.linear chính là bước tính $z = wx + b$. Kiến trúc của mã nguồn có thể được mô tả trực quan ở Hình 4.
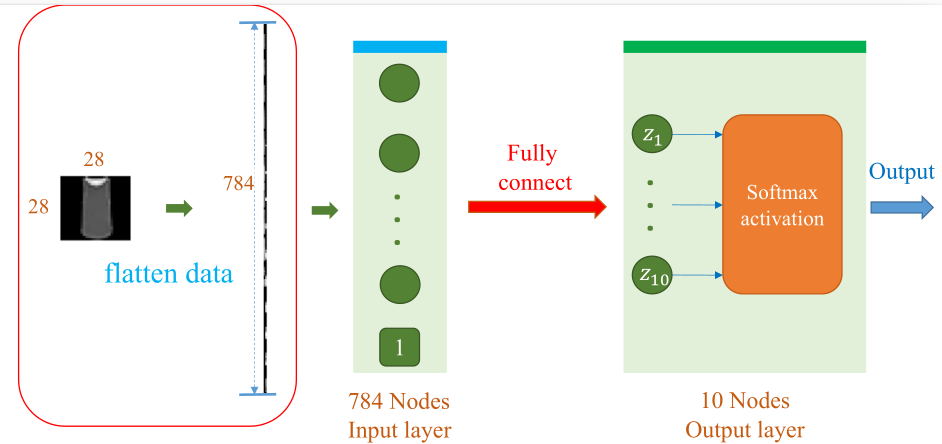
Hình 8. Kiến trúc mạng Softmax Regression cho Fashion-MNIST
Khi chúng ta gọi SoftmaxRegression(x) thì input sẽ được flatten từ [128, 1, 28, 28] sang [128, 784] với x.view(x.size(0), -1). Khi dữ liệu đã ở đúng kích thước đầu vào, lớp tuyến tính self.linear sẽ nhân ma trận trọng số để tạo ra output [128, 10], chính là các logit cuối cùng. Những logit này chính là đầu vào cho hàm softmax trong quá trình tính loss.
Logits có thể được hiểu là các điểm số thô, chưa được chuẩn hóa, và có thể mang bất kỳ giá trị thực nào (âm, dương, lớn hoặc nhỏ). Trong bài toán phân loại đa lớp, mỗi Logit tương ứng với điểm số tự tin của mô hình cho một lớp cụ thể.
Multilayer Perceptron
Tương tự như vậy, chúng ta sẽ xây dựng lớp Multilayer Perceptron bằng cách thêm các lớp ẩn vào giữa input và output.
class MLP(nn.Module):
def __init__(self, input_size=28*28, hidden_size=256, num_classes=10):
super().__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, num_classes)
def forward(self, x):
x = x.view(x.size(0), -1)
return self.fc2(self.relu(self.fc1(x)))
Ở bước khởi tạo, mô hình định nghĩa lớp ẩn self.fc1 nhận vào vector đặc trưng kích thước 784 (sau khi flatten ảnh $28 \times 28$) và biến đổi nó thành một không gian mới có 256 chiều. Thuộc tính self.relu khởi tạo một hàm ánh xạ dữ liệu đầu vào thành dữ liệu phi tuyến tính. Cuối cùng, lớp đầu ra self.fc2 nhận đầu vào là một vector đặc trưng 256 chiều và đưa ra 10 logit tương ứng với 10 lớp mục tiêu. Kiến trúc MLP có thể được mô tả trực quan ở Hình 5.
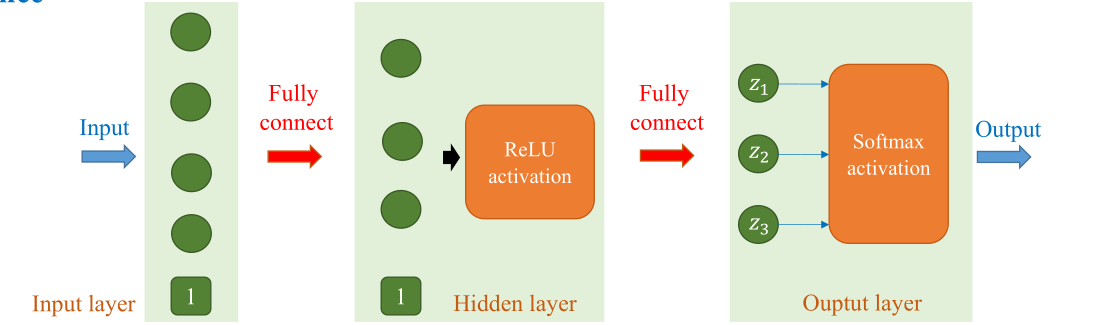
Hình 9. Kiến trúc MLP một lớp ẩn với ReLU
Ảnh đầu vào ban đầu ở dạng [128, 1, 28, 28] được làm phẳng sang [128, 784] bằng x.view(x.size(0), -1). Sau đó dữ liệu đi qua lớp ẩn đầu tiên, được kích hoạt bằng ReLU, rồi đi tiếp vào lớp cuối cùng để tạo ra kết quả dự đoán với shape [128, 10].
Tại sao lại cần hàm kích hoạt phi tuyến tính ReLU ? Nếu không có hàm kích hoạt phi tuyến, thì dù chúng có chồng bao nhiêu lớp nn.Linear lên nhau, về mặt toán học, chúng vẫn chỉ tương đương với một lớp nn.Linear duy nhất (vì tích của các ma trận cũng là một ma trận).
$$ f(x) = W_2(W_1x) = (W_2W_1)x = W_{new}x $$
Huấn luyện mô hình
Chúng ta đã có dữ liệu và mô hình, bây giờ chúng ta sẽ tiến hành huấn luyện chúng. Mã nguồn dưới đây thể hiện vòng lặp cơ bản để huấn luyện một mô hình trong Pytorch.
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
criterion = nn.CrossEntropyLoss()
optimizer_sr = optim.SGD(model_sr.parameters(), lr=0.01, momentum=0.9)
for epoch in range(epochs):
model.train()
for images, labels in train_loader:
images, labels = images.to(device), labels.to(device)
optimizer.zero_grad()
outputs = model(images)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
Trong Pytorch, khi huấn luyện thì lệnh model.train() phải luôn được gọi ở đầu mỗi epoch để báo hiệu cho mô hình biết rằng nó đang ở chế độ huấn luyện. Trong chế độ này, các tính năng đặc thù như Dropout (giúp giảm thiểu overfitting) và Batch Normalization được kích hoạt để đảm bảo quá trình học tập được chính xác.
Vòng lặp bên trong for images, labels in train_loader thực hiện việc học theo từng mini-batch. Đây cũng chính là giải thuật tối ưu Stochastic Gradient Descent (SGD) mà ta đã được học ở các Module trước. SGD cập nhật trọng số dựa trên một tập hợp con nhỏ của dữ liệu huấn luyện, giúp tăng tốc độ xử lý và cải thiện khả năng tổng quát hóa của mô hình.
CPU và GPU có 2 vùng nhớ riêng biệt để lưu trữ dữ liệu, được minh hoạ ở Hình 6. Trong quá trình tính toán, các dữ liệu tensor phải cùng nằm chung một vùng nhớ để chúng có thể "tìm thấy nhau" và thực hiện tính toán. Lệnh to(device) giúp chúng ta đồng bộ toàn bộ dữ liệu tensor trên cùng một vùng nhớ, tránh gây ra lỗi trong quá trình huấn luyện. Biến device được định nghĩa thông qua lệnh torch.device("cuda" if torch.cuda.is_available() else "cpu"), có nghĩa là Pytorch sẽ kiểm tra xem chúng ta có GPU hay không, nếu có thì Pytorch sẽ sử dụng device là GPU, ngược lại thì device sẽ là CPU.
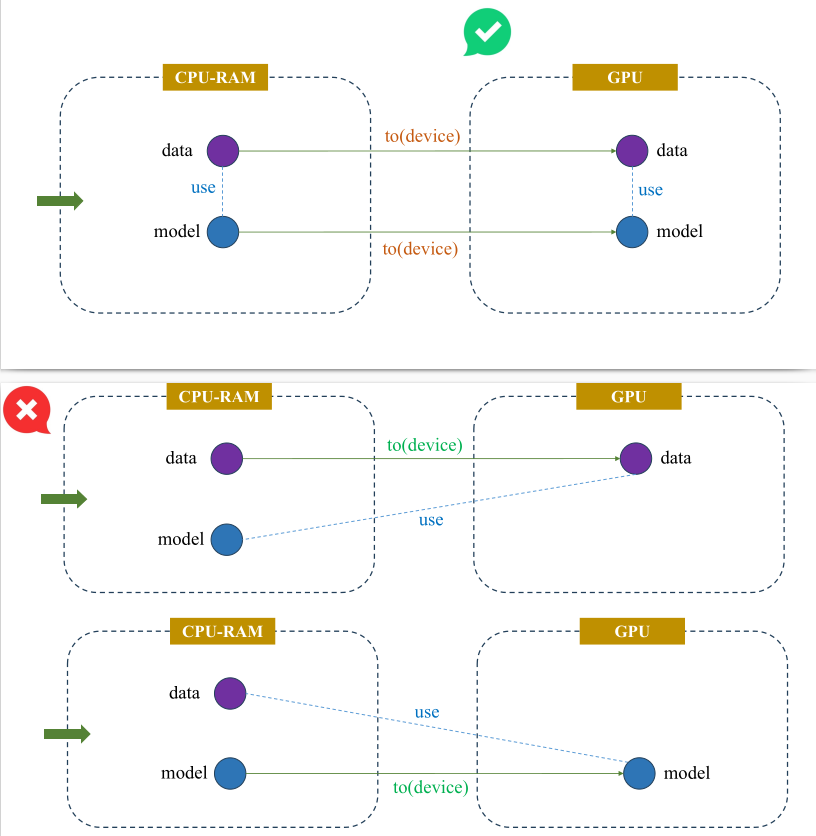
Hình 10. Đồng bộ Data và Model trên cùng một device (GPU)
Trong Pytorch, gradient sẽ được tích luỹ từ các phép toán lan truyền ngược liên tiếp khi gọi lệnh loss.backward() làm sai lệch hướng đi của Gradient Descent và khiến mô hình không hội tụ được hoặc hội tụ đến điểm tối ưu cục bộ không chính xác. Do đó, lệnh optimizer.zero_grad() cần phải được gọi để xóa các gradient cũ (đặt thuộc tính .grad của tất cả các tham số mô hình về 0) đã được tính toán trong bước tối ưu hóa trước đó.
Cuối cùng, chúng ta đưa dữ liệu vào mô hình, sau đó tính toán loss với lệnh criterion(outputs, labels) và thực hiện lan truyền ngược với loss.backward(). Hàm mất mát criterion ở đây chính là Cross Entropy vì chúng ta có 10 lớp mục tiêu cần dự đoán.
Có một điểm cần lưu ý ở đây là hàm mất mát nn.CrossEntropyLoss() của PyTorch đã được thiết kế để Áp dụng Softmax để chuyển đổi Logits thành phân phối xác suất và sử dụng hàm log cho các xác suất này. Chính vì vậy, ở bước thiết kế mô hình thì ta sẽ không áp dụng hàm Softmax ở lớp đầu ra cuối cùng.
Nhận xét
Kết quả sau khi huấn luyện 10 epoch được thể hiện qua Hình 7.
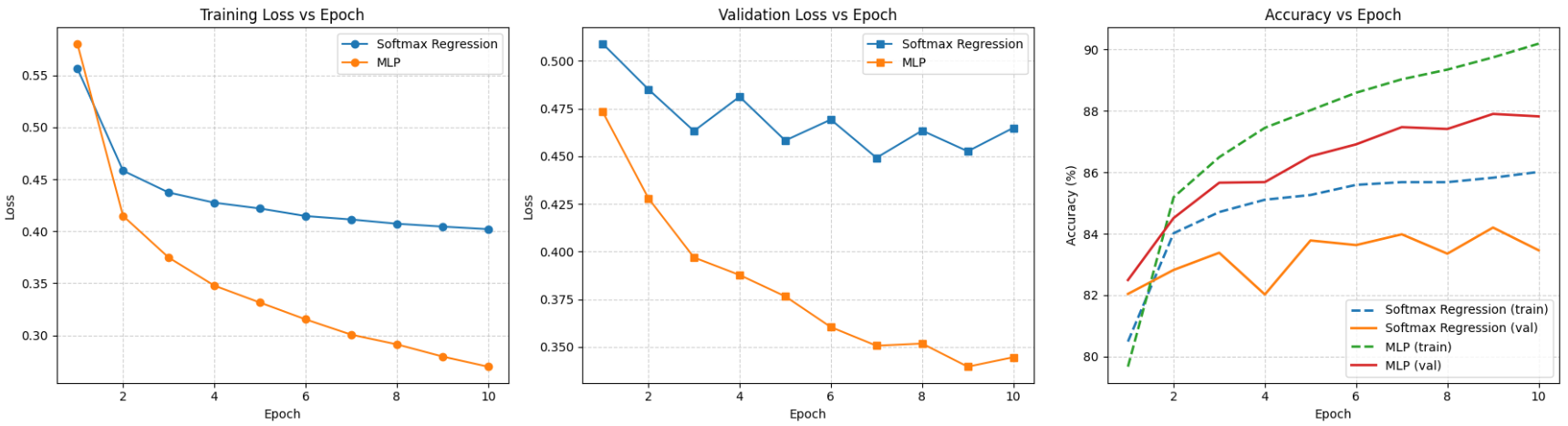
Hình 11. So sánh Softmax Regression và Multilayer Perceptron một lớp ẩn trên Fashion-MNIST
Cả hai mô hình đều cho thấy sự giảm dần của loss trên tập huấn luyện và tập kiểm tra. Tuy nhiên, đường cong loss của Multilayer Perceptron (màu cam) luôn nằm dưới đáng kể so với Softmax Regression (màu xanh), cho thấy Multilayer Perceptron liên tục tìm được các tập tham số tối ưu và hiệu quả hơn. Qua đó, mô hình Multilayer Perceptron đã chứng minh mình vượt trội hơn như thế nào so với đồng nghiệp phía bên kia chiến tuyến là mô hình tuyến tính Softmax Regression khi cùng đánh giá trên bộ dữ liệu Fashion-MNIST.
| Kiến trúc | Val Acc | Val Loss |
|---|---|---|
| Softmax Regression | 84.08% | 0.4706 |
| Multilayer Perceptron | 87.91% | 0.3432 |
Bảng 1. Kết quả đánh giá các kiến trúc trên tập kiểm thử Fashion-MNIST
Multilayer Perceptron đạt độ chính xác cao hơn Softmax Regression 3.83% (87.91% so với 84.08%), đồng thời giảm được mức mất mát (loss) đáng kể, chứng tỏ Multilayer Perceptron học được một ánh xạ phức tạp và chính xác hơn giữa dữ liệu ảnh và nhãn lớp.
Sự cải thiện rõ rệt về hiệu suất chính là bằng chứng rõ ràng nhất về tầm quan trọng của việc thêm các lớp ẩn và hàm kích hoạt phi tuyến tính (ReLU) vào kiến trúc mạng, cho phép mô hình tạo ra các biểu diễn trung gian phong phú, giải quyết hiệu quả các dạng dữ liệu phi tuyến tính như là hình ảnh.
4. MLP cho dữ liệu bảng và văn bản
4.1. Bối cảnh
Do kiến trúc của MLP là mạng kết nối toàn diện, đầu vào bắt buộc phải là các vector có kích thước cố định $x \in \mathbb{R}^n$. Do đó, quá trình trích xuất đặc trưng (Feature Extraction) và biến đổi dữ liệu (Transformation) là bước tiền xử lý bắt buộc.
Đối với dữ liệu bảng
Quy trình chuẩn hóa dữ liệu bảng cho MLP tập trung vào việc xử lý sự khác biệt về thang đo và biểu diễn biến định danh.
1. Chuẩn hóa biến số (Numerical Normalization)
Các biến số có độ lớn khác nhau sẽ khiến hàm mất mát trở nên không cân xứng, làm chậm quá trình hội tụ của thuật toán Gradient Descent. Phương pháp tối ưu: Standardization (Z-score normalization).
$$z = \frac{x - \mu}{\sigma}$$
Trong đó $\mu$ là trung bình mẫu và $\sigma$ là độ lệch chuẩn.
2. Mã hóa biến phân loại (Categorical Encoding)
- One-Hot Encoding: Chuyển biến phân loại thành vector nhị phân thưa. Phương pháp này phù hợp với các biến có số lượng giá trị thấp.
- Entity Embeddings: Ánh xạ mỗi giá trị phân loại vào một không gian vector dày đặc có số chiều thấp hơn, cho phép mạng nơ-ron học được mối quan hệ ngữ nghĩa giữa các danh mục trong quá trình huấn luyện backpropagation.
Đối với dữ liệu văn bản
Vì MLP truyền thống không có cơ chế hồi quy để xử lý chuỗi độ dài thay đổi, văn bản cần được tổng hợp thành vector tĩnh (static representation).
1. Mô hình Bag-of-Words (BoW)
Biểu diễn văn bản bằng tần suất xuất hiện của từ, bỏ qua trật tự từ.
2. TF-IDF
Đây là kỹ thuật trích xuất đặc trưng thống kê nhằm đánh giá mức độ quan trọng của một từ trong văn bản.
$$w_{i,j} = tf_{i,j} \times \log(\frac{N}{df_i})$$
Phương pháp này giúp giảm trọng số của các từ nhiễu (stopwords) và tăng trọng số cho các từ mang thông tin đặc trưng. TF-IDF tạo ra đầu vào phù hợp nhất cho MLP khi xử lý văn bản, dù phải đánh đổi việc mất thông tin ngữ cảnh tuần tự.
4.2. Thực nghiệm
California Housing là một bộ dữ liệu kinh điển trong lĩnh vực Machine Learning, được sử dụng rộng rãi để đánh giá các thuật toán hồi quy. Bộ dữ liệu này chứa thông tin về giá nhà trung bình của các khu vực ở California, được thu thập từ điều tra dân số năm 1990. Với 20,640 khu vực và 8 đặc trưng liên tục, bộ dữ liệu này đủ lớn để huấn luyện một mô hình neural network nhưng không quá phức tạp để bắt đầu học. Biến mục tiêu là giá trị trung vị của nhà (median house value) tính bằng đơn vị $100,000.
Các đặc trưng quan trọng bao gồm thu nhập trung bình (MedInc), tuổi nhà (HouseAge), số phòng và phòng ngủ trung bình (AveRooms, AveBedrms), dân số khu vực (Population), số người ở trung bình (AveOccup), cùng với tọa độ địa lý (Latitude, Longitude). Sự kết hợp giữa các yếu tố kinh tế, đặc điểm nhà ở và vị trí địa lý tạo nên những mối quan hệ phi tuyến phức tạp mà MLP có thể khai thác hiệu quả.
Tham số bài toán
| Tham số | Giá trị |
|---|---|
| Learning rate (lr) | 0.001 |
| Số epoch (epochs) | 50 |
| Batch size (batch_size) | 32 |
| Hidden dimensions (hidden_dims) | [64, 32] |
| Input dimensions (input_dims) | 8 |
| Output dimensions (output_dims) | 1 (hồi quy) |
| Train/Val/Test split | 0.64 / 0.16 / 0.20 |
| Seed (random_state) | 42 |
| Loss function | MSELoss |
| Optimizer | Adam |
| Evaluation metric | MAE (Mean Absolute Error) |
Quy trình thực thi
Bước 1: Import thư viện
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader, TensorDataset
Chúng ta sử dụng NumPy và Pandas để xử lý dữ liệu, Matplotlib cho việc trực quan hóa, Sklearn cung cấp bộ dữ liệu và các công cụ tiền xử lý, trong khi PyTorch là framework chính để xây dựng và huấn luyện mô hình neural network.
Bước 2: Định nghĩa tham số bài toán
LEARNING_RATE = 0.001
EPOCHS = 50
BATCH_SIZE=32
SEED=42
Chúng ta định nghĩa các hyperparameter cho toàn bộ quá trình huấn luyện. Learning rate 0.001 là một giá trị phổ biến cho Adam optimizer, 50 epoch thường đủ để mô hình hội tụ trên bộ dữ liệu này, batch size 32 giúp cân bằng giữa tốc độ huấn luyện và độ ổn định của gradient, còn seed 42 đảm bảo kết quả có thể tái lập được.
Bước 3: Tải bộ dữ liệu
housing = fetch_california_housing()
X = housing.data
y = housing.target.reshape(-1, 1)
Hàm fetch_california_housing() tự động tải xuống và trả về dữ liệu ở định dạng sẵn sàng sử dụng. Chúng ta lấy ma trận đặc trưng X với shape (20640, 8) và reshape biến mục tiêu y từ mảng 1 chiều thành 2 chiều (20640, 1) để phù hợp với định dạng đầu ra của PyTorch model.
Bước 4: Phân chia tập train/test
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# Tách Validation từ Train
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=0.2, random_state=42
)
Chúng ta chia dữ liệu thành 3 tập theo tỷ lệ 64:16:20 cho training, validation và test. Việc tách validation ra từ training set là điều quan trọng để theo dõi hiệu suất mô hình trong quá trình huấn luyện. Tập validation giúp chúng ta phát hiện overfitting sớm mà không "lộ" thông tin từ tập test. Tập test được giữ lại hoàn toàn riêng biệt để đánh giá hiệu suất cuối cùng của mô hình trên dữ liệu chưa từng thấy.
Bước 5: Chuẩn hóa dữ liệu
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_val_scaled = scaler.transform(X_val)
X_test_scaled = scaler.transform(X_test)
print("Train shape:", X_train_scaled.shape)
print("Val shape: ", X_val_scaled.shape)
print("Test shape: ", X_test_scaled.shape)
Như đã trình bày ở phần chuẩn hóa biến số, trong bộ dữ liệu này "Population" có thể dao động từ vài chục đến vài nghìn, trong khi "AveOccup" chỉ từ 1 đến 10. Sự chênh lệch này khiến quá trình tối ưu trở nên khó khăn vì gradient của các tham số tương ứng với đặc trưng có scale lớn sẽ chi phối quá trình cập nhật. Vì vậy chúng ta sử dụng StandardScaler để chuẩn hóa.
Chúng ta chỉ fit scaler trên tập training (fit_transform), sau đó áp dụng các tham số đã học được lên tập validation và test (transform). Điều này đảm bảo không có thông tin nào từ tập validation/test rò rỉ vào quá trình huấn luyện.
Bước 6: Chuyển dữ liệu về Pytorch tensor
X_train_tensor = torch.tensor(X_train_scaled, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32)
X_val_tensor = torch.tensor(X_val_scaled, dtype=torch.float32)
y_val_tensor = torch.tensor(y_val, dtype=torch.float32)
X_test_tensor = torch.tensor(X_test_scaled, dtype=torch.float32)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32)
train_loader = DataLoader(TensorDataset(X_train_tensor, y_train_tensor), batch_size=BATCH_SIZE, shuffle=True)
val_loader = DataLoader(TensorDataset(X_val_tensor, y_val_tensor), batch_size=BATCH_SIZE, shuffle=False)
test_loader = DataLoader(TensorDataset(X_test_tensor, y_test_tensor), batch_size=BATCH_SIZE, shuffle=False)
PyTorch yêu cầu dữ liệu phải ở dạng tensor để có thể tính toán gradient và tận dụng GPU, do đó chúng ta chuyển đổi các mảng NumPy sang tensor với kiểu float32. TensorDataset đơn giản là gom cặp (X, y) lại thành dataset object, trong khi DataLoader đóng vai trò quan trọng hơn nhiều.
Trong thực tế, chúng ta hiếm khi đưa toàn bộ dữ liệu vào mô hình cùng lúc vì điều này không chỉ làm tràn bộ nhớ mà còn khiến việc tính gradient trở nên chậm chạp. DataLoader chia dữ liệu thành các mini-batch kích thước 32 để xử lý song song, giúp tăng tốc độ huấn luyện đáng kể. shuffle=True cho training set xáo trộn thứ tự dữ liệu sau mỗi epoch, đảm bảo mô hình không học vẹt theo thứ tự xuất hiện của các mẫu. Ngược lại, validation và test set không cần shuffle vì chỉ dùng để đánh giá.
Bước 7: Xây dựng mô hình MLP
class MLPRegressor(nn.Module):
def __init__(self, input_dim):
super(MLPRegressor, self).__init__()
self.fc1 = nn.Linear(input_dim, 64)
self.fc2 = nn.Linear(64, 32)
self.dropout = nn.Dropout(0.2)
self.out = nn.Linear(32, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.dropout(x)
return self.out(x)
Kiến trúc MLP của chúng ta được thiết kế với hai lớp ẩn:
-
Lớp ẩn đầu tiên (
self.fc1):
Nhận 8 đặc trưng đầu vào và mở rộng lên không gian 64 chiều thông qua phép biến đổi tuyến tính:
$$z = wx + b$$
Sau đó, hàm kích hoạt ReLU ($\text{ReLU}(x) = \max(0, x)$) tạo ra tính phi tuyến cần thiết.
Nếu thiếu ReLU, dù chúng ta chồng bao nhiêu lớp tuyến tính lên nhau thì về mặt toán học chúng vẫn chỉ tương đương với một lớp tuyến tính duy nhất vì:
$$W_2(W_1x) = (W_2W_1)x = W_{new}x$$ -
Lớp ẩn thứ hai (
self.fc2):
Thu hẹp từ 64 chiều xuống 32 chiều, tiếp tục được kích hoạt bởi ReLU. -
Lớp Dropout:
Áp dụng tỷ lệ 0.2, nghĩa là trong quá trình huấn luyện, 20% các nơ-ron sẽ bị "tắt" ngẫu nhiên. Kỹ thuật này buộc mô hình không quá phụ thuộc vào một vài nơ-ron cụ thể, từ đó giảm overfitting và tăng khả năng tổng quát hóa. -
Lớp đầu ra (
self.out):
Ánh xạ từ 32 chiều xuống 1 giá trị duy nhất - dự đoán giá nhà.
Trong đó, sự khác biệt với bài toán phân loại là lớp đầu ra không sử dụng hàm kích hoạt.
- Trong phân loại, chúng ta cần Softmax để chuyển logits thành phân phối xác suất.
- Với hồi quy, chúng ta muốn mô hình tự do dự đoán bất kỳ giá trị thực nào mà không bị giới hạn trong một khoảng cụ thể.
Xét về luồng dữ liệu, khi gọi model(x), dữ liệu sẽ đi qua tuần tự:
Input (8) → Linear + ReLU (64) → Linear + ReLU (32) → Dropout → Linear (1) → Output
Bước 8: Huấn luyện mô hình
model = MLPRegressor(input_dim=X_train_scaled.shape[1])
device = "cuda" if torch.cuda.is_available() else "cpu"
model.to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=LEARNING_RATE)
train_losses, val_losses = [], []
train_mae_hist, val_mae_hist = [], []
def mae(pred, target):
return torch.mean(torch.abs(pred - target))
EPOCHS = 50
for epoch in range(EPOCHS):
# ---- TRAIN ----
model.train()
batch_train_loss = []
batch_train_mae = []
for xb, yb in train_loader:
xb, yb = xb.to(device), yb.to(device)
optimizer.zero_grad()
preds = model(xb)
loss = criterion(preds, yb)
loss.backward()
optimizer.step()
batch_train_loss.append(loss.item())
batch_train_mae.append(mae(preds, yb).item())
train_losses.append(np.mean(batch_train_loss))
train_mae_hist.append(np.mean(batch_train_mae))
# ---- VALIDATION ----
model.eval()
batch_val_loss = []
batch_val_mae = []
with torch.no_grad():
for xb, yb in val_loader:
xb, yb = xb.to(device), yb.to(device)
preds = model(xb)
batch_val_loss.append(criterion(preds, yb).item())
batch_val_mae.append(mae(preds, yb).item())
val_losses.append(np.mean(batch_val_loss))
val_mae_hist.append(np.mean(batch_val_mae))
if (epoch + 1) % 10 == 0:
print(f"[Epoch {epoch+1}] Train Loss={train_losses[-1]:.4f} Val Loss={val_losses[-1]:.4f}")
Trước khi bắt đầu huấn luyện, chúng ta khởi tạo mô hình và chuyển nó lên biến device (tự động kiểm tra GPU) để tận dụng sức mạnh tính toán, đồng thời thiết lập hàm mất mát nn.MSELoss() tính Mean Squared Error theo công thức $\text{MSE} = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2$ nhằm phạt nặng các sai lệch lớn, và lựa chọn Adam optimizer giúp tự động điều chỉnh learning rate để hội tụ ổn định hơn trên dữ liệu dạng bảng. Vòng lặp huấn luyện bắt đầu bằng lệnh model.train() để kích hoạt Dropout; với mỗi mini-batch, chúng ta buộc phải gọi optimizer.zero_grad() để xóa gradient tích lũy cũ nhằm tránh sai lệch hướng cập nhật, sau đó đảm bảo dữ liệu đầu vào xb, yb được chuyển sang cùng device với mô hình trước khi thực hiện tính toán loss, loss.backward() và cập nhật trọng số bằng optimizer.step(). Kết thúc mỗi epoch, quy trình chuyển sang chế độ đánh giá với model.eval() (tắt Dropout) và sử dụng khối with torch.no_grad() để ngắt tính toán gradient giúp tiết kiệm tài nguyên, tại đây bên cạnh MSE, chúng ta theo dõi thêm chỉ số MAE ($\text{MAE} = \frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y}_i|$) vì nó cung cấp cái nhìn trực quan hơn do cùng đơn vị với biến mục tiêu (ví dụ MAE = 0.5 tương đương sai lệch $50,000 so với giá thực).
Nhận xét
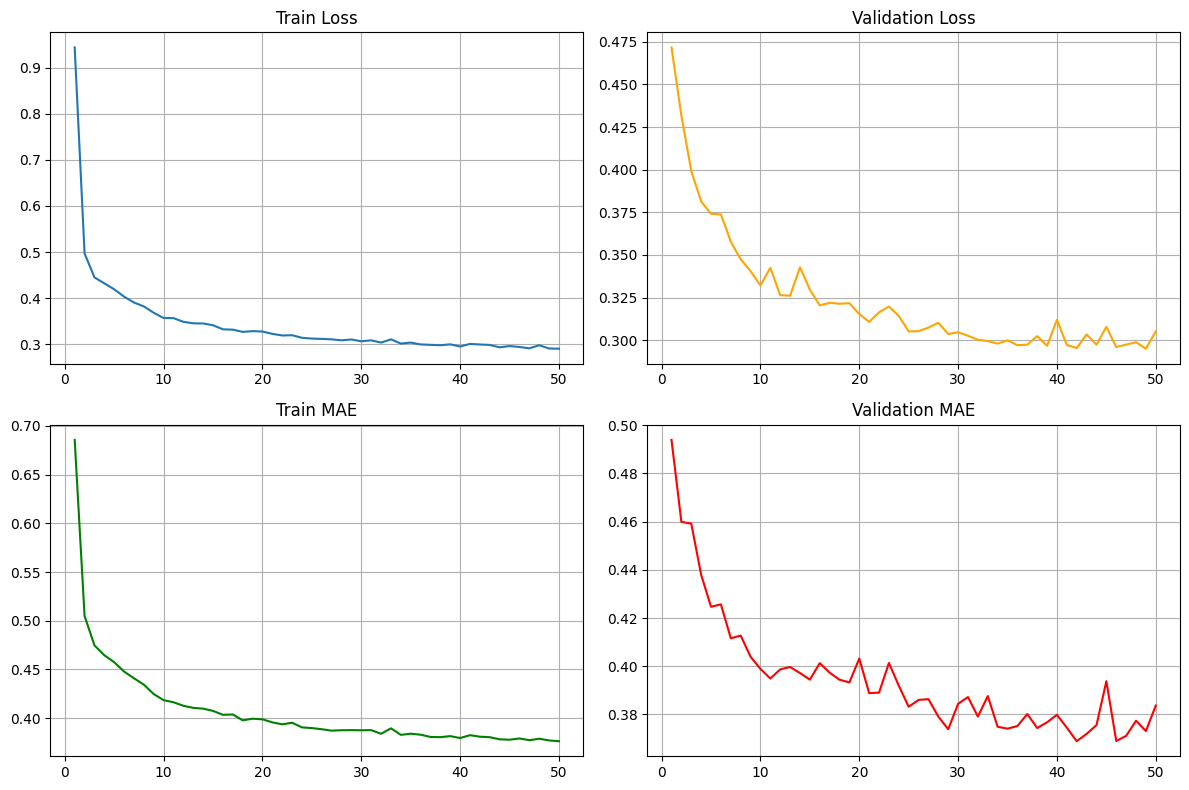
Hình 12. Biểu đồ Loss và MAE của tập huấn luyện và tập kiểm định trong 50 epochs
Dựa trên các biểu đồ loss và MAE của mô hình MLP trên tập dữ liệu California Housing, có thể thấy rằng mô hình đã học khá tốt và hội tụ ổn định. Cả Train Loss và Validation Loss đều giảm mạnh ở những epoch đầu và tiếp tục giảm từ từ về sau, cho thấy quá trình tối ưu diễn ra hiệu quả. Đặc biệt, Validation Loss bám sát Train Loss và dao động nhẹ quanh mức 0.30 ở các epoch cuối, chứng tỏ mô hình không bị overfitting và có khả năng tổng quát hóa tốt. Các đường MAE cũng thể hiện xu hướng tương tự: Train MAE giảm đều về khoảng 0.37, trong khi Validation MAE ổn định quanh mức 0.37–0.38. Việc hai chỉ số MAE gần nhau cho thấy mô hình dự đoán nhất quán trên cả dữ liệu huấn luyện và dữ liệu kiểm định. Nhìn chung, MLP đạt hiệu suất tốt trên tập California Housing, sai số thấp và ổn định, chứng minh mô hình đã nắm bắt được mối quan hệ giữa các đặc trưng và giá nhà. Đây là một kết quả khả quan và có thể làm cơ sở để tiếp tục tối ưu mô hình hoặc thử nghiệm thêm các kiến trúc khác.
4.3. So sánh các mô hình khác
Mặc dù MLP là nền tảng của Deep Learning, việc lựa chọn mô hình cần dựa trên bản chất dữ liệu. Dưới đây là sự so sánh chi tiết giữa MLP và các kiến trúc tối ưu hóa (State-of-the-art) cho từng loại dữ liệu.
Đối với dữ liệu bảng
Dữ liệu bảng thường chứa các quy tắc rời rạc (ví dụ: Tuổi > 18 và Thu nhập > 10 triệu).
1. Ensemble Learning (Gradient Boosting Decision Trees - GBDT)
MLP cố gắng nhân và cộng tất cả các đặc trưng lại với nhau để tạo ra một đường cong mượt mà. Để MLP học được một quy tắc đơn giản như "Nếu A > 5 thì chọn B", nó phải dùng rất nhiều nơ-ron và dữ liệu để xấp xỉ, trong khi GBDT chỉ cần một nút phân nhánh đơn giản. Do đó, GBDT thường học nhanh hơn và chính xác hơn trên dữ liệu bảng.
2. TabNet
Trong MLP, mọi đặc trưng đầu vào đều được tham gia tính toán (kết nối toàn diện - dense), kể cả các đặc trưng nhiễu hoặc không liên quan, dẫn đến dễ bị nhiễu. Ngược lại, TabNet có cơ chế "mặt nạ" (masking) giúp nó học cách bỏ qua các cột không cần thiết cho từng mẫu cụ thể, giống như cách cây quyết định chọn lọc đặc trưng quan trọng
3. TabTransformer
MLP thường xử lý các biến phân loại một cách rời rạc (One-hot encoding), tức là nó không hiểu mối liên hệ giữa "Hà Nội" và "TP.HCM" trừ khi có rất nhiều dữ liệu. TabTransformer sử dụng cơ chế Attention để đặt các biến này vào "ngữ cảnh" của các biến khác, giúp mô hình hiểu sâu hơn mối quan hệ ràng buộc giữa các cột dữ liệu phức tạp.
Đối với dữ liệu văn bản
Sự chuyển dịch từ MLP sang các mô hình hiện đại là sự chuyển dịch từ xử lý tĩnh (static processing) sang xử lý cấu trúc (structural processing).
1. Convolutional Neural Networks (CNN)
MLP nhìn nhận văn bản như một vector đặc trưng phẳng (flat vector) và bất biến toàn cục, dẫn đến việc mất thông tin về vị trí cục bộ. CNN khắc phục điều này bằng cách sử dụng các bộ lọc (filters) trượt qua văn bản để trích xuất các mẫu cục bộ (local patterns) như n-grams. Tư duy của CNN là tìm kiếm các đặc trưng bất biến qua vị trí (translation invariance), trong khi MLP buộc phải học lại một mẫu nếu nó xuất hiện ở vị trí khác trong câu.
2. Recurrent Neural Networks (RNN/LSTM)
Hạn chế lớn nhất của MLP là yêu cầu đầu vào có kích thước cố định, buộc phải cắt gọt hoặc đệm (padding) dữ liệu, đồng thời không có khái niệm về "thời gian". RNN thay đổi hoàn toàn tư duy này bằng cách xử lý dữ liệu theo chuỗi tuần tự (sequential processing). Mô hình duy trì một trạng thái ẩn (hidden state) đóng vai trò như bộ nhớ, cho phép thông tin từ các từ trước đó ảnh hưởng đến việc xử lý từ hiện tại, điều mà kiến trúc feed-forward của MLP không thể thực hiện.
3. Transformer (BERT, GPT)
Nếu MLP xử lý các từ một cách độc lập (hoặc thông qua thống kê tần suất như TF-IDF) và RNN xử lý tuần tự, thì Transformer tiếp cận bằng cơ chế Self-Attention toàn cục. Transformer tính toán sự tương quan giữa mọi cặp từ trong câu cùng một lúc, bất kể khoảng cách vị trí. Cách tiếp cận này loại bỏ rào cản về độ dài chuỗi của RNN và sự thiếu hụt ngữ cảnh của MLP, cho phép mô hình nắm bắt được ngữ nghĩa sâu sắc dựa trên mối quan hệ giữa các từ trong toàn bộ văn bản.
Chưa có bình luận nào. Hãy là người đầu tiên!