Sigmoid và Tanh trong học sâu: Hai “anh em” cùng gốc logistic

1. Giới thiệu

Khi mới bước vào học sâu (deep learning), ta thường gặp ngay hai hàm kích hoạt kinh điển:

• Sigmoid
• Tanh (hyperbolic tangent)

Chúng xuất hiện trong logistic regression, MLP cổ điển, RNN, LSTM,…

Nhìn thì khác nhau, nhưng thực ra có quan hệ rất chặt chẽ: tanh về cơ bản chỉ là sigmoid được co dãn và tịnh tiến lại.

Trong bài viết này, ta sẽ:

1. Ôn lại cơ sở lý thuyết của sigmoid và tanh
2. Hiểu rõ mối liên hệ toán học giữa chúng
3. Xem cách dùng trong deep learning, ưu – nhược điểm
4. Lướt qua ứng dụng thực tế
5. Xem code minh họa bằng PyTorch

2. Cơ sở lý thuyết

2.1. Hàm sigmoid

Hàm sigmoid (logistic):

$$σ(x) = \frac{1}{1 + e^{-x}}$$

Tính chất:

• Miền giá trị: (0,1)

• σ(0) = 0.5

• Khi $x \to +\infty$ → $\sigma(x) \to 1$

• Khi $x \to -\infty$ thì $\sigma(x) \to 0$.

Đạo hàm:

• $\sigma'(x) = \sigma(x)\big(1 - \sigma(x)\big)$

Ý nghĩa trong logistic regression:

• $\sigma(w^\top x + b)$ được diễn giải là xác suất $\Pr(y = 1 \mid x)$.

• Mối liên hệ với log-odds: $\log \dfrac{p}{1 - p} = w^\top x + b$, với $p = \sigma(w^\top x + b)$.

2.2. Hàm tanh

Hàm hyperbolic tangent

Hàm tanh được định nghĩa:

$$ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$

Tính chất:

• Miền giá trị: $(-1, 1)$
• $\tanh(0) = 0$
• $\tanh(x)$ là hàm lẻ: $\tanh(-x) = -\tanh(x)$
• Đối xứng qua gốc toạ độ (zero-centered)

Đạo hàm:

$$ \frac{d}{dx}\tanh(x) = 1 - \tanh^2(x) $$

Cả sigmoid và $\tanh$ đều là hàm trơn, bão hòa (saturate) ở hai đầu, nên đều có nguy cơ vanishing gradient khi $|x|$ lớn.

3. Mối liên hệ giữa sigmoid và tanh

Hàm sigmoid

Hàm sigmoid được định nghĩa:

$$ \sigma(x) = \frac{1}{1 + e^{-x}} $$

Ta có thể biểu diễn $\tanh$ qua sigmoid bằng công thức:

$$ \tanh(x) = 2\sigma(2x) - 1 $$

Giải thích nhanh

Bắt đầu từ vế phải:

$$ 2\sigma(2x) - 1 = 2 \cdot \frac{1}{1 + e^{-2x}} - 1 = \frac{2}{1 + e^{-2x}} - 1 $$

Quy đồng mẫu:

$$ \frac{2}{1 + e^{-2x}} - 1 = \frac{2 - (1 + e^{-2x})}{1 + e^{-2x}} = \frac{1 - e^{-2x}}{1 + e^{-2x}} $$

Nhân cả tử và mẫu với $e^{2x}$:

$$ \frac{1 - e^{-2x}}{1 + e^{-2x}} = \frac{e^{2x} - 1}{e^{2x} + 1} = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \tanh(x) $$

Vậy:

$$ \tanh(x) = 2\sigma(2x) - 1 $$

Nhận xét

• $\sigma(x)$ (sigmoid): miền giá trị $(0, 1)$, không zero-centered
• $\tanh(x)$: miền giá trị $(-1, 1)$, zero-centered

Do đó, trong nhiều kiến trúc mạng nơ-ron cổ điển, người ta thường thích dùng $\tanh$ hơn sigmoid cho các layer ẩn, vì đầu ra cân quanh 0, giúp gradient “dễ thở” hơn.

• Hình đồ thị minh họa của hai hàm:

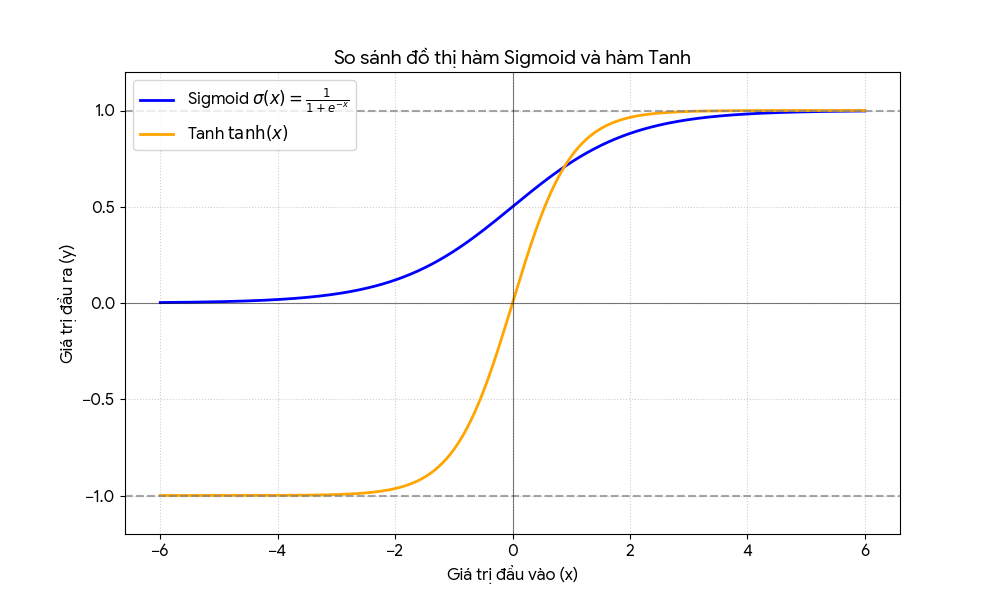
4. Cách dùng trong học sâu

4.1. Sigmoid – khi nào dùng?

Các chỗ điển hình:

1. Output của bài toán nhị phân
   • Ví dụ: logistic regression, binary classification
   • Layer cuối: Linear → Sigmoid
   • Loss thường dùng: Binary Cross-Entropy (BCE)
2. Multi-label classification
   • Mỗi class là một Bernoulli độc lập
   • Dùng sigmoid riêng cho từng đầu ra, thay vì softmax.

Ưu điểm:

• Giải thích rõ ràng dưới dạng xác suất
• Phù hợp tự nhiên cho các bài toán nhị phân.

Nhược điểm:

• Không zero-centered → gradient có thể “lệch” về một phía
• Saturation ở vùng biên (gần 0 hoặc 1) → vanishing gradient.

4.2. Tanh – khi nào dùng?

Các chỗ điển hình:

1. Hidden layer trong MLP / RNN cổ điển
   • Trước thời ReLU thống trị, tanh là lựa chọn rất phổ biến.
2. Bên trong LSTM/GRU
   • Các “candidate state” thường dùng tanh để đưa giá trị vào khoảng [−1,1]
   • Ví dụ:
     • $\tilde{h}_t = \tanh(W x_t + U h_{t-1} + b)$

Ưu điểm:

• Zero-centered → giúp gradient “cân đối” quanh 0 hơn sigmoid
• Thường cho hiệu quả tốt hơn sigmoid khi dùng làm activation ẩn.

Nhược điểm:

• Vẫn bị vanishing gradient khi |x| lớn
• Trong nhiều kiến trúc hiện đại, tanh dần nhường chỗ cho ReLU, LeakyReLU, GELU,…

4.3. So sánh nhanh Sigmoid vs Tanh vs ReLU

• Sigmoid
  • Range: (0, 1)
  • Không zero-centered
  • Vanishing gradient mạnh khi |x| lớn
  • Dùng rất hợp cho output nhị phân
• Tanh
  • Range: (-1, 1)
  • Zero-centered
  • Vanishing gradient vẫn tồn tại
  • Tốt hơn sigmoid cho hidden layer trong nhiều trường hợp cổ điển
• ReLU
  • Range: [0, +∞)
  • Không bão hòa phía dương → gradient giữ được cho x>0
  • Đơn giản, train nhanh, phổ biến trong mạng sâu hiện đại
  • Có vấn đề “dead ReLU” khi gradient về 0 ở nửa âm.

5. Ứng dụng thực tế

5.1. Logistic regression & output nhị phân

Ở bài toán logistic regression:

$$ \hat{p}(y = 1 \mid x) = \sigma(w^\top x + b) $$

→ Sigmoid đóng vai trò map score tuyến tính → xác suất.

Trong deep learning:

• Binary classifier với CNN/MLP:
  • features → Linear → Sigmoid
• Khi dự đoán mỗi pixel là nền/foreground, hoặc mỗi bounding box có/không có object,… sigmoid vẫn là lựa chọn tự nhiên.

5.2. Mạng tuần tự: RNN, LSTM, GRU

Trong LSTM/GRU, ta thường gặp:

• Sigmoid: dùng cho gate (cổng vào/ra/quên)

  → vì ta muốn giá trị trong [0,1] như “tỷ lệ đóng/mở”

• Tanh: dùng cho candidate state / output

  → vì ta muốn thông tin được “bóp” vào khoảng [-1,1]

Ví dụ (LSTM đơn giản):

• $i_t = \sigma(W_i x_t + U_i h_{t-1} + b_i)$ — input gate
• $f_t = \sigma(W_f x_t + U_f h_{t-1} + b_f)$ — forget gate
• $\tilde{c}_t = \tanh(W_c x_t + U_c h_{t-1} + b_c)$ — candidate cell
• $c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t$ — cell state update

→ Ở đây, sigmoid và tanh làm đúng vai trò của “cửa” và “nội dung”.

6. Code minh họa (PyTorch)

6.1 Dưới đây là một ví dụ nhỏ dùng PyTorch để:

1. Định nghĩa hai mô hình MLP:
   • Một dùng tanh ở hidden layer
   • Một dùng sigmoid ở hidden layer
2. Train thử trên dữ liệu toy nhị phân (vòng tròn vs không vòng tròn)

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt # IMPORT THƯ VIỆN VẼ HÌNH

# Để kết quả ổn định, dễ so sánh
torch.manual_seed(42)

# --- 1. Tạo dữ liệu ---
X, y = make_circles(n_samples=2000, factor=0.5, noise=0.1, random_state=42)
X = StandardScaler().fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

X_train = torch.tensor(X_train, dtype=torch.float32)
X_test  = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32).view(-1, 1)
y_test  = torch.tensor(y_test, dtype=torch.float32).view(-1, 1)

# --- 2. Định nghĩa 2 mô hình ---
class MLP_Sigmoid(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(2, 16),
            nn.Sigmoid(), # Hidden layer là Sigmoid
            nn.Linear(16, 1),
            nn.Sigmoid()
        )
    def forward(self, x):
        return self.net(x)

class MLP_Tanh(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(2, 16),
            nn.Tanh(),    # Hidden layer là Tanh
            nn.Linear(16, 1),
            nn.Sigmoid()
        )
    def forward(self, x):
        return self.net(x)

model_sig = MLP_Sigmoid()
model_tanh = MLP_Tanh()

# --- 3. Hàm train chung (ĐÃ SỬA ĐỔI ĐỂ GHI LẠI LỊCH SỬ) ---
def train_model_with_history(model, X_train, y_train, epochs=1000, lr=1e-2):
    criterion = nn.BCELoss()
    optimizer = optim.Adam(model.parameters(), lr=lr)

    # Danh sách để lưu lịch sử
    loss_history = []
    acc_history = []

    print(f"Đang train mô hình: {type(model).__name__}...")
    for epoch in range(epochs):
        model.train()
        optimizer.zero_grad()

        y_pred = model(X_train)
        loss = criterion(y_pred, y_train)

        loss.backward()
        optimizer.step()

        # Tính accuracy và lưu lại loss mỗi epoch
        with torch.no_grad():
            preds = (y_pred > 0.5).float()
            acc = (preds == y_train).float().mean().item()

        # Lưu vào lịch sử
        loss_history.append(loss.item())
        acc_history.append(acc)

        if (epoch+1) % 200 == 0:
            print(f"Epoch {epoch+1:4d} | Loss: {loss.item():.4f} | Acc: {acc:.4f}")

    # Trả về thêm lịch sử
    return model, loss_history, acc_history

# --- Train và nhận lại lịch sử ---
print("==== Bắt đầu huấn luyện ====")
# Train Sigmoid và lưu lịch sử
model_sig, loss_sig_hist, acc_sig_hist = train_model_with_history(
    model_sig, X_train, y_train, epochs=800, lr=1e-2
)
print("-" * 30)
# Train Tanh và lưu lịch sử
model_tanh, loss_tanh_hist, acc_tanh_hist = train_model_with_history(
    model_tanh, X_train, y_train, epochs=800, lr=1e-2
)

# --- 4. VẼ ĐỒ THỊ SO SÁNH (PHẦN MỚI) ---
epochs_range = range(1, len(loss_sig_hist) + 1)

plt.figure(figsize=(14, 6)) # Tạo khung vẽ kích thước 14x6

# Đồ thị 1: So sánh LOSS
plt.subplot(1, 2, 1) # Vị trí bên trái
plt.plot(epochs_range, loss_sig_hist, label='Hidden Sigmoid Loss', color='blue', linestyle='--')
plt.plot(epochs_range, loss_tanh_hist, label='Hidden Tanh Loss', color='red')
plt.title('Training Loss Comparison')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)

# Đồ thị 2: So sánh ACCURACY
plt.subplot(1, 2, 2) # Vị trí bên phải
plt.plot(epochs_range, acc_sig_hist, label='Hidden Sigmoid Acc', color='blue', linestyle='--')
plt.plot(epochs_range, acc_tanh_hist, label='Hidden Tanh Acc', color='red')
plt.title('Training Accuracy Comparison')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim(0.9, 1.0) # Zoom vào khoảng accuracy cao để dễ nhìn
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()

# --- 5. Đánh giá cuối cùng (như cũ) ---
def eval_model(model, X_test, y_test):
    model.eval()
    with torch.no_grad():
        y_pred = model(X_test)
        preds = (y_pred > 0.5).float()
        acc = (preds == y_test).float().mean().item()
    return acc

acc_sig_final = eval_model(model_sig, X_test, y_test)
acc_tanh_final = eval_model(model_tanh, X_test, y_test)

print(f"\nFinal Test Accuracy (Sigmoid): {acc_sig_final:.4f}")
print(f"Final Test Accuracy (Tanh)   : {acc_tanh_final:.4f}")

6.2 Kết quả chạy thực nghiệm:

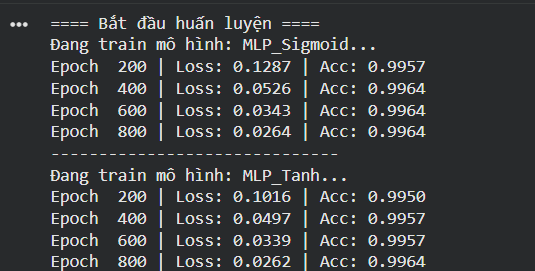
1. Phân tích số liệu định lượng qua bảng.

• Đánh giá chi tiết dựa trên bản chất toán học. Tại sao lại có sự chênh lệch số liệu như trên?
  Dưới đây là giải thích sâu về cơ chế bên trong:
  A. Giai đoạn đầu (Epoch 0 - 200):

• Sự vượt trội của TanhSố liệu tại Epoch 200 cho thấy Loss của Tanh (0.1016) thấp hơn đáng kể so với Sigmoid (0.1287).

• Nguyên nhân - "Zero-centered" (Tâm 0):Hàm Tanh có miền giá trị $(-1, 1)$, trung bình cộng của đầu ra xấp xỉ 0. Điều này giúp các trọng số (weights) trong mạng có thể được cập nhật theo các hướng âm/dương linh hoạt ngay từ đầu.

• Hàm Sigmoid có miền giá trị $(0, 1)$, đầu ra luôn dương. Điều này khiến gradient (đạo hàm dùng để sửa lỗi) truyền về các lớp trước đó luôn cùng dấu.

• Hệ quả là vector trọng số phải di chuyển theo đường "ziczac" để đến đích, làm chậm quá trình học.Kết luận từ số liệu: Con số 0.1016 so với 0.1287 là bằng chứng thực tế cho thấy Tanh đi "thẳng đường" hơn Sigmoid.

B. Giai đoạn sau (Epoch 400 - 800):
Sự bám đuổi của SigmoidTại Epoch 800, Loss của hai mô hình gần như bằng nhau (0.0264 vs 0.0262).
Phân tích:

• Dù khởi đầu chậm chạp, nhưng với bài toán đơn giản này, Sigmoid vẫn đủ khả năng để học được quy luật phân chia dữ liệu.

• Optimizer (Adam) cũng giúp giảm thiểu nhược điểm của Sigmoid bằng cách điều chỉnh tốc độ học (learning rate) thích ứng cho từng tham số.

• Tuy nhiên, nếu bài toán phức tạp hơn (nhiều lớp ẩn hơn), khoảng cách này sẽ không bao giờ được san lấp, và Sigmoid có thể bị kẹt lại ở mức lỗi cao do hiện tượng "Biến mất Gradient" (Vanishing Gradient).

C. Độ chính xác cuối cùng (Test Accuracy)Kết quả kiểm thử cho thấy Tanh (0.9950) chiến thắng sát nút Sigmoid (0.9933).

• Ý nghĩa:Mặc dù chênh lệch chỉ là ~0.17%, nhưng nó phản ánh sự ổn định tốt hơn của Tanh.Với Tanh, ranh giới phân lớp (decision boundary) được mạng vẽ ra dứt khoát và rõ ràng hơn nhờ biên độ đạo hàm lớn hơn (đạo hàm cực đại của Tanh là 1.0, trong khi Sigmoid chỉ là 0.25). Tín hiệu học mạnh hơn giúp mạng "tự tin" hơn với các quyết định của mình.

2. Phân tích qua biểu đồ.

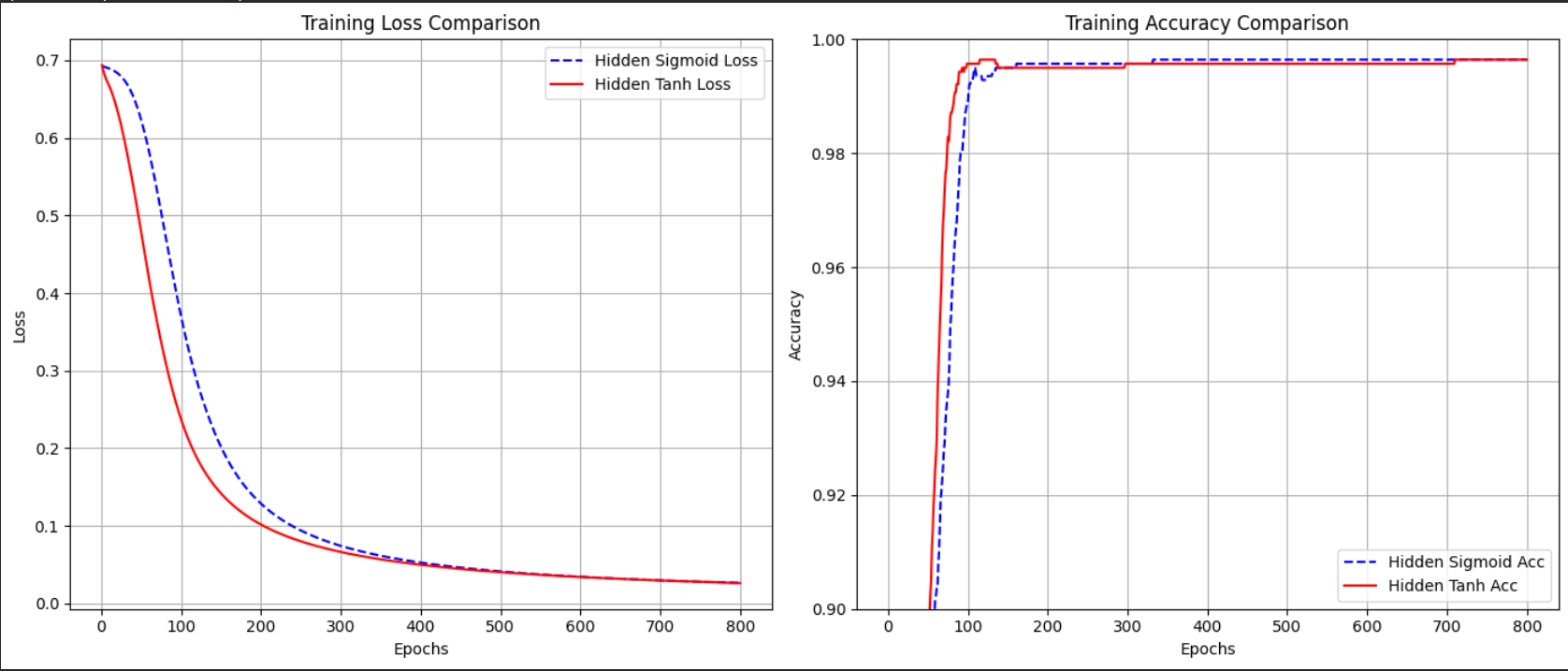
Khi chạy đoạn code có vẽ đồ thị (Matplotlib), chúng ta quan sát thấy hai hiện tượng rõ rệt tương ứng với lý thuyết trên:

Biểu đồ 1: Tốc độ giảm Loss (Training Loss)
Quan sát: Đường Loss của Tanh (màu đỏ) lao dốc gần như thẳng đứng ngay trong 100-200 epoch đầu tiên. Trong khi đó, đường Sigmoid (màu xanh) giảm từ từ và mất nhiều thời gian hơn để đạt đến mức Loss thấp tương tự.

Giải thích: Do đặc tính Zero-centered, Tanh cho phép bộ tối ưu hóa (Adam) tìm ra hướng giảm lỗi nhanh hơn. Sigmoid bị hạn chế bởi hiện tượng "ziczac" của gradient (do đầu ra luôn dương), nên nó mất nhiều bước lặp hơn để điều chỉnh các trọng số về đúng vị trí tối ưu phân chia ranh giới giữa hai hình tròn.

Biểu đồ 2: Độ chính xác (Accuracy)
Quan sát: Mô hình Tanh đạt độ chính xác >99% rất sớm. Sigmoid cũng đạt được độ chính xác này nhưng trễ hơn (thường trễ hơn khoảng 100-300 epochs tùy vào cách khởi tạo ngẫu nhiên).

Giải thích: Mặc dù cả hai hàm đều có khả năng xấp xỉ hàm phi tuyến tính (Universal Approximation Theorem), nhưng Tanh là một bộ xấp xỉ hiệu quả hơn trong các mạng nơ-ron sâu hoặc mạng cơ bản nhờ biên độ đạo hàm lớn.

• Thử thay nn.Sigmoid() ở hidden bằng nn.ReLU() và so sánh
• Thử tăng số layer, hoặc tăng số neuron để xem hiệu quả.

7. Kết luận

• Sigmoid và tanh là hai hàm kích hoạt “anh em” cùng gốc logistic:
  • Sigmoid: (0,1), không zero-centered
  • Tanh: (−1,1), zero-centered
  • Liên hệ: $$tanh⁡(x)=2σ(2x)−1\tanh(x) = 2\sigma(2x) - 1tanh(x)=2σ(2x)−1$$
• Trong deep learning:
  • Sigmoid cực kỳ phù hợp cho output nhị phân và các gate trong RNN/LSTM
  • Tanh hợp lý cho hidden state cần giá trị đối xứng quanh 0, đặc biệt trong mạng tuần tự.