Bạn có bao giờ tự hỏi tại sao mạng neural network của mình không học được khi có quá nhiều lớp? Hay tại sao một số neuron lại "chết" và không bao giờ hoạt động trở lại? Mình đã từng gặp những vấn đề này và phải mất nhiều thời gian mới hiểu được cơ chế đằng sau chúng. Trong bài viết này, mình sẽ cùng các bạn khám phá hai vấn đề "kinh điển" trong deep learning: Gradient Vanishing và Dying ReLU, thông qua các ví dụ tính toán cụ thể với số liệu thực tế.
1. Vấn đề Gradient Vanishing (Tiêu biến Gradient) - Khi Gradient "Biến mất"
Gradient Vanishing xảy ra khi độ dốc (gradient) của hàm mất mát trở nên cực kỳ nhỏ khi lan truyền ngược (backpropagation) về các lớp đầu tiên. Điều này khiến việc cập nhật trọng số ở các lớp sâu (gần đầu vào) diễn ra rất chậm hoặc gần như không xảy ra, làm cho mạng không học được.
Mình đã từng "đau đầu" khi thấy mạng neural network của mình không học được gì sau nhiều epoch, và sau đó mới phát hiện ra rằng gradient đã "biến mất" hoàn toàn ở các lớp đầu!
1.1. Phân tích hàm Sigmoid - "Thủ phạm" chính
Hàm Sigmoid được định nghĩa là:
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
Đạo hàm của nó là:
$$\sigma'(x) = \sigma(x)(1 - \sigma(x))$$
Tính toán cụ thể:
- Đạo hàm tối đa: Giá trị lớn nhất của $\sigma'(x)$ xảy ra khi $x = 0$, lúc này $\sigma(0) = 0.5$.
$$\sigma'(0) = 0.5 \times (1 - 0.5) = 0.25$$
Đây là giá trị lớn nhất mà đạo hàm Sigmoid có thể đạt được!
- Trường hợp bão hòa (Saturation): Khi $x$ rất lớn hoặc rất nhỏ, hàm Sigmoid bị "bão hòa," tức là giá trị đầu ra gần 0 hoặc gần 1.
- Nếu $x = 5$: $\sigma(5) \approx 0.993$, $\sigma'(5) \approx 0.993 \times (1 - 0.993) \approx 0.0069$
- Nếu $x = -5$: $\sigma(-5) \approx 0.0067$, $\sigma'(-5) \approx 0.0067 \times (1 - 0.0067) \approx 0.0066$
Như bạn thấy, khi đầu vào nằm ngoài vùng trung tâm, đạo hàm trở nên rất nhỏ!
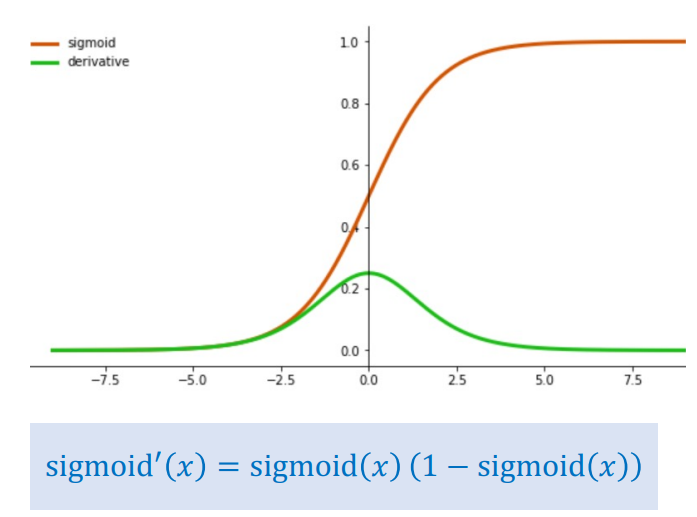
Hình 1: Hàm Sigmoid
Ví dụ Tính tay: Gradient Vanishing qua Nhiều Lớp Ẩn
Bây giờ, hãy xem điều gì xảy ra khi gradient lan truyền qua một mạng có nhiều lớp ẩn sử dụng Sigmoid.
Kiến trúc mạng cho ví dụ Gradient Vanishing:
- Lớp đầu vào (Input Layer): 4 features + 1 bias
- Lớp ẩn 1 (Hidden Layer 1): Nhiều neurons (ví dụ: 3+ neurons) với hàm kích hoạt Sigmoid
- Lớp ẩn 2, 3, ... (Hidden Layers): Nhiều lớp ẩn tiếp theo, mỗi lớp có nhiều neurons, tất cả đều sử dụng hàm kích hoạt Sigmoid (fully connected)
- Lớp đầu ra (Output Layer): 3 neurons ($z_1$, $z_2$, $z_3$) với hàm kích hoạt Softmax
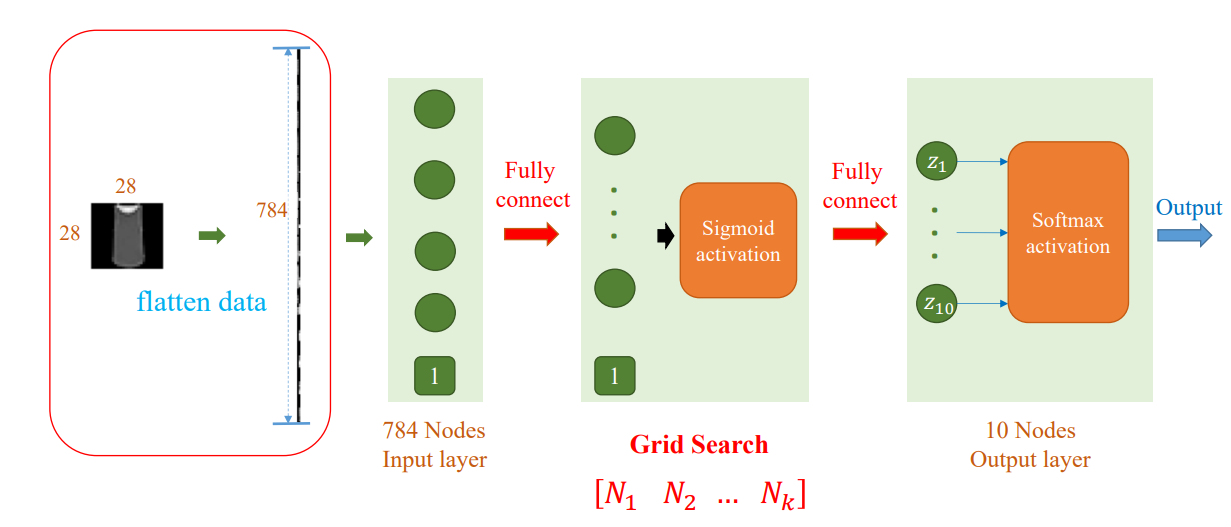
Hình 2: MLP Architecture
Giả sử:
- Mạng có 5 lớp ẩn, tất cả đều sử dụng hàm kích hoạt Sigmoid
- Trong quá trình lan truyền ngược, gradient ban đầu từ lớp đầu ra là: $\nabla_{output} L = 1.0$
- Tất cả các đầu vào pre-activation đều nằm trong vùng bão hòa, với đạo hàm trung bình là $0.1$ (nhỏ hơn giá trị tối đa $0.25$)
<
Tính toán gradient qua từng lớp:*
Lớp 5 (gần đầu ra nhất):
$$\nabla_{layer5} L = \nabla_{output} L \times \sigma'(h_5) = 1.0 \times 0.1 = 0.1$$
Lớp 4:
$$\nabla_{layer4} L = \nabla_{layer5} L \times \sigma'(h_4) = 0.1 \times 0.1 = 0.01$$
Lớp 3:
$$\nabla_{layer3} L = \nabla_{layer4} L \times \sigma'(h_3) = 0.01 \times 0.1 = 0.001$$
Lớp 2:
$$\nabla_{layer2} L = \nabla_{layer3} L \times \sigma'(h_2) = 0.001 \times 0.1 = 0.0001$$
Lớp 1 (gần đầu vào nhất):
$$\nabla_{layer1} L = \nabla_{layer2} L \times \sigma'(h_1) = 0.0001 \times 0.1 = 0.00001$$
Kết quả:
Như bạn thấy, sau 5 lớp, gradient đã giảm xuống còn 0.00001, tức là chỉ còn 0.001% so với gradient ban đầu! Điều này có nghĩa là:
- Các trọng số ở lớp 1 sẽ được cập nhật với learning rate cực kỳ nhỏ
- Nếu learning rate là $0.01$, thì cập nhật thực tế sẽ là: $\Delta w_1 = 0.00001 \times 0.01 = 0.0000001$ (gần như bằng 0!)
- Mạng sẽ không học được gì ở các lớp đầu, dẫn đến hiện tượng Gradient Vanishing
1.3. Phân tích hàm Tanh - Tốt hơn nhưng vẫn có vấn đề
Hàm Tanh (Hyperbolic Tangent) có phạm vi giá trị từ $[-1, 1]$, lớn hơn Sigmoid $[0, 1]$. Đạo hàm của nó là:
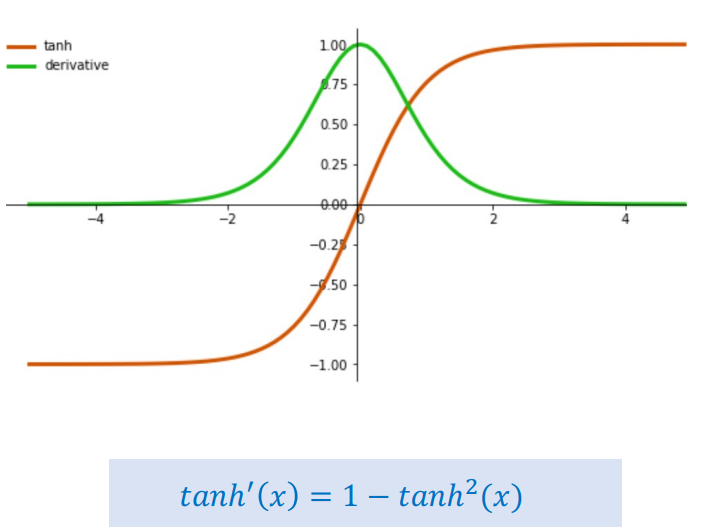
Hình 3: Hàm Tanh
$$\tanh'(x) = 1 - \tanh^2(x)$$
So sánh với Sigmoid:
- Đạo hàm tối đa: $\tanh'(0) = 1.0$ (lớn hơn $0.25$ của Sigmoid)
- Vấn đề bão hòa: Tương tự như Sigmoid, Tanh vẫn bị bão hòa khi giá trị đầu vào $x$ tiến về $\pm 2$
Ví dụ:
- $x = 2$: $\tanh(2) \approx 0.964$, $\tanh'(2) \approx 1 - 0.964^2 \approx 0.071$
- $x = 3$: $\tanh(3) \approx 0.995$, $\tanh'(3) \approx 1 - 0.995^2 \approx 0.010$
1.4. Các hàm Activation khác - Giải pháp cho Gradient Vanishing
Để giải quyết vấn đề Gradient Vanishing, nhiều hàm activation mới đã được phát triển qua các năm. Dưới đây là một số hàm activation phổ biến:
ReLU (Rectified Linear Unit)
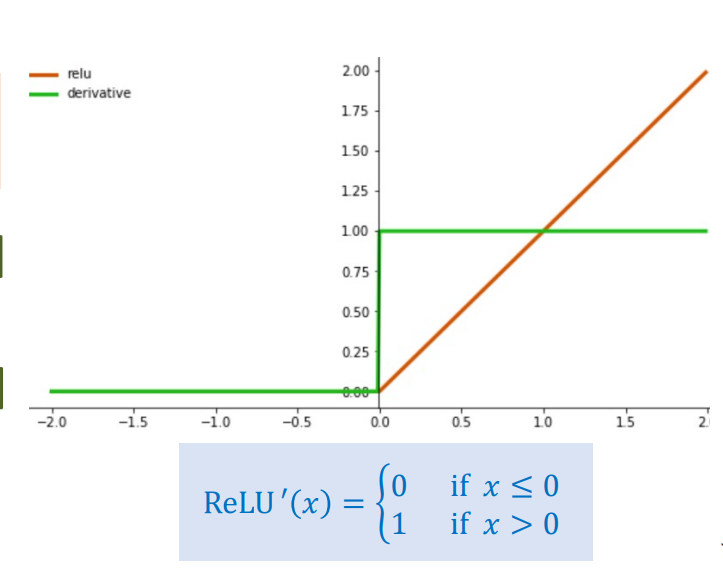
Hình 4: Hàm ReLU
$$\text{ReLU}(x) = \max(0, x) = \begin{cases} 0 & \text{nếu } x < 0 \\ x & \text{nếu } x \geq 0 \end{cases}$$
ReLU giải quyết được vấn đề gradient vanishing khi $x > 0$ (đạo hàm = 1), nhưng lại gặp vấn đề Dying ReLU khi $x \leq 0$ (đạo hàm = 0). Chúng ta sẽ phân tích chi tiết vấn đề này trong phần 2.
Softplus:
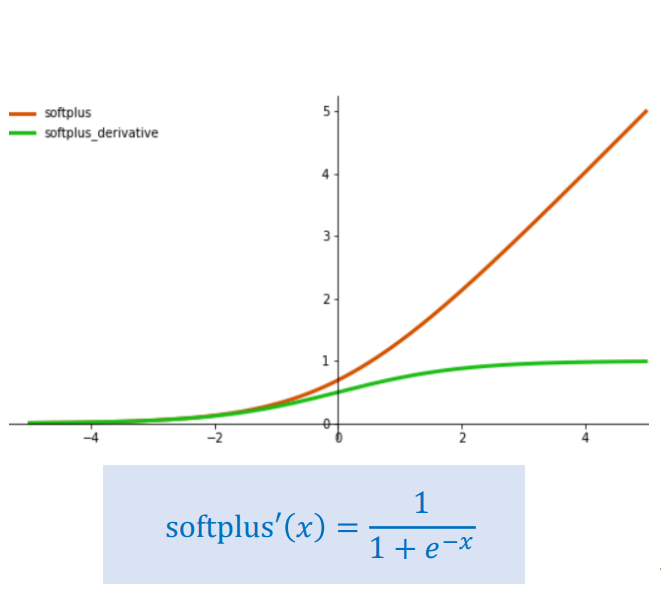
Hình 5: Hàm Softplus
$$\text{Softplus}(x) = \log(1 + e^x)$$
Softplus là phiên bản "mềm" của ReLU, có đạo hàm luôn dương nhưng không bằng 0, giúp tránh được Dying ReLU.
ELU (Exponential Linear Unit)
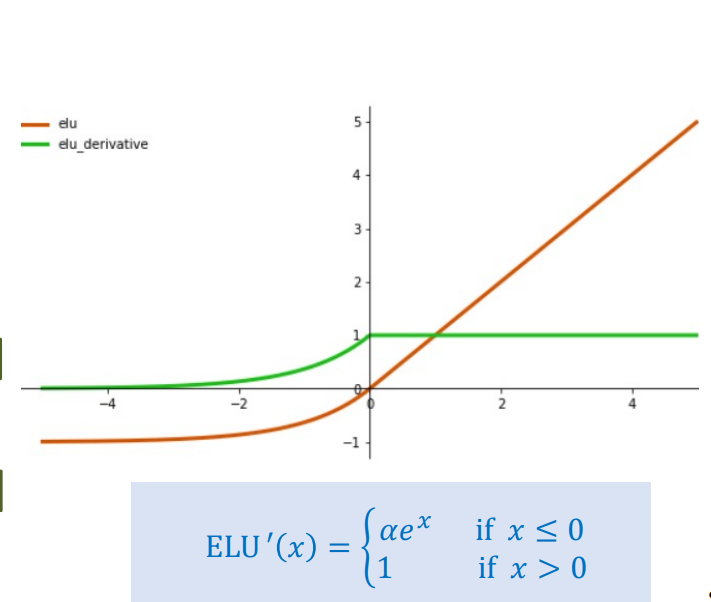
Hình 6: Hàm ELU
$$\text{ELU}(x) = \begin{cases} \alpha(e^x - 1) & \text{nếu } x < 0 \\ x & \text{nếu } x \geq 0 \end{cases}$$
ELU có đạo hàm âm nhỏ khi $x < 0$ (thay vì bằng 0 như ReLU), giúp tránh Dying ReLU và cho phép gradient lan truyền ngược ngay cả khi đầu vào âm.
PReLU (Parametric ReLU)
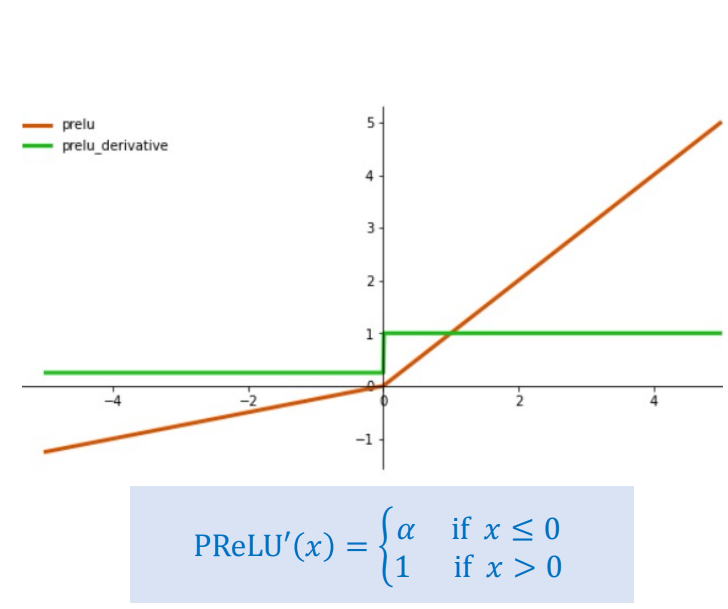
Hình 7: Hàm PReLU
$$\text{PReLU}(x) = \begin{cases} \alpha x & \text{nếu } x < 0 \\ x & \text{nếu } x \geq 0 \end{cases}$$
PReLU tương tự ELU nhưng hệ số $\alpha$ là tham số có thể học được, cho phép mô hình tự điều chỉnh độ dốc khi $x < 0$.
Swish
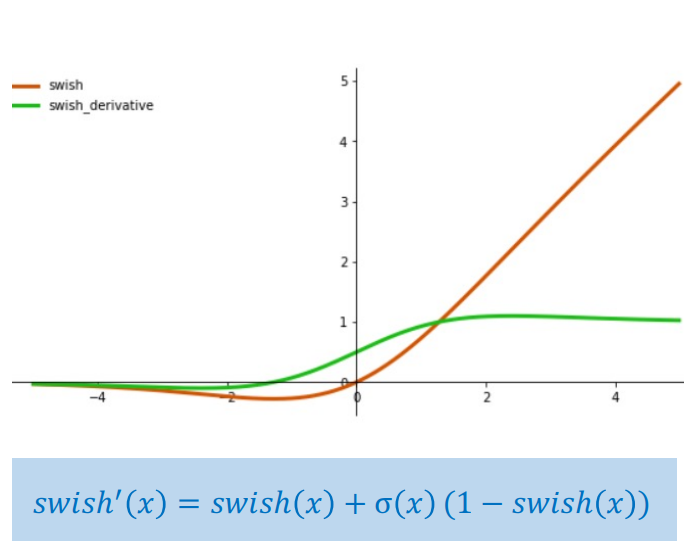
Hình 8: Hàm Swish
$$\text{Swish}(x) = x \cdot \sigma(x) = x \cdot \frac{1}{1 + e^{-x}}$$
Swish là tích của $x$ và Sigmoid, có đạo hàm luôn dương và không bị bão hòa như Sigmoid thuần túy.
GELU (Gaussian Error Linear Unit)
$$\text{GELU}(x) = x \Phi(x) \approx x \cdot \sigma(1.702x)$$
GELU sử dụng phân phối chuẩn tích lũy $\Phi(x)$, được xấp xỉ bằng $x$ nhân với Sigmoid. GELU được sử dụng rộng rãi trong các mô hình transformer hiện đại.
2. Vấn đề Dying ReLU (ReLU Chết) - Khi Neuron "Chết"
Để giải quyết vấn đề Gradient Vanishing, hàm ReLU (Rectified Linear Unit) được phát minh:
Trước khi đi sâu vào các vấn đề, hãy cùng xem các kiến trúc MLP cụ thể mà chúng ta sẽ sử dụng trong các ví dụ. Mỗi vấn đề sẽ sử dụng một kiến trúc phù hợp để minh họa rõ ràng nhất:
Kiến trúc cho ví dụ Dying ReLU
Kiến trúc mạng:
- Lớp đầu vào (Input Layer): 2 features ($x_1$, $x_2$) + 1 bias = 3 nodes
- Lớp ẩn (Hidden Layer): 2 neurons ($h_1$, $h_2$) với hàm kích hoạt ReLU
- Lớp đầu ra (Output Layer): 3 neurons ($z_1$, $z_2$, $z_3$) với hàm kích hoạt Softmax
- Hàm mất mát (Loss Function): Cross-entropy loss
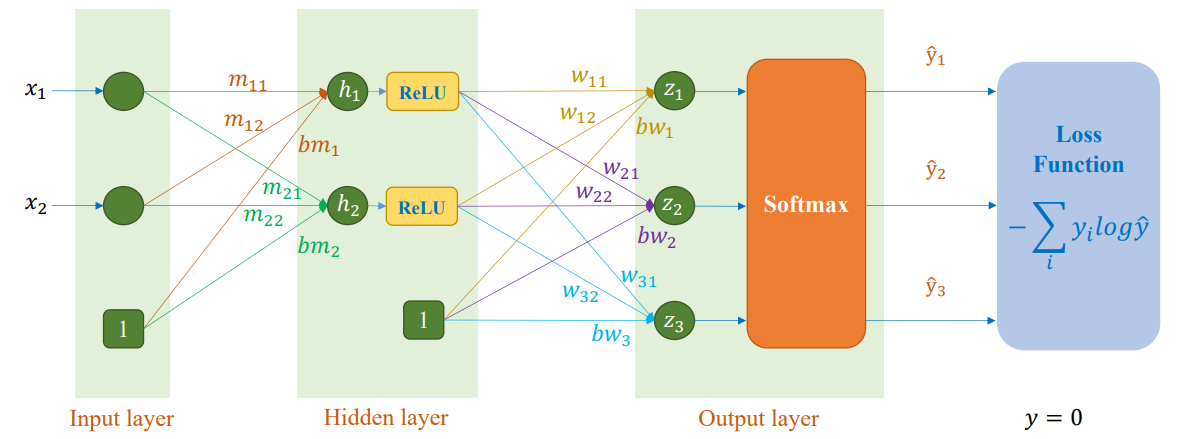
Hình 10: MLP Architecture
$$\text{ReLU}(x) = \max(0, x)$$
Đạo hàm của ReLU là:
- $\text{ReLU}'(x) = 1$ nếu $x > 0$
- $\text{ReLU}'(x) = 0$ nếu $x \leq 0$
Điều này giúp duy trì gradient lớn khi $x > 0$, giải quyết được vấn đề gradient vanishing. Tuy nhiên, ReLU lại sinh ra vấn đề Dying ReLU, xảy ra khi một neuron luôn đưa ra kết quả bằng 0 cho tất cả các mẫu dữ liệu, khiến gradient của nó luôn bằng 0 và neuron đó ngừng học vĩnh viễn.
Mình đã từng thấy một mạng neural network có đến 30% neurons "chết" sau vài epoch, và điều này làm giảm đáng kể khả năng học của mô hình!
2.1. Ví dụ Tính tay: Dying ReLU
Chúng ta sẽ xem xét một ví dụ MLP cụ thể với kiến trúc rõ ràng và minh họa quá trình lan truyền ngược khi một node bị chết.
Cấu hình Mô hình và Dữ liệu:
- Đầu vào: $x = [1.5, 0.2]$ (sau khi thêm bias: $x = [1.0, 1.5, 0.2]$)
- Nhãn: $y = 0$ (mã hóa one-hot: $y = [1, 0, 0]$)
- Cấu trúc mạng:
- Lớp ẩn 1: 2 neurons ($h_1, h_2$) sử dụng ReLU
- Lớp đầu ra: 3 neurons sử dụng Softmax
Trọng số và Bias ban đầu (Lớp Ẩn 1):
Ma trận trọng số $M$ (kích thước $3 \times 2$, bao gồm bias ở hàng đầu tiên):
$$M = \begin{bmatrix} 0.0 & 0.0 \\ 0.86 & -1.04 \\ 0.41 & -0.65 \end{bmatrix}$$
Bias $b_m = [0.0, 0.0]$ (đã được gộp vào $M$ trong phép tính $h = x \times M$)
Trọng số lớp đầu ra (từ hidden layer đến output layer):
$$W_{out} = \begin{bmatrix} 0.5 & 0.3 & -0.2 \\ -0.1 & 0.4 & 0.6 \end{bmatrix}$$
Bước 1: Lan truyền thuận (Forward Propagation)
1. Tính toán đầu vào cho lớp ẩn (pre-activation):
$$h = x \times M = [1.0, 1.5, 0.2] \times \begin{bmatrix} 0.0 & 0.0 \\ 0.86 & -1.04 \\ 0.41 & -0.65 \end{bmatrix}$$
Tính từng phần tử:
- $h_1 = (1.0 \times 0.0) + (1.5 \times 0.86) + (0.2 \times 0.41) = 0 + 1.29 + 0.082 = 1.372$
- $h_2 = (1.0 \times 0.0) + (1.5 \times -1.04) + (0.2 \times -0.65) = 0 - 1.56 - 0.13 = -1.69$
Vậy: $h = [1.372, -1.69]$
2. Áp dụng ReLU:
$$\text{ReLU}(h) = [\max(0, 1.372), \max(0, -1.69)] = [1.372, 0.0]$$
Kết quả quan trọng: Node thứ hai ($h_2$) đã "chết" vì đầu vào pre-activation của nó là âm ($-1.69$), khiến đầu ra ReLU bằng 0.
3. Lan truyền đến lớp đầu ra:
Đầu vào lớp đầu ra:
$$
z = \text{ReLU}(\mathbf{h}) \cdot \mathbf{W}_{\text{out}} =
\begin{bmatrix} 1.372 & 0 \end{bmatrix}
\begin{bmatrix}
0.5 & 0.3 & -0.2 \\
-0.1 & 0.4 & 0.6
\end{bmatrix}
$$
Tính từng phần tử:
- $z_1 = (1.372 \times 0.5) + (0.0 \times -0.1) = 0.686 + 0 = 0.686$
4. Áp dụng Softmax và tính Loss:
Softmax probabilities:
- $p_1 = \frac{e^{0.686}}{e^{0.686} + e^{0.412} + e^{-0.274}} = \frac{1.986}{1.986 + 1.510 + 0.760} = \frac{1.986}{4.256} = 0.467$
- $p_2 = \frac{1.510}{4.256} = 0.355$
- $p_3 = \frac{0.760}{4.256} = 0.178$
Cross-Entropy Loss với nhãn $y = [1, 0, 0]$:
$$L = -\log(p_1) = -\log(0.467) = 0.761$$
Bước 2: Lan truyền ngược (Backward Propagation) - Vấn đề xuất hiện
Trong lan truyền ngược, chúng ta tính toán gradient của mất mát ($L$) đối với các trọng số.
1. Tính $\nabla_z L$ (Gradient lớp đầu ra):
Với Cross-Entropy Loss và Softmax:
$$\nabla_z L = \text{softmax}(z) - y = [0.467, 0.355, 0.178] - [1, 0, 0] = [-0.533, 0.355, 0.178]$$
2. Tính $\nabla_{\text{ReLU}} L$ (Gradient sau ReLU):
Đây là gradient của mất mát đối với đầu ra của lớp ẩn:
$$\nabla_{\text{ReLU}} L = W_{out}^T \times \nabla_z L = \begin{bmatrix} 0.5 & -0.1 \\ 0.3 & 0.4 \\ -0.2 & 0.6 \end{bmatrix} \times \begin{bmatrix} -0.533 \\ 0.355 \\ 0.178 \end{bmatrix}$$
Tính từng phần tử:
- $\nabla_{\text{ReLU}_1} L = (0.5 \times -0.533) + (0.3 \times 0.355) + (-0.2 \times 0.178) = -0.267 + 0.107 - 0.036 = -0.196$
- $\nabla_{\text{ReLU}_2} L = (-0.1 \times -0.533) + (0.4 \times 0.355) + (0.6 \times 0.178) = 0.053 + 0.142 + 0.107 = 0.302$
Vậy: $\nabla_{\text{ReLU}} L = [-0.196, 0.302]$
3. Tính $\nabla_h L$ (Gradient trước ReLU) - Đây là điểm xảy ra vấn đề Dying ReLU:
Ta sử dụng đạo hàm của ReLU:
$$\frac{\partial L}{\partial h_j} = \frac{\partial L}{\partial \text{ReLU}_j} \times \text{ReLU}'(h_j)$$
- Đối với node $h_1$ (sống): $h_1 = 1.372 > 0$, nên $\text{ReLU}'(h_1) = 1$
$$\frac{\partial L}{\partial h_1} = \nabla_{\text{ReLU}_1} L \times 1 = -0.196 \times 1 = -0.196$$
- Đối với node $h_2$ (chết): $h_2 = -1.69 \leq 0$, nên $\text{ReLU}'(h_2) = 0$
$$\frac{\partial L}{\partial h_2} = \nabla_{\text{ReLU}_2} L \times 0 = 0.302 \times 0 = 0.0$$
Kết quả quan trọng: Gradient của node $h_2$ bằng 0, mặc dù gradient từ lớp sau ($\nabla_{\text{ReLU}_2} L = 0.302$) không phải là 0!
4. Tính $\nabla_M L$ (Gradient của trọng số lớp ẩn):
Gradient của trọng số được tính dựa trên $\nabla_h L$ và đầu vào $x$:
$$\nabla_M L = x^T \times \nabla_h L = \begin{bmatrix} 1.0 \\ 1.5 \\ 0.2 \end{bmatrix} \times [-0.196, 0.0]$$
Tính từng phần tử:
Cột 1 (kết nối với $h_1$ - node sống):
- $\frac{\partial L}{\partial m_{11}} = 1.0 \times -0.196 = -0.196$
- $\frac{\partial L}{\partial m_{21}} = 1.5 \times -0.196 = -0.294$
- $\frac{\partial L}{\partial m_{31}} = 0.2 \times -0.196 = -0.039$
Cột 2 (kết nối với $h_2$ - node chết):
- $\frac{\partial L}{\partial m_{12}} = 1.0 \times 0.0 = 0.0$
- $\frac{\partial L}{\partial m_{22}} = 1.5 \times 0.0 = 0.0$
- $\frac{\partial L}{\partial m_{32}} = 0.2 \times 0.0 = 0.0$
Vậy ma trận gradient:
$$\nabla_M L = \begin{bmatrix} -0.196 & 0.0 \\ -0.294 & 0.0 \\ -0.039 & 0.0 \end{bmatrix}$$
Kết luận Dying ReLU:
Do gradient cho các trọng số dẫn đến node $h_2$ bằng 0, những trọng số đó sẽ không bao giờ được cập nhật:
- Nếu learning rate là $\eta = 0.01$, thì cập nhật trọng số:
- $\Delta m_{12} = -\eta \times 0.0 = 0.0$
- $\Delta m_{22} = -\eta \times 0.0 = 0.0$
- $\Delta m_{32} = -\eta \times 0.0 = 0.0$
Node $h_2$ mãi mãi nằm trong vùng âm khi lan truyền thuận (vì trọng số không thay đổi), và mãi mãi có gradient bằng 0 khi lan truyền ngược. Node này đã "chết" và không còn đóng góp vào quá trình học của mô hình.
Tóm Lược và Giải Pháp Khắc Phục
Sau khi hiểu rõ cơ chế của hai vấn đề này, mình đã tổng hợp lại bảng so sánh và giải pháp:
| Vấn đề | Hàm kích hoạt liên quan | Nguyên nhân cơ chế | Đạo hàm (Max) | Giải pháp gợi ý |
|---|---|---|---|---|
| Gradient Vanishing | Sigmoid, Tanh | Đạo hàm rất nhỏ khi bị bão hòa (Saturation) | Sigmoid: 0.25 Tanh: 1.0 |
Dùng ReLU, GELU, SWISH, Skip Connection |
| Dying ReLU | ReLU | Đầu vào pre-activation âm ($\leq 0$), khiến đạo hàm bằng 0 | ReLU: 1 (khi $x > 0$) 0 (khi $x \leq 0$) |
Dùng LeakyReLU, PReLU, ELU (cho đạo hàm nhỏ hơn 0.01)) |
3. Vấn đề Zero Initialization (Khởi tạo bằng 0) - Tại sao MLP không thể khởi tạo bằng 0?
Khi mới bắt đầu học deep learning, mình đã từng thắc mắc: "Tại sao Linear Regression có thể khởi tạo trọng số bằng 0, nhưng MLP thì không?" Câu trả lời nằm ở vấn đề Symmetry Problem (Vấn đề Đối xứng). Hãy cùng mình chứng minh điều này qua các ví dụ tính toán cụ thể.
3.1. Tại sao Linear Regression có thể khởi tạo bằng 0?
Mô hình Linear Regression:
$$\hat{y} = w_1x_1 + w_2x_2 + w_3x_3 + b$$
Loss Function (MSE):
$$L = \frac{1}{2}(\hat{y} - y)^2$$
Gradient:
$$\frac{\partial L}{\partial w_1} = (\hat{y} - y) \times x_1$$
$$\frac{\partial L}{\partial w_2} = (\hat{y} - y) \times x_2$$
$$\frac{\partial L}{\partial w_3} = (\hat{y} - y) \times x_3$$
$$\frac{\partial L}{\partial b} = (\hat{y} - y)$$
Ví dụ tính toán với khởi tạo bằng 0:
- Đầu vào: $x = [2.0, 3.0, 1.0]$
- Nhãn thực tế: $y = 5.0$
- Khởi tạo: $w_1 = 0, w_2 = 0, w_3 = 0, b = 0$
Forward pass:
$$\hat{y} = 0 \times 2.0 + 0 \times 3.0 + 0 \times 1.0 + 0 = 0$$
Backward pass:
- $\frac{\partial L}{\partial w_1} = (0 - 5.0) \times 2.0 = -10.0$
- $\frac{\partial L}{\partial w_2} = (0 - 5.0) \times 3.0 = -15.0$
- $\frac{\partial L}{\partial w_3} = (0 - 5.0) \times 1.0 = -5.0$
- $\frac{\partial L}{\partial b} = (0 - 5.0) = -5.0$
Cập nhật (learning rate $\eta = 0.01$):
- $w_1 = 0 - 0.01 \times (-10.0) = 0.1$
- $w_2 = 0 - 0.01 \times (-15.0) = 0.15$
- $w_3 = 0 - 0.01 \times (-5.0) = 0.05$
- $b = 0 - 0.01 \times (-5.0) = 0.05$
Kết luận: Mỗi trọng số nhận được gradient khác nhau dựa trên giá trị đầu vào tương ứng ($x_1, x_2, x_3$). Do đó, chúng sẽ được cập nhật theo các hướng khác nhau và mô hình có thể học được.
3.2. Tại sao Logistic Regression có thể khởi tạo bằng 0?
Mô hình Logistic Regression:
$$\hat{y} = \sigma(w_1x_1 + w_2x_2 + b) = \frac{1}{1 + e^{-(w_1x_1 + w_2x_2 + b)}}$$
Loss Function (Cross-Entropy):
$$L = -[y \log(\hat{y}) + (1-y) \log(1-\hat{y})]$$
Gradient:
$$\frac{\partial L}{\partial w_1} = (\hat{y} - y) \times x_1$$
$$\frac{\partial L}{\partial w_2} = (\hat{y} - y) \times x_2$$
$$\frac{\partial L}{\partial b} = (\hat{y} - y)$$
Ví dụ tính toán với khởi tạo bằng 0:
- Đầu vào: $x = [1.5, 2.0]$
- Nhãn thực tế: $y = 1$
- Khởi tạo: $w_1 = 0, w_2 = 0, b = 0$
Forward pass:
- $z = 0 \times 1.5 + 0 \times 2.0 + 0 = 0$
- $\hat{y} = \sigma(0) = \frac{1}{1 + e^0} = 0.5$
Backward pass:
- $\frac{\partial L}{\partial w_1} = (0.5 - 1) \times 1.5 = -0.75$
- $\frac{\partial L}{\partial w_2} = (0.5 - 1) \times 2.0 = -1.0$
- $\frac{\partial L}{\partial b} = (0.5 - 1) = -0.5$
Cập nhật (learning rate $\eta = 0.01$):
- $w_1 = 0 - 0.01 \times (-0.75) = 0.0075$
- $w_2 = 0 - 0.01 \times (-1.0) = 0.01$
- $b = 0 - 0.01 \times (-0.5) = 0.005$
Kết luận: Tương tự Linear Regression, mỗi trọng số nhận được gradient khác nhau và có thể học được.
3.3. Tại sao Softmax Regression có thể khởi tạo bằng 0?
Mô hình Softmax Regression (3 classes):
$$z_1 = w_{11}x_1 + w_{12}x_2 + b_1$$
$$z_2 = w_{21}x_1 + w_{22}x_2 + b_2$$
$$z_3 = w_{31}x_1 + w_{32}x_2 + b_3$$
$$\hat{y}_1 = \frac{e^{z_1}}{e^{z_1} + e^{z_2} + e^{z_3}}$$
$$\hat{y}_2 = \frac{e^{z_2}}{e^{z_1} + e^{z_2} + e^{z_3}}$$
$$\hat{y}_3 = \frac{e^{z_3}}{e^{z_1} + e^{z_2} + e^{z_3}}$$
Ví dụ tính toán với khởi tạo bằng 0:
- Đầu vào: $x = [1.0, 2.0]$
- Nhãn thực tế: $y = [1, 0, 0]$ (one-hot)
- Khởi tạo: Tất cả $w_{ij} = 0$, $b_i = 0$
Forward pass:
- $z_1 = 0 \times 1.0 + 0 \times 2.0 + 0 = 0$
- $z_2 = 0 \times 1.0 + 0 \times 2.0 + 0 = 0$
- $z_3 = 0 \times 1.0 + 0 \times 2.0 + 0 = 0$
- $\hat{y}_1 = \frac{e^0}{e^0 + e^0 + e^0} = \frac{1}{3} = 0.333$
- $\hat{y}_2 = \frac{1}{3} = 0.333$
- $\hat{y}_3 = \frac{1}{3} = 0.333$
Backward pass (Cross-Entropy Loss):
$$\frac{\partial L}{\partial z_i} = \hat{y}_i - y_i$$
- $\frac{\partial L}{\partial z_1} = 0.333 - 1 = -0.667$
- $\frac{\partial L}{\partial z_2} = 0.333 - 0 = 0.333$
- $\frac{\partial L}{\partial z_3} = 0.333 - 0 = 0.333$
Gradient cho trọng số:
- $\frac{\partial L}{\partial w_{11}} = \frac{\partial L}{\partial z_1} \times x_1 = -0.667 \times 1.0 = -0.667$
- $\frac{\partial L}{\partial w_{12}} = \frac{\partial L}{\partial z_1} \times x_2 = -0.667 \times 2.0 = -1.334$
- $\frac{\partial L}{\partial w_{21}} = 0.333 \times 1.0 = 0.333$
- $\frac{\partial L}{\partial w_{22}} = 0.333 \times 2.0 = 0.666$
- $\frac{\partial L}{\partial w_{31}} = 0.333 \times 1.0 = 0.333$
- $\frac{\partial L}{\partial w_{32}} = 0.333 \times 2.0 = 0.666$
Kết luận: Mặc dù tất cả $z_i$ ban đầu bằng nhau (dẫn đến $\hat{y}_i$ bằng nhau), nhưng gradient cho mỗi lớp khác nhau dựa trên nhãn thực tế. Do đó, các trọng số sẽ được cập nhật khác nhau và mô hình có thể học được.
3.4. Tại sao MLP KHÔNG THỂ khởi tạo bằng 0? - Vấn đề Đối xứng
Bây giờ, hãy xem điều gì xảy ra với MLP khi khởi tạo bằng 0.
Cấu hình Mô hình:
- Lớp đầu vào: 2 features ($x_1$, $x_2$) + 1 bias
- Lớp ẩn: 2 neurons ($h_1, h_2$) sử dụng ReLU
- Lớp đầu ra: 3 neurons ($z_1$, $z_2$, $z_3$) sử dụng Softmax
Dữ liệu đầu vào (3 samples):
$$x = \begin{bmatrix} x_1^{(1)} & x_2^{(1)} \\ x_1^{(2)} & x_2^{(2)} \\ x_1^{(3)} & x_2^{(3)} \end{bmatrix} = \begin{bmatrix} 1.5 & 0.2 \\ 4.7 & 1.6 \\ 5.6 & 2.2 \end{bmatrix}$$
Sau khi thêm bias (augment với cột 1 ở đầu): $[1, x_1, x_2]$ cho mỗi sample
Nhãn thực tế (one-hot encoding):
$$y = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$
(Sample 1 thuộc class 0, Sample 2 thuộc class 1, Sample 3 thuộc class 2)
Trọng số khởi tạo bằng 0:
Ma trận trọng số lớp ẩn $M$ (kích thước $3 \times 2$, bao gồm bias ở hàng đầu tiên):
$$M = \begin{bmatrix} bm_1 & bm_2 \\ m_{11} & m_{12} \\ m_{21} & m_{22} \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 \\ 0.0 & 0.0 \\ 0.0 & 0.0 \end{bmatrix}$$
Ma trận trọng số lớp đầu ra $W$ (kích thước $2 \times 3$, không bao gồm bias - bias được thêm riêng):
$$W = \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 \end{bmatrix}$$
Bias cho lớp đầu ra: $bw = [bw_1, bw_2, bw_3] = [0.0, 0.0, 0.0]$
Bước 1: Lan truyền thuận (Forward Propagation)
1. Tính toán đầu vào cho lớp ẩn (pre-activation):
Với mỗi sample, ta tính $h = [1, x_1, x_2] \times M$. Vì tất cả trọng số trong $M$ đều bằng 0, kết quả cho cả 3 samples là:
$$h = \begin{bmatrix} h_1^{(1)} & h_2^{(1)} \\ h_1^{(2)} & h_2^{(2)} \\ h_1^{(3)} & h_2^{(3)} \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 \\ 0.0 & 0.0 \\ 0.0 & 0.0 \end{bmatrix}$$
Tính chi tiết cho sample 1:
- $h_1^{(1)} = 1 \times 0.0 + 1.5 \times 0.0 + 0.2 \times 0.0 = 0.0$
- $h_2^{(1)} = 1 \times 0.0 + 1.5 \times 0.0 + 0.2 \times 0.0 = 0.0$
Tương tự, tất cả các samples đều có $h = [0.0, 0.0]$
2. Áp dụng ReLU:
$$\text{ReLU}(h) = \begin{bmatrix} \max(0, 0.0) & \max(0, 0.0) \\ \max(0, 0.0) & \max(0, 0.0) \\ \max(0, 0.0) & \max(0, 0.0) \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 \\ 0.0 & 0.0 \\ 0.0 & 0.0 \end{bmatrix}$$
Kết quả quan trọng: Tất cả neurons trong tất cả samples đều có đầu ra bằng 0!
3. Lan truyền đến lớp đầu ra (pre-activation):
Với mỗi sample: $z = \text{ReLU}(h) \times W + bw$. Vì $\text{ReLU}(h)$, $W$, và $bw$ đều bằng 0:
$$z = \begin{bmatrix} z_1^{(1)} & z_2^{(1)} & z_3^{(1)} \\ z_1^{(2)} & z_2^{(2)} & z_3^{(2)} \\ z_1^{(3)} & z_2^{(3)} & z_3^{(3)} \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 \end{bmatrix}$$
Tính chi tiết cho sample 1:
- $z_1^{(1)} = (0.0 \times 0.0) + (0.0 \times 0.0) + 0.0 = 0.0$
- $z_2^{(1)} = (0.0 \times 0.0) + (0.0 \times 0.0) + 0.0 = 0.0$
- $z_3^{(1)} = (0.0 \times 0.0) + (0.0 \times 0.0) + 0.0 = 0.0$
4. Áp dụng Softmax:
Vì tất cả $z_i$ đều bằng 0 cho mỗi sample, Softmax sẽ cho xác suất đồng đều:
$$\hat{y} = \begin{bmatrix} \hat{y}_1^{(1)} & \hat{y}_2^{(1)} & \hat{y}_3^{(1)} \\ \hat{y}_1^{(2)} & \hat{y}_2^{(2)} & \hat{y}_3^{(2)} \\ \hat{y}_1^{(3)} & \hat{y}_2^{(3)} & \hat{y}_3^{(3)} \end{bmatrix} = \begin{bmatrix} 0.333 & 0.333 & 0.333 \\ 0.333 & 0.333 & 0.333 \\ 0.333 & 0.333 & 0.333 \end{bmatrix}$$
5. Tính Loss (Cross-Entropy):
Với công thức $L = -\sum_i y_i \log(\hat{y}_i)$, loss cho mỗi sample là:
$$L = \begin{bmatrix} -\log(0.333) \\ -\log(0.333) \\ -\log(0.333) \end{bmatrix}$$
Mô hình dự đoán mọi sample với xác suất bằng nhau cho mỗi lớp, bất kể nhãn thực tế!
Bước 2: Lan truyền ngược (Backward Propagation) - Vấn đề Đối xứng xuất hiện
1. Tính $\nabla_z L$ (Gradient lớp đầu ra):
Với Cross-Entropy Loss và Softmax, gradient cho mỗi sample: $\nabla_z L = \hat{y} - y$
$$\nabla_z L = \begin{bmatrix} \nabla_{z_1}^{(1)} & \nabla_{z_2}^{(1)} & \nabla_{z_3}^{(1)} \\ \nabla_{z_1}^{(2)} & \nabla_{z_2}^{(2)} & \nabla_{z_3}^{(2)} \\ \nabla_{z_1}^{(3)} & \nabla_{z_2}^{(3)} & \nabla_{z_3}^{(3)} \end{bmatrix} = \begin{bmatrix} 0.333 & 0.333 & 0.333 \\ 0.333 & 0.333 & 0.333 \\ 0.333 & 0.333 & 0.333 \end{bmatrix} - \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} -0.667 & 0.333 & 0.333 \\ 0.333 & -0.667 & 0.333 \\ 0.333 & 0.333 & -0.667 \end{bmatrix}$$
2. Tính $\nabla_{W} L$ (Gradient trọng số lớp đầu ra):
Gradient được tính bằng tổng gradient từ tất cả samples. Vì $\text{ReLU}(h)$ cho tất cả samples đều bằng 0:
$$\nabla_{W} L = \sum_{i=1}^{3} \text{ReLU}(h^{(i)})^T \times \nabla_z^{(i)} L = \begin{bmatrix} 0.0 \\ 0.0 \end{bmatrix} \times (\text{tổng các gradient}) = \begin{bmatrix} 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 \end{bmatrix}$$
Tính chi tiết:
- $\frac{\partial L}{\partial w_{11}} = 0.0 \times (-0.667) + 0.0 \times 0.333 + 0.0 \times 0.333 = 0.0$
- $\frac{\partial L}{\partial w_{12}} = 0.0 \times 0.333 + 0.0 \times (-0.667) + 0.0 \times 0.333 = 0.0$
- Tương tự, tất cả gradient của $W$ đều bằng 0.0
3. Tính $\nabla_{\text{ReLU}} L$ (Gradient sau ReLU):
Vì $W$ cũng bằng 0, gradient sau ReLU cho tất cả samples:
$$\nabla_{\text{ReLU}} L = W^T \times \nabla_z L = \begin{bmatrix} 0.0 & 0.0 \\ 0.0 & 0.0 \\ 0.0 & 0.0 \end{bmatrix} \times \nabla_z L = \begin{bmatrix} 0.0 & 0.0 \\ 0.0 & 0.0 \\ 0.0 & 0.0 \end{bmatrix}$$
4. Tính $\nabla_h L$ (Gradient trước ReLU):
Vì tất cả $h$ đều bằng 0.0, và ReLU'(0) = 0:
$$\frac{\partial L}{\partial h_j} = \nabla_{\text{ReLU}_j} L \times \text{ReLU}'(0) = 0.0 \times 0 = 0.0$$
Cho tất cả samples và tất cả neurons:
$$
\nabla_h L =
\begin{bmatrix}
0.0 & 0.0 \\
0.0 & 0.0 \\
0.0 & 0.0
\end{bmatrix}
$$
5. Tính $\nabla_M L$ (Gradient trọng số lớp ẩn):
Gradient được tính bằng tổng gradient từ tất cả samples:
$$\nabla_M L = \sum_{i=1}^{3} [1, x_1^{(i)}, x_2^{(i)}]^T \times \nabla_h^{(i)} L$$
Vì tất cả $\nabla_h^{(i)} L = [0.0, 0.0]$, nên:
$$\nabla_M L = \begin{bmatrix} 0.0 & 0.0 \\ 0.0 & 0.0 \\ 0.0 & 0.0 \end{bmatrix}$$
Kết quả thảm họa:
Tất cả gradient đều bằng 0 cho tất cả samples! Điều này có nghĩa là:
- Tất cả trọng số sẽ không được cập nhật: $\Delta w = -\eta \times 0 = 0$ cho mọi trọng số
- Tất cả neurons trong lớp ẩn sẽ mãi mãi có cùng giá trị (0.0) cho mọi sample
- Chúng sẽ nhận được cùng gradient (0.0) trong mọi lần cập nhật, bất kể dữ liệu đầu vào là gì
- Mạng sẽ không bao giờ học được gì! Mô hình sẽ mãi mãi dự đoán xác suất đồng đều [0.333, 0.333, 0.333] cho mọi sample
Vấn đề đối xứng: Tất cả neurons trong cùng một lớp ẩn đều có cùng giá trị (0.0) và nhận cùng gradient (0.0), khiến chúng không thể phân biệt và học các đặc trưng khác nhau. Đây chính là Symmetry Problem - vấn đề đối xứng khi khởi tạo bằng 0.
Lời Kết
Deep learning không phải là "magic" - mỗi vấn đề đều có nguyên nhân toán học rõ ràng. Bằng cách hiểu sâu các cơ chế này, chúng ta có thể xây dựng những mô hình mạnh mẽ và hiệu quả hơn.
Hy vọng bài viết này giúp các bạn hiểu rõ hơn về ba vấn đề "kinh điển" này và cách khắc phục chúng. Nếu có câu hỏi hoặc muốn thảo luận thêm, đừng ngần ngại để lại comment nhé!
Happy learning! 🚀
References
[1] Ảnh được lấy từ slide Insight into Multi-layer Perceptron, AIO Module 06 – Tuần 3, AIO 2025, Dr. Quang Vinh.
Chưa có bình luận nào. Hãy là người đầu tiên!