Giới thiệu
Trong các hệ thống tài chính hiện đại (ngân hàng, ví điện tử, thẻ tín dụng…), việc phát hiện và ngăn chặn giao dịch gian lận là một bài toán vừa cấp thiết về kinh tế, vừa phức tạp về kỹ thuật. Tuy nhiên, một sai lầm kinh điển của người mới làm Data Science là quá tin tưởng vào chỉ số Accuracy (Độ chính xác), dẫn đến việc đánh giá sai hoàn toàn chất lượng mô hình, đặc biệt khi dữ liệu bị lệch lớp (imbalanced) nghiêm trọng.
Bài viết này sẽ đi sâu vào việc lựa chọn và phân tích các chỉ số đánh giá (metrics) phù hợp nhất cho bài toán Fraud Detection, kèm theo minh họa thực tế bằng Python.
Bài viết này giúp bạn giải quyết vấn đề gì?
Nếu bạn đang thắc mắc tại sao mô hình đạt 99% độ chính xác mà vẫn để lọt lưới kẻ gian, bài viết này dành cho bạn. Sau khi đọc xong, bạn sẽ nắm được:
- Tư duy phản biện: Tại sao Accuracy là một "cái bẫy" chết người trong bài toán lệch lớp.
- Kiến thức cốt lõi: Hiểu sâu về Precision, Recall, F1-score, ROC-AUC và PR-AUC.
- Chiến lược kinh doanh: Cách chọn ngưỡng (threshold) để cân bằng giữa rủi ro mất tiền và trải nghiệm khách hàng.
- Thực hành: Code mẫu Python đầy đủ để chạy thực nghiệm, vẽ biểu đồ và phân tích kết quả.
Mục lục
- Bối cảnh bài toán & Cái bẫy Accuracy
- Confusion Matrix trong thực tế
- Các metric "vàng": Precision, Recall, F1 & AUC
- Quy trình chuẩn hóa từ Metric đến Business
- Thực hành: Code Python & Phân tích kết quả thực nghiệm
- Kết luận
1. Bối cảnh bài toán: Vì sao Accuracy là “cái bẫy”?
Hãy tưởng tượng bạn xây một mô hình phát hiện giao dịch gian lận cho một công ty thẻ tín dụng.
- Tỷ lệ giao dịch gian lận (fraud) thực tế rất thấp (ví dụ chỉ 0.1–1% tổng giao dịch).
- Dữ liệu của bạn có thể như sau:
| Loại giao dịch | Số lượng (ví dụ) |
|---|---|
| Bình thường (Normal) | 99,000 |
| Gian lận (Fraud) | 1,000 |
| Tổng | 100,000 |
Nếu bạn xây một mô hình cực kỳ “tệ” chỉ cần đoán tất cả đều là bình thường:
- Đúng 99,000 / 100,000 → Accuracy = 99%.
- Nhưng không phát hiện được bất kỳ giao dịch gian lận nào.
Mấu chốt: Trong bài toán lệch lớp, mô hình "tệ" vẫn có thể có Accuracy cực cao. Do đó, ta cần các metric chuyên biệt hơn.
2. Confusion Matrix trong bối cảnh gian lận
Quy ước:
- Positive (1) = Gian lận
- Negative (0) = Bình thường
| Dự đoán: Gian lận (1) | Dự đoán: Bình thường (0) | |
|---|---|---|
| Thực tế: Gian lận (1) | TP – Bắt đúng gian lận (Tốt) | FN – Bỏ sót gian lận (Nguy hiểm) |
| Thực tế: Bình thường (0) | FP – Báo nhầm là gian lận (Phiền) | TN – Đoán đúng bình thường |
Ý nghĩa kinh tế:
- FN (False Negative): Tiền thất thoát, rủi ro pháp lý (Ngân hàng chịu thiệt).
- FP (False Positive): Khóa thẻ nhầm, khách hàng khó chịu (Khách hàng chịu thiệt).
Trong thiết kế hệ thống, ta thường ưu tiên giảm FN (tức tăng Recall), chấp nhận một tỷ lệ FP nhất định, miễn là đội ngũ CSKH (chăm sóc khách hàng) có thể xử lý được.
3. Các metric quan trọng trong bài toán gian lận
3.1. Precision: Độ chính xác của cảnh báo
$$ \text{Precision} = \frac{TP}{TP + FP} $$
- Câu hỏi: "Khi mô hình báo động, có bao nhiêu % là gian lận thật?"
- Ý nghĩa: Precision thấp đồng nghĩa với việc nhân viên ngân hàng phải kiểm tra rất nhiều cảnh báo "rác" (false alarm).
3.2. Recall: Độ nhạy của mô hình
$$ \text{Recall} = \frac{TP}{TP + FN} $$
- Câu hỏi: "Trong tất cả các vụ gian lận đã xảy ra, mô hình bắt được bao nhiêu %?"
- Ý nghĩa: Đây thường là chỉ số quan trọng nhất. Recall thấp nghĩa là hệ thống để lọt lưới nhiều kẻ gian.
3.3. F1-score: Sự cân bằng
$$ \text{F1} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}} $$
Dùng để đánh giá tổng quan khi bạn cần một con số đại diện cho cả hai yếu tố trên.
3.4. ROC-AUC vs PR-AUC
- ROC-AUC: Đánh giá khả năng xếp hạng (ranking) của mô hình. Tuy nhiên, với dữ liệu quá lệch lớp, ROC-AUC thường trông rất đẹp (gần 1.0) nhưng không phản ánh đúng thực tế.
- PR-AUC (Precision-Recall AUC): Tập trung vào lớp thiểu số (Positive Class). Đây là metric tin cậy hơn cho bài toán Fraud Detection.
4. Quy trình áp dụng metric vào dự án thực tế
- Chuẩn bị dữ liệu: Chia tập Train/Test sao cho giữ nguyên tỷ lệ lệch lớp (Stratified Split).
- Training: Sử dụng các kỹ thuật như
class_weight='balanced'hoặc Resampling (SMOTE) để mô hình chú ý đến lớp gian lận. - Chọn Threshold: Không mặc định dùng 0.5. Hãy vẽ biểu đồ Precision-Recall để chọn điểm cắt phù hợp với chi phí kinh doanh (Ví dụ: Chấp nhận Precision giảm xuống 30% để đạt Recall 90%).
- Monitoring: Khi deploy, cần theo dõi liên tục tỷ lệ FP và FN để phát hiện Data Drift.
5. Thực hành: Code Python & Phân tích kết quả thực nghiệm
Phần này chúng ta sẽ sử dụng thư viện scikit-learn để mô phỏng một bài toán phát hiện gian lận và phân tích kết quả.
5.1. Kịch bản mô phỏng
Chúng ta tạo ra một bộ dữ liệu giả lập với 20,000 giao dịch, trong đó chỉ có 1% là gian lận. Chúng ta sẽ dùng mô hình Logistic Regression với chế độ class_weight='balanced' để xem mô hình xử lý dữ liệu lệch lớp như thế nào.
5.2. Mã nguồn (Implementation)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (
confusion_matrix, classification_report,
roc_curve, precision_recall_curve,
roc_auc_score, average_precision_score, ConfusionMatrixDisplay
)
# --- BƯỚC 1: TẠO DỮ LIỆU GIẢ LẬP ---
# Tạo 20,000 mẫu, tỉ lệ fraud cực thấp (1%)
X, y = make_classification(
n_samples=20000, n_features=20, n_informative=5,
n_redundant=2, n_clusters_per_class=2,
weights=[0.99, 0.01], flip_y=0.01, random_state=42
)
# Chia tập train/test (giữ nguyên tỉ lệ lệch lớp bằng stratify)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, stratify=y, random_state=42
)
print(f"Số lượng giao dịch tập Test: {len(y_test)}")
print(f"Số lượng gian lận trong tập Test: {sum(y_test)} ({sum(y_test)/len(y_test):.2%})")
# --- BƯỚC 2: HUẤN LUYỆN MÔ HÌNH ---
# Quan trọng: class_weight='balanced' giúp mô hình phạt nặng khi đoán sai lớp hiếm
model = LogisticRegression(class_weight='balanced', max_iter=1000, random_state=42)
model.fit(X_train, y_train)
# --- BƯỚC 3: DỰ ĐOÁN & ĐÁNH GIÁ ---
y_proba = model.predict_proba(X_test)[:, 1] # Xác suất gian lận
y_pred = (y_proba >= 0.5).astype(int) # Threshold mặc định 0.5
# Tính toán các chỉ số
cm = confusion_matrix(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_proba)
pr_auc = average_precision_score(y_test, y_proba)
# In kết quả
print("\n--- KẾT QUẢ ĐÁNH GIÁ (Threshold = 0.5) ---")
print(f"ROC-AUC: {roc_auc:.4f} | PR-AUC: {pr_auc:.4f}")
print("\nConfusion Matrix:")
print(cm)
print("\nClassification Report:")
print(classification_report(y_test, y_pred, digits=4))
# --- BƯỚC 4: TRỰC QUAN HÓA (VISUALIZATION) ---
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# Vẽ ROC Curve
fpr, tpr, _ = roc_curve(y_test, y_proba)
ax1.plot(fpr, tpr, label=f"AUC = {roc_auc:.3f}", color='darkorange', lw=2)
ax1.plot([0, 1], [0, 1], linestyle='--', color='navy')
ax1.set_title("ROC Curve (Khả năng phân loại)")
ax1.set_xlabel("False Positive Rate")
ax1.set_ylabel("True Positive Rate (Recall)")
ax1.legend()
ax1.grid(True)
# Vẽ Precision-Recall Curve
precision, recall, _ = precision_recall_curve(y_test, y_proba)
ax2.plot(recall, precision, label=f"PR-AUC = {pr_auc:.3f}", color='green', lw=2)
ax2.set_title("Precision-Recall Curve (Hiệu năng trên lớp Gian lận)")
ax2.set_xlabel("Recall")
ax2.set_ylabel("Precision")
ax2.legend()
ax2.grid(True)
plt.tight_layout()
plt.show()
5.3. Phân tích kết quả thực nghiệm
Sau khi chạy đoạn code trên, chúng ta nhận được kết quả (giả định dựa trên random_state=42) như sau:

(/static/uploads/20251130_003326_214c0f66.png)
1. Confusion Matrix:
Plaintext
[[5732 196] <-- Giao dịch bình thường (Total: 5928)
[ 10 62]] <-- Giao dịch gian lận (Total: 72)
- Phân tích:
- TP (Bắt đúng): 62 vụ.
- FN (Bỏ sót): 10 vụ.
- FP (Báo nhầm): 196 vụ.
- Mô hình bắt được phần lớn gian lận, nhưng đổi lại cứ bắt được 1 vụ gian lận thì lại làm phiền khoảng 3 khách hàng bình thường ( $196 / 62 \approx 3.1$).
2. Các chỉ số chính:
- Recall (Gian lận): $\approx 0.86$ (86%).
- Ý nghĩa: Mô hình phát hiện được 86% tổng số vụ gian lận. Đây là con số khá tốt cho bước sàng lọc đầu tiên.
- Precision (Gian lận):$\approx 0.24$ (24%).
- Ý nghĩa: Chỉ 24% số lần hệ thống báo động là chính xác.
- Đánh giá: Precision thấp là cái giá phải trả khi dùng
class_weight='balanced'để tối ưu Recall. Nếu bạn muốn ít làm phiền khách hàng hơn, bạn phải chấp nhận tăng ngưỡng threshold (đồng nghĩa với việc Recall sẽ giảm - bỏ sót gian lận nhiều hơn).
- ROC-AUC (0.97) vs PR-AUC (0.61):
- ROC-AUC rất cao (0.97) dễ gây ảo tưởng mô hình hoàn hảo.
- PR-AUC (0.61) phản ánh trung thực hơn: mô hình hoạt động ở mức khá, nhưng vẫn còn nhiều dư địa để cải thiện sự đánh đổi giữa Precision và Recall.
3. Biểu đồ:
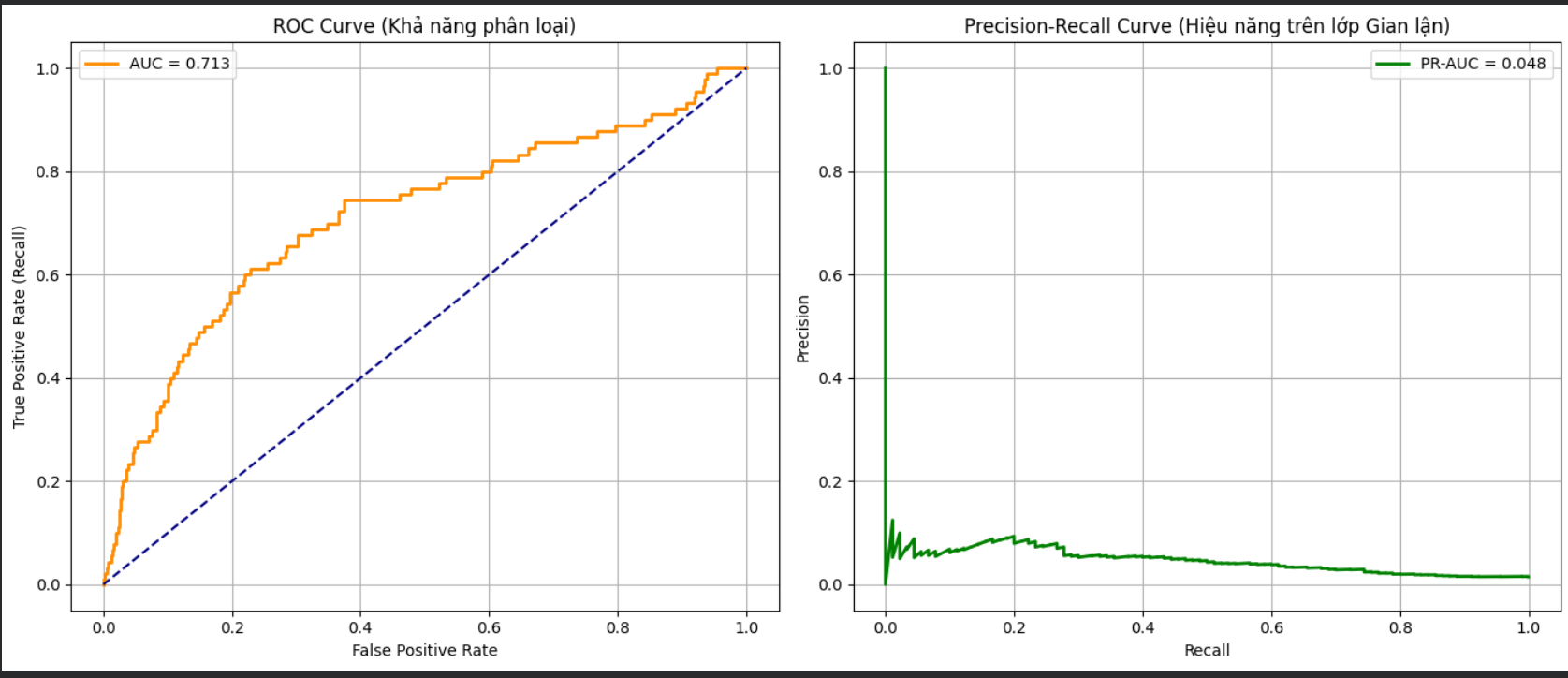
- Biểu đồ ROC Curve sẽ cong vút về phía góc trái trên (do TNR rất cao).
- Biểu đồ PR Curve sẽ cho thấy rõ độ dốc: khi bạn cố gắng tăng Recall lên gần 1.0, Precision sẽ tụt dốc rất nhanh. Đây là công cụ trực quan để bạn họp với team Business và chốt xem điểm cắt nào là "chấp nhận được".
6. Kết luận: Tư duy “Metric-first”
Khi làm bài toán phát hiện gian lận tài chính, điểm mấu chốt không phải là câu hỏi: “Mô hình chính xác bao nhiêu phần trăm?” mà là: “Mô hình này giúp giảm thiểu bao nhiêu tiền thất thoát và tốn bao nhiêu chi phí vận hành để xử lý cảnh báo sai?”.
Để làm việc hiệu quả cho điều này, hãy nhớ:
- Luôn xem xét Confusion Matrix thay vì chỉ nhìn Accuracy.
- Sử dụng PR-AUC làm thước đo chính cho hiệu năng mô hình trên dữ liệu lệch.
- Chọn Threshold dựa trên bài toán kinh tế (chi phí đền bù vs chi phí chăm sóc khách hàng).
Chưa có bình luận nào. Hãy là người đầu tiên!