Giới thiệu
Trong thế giới học máy, một câu hỏi trung tâm mà nhiều người mới bắt đầu đặt ra là: "Tại sao chúng ta cần một framework như PyTorch khi đã có NumPy?" Câu trả lời không chỉ nằm ở khía cạnh kỹ thuật, mà còn phản ánh một sự thay đổi sâu sắc trong ngành. Ngày nay, khoảng cách giữa nghiên cứu (research) và kỹ thuật (engineering) đang dần bị xóa nhòa. Các công ty lớn và ngay cả những startup cạnh tranh nhất không còn tìm kiếm những kỹ sư chỉ biết triển khai mô hình. Yêu cầu tuyển dụng ngày càng khắt khe: để được nhận vào, ứng viên bắt buộc phải có ít nhất một bài báo khoa học đầu ngành (ít nhất một bài paper đầu ngành). Đây là tiêu chuẩn để xây dựng những sản phẩm đẳng cấp thế giới. Trong bối cảnh đó, việc chỉ học "bề mặt" của công cụ là một yếu tố giới hạn sự nghiệp; chúng ta không thể đi xa nếu không hiểu sâu sắc các nguyên lý nền tảng.
Đây chính là lúc PyTorch thể hiện sức mạnh vượt trội. Về bản chất, cú pháp của PyTorch rất tương đồng với NumPy, nhưng nó sở hữu một lợi thế cốt lõi không thể thay thế: khả năng thực thi các phép tính song song trên bộ xử lý đồ họa (GPU). Trong khi NumPy được thiết kế để chạy trên CPU, PyTorch được tối ưu hóa cho GPU, cho phép chúng ta huấn luyện các mô hình học sâu khổng lồ với tốc độ nhanh hơn gấp nhiều lần. Đây là yếu tố then chốt giúp biến những ý tưởng nghiên cứu phức tạp thành các sản phẩm thực tế.
Bài viết này sẽ là một hành trình từng bước, dẫn dắt bạn từ những khái niệm cơ bản nhất của PyTorch đến việc xây dựng các mô hình học máy hoàn chỉnh. Chúng ta sẽ bắt đầu với các khối xây dựng nền tảng, sau đó áp dụng chúng để giải quyết các bài toán từ hồi quy tuyến tính, hồi quy logistic, và cuối cùng là xây dựng mạng nơ-ron đầu tiên để phân loại hình ảnh.
1. Nền tảng PyTorch: Làm quen với Tensor
Tensor là khối xây dựng cơ bản trong PyTorch, tương tự như array trong NumPy, nhưng được trang bị thêm "siêu năng lực" để có thể hoạt động hiệu quả trên GPU. Việc nắm vững cách tạo và thao tác với Tensor là bước đệm quan trọng nhất để làm chủ PyTorch.
Cách tạo một Tensor
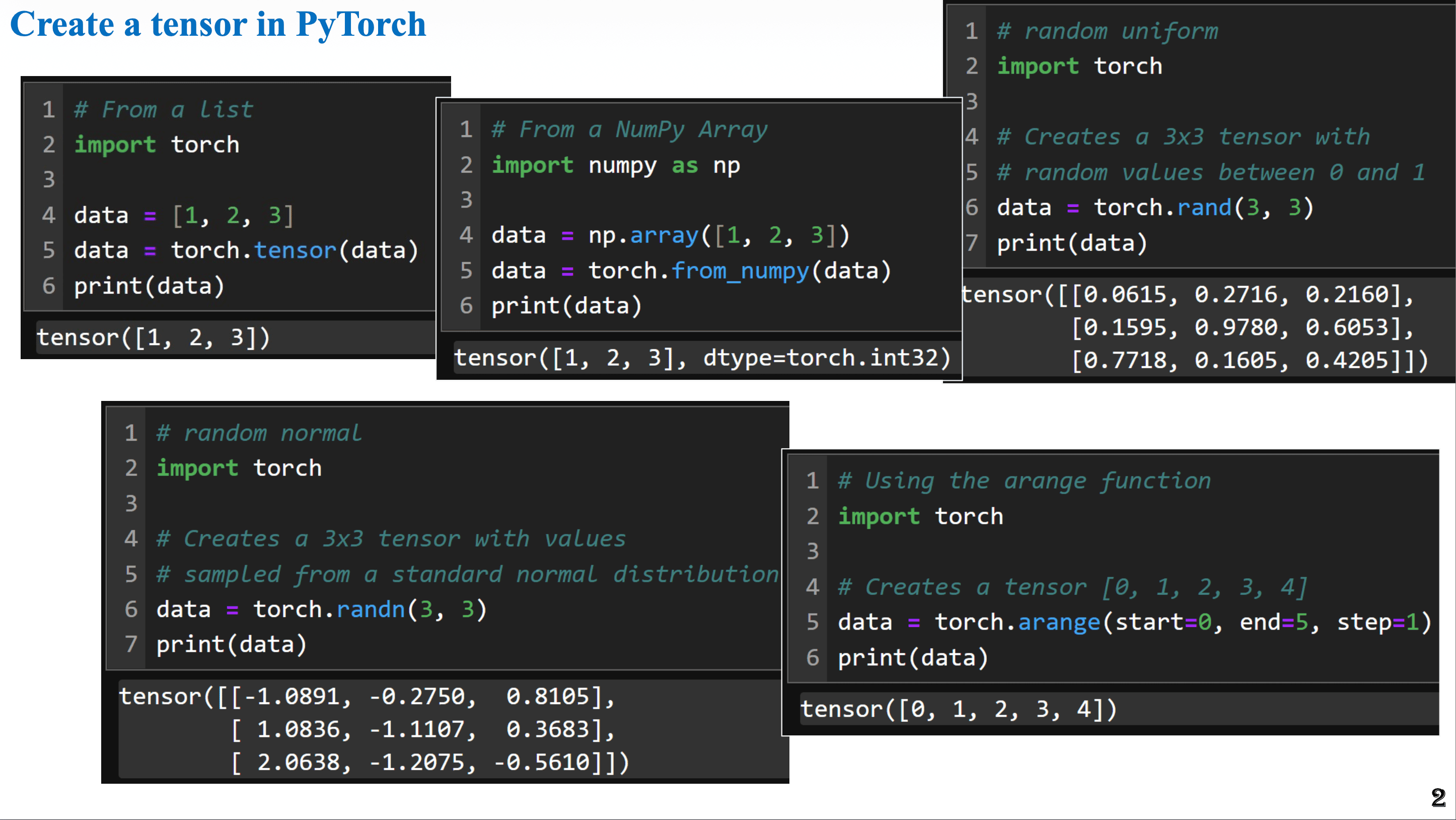
Hình 1. Các hàm cơ bản để tạo Tensor trong Pytorch[1]
Có nhiều cách để tạo ra một Tensor, nhưng đây là những phương pháp phổ biến và hữu ích nhất:
- Từ một List Python: Đây là cách đơn giản nhất để bắt đầu. Bạn chỉ cần truyền một danh sách (list) vào hàm
torch.tensor(). - Từ một NumPy array: PyTorch cung cấp khả năng tương tác liền mạch với NumPy thông qua hàm
torch.from_numpy(). - Tạo ngẫu nhiên: Đây là phương pháp cực kỳ quan trọng trong học máy.
torch.rand(shape): Tạo ra một tensor với các giá trị được lấy ngẫu nhiên từ phân phối đều trong khoảng [0, 1).torch.randn(shape): Tạo ra một tensor với các giá trị được lấy từ phân phối chuẩn (Normal distribution) có giá trị trung bình (mean) là 0 và độ lệch chuẩn (standard deviation) là 1. Hàm này đặc biệt hữu ích cho việc khởi tạo tham số (ví dụ:thetahay trọng sốw) cho mô hình. Việc khởi tạo các trọng số ban đầu là những giá trị nhỏ xung quanh 0 giúp quá trình huấn luyện diễn ra ổn định hơn.
Broadcasting: Phép toán linh hoạt
Giống như NumPy, PyTorch hỗ trợ broadcasting, một cơ chế mạnh mẽ cho phép thực hiện các phép toán trên các Tensor có kích thước không tương thích. Ví dụ, khi bạn trừ một Tensor vector với một số vô hướng (scalar), PyTorch sẽ tự động "mở rộng" số vô hướng đó thành một vector có cùng kích thước để thực hiện phép toán.
x = torch.tensor([1.0, 2.0, 3.0, 4.0])
y = 5.0
# PyTorch tự động "broadcast" số 5 thành tensor [5.0, 5.0, 5.0, 5.0]
# trước khi thực hiện phép trừ.
result = x - y
# result sẽ là tensor([-4., -3., -2., -1.])
Một số hàm hữu ích
PyTorch được xây dựng cho học sâu, vì vậy nó tích hợp sẵn nhiều hàm tiện lợi.
- Mean Squared Error (MSE):
nn.MSELosslà hàm tính toán lỗi bình phương trung bình, một hàm mất mát (loss function) cực kỳ phổ biến cho các bài toán hồi quy. - Lưu ý quan trọng: Hàm loss trong PyTorch thường yêu cầu đầu vào là kiểu dữ liệu
float. Nếu bạn truyền vào số nguyên (ví dụtorch.tensor([1, 2, 3])), chương trình sẽ báo lỗi. Đây là một ràng buộc có chủ đích để đảm bảo tính chính xác trong các phép tính đạo hàm. - Argmax: Hàm
torch.argmax()trả về chỉ số (index) của phần tử có giá trị lớn nhất trong một Tensor. Trong các bài toán phân loại đa lớp (ví dụ Softmax), sau khi mô hình đưa ra một vector xác suất cho các lớp,argmaxđược sử dụng để tìm ra lớp có xác suất cao nhất. Đây là bước then chốt để đưa ra dự đoán cuối cùng và tính toán độ chính xác (accuracy) của mô hình.
Sau khi đã làm quen với Tensor, chúng ta sẽ khám phá tính năng mạnh mẽ và "phép thuật" nhất của PyTorch ở phần tiếp theo.
2. Sức mạnh Cốt lõi của PyTorch: Tự động tính Đạo hàm (Autograd)
Autograd chính là "phép thuật" đằng sau PyTorch. Đây là một công cụ giúp tự động hóa hoàn toàn quá trình tính toán đạo hàm (gradients), giải phóng chúng ta khỏi việc phải tính toán thủ công bằng quy tắc chuỗi (chain rule) phức tạp như khi dùng NumPy. Đây chính là chìa khóa để huấn luyện các mạng nơ-ron hiện đại.

Hình 2. Gradient Computation trong Pytorch[1]
Bật chế độ theo dõi
Để PyTorch bắt đầu theo dõi các phép toán và tính đạo hàm cho một biến, chúng ta phải khai báo Tensor với thuộc tính requires_grad=True.
# Dữ liệu đầu vào thường không cần tính đạo hàm
data = torch.tensor([1.0, 2.0, 3.0])
# Các tham số của mô hình (theta) cần được cập nhật, do đó cần tính đạo hàm
theta = torch.tensor([0.5], requires_grad=True)
Lý do đằng sau thiết kế này rất trực quan: dữ liệu đầu vào (input data) là cố định, chúng ta không bao giờ thay đổi nó trong quá trình huấn luyện. Ngược lại, các tham số của mô hình (trọng số weights và độ chệch biases) là những thứ chúng ta cần điều chỉnh để giảm thiểu sai số, do đó chúng phải có khả năng tính đạo hàm.
Lan truyền ngược với .backward()
Hãy xem sức mạnh của Autograd qua một ví dụ kinh điển. Giả sử chúng ta có các phép toán: y = x² và z = 3y + 2.
Nếu tính bằng tay theo quy tắc chuỗi, đạo hàm của z theo x là: dz/dx = dz/dy * dy/dx = 3 * 2x = 6x
Bây giờ, hãy để PyTorch thực hiện điều này. Với x=3, kết quả mong đợi là 6 * 3 = 18.
# Khởi tạo x, bật theo dõi đạo hàm
x = torch.tensor([3.0], requires_grad=True)
# Xây dựng đồ thị tính toán
y = x**2
z = 3*y + 2
# Yêu cầu PyTorch tính toán tất cả đạo hàm ngược từ z
z.backward()
# In ra đạo hàm dz/dx, được lưu trong thuộc tính .grad của x
print(x.grad) # Kết quả sẽ là tensor([18.]), chính là 6 * 3
Chỉ với một lệnh z.backward(), PyTorch đã tự động lan truyền ngược qua đồ thị tính toán và lưu trữ giá trị đạo hàm chính xác. Để kiểm tra lại, hãy thử với x=2, kết quả phải là 6 * 2 = 12.
x = torch.tensor([2.0], requires_grad=True)
y = x**2
z = 3*y + 2
z.backward()
print(x.grad) # Kết quả chính xác là tensor([12.])
Tối ưu hóa với Optimizer
Sau khi có đạo hàm, chúng ta cần cập nhật các tham số của mô hình. torch.optim cung cấp nhiều thuật toán tối ưu hóa, trong đó SGD (Stochastic Gradient Descent) là thuật toán cơ bản nhất.
Quy trình cập nhật trong một vòng lặp huấn luyện bao gồm hai bước chính:
optimizer.zero_grad(): Reset đạo hàm về 0. Đây là bước bắt buộc trước mỗi vòng lặp. Lý do là PyTorch sẽ cộng dồn các giá trị đạo hàm qua mỗi lần gọi.backward(). Nếu không reset, đạo hàm của batch dữ liệu hiện tại sẽ bị cộng dồn với đạo hàm của batch trước đó, dẫn đến việc cập nhật tham số sai lệch.optimizer.step(): Thực hiện cập nhật tham số. Lệnh này sẽ tự động áp dụng công thứctheta = theta - learning_rate * gradientcho tất cả các tham số đã được đăng ký với optimizer.
Với những công cụ mạnh mẽ này, chúng ta đã sẵn sàng xây dựng và huấn luyện mô hình học máy hoàn chỉnh đầu tiên.
3. Ứng dụng Thực tế I: Hồi quy Tuyến tính (Linear Regression)
Bây giờ, chúng ta sẽ áp dụng các khái niệm về Tensor, Autograd và Optimizer để xây dựng một mô hình hồi quy tuyến tính đơn giản từ đầu. Đây là bước đầu tiên để hiểu quy trình làm việc hoàn chỉnh trong PyTorch, từ dữ liệu đầu vào đến cập nhật trọng số.
Giới thiệu nn.Linear
nn.Linear(in_features, out_features) là một "lớp" (layer) được xây dựng sẵn trong PyTorch, đại diện cho một phép biến đổi tuyến tính y = xW + b. Nó tương đương với một lớp kết nối đầy đủ (fully connected layer).
Đối với bài toán hồi quy tuyến tính đơn giản của chúng ta (1 đặc trưng đầu vào, 1 giá trị đầu ra), chúng ta sẽ khai báo mô hình như sau: model = nn.Linear(1, 1).
Một bước tiến: Forward và Backward Pass
Hãy cùng mô phỏng lại một bước huấn luyện duy nhất với các số liệu cụ thể để thấy rõ quy trình:
- Dữ liệu: Input
x = 6.7, Labely = 9.14.
Để tái tạo chính xác bước tính toán trong bài giảng, chúng ta sẽ bỏ qua các trọng số khởi tạo ngẫu nhiên ban đầu (ví dụ _w = -0.655_, _b = -0.0393_) và gán trực tiếp các giá trị _w = -0.34_ và _b = 0.04_ để phân tích một bước cập nhật cụ thể.
import torch
import torch.nn as nn
# Mô hình
model = nn.Linear(1, 1)
# Gán trọng số ban đầu để kiểm tra (sử dụng .data)
model.weight.data = torch.tensor([[-0.34]])
model.bias.data = torch.tensor([0.04])
# Dữ liệu (Input phải có dạng 2D [batch_size, features])
x = torch.tensor([[6.7]])
y = torch.tensor([[9.14]])
# Hàm loss và Optimizer
loss_fn = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
Bây giờ, hãy thực hiện các bước trong vòng lặp:
- Bước 1: Forward Pass (Lan truyền xuôi): Đưa
xqua mô hình để tính toán dự đoány_hat. - Bước 2: Tính Loss: Tính toán sai số giữa
y_hatvàythực tế. - Bước 3: Backward Pass (Lan truyền ngược): Tính đạo hàm của loss theo các tham số của mô hình.
- Bước 4: Cập nhật Trọng số: Sử dụng optimizer để cập nhật
wvàb. - Lệnh
optimizer.step()đã thực hiện phép tính:w_new = w_old - lr * w_grad(tức là-0.34 - 0.01 * (-151.9292) = 1.179) và tương tự cho bias (b_new = 0.04 - 0.01 * (-22.6760) = 0.26676).
Quy trình forward -> loss -> backward -> step này chính là trái tim của việc huấn luyện hầu hết các mô hình trong PyTorch. Phần tiếp theo sẽ mở rộng quy trình này cho các bài toán phân loại.
4. Ứng dụng Thực tế II: Hồi quy Logistic (Logistic Regression)
Chúng ta sẽ chuyển từ bài toán hồi quy (dự đoán giá trị liên tục) sang bài toán phân loại nhị phân (dự đoán một trong hai lớp). Hồi quy Logistic là mô hình nền tảng cho nhiệm vụ này, có nhiệm vụ chuyển đổi đầu ra của mô hình thành một xác suất.
Kiến trúc Mô hình và Hàm kích hoạt
Kiến trúc cơ bản vẫn sử dụng một lớp nn.Linear. Ví dụ, với 2 đặc trưng đầu vào và 1 đầu ra nhị phân, ta dùng nn.Linear(2, 1). Đầu ra của lớp Linear (gọi là logit) là một giá trị số thực bất kỳ. Để biến nó thành xác suất trong khoảng (0, 1), chúng ta cần hàm kích hoạt Sigmoid.
Lựa chọn Hàm Loss thông minh
Khi làm việc với bài toán phân loại nhị phân, PyTorch cung cấp hai lựa chọn hàm loss chính, nhưng một trong số đó được khuyến khích hơn hẳn:
nn.BCELoss(Binary Cross Entropy Loss): Hàm loss tiêu chuẩn, yêu cầu đầu vào phải là xác suất (đã qua Sigmoid).nn.BCEWithLogitsLoss: Đây là lựa chọn được khuyến khích. Hàm này nhận đầu vào là giá trị logit (đầu ra thô từnn.Linear, trước khi qua Sigmoid). Nó sẽ tự động áp dụng Sigmoid và tính toán BCE trong cùng một bước.
Tại sao lại có sự phức tạp này? Đây là một bài học quan trọng về thiết kế framework. Ở các phiên bản đầu, các nhà nghiên cứu thường xây dựng mô hình với lớp Sigmoid rõ ràng và dùng BCELoss. Tuy nhiên, sau một thời gian, cộng đồng đã "ngộ ra" rằng việc kết hợp hai phép toán (Sigmoid và BCE) vào một hàm duy nhất sẽ giúp tăng tính ổn định về mặt số học (numerical stability), tránh các vấn đề về độ chính xác khi làm việc với các giá trị xác suất rất nhỏ. BCEWithLogitsLoss ra đời chính là vì lý do này, đại diện cho một sự tiến hóa trong tư duy. Triết lý "kết hợp các phép toán để tăng tính ổn định" này là một chủ đề lặp lại trong PyTorch.
Tóm tắt Quy trình
Dưới đây là quy trình được khuyến nghị để xây dựng mô hình Hồi quy Logistic trong PyTorch:
- Xây dựng mô hình chỉ với một lớp
nn.Linearđể tạo ralogits. Không thêm lớp Sigmoid vào mô hình. - Sử dụng
nn.BCEWithLogitsLosslàm hàm loss. - Trong vòng lặp huấn luyện, truyền trực tiếp
logits(đầu ra của mô hình) vàlabels(nhãn thực tế) vào hàm loss. - Tiến hành các bước
loss.backward()vàoptimizer.step()như bình thường.
Sau khi đã giải quyết bài toán hai lớp, chúng ta sẽ nâng cấp lên để xử lý nhiều lớp hơn với Softmax.
5. Ứng dụng Thực tế III: Hồi quy Softmax (Softmax Regression)
Hồi quy Softmax (hay hồi quy logistic đa lớp) là phương pháp tiêu chuẩn cho các bài toán phân loại đa lớp (multi-class classification), nơi mục tiêu là phân loại một đối tượng vào một trong nhiều hơn hai lớp.
Kiến trúc và nn.Sequential
Mô hình Softmax sẽ có một lớp nn.Linear với số nơ-ron đầu ra bằng đúng số lớp cần phân loại. Ví dụ, cho bài toán phân loại có 4 đặc trưng đầu vào và 3 lớp, mô hình sẽ là nn.Linear(4, 3).
Để tổ chức các lớp của mô hình một cách gọn gàng, chúng ta có thể sử dụng nn.Sequential. Đây là một container tiện lợi giúp đóng gói một chuỗi các lớp thành một khối duy nhất.
# Mô hình cho bài toán có 4 features và 3 lớp
model = nn.Sequential(
nn.Linear(4, 3)
)
Hàm Loss CrossEntropyLoss
nn.CrossEntropyLoss là hàm loss tiêu chuẩn cho phân loại đa lớp trong PyTorch. Kế thừa triết lý từ BCEWithLogitsLoss, có một điểm cực kỳ quan trọng cần ghi nhớ:
nn.CrossEntropyLoss đã tích hợp sẵn hàm Softmax bên trong.
Điều này có nghĩa là nó cũng nhận đầu vào là logits (đầu ra thô từ lớp Linear), chứ không phải xác suất đã qua hàm Softmax. Thiết kế này cũng nhằm mục đích tăng cường tính ổn định về mặt số học và đơn giản hóa quy trình làm việc.
Tóm tắt Quy trình
Quy trình xây dựng và huấn luyện mô hình Hồi quy Softmax hiệu quả trong PyTorch như sau:
- Xây dựng mô hình với lớp
nn.Linear(input_features, num_classes)để tạo ralogits. Không thêm lớp Softmax vào kiến trúc mô hình. - Sử dụng
nn.CrossEntropyLosslàm hàm loss. - Trong vòng lặp huấn luyện, truyền trực tiếp
logitsvàlabelsvào hàm loss. - Tiến hành các bước
loss.backward()vàoptimizer.step()như thường lệ.
Tiếp theo, chúng ta sẽ áp dụng mô hình Softmax mạnh mẽ này vào một lĩnh vực trực quan và thú vị hơn: phân loại hình ảnh.
6. Bước vào thế giới Deep Learning: Phân loại Ảnh
Giờ là lúc áp dụng tất cả những gì chúng ta đã học vào một bài toán thực tế hơn: phân loại các chữ số viết tay từ bộ dữ liệu MNIST. Đây là bước đệm hoàn hảo để xây dựng các mạng nơ-ron sâu thực sự.

Hình 3. MNIST dataset[1]
Xử lý Dữ liệu Ảnh
Một ảnh xám (grayscale image) trong bộ MNIST có cấu trúc là một ma trận 2D với kích thước 28x28 pixel. Tuy nhiên, lớp nn.Linear mà chúng ta đã sử dụng chỉ có thể nhận đầu vào là một vector 1D. Để giải quyết vấn đề này, chúng ta cần một lớp đặc biệt:
nn.Flatten: Chức năng của lớp này rất đơn giản nhưng thiết yếu. Nó sẽ "làm phẳng" ma trận ảnh 2D thành một vector 1D. Ví dụ, một ảnh 28x28 sẽ được chuyển đổi thành một vector có 28 * 28 = 784 phần tử.
Mô hình hoàn chỉnh cho MNIST
Với nn.Flatten, chúng ta có thể dễ dàng xây dựng mạng nơ-ron đầu tiên để phân loại 10 lớp chữ số (từ 0 đến 9) trong bộ MNIST. Sử dụng nn.Sequential, kiến trúc hoàn chỉnh sẽ như sau:
# MNIST có ảnh 28x28 (784 pixels) và 10 lớp
model = nn.Sequential(
# Bước 1: Làm phẳng ảnh 2D thành vector 1D
nn.Flatten(),
# Bước 2: Lớp tuyến tính để phân loại từ 784 features sang 10 lớp
nn.Linear(784, 10)
)
Vì đây là bài toán phân loại đa lớp, hàm loss phù hợp nhất vẫn là nn.CrossEntropyLoss. Với kiến trúc đơn giản này, chúng ta đã thành công trong việc xây dựng một mạng nơ-ron có khả năng "nhìn" và phân loại hình ảnh, mở ra cánh cửa cho các kiến trúc phức tạp và mạnh mẽ hơn trong tương lai.
Tổng kết
Trong bài viết này, chúng ta đã thực hiện một hành trình toàn diện để làm quen với PyTorch, bắt đầu từ những khái niệm cơ bản nhất và tiến tới việc xây dựng một mạng nơ-ron thực thụ.
- Chúng ta bắt đầu với
Tensor, đơn vị dữ liệu cơ bản của PyTorch, tương tự như array của NumPy nhưng có khả năng chạy trên GPU. - Tiếp theo, chúng ta khám phá sức mạnh của
Autogradđể tự động hóa hoàn toàn việc tính toán đạo hàm, loại bỏ một trong những công đoạn phức tạp nhất của học máy. - Chúng ta đã học cách sử dụng các lớp như
nn.Linearvà các hàm loss được tối ưu hóa nhưMSELoss,BCEWithLogitsLoss, vàCrossEntropyLossđể xây dựng các mô hình khác nhau. - Chúng ta đã nắm vững quy trình huấn luyện tiêu chuẩn trong PyTorch:
zero_grad→forward→loss→backward→step. - Cuối cùng, chúng ta đã áp dụng tất cả kiến thức để xây dựng một mạng nơ-ron hoàn chỉnh có khả năng phân loại hình ảnh từ bộ dữ liệu MNIST.
Bằng cách xử lý các phần tính toán phức tạp như đạo hàm và cập nhật trọng số, PyTorch cho phép bạn tập trung vào điều quan trọng nhất: thiết kế, thử nghiệm và sáng tạo các kiến trúc mô hình mới để giải quyết những bài toán đầy thách thức.
Reference
[1] Ảnh được lấy từ tài liệu khóa học AIO Module 06 Tuần 01 và 02.
Chưa có bình luận nào. Hãy là người đầu tiên!