Multi-Layer Perceptron (MLP): Từ Lý thuyết Cốt lõi đến Triển khai Thực tế

Tất cả các code trong bài báo dưới đây các bạn có thể tham khảo ở GitHub: MLP-Blog.

1. Multi-Layer Perceptron (MLP) là gì?

Multi-Layer Perceptron (MLP) là một loại mạng nơ-ron nhân tạo truyền thẳng (feedforward neural network). Khác với Perceptron đơn lớp chỉ có thể giải quyết các bài toán tuyến tính (như cổng AND, OR), MLP có khả năng học các mối quan hệ phi tuyến phức tạp nhờ vào việc kết hợp nhiều lớp (layers) và các hàm kích hoạt (activation functions).

Kiến trúc cơ bản của MLP

Một mạng MLP điển hình bao gồm ít nhất ba loại lớp:

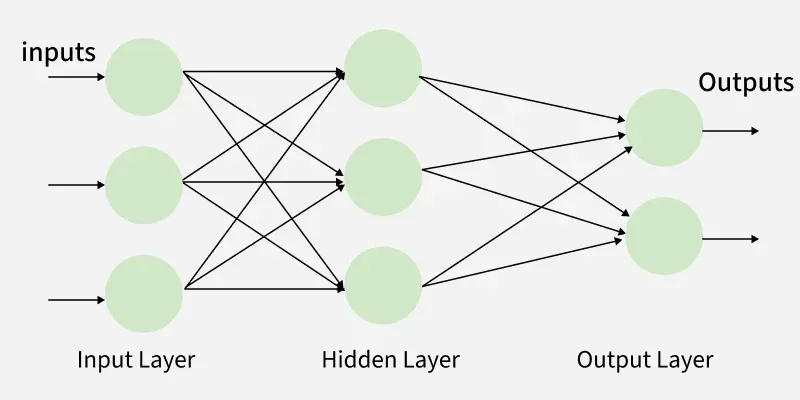
Hình 1: Hình ảnh về kiến trúc cơ bản của MLP [1]

1. Input Layer (Lớp đầu vào):

   • Nhận dữ liệu thô (raw data) từ bên ngoài.

   • Số lượng nơ-ron (node) ở lớp này bằng số lượng đặc trưng (features) của dữ liệu đầu vào.

   • Lớp này không thực hiện tính toán, chỉ truyền dữ liệu đi.

2. Hidden Layers (Các lớp ẩn):

   • Đây là nơi "ma thuật" xảy ra. Một MLP có thể có một hoặc nhiều lớp ẩn.

   • Các lớp này thực hiện các phép biến đổi toán học để trích xuất đặc trưng từ dữ liệu.

   • Các nơ-ron trong lớp ẩn kết nối với tất cả các nơ-ron của lớp trước và lớp sau nó (Fully Connected).

3. Output Layer (Lớp đầu ra):

   • Đưa ra kết quả dự đoán cuối cùng.

   • Số lượng nơ-ron phụ thuộc vào bài toán: 1 node cho hồi quy (regression) hoặc phân loại nhị phân (binary classification), và $N$ nodes cho phân loại đa lớp (multi-class classification) với $N$ là số lớp.

2. Giải phẫu Toán học bên trong một Nơ-ron

Để hiểu cách MLP hoạt động, ta cần nhìn vào từng nơ-ron riêng lẻ. Quá trình tính toán tại một nơ-ron trong lớp ẩn hoặc lớp đầu ra bao gồm hai bước chính: Tổ hợp tuyến tính và Kích hoạt phi tuyến.

2.1. Tổ hợp tuyến tính (Linear Transformation)

Giả sử tại một nơ-ron $j$ thuộc lớp thứ $l$, nó nhận đầu vào là vector $x$ từ lớp trước đó. Giá trị trước khi kích hoạt ($z$) được tính như sau:

$$z = \sum (w_i \cdot x_i) + b$$

Dưới dạng ma trận:
$$Z = W \cdot X + b$$

Trong đó:

• $W$: Ma trận trọng số (Weights) - quyết định mức độ quan trọng của đầu vào.

• $X$: Vector đầu vào.

• $b$: Hệ số chệch (Bias) - giúp tịnh tiến đường phân chia dữ liệu.

2.2. Hàm kích hoạt (Activation Function)

Nếu không có hàm kích hoạt, dù bạn có chồng bao nhiêu lớp ẩn lên nhau, mạng neural vẫn chỉ là một hàm tuyến tính khổng lồ. Hàm kích hoạt giúp mạng học được các mẫu phức tạp.

Dưới đây là các hàm kích hoạt phổ biến và công thức toán học của chúng:

a. Sigmoid Function

Hàm này ép giá trị đầu ra vào khoảng $(0, 1)$, thường dùng cho lớp đầu ra của bài toán phân loại nhị phân.

$$ \sigma(z) = \frac{1}{1 + e^{-z}} $$

• Đạo hàm: $\sigma'(z) = \sigma(z)(1 - \sigma(z))$.

• Nhược điểm: Dễ gặp vấn đề Vanishing Gradient (đạo hàm tiến về 0 khi $|z|$ lớn), làm chậm quá trình học.

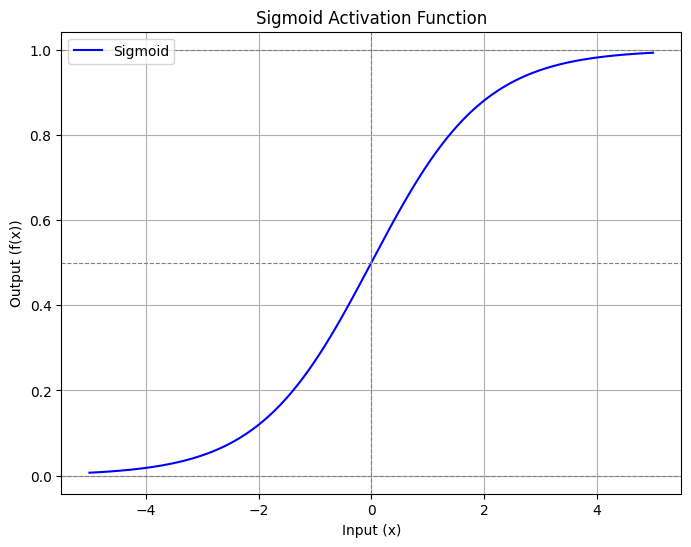
Hình 2: Hình ảnh về hàm kích hoạt Sigmoid

b. Tanh Function (Hyperbolic Tangent)

Hàm Tanh ép giá trị vào khoảng $(-1, 1)$, giúp dữ liệu có trung bình về 0 (zero-centered), tốt hơn Sigmoid cho các lớp ẩn.

$$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$

• Đạo hàm: $\tanh'(x) = 1 - \tanh^2(x)$.

• Nhược điểm: Vẫn bị Vanishing Gradient dù đỡ hơn Sigmoid.

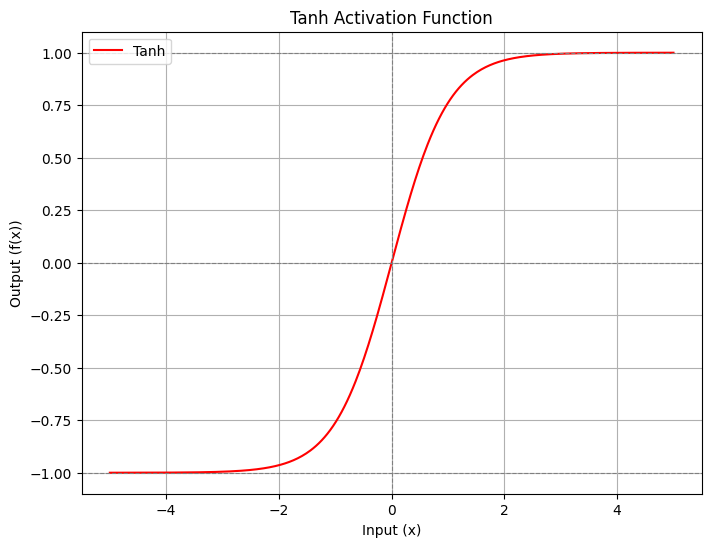
Hình 3: Hình ảnh về hàm kích hoạt Tanh

c. ReLU (Rectified Linear Unit)

Đây là hàm kích hoạt phổ biến nhất hiện nay cho các lớp ẩn vì tính toán đơn giản và giải quyết tốt vấn đề Vanishing Gradient.

$$ReLU(x) = \max(0, x) = \begin{cases} x & \text{nếu } x > 0 \\ 0 & \text{nếu } x \le 0 \end{cases}$$

• Đạo hàm:

$$ \text{ReLU}'(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases} $$

• Nhược điểm: Vấn đề Dying ReLU - khi nơ-ron nhận giá trị âm, đạo hàm bằng 0, nơ-ron đó sẽ ngừng học vĩnh viễn.

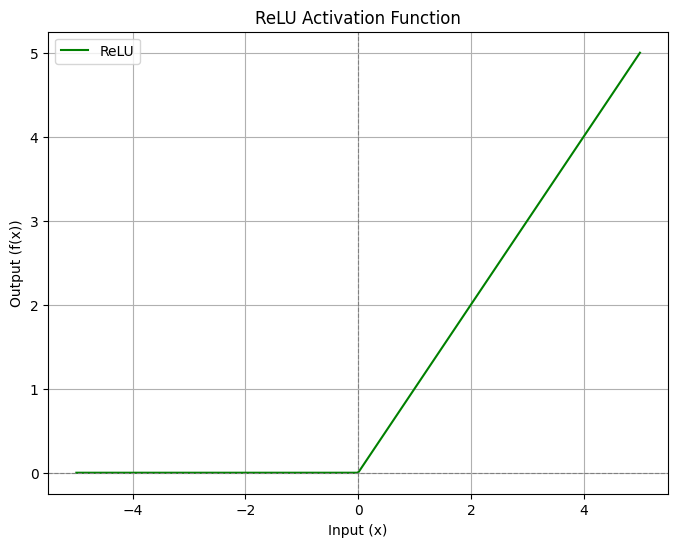
Hình 4: Hình ảnh về hàm kích hoạt ReLU

3. Quá trình Huấn luyện (Training Pipeline)

Quá trình huấn luyện MLP bao gồm 3 giai đoạn lặp đi lặp lại: Forward Propagation, Loss Calculation, và Backpropagation.

3.1. Lan truyền xuôi (Forward Propagation)

Dữ liệu đi từ Input $\rightarrow$ Hidden Layers (nhân trọng số, cộng bias, qua hàm activation) $\rightarrow$ Output Layer $\rightarrow$ Dự đoán $\hat{y}$.

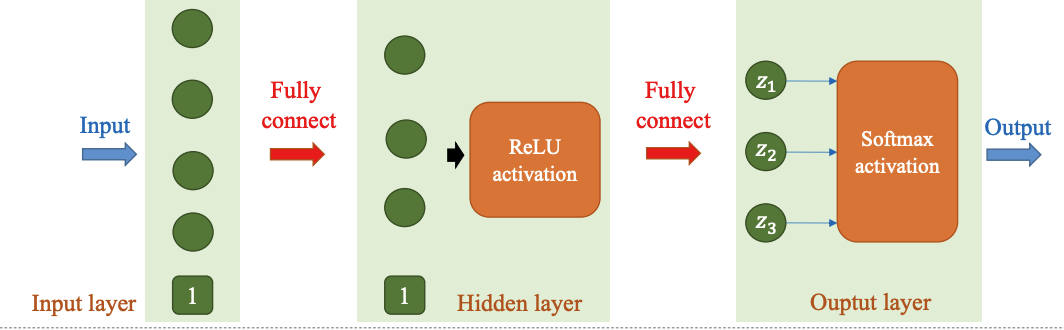
Hình 5: Hình ảnh về Lan truyền xuôi (Forward Propagation) trong MLP[1]

3.2. Hàm mất mát (Loss Function)

Hàm loss đo lường sự sai lệch giữa dự đoán $\hat{y}$ và nhãn thực tế $y$. Mục tiêu là tối thiểu hóa giá trị này.

• Với phân loại nhị phân (Binary Cross Entropy - BCELoss):

$$L(\theta) = - [y \log(\hat{y}) + (1-y) \log(1-\hat{y})]$$

• Với phân loại đa lớp (Cross Entropy Loss):

$$L(\theta) = - \sum_{i} y_i \log(\hat{y}_i)$$

(Trong đó $y$ thường được mã hóa One-hot).

3.3. Lan truyền ngược (Backpropagation) và Tối ưu hóa (Optimization)

Đây là bước cập nhật trọng số $W$ và bias $b$ để giảm Loss. Chúng ta sử dụng thuật toán Gradient Descent:

1. Tính đạo hàm (Gradient) của Loss theo từng trọng số: $\nabla_{\theta}L$.

2. Cập nhật trọng số theo công thức:

   $$\theta_{new} = \theta_{old} - \eta \cdot \nabla_{\theta}L$$

   Trong đó $\eta$ là Learning Rate (tốc độ học).

Các thuật toán tối ưu nâng cao thường dùng: SGD (Stochastic Gradient Descent), Adam, RMSprop.

4. Các kỹ thuật Nâng cao hiệu suất MLP

Để mô hình hoạt động tốt, tránh Overfitting (học vẹt) hoặc Underfitting, ta cần các kỹ thuật sau:

4.1. Weight Initialization (Khởi tạo trọng số)

Không bao giờ khởi tạo tất cả trọng số bằng 0, vì các nơ-ron sẽ học giống hệt nhau (tính đối xứng).

• He Initialization: Tốt cho hàm ReLU.

• Xavier (Glorot) Initialization: Tốt cho Sigmoid/Tanh.

4.2. Batch Normalization

Chuẩn hóa dữ liệu đầu vào của mỗi lớp ẩn để có mean=0 và variance=1. Giúp training nhanh hơn và ổn định hơn.

Công thức:

$$ \hat{x} = \frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} $$

$$ y = \gamma \hat{x} + \beta $$

Lợi ích:

• Training nhanh hơn.

• Cho phép learning rate lớn hơn.

• Giảm phụ thuộc vào weight initialization.

4.3. Dropout

Ngẫu nhiên "tắt" một số nơ-ron trong quá trình training với xác suất $p$. Điều này buộc mạng phải học các đặc trưng mạnh mẽ hơn và giảm Overfitting.

Công thức:

$$ y = \text{Dropout}(x, p) = \begin{cases} \frac{x}{1-p} & \text{với xác suất } (1-p) \\ 0 & \text{với xác suất } p \end{cases} $$

Lợi ích:

• Giảm overfitting.

• Tạo ensemble effect (nhiều mô hình con).

4.4. Regularization (L2 - Weight Decay)

Thêm một thành phần phạt vào hàm Loss để ngăn trọng số trở nên quá lớn.

Loss function mới:

$$ L_{\text{total}} = L_{\text{original}} + \lambda \sum_{i} w_i^2 $$

Lợi ích:

• Giảm overfitting.

• Weights nhỏ hơn → mô hình đơn giản hơn.

5. Đánh giá Mô hình (Evaluation Metrics)

Khi huấn luyện MLP, việc nhìn vào Loss (hàm mất mát) giảm dần là chưa đủ. Loss giúp tối ưu hóa trọng số, nhưng Metrics mới là thước đo thực sự để con người hiểu được mô hình đang hoạt động tốt đến đâu.

Tùy thuộc vào bài toán (phân loại nhị phân, đa lớp, hay dữ liệu mất cân bằng), chúng ta cần chọn metric phù hợp. Dưới đây là các chỉ số quan trọng nhất.

5.1. Accuracy (Độ chính xác)

Đây là chỉ số tự nhiên và dễ hiểu nhất. Nó đơn giản là tỉ lệ số mẫu dự đoán đúng trên tổng số mẫu.

Công thức toán học:
$$Accuracy = \frac{\text{Number of Correct Predictions}}{\text{Total Number of Predictions}} = \frac{TP + TN}{TP + TN + FP + FN}$$

Khi nào dùng?

• Chỉ nên dùng khi tập dữ liệu cân bằng (số lượng mẫu giữa các lớp tương đương nhau).

Hạn chế:

• Cạm bẫy dữ liệu mất cân bằng: Giả sử bài toán phát hiện bệnh hiếm (chỉ $1\%$ người mắc bệnh). Nếu mô hình luôn dự đoán "Không bệnh" cho tất cả mọi người, Accuracy vẫn đạt $99\%$, nhưng mô hình này hoàn toàn vô dụng vì không tìm ra người bệnh nào. Lúc này, ta cần các chỉ số chuyên sâu hơn bên dưới.

5.2. Confusion Matrix (Ma trận nhầm lẫn)

Để hiểu sâu hơn về cách mô hình sai sót, chúng ta sử dụng Confusion Matrix. Đây là bảng so sánh giữa giá trị thực tế (Actual) và giá trị dự đoán (Predicted).

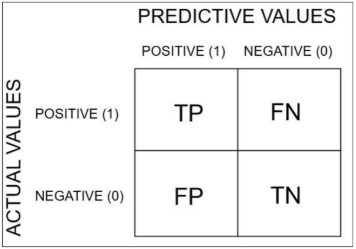
Hình 6: Hình ảnh về ma trận nhầm lẫn

Các thành phần chính:

• True Positive (TP): Thực tế là Dương tính, Mô hình đoán đúng là Dương tính.

• True Negative (TN): Thực tế là Âm tính, Mô hình đoán đúng là Âm tính.

• False Positive (FP): Thực tế là Âm tính, nhưng Mô hình báo nhầm là Dương tính (Báo động giả).

• False Negative (FN): Thực tế là Dương tính, nhưng Mô hình bỏ sót đoán là Âm tính.

5.3. Precision, Recall và F1-Score

Khi dữ liệu mất cân bằng hoặc chi phí của các loại sai lầm (FP và FN) khác nhau, bộ ba này cực kỳ quan trọng.

5.3.1. Precision (Độ chính xác của dự báo dương)

Câu hỏi: "Trong tất cả các mẫu mô hình dự đoán là Positive, có bao nhiêu mẫu đúng?".

$$Precision = \frac{TP}{TP + FP}$$

• Sử dụng khi: Chi phí cho False Positive cao.

• Ví dụ: Hệ thống lọc Spam email. Chúng ta chấp nhận sót email rác (FN) nhưng không được phép đưa email quan trọng vào mục Spam (FP).

5.3.2. Recall (Độ nhạy - Sensitivity)

Câu hỏi: "Trong tất cả các mẫu thực tế là Positive, mô hình tìm được bao nhiêu mẫu?".

$$Recall = \frac{TP}{TP + FN}$$

• Sử dụng khi: Chi phí cho False Negative cao.

• Ví dụ: Dự đoán ung thư. Thà báo nhầm (FP - bệnh nhân đi xét nghiệm lại) còn hơn là bỏ sót bệnh (FN - gây nguy hiểm tính mạng).

5.3.3. F1-Score

Là trung bình điều hòa (harmonic mean) của Precision và Recall.

$$F1 = 2 \times \frac{Precision \times Recall}{Precision + Recall}$$

• Sử dụng khi: Bạn cần sự cân bằng giữa Precision và Recall, hoặc khi dữ liệu bị mất cân bằng (Imbalanced Data). F1-Score sẽ thấp nếu một trong hai chỉ số Precision hoặc Recall quá thấp.

5.4. ROC Curve và AUC

Ngoài các chỉ số trên, ROC (Receiver Operating Characteristic) và AUC (Area Under the Curve) là tiêu chuẩn vàng để đánh giá khả năng phân loại ở các ngưỡng (threshold) khác nhau.

• ROC Curve: Là đồ thị biểu diễn mối quan hệ giữa TPR (True Positive Rate - Recall) và FPR (False Positive Rate).

  • True positive rate (TPR): hay còn được gọi là recall hoặc sensitivity, là tỷ lệ phân loại đúng positive trên tất cả trường hợp thực tế là positive. Chỉ số này sẽ đánh giá mức độ dự đoán của mô hình trên mẫu là positive. Khi giá trị càng cao, mô hình dự đoán càng tốt trên nhóm positive.

  $$TPR/Recall/Sensitivity=\frac{TruePositive}{TotalPositive}=\frac{TP}{TP+FN}$$

  • False positive rate (FPR): Tỷ lệ dự báo sai các trường hợp thực tế là negative thành positive trên tổng số trường hợp thực tế là negative. Nếu một mô hình có FPR càng thấp thì mô hình càng chính xác vì sai số của nó trên nhóm negative càng thấp. Phần bù của FPR là specificity (TNR) đo lường tỷ lệ dự báo đúng các trường hợp negative trên tổng số các trường hợp thực tế là negative.

  $$FPR=1-specificity=\frac{FalsePositive}{TotalNegative}=\frac{FP}{FP+TN}$$

Đồ thị ROC là một đường cong cầu lồi dựa trên TPR và FPR có hình dạng như bên dưới:

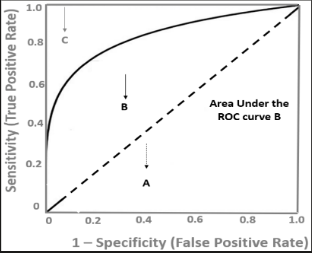
Hình 7: Hình ảnh về đồ thị ROG

• AUC: Là diện tích dưới đường cong ROC.

  • $AUC = 0.5$: Mô hình đoán ngẫu nhiên (tệ nhất).

  • $AUC = 1.0$: Mô hình phân loại hoàn hảo.

Chỉ số này đặc biệt hữu ích khi bạn chưa chốt được ngưỡng quyết định (threshold) là 0.5 hay một số khác.

6. So sánh các hàm kích hoạt trên bài toán Classification

Trong phần này, chúng ta sẽ xây dựng một bài toán classification đơn giản nhưng thú vị để "cân đo đong đếm" hiệu năng của 3 hàm kích hoạt phổ biến nhất: ReLU, Sigmoid và Tanh.

6.1. Chuẩn bị dữ liệu: Thách thức "Phi tuyến"

Chúng ta sẽ sử dụng dataset make_moons từ thư viện sklearn. Dữ liệu này có dạng hai hình bán nguyệt lồng vào nhau, đòi hỏi mô hình phải học được đường ranh giới quyết định (decision boundary) cong và phức tạp.

from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import torch
import torch.nn as nn
import numpy as np

# Thiết lập random seed để kết quả có thể tái lập
random_state = 42

# Tạo dữ liệu phi tuyến (moon-shaped)
# Chúng ta tạo 1000 điểm dữ liệu, thêm một chút nhiễu (noise=0.2) để bài toán thực tế hơn
X, y = make_moons(n_samples=1000, noise=0.2, random_state=random_state)

Output:
Thông qua đoạn code trên chúng ta có thể tạo được 1 phân phối dữ liệu gồm 2 nhóm như hình ảnh dưới đây. Và hình ảnh cho thấy dữ liệu của chúng ta không thể phân chia bằng một đường thẳng đơn giản.

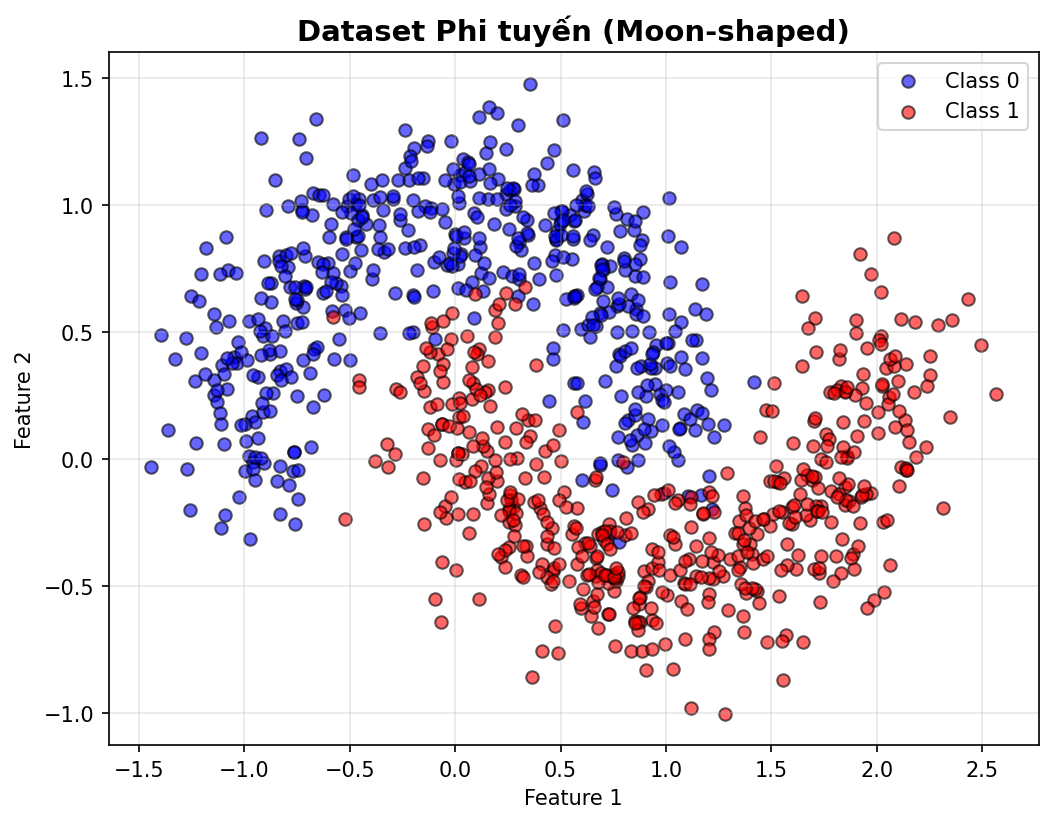
Hình 8: Hình ảnh về dữ liệu

Tiếp theo, chúng ta cần chia dữ liệu thành tập huấn luyện (train) và tập kiểm thử (test), đồng thời chuẩn hóa dữ liệu để giúp mô hình hội tụ nhanh hơn.

# Chia dữ liệu: 80% để huấn luyện, 20% để kiểm tra
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=random_state)

# Chuẩn hóa dữ liệu (Standardization)
# Giúp đưa các feature về cùng một phân phối chuẩn (mean=0, std=1)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# Chuyển đổi dữ liệu sang dạng Tensor của PyTorch để đưa vào mô hình
X_train_torch = torch.FloatTensor(X_train)
y_train_torch = torch.FloatTensor(y_train).unsqueeze(1) # Thêm dimension để khớp với output
X_test_torch = torch.FloatTensor(X_test)
y_test_torch = torch.FloatTensor(y_test).unsqueeze(1)

Thông qua code ở trên ta có thể chia ra $80\%$ dữ liệu dùng để huấn luyện, và $20\%$ còn lại dùng để kiểm tra.

6.2. Xây dựng Kiến trúc MLP Linh hoạt

Bây giờ, chúng ta sẽ định nghĩa một lớp MLP bằng PyTorch. Điểm đặc biệt của class này là nó cho phép chúng ta tùy chọn hàm kích hoạt (activation) ngay khi khởi tạo.

Mô hình của chúng ta sẽ có kiến trúc gồm:

• Input Layer: 2 neurons (tương ứng 2 features của dữ liệu).

• Hidden Layers: 2 lớp ẩn, mỗi lớp 64 neurons để đủ khả năng học các đặc trưng phức tạp.

• Output Layer: 1 neuron (dự đoán xác suất thuộc Class 1).

class MLP(nn.Module):
    """
    Multi-Layer Perceptron với khả năng tùy chọn hàm kích hoạt (activation function).
    """
    def __init__(self, input_dim, hidden_dim, output_dim, activation='relu'):
        super(MLP, self).__init__()
        # Các lớp Linear (Fully Connected)
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, output_dim)

        # Lựa chọn hàm kích hoạt dựa trên tham số truyền vào
        if activation == 'relu':
            self.activation = nn.ReLU()
        elif activation == 'sigmoid':
            self.activation = nn.Sigmoid()
        elif activation == 'tanh':
            self.activation = nn.Tanh()
        else:
            raise ValueError("Activation must be 'relu', 'sigmoid', or 'tanh'")

        # Hàm kích hoạt cho lớp output (Sigmoid cho bài toán phân loại nhị phân)
        self.output_activation = nn.Sigmoid()

    def forward(self, x):
        # Lan truyền dữ liệu qua các lớp
        x = self.activation(self.fc1(x)) # Input -> Hidden 1
        x = self.activation(self.fc2(x)) # Hidden 1 -> Hidden 2
        x = self.output_activation(self.fc3(x)) # Hidden 2 -> Output
        return x

# Định nghĩa các siêu tham số (hyperparameters)
input_dim = 2
hidden_dim = 64
output_dim = 1
learning_rate = 0.01
epochs = 500

6.3. Huấn luyện và So sánh

Để việc so sánh công bằng và gọn gàng, chúng ta viết một hàm train_model tổng quát. Hàm này sẽ nhận vào mô hình, dữ liệu và thực hiện vòng lặp huấn luyện, đồng thời ghi lại lịch sử Loss và Accuracy để chúng ta vẽ biểu đồ sau này.

def train_model(model, X_train, y_train, X_test, y_test, epochs, lr):
    """
    Hàm huấn luyện mô hình và trả về lịch sử loss/accuracy để visualize.
    """
    # Sử dụng Binary Cross Entropy Loss cho bài toán phân loại nhị phân
    criterion = nn.BCELoss()
    # Sử dụng Adam optimizer - thuật toán tối ưu phổ biến và hiệu quả
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)

    train_losses = []
    test_losses = []
    train_accs = []
    test_accs = []

    for epoch in range(epochs):
        # --- Quá trình Training ---
        model.train() # Chuyển mô hình sang chế độ huấn luyện
        optimizer.zero_grad() # Xóa gradient cũ
        outputs = model(X_train) # Forward pass
        loss = criterion(outputs, y_train) # Tính loss
        loss.backward() # Backward pass (tính gradient)
        optimizer.step() # Cập nhật trọng số

        train_losses.append(loss.item())

        # Tính toán accuracy trên tập train
        with torch.no_grad():
            train_pred = (outputs > 0.5).float() # Ngưỡng 0.5 để phân lớp
            train_acc = (train_pred == y_train).float().mean().item()
            train_accs.append(train_acc)

        # --- Quá trình Testing (Validation) ---
        model.eval() # Chuyển mô hình sang chế độ đánh giá
        with torch.no_grad():
            test_outputs = model(X_test)
            test_loss = criterion(test_outputs, y_test)
            test_losses.append(test_loss.item())

            test_pred = (test_outputs > 0.5).float()
            test_acc = (test_pred == y_test).float().mean().item()
            test_accs.append(test_acc)

        # In thông tin mỗi 100 epochs để theo dõi tiến độ
        if (epoch + 1) % 100 == 0:
            print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}, '
                  f'Train Acc: {train_acc:.4f}, Test Acc: {test_acc:.4f}')

    return train_losses, test_losses, train_accs, test_accs

Đựa trên hàm huấn luyện bên trên ta có thể tạo ra 3 phiên bản để lần lượt huấn luyêh với những model có hàm kích hoạt khác nhau như sau:

• Đối với hàm kích hoạt ReLU:

# 1. Huấn luyện với hàm kích hoạt ReLU
model_relu = MLP(input_dim, hidden_dim, output_dim, activation='relu')
relu_train_loss, relu_test_loss, relu_train_acc, relu_test_acc = train_model(
    model_relu, X_train_torch, y_train_torch, X_test_torch, y_test_torch, epochs, learning_rate
)

• Đối với hàm kích hoạt Sigmoid:

# 2. Huấn luyện với hàm kích hoạt Sigmoid
model_sigmoid = MLP(input_dim, hidden_dim, output_dim, activation='sigmoid')
sigmoid_train_loss, sigmoid_test_loss, sigmoid_train_acc, sigmoid_test_acc = train_model(
    model_sigmoid, X_train_torch, y_train_torch, X_test_torch, y_test_torch, epochs, learning_rate
)

• Đối với hàm kích hoạt Tanh:

# 3. Huấn luyện với hàm kích hoạt Tanh
model_tanh = MLP(input_dim, hidden_dim, output_dim, activation='tanh')
tanh_train_loss, tanh_test_loss, tanh_train_acc, tanh_test_acc = train_model(
    model_tanh, X_train_torch, y_train_torch, X_test_torch, y_test_torch, epochs, learning_rate
)

6.4. Kết quả đối đầu: Ai là người chiến thắng?

Sau khi huấn luyện xong cả 3 mô hình, giờ là lúc chúng ta trực quan hóa kết quả. Chúng ta sẽ xem xét hai yếu tố quan trọng:

1. Tốc độ hội tụ (Loss): Hàm nào giúp mô hình giảm lỗi nhanh nhất?

2. Độ chính xác (Accuracy): Hàm nào giúp mô hình dự đoán đúng nhiều nhất?

Kết quả so sánh: Sau khi chạy 3 hàm training với hàm kích hoạt khác nhau và biểu diễn nó qua hình ảnh dưới đây.

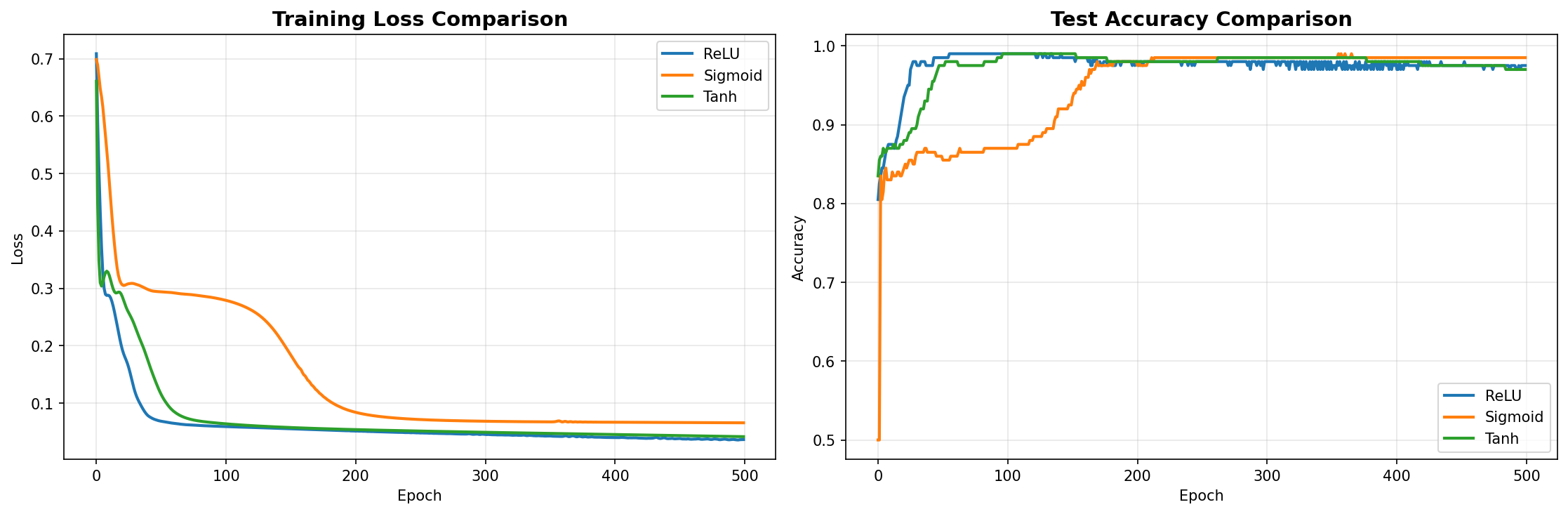
Hình 9: Hình ảnh về kết qủa huấn luyện

Bảng so sánh kết quả:

==========================================================
FINAL RESULTS COMPARISON
==========================================================
ReLU    - Train Acc: 0.9812 | Test Acc: 0.9800
Sigmoid - Train Acc: 0.9750 | Test Acc: 0.9850
Tanh    - Train Acc: 0.9825 | Test Acc: 0.9750

6.5. Nhìn thấu "Tư duy" của mô hình: Decision Boundary

Để thực sự hiểu các hàm kích hoạt ảnh hưởng thế nào đến cách mô hình "học", chúng ta sẽ vẽ Decision Boundary (đường ranh giới quyết định). Đường này cho thấy mô hình phân chia không gian dữ liệu như thế nào để phân loại các điểm xanh (Class 0) và đỏ (Class 1).

Decision Boundaries:

Quan sát hình ảnh dưới đây, bạn sẽ thấy sự khác biệt rõ rệt trong cách mỗi hàm kích hoạt vẽ nên ranh giới:

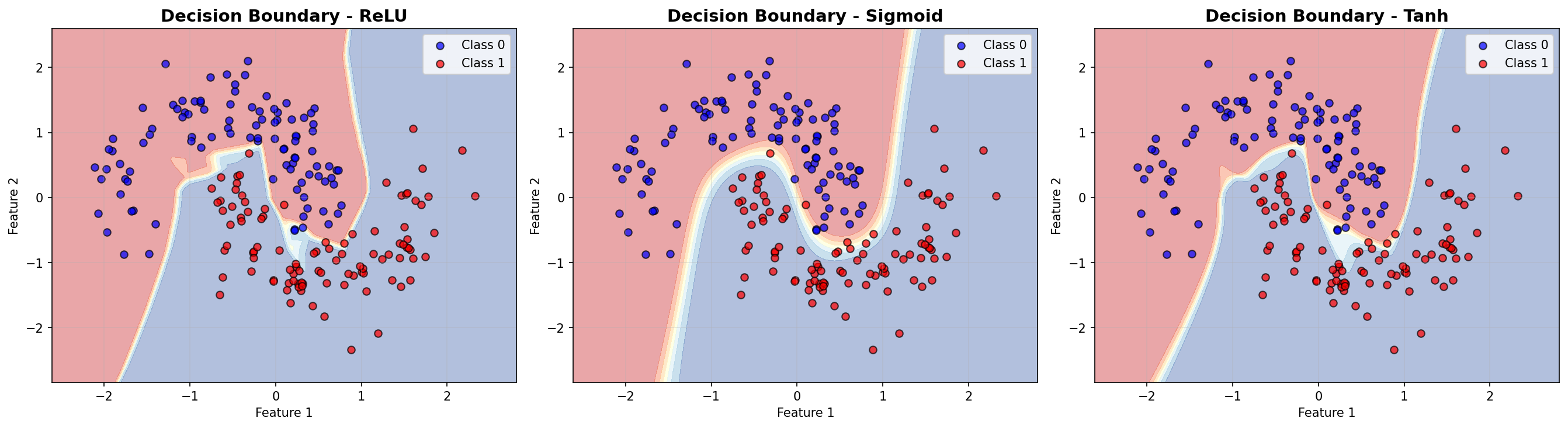
Hình 10: Hình ảnh về Decision Boundaries

Tổng kết và Nhận xét:

1. ReLU (Rectified Linear Unit):

• Hiệu năng: Thường là người chiến thắng về tốc độ hội tụ và độ chính xác cuối cùng.

• Lý do: ReLU không bị bão hòa ở miền dương (gradient luôn bằng 1), giúp tránh hiện tượng Vanishing Gradient. Đường phân chia của nó thường sắc nét và gấp khúc hơn.

• Lời khuyên: Đây nên là lựa chọn mặc định khi bạn bắt đầu xây dựng các mạng Deep Learning.

2. Sigmoid:

• Hiệu năng: Thường kém nhất trong 3 hàm này. Tốc độ học chậm và có thể kẹt ở độ chính xác thấp hơn.

• Lý do: Bị ảnh hưởng nặng nề bởi Vanishing Gradient. Khi giá trị đầu vào lớn hoặc nhỏ, đạo hàm tiến về 0, khiến trọng số gần như không được cập nhật.

• Lời khuyên: Hạn chế dùng ở các lớp ẩn (hidden layers). Chỉ nên dùng ở lớp đầu ra (output layer) cho bài toán xác suất nhị phân.

3. Tanh (Hyperbolic Tangent):

• Hiệu năng: Tốt hơn Sigmoid và đôi khi tiệm cận ReLU.

• Lý do: Giống Sigmoid nhưng có lợi thế là "zero-centered" (trung bình về 0), giúp việc tối ưu hóa dễ dàng hơn một chút. Tuy nhiên, nó vẫn không thoát khỏi vấn đề bão hòa gradient ở hai đầu.

• Lời khuyên: Có thể là một sự thay thế tốt nếu ReLU không hoạt động hiệu quả trên dữ liệu cụ thể của bạn.

7. Áp dụng các kỹ thuật cải thiện

Ta có thể áp dụng những kỹ thuật cải tiến như sau để có thể cải thiện dự đoán của mô hình cho những bài toán phức tạp hơn.

7.1. MLP với Dropout

Dropout là một kỹ thuật chống overfitting bằng cách ngẫu nhiên "tắt" một số nơ-ron trong quá trình huấn luyện. Điều này buộc mạng phải học các đặc trưng mạnh mẽ hơn thay vì phụ thuộc vào một vài nơ-ron cụ thể.

class MLP_Dropout(nn.Module):
    """
    MLP với Dropout để giảm overfitting
    """
    def __init__(self, input_dim, hidden_dim, output_dim, dropout_rate=0.5):
        super(MLP_Dropout, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(p=dropout_rate)
        self.activation = nn.ReLU()
        self.output_activation = nn.Sigmoid()

    def forward(self, x):
        x = self.activation(self.fc1(x))
        x = self.dropout(x)  # Dropout sau activation
        x = self.activation(self.fc2(x))
        x = self.dropout(x)
        x = self.output_activation(self.fc3(x))
        return x

7.2. MLP với Batch Normalization

Batch Normalization chuẩn hóa dữ liệu đầu vào của mỗi lớp về phân phối chuẩn (mean=0, variance=1). Kỹ thuật này giúp mạng hội tụ nhanh hơn, ổn định hơn và cho phép sử dụng learning rate lớn hơn mà không sợ phân kỳ.

class MLP_BatchNorm(nn.Module):
    """
    MLP với Batch Normalization
    """
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(MLP_BatchNorm, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.bn1 = nn.BatchNorm1d(hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.bn2 = nn.BatchNorm1d(hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, output_dim)
        self.activation = nn.ReLU()
        self.output_activation = nn.Sigmoid()

    def forward(self, x):
        x = self.fc1(x)
        x = self.bn1(x)  # Batch Norm trước activation
        x = self.activation(x)

        x = self.fc2(x)
        x = self.bn2(x)
        x = self.activation(x)

        x = self.output_activation(self.fc3(x))
        return x

7.3. MLP với L2 Regularization (Weight Decay)

L2 Regularization (hay Weight Decay) thêm một thành phần phạt vào hàm mất mát dựa trên độ lớn của trọng số. Nó ngăn chặn trọng số trở nên quá lớn, giúp mô hình đơn giản hơn và tránh overfitting.

def train_model_with_l2(model, X_train, y_train, X_test, y_test, epochs, lr, weight_decay=0.01):
    """
    Training model với L2 regularization (weight decay)
    """
    criterion = nn.BCELoss()
    # Thêm weight_decay vào optimizer
    optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=weight_decay)

    train_losses = []
    test_losses = []
    train_accs = []
    test_accs = []

    for epoch in range(epochs):
        model.train()
        optimizer.zero_grad()
        outputs = model(X_train)
        loss = criterion(outputs, y_train)
        loss.backward()
        optimizer.step()

        train_losses.append(loss.item())

        with torch.no_grad():
            train_pred = (outputs > 0.5).float()
            train_acc = (train_pred == y_train).float().mean().item()
            train_accs.append(train_acc)

        model.eval()
        with torch.no_grad():
            test_outputs = model(X_test)
            test_loss = criterion(test_outputs, y_test)
            test_losses.append(test_loss.item())

            test_pred = (test_outputs > 0.5).float()
            test_acc = (test_pred == y_test).float().mean().item()
            test_accs.append(test_acc)

        if (epoch + 1) % 100 == 0:
            print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}, '
                  f'Train Acc: {train_acc:.4f}, Test Acc: {test_acc:.4f}')

    return train_losses, test_losses, train_accs, test_accs

7.4. So sánh tất cả các kỹ thuật

Sau khi áp dụng các kỹ thuật trên, chúng ta sẽ so sánh hiệu suất của chúng với mô hình Baseline (chỉ dùng ReLU). Việc này giúp ta thấy rõ tác động của từng phương pháp lên quá trình huấn luyện và kết quả kiểm thử.

Kết quả so sánh các kỹ thuật:

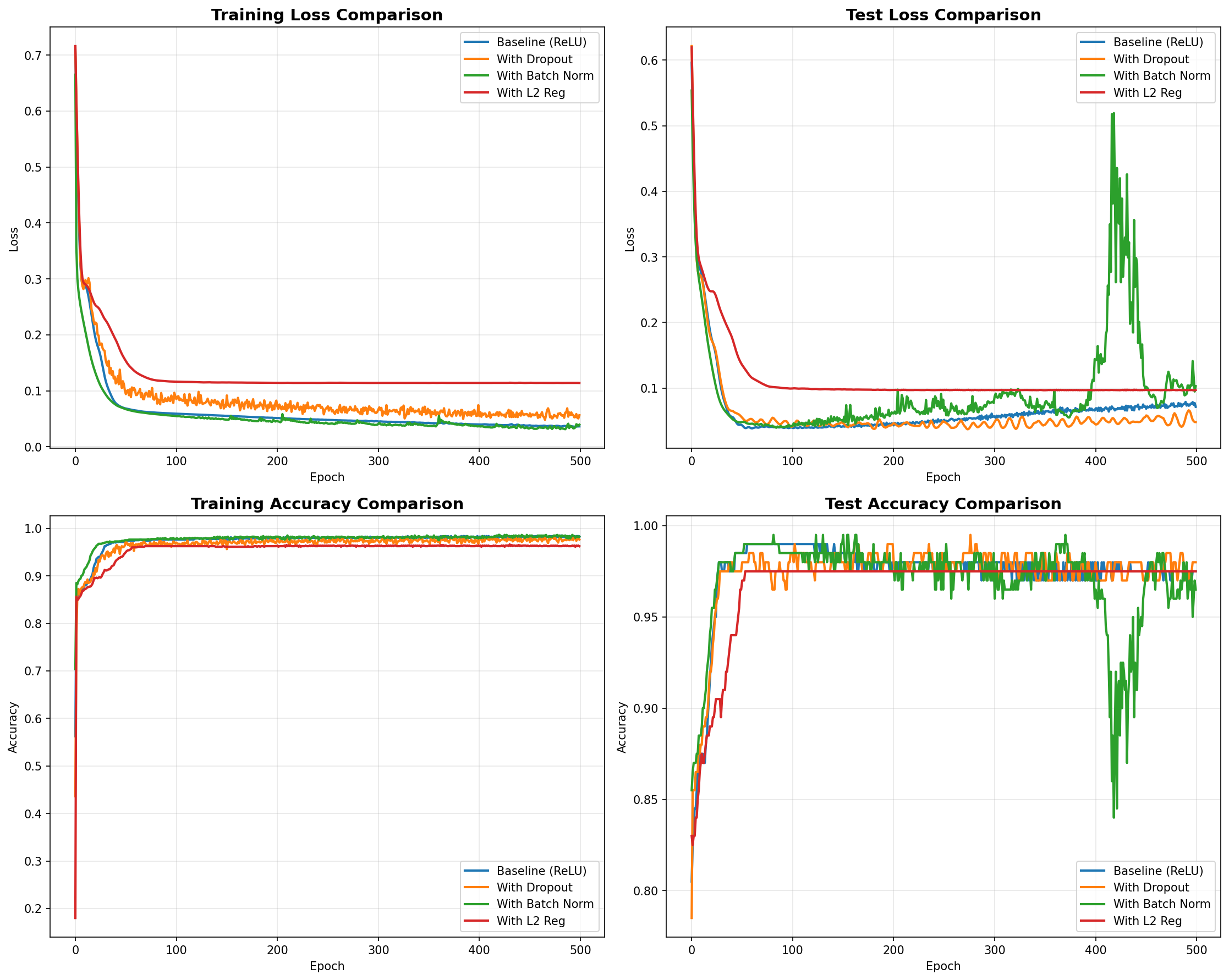
Hình 11: Hình ảnh của việc huấn luyện mô hình khi áp dụng những kỹ thuật cải thiện

Để đánh giá mức độ overfitting, ta tính chênh lệch (gap) giữa độ chính xác trên tập huấn luyện và tập kiểm thử. Gap càng nhỏ chứng tỏ mô hình tổng quát hóa càng tốt.

print(f"Baseline (ReLU): {relu_train_acc[-1] - relu_test_acc[-1]:.4f}")
print(f"With Dropout:    {dropout_train_acc[-1] - dropout_test_acc[-1]:.4f}")
print(f"With Batch Norm: {bn_train_acc[-1] - bn_test_acc[-1]:.4f}")
print(f"With L2 Reg:     {l2_train_acc[-1] - l2_test_acc[-1]:.4f}")

Bảng phân tích đánh giá.

==========================================================
OVERFITTING ANALYSIS (Train-Test Accuracy Gap)
==========================================================
Baseline (ReLU): 0.0012
With Dropout:    0.0025
With Batch Norm: 0.0163
With L2 Reg:     -0.0125

Note: Gap nhỏ hơn = ít overfitting hơn

Nhận xét:

• Dropout: Giảm overfitting hiệu quả, train acc thấp hơn nhưng test acc tốt hơn.

• Batch Normalization: Training nhanh hơn, ổn định hơn.

• L2 Regularization: Giảm weights lớn, giúp model đơn giản hơn.

8. Kết luận

Multi-Layer Perceptron (MLP) là bước đệm quan trọng để bước vào thế giới Deep Learning. Mặc dù đối với dữ liệu ảnh phức tạp, MLP không hiệu quả bằng Convolutional Neural Networks (CNN) do làm mất thông tin không gian khi duỗi phẳng ảnh (Flatten), nhưng nó vẫn cực kỳ mạnh mẽ đối với dữ liệu dạng bảng (tabular data) và là thành phần cốt lõi nằm trong các kiến trúc lớn hơn (ví dụ: lớp Fully Connected cuối cùng trong CNN hay trong Transformer).

Hy vọng bài viết này đã giúp bạn nắm vững từ lý thuyết toán học đến cách code một mạng MLP hoàn chỉnh. Chúc bạn thành công trên con đường chinh phục AI!

Refernces

[1] Ảnh được lấy từ tài liệu khóa học AIO Module 06 Tuần 03

[2] Code về MLP được lấy trong repo sau: MLP-Blog.