Bạn có bao giờ tự hỏi: "Tại sao mình không thể dùng accuracy cho regression như classification?" Hay "MAE và MSE khác nhau như thế nào, và khi nào nên dùng cái nào?" Mình cũng từng như vậy, và sau nhiều lần "đau đầu" với các metrics.
Trong bài viết này, mình sẽ cùng các bạn khám phá các loại metrics và loss functions cho regression, kèm theo những ví dụ cụ thể mà mình đã gặp trong thực tế. Hy vọng sẽ giúp các bạn tránh được những "cạm bẫy" mà mình đã từng vấp phải!
I. Nhóm Sai số Phụ thuộc vào Thang đo (Scale-dependent Errors)
Đầu tiên, mình muốn nói về nhóm metrics này vì chúng là những cái "cơ bản nhất" mà ai cũng sẽ gặp khi làm regression. Nhưng đừng vội coi thường nhé, vì chúng có những "cạm bẫy" mà mình đã từng mắc phải!
Các sai số này phụ thuộc vào thang đo (đơn vị) của dữ liệu, nghĩa là nếu bạn đổi đơn vị (ví dụ từ triệu VND sang nghìn VND), giá trị của metric sẽ thay đổi. Điều này có thể gây khó khăn khi so sánh giữa các dự án khác nhau.
1. Sai số Trung bình (Mean Error - ME) - Đơn giản nhưng đầy "bẫy"
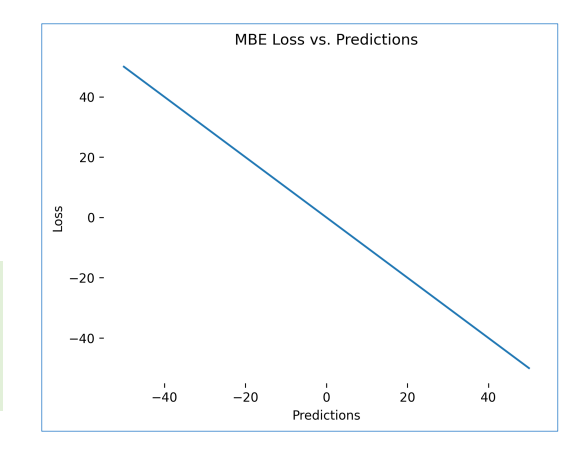
Hình 1: Mean Error Loss
Công thức:
$$ME = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)$$
Trong đó:
- yi: Giá trị thực tế
- ŷi: Giá trị dự đoán
- n: Số lượng mẫu
Ví dụ cụ thể:
Giả sử chúng ta có 5 mẫu dự đoán giá nhà (đơn vị: triệu VND):
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | Sai số (yi - ŷi) |
|---|---|---|
| 1000 | 1050 | -50 |
| 2000 | 1950 | 50 |
| 1500 | 1480 | 20 |
| 3000 | 3020 | -20 |
| 2500 | 2450 | 50 |
ME = (-50 + 50 + 20 - 20 + 50) / 5 = $\frac{50}{5}$ = 10
Giải thích: ME = 10 > 0 cho thấy mô hình có xu hướng dự đoán thấp hơn giá trị thực tế (underestimate) trung bình 10 triệu VND. Đây là một thông tin hữu ích về bias của mô hình, nhưng như bạn sẽ thấy ở ví dụ tiếp theo, ME có một "cạm bẫy" lớn!
Ví dụ về Error Cancellation:
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | Sai số (yi - ŷi) |
|---|---|---|
| 100 | 150 | -50 |
| 200 | 150 | 50 |
| 300 | 350 | -50 |
| 400 | 350 | 50 |
| 500 | 500 | 0 |
ME = (-50 + 50 - 50 + 50 + 0) / 5 = 0
Đây chính là "cạm bẫy" mà mình đã nói! Mặc dù ME = 0, nhưng mô hình vẫn có sai số đáng kể! Các sai số dương và âm đã triệt tiêu lẫn nhau. Mình đã từng "vỡ mộng" khi thấy ME = 0 và nghĩ rằng mô hình của mình hoàn hảo, nhưng thực ra nó vẫn sai rất nhiều. Đây là lý do tại sao chúng ta cần các metrics khác như MAE.
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Đơn giản, dễ tính toán | Các sai số dương và âm có thể triệt tiêu lẫn nhau, gây hiểu lầm |
| Cung cấp thông tin về hướng của độ lệch (bias) | ME = 0 không đảm bảo mô hình chính xác |
| ME < 0: mô hình overestimate | Không phản ánh độ lớn của sai số |
| ME > 0: mô hình underestimate | Dễ bị ảnh hưởng bởi các giá trị ngoại lai lớn |
| ME = 0: không có độ lệch hệ thống | Không thể so sánh giữa các tập dữ liệu có thang đo khác nhau |
2. Sai số Tuyệt đối Trung bình (Mean Absolute Error - MAE) - "Cứu tinh" của ME
Sau khi "vỡ mộng" với ME, mình đã tìm đến MAE như một giải pháp. MAE khắc phục nhược điểm triệt tiêu của ME bằng cách sử dụng giá trị tuyệt đối. Đây là một trong những metrics mà mình thích nhất vì nó đơn giản và dễ hiểu.
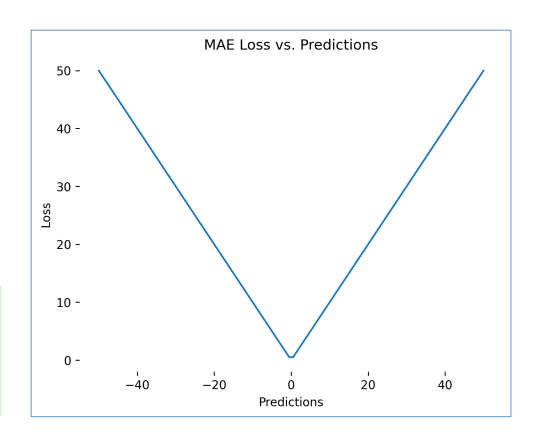
Hình 2: Mean Absolute Error
Công thức:
$$MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$$
Ví dụ cụ thể:
Sử dụng cùng dữ liệu giá nhà ở trên:
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | |yi - ŷi| |
|---|---|---|
| 1000 | 1050 | 50 |
| 2000 | 1950 | 50 |
| 1500 | 1480 | 20 |
| 3000 | 3020 | 20 |
| 2500 | 2450 | 50 |
MAE = (50 + 50 + 20 + 20 + 50) / 5 = $\frac{190}{5}$ = 38 triệu VND
Giải thích: Trung bình, mô hình sai lệch 38 triệu VND so với giá trị thực tế.
Ví dụ so sánh với Outliers:
Trường hợp 1: Không có outlier
| yi | ŷi | |yi - ŷi| |
|---|---|---|
| 10 | 11 | 1 |
| 12 | 13 | 1 |
| 15 | 14 | 1 |
| 18 | 17 | 1 |
| 20 | 19 | 1 |
MAE = (1 + 1 + 1 + 1 + 1) / 5 = 1.0
Trường hợp 2: Có 1 outlier
| yi | ŷi | |yi - ŷi| |
|---|---|---|
| 10 | 11 | 1 |
| 12 | 13 | 1 |
| 15 | 14 | 1 |
| 18 | 17 | 1 |
| 7 | 20 | 13 |
MAE = (1 + 1 + 1 + 1 + 13) / 5 = 3.4
MAE tăng từ 1.0 lên 3.4 (tăng 3.4 lần), nhưng ít nhạy cảm hơn so với MSE (sẽ thấy ở phần sau). Đây là một điểm mạnh của MAE - nó không bị "điên cuồng" khi gặp outliers như MSE. Nhưng điều này cũng có nghĩa là nó có thể "bỏ qua" những lỗi lớn mà bạn muốn mô hình chú ý đến.
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Đơn giản, dễ hiểu và tính toán | Không cho biết hướng của sai số (over/underestimate) |
| Khắc phục nhược điểm triệt tiêu của ME | Không cung cấp thông tin về phương sai hoặc độ phân tán |
| Ít nhạy cảm với outliers hơn MSE | Áp dụng trọng số bằng nhau cho tất cả sai số |
| Dễ diễn giải: "sai lệch trung bình X đơn vị" | Ít nhạy cảm với các lỗi lớn so với MSE |
| Phù hợp khi muốn mô hình tập trung vào median | Phụ thuộc vào thang đo của dữ liệu |
3. Sai số Bình phương Trung bình (Mean Squared Error - MSE) - "Kẻ phạt nặng"
Nếu MAE là người "hiền lành", thì MSE là "kẻ phạt nặng". MSE trừng phạt các sai số lớn rất nghiêm khắc bằng cách bình phương chúng. Điều này có thể tốt hoặc xấu, tùy thuộc vào dữ liệu của bạn. Mình đã từng dùng MSE cho một dataset có nhiều outliers và kết quả là... mô hình của mình bị "ám ảnh" bởi những điểm ngoại lai đó!
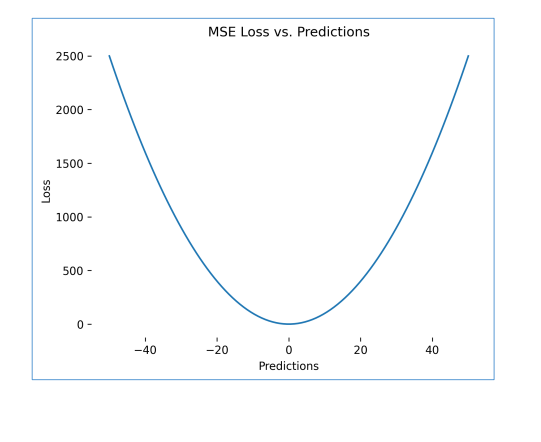
Hình 3: Mean Squared Error
Công thức:
$$MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$$
Ví dụ cụ thể:
Sử dụng cùng dữ liệu giá nhà:
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | (yi - ŷi) | (yi - ŷi)² |
|---|---|---|---|
| 1000 | 1050 | -50 | 2500 |
| 2000 | 1950 | 50 | 2500 |
| 1500 | 1480 | 20 | 400 |
| 3000 | 3020 | -20 | 400 |
| 2500 | 2450 | 50 | 2500 |
MSE = (2500 + 2500 + 400 + 400 + 2500) / 5 = $\frac{8300}{5}$ = 1660
Giải thích: MSE = 1660 (triệu VND)². Lưu ý đơn vị là bình phương!
Ví dụ về độ nhạy cảm với Outliers:
Trường hợp 1: Không có outlier
| yi | ŷi | (yi - ŷi) | (yi - ŷi)² |
|---|---|---|---|
| 10 | 11 | -1 | 1 |
| 12 | 13 | -1 | 1 |
| 15 | 14 | 1 | 1 |
| 18 | 17 | 1 | 1 |
| 20 | 19 | 1 | 1 |
MSE = (1 + 1 + 1 + 1 + 1) / 5 = 1.0
Trường hợp 2: Có 1 outlier
| yi | ŷi | (yi - ŷi) | (yi - ŷi)² |
|---|---|---|---|
| 10 | 11 | -1 | 1 |
| 12 | 13 | -1 | 1 |
| 15 | 14 | 1 | 1 |
| 18 | 17 | 1 | 1 |
| 7 | 20 | -13 | 169 |
MSE = (1 + 1 + 1 + 1 + 169) / 5 = 34.6
MSE tăng từ 1.0 lên 34.6 (tăng 34.6 lần!), trong khi MAE chỉ tăng 3.4 lần. Đây chính là lý do tại sao mình nói MSE là "kẻ phạt nặng"! Một điểm outlier có thể làm "nổ tung" giá trị MSE. Điều này có thể tốt nếu bạn muốn mô hình chú ý đến những lỗi lớn, nhưng cũng có thể dẫn đến overfitting nếu dữ liệu của bạn có nhiều noise.
Ví dụ về phụ thuộc thang đo:
- Dữ liệu gốc (triệu VND): MSE = 1660
- Nếu đổi sang nghìn VND: MSE = 1,660,000,000
- Nếu đổi sang tỷ VND: MSE = 0.00166
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Trừng phạt các sai số lớn nghiêm khắc hơn | Rất nhạy cảm với outliers |
| Khuyến khích mô hình robust hơn | Có thể dẫn đến overfitting |
| Phù hợp khi muốn mô hình tập trung vào mean | Phụ thuộc vào thang đo của dữ liệu |
| Có đạo hàm liên tục, dễ tối ưu hóa | Đơn vị là bình phương, khó diễn giải trực tiếp |
| Được sử dụng rộng rãi trong thống kê | Không thể so sánh giữa các tập dữ liệu khác nhau |
4. Sai số Bình phương Trung bình Gốc (Root Mean Squared Error - RMSE)
Công thức:
$$RMSE = \sqrt{MSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}$$
Ví dụ cụ thể:
Từ ví dụ MSE ở trên: MSE = 1660
RMSE = √1660 ≈ 40.74 triệu VND
Giải thích: RMSE có cùng đơn vị với dữ liệu gốc, dễ diễn giải hơn MSE.
So sánh MAE vs RMSE:
| yi | ŷi | |yi - ŷi| | (yi - ŷi)² |
|---|---|---|---|
| 10 | 11 | 1 | 1 |
| 10 | 12 | 2 | 4 |
| 10 | 13 | 3 | 9 |
| 10 | 14 | 4 | 16 |
| 10 | 15 | 5 | 25 |
MAE = (1 + 2 + 3 + 4 + 5) / 5 = 3.0
MSE = (1 + 4 + 9 + 16 + 25) / 5 = $\frac{55}{5}$ = 11.0
RMSE = √11.0 ≈ 3.32
RMSE luôn lớn hơn hoặc bằng MAE (RMSE ≥ MAE) vì phép bình phương làm tăng trọng số của các sai số lớn.
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Có cùng đơn vị với dữ liệu gốc, dễ diễn giải | Vẫn nhạy cảm với outliers (như MSE) |
| Trừng phạt các sai số lớn nghiêm khắc | Phụ thuộc vào thang đo |
| Được sử dụng rộng rãi trong thực tế | Không thể so sánh giữa các tập dữ liệu khác nhau |
| Phù hợp khi muốn mô hình tập trung vào mean | Có thể dẫn đến overfitting |
II. Nhóm Sai số Dựa trên Tỷ lệ Phần trăm (Percentage Errors) - So sánh "công bằng" hơn
Sau khi làm việc với nhiều dự án khác nhau, mình nhận ra một vấn đề: làm sao để so sánh hiệu suất của một mô hình dự đoán giá nhà (triệu VND) với một mô hình dự đoán giá sản phẩm (nghìn VND)? Đây là lúc các metrics dựa trên phần trăm phát huy tác dụng!
Các metrics này giúp so sánh hiệu suất giữa các bộ dữ liệu có thang đo khác nhau bằng cách chuẩn hóa theo phần trăm. Nhưng như mọi thứ trong cuộc sống, chúng cũng có những "cạm bẫy" riêng.
1. Sai số Phần trăm Tuyệt đối Trung bình (Mean Absolute Percentage Error - MAPE)
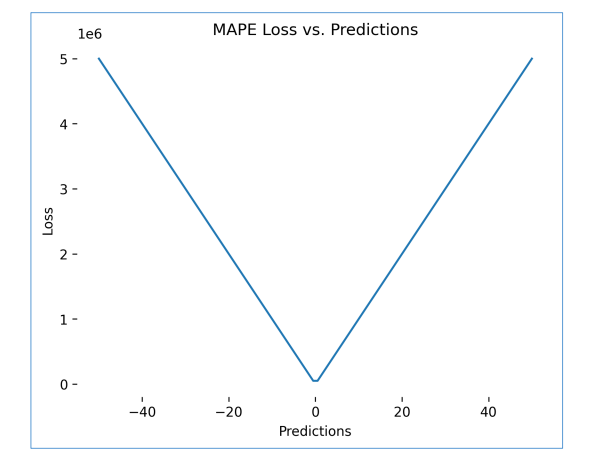
Hình 4: Mean Absolute Percentage Error
Công thức:
$$MAPE = \frac{1}{n} \sum_{i=1}^{n} \left|\frac{y_i - \hat{y}_i}{y_i}\right| \times 100\%$$
Ví dụ cụ thể:
Dự đoán giá sản phẩm (nghìn VND):
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | |yi - ŷi| | |(yi - ŷi)/yi| × 100% |
|---|---|---|---|
| 100 | 110 | 10 | 10% |
| 200 | 190 | 10 | 5% |
| 300 | 315 | 15 | 5% |
| 400 | 380 | 20 | 5% |
| 500 | 520 | 20 | 4% |
MAPE = (10% + 5% + 5% + 5% + 4%) / 5 = 5.8%
Giải thích: Trung bình, mô hình sai lệch 5.8% so với giá trị thực tế.
Ví dụ về tính bất đối xứng:
Trường hợp 1: Overforecast (dự đoán quá cao)
- Giá trị thực tế: 100
- Giá trị dự đoán: 150
- Sai số tuyệt đối: 50
- MAPE = |(100 - 150) / 100| × 100% = 50%
Trường hợp 2: Underforecast (dự đoán quá thấp)
- Giá trị thực tế: 150
- Giá trị dự đoán: 100
- Sai số tuyệt đối: 50 (cùng giá trị!)
- MAPE = |(150 - 100) / 150| × 100% = 33.3%
Đây là một điều thú vị mà mình đã phát hiện ra: cùng một sai số tuyệt đối (50), nhưng MAPE xử lý khác nhau! Overforecast (dự đoán quá cao) bị phạt nặng hơn underforecast (dự đoán quá thấp). Điều này có thể gây ra bias trong đánh giá, đặc biệt là khi bạn có nhiều giá trị nhỏ trong dataset.
Ví dụ về nhạy cảm với giá trị nhỏ:
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | Sai số tuyệt đối | MAPE |
|---|---|---|---|
| 10 | 15 | 5 | 50% |
| 100 | 105 | 5 | 5% |
| 1000 | 1005 | 5 | 0.5% |
Cùng một sai số tuyệt đối (5), nhưng MAPE phạt rất nặng khi giá trị thực tế nhỏ!
Ví dụ về giá trị 0:
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | MAPE |
|---|---|---|
| 0 | 10 | Không xác định (chia cho 0) |
| 0 | 0 | Không xác định (0/0) |
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Độc lập với thang đo (Scale-independent) | Bất đối xứng: xử lý overforecast và underforecast khác nhau |
| Dễ so sánh hiệu suất giữa các tập dữ liệu khác nhau | Nhạy cảm với giá trị thực tế nhỏ |
| Dễ diễn giải: "sai lệch X%" | Không xác định khi giá trị thực tế = 0 |
| Phù hợp cho dữ liệu có thang đo lớn | Phạt nặng các sai số ở giá trị nhỏ, bất kể tác động thực tế |
| Được sử dụng rộng rãi trong forecasting | Có thể gây hiểu lầm khi giá trị thực tế gần 0 |
2. Sai số Phần trăm Tuyệt đối Trung bình Đối xứng (Symmetric Mean Absolute Percentage Error - sMAPE)
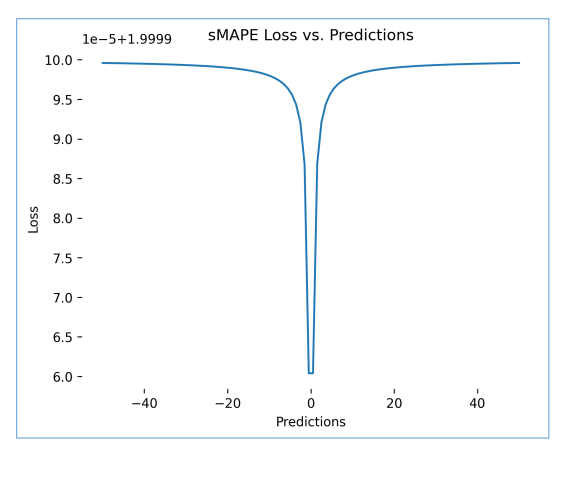
Hình 5: Symmetric Mean Absolute Percentage Error
Công thức:
$$sMAPE = \frac{1}{n} \sum_{i=1}^{n} \frac{|y_i - \hat{y}_i|}{(|y_i| + |\hat{y}_i|) / 2} \times 100\%$$
Ví dụ cụ thể:
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | |yi - ŷi| | (|yi| + |ŷi|)/2 | sMAPE (%) |
|---|---|---|---|---|
| 100 | 110 | 10 | 105 | 9.52% |
| 200 | 190 | 10 | 195 | 5.13% |
| 300 | 315 | 15 | 307.5 | 4.88% |
| 400 | 380 | 20 | 390 | 5.13% |
| 500 | 520 | 20 | 510 | 3.92% |
sMAPE = (9.52% + 5.13% + 4.88% + 5.13% + 3.92%) / 5 = 5.72%
Ví dụ so sánh MAPE vs sMAPE:
Trường hợp 1: Overforecast
- $y_i = 100$, $\hat{y}_i = 150$
- MAPE = |(100 - 150) / 100| × 100% = 50%
- sMAPE = |100 - 150| / ((100 + 150) / 2) × 100% = 50 / 125 × 100% = 40%
Trường hợp 2: Underforecast
- $y_i = 150$, $\hat{y}_i = 100$
- MAPE = |(150 - 100) / 150| × 100% = 33.3%
- sMAPE = |150 - 100| / ((150 + 100) / 2) × 100% = 50 / 125 × 100% = 40%
sMAPE xử lý đối xứng hơn MAPE (cùng 40% cho cả hai trường hợp), nhưng vẫn chưa hoàn toàn đối xứng.
Ví dụ về giá trị > 100%:
- $y_i = 10$, $\hat{y}_i = 100$
- sMAPE = |10 - 100| / ((10 + 100) / 2) × 100% = 90 / 55 × 100% = 163.6%
sMAPE có thể vượt quá 100%, gây khó khăn trong diễn giải.
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Độc lập với thang đo | Chỉ giảm một phần tính bất đối xứng, chưa hoàn toàn đối xứng |
| Giảm độ nhạy cảm với giá trị 0 hơn MAPE | Có thể tạo ra kết quả khó hiểu với một số phân phối dữ liệu |
| Xử lý overforecast và underforecast đối xứng hơn MAPE | Có thể vượt quá 100%, khó diễn giải |
| Ổn định hơn MAPE | Khó diễn giải hơn MAPE ở các giá trị cao |
| Phù hợp khi cần tính đối xứng | Phụ thuộc vào cả giá trị thực tế và dự đoán |
III. Nhóm Sai số Tương đối và Tỷ lệ (Relative and Scaled Errors)
Các metrics này so sánh hiệu suất của mô hình với một phương pháp chuẩn (benchmark).
1. Sai số Tuyệt đối Tương đối Trung bình (Mean Relative Absolute Error - MRAE)
Công thức:
$$MRAE = \frac{1}{n} \sum_{i=1}^{n} \frac{|y_i - \hat{y}_i|}{|y_i - \hat{y}_{i,benchmark}|}$$
Trong đó $\hat{y}_{i,benchmark}$ là dự đoán từ phương pháp chuẩn (ví dụ: Naive method - dự đoán bằng giá trị trước đó).
Ví dụ cụ thể:
Dự đoán doanh số hàng tháng (triệu VND) với Naive method (dự đoán = giá trị tháng trước):
| Tháng | Giá trị thực tế (yi) | Naive (ŷi_naive) | Mô hình (ŷi) | |yi - ŷi| | |yi - ŷi_naive| | MRAE |
|---|---|---|---|---|---|---|
| 1 | 100 | - | 105 | - | - | - |
| 2 | 120 | 100 | 118 | 2 | 20 | 0.1 |
| 3 | 110 | 120 | 112 | 2 | 10 | 0.2 |
| 4 | 130 | 110 | 128 | 2 | 20 | 0.1 |
| 5 | 125 | 130 | 124 | 1 | 5 | 0.2 |
MRAE = (0.1 + 0.2 + 0.1 + 0.2) / 4 = 0.15
Giải thích: MRAE = 0.15 < 1, nghĩa là mô hình tốt hơn Naive method 6.67 lần (1/0.15).
Ví dụ về MRAE > 1:
| yi | ŷi_naive | ŷi | |yi - ŷi| | |yi - ŷi_naive| | MRAE |
|---|---|---|---|---|---|
| 100 | 90 | 95 | 5 | 10 | 0.5 |
| 120 | 100 | 130 | 10 | 20 | 0.5 |
| 110 | 120 | 90 | 20 | 10 | 2.0 |
| 130 | 110 | 100 | 30 | 20 | 1.5 |
MRAE = (0.5 + 0.5 + 2.0 + 1.5) / 4 = 1.125
MRAE > 1 cho thấy mô hình hoạt động kém hơn Naive method.
Ví dụ về chia cho 0:
| yi | ŷi_naive | ŷi | |yi - ŷi| | |yi - ŷi_naive| | MRAE |
|---|---|---|---|---|---|
| 100 | 100 | 105 | 5 | 0 | Không xác định (chia cho 0) |
Khi Naive method dự đoán chính xác ($y_i = \hat{y}_{i,naive}$), MRAE không xác định.
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Độc lập với thang đo | Không xác định khi sai số benchmark = 0 |
| Dễ diễn giải: MRAE < 1 = tốt hơn benchmark | Phụ thuộc vào benchmark được chọn |
| Cho phép so sánh với phương pháp cơ bản | Nhạy cảm với mẫu số nhỏ |
| Hữu ích trong forecasting | Nếu benchmark không có ý nghĩa, kết quả khó diễn giải |
| Có thể so sánh giữa các mô hình khác nhau | Sai số tương đối có thể bị phóng đại quá mức |
2. Sai số Tuyệt đối Trung bình Theo Tỷ lệ (Mean Absolute Scaled Error - MASE)
Công thức:
$$MASE = \frac{MAE_{model}}{MAE_{naive\_in-sample}}$$
Trong đó:
- MAE_model: MAE của mô hình trên tập test
- MAE_naive_in-sample: MAE của Naive method trên tập train
Ví dụ cụ thể:
Tập Train (in-sample):
| Tháng | yi | yi-1 (giá trị trước) | |yi - yi-1| |
|---|---|---|---|
| 1 | 100 | - | - |
| 2 | 120 | 100 | 20 |
| 3 | 110 | 120 | 10 |
| 4 | 130 | 110 | 20 |
| 5 | 125 | 130 | 5 |
MAE_naive_in-sample = (20 + 10 + 20 + 5) / 4 = 13.75
Tập Test:
| Tháng | yi | ŷi (mô hình) | |yi - ŷi| |
|---|---|---|---|
| 6 | 140 | 138 | 2 |
| 7 | 135 | 137 | 2 |
| 8 | 145 | 143 | 2 |
| 9 | 150 | 148 | 2 |
MAE_model = (2 + 2 + 2 + 2) / 4 = 2.0
MASE = $\frac{2.0}{13.75}$ = 0.145
Giải thích: MASE = 0.145 < 1, nghĩa là mô hình tốt hơn Naive method khoảng 6.9 lần (1/0.145).
Ví dụ về MASE > 1:
Giả sử mô hình kém hơn:
- MAE_model = 20.0
- MAE_naive_in-sample = 13.75
- MASE = $\frac{20.0}{13.75}$ = 1.45
MASE > 1 cho thấy mô hình hoạt động kém hơn Naive method.
Ví dụ về chia cho 0:
Nếu tất cả các giá trị trong tập train đều bằng nhau:
- $y_i = [100, 100, 100, 100, 100]$
- MAE_naive_in-sample = 0 (vì tất cả $|y_i - y_{i-1}| = 0$)
- MASE không xác định (chia cho 0)
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Độc lập với thang đo | Không xác định khi tất cả quan sát lịch sử bằng nhau |
| Cho phép so sánh giữa các chuỗi dữ liệu khác nhau | Phụ thuộc vào phương pháp benchmark (thường là Naive) |
| Thích hợp ngay cả khi dữ liệu có xu hướng hoặc tính thời vụ | Cần tính toán trên cả tập train và test |
| Dễ diễn giải: MASE < 1 = tốt hơn benchmark | Có thể khó hiểu nếu không quen với khái niệm scaling |
| Không bị ảnh hưởng bởi scale của dữ liệu | Ít được sử dụng hơn MAPE trong một số lĩnh vực |
IV. Các Metrics Quan trọng Khác
Sai số Logarit Bình phương Trung bình Gốc (Root Mean Squared Logarithmic Error - RMSLE)
Công thức:
$$RMSLE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} [\log(1 + y_i) - \log(1 + \hat{y}_i)]^2}$$
Ví dụ cụ thể:
Dự đoán giá nhà (triệu VND):
| Giá trị thực tế (yi) | Giá trị dự đoán (ŷi) | log(1 + yi) | log(1 + ŷi) | (log(1 + yi) - log(1 + ŷi))² |
|---|---|---|---|---|
| 1000 | 1050 | 6.908 | 6.957 | 0.0024 |
| 2000 | 1950 | 7.601 | 7.576 | 0.0006 |
| 1500 | 1480 | 7.314 | 7.300 | 0.0002 |
| 3000 | 3020 | 8.006 | 8.014 | 0.0001 |
| 2500 | 2450 | 7.824 | 7.803 | 0.0004 |
RMSLE = √[(0.0024 + 0.0006 + 0.0002 + 0.0001 + 0.0004) / 5] = √$\frac{0.0037}{5}$ = √0.00074 ≈ 0.027
Ví dụ về xử lý outliers:
Trường hợp 1: Không có outlier
| yi | ŷi | (yi - ŷi)² | (log(1 + yi) - log(1 + ŷi))² |
|---|---|---|---|
| 10 | 11 | 1 | 0.0009 |
| 12 | 13 | 1 | 0.0008 |
| 15 | 14 | 1 | 0.0006 |
RMSE ≈ 1.0, RMSLE ≈ 0.028
Trường hợp 2: Có outlier
| yi | ŷi | (yi - ŷi)² | (log(1 + yi) - log(1 + ŷi))² |
|---|---|---|---|
| 10 | 11 | 1 | 0.0009 |
| 12 | 13 | 1 | 0.0008 |
| 7 | 20 | 169 | 0.1089 |
RMSE ≈ 7.5 (tăng mạnh), RMSLE ≈ 0.19 (tăng ít hơn)
RMSLE ít nhạy cảm với outliers hơn RMSE nhờ phép biến đổi logarit.
Ví dụ về tính bất đối xứng:
Trường hợp 1: Underforecast (dự đoán thấp)
- $y_i = 1000$, $\hat{y}_i = 500$
- RMSLE contribution = (log(1001) - log(501))² = (6.908 - 6.217)² = 0.477
Trường hợp 2: Overforecast (dự đoán cao)
- $y_i = 500$, $\hat{y}_i = 1000$
- RMSLE contribution = (log(501) - log(1001))² = (6.217 - 6.908)² = 0.477
RMSLE xử lý đối xứng hơn MAPE, nhưng vẫn có một số bất đối xứng với các giá trị cụ thể.
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Độc lập với thang đo | Vẫn có một số tính bất đối xứng (như MAPE) |
| Ít nhạy cảm với outliers hơn RMSE | Khó diễn giải hơn các metrics đơn giản |
| Phù hợp cho dữ liệu có phạm vi rộng | Không thể áp dụng khi có giá trị âm |
| Phép biến đổi logarit giúp xử lý dữ liệu có phân phối lệch | Cần hiểu về phép biến đổi logarit |
| Được sử dụng trong các cuộc thi như Kaggle | Có thể gây khó hiểu cho người không quen thuộc |
V. Từ Metrics đến Hàm Loss (Loss Functions) - Mối liên kết quan trọng
Đây là phần mà mình nghĩ là quan trọng nhất nhưng lại ít được chú ý: mối quan hệ giữa Metrics và Loss Functions. Khi mới bắt đầu, mình đã từng tối ưu hóa với MSE nhưng lại đánh giá bằng MAE, và kết quả là... mô hình của mình không hoạt động như mong đợi!
Metrics đánh giá hiệu suất của mô hình, nhưng khi sử dụng chúng để tối ưu hóa, chúng trở thành Hàm Loss. Điều quan trọng là bạn cần hiểu rằng chúng nên có cùng tính chất - nếu bạn tối ưu hóa với MAE, hãy đánh giá bằng MAE!
Mối quan hệ giữa Loss và Metrics
Ví dụ minh họa:
Giả sử chúng ta có phân phối lỗi như sau:
- Lỗi: [-10, -5, 0, 5, 10, 15, 20]
- Median (trung vị): 5
- Mean (trung bình): 5
Khi sử dụng MAE làm Loss:
- Mô hình sẽ được tối ưu để giảm thiểu tổng $|y_i - \hat{y}_i|$
- Điều này kéo các dự đoán về phía median của phân phối
- Ít bị ảnh hưởng bởi outliers
Khi sử dụng MSE làm Loss:
- Mô hình sẽ được tối ưu để giảm thiểu tổng $(y_i - \hat{y}_i)^2$
- Điều này kéo các dự đoán về phía mean của phân phối
- Rất nhạy cảm với outliers
Ví dụ cụ thể:
Phân phối giá nhà thực tế: [500, 600, 700, 800, 900, 1000, 5000]
- Median = 800
- Mean = 1214.3
Mô hình A (tối ưu với MAE):
- Dự đoán trung bình ≈ 800 (gần median)
- MAE thấp, nhưng có thể bỏ qua các giá trị ngoại lai
Mô hình B (tối ưu với MSE):
- Dự đoán trung bình ≈ 1214 (gần mean)
- MSE thấp, nhưng bị ảnh hưởng mạnh bởi giá trị 5000
Nguyên tắc quan trọng: Hàm loss được sử dụng để tối ưu hóa mô hình và tiêu chí đánh giá (metrics) nên có cùng tính chất (tối ưu hóa cùng một thống kê của phân phối).
Bảng so sánh:
| Loss Function | Tối ưu hóa về | Nhạy cảm với Outliers | Phù hợp khi |
|---|---|---|---|
| MAE | Median | Thấp | Có nhiều outliers, muốn robust |
| MSE | Mean | Cao | Muốn trừng phạt lỗi lớn |
| RMSE | Mean | Cao | Muốn trừng phạt lỗi lớn, dễ diễn giải |
| Huber Loss | Cân bằng | Trung bình | Cần cân bằng giữa MAE và MSE |
Huber Loss
Công thức:
$$L_{\delta}(y, \hat{y}) = \begin{cases} 0.5 \times (y - \hat{y})^2 & \text{nếu } |y - \hat{y}| \leq \delta \\ \delta \times |y - \hat{y}| - 0.5 \times \delta^2 & \text{nếu } |y - \hat{y}| > \delta \end{cases}$$
Trong đó δ (delta) là tham số ngưỡng.
Ví dụ cụ thể:
Giả sử δ = 5:
| yi | ŷi | |yi - ŷi| | Loss (δ = 5) |
|---|---|---|---|
| 10 | 12 | 2 | 0.5 × 2² = 2.0 (MSE) |
| 10 | 13 | 3 | 0.5 × 3² = 4.5 (MSE) |
| 10 | 14 | 4 | 0.5 × 4² = 8.0 (MSE) |
| 10 | 15 | 5 | 0.5 × 5² = 12.5 (MSE) |
| 10 | 18 | 8 | 5 × 8 - 0.5 × 5² = 27.5 (MAE-like) |
| 10 | 25 | 15 | 5 × 15 - 0.5 × 5² = 62.5 (MAE-like) |
Giải thích:
- Khi sai số nhỏ (≤ 5): Huber Loss hoạt động như MSE (bình phương)
- Khi sai số lớn (> 5): Huber Loss hoạt động như MAE (tuyến tính)
So sánh với MAE và MSE:
| |yi - ŷi| | MAE | MSE | Huber (δ=5) |
|---|---|---|---|
| 1 | 1 | 1 | 0.5 |
| 3 | 3 | 9 | 4.5 |
| 5 | 5 | 25 | 12.5 |
| 10 | 10 | 100 | 27.5 |
| 20 | 20 | 400 | 62.5 |
Huber Loss tăng chậm hơn MSE nhưng nhanh hơn MAE cho các lỗi lớn.
Ví dụ về lựa chọn δ:
δ = 1 (nhạy cảm hơn với outliers):
- Nhiều lỗi được xử lý như MAE
- Ít nhạy cảm với outliers hơn
δ = 10 (nhạy cảm hơn với lỗi nhỏ):
- Nhiều lỗi được xử lý như MSE
- Nhạy cảm hơn với lỗi nhỏ
Bảng Ưu điểm và Nhược điểm:
| Ưu điểm | Nhược điểm |
|---|---|
| Kết hợp ưu điểm của MAE và MSE | Cần chọn tham số δ phù hợp |
| Ít nhạy cảm với outliers hơn MSE | Phức tạp hơn MAE và MSE |
| Trừng phạt lỗi lớn hơn MAE | Cần điều chỉnh δ cho từng bài toán |
| Có đạo hàm liên tục, dễ tối ưu hóa | Ít được sử dụng hơn MAE/MSE trong thực tế |
| Phù hợp khi cần cân bằng giữa robust và sensitivity | Có thể khó diễn giải cho người không quen thuộc |
Tóm lại
Việc lựa chọn metrics đánh giá và hàm loss phù hợp là chìa khóa để xây dựng mô hình hồi quy hiệu quả.
Bảng Hướng dẫn Lựa chọn
| Tình huống | Metrics/Loss được khuyến nghị | Lý do |
|---|---|---|
| Có nhiều outliers, muốn robust | MAE | Ít nhạy cảm với outliers, tập trung vào median |
| Muốn trừng phạt nghiêm khắc lỗi lớn | MSE/RMSE | Bình phương làm tăng trọng số lỗi lớn |
| So sánh giữa các tập dữ liệu khác nhau | MAPE, MASE, MRAE | Độc lập với thang đo |
| Cần cân bằng giữa MAE và MSE | Huber Loss | Kết hợp ưu điểm của cả hai |
| Dữ liệu có phạm vi rộng, có outliers | RMSLE | Logarit giúp giảm ảnh hưởng outliers |
| Forecasting, cần so sánh với baseline | MASE | So sánh với Naive method, độc lập thang đo |
| Cần diễn giải dễ hiểu | MAE, RMSE, MAPE | Đơn giản, dễ giải thích |
Nguyên tắc vàng
-
Đồng nhất Loss và Metrics: Nếu bạn tối ưu hóa với MAE, hãy đánh giá bằng MAE. Tương tự với MSE/RMSE.
-
Hiểu rõ dữ liệu: Xem xét phân phối, outliers, và scale của dữ liệu trước khi chọn metrics.
-
Xem xét ngữ cảnh: Metrics phù hợp phụ thuộc vào mục tiêu kinh doanh và rủi ro của từng loại lỗi.
-
Sử dụng nhiều metrics: Không chỉ dựa vào một metric duy nhất, hãy xem xét nhiều góc độ.
Việc lựa chọn đúng công cụ đánh giá, giống như việc chọn đúng ống kính máy ảnh, sẽ giúp bạn nhìn thấy rõ bức tranh về hiệu suất mô hình của mình. Mỗi metric là một góc nhìn khác nhau, và việc hiểu rõ chúng sẽ giúp bạn đưa ra quyết định tốt hơn trong quá trình xây dựng và tối ưu hóa mô hình.
References
[1] Ảnh được lấy từ tài liệu khóa học AIO Module 06 – Tuần 1, AIO 2025.
Chưa có bình luận nào. Hãy là người đầu tiên!