
Mở đầu
Trong các bài toán về phân loại (Classification) chúng ta thường dùng các các chỉ số như Accuracy (Độ chính xác), Log Loss, vân vân mây mây để đánh giá mô hình.
Thế nhưng trong các bài toán dự đoán giá trị liên tục (Regression) như giá nhà hay chứng khoán, các chỉ số Accuracy không thể tính được vì không có khái niệm đúng/sai tuyệt đối như trong bài toán phân loại (Classification).
Do đó 🧐, để xác định mô hình nào (A hay B) tốt hơn trên cùng một bộ dữ liệu, chúng ta cần sử dụng bộ metrics (các chỉ số đánh giá) dành riêng cho bài toán hồi quy. Các chỉ số này thay thế cho Accuracy, tập trung vào việc đánh giá sai số, độ lệch và mức độ phù hợp của giải thuật.
Giới thiệu về Evaluation Metrics
Để khám phá các khía cạnh cốt lõi của Evaluation Metrics, từ định nghĩa, cách thức hoạt động đến thời điểm sử dụng, chúng ta sẽ dựa vào các tiêu chí sau đây:
1. What: Evaluation Metrics là gì? 😳
Evaluation Metrics (Chỉ số đánh giá mô hình) là công cụ định lượng hiệu suất của một mô hình (Quantify the performance of a model).
Nó biến độ "tốt" hay "xấu" của mô hình thành một con số cụ thể, dễ dàng so sánh và theo dõi các mô hình với nhau.
2. How: Evaluation Metrics hoạt động như thế nào? 🤨
Evaluation Metrics diễn ra bằng cách so sánh các dự đoán của mô hình với các giá trị thực tế (ground truth).
Ví dụ: Nếu mô hình dự đoán giá nhà là 5 tỷ, nhưng giá thực tế là 6 tỷ, Evaluation Metrics sẽ tính toán độ sai lệch (1 tỷ) này.
3. Why: Tại sao chúng ta lại cần Evaluation Metrics? 😫
- Tìm ra lỗ hổng hiệu suất (Identify performance gaps): Giúp xác định mô hình đang sai ở đâu để tối ưu hóa thêm.
- Lựa chọn mô hình tốt nhất (Choose the best model): Dùng để so sánh và chọn ra mô hình có trọng số (weight) hoặc cấu hình tốt nhất cho một nhiệm vụ cụ thể.
- Đo lường độ tin cậy (Measure reliability): Đảm bảo rằng các dự đoán của mô hình đáp ứng được các yêu cầu và mục tiêu kinh doanh hoặc ứng dụng cuối cùng.
4. When: Khi nào chúng ta sử dụng Evaluation Metrics? 🕒
Evaluation Metrics không chỉ dùng ở cuối quá trình mà còn được sử dụng liên tục trong vòng đời phát triển mô hình:
- Lựa chọn Mô hình (Model Selection): Dùng để tìm mô hình tốt nhất trong một tập hợp các ứng viên (ví dụ: so sánh giữa Hồi quy Tuyến tính và Rừng Ngẫu nhiên).
- Điều chỉnh Mô hình (Model Tuning): Đo lường tác động của việc điều chỉnh các tham số siêu cấp (hyperparameter) để xem cấu hình nào mang lại kết quả tốt nhất.
- Kiểm tra Mô hình (Model Testing): Truy cập hiệu suất cuối cùng của mô hình trước khi triển khai.
- Giám sát (Monitoring): Theo dõi liên tục hiệu suất của mô hình đã triển khai trong môi trường thực tế để phát hiện sự suy giảm hiệu suất theo thời gian (drift).
5. Types: Các loại metrics tương ứng? 🍁
Evaluation Metrics được chia làm nhiều loại dành cho các bài toán riêng biệt , tùy thuộc vào loại dữ liệu đầu ra mà mô hình dự đoán:
| Loại Mô hình | Đặc điểm | Metrics đại diện |
|---|---|---|
| Phân loại (Classification) | Dự đoán đầu ra là biến phân loại (categorical variable), ví dụ: "Có/Không", "Chó/Mèo", "Loại A/B/C". | Accuracy, Precision, Recall, F1-Score, AUC. |
| Hồi quy (Regression) | Dự đoán đầu ra là biến số (numerical variable) hoặc giá trị liên tục, ví dụ: "Giá nhà là 5 tỷ", "Nhiệt độ ngày mai là 30°C". | MAE, MSE, RMSE, R-squared. |
| Phân cụm (Clustering) | Không có nhãn (unsupervised), mô hình tự nhóm dữ liệu thành các cụm dựa trên độ giống nhau. | Silhouette Score, Davies--Bouldin Index, Calinski--Harabasz, ARI, NMI. |
| Xếp hạng/Tìm kiếm (Ranking / Retrieval) | Dùng để xếp hạng hoặc tìm kiếm: đề xuất video, kết quả tìm kiếm, sản phẩm gợi ý. | Precision@K, Recall@K, MAP, MRR, NDCG. |
| Dịch/Tóm tắt/NLP Generation (NLP Metrics) | Đánh giá chất lượng văn bản sinh ra hoặc dịch so với câu gốc. | BLEU, ROUGE, METEOR, BERTScore, Perplexity. |
| Phát hiện vật thể / Nhận diện ảnh (Object Detection) | Dự đoán vị trí (bbox) + nhãn của vật thể trong ảnh. | mAP, AP50/AP75, IoU. |
Và nội dung bài blog hôm nay chúng ta sẽ tập trung chủ yếu vào các Evaluation Metric (Chỉ số đánh giá) của bài toán Regression.
Error metrics phổ biến và các metrics tương ứng.
1. Scale-dependent errors
Scale-dependent errors là loại lỗi mà độ lớn của nó thay đổi khi đơn vị đo lường (scale) của dữ liệu hoặc mục tiêu dự đoán thay đổi.
Các metrics phổ biến của Scale-dependent errors bao gồm: ME, MAE và MSE.
ME (Mean Error)
ME (Mean Error) được tính bằng cách lấy trung bình cộng của tất cả các sai số (lỗi) mà mô hình mắc phải.
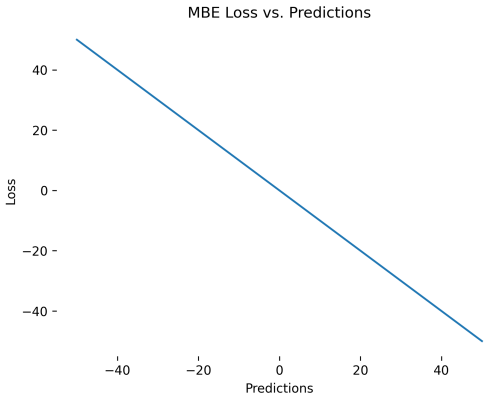
Hình 1: ME dạng đồ thị
Công thức:
$$ ME = \frac{1}{n}\sum_{t=1}^{n} (y_t - \hat{y}_t) $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
Đặc điểm:
- ME > 0: Giá trị dự đoán $\hat{y}_t$ lớn hơn giá trị thực tế $y_t$ ⇒ Mô hình Underestimate.
- ME = 0: Giá trị dự đoán $\hat{y}_t$ bằng giá trị thực tế $y_t$ ⇒ Mô hình hoàn hảo.
- ME < 0: Giá trị dự đoán $\hat{y}_t$ nhỏ hơn giá trị thực tế $y_t$ ⇒ Mô hình Overestimate.
Ưu điểm
- Mô hình đơn giản chỉ là tính trung bình cộng của các sai số.
- Dễ dàng biết được mô hình có xu hướng dự đoán cao hơn hay thấp hơn giá trị thực tế ⇒ Phát hiện liệu mô hình đang đánh giá quá cao [overestimating] hay đánh giá quá thấp [underestimating] một cách hệ thống.
Nhược điểm:
- Nếu các thành phần tử số dương và tử số âm triệt tiêu lẫn nhau ⇒ tử số = 0 ⇒ ME = 0 dẫn đễn lầm tưởng rằng nó là mô hình hoàn hảo dù thật ra một sự thật đang bị che giấu là mô hình vẫn đang mắc lỗi lớn.
- Một vài giá trị ngoại lai (Outliers) lớn có thể làm sai lệch ME và dẫn đến kết luận sai lầm.
Ví dụ về mã nguồn:
def me(actual, predicted):
actual, predicted = np.array(actual), np.array(predicted)
errors = actual - predicted
return np.mean(errors)
Tóm lại:
ME chỉ dùng khi bạn muốn biết hướng đi của lỗi. Nó giúp bạn biết mô hình của mình có xu hướng dự đoán cao hơn hay thấp hơn giá trị thực tế một cách nhất quán hay không.
MAE (Mean Absolute Error)
Mean Absolute Error (MAE) đo sai số trung bình tuyệt đối giữa giá trị dự đoán và thực tế.
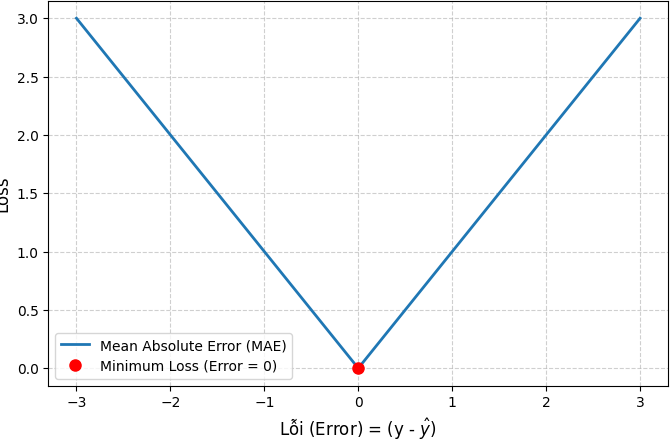
Hình 2: MAE dạng đồ thị
Công thức:
$$ MAE = \frac{1}{n}\sum_{i=1}^{n} |y_i - \hat{y}_i| $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
- $|y_i - \hat{y}_i|$: Trị tuyệt đối sai số giữa giá trị dự đoán và giá trị thực tế.
Đặc điểm:
- MAE > 0: Càng lớn thì mô hình càng dự báo sai , gần về 0 thì càng tốt.
- MAE = 0: Mô hình hoàn hảo.
- MAE < 0: Không thể xảy ra ⇒ mô hình đang bị sai.
Ưu điểm
- Đơn giản và Trực quan: Mô hình đơn giản, dễ tính toán và dễ hiểu. Giá trị của MAE có cùng đơn vị với biến mục tiêu.
- Ít nhạy cảm với các outlier: Vì nó xử lý lỗi một cách tuyến tính.
- Khắc phục Triệt tiêu Lỗi: Việc sử dụng trị tuyệt đối ($|...|$) ngăn lỗi dương và lỗi âm triệt tiêu lẫn nhau, giúp MAE phản ánh độ lớn thực sự của sai số trung bình (khắc phục nhược điểm của ME).
Nhược điểm:
- Không biết được hướng của lỗi: Không thể biết liệu mô hình có xu hướng Overestimate hay Underestimate trong hệ thống hay không.
- Một vài giá trị ngoại lai (Outliers) lớn có thể làm sai lệch và dẫn đến kết luận sai lầm.
- Scale-dependent: Giá trị của chúng phụ thuộc vào đơn vị và độ lớn của dữ liệu, khiến bạn không thể so sánh mô hình hoặc dữ liệu khác scale và dễ hiểu sai về mức độ sai số.
Ví dụ về mã nguồn:
def mae(actual, predicted):
actual, predicted = np.array(actual), np.array(predicted)
errors = np.abs(actual - predicted)
return np.mean(errors)
Tóm lại:
Dùng Mô hình Mean Absolute Error (MAE) khi bạn cần một metric dễ hiểu, ổn định, không bị outlier phá hỏng và phản ánh đúng sai số trung bình theo đơn vị gốc.
MSE (Mean Squared Error)
MSE (Mean Squared Error) đo sai số trung bình bình phương giữa giá trị dự đoán và giá trị thực tế.
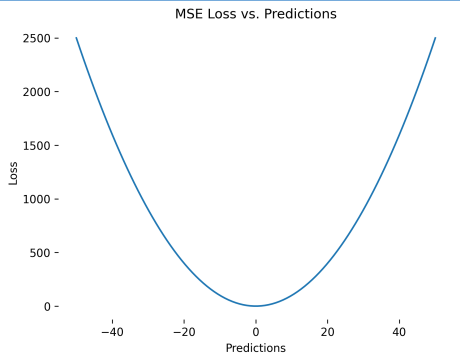
Hình 3: MSE dạng đồ thị
Công thức:
$$ MSE = \frac{1}{n}\sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
- $(y_i - \hat{y}_i)^2$: Bình phương sai số giữa giá trị dự đoán và giá trị thực tế.
Đặc điểm:
- MSE > 0: Càng lớn thì mô hình càng dự báo sai , gần về 0 thì càng tốt.
- MSE = 0: Mô hình hoàn hảo.
- MSE < 0: Không thể xảy ra ⇒ mô hình đang bị sai.
Ưu điểm
- Phạt các Lỗi Lớn một cách Nghiêm khắc: MSE sử dụng hàm bậc hai, nghĩa là nếu lỗi tăng gấp đôi (ví dụ: từ 5 lên 10), thì hình phạt sẽ tăng gấp bốn lần (từ 25 lên 100).
- Khắc phục được việc triệt tiêu lỗi của ME.
Nhược điểm:
- Rất Nhạy cảm với Giá trị Ngoại lai do bình phương lỗi ⇒ mô hình dễ bị overfitting.
- Không biết được hướng của lỗi: Không thể biết liệu mô hình có xu hướng Overestimate hay Underestimate hệ thống hay không.
- Scale-dependent: Giá trị của chúng phụ thuộc vào đơn vị và độ lớn của dữ liệu, khiến bạn không thể so sánh mô hình hoặc dữ liệu khác scale và dễ hiểu sai về mức độ sai số.
Ví dụ về mã nguồn:
def mse(actual, predicted):
actual, predicted = np.array(actual), np.array(predicted)
errors = (actual - predicted)**2
return np.mean(errors)
Tóm lại: Dùng MSE (Mean Squared Error) khi mục tiêu của bạn là tối ưu hóa mô hình và phạt nặng các lỗi lớn.
Bảng tóm tắt các trường hợp nên dùng của mỗi loại mô hình:
| Metric | Khi nào nên dùng |
|---|---|
| ME (Mean Error) | - Khi muốn biết một mô hình đang dự đoán cao hơn hay thấp hơn so với thực tế (bias). - Tốt trong việc kiểm tra "mô hình lệch hướng". |
| MAE (Mean Absolute Error) | - Khi dữ liệu có nhiều outliers. - Khi muốn metric dễ hiểu cho business (đơn vị thực). - Khi ưu tiên việc ổn định và mong lỗi phân bố đều. |
| MSE (Mean Squared Error) | - Khi muốn phạt mạnh các lỗi lớn. - Khi mô hình cần tính trơn để tối ưu deep learning. - Khi outliers là thông tin quan trọng chứ không phải nhiễu. |
Vấn đề:
ME, MSE, và MAE đều sử dụng đơn vị gốc của dữ liệu (ví dụ: USD, Kilogram) để tính toán sai số.
Giả sử ta có 2 mô hình dưới đây:
| Mô hình | Dự báo | Quy mô Giá trị Thực tế | MAE báo cáo |
|---|---|---|---|
| A | Doanh số Điện thoại (USD) | 1,000,000 USD | 100 USD |
| B | Số lượng Khách hàng mới (người) | 500 người | 50 người |
Khi nhìn vào vào số 100 và 50, bạn có thể kết luận rằng lỗi 100 USD của Mô hình A lớn hơn lỗi 50 người của Mô hình B.
Trong khi thực tế thì:
- Mô hình A: Lỗi 100 USD là rất nhỏ so với tổng doanh số 1,000,000 USD (tương đương 0.01% lỗi).
- Mô hình B: Lỗi 50 người là rất lớn so với tổng số 500 khách hàng (tương đương 10% lỗi).
ME/MAE/MSE không cho bạn biết mô hình nào tốt hơn khi quy mô khác nhau. Do đó bạn cần các metric Scale-Independent để đưa ra so sánh công bằng bao gồm các metric phía dưới đây.
2. Percentage Errors
Percentage Errors (Các loại lỗi theo phần trăm) là nhóm các thước đo đánh giá mô hình dự đoán bằng cách biểu diễn sai số dưới dạng phần trăm (%) so với giá trị thật. Do đó ta có thể tránh được nhược điểm Scale-dependent của 3 mô hình trên.
Một số mô hình tiêu biểu như là : MAPE, sMAPE.
MAPE (Mean Absolute Percentage Error)
MAPE (Mean Absolute Percentage Error) đo lường mức độ sai lệch trung bình giữa giá trị dự báo và giá trị thực tế biểu diễn dưới dạng phần trăm.
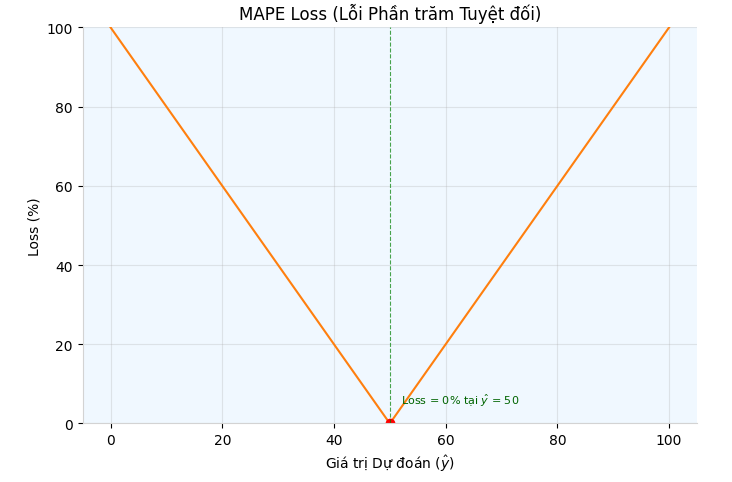
Hình 4: MAPE dạng đồ thị
Công thức:
$$ MAPE = \frac{1}{n}\sum_{t=1}^{n} \left|\frac{y_t - \hat{y}_t}{y_t}\right| \times 100\% $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
- $\left|\frac{y_t - \hat{y}_t}{y_t}\right|$ : Trị tuyệt đối sai số chia cho giá trị thực tế.
Đặc điểm:
MAPE > 0: Càng lớn thì mô hình càng dự báo sai , gần về 0 thì càng tốt.
MAPE = 0: Mô hình hoàn hảo.
MAPE < 0: Không thể xảy ra ⇒ mô hình đang bị sai.
Ưu điểm
- Độc lập với Tỉ lệ (Scale-independency): MAPE không bị ảnh hưởng bởi đơn vị đo lường của dữ liệu.
- Dễ giải thích do MAPE cung cấp lỗi dưới dạng phần trăm. Nếu MAPE = $5\%$, điều đó có nghĩa là dự báo trung bình bị sai lệch $5\%$ so với giá trị thực tế.
Nhược điểm:
- Nhạy cảm với Số 0 & Không xác định: Khi giá trị thực tế ($y_t$) bằng 0 hoặc rất gần 0, MAPE trở nên không xác định (undefined) hoặc cho kết quả vô cùng lớn (infinite) Ví dụ hen: Nếu bạn dự báo doanh số của một mặt hàng mà doanh số thực tế ($y_t$) bằng 0, công thức MAPE yêu cầu phép chia cho 0 ⇒ lỗi rồi đó. 🙂
- Xử lý Lỗi Bất đối xứng: Vì nó phạt lỗi Overestimate (dự đoán cao) nặng hơn và không giới hạn (có thể vượt $100\%$), trong khi lỗi Underestimate (dự đoán thấp) bị giới hạn ở $100\%$, dẫn đến thiên vị hệ thống trong mô hình.
Ví dụ về mã nguồn:
actual = [3, 5, 2, 8, 7]
predicted1 = [2, 2, 2, 2, 2]
predicted2 = [5, 5, 5, 5, 5]
predicted3 = [7, 7, 7, 7, 7]
def mape(actual, predicted):
actual, predicted = np.array(actual), np.array(predicted)
percentage_errors = np.abs((actual - predicted) / actual) * 100
return np.mean(percentage_errors)
# or
from sklearn.metrics import mean_absolute_percentage_error
Tóm lại:
MAPE (Mean Absolute Percentage Error) được sử dụng chủ yếu khi bạn cần một chỉ số lỗi độc lập với tỉ lệ (Scale-independent) và muốn báo cáo hiệu suất dự báo dưới dạng phần trăm.
sMAPE (Symmetric Mean Absolute Percentage Error)
sMAPE (Symmetric Mean Absolute Percentage Error) là một chỉ số lỗi tương đối (Scale-independent) được thiết kế để khắc phục nhược điểm bất đối xứng (asymmetry) và nhạy cảm với số 0 của MAPE.
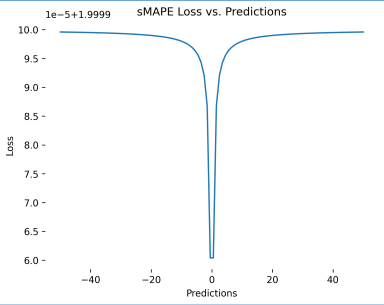
Hình 5: sMAPE dạng đồ thị
Công thức:
$$ sMAPE = \frac{1}{n}\sum_{t=1}^{n} \frac{|y_t - \hat{y}_t|}{(|y_t| + |\hat{y}_t|) / 2} \times 100\% $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
Đặc điểm:
- sMAPE > 0: Càng lớn thì mô hình càng dự báo sai , gần về 0 thì càng tốt.
- sMAPE = 0: Mô hình hoàn hảo.
- sMAPE < 0: Không thể xảy ra ⇒ mô hình đang bị sai.
Ưu điểm:
Có các ưu điểm của MAPE cộng thêm:
- Độc lập với Tỉ lệ (Scale-independency): sMAPE không bị ảnh hưởng bởi đơn vị đo lường của dữ liệu.
- Cân bằng lỗi tốt hơn: Việc chia cho trung bình của cả $y_t$ và $\hat{y}_t$ giúp hình phạt của lỗi Overestimate và Underestimate trở nên cân bằng hơn, giảm thiểu thiên vị hệ thống của MAPE.
Nhược điểm:
-
Khó trong việc giải thích: Nếu giá trị thực tế là $10$ và dự đoán là $100$, sMAPE sẽ là khoảng $163.6\%$, một con số khó hiểu.
-
Phức tạp trong sử dụng: Đối với một số phân phối dữ liệu (đặc biệt khi dữ liệu mất cân bằng nghiêm trọng), sMAPE vẫn có thể tạo ra các kết quả không trực quan.
Ví dụ: Khi một chuỗi thời gian có nhiều giá trị âm và dương gần 0, việc sử dụng giá trị tuyệt đối trong mẫu số vẫn có thể tạo ra các kết quả kỳ lạ.
Ví dụ về mã nguồn:
actual = np.array([3, 5, 2, 8, 7])
predicted1 = np.array([2, 2, 2, 2, 2])
predicted2 = np.array([5, 5, 5, 5, 5])
predicted3 = np.array([7, 7, 7, 7, 7])
def smape(actual, predicted):
actual, predicted = np.array(actual), np.array(predicted)
numerator = np.abs(actual - predicted)
denominator = np.abs(actual) + np.abs(predicted)
smape_values = numerator / denominator
return np.mean(smape_values) * 200
#hoặc dùng thư viện
from sktime.performance_metrics.forecasting import MeanAbsolutePercentageError
Tóm lại: sMAPE là một sự cải tiến so với MAPE khi bạn cần một chỉ số phần trăm ổn định và ít thiên vị hơn, đặc biệt khi dữ liệu có thể chứa các giá trị gần hoặc bằng 0.
Bảng tóm tắt các trường hợp nên dùng của mỗi loại mô hình:
| Metric | Khi nào nên dùng |
|---|---|
| MAPE (Mean Absolute Percentage Error) | - Khi giá trị thực tế luôn dương và khác 0. - Khi cần metric dễ hiểu và truyền đạt (sai số là X% so với giá trị thực tế). - Khi chấp nhận việc metric này sẽ phạt nặng hơn đối với các trường hợp dự báo cao hơn thực tế (Over-forecasting). |
| sMAPE (Symmetric Mean Absolute Percentage Error) | - Khi dữ liệu có thể chứa giá trị 0 hoặc gần 0 (tránh lỗi chia cho 0). - Khi muốn có một metric đối xứng hơn xử phạt lỗi dự báo cao hơn và thấp hơn tương đối cân bằng. - Khi muốn có một metric có phạm vi giá trị xác định (thường tối đa là 200%). |
3. Relative Errors
Relative Errors (Lỗi Tương đối) là sai số của mô hình được chia cho sai số của một phương pháp chuẩn (benchmark) tại từng điểm dữ liệu, thường là mô hình Naive.
$$ \text{Tư duy:} \quad \text{Trung bình của } \left(\frac{\text{Lỗi của bạn}}{\text{Lỗi của Chuẩn}}\right) $$
Naive Method (phương pháp dự báo ngây thơ) là cách dự báo đơn giản nhất trong đó :
👉 Dự báo giá trị tiếp theo bằng chính giá trị ngay trước đó.
Ví dụ:
Nhiệt độ hôm qua = 30°C → dự báo hôm nay =30°C.
MRAE (Mean Relative Absolute Error)
MRAE (Mean Relative Absolute Error) là một trong những thước đo lỗi dựa trên tỷ lệ so với một baseline (thường là phương pháp dự đoán ngây thơ -- naive method). Thay vì đo lỗi tuyệt đối, MRAE trả lời câu hỏi:
"Mô hình của bạn tốt hơn baseline bao nhiêu lần?"
Công thức:
$$ MRAE = \frac{1}{n}\sum_{t=1}^{n} \left|\frac{y_t - \hat{y}_t}{y_t - \hat{y}_t^b}\right| $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
- $\hat{y}_t^b$: Giá trị dự đoán của một mô hình cơ sở (benchmark model).
Đặc điểm:
- MRAE = 0: Mô hình tuyệt vời.
- MRAE < 1: Điều này có nghĩa là lỗi tuyệt đối trung bình của mô hình bạn đang đánh giá nhỏ hơn lỗi tuyệt đối trung bình của mô hình cơ sở. Do đó, mô hình của bạn tốt hơn mô hình cơ sở.
- MRAE > 1: Mô hình bạn đang đánh giá tệ hơn mô hình cơ sở.
- MRAE = 1: Hiệu suất của hai mô hình là tương đương.
Ưu điểm:
- Độc lập với Tỉ lệ (Scale-independency): MRAE không bị ảnh hưởng bởi đơn vị đo lường của dữ liệu vì nó so sánh cùng đơn vị.
- Dễ diễn giải: MRAE cho biết mô hình tốt hơn (hoặc tệ hơn) baseline bao nhiêu lần.
Ví dụ:
- MRAE = 0.5 → mô hình tốt gấp đôi baseline.
- MRAE = 1 → mô hình ngang baseline.
- MRAE = 2 → mô hình tệ gấp đôi baseline.
Nhược điểm:
-
Có thể cho kết quả không xác định.
-
Nhạy với mẫu số quá nhỏ: Nếu baseline sai rất ít, mẫu số gần 0 → MRAE tăng vọt → giá trị cực lớn, không ổn định, dù mô hình không hẳn tệ.
-
Phụ thuộc vào baseline: MRAE đánh giá mô hình dựa trên baseline, nên nếu baseline chọn không hợp lý, kết quả sẽ trở nên vô nghĩa.
Ví dụ:
Baseline quá tốt → mô hình "bình thường" trông như rất tệ.
Baseline quá tệ → mô hình kém cũng trông như rất tốt.
Baseline không liên quan → metric mất ý nghĩa.
Ví dụ về mã nguồn:
actual = np.array([3, 5, 2, 8, 7], dtype=float)
# Random-walk naive forecast (shifted actual values)
naive = np.roll(actual, 1) # Shift the actual values by 1
naive[0] = np.nan # First value is undefined for random-walk method
predicted1 = np.array([3.5, 3, 5, 2, 8])
predicted2 = np.array([3.5, 5.3, 2.1, 8.2, 7.5])
predicted3 = np.array([3.5, 2, 6, 1, 9])
def mrae(actual, predicted, naive):
actual, predicted, naive = np.array(actual), np.array(predicted), np.array(naive)
rae = np.abs(actual - predicted) / np.abs(actual - naive)
return np.mean(rae)
Tóm lại:
MRAE (Mean Relative Absolute Error) được dùng khi bạn muốn đo mức độ sai số tương đối của mô hình so với một mô hình baseline đơn giản.
GMRMAE ( Geometric Mean Relative Absolute Error)
GMRMAE là một phiên bản cải tiến của MRAE (Mean Relative Absolute Error). Thay vì sử dụng trung bình cộng (Arithmetic Mean) để tổng hợp các lỗi tương đối (như MRAE), GMRMAE sử dụng trung bình hình học (Geometric Mean).
Sự khác nhau giữa Trung bình cộng và Trung bình hình học:
| Loại trung bình | Dùng khi dữ liệu... | Ví dụ |
|---|---|---|
| Trung bình cộng | Thay đổi theo cộng/trừ | Cân nặng, chiều cao, điểm số, lỗi MAE |
| Trung bình hình học | Thay đổi theo nhân/chia hoặc tỷ lệ % | Tăng trưởng, tỷ lệ lợi nhuận, relative errors |
Công thức:
$$ \mathbf{GMRMAE} = \sqrt[n]{\prod_{t=1}^{n} \left|\frac{y_t - \hat{y}_t}{y_t - \hat{y}_t^b}\right|} $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
- $\hat{y}_t^b$: Giá trị dự đoán của một mô hình cơ sở (benchmark model).
Đặc điểm:
- GMRAE = 0: Mô hình hoàn hảo.
- GMRAE < 1: Mô hình của bạn tốt hơn mô hình cơ sở.
- GMRAE > 1: Mô hình bạn đang đánh giá tệ hơn mô hình cơ sở.
- GMRAE = 1: Hiệu suất của hai mô hình là tương đương.
Ưu điểm:
GMRAE có các ưu điểm giống với MRAE, ngoài ra:
- Trung bình hình học (dùng trong GMRMAE) hoạt động như một "bộ giảm thanh", nó giảm bớt ảnh hưởng của các lỗi tương đối cực lớn ⇒ GMRMAE giúp mô hình của bạn đạt được khả năng bền vững tốt hơn trước các outliers so với MRAE.
Nhược điểm:
- Có thể cho kết quả không xác định.
- Nhạy với baseline bị sai lớn: Nếu baseline sai quá nhiều, mẫu số lớn → GMRAE nhỏ bất thường → phóng đại mức tốt của mô hình, làm metric mất độ tin cậy.
- Nhạy với mẫu số quá nhỏ: Nếu baseline sai rất ít, mẫu số gần 0 → GMRAE tăng vọt → giá trị cực lớn, không ổn định, dù mô hình không hẳn tệ.
- Phụ thuộc vào phương pháp baseline: GMRAE đánh giá mô hình dựa trên baseline, nên nếu baseline chọn không hợp lý, kết quả sẽ trở nên vô nghĩa.
Ví dụ về mã nguồn:
actual = np.array([3, 5, 2, 8, 7], dtype=float)
# Random-walk naive forecast (shifted actual values)
naive = np.roll(actual, 1) # Shift the actual values by 1
naive[0] = np.nan # First value is undefined for random-walk method
predicted1 = np.array([3.5, 3, 5, 2, 8])
predicted2 = np.array([3.5, 5.3, 2.1, 8.2, 7.5])
predicted3 = np.array([3.5, 2, 6, 1, 9])
def gmrae(actual, predicted, naive):
return np.prod(np.abs((actual - predicted) / (actual - naive))) ** (1 / len(actual))
#or
from sktime.performance_metrics.forecasting import GeometricMeanRelativeAbsoluteError
Tóm lại: GMRMAE (Geometric Mean Relative Mean Absolute Error) được dùng khi bạn muốn đo hiệu suất mô hình so với baseline nhưng cần một chỉ số ổn định, giảm ảnh hưởng của vài sai số cực lớn (outliers).
Bảng tóm tắt các trường hợp nên dùng của mỗi loại mô hình:
| Metric | Khi nào nên dùng |
|---|---|
| MRAE (Mean Relative Absolute Error) | - Khi muốn tránh vấn đề chia cho 0 của MAPE. - Khi cần một chỉ số độc lập với quy mô (scale-independent) bằng cách chia sai số tuyệt đối cho một mô hình cơ sở (thường là Naive). |
| GMRMAE (Geometric Mean Relative Absolute Error) | - Phù hợp cho nhiều chuỗi thời gian. - Khi muốn so sánh hiệu suất tương đối trên nhiều chuỗi thời gian, cung cấp kết quả tổng thể mượt hơn. - Muốn giảm ảnh hưởng của Outliers. |
4. Relative Measures
Relative Measures là thước đo lỗi dạng "so sánh" trên toàn bộ tập dữ liệu, so sánh hiệu quả mô hình với mô hình chuẩn bằng cách lấy lỗi tổng hợp của mô hình chia cho lỗi tổng hợp của mô hình chuẩn.
$$ \text{Tư duy:} \quad \frac{\text{Tổng Lỗi của bạn}}{\text{Tổng Lỗi của Chuẩn}} $$
Đây là nhóm chỉ số hoạt động theo cách "Trung bình của các Tỉ lệ" (Mean of Ratios).
Bao gồm các mô hình tiêu biểu sau đây:
RelMAE ( Relative Mean Absolute Error)
RelMAE được định nghĩa là tỷ lệ giữa MAE (Mean Absolute Error) của mô hình bạn đang đánh giá và MAE của mô hình cơ sở (thường là mô hình Naive/Random Walk).
Công thức:
$$ RelMAE = \frac{\sum_{t=1}^{n} |y_t - \hat{y}_t|}{\sum_{t=1}^{n} |y_t - \hat{y}_t^b|} $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
Đặc điểm:
- RelMAE = 0: Mô hình hoàn hảo.
- RelMAE < 1: Mô hình của bạn tốt hơn mô hình cơ sở.
- RelMAE > 1: Mô hình bạn đang đánh giá tệ hơn mô hình cơ sở.
- RelMAE = 1: Hiệu suất của hai mô hình là tương đương.
Ưu điểm:
- Giống như MAE, RelMAE dựa trên sai số tuyệt đối nên ít bị ảnh hưởng bởi outliers.
- Độc lập với tỉ lệ (Scale-independency).
- Dễ dàng giải thích.
Nhược điểm:
- Phụ thuộc vào baseline: RelMAE đánh giá mô hình dựa trên baseline, nên nếu baseline chọn không hợp lý, kết quả sẽ trở nên vô nghĩa.
- Có nguy cơ xuất hiện chia cho 0 dẫn đến chỉ số mất tính ổn định và không thể tính toán được.
Ví dụ về mã nguồn:
import numpy as np
# Dữ liệu của bạn
actual = [3, 5, 2, 8, 7]
predicted1 = [2, 2, 2, 2, 2]
predicted2 = [5, 5, 5, 5, 5]
predicted3 = [7, 7, 7, 7, 7]
def rel_mae(actual, predicted):
actual, predicted = np.array(actual), np.array(predicted)
# Tính tử số: Tổng sai số tuyệt đối
sum_abs_error = np.sum(np.abs(actual - predicted))
# Tính mẫu số: Tổng giá trị tuyệt đối của thực tế
sum_abs_actual = np.sum(np.abs(actual))
# Trả về kết quả
return sum_abs_error / sum_abs_actual
# --- Chạy thử nghiệm ---
print(f"RelMAE 1: {rel_mae(actual, predicted1):.4f}")
print(f"RelMAE 2: {rel_mae(actual, predicted2):.4f}")
print(f"RelMAE 3: {rel_mae(actual, predicted3):.4f}")
Tóm lại:
RelMAE ( Relative Mean Absolute Error) được dùng khi bạn muốn so sánh sai số của mô hình với sai số của một mô hình baseline bất kỳ, để xem mô hình tốt hơn hay tệ hơn bao nhiêu lần.
RSE ( Root Relative Squared Error)
RSE (Relative Squared Error) là tỷ lệ giữa tổng bình phương sai số của mô hình và tổng bình phương sai số của baseline (hoặc độ biến thiên của dữ liệu).
Công thức:
$$RSE = \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}$$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
Đặc điểm:
- RSE = 0: Mô hình hoàn hảo.
- RSE < 1: Mô hình của bạn tốt hơn mô hình cơ sở.
- RSE > 1: Mô hình bạn đang đánh giá tệ hơn mô hình cơ sở.
- RSE = 1: Hiệu suất của hai mô hình là tương đương.
Ưu điểm:
- Nhạy với outliers: RSE sử dụng lỗi bình phương → các sai số lớn sẽ bị phạt nặng.
- Không phụ thuộc vào scale dữ liệu.
Nhược điểm:
- Có nguy cơ xuất hiện chia cho 0 dẫn đến chỉ số mất tính ổn định và không thể tính toán được.
- Phụ thuộc vào baseline.
Ví dụ: Dùng giá trị trung bình làm baseline cho chuỗi thời gian có xu hướng tăng → RSE thường cho kết quả tệ, dù mô hình dự đoán tốt.
Ví dụ về mã nguồn:
import numpy as np
def rae(actual, predicted):
actual, predicted = np.array(actual), np.array(predicted)
numerator = np.sum(np.abs(actual - predicted))
denominator = np.sum(np.abs(actual - np.mean(actual)))
epsilon = 1e-10
return numerator / (denominator + epsilon)
Tóm lại:
RSE ( Root Relative Squared Error) được dùng khi bạn muốn đánh giá mô hình bằng cách so sánh sai số bình phương của mô hình với sai số bình phương của một mô hình baseline đơn giản (thường là dự đoán bằng giá trị trung bình).
Bảng tóm tắt các trường hợp nên dùng của mỗi loại mô hình:
| Metric | Khi nào nên dùng |
|---|---|
| RelMAE (Relative Mean Absolute Error) | - Cần metric độc lập với quy mô (scale-independent). - Ưu tiên khi cần dễ dàng diễn giải hiệu suất tương đối. |
| RSE (Relative Squared Error) | - So sánh với mô hình cơ sở và phạt mạnh các lỗi lớn (outliers). - Cần metric độc lập với quy mô nhưng nhạy cảm với lỗi (do sử dụng bình phương sai số). - Thích hợp để tối ưu hóa giảm thiểu phương sai sai số. |
5. Scale Errors
Scaled Errors là nhóm chỉ số chuẩn hóa lỗi so với một baseline, giúp không còn phụ thuộc vào đơn vị đo và dễ so sánh giữa các chuỗi khác nhau.
Bao gồm các metric tiêu biểu sau đây:
MASE (Mean Absolute Scaled Error)
MASE là một metric đo sai số bằng cách chuẩn hóa MAE của mô hình bằng MAE của mô hình baseline, thường là naive forecast (dự đoán yₜ ≈ yₜ₋₁).
Công thức:
$$ MASE = \frac{1}{n} \sum_{t=1}^{n} \left| \frac{y_t - \hat{y}_t}{\frac{1}{n-1} \sum_{i=2}^{n} |y_i - y_{i-1}|} \right| = \frac{\frac{1}{n}\sum_{t=1}^{n} |y_t - \hat{y}_t|}{\frac{1}{n-1}\sum_{i=2}^{n} |y_i - y_{i-1}|} $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
- $y_i - y_{i-1}$: Sự chênh lệch giữa giá trị hiện tại và giá trị ngay trước đó.
Đặc điểm:
- MASE = 0: Mô hình hoàn hảo.
- MASE < 1: Mô hình của bạn tốt hơn mô hình cơ sở.
- MASE > 1: Mô hình bạn đang đánh giá tệ hơn mô hình cơ sở.
- MASE = 1: Hiệu suất của hai mô hình là tương đương.
Ưu điểm:
- Tính ứng dụng rộng rãi: MASE cực kỳ linh hoạt và "dễ tính". Nó hoạt động hiệu quả trong nhiều tình huống dự báo khác nhau. Đặc biệt, MASE vẫn giữ được độ tin cậy ngay cả khi dữ liệu của bạn phức tạp, ví dụ như khi dữ liệu thể hiện rõ xu hướng tăng giảm (trend) hoặc có tính chu kỳ mùa vụ (seasonal pattern).
- Không phụ thuộc vào scale dữ liệu (Scale-independency).
Nhược điểm:
- Có nguy cơ xuất hiện chia cho 0.
- Đối xử "bình đẳng" giữa sai số âm và dương giống mô hình MAE, MASE.
Ví dụ về mã nguồn:
import numpy as np
# Dữ liệu lịch sử (dùng để tính mẫu số - độ biến động của chuỗi)
y_train = [3, 4, 3, 5, 6]
# Dữ liệu thực tế cần dự báo (Test set)
actual = [3, 5, 2, 8, 7]
# Các mô hình dự báo
predicted1 = [2, 2, 2, 2, 2]
predicted2 = [5, 5, 5, 5, 5]
predicted3 = [7, 7, 7, 7, 7]
def mase(y_train, actual, predicted):
"""
Tính MASE: Mean Absolute Scaled Error
y_train: Dữ liệu lịch sử (để tính mẫu số - scale)
actual: Dữ liệu thực tế (test set)
predicted: Dữ liệu dự báo
"""
y_train = np.array(y_train)
actual = np.array(actual)
predicted = np.array(predicted)
# 1. Tính MAE của dự đoán (Tử số)
mae_forecast = np.mean(np.abs(actual - predicted))
# 2. Tính MAE của phương pháp Naive trên tập train (Mẫu số - Scale)
# Naive: Dự đoán ngày hôm nay bằng giá trị ngày hôm qua (y[t] = y[t-1])
# np.diff(y_train) tương đương với (y[t] - y[t-1])
n = len(y_train)
if n <= 1:
return np.inf # Không đủ dữ liệu để tính scale
mae_naive = np.sum(np.abs(np.diff(y_train))) / (n - 1)
# 3. Tính MASE
# Tránh chia cho 0 nếu chuỗi hằng số
if mae_naive == 0:
return np.inf
return mae_forecast / mae_naive
# --- Chạy thử nghiệm ---
print(f"MASE 1: {mase(y_train, actual, predicted1):.4f}")
print(f"MASE 2: {mase(y_train, actual, predicted2):.4f}")
print(f"MASE 3: {mase(y_train, actual, predicted3):.4f}")
Tóm lại:
MASE là một công cụ tuyệt vời để so sánh hiệu quả dự báo trên đa dạng dữ liệu, miễn là dữ liệu lịch sử của bạn có sự biến động.
RMSSE (Root Mean Squared Scaled Error)
Công thức RMSSE là căn bậc hai của tỷ lệ giữa MSE dự báo và MSE của mô hình Naive (sử dụng sai phân bậc nhất) trên dữ liệu huấn luyện.
Công thức:
$$RMSSE = \sqrt{\frac{\frac{1}{n} \sum_{t=1}^{n} (y_t - \hat{y}_t)^2}{\frac{1}{n-1} \sum_{i=2}^{n} (y_i - y_{i-1})^2}} $$
Trong đó:
- $n$ : Tổng số mẫu dữ liệu (số lượng quan sát).
- $y_t$: Giá trị thực tế (actual value) của mẫu thứ t.
- $\hat{y}_t$ : Giá trị dự đoán (predicted value) của mô hình cho mẫu thứ t.
- $y_i - y_{i-1}$: Sự chênh lệch giữa giá trị hiện tại và giá trị ngay trước đó.
Đặc điểm:
- RMSSE = 0: Mô hình hoàn hảo.
- RMSSE < 1: Mô hình của bạn tốt hơn mô hình cơ sở.
- RMSSE > 1: Mô hình bạn đang đánh giá tệ hơn mô hình cơ sở.
- RMSSE = 1: Hiệu suất của hai mô hình là tương đương.
Ưu điểm:
- Phạt cực nặng các sai số lớn.
- Độc lập với tỉ lệ (Scale-independency).
Nhược điểm:
- Cực kỳ nhạy cảm với Outliers.
- Có nguy cơ xuất hiện chia cho 0.
Ví dụ về mã nguồn:
import numpy as np
# Dữ liệu lịch sử (Bắt buộc để tính Scale - mẫu số)
train = [3, 4, 3, 5, 6]
# Dữ liệu thực tế & Dự báo
actual = [3, 5, 2, 8, 7]
predicted1 = [2, 2, 2, 2, 2]
predicted2 = [5, 5, 5, 5, 5]
predicted3 = [7, 7, 7, 7, 7]
def rmsse(train, actual, predicted):
"""
RMSSE = Căn bậc hai (MSE dự báo / MSE naive trên tập train)
"""
train = np.array(train)
actual, predicted = np.array(actual), np.array(predicted)
# 1. Tử số: Mean Squared Error của dự báo
mse_forecast = np.mean((actual - predicted) ** 2)
# 2. Mẫu số: Mean Squared Error của Naive trên tập train
# np.diff(train) tương đương: train[t] - train[t-1]
mse_naive = np.mean(np.diff(train) ** 2)
# 3. Kết quả: Căn bậc hai của tỷ lệ
return np.sqrt(mse_forecast / mse_naive)
# --- Kiểm tra kết quả ---
print(f"RMSSE 1: {rmsse(train, actual, predicted1):.4f}")
print(f"RMSSE 2: {rmsse(train, actual, predicted2):.4f}")
print(f"RMSSE 3: {rmsse(train, actual, predicted3):.4f}")
Tóm lại: RMSSE là lựa chọn tối ưu khi bạn cần một chỉ số chuẩn hóa để so sánh các chuỗi dữ liệu khác nhau, đồng thời muốn phạt thật nặng các dự báo sai lệch lớn.
Bảng tóm tắt các trường hợp nên dùng của mỗi loại mô hình:
| Metric | Khi nào nên dùng |
|---|---|
| MASE (Mean Absolute Scaled Error) | - Khi cần một metric độc lập với quy mô (scale-independent) và không bị ảnh hưởng bởi giá trị 0 hoặc gần 0 (khắc phục nhược điểm của MAPE/sMAPE). - So sánh chính xác hiệu suất của mô hình với một mô hình cơ sở Naive trên nhiều chuỗi thời gian khác nhau. - Dễ dàng diễn giải: MASE < 1 nghĩa là mô hình của bạn tốt hơn mô hình Naive. |
| RMSSE (Root Mean Squared Scaled Error) | - Khi cần một metric độc lập với quy mô (giống MASE), nhưng muốn phạt mạnh hơn đối với các lỗi lớn (do sử dụng bình phương sai số, tương tự như RMSE). - Thường được sử dụng trong các cuộc thi dự báo lớn (ví dụ: M5 Forecasting Competition) vì nó kết hợp ưu điểm của việc chuẩn hóa (của MASE) và hình phạt lỗi lớn (của RMSE). - Mục tiêu là giảm thiểu tổng phương sai sai số so với mô hình cơ sở. |
Từ Evaluation Metrics đến Loss Function (Mở rộng)
Như các bạn có thể thấy có một số Evaluation Metric (chỉ số đánh giá) và Loss Function( hàm mất mát) thường có công thức tương đồng nhau (MAE, MSE,...) thế nhưng nó lại phục vụ cho hai mục đích khác nhau:
- Về Evaluation Metric (Chỉ số đánh giá): Dùng để đánh giá hiệu suất của mô hình sau khi đã huấn luyện xong.
- Về Loss Function (Hàm mất mát): Dùng trong quá trình huấn luyện (training) để hướng dẫn mô hình điều chỉnh tham số sao cho đầu ra ngày càng chính xác hơn.
Về nôm na:
Metric là mục tiêu cuối cùng, còn Loss Function là con đường dẫn đến mục tiêu đó
Vậy để mô hình được đánh giá hiệu suất cao nhất thì bản thân mô hình lúc huấn luyện cần có hàm loss tối ưu. Việc nắm vững bản chất của các chỉ số đánh giá (Evaluation Metrics) là bước đi đầu tiên và quan trọng nhất để bạn có thể tự xây dựng hoặc lựa chọn hàm mất mát (Loss Function) phù hợp cho mô hình của mình. Như việc MSE quá nhạy cảm với outliers, còn MAE khó tối ưu hóa (khó tính đạo hàm tại điểm 0) ⇒ xây dựng Huber Loss là kết hợp những ưu điểm của cả MSE và MAE.
Công thức Huber Loss
$$ L_{\delta}(y, f(x)) = \begin{cases} \frac{1}{2}(y - f(x))^2 & \text{nếu } |y - f(x)| \le \delta \\ \delta \cdot \left(|y - f(x)| - \frac{1}{2}\delta\right) & \text{nếu } |y - f(x)| > \delta \end{cases} $$
Trong đó:
- y: Giá trị thực tế (Ground Truth).
- f(x): Giá trị dự báo của mô hình (Prediction).
- δ (Delta): Tham số ngưỡng (Threshold) do bạn tự chọn. Nó xác định ranh giới giữa việc coi một sai số là "nhỏ" (bình thường) hay "lớn" (ngoại lai).
Cách hoạt động:
Huber Loss sẽ đặt ra 1 ngưỡng δ (delta) sau đó so sánh sai số với delta đó:
- Lớn hơn δ: hoạt động giống MAE.
- Nhỏ hơn δ: hoạt động giống MSE.
Vậy để mô hình đạt hiệu suất cao nhất:
1. Xác định Metric
Luôn bắt đầu bằng việc chọn Evaluation Metric phản ánh đúng mục tiêu mình cần.
Metric dùng để đánh giá mô hình sau cùng, không phải để huấn luyện.
2. Chọn Loss Function phù hợp
Chọn một Loss Function có tính chất tương đồng với Metric bạn muốn tối ưu, cụ thể:
- Nếu metric khó tối ưu trực tiếp (như F1, MAPE, Accuracy, AUC) ⇒ chọn Loss khả vi nhưng tương quan cao với Metric đó.
- Nếu metric là MAE:
- Tránh MAE thuần vì đạo hàm không mượt.
- Dùng Huber Loss hoặc Smooth L1 để mô hình học ổn định hơn.
Nguồn tài liệu tham khảo:
Ảnh được lấy từ tài liệu khóa học AIO Module 06 Tuần 02.
Chưa có bình luận nào. Hãy là người đầu tiên!