Logistic Regression
1. Dẫn nhập từ Linear Regression
- Chúng ta đã học qua Linear Regression, một thuật toán dùng để dự đoán những giá trị số liên tục một cách tuyến tính. Nó giải quyết một vài vấn đề như là Dự đoán giá nhà, Dự đoán điểm số,… Trong thực tế, nhiều lúc bài toán sẽ không còn là dự đoán một con số tuyến tính mà thay vào đó sẽ là những bài toán nhị phân. Ví dụ như là bệnh nhân có mắc ung thư hay không, hay một trong những bài toán kinh điển chính là dự đoán hành khách trên tàu Titanic có sống sót hay không.
- Để giải quyết những vấn đề trên, chúng ta cần có những kỹ thuật để biến những giá trị dự đoán bằng chữ “Có” hay “Không” thành những giá trị số. Thông thường thì chúng ta sẽ biểu diễn “Có” với kí hiệu số 1 và “Không” với kí hiệu số 0 tương ứng với xác suất mà một sự việc nào đó “Có” xảy ra hay “Không” xảy ra. Vậy lúc này, dataset của chúng ta sẽ có hình dạng như nào?
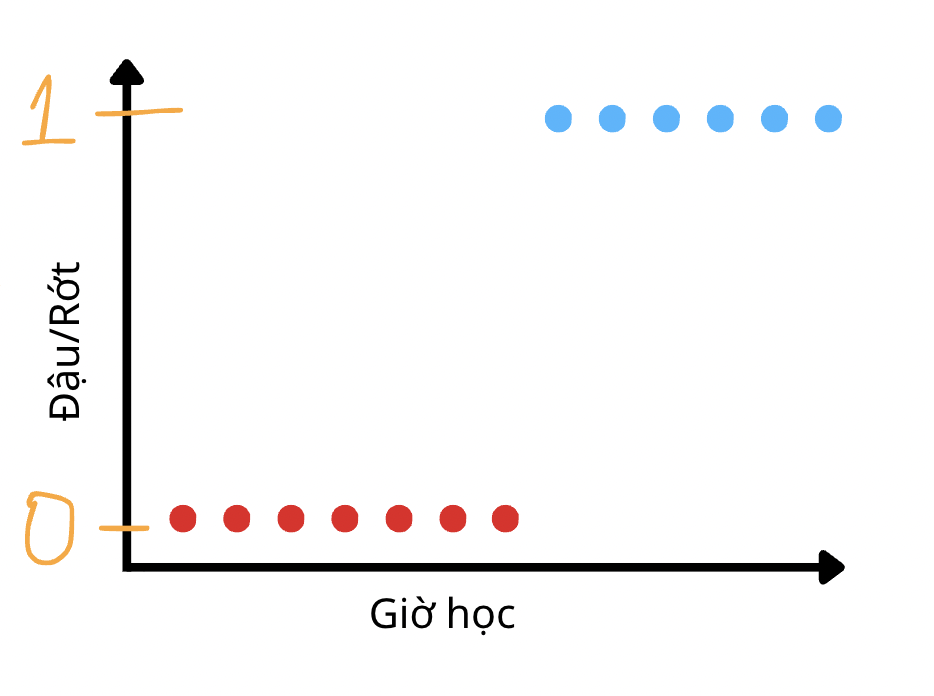
- Có phải nó sẽ được chia đôi ra thành 2 đầu của trục y tại như vậy không? Trong trường hợp này thì cách để chúng ta dự đoán bằng cách huấn luyện một đường thẳng tối ưu nhất trong dữ liệu trên sẽ trông như thế này.
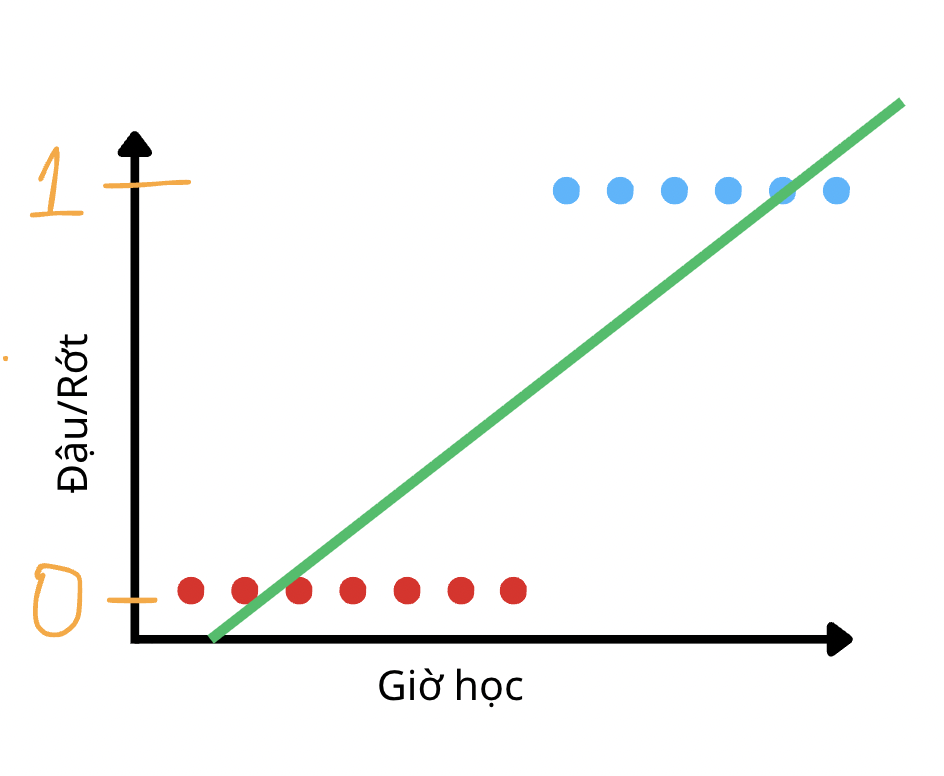
- Thoạt nhìn qua thì chúng ta nghĩ rằng nếu chọn 1 threshold ở giữa và lấy các giá trị predictions và phân loại dựa theo threshold thì dường như bài toán này sẽ được giải quyết bằng Linear Regression. Nhưng mà nếu chúng ta để ý thấy thì đường thẳng đó sẽ kéo dài đến vô cùng và sẽ xuất hiện giá trị ngoài vùng 0 và 1. Như vật thì nếu diễn giải theo Linear Regression, chúng ta sẽ dự đoán cho datapoint đầu tiên (màu đỏ từ trái sang phải) mang một giá trị âm. Hay nói cách khác datapoint đó có -0,05% là màu xanh dương?
- Để giải quyết được vấn đề trên thì chúng ta hãy tìm hiểu vào thuật toán của ngày hôm nay, Logistic Regression.
2. Logistic Regression là gì?
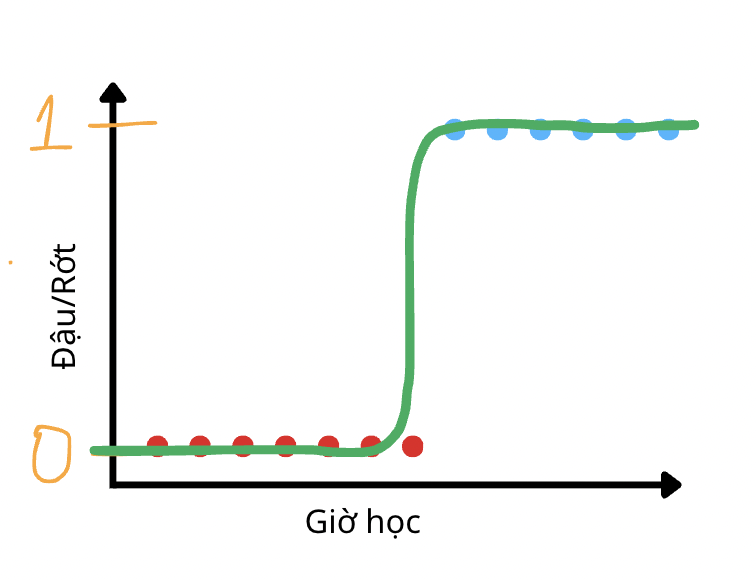
- Nhìn vào bức hình này thì nếu chúng ta biến đường thẳng tuyến tính ở phần 1 trở thành một đồ thị như trên thì sẽ phù hợp hơn với bài toán phân loại nhị phân. Vấn đề chính đó là cho dù chúng ta có chỉnh sửa hình dạng của đồ thị, vẫn phải giữ được sự linh hoạt trong quá trình học dataset của mô hình. Vì thế, người ta sử dùng một hàm được gọi là Sigmoid:
$$ g(z) = \frac{1}{1 + e^{-z}} $$
- $g(z)$: hàm Sigmoid hay còn gọi là Logistic Function
- $z$: giá trị đầu vào, trong trường hợp Logistic Regression thì giá trị đầu vào chính là hàm Linear Regression. Nói cách khác, $z = wx + b$
- Hàm Sigmoid được thiết kế để với mọi giá trị của mô hình Linear Regression đều sẽ bị thu hẹp trong khoảng từ 0 tới 1 trên toàn miền giá trị.
-
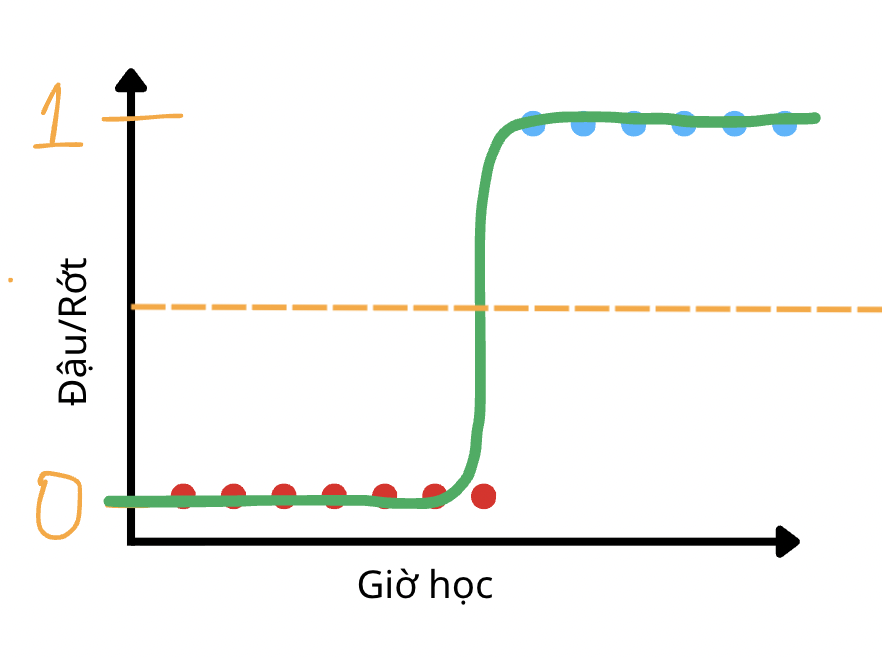
Để phù hợp hơn trong bài toàn phân loại nhị phân, người thường sẽ xét một ngưỡng threshold (thường là 0,5) để phần loại dự đoán từ mô hình thành 0 và 1.
-
Những giá trị thấp hơn threshold (đường kẻ nét đứt màu cam) đều sẽ được dự đoán là thuộc nhóm màu đỏ và ngược lại.
3. Hàm mất mát mới: Binary Cross Entropy
3.1. Tại sao chúng ta cần có hàm mất mát mới?
-
Hãy xem qua ví dụ sau:
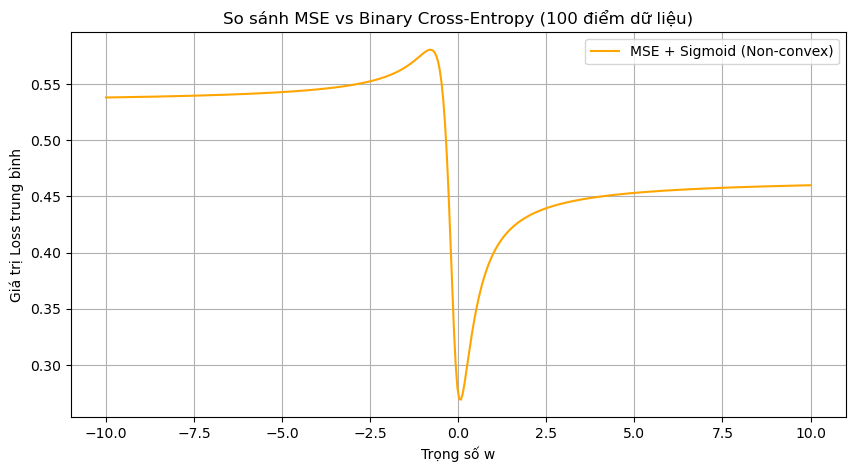
-
Đây là đồ thị hàm loss và weights của mô hình Logistic Regression kết hợp vớ hàm loss thông thường MSE.
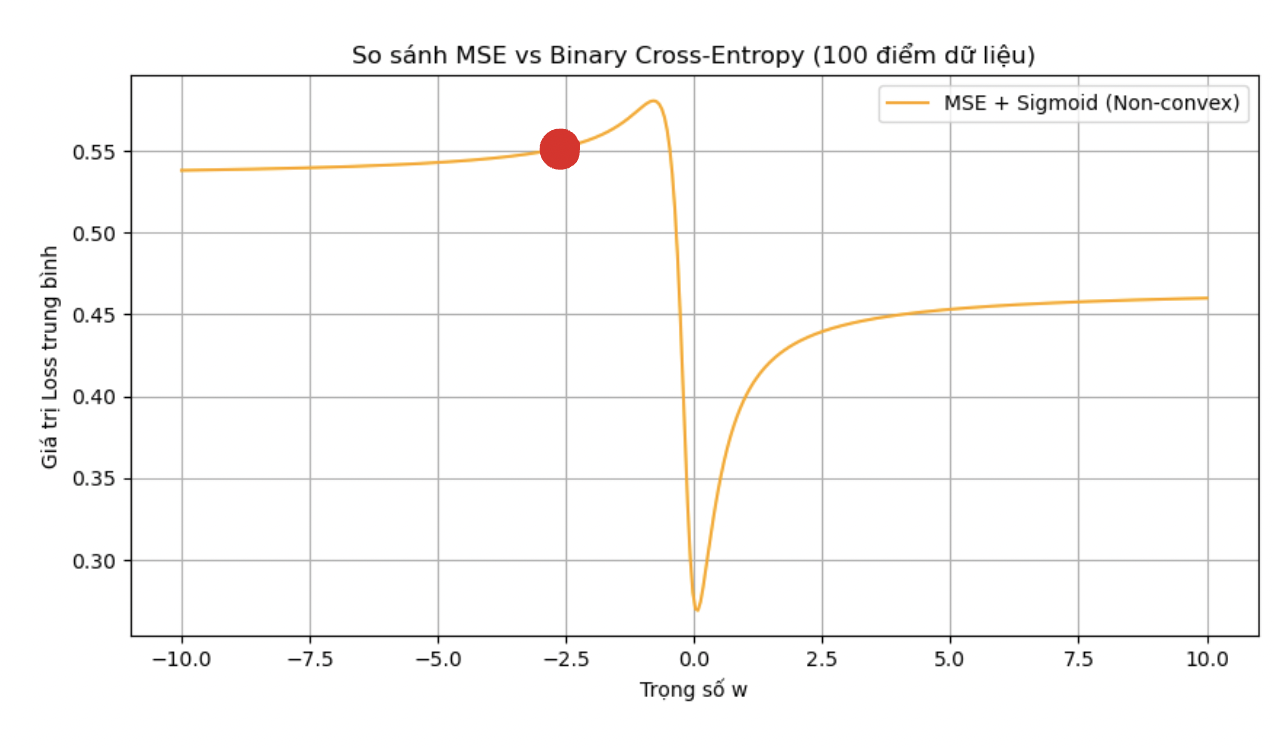
-
Nếu ta nhìn vào chấm màu đỏ thì có thể nhận thấy rằng nếu chúng ta tính toán Gradient tại điểm đó, những update của Weights sau đó đều sẽ đi về phía bên trái, cho dù là cực tiểu của bài toán đang nằm ở bên phải. Do đó điểm màu đỏ đấy được gọi là cực tiểu địa phương và chỗ lõm sâu nhất trên biểu đồ chính là cực tiểu toàn cục mà chúng ta đang nhắm đến. Chúng ta có thể thấy được việc sử dụng MSE kết hợp với Logistic Regression sẽ khiến cho mô hình khó hoặc không thể hội tụ theo đúng ý chúng ta muốn.
- Kế đến hãy xem xét đồ thị khi sử dụng kết hợp với hàm Loss BCE:
$$ L = -[y \log(\hat{y}) + (1 - y)\log(1 - \hat{y})] $$
- Với $y$ là giá trị thực tế
- $\hat{y}$ chính là giá trị dự đoán từ mô hình (ở dạng xác suất)
→ Diễn giải ý nghĩa của hàm loss như sau:
| Dự đoán gần 1 (0,9) | Dự đoán gần 0 (0,1) | |
|---|---|---|
| Giá trị thực 1 | L = -log(0.9) = 0,045… | L = -log(0,1) = 1 |
| Giá trị thực 0 | L = -log(0,1) = 1 | L = -log(0,9) = 0,045… |
- Với xác suất dự đoán của mô hình càng gần với giá trị thực thì hàm loss sẽ trừng phạt rất ít. Nhưng nếu xác suất dự đoán của mô hình càng xa với giá trị thực thì hàm loss sẽ càng tăng nhiều.
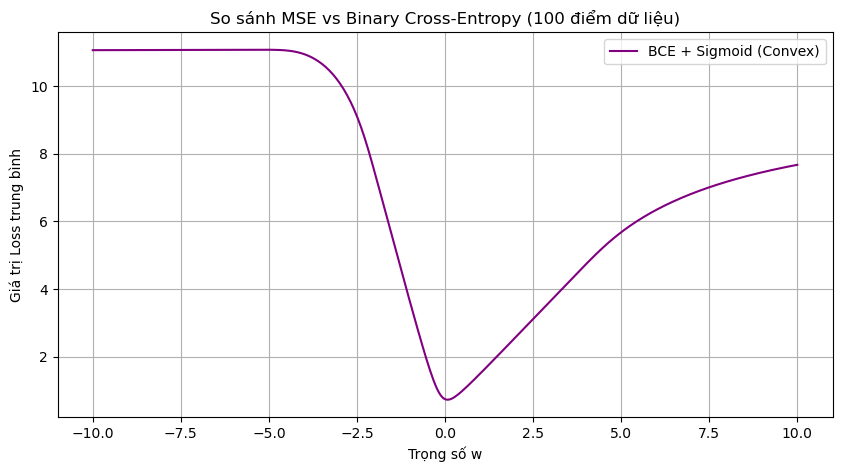
- Do đó, trong bài toán phân loại nhị phân chúng ta thường sẽ sử dụng Logistic Regression kết hợp với BCE.
4. Cách tính Gradient cho Logistic Regression
4.1. The Chain Rule
- Như đã học từ những bài trước, để tối ưu một mô hình từ hàm Loss, chúng ta sẽ áp dụng Chain Rule. Ví dụ như trong bài Linear Regression chúng ta muốn tính:
$$ \frac{\partial L}{\partial W} $$
- Chúng ta cần tính toán những đạo hàm sau:
$$ \frac{\partial L}{\partial W} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial W} $$
- Trong mô hình Logistic Regression, giá trị dự đoán của mô hình Linear Regression (hay chính là $\hat{y}$) sẽ được bỏ thêm vào một hàm Sigmoid. Vậy thì đạo hàm của $\frac{\partial L}{\partial W}$ sẽ trở thành:
$$ \frac{\partial L}{\partial \hat{y}}\cdot \frac{\partial \hat{y}}{\partial z}\cdot \frac{\partial z}{\partial W} $$
- Với $z$ chính là đầu vào của hàm Sigmoid ($z = xw + b$) và $\hat{y}$ chính là đầu ra của hàm Sigmoid đó
4.2. Cách tính đạo hàm giá trị dự đoán theo z
- Nhắc lại công thức Sigmoid mà chúng ta đang xét:
$$ g(z) = \frac{1}{1 + e^{-z}} $$
- Áp dụng đạo hàm hàm hợp của $(\frac{1}{u})' =-\frac{u'}{u^{2}}$:
$$ \frac{e^{-z}}{(1 + e^{-z})^2} $$
- Phân tích biểu thức ta nhận thấy:
$$ g'(z) = \frac{1}{1 + e^{-z}} \cdot \frac{e^{-z}}{1 + e^{-z}} $$
- Ngoài ra:
$$ \frac{e^{-z}}{1 + e^{-z}} = 1 - \frac{1}{1 + e^{-z}} = 1 - g(z) $$
- Suy ra:
$$ g'(z) = g(z)\big(1 - g(z)\big) $$
- Hay trong trường hợp của chúng ta $g(z)$ chính là $\hat{y}$:
$$ \frac{d\hat{y}}{dz} = \hat{y}\big(1 - \hat{y}\big) $$
5. Tổng kết
- Blog hôm nay cho chúng ta biết được lý do tại sao chúng ta lại cần Logistic Regression. Ứng dụng trong những bài toán phân loại nhị phân. Giúp chúng ta dự đoán được xác suất, học được những mối quan hệ phi tuyến hơn là mô hình Linear Regression có thể cho ra giá trị nằm ngoài đoạn [0,1], chỉ học được mối quan hệ tuyến tính.
- Ngoài ra, chúng ta còn biết đến một hàm loss mới chính là Binary Cross Entropy được ứng dụng rất nhiều trong các bài toán phân loại, nơi mà các giá trị phân loại đều rời rạc.
- Cuối cùng thì chúng ta biết đến cách để tính đạo hàm của hàm Logistic Regression, hiểu về thuật toán chạy đằng sau để áp dụng vào những bài toán sau này.
6. Mở rộng
- Logistic Regression chỉ áp dụng được cho bài toán phân loại nhị phần. Ở phần tiếp theo của blog chúng ta sẽ tìm hiểu thêm về cách để giải quyết bài toán phân loại nhiều lớp thông quá thuật toán Softmax Regression.
Softmax Regression
1. Giới thiệu về Softmax Regression
Softmax Regression (Hồi quy Softmax) là một mô hình hồi quy được sử dụng cho bài toán Phân Loại đa lớp (Multi-class Classfication) (ví dụ: dự đoán một datapoint động vật với các feature màu lông, chiều cao, cân nặng,…. và dự đoán là chó, mèo hay khỉ,…).
Trước hết, câu hỏi đặt ra là “Vì sao phải dùng đến Softmax Regression?”, hay đúng hơn là “Có kĩ thuật nào trước đó có thể được sử dụng cho bài toán Multi-class Classification hay không?”. Chúng ta hãy đi qua một số phân tích để hiểu hơn về vấn đề này.
1.1. Vì sao không tạo ra một mô hình học trực tiếp từ nhãn (label) rời rạc mà phải dùng mô hình hồi quy (Regression)?
Giả sử bạn đang xây dựng một mô hình nhận diện trái cây 🍎🍌🍊. Bạn có ba loại trái cây: táo (0), chuối (1), cam (2).
Và bạn nói với mô hình:
“Hãy nhìn ảnh, và dự đoán xem nó là 0 (táo), 1 (chuối) hay 2 (cam) nhé.”
Giả sử bạn đưa bài toán này vào mô hình hồi quy tuyến tính cổ điển (Linear Regression):
$$ \hat{y}=w^Tx+b $$
rồi huấn luyện sao cho $\hat{y}$ gần với nhãn thật (0, 1, 2).
⇒ Mô hình sẽ xem 0, 1 và 2 là những con số có thứ tự (vì Linear Regression hoạt động trên dữ liệu liên tục)
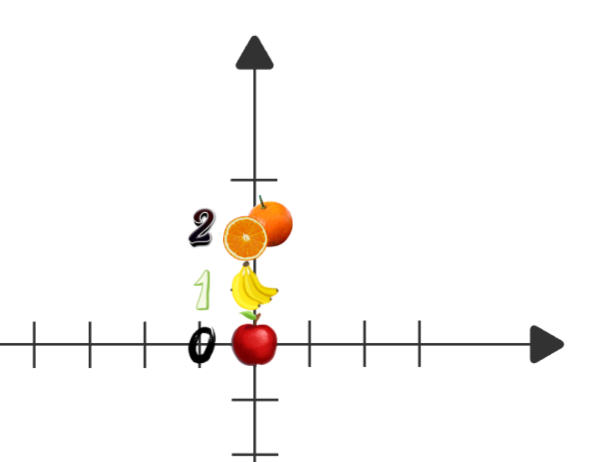
⇒ “Chuối” (1) bị hiểu là nằm giữa “táo” (0) và “cam” (2), như thể có một trục số tuyến tính 0 → 1 → 2.
⇒ Mô hình sẽ cố gắng dịch chuyển ảnh “chuối” về giữa hai đầu, vì đó là cách tốt nhất để giảm MSE.
Nhưng trong thực tế, không có mối liên hệ tuyến tính như vậy. Một bức ảnh “chuối” không “nằm giữa” táo và cam theo bất kỳ nghĩa nào. Điều đó cũng khiến cho hướng đạo hàm (gradient) cũng trở nên sai lệch, vì mô hình không hiểu mình sai bao nhiêu, hay sai theo hướng nào.
Để mô hình có thể học, ta cần:
- Một đại lượng liên tục để đo “mức độ sai”
- Một hàm khả vi để tính gradient
⇒ Khi mô hình sai, nó cần biết phải điều chỉnh theo hướng nào.
Nhãn rời rạc không có hai đặc tính này. Vì vậy, ta buộc phải chuyển bài toán rời rạc sang một không gian liên tục. Nghĩa là ta không còn nói:
“Ảnh này là 0 hay 1 hay 2,”
mà nói:
“Ảnh này giống táo 80%, giống chuối 10%, giống cam 10%.”
Tức là ta ước lượng mức độ tin tưởng (confidence) cho từng lớp.
Khi đó, nếu mô hình dự đoán 60% cho “táo” mà thực tế là “táo”, ta biết cần tăng nó lên; nếu mô hình dự đoán 90% cho “chuối” mà sai, ta biết cần giảm nó xuống.
⇒ Mọi điều chỉnh này giờ đây có thể mô tả bằng gradient, vì đầu ra là các giá trị thực, liên tục, khả vi.
1.2. Vì sao không dùng hồi quy tuyến tính (Linear Regression)?
Giả sử sau khi biết rằng “ta phải học xác suất”, ta thử áp dụng một mô hình tuyến tính nhiều đầu ra (multi-output linear regression):
$$ z_k = w_k^T x + b_k,\quad k = 1, 2, …, K $$
Mỗi lớp $k$ có trọng số riêng $w_k, b_k$. Khi cho ảnh vào, ta nhận được một loạt giá trị $z_1, z_2, …, z_K$.
Ý tưởng nghe có vẻ hợp lý:
“Chỉ cần chọn lớp có $z_k$ lớn nhất làm kết quả.”
⇒ Sử dụng hàm loss ArgMax
Tuy nhiên, có 3 vấn đề lớn xảy ra:
-
Hàm argmax không khả vi (non-differentiable)
ArgMax chỉ “chọn” lớp cao nhất, nhưng nó không cho biết lớp đó cao hơn bao nhiêu, và quan trọng hơn: nó không có đạo hàm.
-
Không giới hạn trong $[0,1]$
Giá trị $z_k = w_k^T x + b_k$ có thể là $5$, $-3$, hay $12.7$.
Nếu ta muốn $z_k$ đại diện cho “mức độ tin tưởng” hay “xác suất thuộc về lớp k”, điều đó không thể, vì:
Một xác suất hợp lệ phải luôn nằm trong khoảng $[0,1]$.
Khi $z_k = 7.2$ hay $z_k = -4$, ta không thể diễn giải được:
- $7.2$ xác suất nghĩa là gì?
- Âm xác suất có nghĩa gì?
→ Không có diễn giải xác suất hợp lệ nào cả.
-
Không có sự cạnh tranh giữa các lớp
Một đặc điểm quan trọng của xác suất là nếu một lớp tăng, lớp khác phải giảm.
Ví dụ: Nếu ta tin 80% rằng ảnh là “táo”, thì phần còn lại (20%) phải chia cho “cam” và “chuối”.
Trong linear regression, điều đó không xảy ra. Khi $z_1$ tăng, $z_2, z_3$ không bị ảnh hưởng gì. Thậm chí mô hình có thể cho ra:
Lớp Giá trị (z_k) Táo 100 Chuối 120 Cam 90 ⇒ Vô lý vì mô hình không thể “tự tin” rằng 1 datapoint thuộc tất cả các class được.
⇒ Linear Regression thất bại khi ta muốn mô hình hóa xác suất đa lớp.
1.3. Vì sao không dùng hồi quy Logistic (Logistic Regression)?
Vậy là Linear Regression đã thất bại, ta có thể nghĩ ngay đến một lựa chọn khác hợp lý hơn, đó là Logistic Regression – mô hình phân loại nhị phân mà ta đã đề cập ở phần trước.
Logistic Regression có một ưu điểm lớn: nó biến đầu ra tuyến tính
$$ z = w^\top x + b $$
thành xác suất trong [0, 1] bằng hàm sigmoid:
$$ P(y=k|x) = \frac{1}{1 + e^{-z}} {} ,\space k \in \{0, 1\} $$
Nghe có vẻ đúng hướng, vì classification rõ ràng cần xác suất. Tuy nhiên, mô hình này chỉ áp dụng được cho Binary Classification.
Vậy để áp dụng cho Multi-class Clasification, ta có thể:
-
Điều chỉnh Logistic Regression thành Logistic Regression cho từng class, với bộ tham số riêng cho từng mô hình tương ứng với từng class
⇒ Vấn đề: Các mô hình không cạnh tranh với nhau, class 1 được tăng độ tự tin không ảnh hưởng đến độ tự tin của class 2.
⇒ Vô lý bởi vì tất cả các class đều đang chia sẻ cùng 1 “miếng bánh” 100% độ tự tin.
-
Vậy nếu dùng chung bộ tham số thì sao?
⇒ Vấn đề: Tổng các xác suất không bằng 1 (không phù hợp với xác suất), và mô hình có thể tự tin với nhiều class (vô lý, và cũng không thể xử lí bằng ArgMax với lí do đã nêu ở phần Linear Regression).
⇒ Logistic Regression cũng thất bại khi ta muốn mô hình hóa xác suất đa lớp.
Hiểu được lí do vì sao các mô hình khác không thể xử lí bài toán Phân Loại đa lớp (Multi-class Classfication). Ta hãy đi vào tìm hiểu về Softmax Regression và cách hoạt động của nó.
2. Cơ chế hoạt động của Softmax Regression
Cũng tương tự với Logistic Regression, Softmax Regression cũng sử dụng các giá trị đầu vào là $z$ được chạy trên mô hình Linear Regression. Tuy nhiên, đối với $K$ class trong Softmax Regression, ta cần $k$ biến $z$ làm logit thể hiện “điểm số” cho từng class:
$$ z_k = {w_k}^Tx+b_k, \space k \in \{0,1,...,K-1\} $$
- $z_k$: “điểm số” cho class $k$
- $w_k$: vector trọng số cho mô hình linear regression cho logit $z_k$
- $b_k$: bias cho mô hình linear regression cho logit $z_k$
$z_k$ càng lớn ⇒ Độ tự tin của mô hình cho rằng input thuộc class $k$ càng cao
Lúc này, ta sẽ áp dụng hàm Softmax lên các logits $z_k$ vừa tính để có được xác suất mà mô hình cho rằng input sẽ thuộc class $k$
$$ \hat{y_k} = P(y = k \mid x) = \frac{e^{z_k}}{\sum_{j=1}^{K} e^{z_j}} $$
- $\hat{y_k}$: dự đoán của mô hình dưới dạng xác suất
- $P(y = k \mid x)$: xác suất input sẽ thuộc class $k$
- $e^{z_j}$: hàm $e$ mũ logit $z_j$
⇒ Đối với cùng 1 input $x$, ta sẽ predict $x$ thuộc class $k$ nếu:
$$ z_k > z_j \ \forall \ j \in \{0, 1, …, K-1\} \backslash \{k\} $$
Nghĩa là class $k$ với $z_k$ lớn nhất sẽ được chọn làm prediction cho input $x$.
3. Cross Entropy Loss
Như các bạn đã biết ở phần Logistic Regression, hàm Binary Cross Entropy Loss được sử dụng để đo trung bình độ hỗn loạn của prediction cho bài toán phân loại nhị phân (Binary Classification)
$$ BCE\_Loss = -\sum_{i=1}^{N} \ [y_i \log(\hat{y_i}) + (1 - y_i)\log(1 - \hat{y_i})] $$
Trong đó:
- $N$ là số lượng mẫu
- $y_i \in \{0,1\}$ là nhãn thực của mẫu thứ iii
- $\hat{y_i}$ là xác suất dự đoán cho nhãn $1$
Đối với bài toán Phân Loại đa lớp (Multi-class Classification), ý tưởng vẫn giống nhau: so sánh xác suất dự đoán với nhãn thật. Tuy nhiên, vì mỗi mẫu có nhiều lớp, ta sử dụng one-hot encoding cho nhãn và tổng hợp cross-entropy theo từng lớp:
$$ CE\_Loss = - \sum_{i=1}^{N} \sum_{k=1}^{K} y_{ik} \, \log \hat{y}_{ik} = - \sum_{i=1}^{N} \sum_{k=1}^{K} y_{ik} \, \log \frac{e^{z_k}}{\sum_{j=1}^{K} e^{z_j}} $$
Trong đó:
- $K$ là số lớp
- $y_{ik} = 1$ nếu mẫu i thuộc lớp $k$, ngược lại $0$
- $\hat{y}_{ik}$ là xác suất dự đoán của mẫu $i$ cho lớp $k$ (đầu ra của hàm softmax)
Khi dự đoán càng gần với nhãn thật (tức là $\hat{y}_{i y_i} \to 1$), giá trị loss càng nhỏ.
Ngược lại, khi dự đoán sai hoặc không chắc chắn (tức là $\hat{y}_{i y_i} \ll 1$), giá trị loss càng lớn.
Như vậy, hàm loss này khuyến khích mô hình tăng xác suất $\hat{y}_{i k}$ cho lớp đúng $k = y_i$ và giảm xác suất cho các lớp sai $k \neq y_{i}$, giống như cách Binary Cross-Entropy làm trong nhị phân, nhưng được mở rộng cho nhiều lớp.
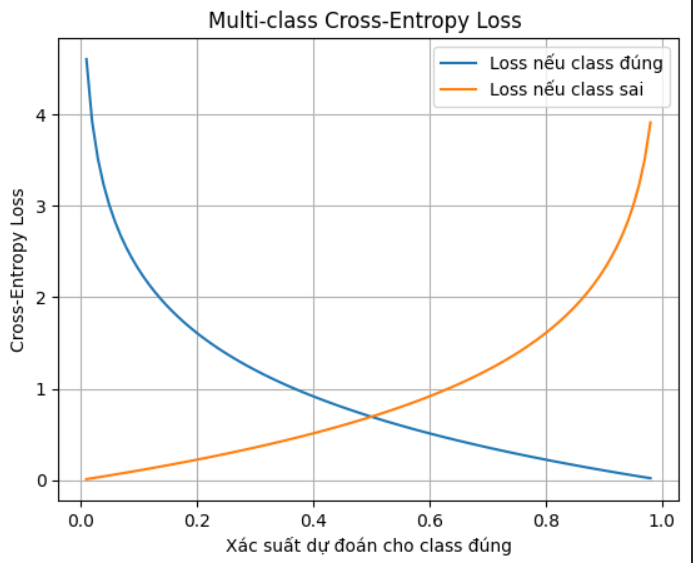
Giả sử:
- Có 3 lớp: Táo, Chuối, Cam
- Nhãn thật: Táo → one-hot: $y=[1,0,0]$
- Mô hình dự đoán xác suất (softmax output): $\hat{y} = [0.7, 0.2, 0.1]$
Cross-entropy loss cho sample này:
$$ L = - \sum_{k=1}^{3} y_k \log \hat{y}_k = - \big(1*\log 0.7 + 0*\log 0.2 + 0 *\log 0.1 \big) = - \log 0.7 \approx 0.357 $$
| Lớp (k) | Nhãn thật $(y_k)$ | Xác suất dự đoán $(\hat{y}_k)$ | $(y_k * \log \hat{y}_k)$ |
|---|---|---|---|
| Táo | 1 | 0.7 | $(\log 0.7 \approx -0.357)$ |
| Chuối | 0 | 0.2 | 0 |
| Cam | 0 | 0.1 | 0 |
4. Cách tính đạo hàm (Gradient) cho hàm Softmax Regression
4.1. Notation
- $N$: số mẫu.
- $D$: số đặc trưng.
- $K$: số lớp.
- Input: $\mathbf{x}_i \in \mathbb{R}^D$, nhãn $y_i \in \{1,...,K\}$.
- One-hot encoding: $y_{ik} = 1$ nếu $k=y_i$, $0$ nếu không.
-
Parameters:
$\mathbf{W} \in \mathbb{R}^{D \times K}$, $\mathbf{b} \in \mathbb{R}^K$
-
Logits:
$$z_{ik} = \mathbf{x}_i^\top \mathbf{w}_k + b_k$$
- Softmax:
$$p_{ik} = \frac{e^{z_{ik}}}{\sum_{l=1}^K e^{z_{il}}}$$
- Loss (cross-entropy, toàn batch):
$$L = - \sum_{i=1}^N \sum_{k=1}^K y_{ik} \log p_{ik}$$
Lưu ý: Ở đây sử dụng $p_{ik}$ thay cho $\hat{y_{ik}}$ để dễ hiểu đây là giá trị xác suất, không nhãn của class.
4.2. Mục tiêu
Tính đạo hàm:
$$\frac{\partial L}{\partial \mathbf{w}_j}, \quad \frac{\partial L}{\partial b_j}$$
4.3. Bắt đầu từ single sample $i$
Loss cho mẫu $i$:
$$L_i = - \sum_{k=1}^K y_{ik} \log p_{ik}$$
Đạo hàm theo logits $z_{ij}$:
$$\frac{\partial L_i}{\partial z_{ij}} = - \sum_{k=1}^K y_{ik} \frac{\partial \log p_{ik}}{\partial z_{ij}}$$
Đạo hàm log softmax
-
$\log p_{ik} = z_{ik} - \log \sum_{l=1}^K e^{z_{il}}$
Suy ra: $$\frac{\partial \log p_{ik}}{\partial z_{ij}} = \frac{\partial z_{ik}}{\partial z_{ij}} - \frac{1}{\sum_l e^{z_{il}}} \frac{\partial \sum_l e^{z_{il}}}{\partial z_{ij}}$$
-
$\frac{\partial z_{ik}}{\partial z_{ij}} = \delta_{kj}$
-
$\frac{\partial \sum_l e^{z_{il}}}{\partial z_{ij}} = e^{z_{ij}}$
Kết hợp:
⇒ $$\frac{\partial \log p_{ik}}{\partial z_{ij}} = \delta_{kj} - \frac{e^{z_{ij}}}{\sum_l e^{z_{il}}} = \delta_{kj} - p_{ij}$$
4.4. Gradient theo logits
$$\frac{\partial L_i}{\partial z_{ij}} = - \sum_{k=1}^K y_{ik} (\delta_{kj} - p_{ij}) = - (y_{ij} - y_{ij} p_{ij}) + \sum_{k \neq j} y_{ik} p_{ij} = p_{ij} - y_{ij}$$
- Trường hợp $j$ là lớp đúng: $y_{ij} = 1$, gradient $p_{ij}-1$ (âm nếu $p_{ij}<1$, đẩy tăng xác suất).
- Trường hợp $j$ là lớp sai: $y_{ij} = 0$, gradient $p_{ij}-0 = p_{ij}$ (dương, giảm xác suất).
4.5. Gradient theo weights $\mathbf{w}_j$ và bias $b_j$
Với $z_{ij} = {x}_i^\top {w}_j + b_j$:
$$\frac{\partial z_{ij}}{\partial {w}_j} = {x}_i, \quad \frac{\partial z_{ij}}{\partial b_j} = 1$$
Áp dụng chain rule:
Suy ra:
- $$\frac{\partial L_i}{\partial {w}_j} = \frac{\partial L_i}{\partial z_{ij}} \frac{\partial z_{ij}}{\partial {w}_j} = (p_{ij}-y_{ij}) {x}_i$$
- $$\frac{\partial L_i}{\partial b_j} = \frac{\partial L_i}{\partial z_{ij}} \frac{\partial z_{ij}}{\partial b_j} = p_{ij}-y_{ij}$$
trong đó:
- $\mathbf{x}_i$: vector input
- $p_{ij}$: xác suất của model dự đoán $\mathbf{x}_i$ thuộc class $j$
- $y_{ij} = 1$ nếu $j$ là lớp đúng, $y_{ij} = 0$ nếu $j$ là lớp sai
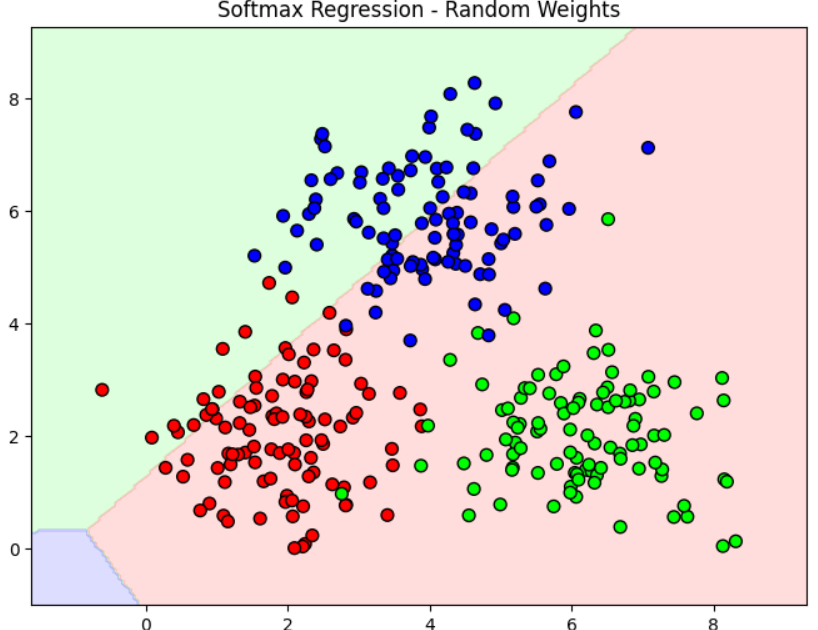
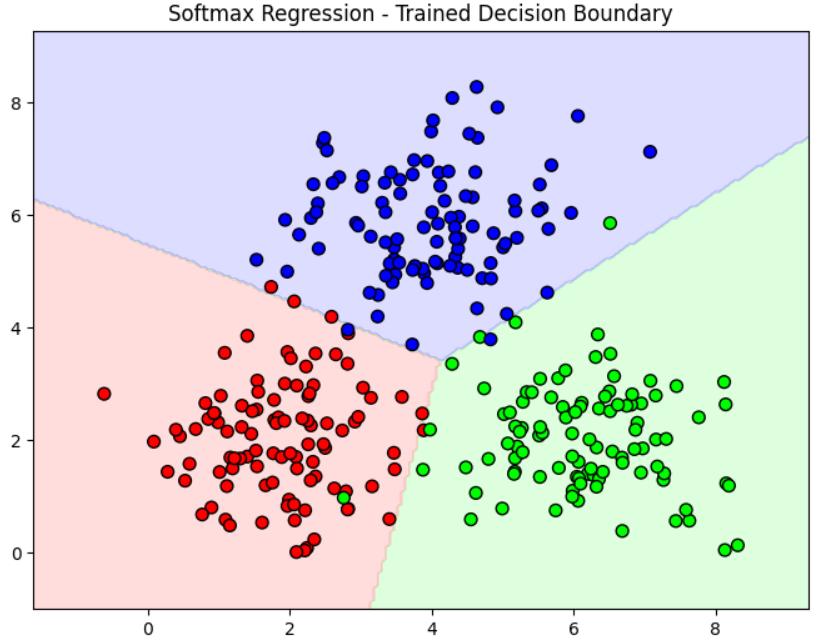
Sau khi mô hình cập nhật trọng số, khả năng predict class của mô hình sẽ tốt hơn sau mỗi bước. Sau đây là minh họa cho sự khác nhau giữa trước khi và sau khi train Softmax Regression sử dụng Cross Entropy Loss:
5. Giải thích sâu hơn về nguyên lí đằng sau Softmax Regression
5.1. Khởi điểm: từ logistic regression nhị phân (khi K = 2)
Với bài toán nhị phân (hai lớp: 0 và 1), logistic regression mô tả log-odds bằng một hàm tuyến tính:
$$ \log\frac{P(y=1\mid x)}{P(y=0\mid x)} = w^\top x + b. $$
Từ đó ta suy ra xác suất:
$$ ⁍ $$
Ý nghĩa: mô hình hồi quy lên log-odds — log(tỉ xác suất) là tuyến tính theo $x$. Đây là mô hình log-linear trong trường hợp K=2.
5.2. Mở rộng ý tưởng: log-odds so với một lớp tham chiếu khi K > 2
Khi có $K$ lớp $\{1,\dots,K\}$, ta không thể ghi một log-odds duy nhất nữa. Một cách tự nhiên (thống kê cổ điển) là chọn một lớp làm tham chiếu — gọi là lớp $K$ — rồi mô hình hóa log-odds của mọi lớp so với lớp tham chiếu bằng các hàm tuyến tính:
Định nghĩa (multinomial logit, reference class = K):
$$ \log\frac{P(y=k\mid x)}{P(y=K\mid x)} = w_k^\top x + b_k,\qquad k=1,\dots,K-1 \tag{1}. $$
- Ở đây $w_k\in\mathbb R^D, b_k\in\mathbb R$ là tham số cho lớp $k$.
- Lưu ý: không định nghĩa $w_K,b_K$ (ta có thể hiểu $w_K=0,b_K=0$ như 1 quy ước).
Trực giác: (1) nói rằng log-tỉ lệ giữa xác suất của lớp kkk và xác suất của lớp tham chiếu $K$ là một hàm tuyến tính của $x$.
5.3. Từ log-odds sang tỉ lệ — biểu thức tỉ lệ giữa P(y=k) và P(y=K)
Từ (1) lấy mũ hai vế:
$$ \frac{P(y=k\mid x)}{P(y=K\mid x)} = \exp(w_k^\top x + b_k),\qquad k=1,\dots,K-1.\tag{2} $$
Suy ra:
$$ P(y=k\mid x) = P(y=K\mid x)\,\exp(w_k^\top x + b_k),\qquad k=1,\dots,K-1. \ \tag{3} $$
Đây là biểu thức rất trực quan: xác suất của lớp kkk tỉ lệ với xác suất của lớp $K$ nhân một hệ số $e^{\text{score}_k}$.
5.4. Dùng ràng buộc tổng xác suất = 1 để giải $P(y=K\mid x)$
Ta có ràng buộc cơ bản của xác suất:
$$\sum_{j=1}^{K} P(y=j\mid x) = 1.$$
Thay (3) vào tổng trên (với $k=1,\dots,K-1$ biểu diễn bằng (3) và để lại $P(y=K\mid x)$ ở vế cuối):
$$\sum_{k=1}^{K-1} P(y=K\mid x)\,e^{w_k^\top x + b_k} + P(y=K\mid x) = 1$$.
Gom $P(y=K\mid x)$ ra ngoài:
$$P(y=K\mid x)\Big(1 + \sum_{k=1}^{K-1} e^{w_k^\top x + b_k}\Big) = 1.$$
Do đó:
$$ \boxed{\,P(y=K\mid x) = \frac{1}{\,1 + \sum_{k=1}^{K-1} e^{w_k^\top x + b_k}\,}\, }. \tag{4} $$
5.5. Biểu thức cho mọi $P(y=k\mid x)$ (k = 1..K-1) — đưa về dạng chuẩn
Từ (3) và (4):
$$ P(y=k\mid x) = \frac{e^{w_k^\top x + b_k}}{\,1 + \sum_{j=1}^{K-1} e^{w_j^\top x + b_j}\,},\qquad k=1,\dots,K-1.\tag{5} $$
và $P(y=K\mid x)$ là (4). Đây là dạng multinomial logistic with reference class.
5.6. Chuyển sang dạng softmax (đưa tất cả các lớp vào mẫu số)
Để viết công thức theo một quy ước đối xứng hơn (mẫu số chạy từ $1$ tới $K$), ta giả sử (hoặc đặt quy ước) rằng:
$$ w_K = 0,\qquad b_K = 0. $$
Khi đó $e^{w_K^\top x + b_K} = e^0 = 1$. Dùng điều này, (5) và (4) có thể viết gọn thành:
$$ {\,P(y=k\mid x) = \frac{e^{w_k^\top x + b_k}}{\sum_{j=1}^{K} e^{w_j^\top x + b_j}},\qquad k=1,\dots,K.\,}\tag{6} $$
Đây chính là hàm Softmax — dạng chuẩn mà ta thường thấy.
Ghi chú quan trọng: việc chọn $w_K=b_K=0$ không làm mất tính tổng quát — nó chỉ là một gauge fixing (fix identifiability). Lý do: nếu ta cộng cùng một hằng số $c(x)$ vào mọi $w_j^\top x + b_j$, phân phối $P$ không đổi (xem phần 7).
5.7. Tính bất biến khi thêm cùng một hằng số vào mọi logits (identifiability)
Đặt $z_j = w_j^\top x + b_j$. Nếu ta thay $z_j \leftarrow z_j + c$ (thêm cùng $c$ cho mọi $j$), thì
$$ \frac{e^{z_k + c}}{\sum_j e^{z_j + c}} = \frac{e^c e^{z_k}}{e^c\sum_j e^{z_j}} = \frac{e^{z_k}}{\sum_j e^{z_j}}. $$
=> Softmax không thay đổi. Vì vậy vector $z$ chỉ xác định xác suất lên simplex với K−1 độ tự do. Để ước lượng tham số duy nhất, ta cần fix một chiều (ví dụ $z_K=0$ tương đương $w_K=b_K=0$), hoặc đặt ràng buộc khác như $\sum_j z_j = 0$.
5.8. So sánh trực tiếp hai lớp (pairwise log-odds)
Từ (6) suy ra log-odds giữa hai lớp $i$ và $j$:
$$\log\frac{P(y=i\mid x)}{P(y=j\mid x)} = (w_i^\top x + b_i) - (w_j^\top x + b_j).$$
Đặc biệt, nếu ta chọn $j=K$ như lớp tham chiếu và đặt $w_K=b_K=0$, ta trở lại (1).
=> Tất cả các log-odds cặp đôi đều là hiệu của hai logits tuyến tính.
5.9. Tổng kết logic các bước (một mạch ngắn gọn)
- Với K=2, logistic regression mô tả log-odds bằng hàm tuyến tính.
- Mở rộng lên K lớp: mô tả K−1 log-odds so với lớp tham chiếu KKK bằng các hàm tuyến tính (đúng số DOF).
- Lấy mũ để có tỉ lệ $P(y=k)/P(y=K)$.
- Dùng ràng buộc tổng xác suất = 1 để giải ra $P(y=K)$.
- Thay ngược để được biểu thức cho mọi $P(y=k)$ — chuyển về dạng đối xứng bằng cách đặt $w_K=b_K=0$.
- Kết quả là softmax: $P(y=k) = e^{z_k} / \sum_j e^{z_j}$.
- Softmax invariant dưới phép cộng hằng số cho mọi logits → chỉ có K−1 DOF → cần fix gauge để tham số hoá duy nhất.
5.10. Ví dụ số nhỏ (K = 3) — để kiểm chứng
Chọn $w_1^\top x + b_1 = 2$, $w_2^\top x + b_2 = 1$, lớp tham chiếu $K=3$ ⇒ $z_3=0$.
Tính:
$$e^{z} = [e^2, e^1, e^0] \approx [7.389,\,2.718,\,1].$$
$\text{mẫu số} = 7.389 + 2.718 + 1 \approx 11.107.$
$$P = [7.389/11.107,\;2.718/11.107,\;1/11.107]\approx[0.665,\,0.245,\,0.090].$$
Nếu trước đó ta dùng công thức tham chiếu (4)-(5) với $P_3 = 1/(1+e^2+e^1)$, ta sẽ nhận đúng kết quả trên. Nếu thêm hằng số $c=−1$ vào mọi logits: $z=[1,0,−1]$ vẫn cho cùng $P$.
5.11. Hệ quả thực tiễn & giải thích trực giác
- K−1 độ tự do: vì xác suất tổng bằng 1, vector xác suất sống trên simplex (kích thước K−1). Do đó việc mô hình hóa K−1 log-odds là tự nhiên và đủ.
- Chọn lớp mốc chỉ là quy ước để tránh dư thừa tham số (identifiability). Kết quả dự đoán không phụ thuộc vào lớp mốc (nếu ta thay đổi tham số tương ứng).
- Softmax cho “cạnh tranh toàn cục”: mỗi $e^{z_k}$ đóng góp vào mẫu số chung; tăng zkz_kzk làm giảm tỉ trọng tương đối của các $e^{z_j}$ khác. Đây chính là tính “cạnh tranh” giữa các lớp mà linear multi-output thiếu.
- Log-linear: log-tỉ số giữa hai lớp là tuyến tính theo $x$ — nên mô hình dễ giải thích, gradient đơn giản, và cross-entropy là negative log-likelihood tư nhiên.
Chưa có bình luận nào. Hãy là người đầu tiên!