From Binary to Multi-Class: A Guide to Logistic and Softmax Regression

1. Logistic Regression for binary classification

Logistic Regression là một trong những thuật toán Supervised-Learning nền tảng quan trọng nhất.

Khác với Linear Regression (dự đoán giá trị liên tục), Logistic Regression giải quyết bài toán phân loại nhị phân (Binary Classification), nơi đầu ra chỉ thuộc một trong hai lớp (ví dụ: 0 hoặc 1, Yes hoặc No, True hoặc False).

Mục tiêu của Logistic Regression là dự đoán xác suất đầu vào thuộc về lớp 1 (positive class). Mô hình sử dụng hàm Sigmoid để chuyển đổi đầu vào thành giá trị xác suất trong khoảng từ 0 đến 1.

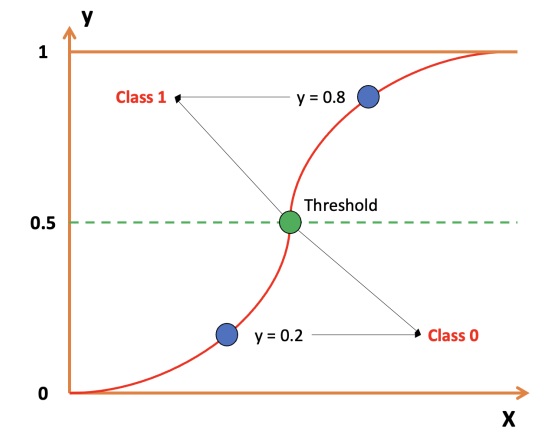
Hình 1: Cách Sigmoid quyết định Class cho dữ liệu[1]

Ví dụ đơn giản: Giả sử chúng ta có 2 lớp [0, 1]. Khi đưa dữ liệu (3 sample) đầu vào, mô hình Binary Classification trả về xác suất như sau [0.2, 0.8, 0.4]. Ở đây ta đặt ngưỡng (Threshold) là 0.5.

• 0.2 < 0.5 $\rightarrow$ thuộc lớp 0
• 0.8 > 0.5 $\rightarrow$ thuộc lớp 1
• 0.4 < 0.5 $\rightarrow$ thuộc lớp 0

Kết quả dự đoán cuối cùng (output) của model là: [0, 1, 0].

Quy trình hoạt động (Pipeline)

Để xây dựng và vận hành Logistic Regression, chúng ta đi theo một luồng xử lý tuần tự từ chuẩn bị dữ liệu, tính toán đến ra quyết định cuối cùng.

Hình 2: Pipeline đơn giản của Logistic Regression[1]

Bước 1: Chuẩn bị Dữ liệu và Tham số

Mọi quá trình đều bắt đầu từ dữ liệu.

• Dữ liệu đầu vào ($X$): Là ma trận chứa các đặc trưng (features).
  $$ X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix} $$

• Nhãn ($Y$): Trong Logistic Regression, $Y$ là giá trị nhị phân đại diện cho 2 lớp.
  $$ Y = \begin{cases} 0 & \text{if } Class\ 0 \\ 1 & \text{if } Class\ 1 \end{cases} $$

• Khởi tạo tham số ($w, b$): Trước khi tính toán, mô hình cần khởi tạo trọng số $w$ (weights) và hệ số chệch $b$ (bias). Thông thường, chúng được khởi tạo ngẫu nhiên nhỏ hoặc bằng 0.

Bước 2: Tính toán chiều xuôi (Forward Pass)

Sau khi có dữ liệu và tham số, mô hình thực hiện tính toán để đưa ra dự đoán xác suất.

1. Tính điểm tuyến tính (Linear Score):
   Áp dụng hàm tuyến tính lên dữ liệu đầu vào $X$ với bộ tham số hiện tại.
   $$z = \omega \cdot X + b$$

2. Hàm kích hoạt Sigmoid (Activation):
   Vì $z$ có thể là bất kỳ số thực nào ($-\infty$ đến $+\infty$), ta đưa $z$ qua hàm Sigmoid để chuẩn hóa thành xác suất $\hat{y}$ trong khoảng $(0, 1)$.
   $$\hat{y} = \sigma(z) = \frac{1}{1 + e^{-z}}$$

Bước 3: Tính toán lỗi (Loss Function)

Để biết mô hình đang dự đoán tốt hay tệ, ta so sánh kết quả xác suất $\hat{y}$ vừa tính được với nhãn thực tế $y$ thông qua hàm Binary Cross-Entropy.

$$L = -[y \log(\hat{y}) + (1 - y) \log(1 - \hat{y})]$$

• Mục tiêu của quá trình huấn luyện là tìm bộ tham số $(\omega, b)$ sao cho giá trị Loss $L$ là nhỏ nhất.

Bước 4: Tối ưu hóa (Backward Pass)

Đây là bước "học" của mô hình. Chúng ta sử dụng thuật toán Gradient Descent để cập nhật tham số dựa trên sai số vừa tính được.

$$\theta = \theta - \eta \nabla_{\theta}L$$

Trong đó:

• $\nabla_{\theta}L$: Đạo hàm (Gradient) cho biết hướng và độ lớn cần điều chỉnh của tham số.

• $\eta$: Learning rate (tốc độ học).

Lưu ý: Quá trình từ Bước 2 đến Bước 4 sẽ được lặp đi lặp lại nhiều lần (Epochs) cho đến khi hàm Loss hội tụ.

Bước 5: Ra quyết định (Inference/Thresholding)

Sau khi mô hình đã được huấn luyện, để có kết quả phân loại cuối cùng (0 hoặc 1), ta sử dụng xác suất $\hat{y}$ từ Bước 2 để so sánh với một ngưỡng (Threshold), thường là 0.5.

• Nếu $\hat{y} \geq 0.5 \rightarrow$ Dự đoán là Class 1.
• Nếu $\hat{y} < 0.5 \rightarrow$ Dự đoán là Class 0.

2. Code triển khai của Logistic Regression

Để hiểu rõ cách Logistic Regression hoạt động "bên dưới lớp vỏ" (under the hood), thay vì dùng ngay các thư viện có sẵn như Scikit-learn, chúng ta sẽ tự xây dựng thuật toán bằng phương pháp Vectorization với thư viện NumPy.

Phương pháp này sử dụng các phép toán ma trận để tính toán song song trên toàn bộ dữ liệu, giúp tốc độ xử lý nhanh hơn hàng trăm lần so với việc dùng vòng lặp for truyền thống.

Bước 1: Chuẩn bị dữ liệu giả lập

Trước hết, chúng ta tạo một bộ dữ liệu đơn giản gồm 2 lớp phân biệt để thử nghiệm thuật toán. Chúng ta sẽ chia dữ liệu thành tập huấn luyện (train) và tập kiểm tra (test).

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 1. Tạo dữ liệu giả lập (500 mẫu, 2 đặc trưng, 2 lớp)
X, y = make_blobs(n_samples=500, centers=2, n_features=2, random_state=42, cluster_std=1.5)
y = y.reshape(-1, 1) # Chuyển y thành vector cột

# 2. Chia tập train/test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

print(f"Training set: {X_train.shape}")
print(f"Test set: {X_test.shape}")

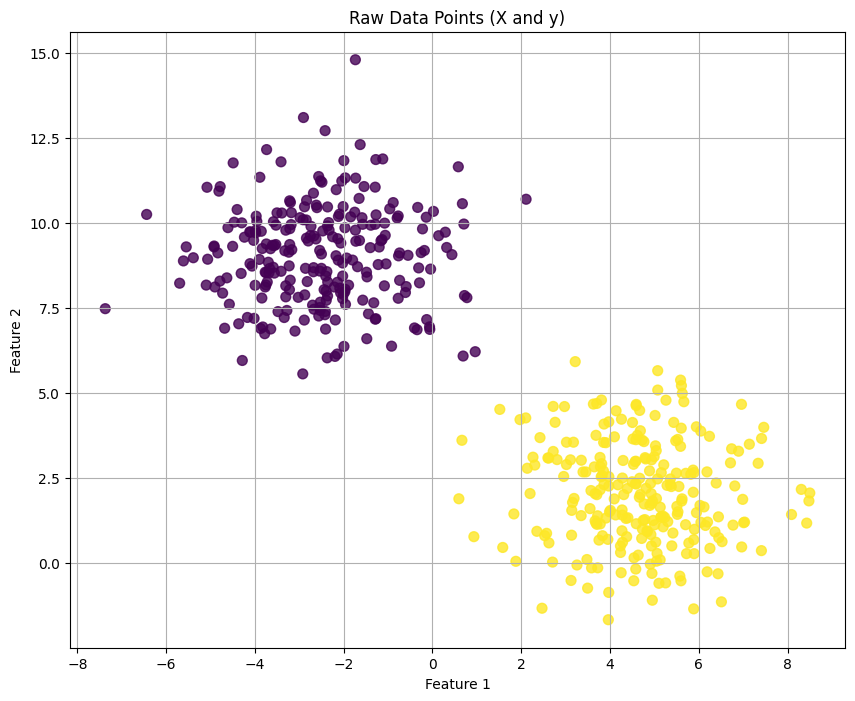
Hình 3: Hình ảnh về dữ liệu

Bước 2: Xây dựng và Huấn luyện mô hình (Vectorization)

Chúng ta sẽ thực hiện quy trình gồm 3 bước chính trong vòng lặp huấn luyện:

1. Forward Pass: Tính toán giá trị tuyến tính $z = w \cdot X + b$ và đưa qua hàm Sigmoid để dự đoán xác suất $\hat{y}$.

2. Loss Computation: Tính sai số giữa dự đoán và thực tế bằng hàm Binary Cross-Entropy.

3. Backward Pass: Tính đạo hàm (Gradient) và cập nhật tham số $w, b$ theo chiều ngược lại của Gradient Descent.

# Cấu hình tham số (Hyperparameters)
learning_rate = 0.01
epochs = 1000
n_samples, n_features = X_train.shape

# Khởi tạo tham số w (trọng số) và b (hệ số chặn)
w = np.zeros((n_features, 1))
b = 0

losses = [] # Lưu lịch sử lỗi để vẽ đồ thị

# --- VÒNG LẶP HUẤN LUYỆN ---
for epoch in range(epochs):
    # 1. Forward Pass (Tính toán cho toàn bộ batch)
    z = np.dot(X_train, w) + b
    y_hat = 1 / (1 + np.exp(-z)) # Hàm Sigmoid

    # 2. Tính Loss (Binary Cross-Entropy)
    # Thêm 1e-15 để tránh lỗi log(0)
    loss = -(1/n_samples) * np.sum(y_train * np.log(y_hat + 1e-15) + (1 - y_train) * np.log(1 - y_hat + 1e-15))
    losses.append(loss)

    # 3. Tính đạo hàm (Gradient)
    dw = (1/n_samples) * np.dot(X_train.T, (y_hat - y_train))
    db = (1/n_samples) * np.sum(y_hat - y_train)

    # 4. Cập nhật tham số (Gradient Descent)
    w = w - learning_rate * dw
    b = b - learning_rate * db

    # In loss sau mỗi 100 epochs
    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss:.4f}')

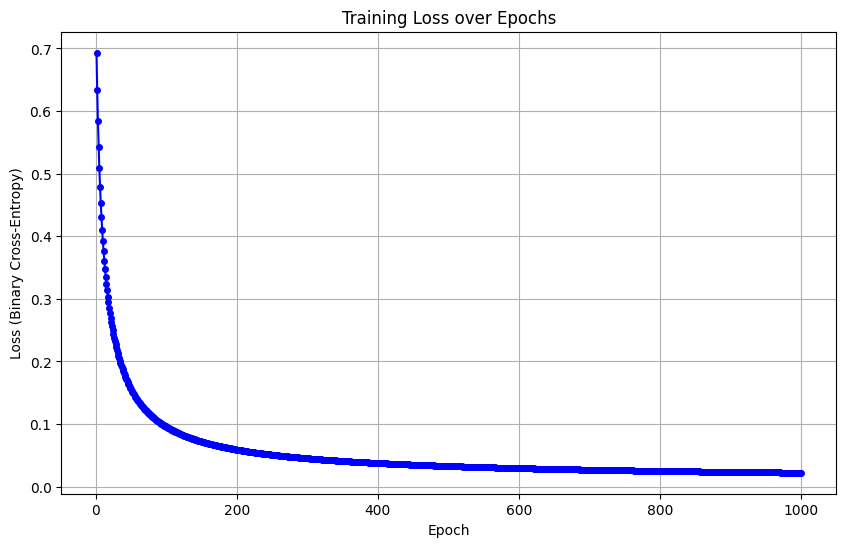
Hình 4: Kết qủa huấn luyện loss của mô hình

Bước 3: Đánh giá kết quả

Sau khi huấn luyện xong, ta sử dụng bộ tham số $w$ và $b$ đã tìm được để dự đoán trên tập kiểm tra (Test set). Nếu xác suất $> 0.5$ ta gán nhãn 1, ngược lại gán nhãn 0.

# Dự đoán trên tập Test
z_test = np.dot(X_test, w) + b
y_pred_proba = 1 / (1 + np.exp(-z_test))

# Chuyển xác suất thành nhãn lớp (Ngưỡng 0.5)
y_pred = (y_pred_proba > 0.5).astype(int)

# Đánh giá độ chính xác
acc = accuracy_score(y_test, y_pred)
print(f"\n--- Kết quả ---")
print(f"Trọng số w tìm được: {w.flatten()}")
print(f"Bias b tìm được: {b:.4f}")
print(f"Độ chính xác (Accuracy): {acc:.4f}")

Sau khi huấn luyện mô hình Logistic Regression ta được kết quả như sau.

--- Kết quả ---
Trọng số w tìm được: [ 1.23553191 -0.37815406]
Bias b tìm được: 0.1781
Độ chính xác (Accuracy): 1.0000

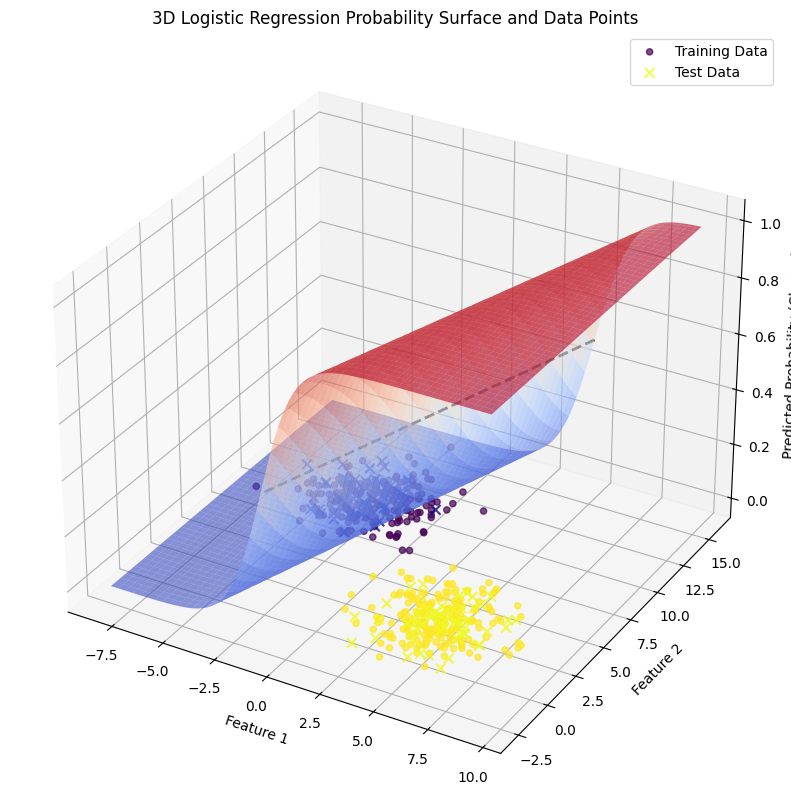
Hình 5: Hình ảnh của dữ liệu và hàm Logistic

Lưu ý: Cách triển khai trên minh họa bản chất toán học của thuật toán. Trong thực tế sản xuất (production), bạn nên sử dụng LogisticRegression từ thư viện scikit-learn hoặc PyTorch để tối ưu hóa hiệu năng, độ ổn định, cũng như hỗ trợ các kỹ thuật nâng cao như Regularization.

3. Softmax Regression for multiple classification

Tiếp theo, chúng ta sẽ tìm hiểu về Softmax Regression, một kỹ thuật mở rộng dựa trên Logistic Regression để xử lý các bài toán phân loại đa lớp (Multi-class Classification).

• Logistic Regression: Chỉ phân loại 2 lớp (Binary), ví dụ: 0 hoặc 1, Chó hoặc Mèo.
• Softmax Regression: Phân loại dữ liệu vào nhiều hơn hai lớp (Multi-class), ví dụ: lớp 1, 2, 3, ..., $K$ (phân loại chữ số viết tay từ 0-9).

Mục tiêu của Softmax Regression là tính toán và đưa ra một phân phối xác suất cho tất cả các lớp. Lớp nào có xác suất cao nhất sẽ được chọn làm kết quả dự đoán.

Ví dụ đơn giản: Giả sử bài toán có 3 lớp [0, 1, 2]. Khi đưa một ảnh đầu vào, mô hình Softmax dự đoán xác suất cho 3 lớp lần lượt là [0.3, 0.5, 0.2].

• Xác suất là lớp 0: 30%
• Xác suất là lớp 1: 50% (Cao nhất)
• Xác suất là lớp 2: 20%

$\rightarrow$ Kết luận: Input thuộc về lớp 1.

Quy trình hoạt động (Pipeline)

Tương tự như Logistic Regression, Softmax Regression cũng tuân theo luồng xử lý tuần tự từ chuẩn bị dữ liệu đến ra quyết định.

Hình 6: Pipeline đơn giản của Softmax Regression[1]

Bước 1: Chuẩn bị Dữ liệu và Tham số

Sự khác biệt lớn nhất nằm ở cách chúng ta xử lý nhãn (Label) và kích thước tham số.

• Dữ liệu đầu vào ($X$): Vẫn là ma trận đặc trưng kích thước $(n, m)$.

  $$ X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix} $$

• Nhãn ($Y$) - One-Hot Encoding:
  Trong bài toán đa lớp, chúng ta không để nhãn dạng số (0, 1, 2...) mà chuyển đổi sang dạng vector One-Hot.
  Ví dụ với 3 lớp:

  • Lớp 0 $\rightarrow$ [1, 0, 0]
  • Lớp 1 $\rightarrow$ [0, 1, 0]
  • Lớp 2 $\rightarrow$ [0, 0, 1]

• Khởi tạo tham số ($W, b$):
  Vì có $K$ lớp đầu ra, ta cần một bộ trọng số riêng cho từng lớp. Do đó, $W$ sẽ là một ma trận (thay vì vector như Logistic) và $b$ là một vector chứa các hệ số chệch cho từng lớp.

Bước 2: Tính toán chiều xuôi (Forward Pass)

Mô hình thực hiện tính toán để chuyển input thành xác suất thông qua 2 giai đoạn:

1. Tính điểm tuyến tính (Linear Score):
   Với mỗi lớp $k$, mô hình tính một điểm số $z_k$.
   $$z = W \cdot X + b$$
   Kết quả $z$ là một vector chứa điểm số của tất cả các lớp (ví dụ: $[z_1, z_2, ..., z_K]$).

2. Hàm Softmax (Activation):
   Chuyển đổi vector điểm số $z$ thành vector xác suất $\hat{y}$ (hay $\hat{p}$).
   $$\hat{y}_k = \sigma(z)_k = \frac{e^{z_k}}{\sum_{j=1}^{K} e^{z_j}}$$

   Hàm này đảm bảo:
   - Mọi xác suất $\hat{y}_k$ đều nằm trong khoảng $(0, 1)$.
   - Tổng các xác suất của tất cả các lớp bằng 1 ($\sum \hat{y}_k = 1$).

Bước 3: Tính toán lỗi (Loss Function)

Để đo lường độ sai lệch giữa phân phối xác suất dự đoán ($\hat{y}$) và nhãn thực tế ($y$ - dạng one-hot), ta sử dụng hàm Cross-Entropy Loss.

$$L = -\sum_{k=1}^{K} y_k \log(\hat{y}_k)$$

Vì $y$ là one-hot vector (chỉ có một vị trí bằng 1, còn lại bằng 0), hàm loss thực chất chỉ quan tâm đến xác suất mà mô hình dự đoán cho lớp đúng.

• Mục tiêu: Tối đa hóa xác suất của lớp đúng $\rightarrow$ Tối thiểu hóa $L$.

Bước 4: Tối ưu hóa (Backward Pass)

Tương tự Logistic Regression, chúng ta sử dụng Gradient Descent để cập nhật toàn bộ ma trận trọng số $W$ và vector bias $b$.

$$\theta = \theta - \eta \nabla_{\theta}L$$

Trong đó, $\nabla_{\theta}L$ được tính toán dựa trên sai số giữa vector dự đoán và vector nhãn one-hot.

Lưu ý: Quá trình từ Bước 2 đến Bước 4 được lặp lại nhiều lần (Epochs) cho đến khi mô hình hội tụ.

Bước 5: Ra quyết định (Inference/Argmax)

Sau khi huấn luyện, để đưa ra kết quả cuối cùng cho một dữ liệu mới, ta lấy lớp có xác suất cao nhất. Kỹ thuật này gọi là argmax.

$$\text{Predicted Class} = \text{argmax}(\hat{y})$$

Ví dụ: Nếu $\hat{y} = [0.1, 0.7, 0.2]$, hàm argmax sẽ trả về chỉ số 1 (tương ứng với xác suất 0.7).

4. Code triển khai của Softmax Regression

Tương tự như phần Logistic Regression, để thực sự hiểu cách mô hình xử lý dữ liệu đa lớp, chúng ta sẽ tự xây dựng Softmax Regression từ đầu (from scratch) sử dụng NumPy.

Cách tiếp cận này giúp bạn thấy rõ cách ma trận trọng số hoạt động và cách hàm Softmax chuyển đổi điểm số (logits) thành xác suất như thế nào.

Bước 1: Chuẩn bị dữ liệu và One-Hot Encoding

Khác với bài toán nhị phân (nhãn là 0 hoặc 1), trong bài toán đa lớp, chúng ta thường cần chuyển đổi nhãn $y$ sang dạng One-Hot Vector để tính toán hàm mất mát dễ dàng hơn.

Ví dụ: Nếu có 3 lớp, nhãn 1 sẽ được chuyển thành vector [0, 1, 0].

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 1. Tạo dữ liệu giả lập (1000 mẫu, 4 lớp)
X, y = make_blobs(n_samples=1000, centers=4, n_features=2, random_state=42, cluster_std=1.5)

# 2. Hàm chuyển đổi One-Hot Encoding
def to_one_hot(y, n_classes):
    # Tạo ma trận 0 kích thước (số mẫu, số lớp)
    one_hot = np.zeros((y.shape[0], n_classes))
    # Đánh dấu 1 tại vị trí đúng class
    one_hot[np.arange(y.shape[0]), y] = 1
    return one_hot

# 3. Chia tập dữ liệu và One-hot
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

n_classes = len(np.unique(y))
y_train_enc = to_one_hot(y_train, n_classes)
y_test_enc = to_one_hot(y_test, n_classes)

print(f"Input shape: {X_train.shape}")
print(f"One-hot label shape: {y_train_enc.shape}") 
# Ví dụ: Input (800, 2) -> Output (800, 4)

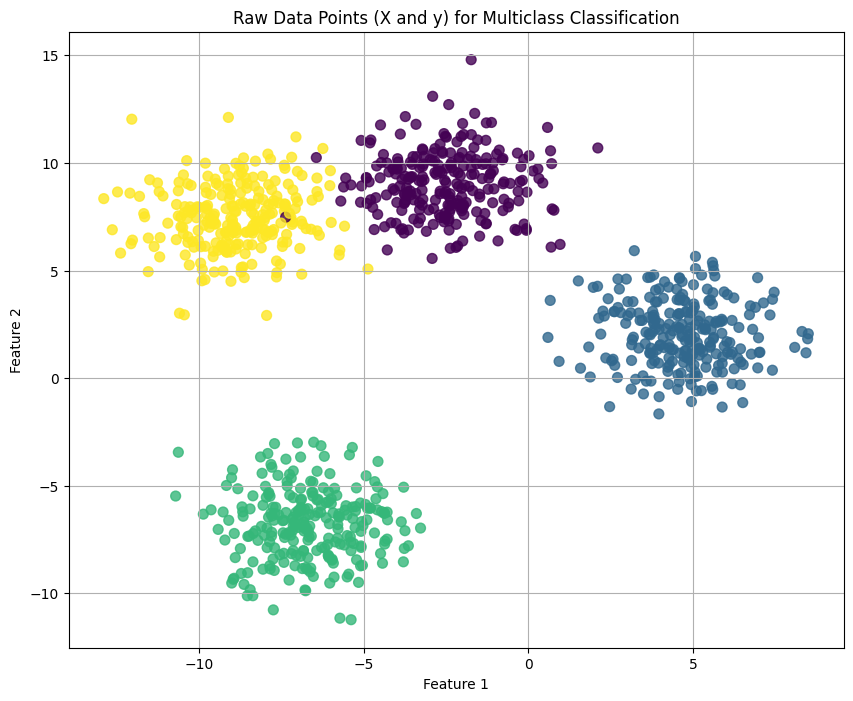
Hình 7: Hình ảnh của dữ liệu trước khi huấn luyện Softmax Regression

Bước 2: Xây dựng hàm Softmax và Vòng lặp Huấn luyện

Tại đây, chúng ta sẽ triển khai 2 thành phần cốt lõi:

1. Hàm softmax(z): Chuyển đổi vector điểm số thành xác suất. Lưu ý kỹ thuật trừ đi max(z) để giữ ổn định số học (numerical stability), tránh tràn số (overflow) khi tính mũ $e^z$.

def softmax(z):
    exp_z = np.exp(z - np.max(z, axis=1, keepdims=True))
    return exp_z / np.sum(exp_z, axis=1, keepdims=True)

2. Vòng lặp Gradient Descent:

   • Forward: Tính $Z = X \cdot W + b$ và $\hat{y} = \text{softmax}(Z)$.

   • Loss: Tính Cross-Entropy Loss: $-\sum y \log(\hat{y})$.

   python def cross_entropy_loss(y_true, y_pred): m = y_true.shape[0] return -np.sum(y_true * np.log(y_pred + 1e-15)) / m

   • Backward: Tính đạo hàm. Một điều thú vị của toán học là đạo hàm của Softmax + Cross-Entropy có dạng rất giống Logistic Regression: $\text{Gradient} = \hat{y} - y$ (với $y$ là one-hot).

# --- KHỞI TẠO THAM SỐ ---
n_samples, n_features = X_train.shape
learning_rate = 0.1
epochs = 1000

# W là ma trận (n_features x n_classes)
W = np.zeros((n_features, n_classes)) 
# b là vector (1 x n_classes)
b = np.zeros((1, n_classes))

losses = []

# --- VÒNG LẶP TRAINING ---
for epoch in range(epochs):
    # 1. Forward Pass
    Z = np.dot(X_train, W) + b
    A = softmax(Z) # A chính là y_hat (xác suất dự đoán)

    # 2. Tính Loss
    loss = cross_entropy_loss(y_train_enc, A)
    losses.append(loss)

    # 3. Backward Pass (Gradient Descent)
    # Đạo hàm của Loss theo Z chính là (A - Y)
    dZ = A - y_train_enc

    dW = (1/n_samples) * np.dot(X_train.T, dZ)
    db = (1/n_samples) * np.sum(dZ, axis=0, keepdims=True)

    # 4. Cập nhật tham số
    W = W - learning_rate * dW
    b = b - learning_rate * db

    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss:.4f}')

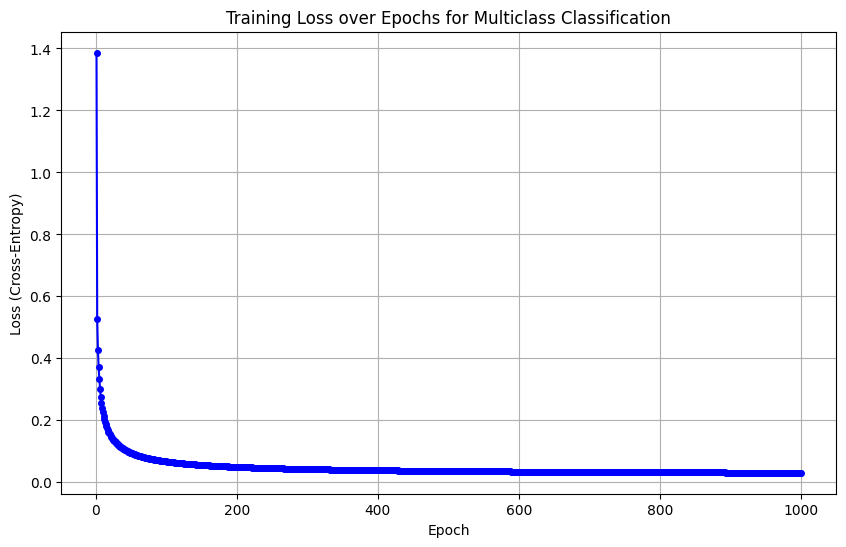
Hình 8: Hình ảnh của hàm loss trong huấn luyện mô hình

Bước 3: Dự đoán và Đánh giá

Sau khi tìm được ma trận trọng số $W$ và vector bias $b$ tối ưu, để dự đoán nhãn cho dữ liệu mới, ta thực hiện:
1. Tính xác suất cho tất cả các lớp.
2. Sử dụng hàm argmax để chọn ra lớp có xác suất cao nhất làm kết quả cuối cùng.

# --- DỰ ĐOÁN TRÊN TẬP TEST ---

# 1. Tính toán xuôi
Z_test = np.dot(X_test, W) + b
A_test = softmax(Z_test) # Xác suất của 4 lớp

# 2. Chọn lớp có xác suất cao nhất (argmax)
y_pred = np.argmax(A_test, axis=1)

# --- ĐÁNH GIÁ ---
acc = accuracy_score(y_test, y_pred)

print("\n--- Kết quả Softmax from Scratch ---")
print(f"Kích thước ma trận trọng số W: {W.shape}") # (2, 4)
print(f"Bias b: {b}")
print(f"Độ chính xác (Accuracy): {acc:.4f}")

# Kiểm tra thử 1 mẫu
print(f"\nMẫu đầu tiên thực tế: Class {y_test[0]}")
print(f"Mẫu đầu tiên dự đoán: Class {y_pred[0]} với xác suất {np.max(A_test[0]):.2f}")

Sau khi huấn luyện mô hình Softmax Regression ta được kết quả như sau.

--- Kết quả Softmax from Scratch ---
Kích thước ma trận trọng số W: (2, 4)
Bias b: [[-0.17793044  0.4940701   0.13795072 -0.45409038]]
Độ chính xác (Accuracy): 0.9950

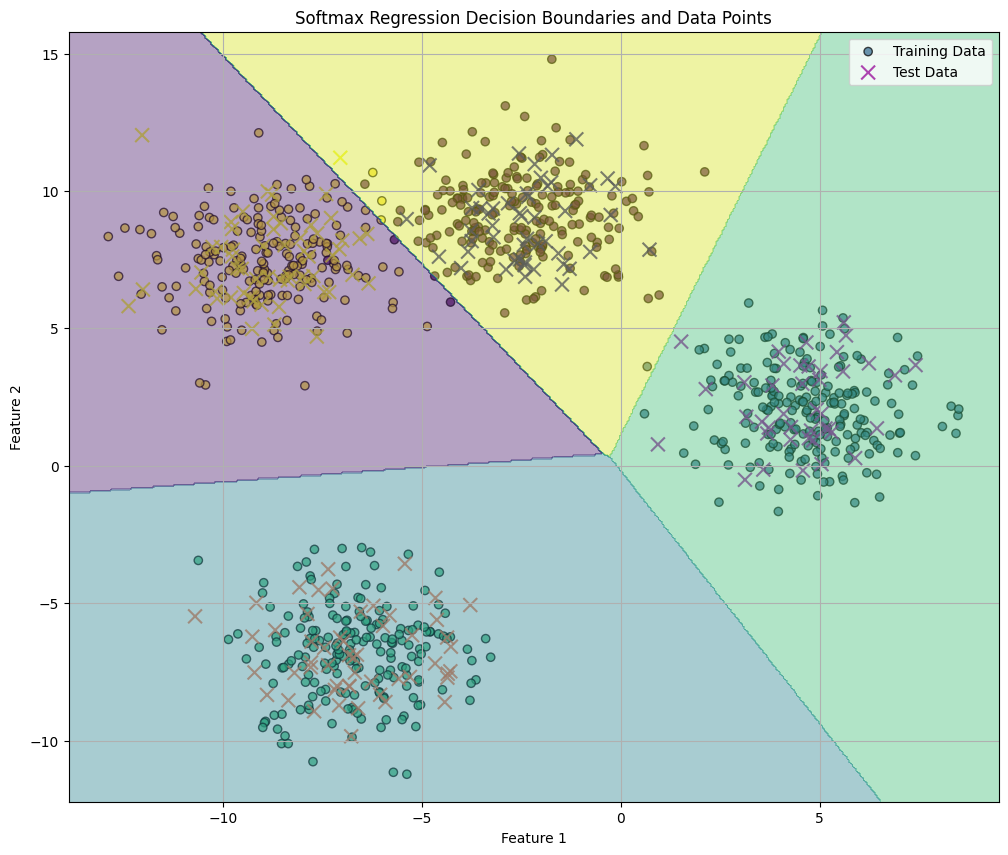
Hình 9: Hình ảnh kết quả dự đoán của mô hình

Tổng kết: Bằng cách tự triển khai, ta thấy rằng Softmax Regression thực chất là việc duy trì $K$ bộ trọng số riêng biệt (một bộ cho mỗi lớp). Hàm Softmax đóng vai trò như một "người trọng tài", so sánh điểm số của các lớp và chuẩn hóa chúng thành một phân phối xác suất hợp lệ.

5. Advance technique

5.1. Xử lý overfitting

Với bài toán Softmax Regression, ta có hàm mất mát (loss function) như sau:

$$ \mathcal{L}(\mathbf{W}) = -\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K}y_{i,k}\log(\hat{y}_{i,k}) $$

Trong đó:
- $N$: số mẫu
- $K$: số lớp
- $y_{i,k}$: nhãn one-hot (1 nếu mẫu $i$ thuộc lớp $k$, 0 nếu không)
- $\hat{y}_{i,k}$: xác suất dự đoán (softmax)

Mục tiêu: Tối thiểu $\mathcal{L}(\mathbf{W})$

Khi đó, để chống overfitting, ta có thể sử dụng L1/L2 Regularization:

$$ \mathcal{L}(\mathbf{W})_{\text{L2}} = \mathcal{L}(\mathbf{W}) + \lambda||\mathbf{W}||_2^2 \quad \text{với} \quad \lambda||\mathbf{W}||_2^2 = \sum_{i,j} w_{ij}^2 $$

$$ \mathcal{L}(\mathbf{W})_{\text{L1}} = \mathcal{L}(\mathbf{W}) + \lambda||\mathbf{W}||_1 \quad \text{với} \quad \lambda||\mathbf{W}||_1 = \sum_{i,j} |w_{ij}| $$

Với thư viện Scikit-learn, ta có thể điều chỉnh bằng các tham số:

• C: $C=1/(2\lambda)$, nghĩa là giá trị của C sẽ ngược lại với độ mạnh regularization (C nhỏ = regularization mạnh).

• penalty='l1'(L1 Regularization - Lasso): sử dụng để chọn đặc trưng có ý nghĩa khi bộ dữ liệu có nhiều features không quan trọng.

from sklearn.linear_model import LogisticRegression
model = LogisticRegression(penalty='l1', C=0.1, solver='saga')

• penalty='l2' (L2 Regularization - Ridge) - Default choice: dùng để tránh overfitting, vẫn giữ tất cả features.

from sklearn.linear_model import LogisticRegression
model = LogisticRegression(penalty='l2', C=1.0, solver='lbfgs')

• penalty='elasticnet': cân bằng giữa l1 và l2. Điều chỉnh l1_ratio để tùy chỉnh (l1_ratio=0: chỉ L2, l1_ratio=1: chỉ L1, l1_ratio=0.5: cân bằng, l1_ratio=None: không regularization):

# Kết hợp cả L1 và L2, cân bằng giữa feature selection và stability
model = LogisticRegression(penalty='elasticnet', l1_ratio=0.5, solver='saga', C=0.5)

Thư viện PyTorch cho phép điều chỉnh giá trị L2 regularization trong optimizer với tham số weight_decay:

optimizer = optim.Adam(model.parameters(), lr=0.01, weight_decay=1e-4)

5.2. Một số tùy chỉnh nâng cao trong thư viện Scikit-learn

Class Imbalance Handling - Xử lý mất cân bằng lớp:

Khi dữ liệu bị mất cân bằng giữa các lớp, ta có thể tùy chỉnh tham số class_weight để model không bị bias về class đông hơn. Các giá trị của class_weight có thể là:

• None: Mặc định.

• balanced:

python # Tự động điều chỉnh trọng số cho classes không cân bằng model = LogisticRegression(class_weight='balanced')

• Hoặc 1 dict tự định nghĩa:

python # Class 1 quan trọng hơn model = LogisticRegression(class_weight={0: 1, 1: 3})

Multi class Selection - Chế độ đa lớp:

Gồm các lựa chọn sau:

• auto: Tự động chọn dựa trên dữ liệu.

• ovr (One-vs-Rest): Dùng nhiều mô hình nhị phân (thường dùng cho các thuật toán không hỗ trợ đa lớp gốc).

• multinomial: Tương đương Softmax Regression.

model = LogisticRegression(multi_class='multinomial', solver='saga')

5.3. Temperature Scaling

Tham số nhiệt độ được sử dụng để điều chỉnh hàm Softmax bằng cách chia các input logit ($z_i$) cho 1 tham số nhiệt độ $\mathcal{T}$. Nó giúp kiểm soát "độ mềm" (softness) và "độ đỉnh" (peakness) của phân phối xác suất đầu ra. Khi đó, ta có công thức toán học sau:

$$ P_i = \frac{e^{z_i/\mathcal{T}}}{\sum_j e^{z_j/\mathcal{T}}} $$

Có thể thấy:

• $\mathcal{T} = 1$: Phân phối xác suất đầu ra giống với phân phối của Softmax chuẩn.

• $\mathcal{T} > 1$: Các logit đầu vào sẽ giảm xuống và gần nhau hơn. Khi đó, phân phối xác suất sẽ trở nên "phẳng" hơn. Điều này giúp model trở nên bớt tự tin và tăng tính ngẫu nhiên.

• $\mathcal{T} < 1$: Phân phối đầu ra sẽ trở nên nhọn hơn. Khi đó, model trở nên đáng tin cậy (tự tin cao vào lớp có điểm cao nhất) và giảm tính ngẫu nhiên.

Các ứng dụng phổ biến:

• Xử lý ngôn ngữ tự nhiên (NLP): Nhiệt độ là một siêu tham số được sử dụng trong các mô hình ngôn ngữ như GPT-2, GPT-3 và BERT để kiểm soát tính ngẫu nhiên của văn bản được tạo ra. Nhiệt độ cao khuyến khích đầu ra sáng tạo hơn, tránh lặp lại từ gây nhàm chán. Trong khi nhiệt độ thấp giúp mô hình tập trung và dễ dự đoán hơn.

• Knowledge Distillation: Được sử dụng trong việc huấn luyện một mô hình nhỏ hơn (Student) để mô phỏng đầu ra của một mô hình lớn hơn (Teacher) bằng cách cho phép mô hình nhỏ hơn học hỏi từ các xác suất "mềm hơn" (soft targets) của mô hình lớn.

5.4. Focal Loss

Focal Loss là một hàm loss được thiết kế để giải quyết vấn đề mất cân bằng lớp (class imbalance), đặc biệt trong các bài toán như Object Detection (các bài toán tìm vật thể nhỏ trong background lớn), chẩn đoán y tế (các bệnh hiếm gặp)...

Hãy xem xét 2 hàm loss sau:

• Cross Entropy:
  $$CE(p_t) = -\log(p_t)$$

• Focal Loss:
  $$FL(p_t) = -(1-p_t)^\gamma \log(p_t)$$

Trong đó: $\gamma \ge 0$ là tham số tập trung (focusing parameter).

• Nếu $\gamma = 0$, Focal Loss trở thành Cross Entropy.

• $\gamma$ thường được chọn từ 1 - 5, thường dùng nhất là 2.

Cơ chế hoạt động:
- Với các mẫu dễ (mô hình dự đoán đúng với xác suất cao, $p_t \to 1$): Giá trị $(1-p_t)^\gamma \to 0$, khiến loss của các mẫu này giảm đi đáng kể, do đó chúng không còn đóng góp nhiều trong quá trình training (tránh việc model bị áp đảo bởi quá nhiều mẫu dễ).

• Ngược lại, với các mẫu khó (mô hình dự đoán sai hoặc xác suất thấp, $p_t$ nhỏ): Giá trị $(1-p_t)^\gamma$ gần bằng 1, giúp giữ nguyên mức độ ảnh hưởng của loss, buộc mô hình phải tập trung học các mẫu này nhiều hơn.

Ta cũng có thể gán cho mỗi lớp 1 trọng số cân bằng $\alpha_t \in (0,1)$ như sau:

$$ FL(p_t) = -\alpha_t(1-p_t)^\gamma \log(p_t) $$

6. Reference

[1] Ảnh được lấy từ tài liệu khóa học AIO Module 06 Tuần 01, 02