1. Problem Introduction

Dự báo giá cổ phiếu là một trong những bài toán thách thức nhất trong lĩnh vực tài chính và machine learning. Trong LTSF-Linear Forecasting Challenge, chúng ta đối mặt với bài toán dự báo giá cổ phiếu FPT cho 100 ngày tương lai - một khoảng thời gian đủ dài để sai số tích lũy và đòi hỏi mô hình phải có khả năng tổng quát hóa tốt.

Thách thức chính:

• Dữ liệu tài chính có tính phi tuyến cao và nhiễu lớn
• Dự báo dài hạn (100 ngày) với cơ chế recursive - sai số từ bước trước sẽ lan truyền sang bước sau
• Giới hạn chỉ sử dụng các mô hình tuyến tính (Linear, NLinear, DLinear)
• Metric đánh giá: MSE (Mean Squared Error) trên tập public và private test

Baseline approach:

• Model: Linear đơn giản với 1 biến đầu vào (giá close)
• Input window: 14 ngày → Output: 3 ngày/bước
• Log transform đơn giản trên giá close

Mục tiêu nhóm là cải tiến baseline bằng cách khai thác nhiều đặc trưng hơn và sử dụng kiến trúc DLinear với khả năng phân tách xu hướng (trend) và mùa vụ (seasonality).

2. Proposed Approach

2.1. Điều chỉnh Input Window:

    """
    day: từ 1 đến TOTAL_PREDICT_DAYS
    Trả về window được dùng để ensemble cho ngày đó.
    Logic:
    1-30  : [30]
    31-50 : [30,50]
    51-70 : [50,70]
    71-90 : [70,90]
    91-100: [90,100]
    """
WINDOWS = [30, 50, 70, 90, 100]
OUTPUT_LENS = 1

if 1 <= day <= 30:
    return [30], [1]

elif 31 <= day <= 50:
    return [30, 50], [3.5, 6.5]

elif 51 <= day <= 70:
    return [50, 70], [3.5, 6.5]

elif 71 <= day <= 90:
    return [70, 90], [3.5, 6.5]

elif 91 <= day <= 100:
    return [90, 100], [3.5, 6.5]
else:
    raise ValueError(f"Ngày {day} vượt range")

Áp dụng phương pháp ensemble model, nhóm sẽ thực hiện train 5 model với 5 sliding window khác nhau, sau đó dạy mô hình học quan hệ giữa mỗi cửa sổ lịch sử và 1 ngày tương lai (multi-step forecast). Với mỗi ngày dự đoán, ta sẽ có công thức tính trọng số như sau:
$$w = \frac{(w_s * 3.5 + w_l * 6.5)}{3.5 + 6.5}$$
Trong đó, $w_s$ là giá trị trọng số của mô hình cửa sổ các ngày trước đó, có hệ số cố định là 3.5, còn $w_l$ là giá trị trọng số của mô hình cửa sổ hiện tại, có hệ số là 6.5. Phương pháp này giúp cho mô hình đọc hiểu rõ ràng hơn với các thay đổi ngắn hạn, cũng như cân nhắc đến các sự thay đổi dài hạn.

2.2. Multi-Variable Input

Thay vì chỉ dùng giá close, nhóm sử dụng 8 features bao gồm:

• 4 biến giá cơ bản: open, high, low, close (log-transformed)
• 1 biến khối lượng: volume (log1p-transformed)
• 3 biến kỹ thuật: volatility, rate of change, simple moving average

Lợi ích:

• Mô hình có nhiều góc nhìn hơn về chuyển động giá
• Khai thác thông tin tương quan giữa các biến
• Tăng khả năng dự báo trong điều kiện thị trường phức tạp

2.3. DLinear Architecture

Áp dụng mô hình DLinear (Decomposition Linear) với khả năng:

• Tách biệt xu hướng (trend) và dao động (seasonal)
• Xử lý riêng hai thành phần bằng hai nhánh linear độc lập
• Tổng hợp kết quả để có dự báo cuối cùng

2.4. Data Normalization

Sử dụng StandardScaler để chuẩn hóa toàn bộ features:

• Đưa các biến về cùng thang đo
• Giúp mô hình hội tụ nhanh hơn
• Tránh bias về các biến có giá trị lớn (như volume)

3. Data Preprocessing

3.1. Load và Sắp xếp Dữ liệu

df = pd.read_csv("FPT_train.csv")  
df["time"] = pd.to_datetime(df["time"])  
df= df.sort_values("time").reset_index(drop=True)

3.2. Log Transformation

df["open_log"]= np.log(df["open"])  
df["high_log"]= np.log(df["high"])  
df["low_log"] = np.log(df["low"])  
df["close_log"\] = np.log(df["close"])  
df["volume_log"] = np.log1p(df["volume"])  # log1p để tránh log(0)

Lý do dùng log transform:

• Giá cổ phiếu có phân phối lệch (skewed distribution)
• Log transform giúp ổn định phương sai
• Chuyển tăng trưởng nhân thành tăng trưởng cộng (dễ học hơn với linear model)
• $$log1p(x) = log(1+x)$$ tránh lỗi khi volume = 0

3.3. Standardization

scaler = StandardScaler()  
df_scaled = df.copy()  
df_scaled[FEATURE_COLS] = scaler.fit_transform(df[FEATURE_COLS])

StandardScaler thực hiện công thức:

$$x_{\text{scaled}} = \frac{x - \mu}{\sigma}$$

Trong đó:

• μ: giá trị trung bình
• σ: độ lệch chuẩn

Lợi ích:

• Đưa tất cả features về mean=0, std=1
• Tăng tốc gradient descent convergence
• Tránh hiện tượng một số features chi phối quá trình học

4. Feature Engineering

4.1. Volatility (Độ biến động)

df["volatility"] = (df["high"] - df["low"]) / df["close"]

Ý nghĩa:

• Đo biên độ dao động trong ngày
• Công thức: $$Volatility = (\frac{High - Low}{Close})$$
• High volatility → thị trường biến động mạnh, rủi ro cao
• Low volatility → thị trường ổn định

Tại sao quan trọng?

• Giá trị tương lai phụ thuộc vào mức độ biến động hiện tại
• Volatility là chỉ báo về tâm lý thị trường

4.2. Rate of Change (Tốc độ thay đổi)

df["roc_1"] = df["close"].pct_change().fillna(0)

Ý nghĩa:

• Đo phần trăm thay đổi giá so với ngày hôm trước
• Công thức: $$ROC_t = \frac{Close_t - Close_{t-1}}{Close_{t-1}}$$

Lợi ích:

• Nắm bắt động lượng (momentum) của giá
• Phát hiện trend đảo chiều (từ tăng sang giảm hoặc ngược lại)
• fillna(0) cho ngày đầu tiên không có giá trị trước đó

4.3. Simple Moving Average 5-day (SMA-5)

df["sma_5"] = df["close"].rolling(5).mean().fillna(method="bfill")  
df["sma_5_log"] = np.log(df["sma_5"])

Ý nghĩa:

• Trung bình giá của 5 ngày gần nhất
• Công thức: $$SMA\_{5}(t) = \frac{1}{5} \sum_{i=0}^{4} Close_{t-i}$$

Tại sao dùng SMA-5?

• Làm mượt nhiễu ngắn hạn
• Thể hiện xu hướng gần nhất
• Chỉ báo kỹ thuật phổ biến trong phân tích tài chính
• bfill (backward fill) để xử lý 4 ngày đầu không đủ dữ liệu

4.4. Feature Selection

FEATURE_COLS = [  
    "open_log", "high_log", "low_log", "close_log",  \# 4 biến giá  
    "volume_log",                                      \# 1 biến khối lượng  
    "volatility", "roc_1", "sma_5_log"                \# 3 biến kỹ thuật  
]  
TARGET_COL = "close_log"  # Mục tiêu dự báo

Tổng cộng 8 features đầu vào - tăng đáng kể so với 1 feature của baseline.

5. Multi variables DLinear Model architecture

5.1. Definition

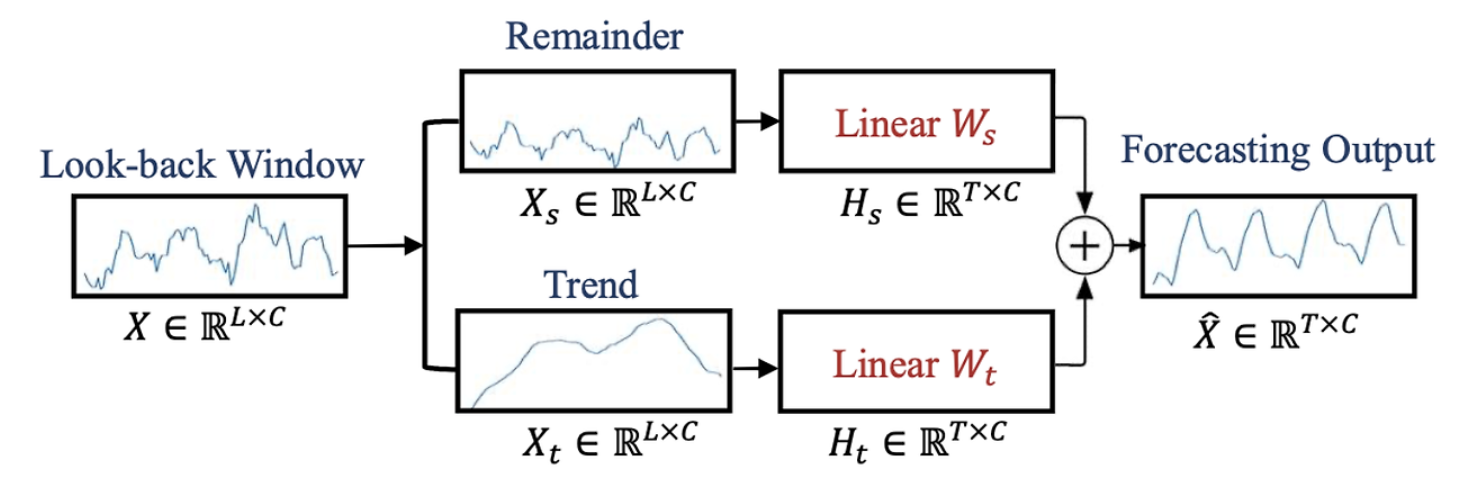
Mô hình DLinear hoạt động bằng cách phân rã chuỗi đầu vào thành 2 thành phần: seasonal và trend. Trong đó, chuỗi trend được dùng để phản ánh xu hướng dài hạn còn chuỗi seasonal sẽ phát hiện những chu kỳ ngắn hạn, lặp lại của dữ liệu. Chúng ta sẽ chiếu 2 chuỗi tuyến tính riêng biệt cho từng phần, sau đó cộng lại để ra kết quả dự báo cuối cùng. Phương pháp này giúp cho mô hình nắm bắt được sự thay đổi dài hạn và ngắn hạn một cách nhạy bén hơn so với các mô hình tuyến tính đơn.

5.2. Architecture

Cơ chế hoạt động của mô hình DLinear được chia thành các bước chính như sau:

• Bước 1: Phân rã chuỗi (decomposition):
  Dữ liệu đầu vào $X$ với độ dài $L$ được tách thành 2 phần:
• Thành phần Xu hướng $(X_{t})$ đại diện cho sự vận động dài hạn, được tính toán bằng cách chạy cửa sổ trượt (Moving Average) để tính trung bình trên chuỗi đầu, sử dụng công thức sau:

$$X_{t} = \frac{1}{k} \sum_{i=0}^{k-1} x_{t-i}$$

Trong đó, t là thời điểm tính xu hướng còn k là kích thước cửa sổ

• Thành phần Mùa vụ $(X_{s})$ đại diện cho các dạo động ngắn hạn, được tính bằng cách lấy chuỗi gốc trừ đi chuỗi xu hướng $(X_{t})$:

$$X_{s} = X - X_{t}$$

• Bước 2: Mô hình hóa tuyến tính (Linear Modelling)

  Sau khi đã có 2 chuỗi riêng biệt, DLinear đưa mỗi chuỗi qua các lớp Tuyến tính độc lập, ta có:
  $$\hat{X}_{t} = X_{t}*W_{t} + b_{t}.$$
  $$\hat{X}_{s} = X_{s}*W_{s} + b_{s}.$$
  DLinear ánh xạ trực tiếp từ $L$ điểm quá khứ sang $H$ điểm tương lai mà không cần vòng lặp hay cơ chế Attention phức tạp.

• Bước 3: Tổng hợp kết quả (Composition):
  Cuối cùng, mô hình cộng gộp 2 kết quả dự báo lại để tạo ra đầu ra cuối cùng $\hat{X}$
  $$\hat{X}_{final} = \hat{X}_{t} + \hat{X}_{s}$$

5.3. Advantages

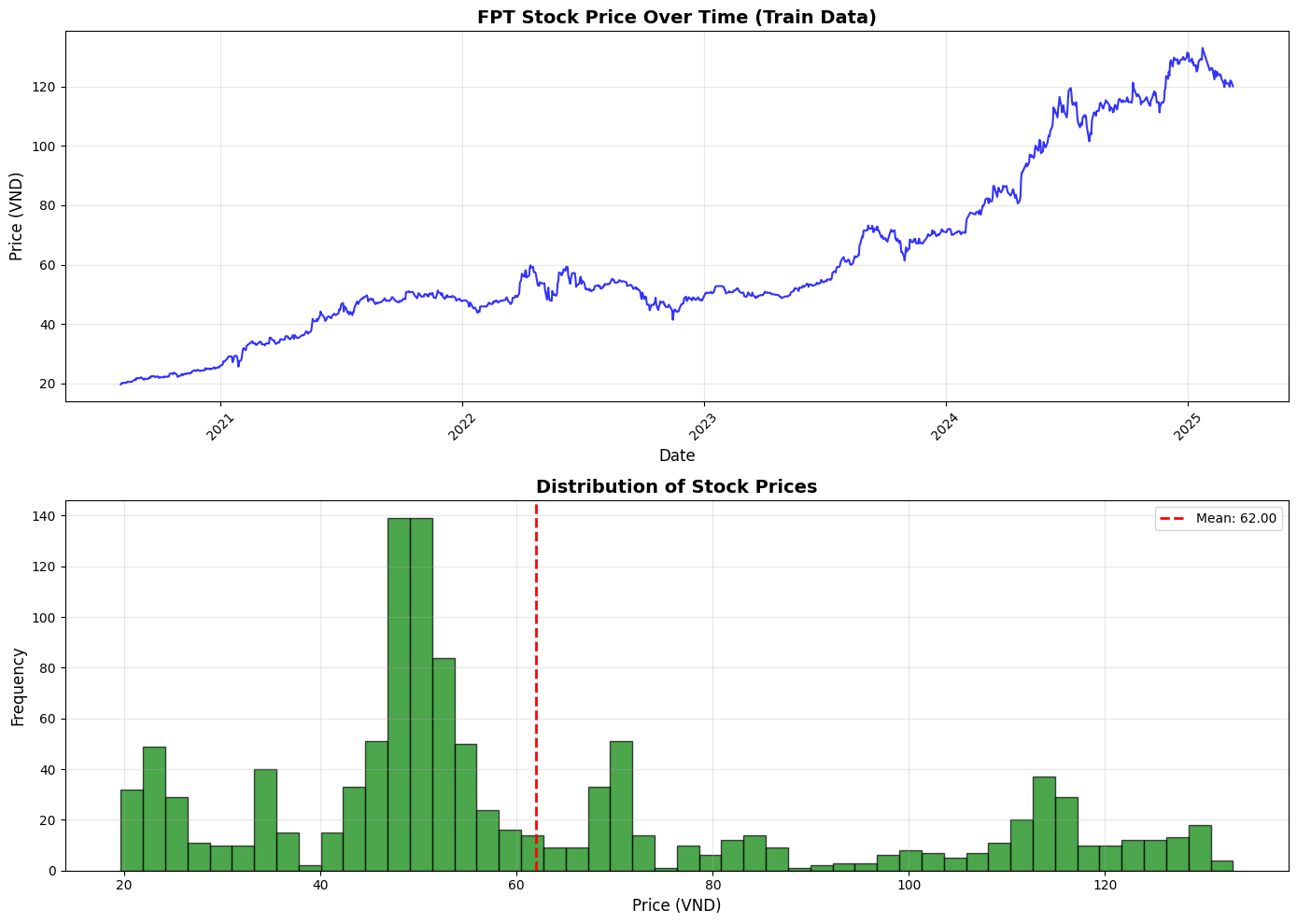
• Với cơ chế Phân rã (decomposition) chia chuỗi dữ liệu thành trend và seasonal, DLinear có lợi thế tốt hơn nhiều so với các mô hình tuyến tính khác như NLinear và Linear trong những bài toán dự báo dài hạn và có xu hướng rõ ràng. Qua hình dưới đây, ta có thể thấy giá cổ phiếu cần dự đoán là FPT có xu hướng tăng đều và ổn định qua các năm, tạo xu hướng rõ ràng. Điều này giúp cho mô hình DLinear là lựa chọn tốt hơn cho bài toán này, trong khi đó mô hình NLinear sẽ mạnh mẽ hơn với loại dữ liệu có biến động mạnh và phân phối thay đổi liên tục.

6. Huấn luyện mô hình

6.1. Khởi tạo dataset và kiến trúc mô hình

Định nghĩa một lớp PyTorch Dataset để xử lý các cửa sổ trượt và mô hình DLinearMulti đa biến.

# Lớp Dataset
class MultiDataset(Dataset):
    def __init__(self, df, input_len, output_len, feature_cols, target_col):
        self.data = df[feature_cols].values
        self.targets = df[target_col].values
        self.input_len = input_len
        self.output_len = output_len

    def __len__(self):
        return len(self.data) - self.input_len - self.output_len

    def __getitem__(self, idx):
        x = self.data[idx : idx + self.input_len]
        y = self.targets[idx + self.input_len : idx + self.input_len + self.output_len]
        return torch.FloatTensor(x), torch.FloatTensor(y)

# Kiến trúc DLinear
class DLinearMulti(nn.Module):
    def __init__(self, input_len, num_features, output_len):
        super().__init__()

        self.input_len = input_len
        self.output_len = output_len
        self.num_features = num_features

        self.linear_trend = nn.Linear(input_len * num_features, output_len)
        self.linear_seasonal = nn.Linear(input_len * num_features, output_len)

    def moving_avg(self, x, kernel=3):
        padding = kernel // 2
        x_pad = torch.nn.functional.pad(x, (0,0, padding, padding), mode='reflect')
        x_smooth = torch.nn.functional.avg_pool1d(
            x_pad.transpose(1,2), 
            kernel_size=kernel, 
            stride=1
        ).transpose(1,2)
        return x_smooth

    def forward(self, x):
        trend_part = self.moving_avg(x)
        seasonal_part = x - trend_part

        trend_flat = trend_part.reshape(x.size(0), -1)
        seasonal_flat = seasonal_part.reshape(x.size(0), -1)

        trend_out = self.linear_trend(trend_flat)
        seasonal_out = self.linear_seasonal(seasonal_flat)

        return trend_out + seasonal_out

6.2. Huấn luyện đa cửa sổ (Multi-window)

Thay vì huấn luyện một mô hình duy nhất, quy trình này huấn luyện 5 mô hình riêng biệt, mỗi mô hình chuyên biệt cho một kích thước cửa sổ khác nhau (30, 50, 70, 90, 100 ngày).

def train_model_for_window(input_len, epochs=EPOCHS, lr=LR, batch_size=BATCH_SIZE):
    print(f"\nTraining model with window = {input_len}")
    dataset = MultiDataset(df_scaled, input_len, OUTPUT_LEN, FEATURE_COLS, TARGET_COL)
    loader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

    model = DLinearMulti(input_len, len(FEATURE_COLS), OUTPUT_LEN).to(device)
    criterion = nn.MSELoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)

    for epoch in range(epochs):
        model.train()
        total_loss = 0.0

        for batch_x, batch_y in loader:
            batch_x, batch_y = batch_x.to(device), batch_y.to(device)

            optimizer.zero_grad()
            out = model(batch_x)                  # [B, 1]
            loss = criterion(out, batch_y)        # batch_y: [B, 1]
            loss.backward()
            optimizer.step()

            total_loss += loss.item()

        if (epoch + 1) % 5 == 0:
            print(f"Epoch {epoch+1}/{epochs} - Loss: {total_loss/len(loader):.6f}")

    return model

6.3. Chiến lược Ensemble Động

Quyết định những mô hình nào sẽ được sử dụng dựa trên khoảng cách thời gian dự đoán trong tương lai.

• Tương lai gần (Ngày 1-30): Chỉ sử dụng mô hình ngắn hạn (Window 30).

• Tương lai xa (Ngày 91-100): Sử dụng các mô hình dài hạn (Window 90, 100) với trọng số cụ thể.

def get_windows_and_weights(day):
    """
    day: từ 1 đến TOTAL_PREDICT_DAYS
    Trả về window được dùng để ensemble cho ngày đó.
    Logic:
    1-30  : [30]
    31-50 : [30,50]
    51-70 : [50,70]
    71-90 : [70,90]
    91-100: [90,100]
    """
    if 1 <= day <= 30:
        return [30], [1]

    elif 31 <= day <= 50:
        return [30, 50], [3.5, 6.5]

    elif 51 <= day <= 70:
        return [50, 70], [3.5, 6.5]

    elif 71 <= day <= 90:
        return [70, 90], [3.5, 6.5]

    elif 91 <= day <= 100:
        return [90, 100], [3.5, 6.5]
    else:
        raise ValueError(f"Ngày {day} vượt range")

6.4. Suy luận Tự hồi quy (Vòng lặp Dự đoán)

Trong giai đoạn dự báo, mô hình sẽ dự đoán từng ngày một. Điểm mấu chốt là mô hình sẽ thêm giá trị vừa dự đoán ngược trở lại vào dữ liệu đầu vào (all_feats) để mô hình có thể sử dụng chính dự đoán trước đó của nó để dự báo ngày tiếp theo.

# %%
# Dùng toàn bộ lịch sử scaled để append dần các ngày tương lai
all_feats = df_scaled[FEATURE_COLS].values.copy()

pred_log_list = []

close_idx = FEATURE_COLS.index("close_log")

for day in range(1, TOTAL_PREDICT_DAYS + 1):

    win_list, weights = get_windows_and_weights(day)

    day_preds = []

    for w in win_list:
        model_w = models[w]
        model_w.eval()

        window_input = all_feats[-w:]

        inp = torch.FloatTensor(window_input).unsqueeze(0).to(device)

        with torch.no_grad():
            out = model_w(inp)[0].cpu().numpy()

        pred_log = float(out[0])
        day_preds.append(pred_log)

    # ensemble theo trọng số các windows trong win_list

    weights = np.array(weights, dtype=float)
    weights = weights / weights.sum()   # chuẩn hóa

    day_preds = np.array(day_preds)

    final_pred_log = float(np.sum(day_preds * weights))

    pred_log_list.append(final_pred_log)

    # cập nhật all_feats: giữ các feature khác, thay close_log bằng pred
    new_row = all_feats[-1].copy()
    new_row[close_idx] = final_pred_log
    all_feats = np.vstack([all_feats, new_row])


pred_close_log_scaled = np.array(pred_log_list)

6.5. Hậu xử lý và Nộp kết quả

Cuối cùng, quy trình đảo ngược việc chuẩn hóa (inverse scaling) và đảo ngược biến đổi log (inverse log) để lấy giá trị giá thực tế (VND), sau đó vẽ biểu đồ kết quả và lưu file CSV.

pred_close_log = np.array(pred_log_list)

close_idx = FEATURE_COLS.index("close_log")
mean = scaler.mean_[close_idx]
std = np.sqrt(scaler.var_[close_idx])

pred_close_log_original = pred_close_log * std + mean
pred_price = np.exp(pred_close_log_original)

df_sub = pd.DataFrame({
    "id": np.arange(1, TOTAL_PREDICT_DAYS + 1),
    "close": pred_price
})

df_sub.to_csv("submission.csv", index=False)
print("Saved submission.csv!")

7. Result

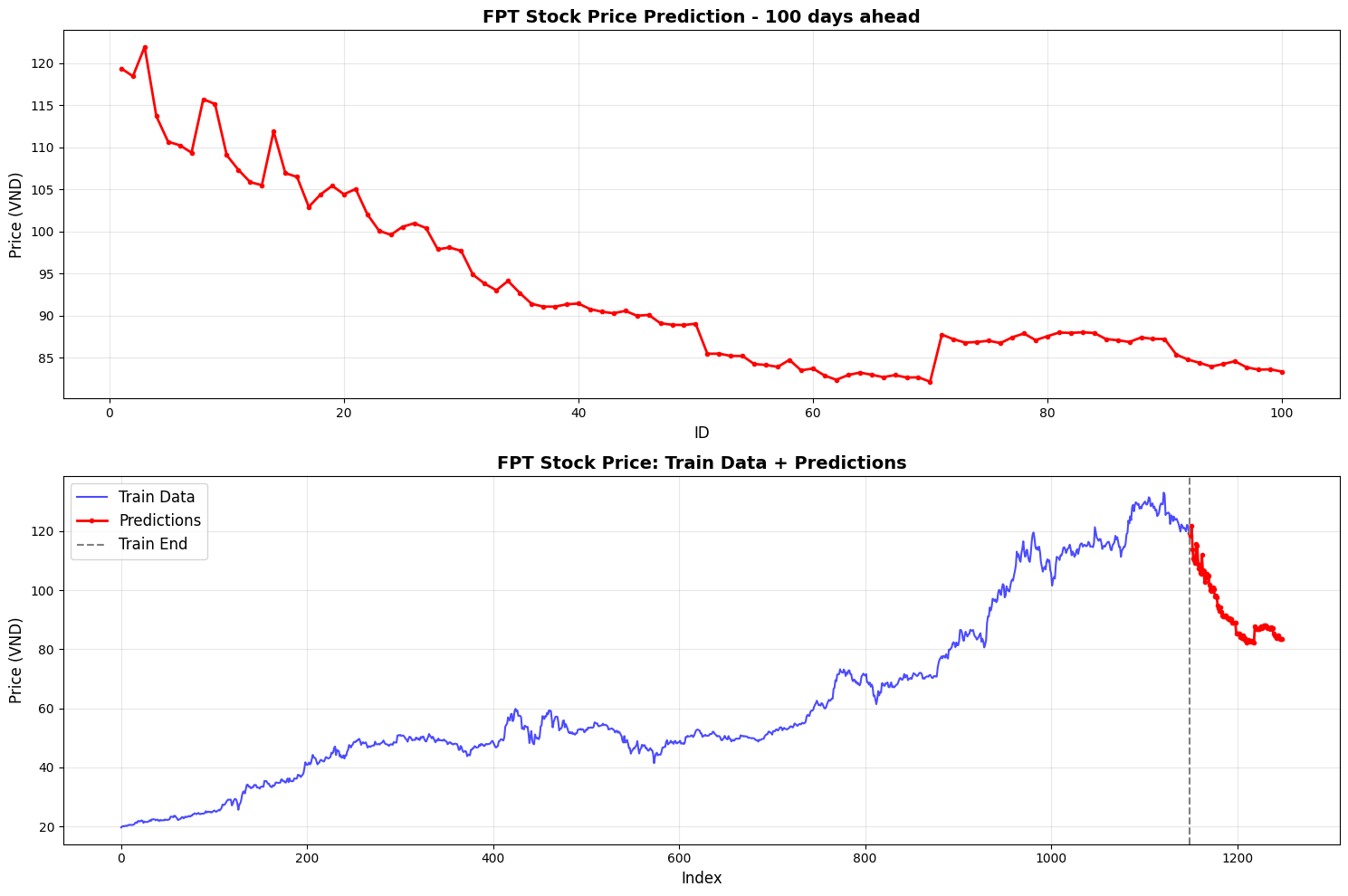
Sau khi qua mô hình, nhóm dự đoán (đường đỏ ở hình dưới) cổ phiếu FPT sẽ có xu hướng đi xuống đáng kể trong thời gian tới, với những ngày thấp nhất có khả năng xuống tới 85.000VND/cổ phiếu. Điều này trùng khớp với dữ liệu thực tế được cung cấp, khi Mean Squared Error (MSE) của mô hình ở thời điểm tốt nhất chỉ còn khoảng 12.9775.