#loss_function #python

9 phút đọc 60 lượt xem 0 thích 0 bình luận

Hồi Quy Softmax: Nền Tảng Cho Phân Loại Đa Lớp Trong Deep Learning

Nguyễn Tuấn Minh , Trần Tuấn Khoa , Nguyễn Thị Hải Mi , Quốc Hiệu Nguyễn , Đinh Nam Khánh

Tác giả chính • 4 đồng tác giả

Xuất bản: 15/12/2025

Cập nhật: 08/01/2026

1. Giới thiệu

Hồi quy softmax, còn được gọi là hồi quy logistic đa lớp, là phần mở rộng của hồi quy logistic để xử lý các vấn đề phân loại đa lớp. Đây là một kỹ thuật cơ bản trong học máy và đóng vai trò quan trọng trong các kiến trúc deep learning, đặc biệt là ở lớp đầu ra của mạng nơ-ron được thiết kế để phân loại dữ liệu vào nhiều lớp. Hàm softmax chuyển đổi các điểm số thô (logits) thành phân bố xác suất trên các lớp, đảm bảo tổng xác suất bằng 1. Báo cáo này tổng hợp các khái niệm cốt lõi từ các slide được cung cấp, bao gồm động lực, xây dựng mô hình, hàm mất mát, tối ưu hóa, triển khai và ví dụ. Nó nhấn mạnh vai trò của softmax trong ngữ cảnh deep learning, nơi nó cho phép các mô hình đưa ra dự đoán xác suất tự tin cho các nhiệm vụ như phân loại hình ảnh hoặc xử lý ngôn ngữ tự nhiên.

2. Nền tảng: Hồi quy tuyến tính và hồi quy logistic

Để hiểu hồi quy softmax, cần ôn lại các tiền đề: hồi quy tuyến tính cho dự đoán liên tục và hồi quy logistic cho phân loại nhị phân.

2.1. Hồi quy tuyến tính

Hồi quy tuyến tính mô hình hóa mối quan hệ tuyến tính giữa các đặc trưng đầu vào và đầu ra liên tục. Mục tiêu là tìm tham số $\theta$ (trọng số $w$ và bias $b$) để giảm thiểu sai số giữa giá trị dự đoán $\hat{y}$ và nhãn thực $y$.

Mô hình là $\hat{y} = \theta^T x = w x + b$, trong đó $x$ là vector đặc trưng.

Sai số thường được đo bằng lỗi bình phương trung bình (MSE), và tham số được tối ưu hóa để phù hợp đường thẳng với các điểm dữ liệu.

Đối với câu hỏi toán học đóng như giải $\theta$ bằng phương pháp bình phương nhỏ nhất, giải pháp được suy ra như sau:

Công thức MSE: $L = \frac{1}{2m} \sum (\hat{y}_i - y_i)^2$, trong đó $m$ là số mẫu.
Phương trình chuẩn: $\theta = (X^T X)^{-1} X^T y$, trong đó $X$ là ma trận thiết kế (đặc trưng với cột bias).

Phương pháp gradient descent thay thế: $\theta = \theta - \eta \nabla L$, trong đó $\nabla L = \frac{1}{m} X^T (\hat{y} - y)$.

2.2. Hồi quy logistic

Hồi quy logistic xử lý phân loại nhị phân bằng cách ánh xạ tổ hợp tuyến tính sang xác suất sử dụng hàm sigmoid.

Hàm sigmoid: $\sigma(z) = \frac{1}{1 + e^{-z}}$, trong đó $z = \theta^T x$.

Xác suất dự đoán $\hat{y} = \sigma(z)$, với $\hat{y} \in [0,1]$.

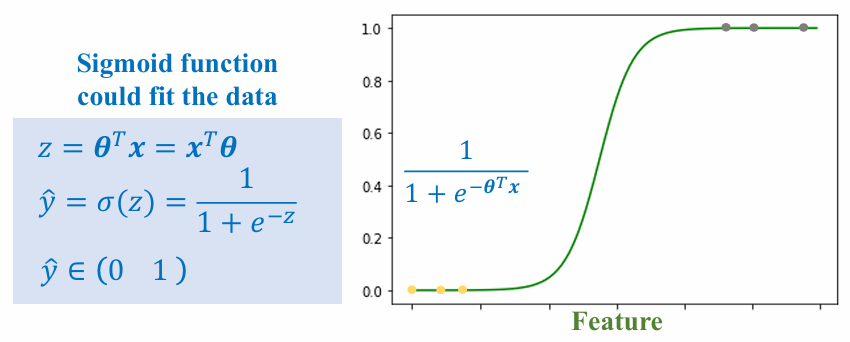
Hàm mất mát là entropy chéo nhị phân: $L = - [y \log(\hat{y}) + (1-y) \log(1-\hat{y})]$.

Để suy ra gradient:

$\frac{\partial L}{\partial z} = \hat{y} - y$ (qua quy tắc chuỗi trên sigmoid và entropy chéo).
Cập nhật $\theta$ bằng gradient descent: $\theta = \theta - \eta x (\hat{y} - y)$.

Điều này tạo ra đường cong hình chữ S phân tách các lớp.

Hồi quy logistic ngầm xử lý xác suất bổ sung (P(y=0) = 1 - P(y=1)), nhưng đối với đa lớp, cách tiếp cận này trở nên không hiệu quả.

3. Hàm softmax

3.1. Động lực cho hồi quy softmax

Trong phân loại nhị phân, hồi quy logistic sử dụng sigmoid để xuất xác suất cho hai lớp, nhưng các xác suất phụ thuộc lẫn nhau. Đối với vấn đề đa lớp (ví dụ: phân loại hoa thành ba loài dựa trên đặc trưng cánh hoa), việc sử dụng nhiều bộ phân loại nhị phân (one-vs-rest) dẫn đến vấn đề như xác suất không chuẩn hóa trên các lớp và tối ưu hóa không hiệu quả.

Softmax giải quyết điều này bằng cách:

Trực tiếp xuất xác suất cho tất cả các lớp với tổng bằng 1.
Cho phép tối ưu hóa độc lập cho logit của mỗi lớp trong khi đảm bảo chuẩn hóa.
Cung cấp diễn giải xác suất phù hợp cho các mô hình deep learning xử lý sự không chắc chắn.

Ví dụ từ slide: Trong tập dữ liệu thời gian học vs. điểm số với các lớp {0,1,2,3}, sigmoid cho từng lớp có thể cho P(class0)=0.3, P(class2)=0.4, nhưng tổng >1. Softmax đảm bảo phân bố hợp lệ.

3.2 Công thức hàm softmax

Hàm softmax là trung tâm của phân loại đa lớp:

$$p_i = \frac{\exp(z_i)}{\sum_j \exp(z_j)}$$

Trong đó: L $i = 1$ đến $k$ là số thứ tự của các lớp.

Nó ánh xạ logits $z$ (vector điểm số thô) sang xác suất $p$, với $p_i \geq 0$ và $\sum p_i = 1$.

Để tránh bất ổn số (tràn từ $z$ lớn), sử dụng softmax ổn định:

$$p_i = \frac{\exp(z_i - \max(z))}{\sum_j \exp(z_j - \max(z))}$$

Suy ra phiên bản ổn định: Phép mũ số lớn có thể gây tràn; trừ max dịch chuyển giá trị sang $\leq 0$, giữ exp trong (0,1].

Trong mã:

def softmax(z): 

    exp_z = np.exp(z - np.max(z)) 

    return exp_z / np.sum(exp_z)

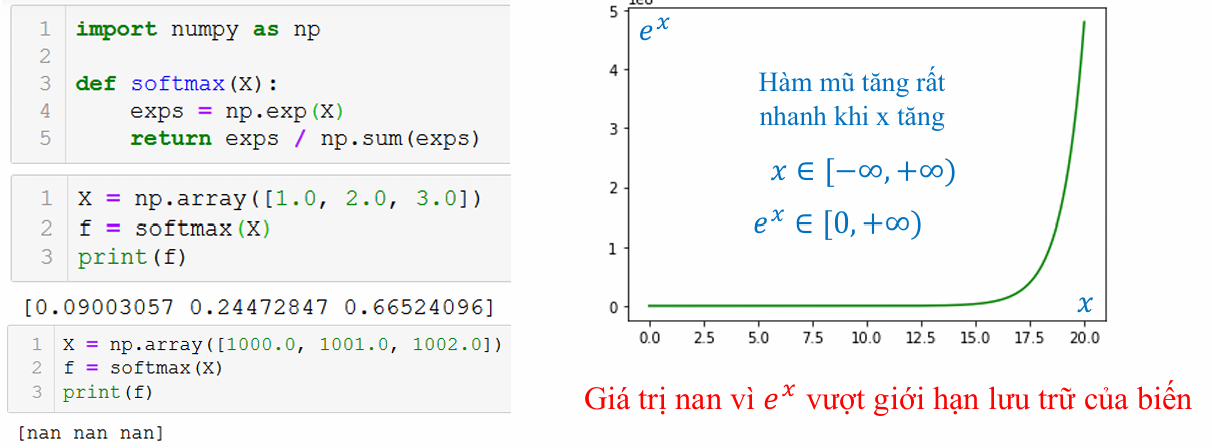
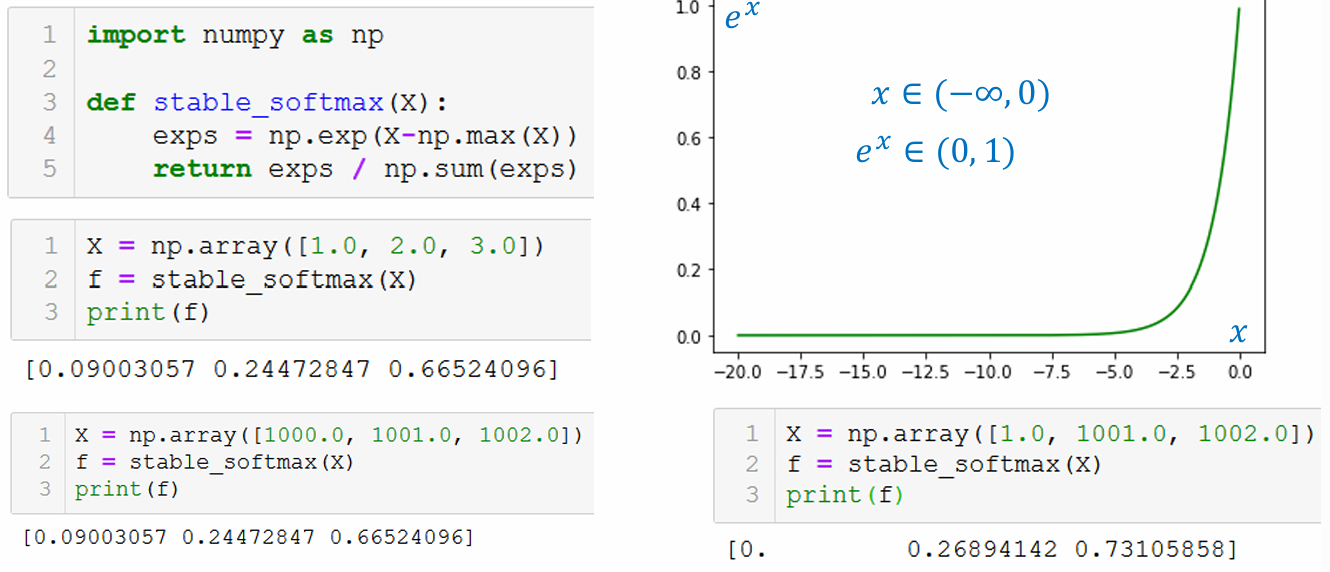
Ngoài ra, hàm Softmax còn có một phiên bản khác được đặt tên là Stable Softmax:

def stable_softmax(X): 

    exps = np.exp(X - np.max(X)) 

    return exps / np.sum(exps)

Hình 4. Hàm Stable Softmax - một phiên bản khác của hàm Softmax

4. Các bước xây dựng softmax

4.1. Xây dựng mô hình

Mô hình là mạng một lớp cho đa lớp:

Đầu vào: vector đặc trưng $x$ (d chiều, thêm bias như $x_0=1$).
Logits: $z = W x + b$, trong đó $W$ là ma trận trọng số $k \times d$, $b$ là $k \times 1$ bias.
Đầu ra: $\hat{y} = softmax(z)$.

Số tham số: $k(d + 1)$.

Ví dụ, với 2 đặc trưng và 3 lớp (như dữ liệu cánh hoa iris):

Nút đầu vào: 3 (bias + 2 đặc trưng).
Nút đầu ra: 3.

Mô hình học các bộ phân loại tuyến tính riêng biệt cho mỗi lớp, được chuẩn hóa bởi softmax.

4.2. Hàm mất mát entropy chéo

Hàm mất mát entropy chéo phân loại đo sự khác biệt giữa xác suất dự đoán $\hat{y}$ và nhãn one-hot thực $y$:

$$L = - \sum_i y_i \log(\hat{y}_i) = - y^T \log(\hat{y})$$

Đối với batch, lấy trung bình trên các mẫu.

Hàm mất mát này thấp khi $\hat{y}$ gán xác suất cao cho lớp đúng.

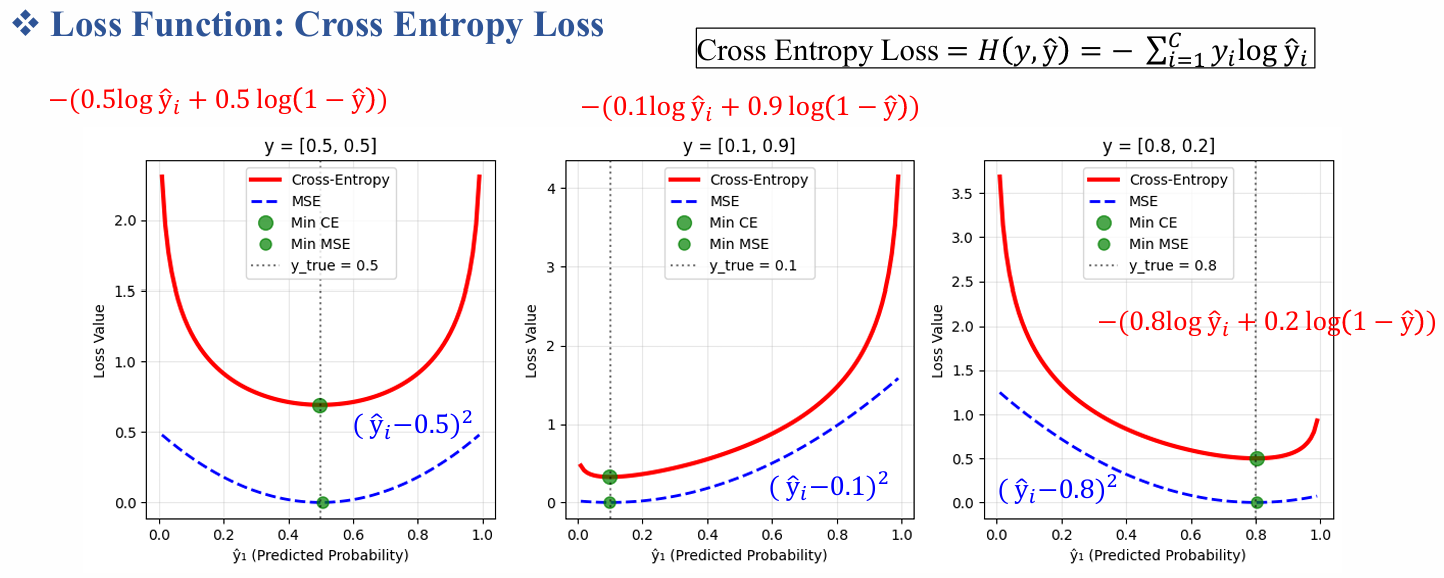
Trong trường hợp nhị phân, nó giảm về entropy chéo nhị phân.

Để suy ra gradient:

$\frac{\partial L}{\partial z_j} = \hat{y}_j - y_j$.

Chứng minh:

$L = - \sum y_i \log(p_i)$, $p_i = softmax(z_i)$.
Sử dụng quy tắc chuỗi và đạo hàm softmax $\frac{\partial p_k}{\partial z_j} = p_k (\delta_{kj} - p_j)$.
Kết quả $\frac{\partial L}{\partial z_j} = p_j - y_j$.

Dạng đơn giản này cho phép tối ưu hóa hiệu quả.

4.3. Tối ưu hóa với gradient descent

Sử dụng gradient descent ngẫu nhiên (SGD) để huấn luyện:

Với mỗi mẫu $(x, y)$:
Tính $z = \theta^T x$ (vector hóa: $\theta$ là ma trận).
$\hat{y} = softmax(z)$.
$L = - y^T \log(\hat{y})$.
$\nabla_\theta L = x (\hat{y} - y)^T$.
$\theta = \theta - \eta \nabla_\theta L$.

Đối với tính toán đạo hàm đóng:

Bắt đầu với:
$$L = - \sum y_i \log( \frac{\exp(z_i)}{\sum \exp(z)} ) = - \sum y_i [z_i - \log(\sum \exp(z))]$$

$$\frac{\partial L}{\partial z_k} = - y_k + (\sum y) \cdot \frac{\exp(z_k)}{\sum} = \hat{y}_k - y_k$$

4.4. Triển khai

Mã giả cho SGD:

for epoch in range(num_epochs): 

    for x, y in training_data: 

        z = theta.T.dot(x)  # logits 

        y_hat = softmax(z) 

        loss = - y.T.dot(np.log(y_hat)) 

        dz = y_hat - y 

        dtheta = x.dot(dz.T) 

        theta -= learning_rate * dtheta

Để ổn định, trong quá trình huấn luyện, ta sử dụng hàm stable softmax.

4.5 Ví dụ

4.5.1. Ví dụ phân loại nhị phân

Dù softmax thường được sử dụng cho phân loại đa lớp, nó cũng có thể áp dụng cho bài toán nhị phân bằng cách dùng hai logit tương ứng với hai lớp. Khi đó, hàm softmax trả về phân bố xác suất gồm hai phần tử, trong đó mỗi giá trị thể hiện xác suất mẫu thuộc từng lớp. Cách tiếp cận này giúp mô hình diễn giải rõ ràng xác suất cho cả hai nhãn, đặc biệt hữu ích trong các hệ thống cần biểu diễn độ tin cậy như phân loại thư rác, phát hiện gian lận hoặc dự đoán bệnh lý. Việc sử dụng softmax cho nhị phân còn đảm bảo tính tổng quát khi mở rộng mô hình sang nhiều lớp trong tương lai.

4.5.2. Ví dụ phân loại đa lớp

Hồi quy softmax là lựa chọn tiêu chuẩn cho các bài toán phân loại nhiều nhãn rời rạc, nơi mỗi mẫu chỉ thuộc đúng một lớp. Nhờ khả năng chuyển logits thành phân bố xác suất chuẩn hóa, softmax giúp mô hình xác định lớp có xác suất cao nhất một cách tự nhiên và trực quan. Nó được ứng dụng rộng rãi trong các nhiệm vụ như phân loại ảnh (nhận dạng chữ số MNIST, phân loại loài hoa Iris), phân loại văn bản, nhận dạng giọng nói, hoặc phân tích cảm xúc. Trong deep learning, softmax đóng vai trò quan trọng ở lớp đầu ra, giúp lan truyền ngược hiệu quả với hàm mất mát entropy chéo và mang lại khả năng dự đoán xác suất đáng tin cậy.

4.6 Vai trò hàm Softmax trong mô hình Deep Learning

Trong deep learning, softmax là hàm kích hoạt ở lớp cuối cho nhiệm vụ đa lớp (ví dụ: phân loại chữ số MNIST). Các nguyên tắc logits, chuẩn hóa xác suất, entropy chéo-giữ nguyên, nhưng trước các lớp ẩn với kích hoạt phi tuyến. Softmax cho phép huấn luyện end-to-end qua lan truyền ngược, nơi gradient chảy từ mất mát qua softmax đến các lớp trước.

Thường gặp trong framework như PyTorch: nn.Softmax + nn.CrossEntropyLoss.

5. Kết luận

Hồi quy softmax đóng vai trò nền tảng trong các bài toán phân loại hiện đại nhờ khả năng tạo ra phân bố xác suất rõ ràng và nhất quán giữa các lớp. Kết hợp với hàm mất mát entropy chéo và các thuật toán tối ưu như gradient descent, phương pháp này mang lại quy trình huấn luyện ổn định và hiệu quả. Bên cạnh đó, việc triển khai đơn giản trong các thư viện như NumPy giúp người học dễ dàng tiếp cận từ mức cơ bản đến nâng cao. Quan trọng hơn, softmax đã trở thành thành phần mặc định trong lớp đầu ra của nhiều mô hình deep learning, góp phần quyết định vào hiệu suất của các hệ thống phân loại trong thực tế.

Tags: #loss_function #python

Chia sẻ: