I. Giới thiệu bài toán

Logistic Regression mặc dù là Regression nhưng lại là một trong số các mô hình classification phổ biến, thường được sử dụng trong bài toán phân loại có 2 classes (Binary classification). Nhưng trong thực tế, các bài toán phân loại thường có nhiều classes (multi classification). Mặc dù vẫn có thể áp dụng Logistic Regression trong trường hợp này nhưng nó cũng bộc lộ một số điểm hạn chế. Softmax Regression là một mô hình tổng quát và hiệu quả hơn để khắc phục những điểm hạn chế đó.

II. Multi class với LogisticRegression

Với multi classification, bài toán đặt ra là hãy phân loại các samples thành $m$ classes khác nhau $(m>2)$.

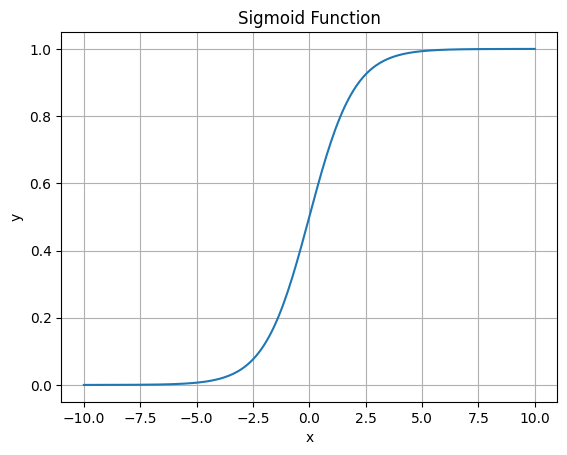
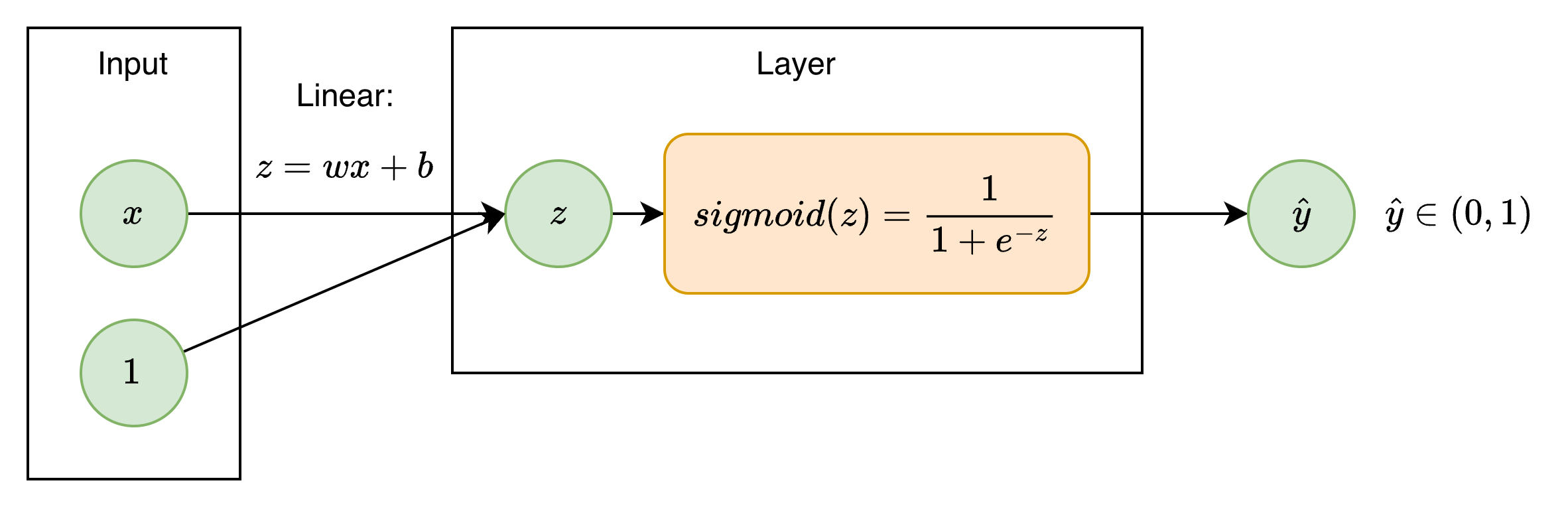
Logistic Regression sử dụng hàm sigmoid để có được đầu ra $\hat y$ nằm trong khoảng $(0, 1)$ là xác suất sample thuộc class 1. Chọn ngưỡng để so sánh, đầu ra sẽ được phân loại thành 0 hoặc 1 (2 classes). Để áp dụng vào multi classification, ta có thể sử dụng một vài phương pháp như one-vs-rest.

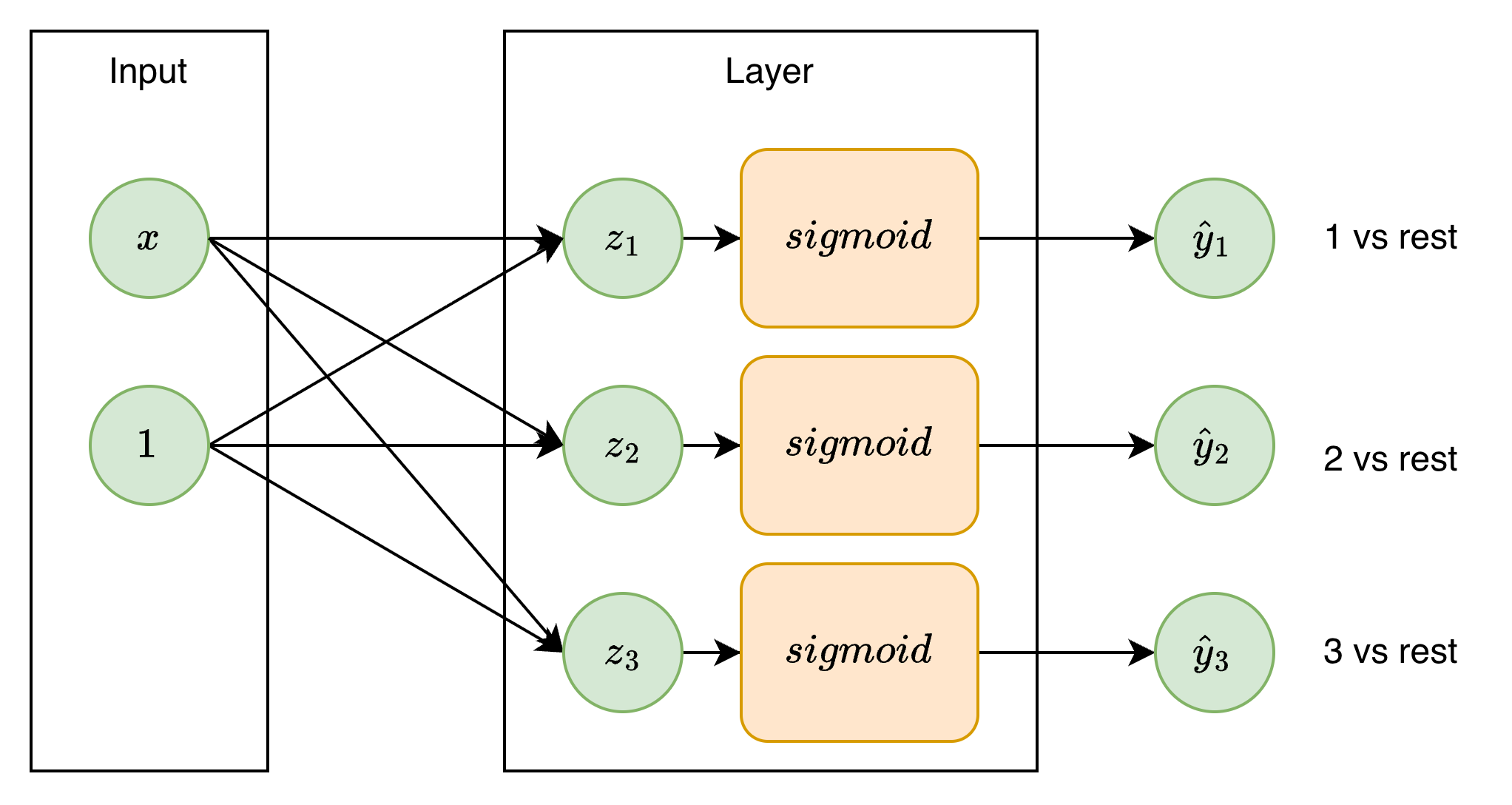
Ý tưởng của one-vs-rest là sử dụng đầu ra $\hat y\in(0,1)$ để phân loại đầu vào thuộc class nào đó hoặc thuộc các class còn lại thay vì 2 class là 0 và 1. Với $m$ classes sẽ có $m$ mô hình Logistic Regression với $m$ bộ tham số khác nhau để phân loại đầu vào thuộc class đó hay các class còn lại, đầu ra cuối cùng sẽ là class có xác suất $(\hat y)$ cao nhất.

Hạn chế của one-vs-rest đó là các giá trị output $(\hat y_1,\hat y_2,\hat y_3,...)$ được tính toàn trực tiếp từ các mô hình Logistic Regression khác nhau và kết quả đầu ra không phụ thuộc vào nhau. Với từng giá trị $(\hat y_1,\hat y_2,\hat y_3,...)$ là đầu ra của các hàm sigmoid riêng biệt và đều $\in(0,1)$ thì tổng của các output có thể $\ne1$. Hay nói cách khác tổng xác suất sample thuộc một class nào đó không bằng 1, điều này có thể làm giảm độ chính xác của kết quả phân loại.

III. Softmax Regression

3.1. Hàm Softmax

$$ \hat y_i=softmax(z_i)=\frac{e^{z_i}}{\sum_{j}e^{z_j}} $$

Hàm softmax biến đổi các input $z_i$ thành output $\hat y_i\in(0,1)$ và tổng các giá trị output bằng 1.

3.2. Softmax Regression

Áp dụng hàm softmax thay cho hàm sigmoid ở trên ta có mô hình Softmax Regression, mô hình này khắc phục được hạn chế kể trên về tổng xác suất. Điều này giúp mô hình hợp lý hơn khi áp dụng phân loại nhiều classes khi mà tổng giá trị xác suất đầu vào thuộc các class khác nhau $\hat y_1+\hat y_2+...+\hat y_i=1$.

Với mỗi input $\bm{x}=[x_1,x_2,...]$ quá trình tính toán của Softmax Regression cho phân loại $k$ class có thể chia làm các bước sau:

Bước 1: Sử dụng hàm linear tính toán giá trị tuyến tính $\bm z$ (logits)

Thay vì tính toán 1 điểm z như với Logistic Regression, ta tính toán $k$ giá trị $z_i$ với k bộ tham số $(w_i, b_i)$ khác nhau:

$$ z_1=\bm{w}_1^T\bm{x}+b_1 \\ z_2=\bm{w}_2^T\bm{x}+b_2 \\ \vdots \\ z_k=\bm{w}_k^T\bm{x}+b_k $$

Bước 2: Chuyển đổi logits thành $k$ giá trị xác suất $\hat y_i$

Sử dụng hàm softmax với input là logits $\bm{z}=\{z_1, z_2,...,z_k\}$ ta có được các giá trị xác suất $\bm{\hat y}=\{\hat y_1, \hat y_2, ..., \hat y_k\}$

$$ \hat y_i=P(y=k|\bm{x})=\frac{e^{z_k}}{\sum_{j=1}^k e^{z_j}} $$

output $y_i$ là xác suất input thuộc class $i$

Hàm Softmax có ý nghĩa:

• Chuẩn hóa: đảm bảo tổng xác suất $y_1+y_2+...+y_k=1$
• Hàm mũ $e^z$ khuếch đại sự khác biệt giữa các logits lên rất nhiều lần, làm cho lớp có logit $z_i$ cao nhất sẽ có xác suất $\hat y_i$ vượt trội. Ví dụ bài toán phân loại (chó, mèo, gà) tính toán được $\bm{z}=\{z_{chó},z_{mèo},z_{gà}\}=\{2,1,-1\}$, áp dụng hàm mũ có được $\bm{e^z}=\{7.39, 2.72, 0.37\}$ và chuẩn hóa có được $\bm{\hat y}=\{P_{chó},P_{mèo},P_{gà}\}=\{0.705,\ 0.260,\ 0.035\}$. Như vậy hàm mũ đã khuếch đại class có điểm logit cao nhất để có xác suất vượt trội so với các class khác

3.3. Hàm loss Categorical Cross Entropy

3.3.1. Binary Cross Entropy và hàm -log(x)

Với Logistic Regression ta có hàm loss là Binary Cross Entropy

$$ L_{BCE}=-ylog(\hat y)-(1-y)log(1-\hat y) $$

Với $y=0;\ L=-log(1-\hat y)=-log(\hat y_0)$. Với $\hat y_0=1-\hat y$: xác suất input thuộc class 0

Với $y=1;\ L=-log(\hat y)=-log(\hat y_1)$. Với $\hat y_1=\hat y$: xác suất input thuộc class 1

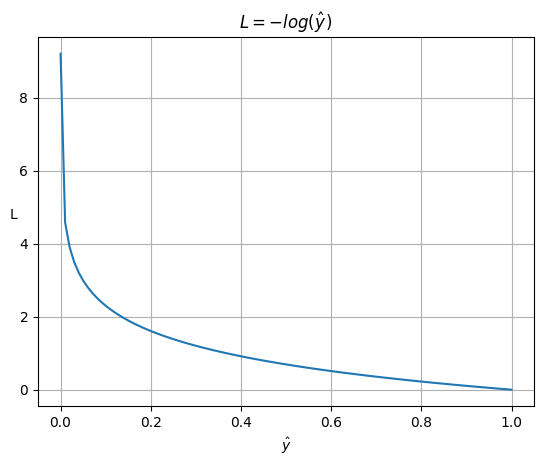
Hàm $L=-log(\hat y)$ có đặc điểm là:

• khi $\hat y=1$ thì $L=-log(\hat y) = 0$
• khi $\hat y\rightarrow0$ thì $L=-log(\hat y)\rightarrow+\infin$

3.3.2. Categorical Cross Entropy

Với Softmax Regression cho bài toán phân loại $k$ class, với mỗi input $x$ có label $y=j$, output của mô hình $\bm y=\{y_1,y_2,...,y_i,...y_k\}$ với $\hat y_i\in(0,1]$ là xác suất input thuộc class $i$.

Tại vị trí $i=j$, $\hat y_j\in(0,1]$ là xác suất input thuộc class $j$ (label). Ta mong muốn hàm loss có tính chất sau:

• Khi $\hat y_j\rightarrow0$: nghĩa là xác suất input thuộc class $i$ thấp, mô hình đang dự đoán sai thì phạt càng lớn, $L\rightarrow+\infin$ và tăng nhanh về phía $\hat y=0$
• Khi $\hat y_j\rightarrow1$: nghĩa là xác suất input thuộc class $i$ cao, mô hình đang dự đoán đúng thì phạt càng ít, $L\rightarrow0$

Hàm loss là $L=-log(\hat y_j)$ có được tính chất này. Một cách tổng quát ta sẽ có hàm loss cho Softmax Regression với 1 đầu vào $\bm x$ như sau:

$$ L=-\sum_{i=1}^m y_ilog(\hat y_i)=-y_1log(\hat y_1)-y_2log(\hat y_2)-...-y_klog(\hat y_k) \tag*{(1)} $$

Trong đó $y_i=1$ nếu input thuộc class $j\ (i=j)$ và 0 với các trường hợp còn lại

Ví dụ: Với các class (1, 2, 3, …) ta có:

• Nếu input thuộc class 1 thì hàm loss ở (1) $L=-log(\hat y_1)$
• Nếu input thuộc class 2 thì hàm loss ở (1) $L=-log(\hat y_2)$

3.4. Gradient Descent cho Softmax Regression

Với hàm loss $L(y,\hat y)$ ở (1) hay quy về $L(W,\bm b)$, ta sử dụng Gradient Descent để tìm ra bộ tham số $(W,\bm b)$ sao cho giá trị hàm loss là nhỏ nhất. Việc tính đạo hàm trực tiếp $\frac{\partial L}{\partial W}$ rất phức tạp nên ta sử dụng phương pháp đạo hàm trung gian

$$ \frac{\partial L}{\partial W}=\frac{\partial L}{\partial \hat y}=\frac{\partial \hat y}{\partial z}=\frac{\partial z}{\partial w} $$

Kết quả cuối cùng ta sẽ có được như sau:

$$ \nabla_{W} L=\frac{\partial L}{\partial W}=(\hat{y}_i - y_i)\, x_i \\ \nabla_{b} L=\frac{\partial L}{\partial b}=(\hat{y}_i - y_i) $$

3.5. Quy trình huấn luyện sử dụng batch Gradient Descent

Cho bài toán phân loại nhiều class $(k)$:

• input là ma trận $X$ với $m$ samples.
• label là ma trận $Y$ có kích thước $m*k$ tạo thành từ $m$ vector $\bm y_i(i\in[1,m])$ là one-hot vector cho sample thứ $i$. $k$ là số lượng class

Quy trình huấn luyện mô hình như sau:

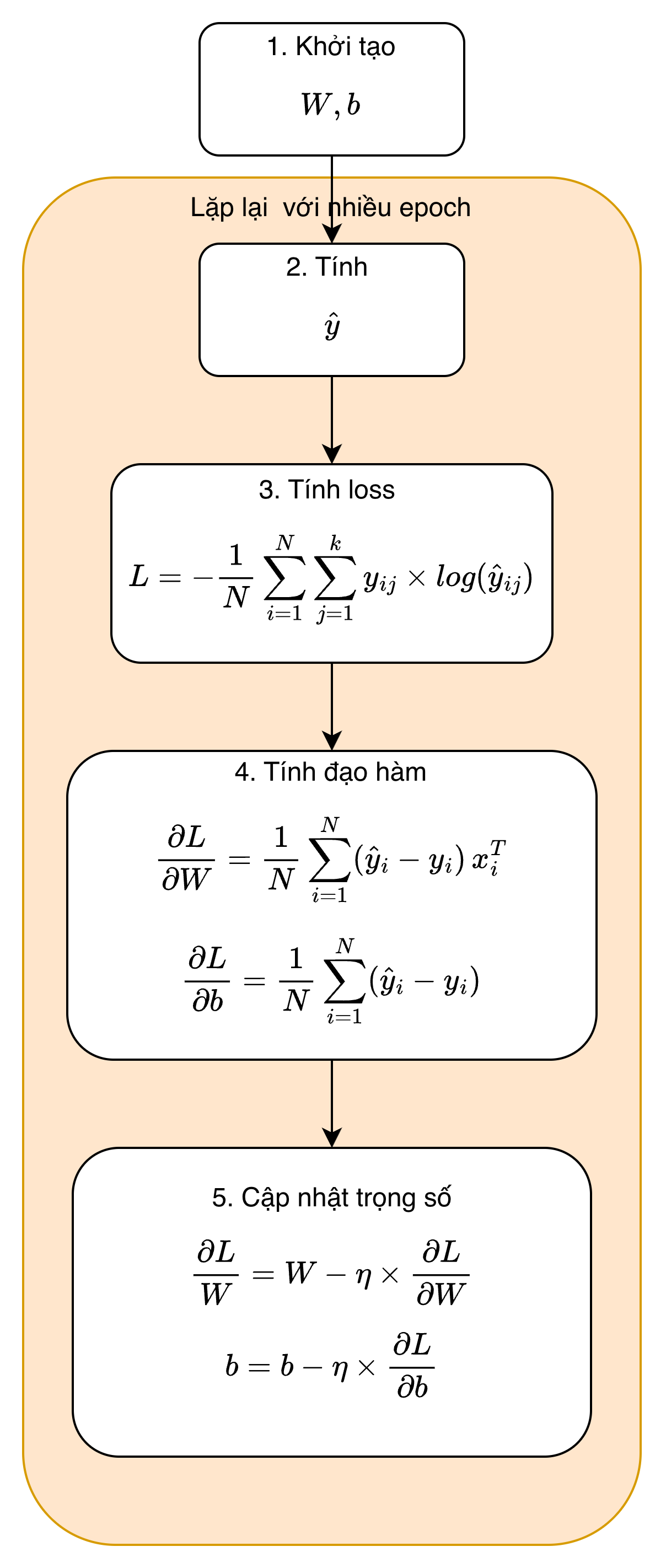
Bước 1: Khởi tạo tham số

• Khởi tạo tham số ban đầu gồm ma trận trọng số $W$ có kích thước $d*k$ và vector $\bm b$ cho bias
• Chọn siêu tham số learning rate $\eta$ và số vòng lặp (epochs) là số lần mô hình học qua $m$ samples

Bước 2: Tính toán xác suất dự đoán $\hat y$

• Tính logits sử dụng hàm tuyến tính: $z_i=Wx_i+b$
• Tính $\hat y_i=\frac{e^{z_i}}{\sum_{j=1}^ke^{z_j}}$

Bước 3: Tính loss

• Tính loss

$$ \displaystyle L = -\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{K} y_{ij}\times \log(\hat{y}_{ij}) $$

Trong đó $y_{ij}=1$ nếu sample i thuộc lớp j và 0 nếu ngược lại

Bước 4: Tính đạo hàm trên toàn bộ mẫu:

$$ \frac{\partial L}{\partial W}= \frac{1}{N} \sum_{i=1}^{N} (\hat{y}_i - y_i)\, x_i^{T},\qquad\frac{\partial L}{\partial b}= \frac{1}{N} \sum_{i=1}^{N} (\hat{y}_i - y_i) $$

Bước 5: Cập nhật trọng số $W$ và $b$

$$ W = W - \eta \times \frac{\partial L}{\partial W},\qquad b = b - \eta \times \frac{\partial L}{\partial b} $$

Lặp lại các bước 2, 3, 4, 5 với số lần lặp epochs để có được bộ tham số tối ưu

IV. Softmax Regression với numpy

Cho tập dataset của hoa Iris với 2 features như sau, xây dựng mô hình phân loại hoa với 3 class

# Dataset
X = np.array([
    [1.5, 0.2],
    [1.4, 0.2],
    [1.6, 0.2],
    [4.7, 1.6],
    [3.3, 1.1],
    [4.6, 1.3],
    [5.6, 2.2],
    [5.1, 1.5],
    [5.6, 1.4]
])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2])

Xử lý dữ liệu:

• Thêm bias vào X
• Sử dụng one-hot-encoding chuyển $N$ samples thành $N$ vector có độ dài $k$ (số class)

# Add bias
intercept = np.ones((X.shape[0], 1))
X = np.concatenate((intercept, X), axis=1)
# Convert label to one-hot
y = one_hot_encoding(y)

Huấn luyện mô hình với 3000 vòng lặp:

N = X.shape[0] # num of samples
d = X.shape[1] # num of features + bias
k = y.shape[1] # num of classes
np.random.seed(42)

learning_rate = 0.01
losses = []
num_epoch = 3000
theta = 0.01 * np.random.randn(d, k)

for epoch in range(num_epoch):
    # compute logits
    z = X.dot(theta) # matrix Nxk

    # compute class probabilities with softmax
    y_hat = softmax(z) # Nxk

    # compute loss
    loss = cross_entropy(y_hat, y)
    losses.append(loss)

    # compute gradient
    grad = gradient(X, y, y_hat) # dxk

    # update parameters
    theta = theta - learning_rate * grad

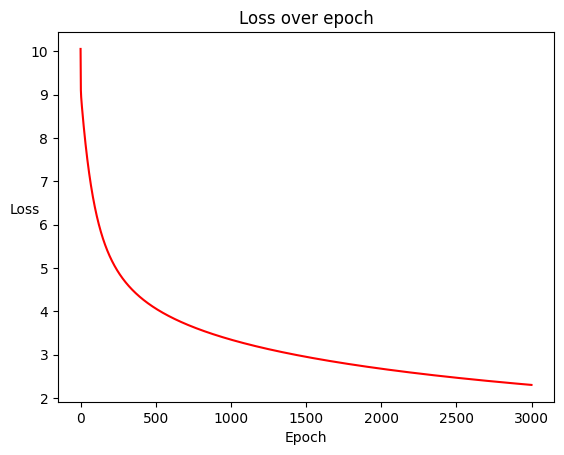
Kết quả thu được có giá trị hàm loss giảm dần

V. Softmax Regression với Pytorch

Xét bộ dataset chữ viết tay MNIST gồm 1000 samples

from sklearn.datasets import fetch_openml
import random
from torch.utils.data import Subset
from torchvision import datasets
import torchvision.transforms as transforms
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
import torch
import matplotlib.pyplot as plt

# Define a transform to convert PIL images to tensors
transform = transforms.Compose([
    transforms.ToTensor(),
])

# Download the training dataset
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)

# Download the test dataset
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)

random.seed(42)

train_indices = random.sample(range(len(train_dataset)), 1000)
small_train_dataset = Subset(train_dataset, train_indices)

test_indices = random.sample(range(len(test_dataset)), 200)
small_test_dataset = Subset(test_dataset, test_indices)

Với dataset lớn, việc tối ưu trên toàn bộ dataset cùng một lúc rất tốn kém, vì vậy ta sử dụng mini-batch để chia nhỏ dataset. DataLoader trong Pytorch là một generator sẽ giúp làm việc đó.

# Define loader
train_loader = DataLoader(small_train_dataset, batch_size=64)
test_loader = DataLoader(small_test_dataset, batch_size=64)rain Accuracy: {epoch_accuracy:.2f}%, Test Accuracy: {test_accuracy:.2f}")

Train mô hình:

# Define model
model = nn.Sequential(
    nn.Flatten(),
    nn.Linear(784, 10)
)
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

# Define training parameters
num_epochs = 300
losses = []

# Train the model
for epoch in range(num_epochs):
    running_loss = 0.0
    running_correct = 0   # to track number of correct predictions
    total = 0             # to track total number of samples

    for i, (inputs, labels) in enumerate(train_loader):
        # Forward pass
        outputs = model(inputs)
        loss = criterion(outputs, labels)

        running_loss += loss.item()
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        running_correct += (predicted == labels).sum().item()

        # Backward and optimize
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    epoch_loss = running_loss / (i + 1)
    losses.append(epoch_loss)

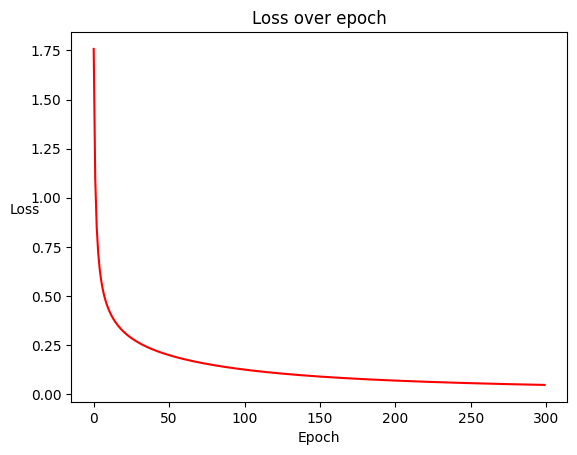
Kết quả thu được có giá trị hàm loss giảm dần

VI. Mở rộng Softmax Regression

6.1. Stable Softmax

Khi tính toán với hàm Softmax, ta cần tính $e^z$, biểu thức này tăng rất nhanh và có thể gây tràn số, ví dụ như với kiểu float64 trong Python, $e^z$ sẽ tràn khi $z\gtrsim709$. Để tránh điều này, trước khi tính hàm mũ, ta có thể trừ đi giá trị lớn nhất trong số các logits

$$ \bm z=\{z_1,z_2,...,z_m\};\ m=max(z_i)\\P_i=stable\_softmax(z_i)=\frac{e^{z_i-m}}{\sum_{j}e^{z_j-m}} $$

Việc cộng hoặc trừ một hằng số vào toàn bộ vector $\bm z$ không làm thay đổi kết quả trong khi giúp việc tính toán trở nên ổn định hơn

$$ softmax(z_i)=\frac{e^{z_i}}{\sum_{j}e^{z_j}}=\frac{e^{-m}e^{z_i}}{e^{-m}\sum_{j}e^{z_j}}=\frac{e^{z_i-m}}{\sum_{j}e^{z_j-m}}=stable\_softmax(z_i) $$

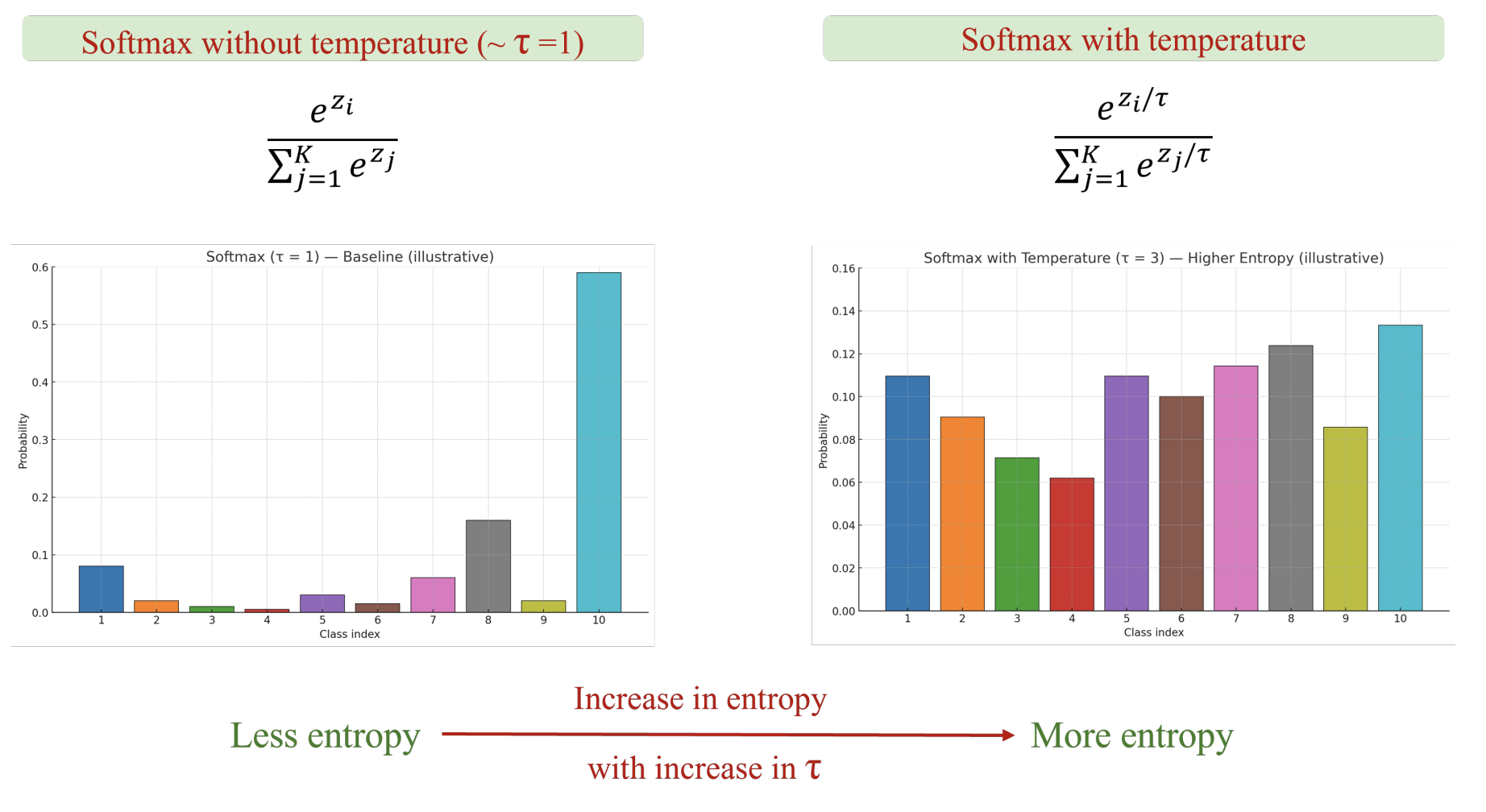
6.2. Softmax với tham số temperature $\tau$

Tham số temperature $\tau$ có thể được thêm vào để điều khiển độ tập trung của phân bố xác suất từ các logits ban đầu.

$$ P_i(\tau)=softmax(\frac{\bm z}{\tau})_i=\frac{e^{z_i/\tau}}{\sum_{j}e^{z_j/\tau}} $$

• Khi $\tau=1$, phân bố xác suất chuẩn
• Khi $\tau$ tăng, độ chênh lệch giữa các $e^{z_i/\tau}$ giảm, phân bố trải đều, do đó entropy sẽ tăng theo
• Ngược lại, khi $\tau$ giảm, độ chênh lệch giữa các $e^{z_i/\tau}$ tăng, phân bố tập trung vào một class, do đó entropy sẽ giảm theo

VII. Tài liệu tham khảo

AI Viet Nam