1. Giới thiệu
Softmax Regression mở rộng Logistic Regression từ phân loại nhị phân sang phân loại đa lớp. Đề tài hướng đến việc xây dựng nền tảng vững chắc để hiểu cách mô hình tuyến tính xử lý dữ liệu khi số lớp lớn hơn hai, thông qua việc sử dụng hàm Softmax để tạo ra phân phối xác suất hợp lệ. Nội dung trọng tâm gồm giải thích cách Softmax chuyển đổi logits thành xác suất, cách hàm mất mát Categorical Cross-Entropy được sử dụng, và cách Gradient Descent tối ưu các tham số của mô hình.
2. Cơ sở lý thuyết
2.1. Khái niệm
Logistic Regression là một mô hình học máy có giám sát dùng để phân loại, đặc biệt là các bài toán phân loại nhị phân (binary classification). Logistic Regression không dự đoán giá trị liên tục như Linear Regression mà dự đoán xác suất một mẫu thuộc lớp "1". Ví dụ:
- Dự đoán email có phải spam hay không (spam = 1, không spam = 0)
- Dự đoán khách hàng có mua hàng hay không (mua = 1, không mua = 0)
Logistic Regression bắt đầu từ một mô hình tuyến tính giống Linear Regression:
$$ z = w^Tx + b $$
Trong đó:
- $x$ là vector đặc trưng đầu vào
- $w$ là vector trọng số
- $b$ là hệ số điều chỉnh (bias)
Giá trị $z$ sau đó được đưa qua hàm sigmoid để biến đổi thành một giá trị xác suất trong khoảng (0, 1):
$$ \sigma(z)=\frac{1}{1+e^{-z}} $$
Logistic Regression không dự đoán trực tiếp xác suất mà mô hình hóa log-odds (logit) như một hàm tuyến tính theo $x$
$$ logit(p) = log(\frac{p}{1-p}) = w^Tx + b $$
Trong đó:
- $p=\sigma(z)$ là xác suất mẫu thuộc lớp 1
- $\frac{p}{1-p}$ là odds (tỷ lệ xảy ra và không xảy ra)
- $log(\frac{p}{1-p})$ là log-odds, tuyến tính theo $x$
2.2. Ý tưởng
Tăng trưởng logistic là một mô hình mô tả sự tăng trưởng của một quần thể, một lượng vật chất, hay một quá trình nào đó theo thời gian, trong bối cảnh nguồn lực bị giới hạn.
Khi một quần thể còn ít, tăng trưởng diễn ra gần như theo hàm mũ vì nguồn lực (thức ăn, không gian) chưa bị giới hạn. Khi quần thể lớn dần, nguồn lực hạn chế sẽ làm giảm tốc độ tăng trưởng. Sau cùng, quần thể sẽ ổn định ở một giới hạn môi trường gọi là carrying capacity K - số lượng tối đa mà môi trường có thể hỗ trợ.
Tăng trưởng logistic được mô tả qua phương trình vi phân sau:
$$ \frac{dP}{dt} = rP(1-\frac{P}{K}) $$
Trong đó:
- P(t): kích thước quân thể tại thời điểm t
- r: tốc độ tăng trưởng nội tại
- K: giới hạn tối đa (carrying capacity)
Giải phương trình vi phân trên ta được hàm logistic:
$$ P(t)=\frac{K}{1+ \frac{K-P_0}{P_0}e^{-rt}} $$
với $P_0$ là kích thước ban đầu của quần thể.
Đường cong $P(t)$ có hình dạng chữ S điển hình.
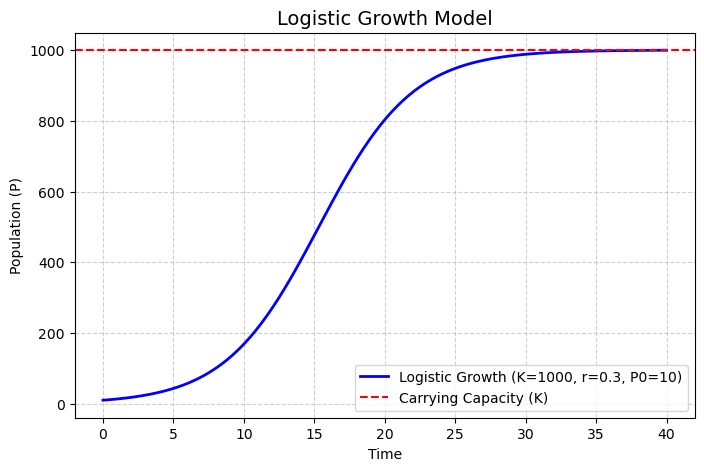
Hình 1. Ví dụ đường cong hàm logistic
Hàm Sigmoid xuất phát từ mô hình tăng trưởng logistic trong sinh học và dân số học, sau đó được chuẩn hóa để sử dụng rộng rãi trong các mô hình học máy. Hàm này có đặc tính biến đổi đầu ra tuyến tính thành giá trị nằm trong khoảng (0,1), phù hợp để diễn giải như xác suất.
$$
\sigma(x)=\frac{1}{1+e^{-x}}
$$
Trong bài toán phân loại nhị phân, mô hình tuyến tính có dạng:
$$
z = w^Tx + b
$$
với w là vector trọng số và b là hệ số chệch (bias). Nếu sử dụng trực tiếp z làm dự đoán, giá trị \hat {y} có thể âm hoặc lớn hơn 1, không phù hợp để diễn giải như xác suất.
Để khắc phục, ta sử dụng hàm Sigmoid:
$$
P(y=1|x)=\sigma(z)=\frac{1}{1+e^{-z}}
$$
- Khi $z → -\infty$, $\sigma(z) → 0$
- Khi $z → +\infty$, $\sigma(z) → 1$
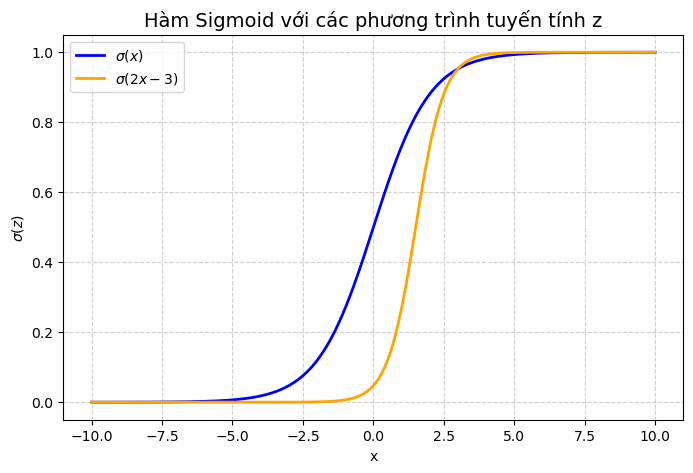
Hình 2. Ví dụ đường cong hàm Sigmoid
Về ngưỡng quyết định, sau khi có được dự đoán giá trị xác suất $\hat{y}$, chúng ta cần đưa ra ngưỡng xác suất phù hợp để quyết định dự đoán mẫu thuộc lớp "1" hay lớp "0". Giá trị ngưỡng thông dụng nhất là 0.5. Ví dụ:
- Nếu $\hat{y} \ge 0.5$ (xác suất email spam lớn hơn hoặc bằng 0.5), phân loại email vào loại "Spam".
- Nếu $\hat{y} < 0.5$ (xác suất email spam nhỏ hơn 0.5), phân loại email vào loại "Không Spam".
2.3. Hàm mất mát
Trong học máy, đặc biệt với thuật toán Gradient Descent, tính lồi (convex) của hàm mất mát đóng vai trò quan trọng. Nếu hàm mất mát là lồi, Gradient Descent đảm bảo hội tụ về cực tiểu toàn cục, tránh bị kẹt ở cực tiểu cục bộ.
Một hàm được coi là hàm lồi nếu các eigenvalues (đại lượng vô hướng) của ma trận Hessian lớn hơn hoặc bằng 0, nghĩa là ma trận Hessian của hàm đó là ma trận nửa xác định dương (Positive Semidefine - PSD).
2.3.1. Mean Squared Error (MSE)
2.3.1.1. MSE trong Linear Regression
Xét mô hình hồi quy tuyến tính:
$$ \begin{aligned} \hat{y} &= \theta^Tx \\ L&=\frac{1}{2}(\hat{y} - y)^2 \\ \end{aligned} $$
Các phương trình đạo hàm như sau:
$$ \begin{aligned} \frac{\partial L}{\partial \hat{y}} &= \hat{y} - y \\ \frac{\partial \hat{y}}{\partial \theta_i} &= x_i\\ \end{aligned} $$
Đạo hàm bậc nhất của $L$ theo $\theta$:
$$ \frac{\partial L}{\partial \theta_i} = \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial \theta_i} = (\hat{y} - y)x_i $$
Đạo hàm bậc hai của $L$ theo $\theta$:
$$ \begin{aligned} \frac{\partial^2 L}{\partial \theta_i^2} &= \frac{\partial [x_i(\hat{y} - y)]}{\partial \theta_i} \\ &= \frac{\partial x_i}{\partial \theta_i} \cdot (\hat{y} - y)+\frac{\partial (\hat{y} - y)}{\partial \theta_i} \cdot x_i \\ &= \frac{\partial (\hat{y} - y)}{\partial \theta_i} \cdot x_i \ \ (1) \\ &= x_i^2 \ge 0 \end{aligned} $$
Trong đó:
$(1)$ $x_i$ là hằng số nên $\frac{\partial x_i}{\partial \theta_i} = 0$
Kết luận: Với đạo hàm bậc hai của $L$ theo $\theta$ không âm, MSE kết hợp với hàm tuyến tính là hàm lồi, đảm bảo hội tụ về cực tiểu toàn cục.
2.3.1.2. MSE trong Logistic Regression
Trong bài toán phân loại nhị phân:
$$ \begin{aligned} y &\in \{0,1\} \\ z &= \theta^Tx \\ \hat{y} &= \sigma (z) = \frac{1}{1+e^{-z}} \\ L(z) &= \frac{1}{2}(\hat{y}-y)^2 \end{aligned} $$
Các phương trình đạo hàm như sau:
$$ \begin{aligned} \frac{\partial L}{\partial \hat{y}} &= \hat{y} - y \\ \frac{\partial \hat{y}}{\partial z} &= -\frac{-e^{-z}}{(1+e^{-z})^2} = \frac{1}{1+e^{-z}} \cdot \frac{1+e^{-z} - 1}{1+e^{-z}} = \hat{y}(1-\hat{y})\\ \frac{\partial z}{\partial \theta_i} &= x_i \end{aligned} $$
Đạo hàm bậc nhất của $L$ theo $\theta$:
$$ \begin{aligned} \frac{\partial L}{\partial \theta_i} &= \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z} \frac{\partial z}{\partial \theta_i} \\ &= x_i\hat{y}(1-\hat{y})(\hat{y} - y) \\ &= -x_i\hat{y}^3 + x_iy\hat{y}^2 + x_i\hat{y}^2 - x_iy\hat{y} \end{aligned} $$
Đạo hàm bậc hai của $L$ theo $\theta$:
$$ \begin{aligned} \frac{\partial^2 L}{\partial \theta_i^2} &= \frac{\partial}{\partial \theta_i} (-x_i\hat{y}^3 + x_iy\hat{y}^2 + x_i\hat{y}^2 - x_iy\hat{y})\\ &= x_i^2\hat{y}(1-\hat{y})(-3\hat{y}^2 + 2y\hat{y} + 2\hat{y} - y) \end{aligned} $$
Vì $x_i^2\hat{y}(1-\hat{y}) \ge 0$ nên dấu của đạo hàm bậc hai chỉ phụ thuộc vào dấu của $-3x_i\hat{y}^2 + 2x_iy\hat{y} + 2x_i\hat{y} - y$.
Do $y$ nhận 2 giá trị $0$ và $1$ nên:
* Khi $y=0$ thì $f(\hat{y}) = -3\hat{y}^2 + 2\hat{y}$. Tồn tại ít nhất 1 trường hợp của $\hat{y}$ để $f(\hat{y}) < 0$. Ví dụ, với $\hat{y} = 0.9$ thì $f(0.9) = -0.63 < 0$.
* Khi $y=1$ thì $f(\hat{y}) = -3\hat{y}^2 + 4\hat{y} - 1$. Tồn tại ít nhất 1 trường hợp của $\hat{y}$ để $f(\hat{y}) < 0$. Ví dụ, với $\hat{y} = 0.2$ thì $f(0.2) = -0.32 < 0$.
Kết luận: Do tồn tại trường hợp đạo hàm bậc hai âm, MSE kết hợp Sigmoid là hàm non-convex. Điều này có thể khiến mô hình rơi vào cực tiểu cục bộ, không đảm bảo tối ưu toàn cục. Vì vậy, MSE không phù hợp cho Logistic Regression.
2.3.2. Binary Cross-Entropy (BCE)
Từ ý tưởng mong muốn kích thích mô hình dự đoán đúng xác suất và phạt nặng dự đoán sai, ta xét hàm số $y=-log(x)$.
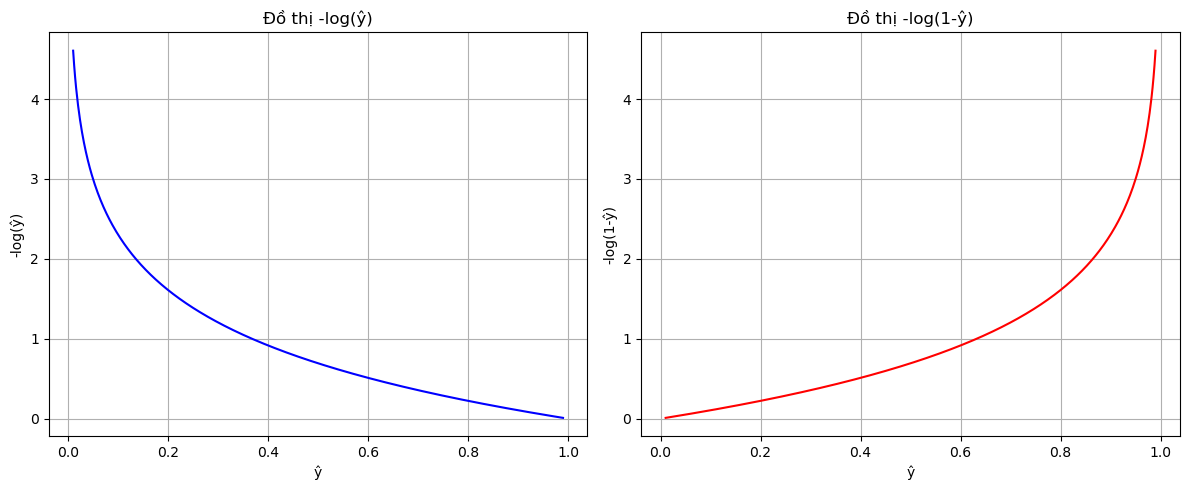
Hình 3. Đồ thị -log(ŷ) và -log(1-ŷ)
Hàm $-log(x)$ có những đặc tính lý tưởng cho xác suất:
* Với $y=1$, khi $\hat{y}$ gần 1 thì mất mát $-log(\hat{y})$ gần 0.
* Với $y=1$, khi $\hat{y}$ gần 0 thì mất mát $-log(\hat{y})$ rất lớn.
* Đối xứng: Với $y=0$, sử dụng $-log(1-\hat{y})$ có cùng hiệu ứng.
Kết hợp hai trường hợp sau:
* Nếu $y=1$ thì $L(\hat{y}) = -log(\hat{y})$
* Nếu $y=0$ thì $L(\hat{y}) = -log(1-\hat{y})$
Ta có công thức tổng quát:
$$ L(y,\hat{y}) = -ylog(\hat{y})-(1-y)log(1-\hat{y}) $$
Xét mô hình Logistic Regression:
$$ \begin{aligned} &y \in \{0,1\} \\ &z=\theta^Tx \\ &\hat{y} = \sigma (z) = \frac{1}{1+e^{-z}} \\ &L = -ylog(\hat{y})-(1-y)log(1-\hat{y}) \end{aligned} $$
Ta có các công thức đạo hàm sau:
$$ \begin{aligned} \frac{\partial L}{\partial \hat{y}} &= -\frac{y}{\hat{y}} + \frac{1-y}{1-\hat{y}} = \frac{\hat{y} - y}{\hat{y}(1-\hat{y})} \\ \frac{\partial \hat{y}}{\partial z} &= \hat{y} (1-\hat{y}) \\ \frac{\partial {z}}{\partial \theta_i} &= x_i \end{aligned} $$
Do đó, đạo hàm bậc nhất theo $\theta_i$:
$$ \frac{\partial L}{\partial \theta_i} = \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z} \frac{\partial z}{\partial \theta_i} = \frac{\hat{y} - y}{\hat{y}(1-\hat{y})} \hat{y} (1-\hat{y}) x_i = x_i(\hat{y} - y) $$
Đạo hàm bậc hai theo $\theta_i$:
$$ \begin{aligned} \frac{\partial^2 L}{\partial \theta_i^2} &= \frac{\partial [x_i(\hat{y} - y)]}{\partial \theta_i} \\ &= \frac{\partial x_i}{\partial \theta_i} ⋅ (\hat{y} - y)+\frac{\partial (\hat{y} - y)}{\partial \theta_i} ⋅ x_i \\ &= \frac{\partial (\hat{y} - y)}{\partial \theta_i} ⋅ x_i \ \ (1)\\ &= \frac{\partial \hat{y}}{\partial \theta_i} ⋅ x_i \\ &= \frac{\partial \hat{y}}{\partial z} \frac{\partial z}{\partial \theta_i} ⋅ x_i \\ &= \hat{y}(1-\hat{y})x_i^2 \ge 0 \ \ (2) \end{aligned} $$
Trong đó:
$(1)$ $x_i$ là hằng số nên $\frac{\partial x_i}{\partial \theta_i} = 0$
$(2)$ $\hat{y}(1-\hat{y}) \ge 0$ với $\hat{y} \in (0,1)$
Kết luận: Vì đạo hàm bậc hai của $L$ theo $\theta$ không âm với mọi $\theta$, ta kết luận rằng hàm mất mát BCE kết hợp với Sigmoid là hàm lồi theo tham số $\theta$, hay đảm bảo hội tụ về cực tiểu toàn cục. Nhờ đặc điểm này, chúng ta đã giải quyết được vấn đề cực tiểu địa phương nếu áp dụng MSE.
2.4. Cơ chế hoạt động của Logistic Regression
Quá trình huấn luyện cho Logistic Regression về cơ bản khá giống với Linear Regression, khi cũng sử dụng Batch Gradient Descent để tối ưu các tham số $w$ và $b$. Toàn bộ các bước huấn luyện được minh họa trong hình sau:
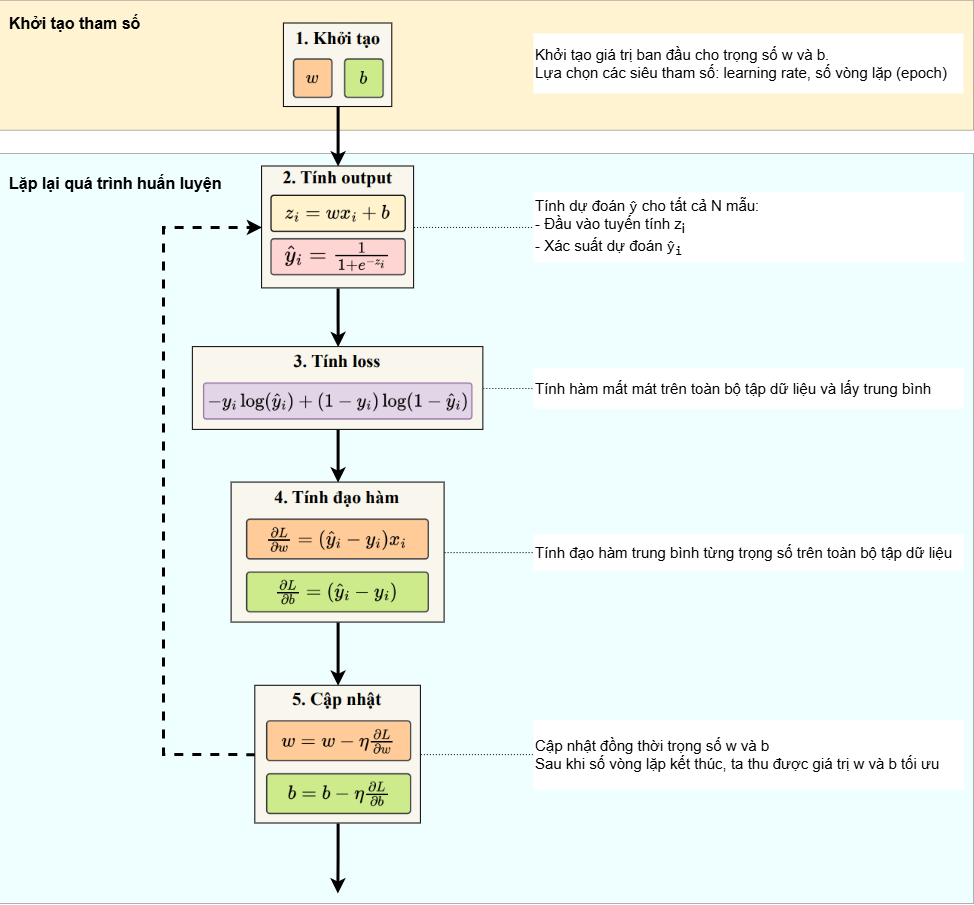
Hình 4. Quy trình huấn luyện mô hình Logistic Regression
Bước 1: Khởi tạo tham số ngẫu nhiên
Khởi tạo vector tham số $\theta$, bao gồm cả trọng số $w$ và bias $b$. Tất cả các giá trị này ban đầu có thể được khởi tạo bằng 0 hoặc ngẫu nhiên
Bước 2: Tính xác suất dự đoán cho N mẫu
Với mỗi mẫu dữ liệu:
- Tính đầu vào tuyến tính:
$$ z_i = x_iw+b $$
- Tính xác suất dự đoán mẫu thuộc lớp 1 thông qua hàm Sigmoid
$$ \hat{y_i} = \frac{1}{1+e^{-z_i}} $$
Bước 3: Tính mất mát trung bình trên toàn bộ tập dữ liệu
Hàm mất mát đo lường sự khác biệt giữa giá trị xác suất dự đoán mẫu thuộc lớp 1
là $\hat{y_i}$ và giá trị lớp thực tế $y_i$.
$$ L(w,b)=-\frac{1}{N} \sum^N_{i=1}[y_ilog(\hat{y_i})+(1-y_i)log(1-\hat{y_i})] $$
Các chỉ số i đại diện cho sample thứ i trong tổng số N samples của tập dữ liệu. Nói cách khác, $\hat{y_i}$ là giá trị dự đoán của sample thứ i, và $y_i$
là giá trị thực tế tương ứng với sample thứ i, với i = 1, 2, . . . , N.
Bước 4: Tính đạo hàm hàm mất mát $L$ theo tham số $w$ và $b$
- Tính trung bình đạo hàm hàm loss theo tham số $w_j$ của N samples
$$ \frac{\partial L}{\partial w_j} = \frac{1}{N}\sum_{i=1}^N(\hat{y_i} - y_i)x_{ij} $$
- Tính trung bình đạo hàm hàm loss theo bias $b$ của N samples
$$ \frac{\partial L}{\partial b} = \frac{1}{N}\sum_{i=1}^N(\hat{y_i} - y_i) $$
Bước 5: Cập nhật tham số
Với vector $\theta$ và vector các giá trị đạo hàm $L'_{\theta}$, ta cập nhật tất
cả các trọng số và bias cùng lúc thông qua công thức sau:
$$ w_j = w_j - \eta \frac{\partial L}{\partial w_j} \\ b = b - \eta \frac{\partial L}{\partial b} $$
với $\eta$ là learning rate.
Quá trình trên được lặp lại cho đến khi hội tụ, tức là hàm loss đạt đến giá trị nhỏ nhất hoặc thay đổi của các tham số rất nhỏ. Nhờ việc lặp lại quy trình tối ưu, mô hình dần dần điều chỉnh và tìm ra bộ tham số phù hợp nhất. Sau mỗi epoch, giá trị hàm mất mát $L(w,b)$ sẽ tiếp tục giảm, và đường quyết định $wx+b=0$ sẽ từng bước dịch chuyển đến vị trí tối ưu để tách biệt hai lớp 0 và 1.
2.5. Minh họa thực hiện thuật toán
Ta tiến hành minh họa thực hiện thuật toán qua bài toán cụ thể, lấy từ tập dữ liệu hoa iris được trình bày qua bài giảng.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('iris_full.csv')
X = df.iloc[:, :-1]
y = df.iloc[:, -1]
# chuẩn hóa đặc trưng
X_max = X.max()
X_min = X.min()
X = (X - X_min) / (X_max - X_min)
intercept = np.ones((X.shape[0], 1))
X = np.concatenate((intercept, X.to_numpy()), axis=1)
y = y.to_numpy()
# shuffle data
inds = np.arange(len(y))
np.random.shuffle(inds)
X = X[inds]
y = y[inds]
# tạo helper functions
def sigmoid(z):
return 1/(1+np.exp(-z))
def predict(X, theta):
return sigmoid(np.dot(X, theta))
def loss_function(y, y_hat):
return -np.dot(y, np.log(y_hat)) - np.dot((1-y), np.log(1-y_hat))
# Chuẩn bị tham số
n_epoch = 500
N = len(y)
theta = np.array([1,1,1,1,1])
lr = 0.01
losses = []
accs = []
# training
for epoch in range(n_epoch):
y_hat = predict(X, theta)
loss = loss_function(y, y_hat)
losses.append(loss)
acc = (np.round(y_hat) == y).sum()/N
accs.append(acc)
grad = np.dot((y_hat - y), X)
theta = theta - lr*grad
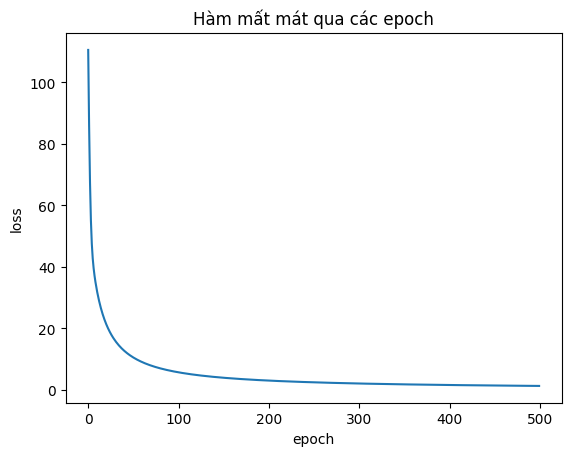
Hình 5. Hàm mất mát BCE qua các epoch
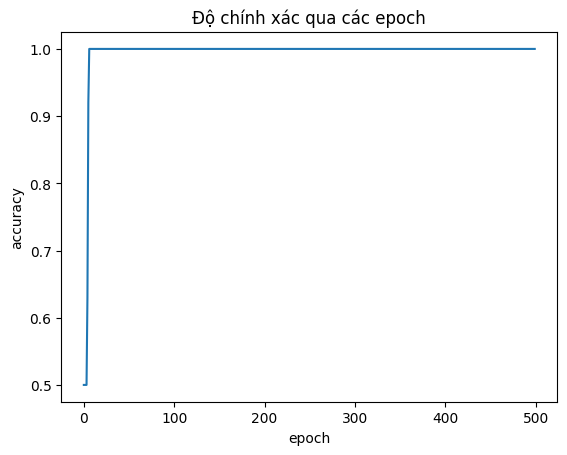
Hình 6. Độ chính xác qua các epoch
| Epoch | Mất mát | Độ chính xác | w0 | w1 | w2 | w3 | b | Dự đoán y_hat (sample 10 với y=0) |
|---|---|---|---|---|---|---|---|---|
| 1 | 110.552703 | 0.5 | 1 | 1 | 1 | 1 | 1 | 0.911354 |
| 2 | 85.974822 | 0.5 | 0.575973 | 0.891906 | 0.741798 | 0.962571 | 0.973732 | 0.837499 |
| 3 | 67.474111 | 0.5 | 0.203595 | 0.800638 | 0.509656 | 0.939362 | 0.959569 | 0.737106 |
| 6 | 42.795006 | 0.92 | -0.517509 | 0.665276 | 0.01494 | 0.989124 | 1.020006 | 0.459575 |
| 11 | 31.775637 | 1 | -0.957608 | 0.707203 | -0.409314 | 1.292551 | 1.310928 | 0.28447 |
| 51 | 10.538705 | 1 | -1.92341 | 1.186915 | -1.778294 | 2.886818 | 2.813393 | 0.061127 |
| 101 | 5.721987 | 1 | -2.403562 | 1.438653 | -2.524632 | 3.777354 | 3.652143 | 0.024785 |
| 251 | 2.46829 | 1 | -3.047369 | 1.767888 | -3.576719 | 5.031136 | 4.834307 | 0.006867 |
| 500 | 1.302646 | 1 | -3.533373 | 2.007025 | -4.402426 | 6.013703 | 5.762189 | 0.002515 |
Bảng 1. Bảng tóm tắt quá trình huấn luyện qua 500 epochs
Từ bảng tóm tắt quá trình huấn luyện trên tập dữ liệu iris, ta thấy:
- Các trọng số liên tục điều chỉnh để tìm ra ranh giới phù hợp nhất với bộ dữ liệu để phân loại.
- Mất mát giảm từ 110 xuống còn 1.3, chứng tỏ rằng mô hình đang học tốt và hội tụ.
- Ví dụ về đoán xác suất $\hat{y}$ của sample thứ 10 (có nhãn $y$ bằng 0) giảm từ 0.9 xuống còn 0.0025, ngày càng chính xác về nhãn thực tế $y=0$.
3. Softmax regression
3.1. Khái niệm
Softmax Regression là mô hình tổng quát hóa của Logistic Regression, được sử dụng cho bài toán phân loại đa lớp (Multi-class Classification), tức là phân loại đối tượng vào một trong $K$ nhóm khác nhau, với $K>2$.
3.2. Ý tưởng
Ý tưởng của hàm Softmax là giải quyết hạn chế của Logistic Regression (chỉ hoạt động hiệu quả cho phân loại nhị phân $K=2$ lớp) bằng cách tạo ra một hàm có khả năng:
- Tính toán $K$ điểm số tuyến tính (Logits) riêng biệt ($z_k$)—một điểm cho mỗi lớp $k$.
- Biến đổi $K$ điểm số này thành $K$ xác suất riêng biệt ($P(y=k|x)$).
- Đảm bảo $K$ xác suất này có tổng bằng 1.
Hàm Softmax thực hiện điều này bằng cách lấy hàm mũ ($e^z$) cho các điểm số (để chúng luôn dương, $e^{z_k} > 0$) và sau đó chuẩn hóa chúng bằng cách chia cho tổng của tất cả các giá trị mũ đó. Công thức tổng quát của hàm Softmax là:
$$\hat{y}_{k} = P(y=k|x) = \frac{e^{z_{k}}}{\sum_{j=1}^{K}e^{z_{j}}}$$
Tuy nhiên, khi các điểm số tuyến tính (Logits) $z_k$ có giá trị rất lớn, hàm mũ $e^{z_k}$ có thể vượt quá giới hạn lưu trữ của kiểu dữ liệu, dẫn đến hiện tượng Overflow (tràn số). Để giải quyết vấn đề này, người ta sử dụng công thức Stable Softmax:$$\hat{y}_{k} = \frac{e^{z_{}-\max(z)}}{\sum_{j=1}^{K}e^{z_{j}-\max(z)}}$$Việc trừ đi $\max(z)$ (giá trị Logit lớn nhất trong vector $z$) trong công thức này đảm bảo rằng số mũ lớn nhất luôn là $e^0=1$, giúp giữ các giá trị tính toán ổn định, tránh được Overflow mà vẫn giữ nguyên kết quả xác suất cuối cùng.
Giả sử ta có một dãy số z như sau:
$$z = [1000, 1001, 1002]$$
Nếu tính Softmax trực tiếp, $e^{1000}$ sẽ gây ra overflow. Để giải quyết vấn đề trên, ta áp dụng Stable Softmax như sau:
$$\text{Softmax}([1000, 1001, 1002]) = \left[\frac{e^{1000-1002}}{e^{1000-1002} + e^{1001-1002} + e^{1002-1002}}, \frac{e^{1001-1002}}{e^{1000-1002} + e^{1001-1002} + e^{1002-1002}}, \frac{e^{1002-1002}}{e^{1000-1002} + e^{1001-1002} + e^{1002-1002}}\right]$$
$$= \left[\frac{e^{-2}}{e^{-2} + e^{-1} + e^{0}}, \frac{e^{-1}}{e^{-2} + e^{-1} + e^{0}}, \frac{e^{0}}{e^{-2} + e^{-1} + e^{0}}\right]$$
$$\approx [0.09, 0.24, 0.67]$$
Kết luận: Stable Softmax giải quyết được vấn đề Overflow và Underflow, kết quả đồng nhất, không làm thay đổi ý nghĩa của phân phối xác suất cuối cùng
3.3. Hàm mất mát
Hàm mất mát tiêu chuẩn được sử dụng cho Softmax Regression là Categorical Cross-Entropy (CE) vì nó đo lường sự khác biệt giữa phân phối xác suất dự đoán ($\hat{y}_i$) và nhãn thực tế (dạng one-hot $y_i$). Nó được suy ra từ việc tổng quát hóa hàm Binary Cross-Entropy (sử dụng trong Logistic Regression) cho $K$ lớp.
Công thức của Cross-Entropy Loss cho một mẫu $i$ là:$$L_{i}=-\sum_{j=1}^{K}y_{ij}\log(\hat{y}_{ij})$$ Trong đó, $y_{i}$ là vector one-hot, $y_{ij}$ là 1 nếu mẫu $i$ thuộc lớp $j$, và 0 nếu ngược lại. $\hat{y}_{ij}$ là xác suất dự đoán mẫu $i$ thuộc về lớp $j$. Mục tiêu của quá trình huấn luyện là tìm ra bộ tham số ($W$ và $b$) làm cho giá trị của hàm mất mát tổng quát $L$ trên toàn bộ $N$ mẫu là nhỏ nhất. Công thức hàm mất mát tổng quát là:$$L=\frac{1}{N}\sum_{i=1}^{N}L_{i}$$
3.4. Cơ chế hoạt động
Quá trình huấn luyện Softmax Regression sử dụng Batch Gradient Descent để tối ưu ma trận trọng số $W$ và vector bias $b$.
- Bước 1: Khởi tạo tham số: Thiết lập giá trị ban đầu cho ma trận trọng số $W$ và vector bias $b$ (thường là ngẫu nhiên cho $W$ và $0$ cho $b$). Thiết lập siêu tham số $\eta$ (learning rate) và số Epoch
-
Bước 2: Tính dự đoán ($\hat{y}_{i}$) cho tất cả N mẫu:
- Tính vector điểm số tuyến tính:
$$z_i = Wx_i + b$$ - Tính vector xác suất dự đoán:
$$\hat{y}_{i} = \text{softmax}(z_i)$$
- Tính vector điểm số tuyến tính:
-
Bước 3: Tính hàm mất mát (Categorical Cross-Entropy) trên toàn bộ tập dữ liệu:
$$L = -\frac{1}{N}\sum_{i=1}^{N}\sum_{j=1}^{K}y_{ij}\log(\hat{y}_{ij})$$ -
Bước 4: Tính đạo hàm trung bình trên N mẫu:
$$\frac{\partial L}{\partial W} = \frac{1}{N}\sum_{i=1}^{N}(\hat{y}_{i}-y_{i})x_{i}^{T}$$
$$\frac{\partial L}{\partial b} = \frac{1}{N}\sum_{i=1}^{N}(\hat{y}_{i}-y_{i})$$ -
Bước 5: Cập nhật tham số: $$W = W - \eta \times \frac{\partial L}{\partial W}$$ $$b = b - \eta \times \frac{\partial L}{\partial b}$$
Ta tiến hành lặp lại các bước cho đến khi đạt số Epoch đã chọn. Sau mỗi epoch, hàm mất mát sẽ giảm xuống và mô hình hội tụ.
Đễ dễ hình dung vì sao tồn tại công thức tại bước c, ta tiến hành chứng minh công thức tính đạo hàm trung bình trên N mẫu như sau:
$$\frac{\partial L}{\partial z_i} = -y_i(1 - \hat{y}_i) - \sum_{k \neq i} y_k \frac{1}{\hat{y}_k} (-\hat{y}_k \hat{y}_i)$$
$$= -y_i(1 - \hat{y}_i) + \sum_{k \neq i} y_k \hat{y}_i$$
$$= -y_i + y_i \hat{y}_i + \sum_{k \neq i} y_k \hat{y}_i$$
$$= \hat{y}_i \left( y_i + \sum_{k \neq i} y_k \right) - y_i$$
$$ = \hat{y}_i - y_i \quad (y_i + \sum_{k \neq i} y_k = 1 \text{ (one-hot)}) $$
Có $z_i = W \cdot x_i + b$ => $\frac{\partial z_i}{\partial W} = x_i^T$, $\frac{\partial z_i}{\partial b} = 1$
$$\frac{\partial L}{\partial W} = \frac{\partial L}{\partial z_i} \cdot \frac{\partial z_i}{\partial W} = (\hat{y}_i - y_i)x_i^T$$
$$\frac{\partial L}{\partial b} = \frac{\partial L}{\partial z_i} \cdot \frac{\partial z_i}{\partial b} = (\hat{y}_i - y_i)$$
Từ đó khái quát lên N mẫu:
$$\frac{\partial L}{\partial W} = \frac{1}{N}\sum_{i=1}^{N}(\hat{y}_{i}-y_{i})x_{i}^{T}$$
$$\frac{\partial L}{\partial b} = \frac{1}{N}\sum_{i=1}^{N}(\hat{y}_{i}-y_{i})$$
3.5. Minh họa thực hiện thuật toán
Bài toán phân loại đa lớp: Dự đoán một mẫu hoa thuộc về 1 trong 3 giống (Lớp 0: Giống A, Lớp 1: Giống B, Lớp 2: Giống C), dựa trên một đặc trưng ($x$: Chiều rộng cánh hoa). Tập dữ liệu: $N=6$ mẫu.
Mục tiêu: Chúng ta sẽ thực hiện tính toán một vòng lặp (epoch) của Batch Gradient Descent để tìm ra các giá trị mới cho ma trận trọng số W và vector độ chệch b
import numpy as np
import pandas as pd
X_raw = np.array([[1.0, 2.5, 4.0, 5.5, 7.0, 8.0]])
N = X_raw.shape[1]
X_aug = np.vstack([np.ones((1, N)), X_raw])
Y_true_OH = np.array([[1, 1, 0, 0, 0, 0], [0, 0, 1, 1, 0, 0], [0, 0, 0, 0, 1, 1]])
K = Y_true_OH.shape[0]
D_aug = X_aug.shape[0]
lr = 0.2
Theta = np.zeros((K, D_aug))
EPOCH_MILESTONES = [1, 10, 500, 2000, 10000]
RESULTS = []
def stable_softmax(Z):
"""Tính toán Softmax ổn định."""
max_Z = np.max(Z, axis=0, keepdims=True)
exp_Z = np.exp(Z - max_Z)
return exp_Z / np.sum(exp_Z, axis=0, keepdims=True)
def cross_entropy_loss(Y_true, Y_pred, N):
"""Tính Loss Categorical Cross-Entropy."""
Y_pred = np.clip(Y_pred, 1e-12, 1.0)
return -np.sum(Y_true * np.log(Y_pred)) / N
def get_prediction_x8(theta, x_aug):
Z_x6 = theta @ x_aug[:, [-1]]
return stable_softmax(Z_x6)[2, 0]
MAX_EPOCHS = 10000
initial_loss = cross_entropy_loss(Y_true_OH, stable_softmax(Theta @ X_aug), N)
RESULTS.append({
'Epoch': 0,
'Trọng số W': '(0.00, 0.00, 0.00)',
'Độ chệch b': '(0.00, 0.00, 0.00)',
'Mất mát (CE)': initial_loss,
'Dự đoán y^ (x=8.0)': 1/3
})
print(f"--- BẮT ĐẦU HUẤN LUYỆN {MAX_EPOCHS} EPOCH ---")
for epoch in range(1, MAX_EPOCHS + 1):
Z = Theta @ X_aug
Y_pred = stable_softmax(Z)
Loss = cross_entropy_loss(Y_true_OH, Y_pred, N)
E = Y_pred - Y_true_OH
grad_Theta = (E @ X_aug.T) / N
Theta = Theta - lr * grad_Theta
if epoch in EPOCH_MILESTONES:
W_curr = Theta[:, 1]
b_curr = Theta[:, 0]
P_x8 = get_prediction_x8(Theta, X_aug)
RESULTS.append({
'Epoch': epoch,
'Trọng số W': f"({W_curr[0]:.2f}, {W_curr[1]:.2f}, {W_curr[2]:.2f})",
'Độ chệch b': f"({b_curr[0]:.2f}, {b_curr[1]:.2f}, {b_curr[2]:.2f})",
'Mất mát (CE)': Loss,
'Dự đoán y^ (x=8.0)': P_x8
})
df = pd.DataFrame(RESULTS)
df['Mất mát (CE)'] = df['Mất mát (CE)'].apply(lambda x: f"{x:.4f}")
df['Dự đoán y^ (x=8.0)'] = df['Dự đoán y^ (x=8.0)'].apply(lambda x: f"{x:.4f}")
print("\n" + "="*80)
print("Bảng: Tóm tắt quá trình huấn luyện Softmax (Mô phỏng 10000 Epochs)")
print("="*80)
print(df.to_markdown(index=False, numalign="center", stralign="center"))
| Epoch | Trọng số W | Độ chệch b | Mất mát (CE) | Dự đoán $\hat{y}$ (x=8.0) |
|---|---|---|---|---|
| 0 | (0.00, 0.00, 0.00) | (0.00, 0.00, 0.00) | 1.0986 | 0.3333 |
| 1 | (-0.19, 0.01, 0.19) | (0.00, 0.00, 0.00) | 1.0986 | 0.7829 |
| 10 | (-0.16, 0.11, 0.05) | (0.30, 0.01, -0.30) | 1.0685 | 0.2845 |
| 500 | (-1.30, 0.19, 1.11) | (4.88, 0.28, -5.16) | 0.2917 | 0.8780 |
| 2000 | (-2.34, 0.28, 2.06) | (9.14, 0.88, -10.02) | 0.1343 | 0.9664 |
| 10000 | (-4.08, 0.36, 3.71) | (16.40, 2.19, -18.59) | 0.0388 | 0.9975 |
Bảng 2. Kết quả huấn luyện Softmax Regression
Nhận xét kết quả huấn luyện qua các epoch:
- Ma trận trọng số W: Các trọng số phân hóa rõ rệt. $w_0$ ('Giống A') trở nên rất âm, $w_2$ ('Giống C') trở nên rất dương. Điều này cho thấy mô hình đã học được rằng x (chiều rộng) tăng thì điểm (logit) cho lớp 'Giống A' giảm và điểm cho lớp 'Giống C' tăng.
- Vector độ chệch b: Các độ chệch $b_0$, $b_1$, $b_2$ cũng phân tách để tìm ra các ranh giới quyết định. $b_0$ dương và $b_2$ âm cho thấy ngay cả khi x = 0, mô hình cũng ưu tiên 'Giống A' ($b_0$ lớn nhất) và chỉ khi x đủ lớn (để bù lại $b_2$ âm) thì mới dự đoán 'Giống C'.
- Mất mát (CE): Giảm từ 1.0986 (dự đoán ngẫu nhiên) xuống còn 0.0388. Đây là bằng chứng rõ ràng nhất cho thấy mô hình đang học tốt và hội tụ.
- Dự đoán $\hat{y}$ (cho x = 8.0): Dự đoán cho mẫu hoa có x = 8.0 (nhãn y = 2) tăng từ 33.3% lên 78.3% (sau 1 epoch), và hội tụ về ≈ 0.9975 (99.75%), ngày càng tự tin hơn về nhãn thực tế y = 2
Chưa có bình luận nào. Hãy là người đầu tiên!