Hồi quy tuyến tính (Linear Regression): Viên gạch đầu tiên trên con đường Machine Learning
Trong lĩnh vực Trí tuệ nhân tạo và Khoa học dữ liệu, trước khi tiếp cận các thuật toán phức tạp, việc nắm vững những kiến thức nền tảng là điều tất yếu. Hồi quy tuyến tính (Linear Regression) chính là một trong những thuật toán quan trọng nhất mà mọi người học Machine Learning cần phải thành thạo. Bài viết này cung cấp một cẩm nang chi tiết về thuật toán kinh điển này, từ lý thuyết đến thực hành.
1. Giới thiệu
Hồi quy tuyến tính là một thuật toán học có giám sát (supervised learning) được sử dụng để dự đoán một giá trị số dựa trên các thông tin đầu vào. Hãy nghĩ về nó như một cách để máy tính "học" mối liên hệ giữa nguyên nhân và kết quả từ những ví dụ có sẵn.
Ví dụ thực tế dễ hiểu: Bạn muốn biết giá một căn nhà sẽ là bao nhiêu. Bạn có thông tin về diện tích nhà. Bạn cũng có dữ liệu về nhiều căn nhà khác với diện tích và giá của chúng. Hồi quy tuyến tính sẽ giúp bạn tìm ra công thức để tính giá nhà dựa trên diện tích. Một ví dụ khác là dự đoán doanh số bán hàng dựa trên số tiền bạn bỏ ra cho quảng cáo.
Điều đặc biệt của thuật toán này là nó giả định rằng có một "đường thẳng" nào đó có thể mô tả được mối quan hệ giữa cái bạn biết (diện tích nhà) và cái bạn muốn dự đoán (giá nhà). Mục tiêu của chúng ta là tìm ra đường thẳng đó.
Để hình dung đơn giản hơn, bạn có thể nghĩ về hồi quy tuyến tính như việc tìm ra một công thức toán học cơ bản nhất: $y = ax + b$. Trong đó, $x$ là thông tin bạn có (ví dụ: diện tích nhà), $y$ là thứ bạn muốn dự đoán (ví dụ: giá nhà), còn $a$ và $b$ là những con số mà máy tính cần phải tự "học" từ dữ liệu. Một khi máy đã tìm ra được $a$ và $b$, bạn chỉ cần thay số vào công thức là có thể dự đoán giá cho bất kỳ căn nhà nào.
2. Cơ sở lý thuyết
2.1. Ý tưởng nền tảng
Hồi quy tuyến tính hoạt động dựa trên một ý tưởng đơn giản: khi một thứ thay đổi, thứ kia cũng thay đổi theo một tỷ lệ nhất định và có thể dự đoán được. Nói cách khác, nếu bạn vẽ các điểm dữ liệu lên giấy (hoặc trên màn hình), bạn có thể kẻ một đường thẳng đi qua chúng sao cho đường thẳng đó "đại diện" tốt nhất cho xu hướng của dữ liệu.
Hãy tưởng tượng bạn là người bán nhà. Qua nhiều năm kinh nghiệm, bạn nhận thấy một quy luật: mỗi khi diện tích nhà tăng thêm mười mét vuông, giá nhà thường tăng thêm khoảng năm mươi triệu đồng. Đây chính là một mối quan hệ "tuyến tính" - tức là có thể biểu diễn bằng đường thẳng. Hồi quy tuyến tính giúp chúng ta tìm ra con số chính xác của mối quan hệ này không phải bằng cảm tính, mà bằng phép tính toán từ dữ liệu thực tế.
Nhiệm vụ của chúng ta là tìm ra đường thẳng nào "khớp" nhất với tất cả các điểm dữ liệu chúng ta có. "Khớp nhất" ở đây nghĩa là tổng khoảng cách từ các điểm đến đường thẳng là nhỏ nhất có thể.
2.2. Mô hình toán học
Hồi quy tuyến tính đơn (Simple Linear Regression)
Đây là trường hợp đơn giản nhất khi chúng ta chỉ có một yếu tố ảnh hưởng (ví dụ: chỉ có diện tích) để dự đoán kết quả (giá nhà). Công thức toán học trông như thế này:
$$ Y = \beta_0 + \beta_1 X + \epsilon $$
Đừng lo nếu bạn thấy các ký hiệu lạ. Hãy để tôi giải thích từng phần một cách dễ hiểu:
- $Y$ là cái bạn muốn dự đoán, chẳng hạn như giá nhà
- $X$ là thông tin bạn có sẵn, chẳng hạn như diện tích nhà
- $\beta_0$ (đọc là "beta không") là giá trị khởi điểm. Nói cách khác, nếu diện tích bằng không (tức $X = 0$), thì giá trị của $Y$ sẽ là bao nhiêu. Bạn có thể hiểu nó như "giá cơ bản" hay "điểm xuất phát"
- $\beta_1$ (đọc là "beta một") cho biết khi $X$ tăng thêm một đơn vị thì $Y$ sẽ tăng thêm bao nhiêu. Ví dụ: khi diện tích tăng thêm một mét vuông thì giá nhà tăng thêm bao nhiêu triệu
- $\epsilon$ (đọc là "epsilon") là phần "sai số ngẫu nhiên". Trong thực tế, không có công thức nào hoàn hảo một trăm phần trăm. Luôn có những yếu tố nhỏ chúng ta không tính đến, khiến giá trị thực tế lệch một chút so với dự đoán. Đó chính là $\epsilon$
Ví dụ cụ thể để bạn hình dung rõ hơn: Giả sử sau khi phân tích dữ liệu, máy tính tìm ra $\beta_0 = 100$ triệu và $\beta_1 = 5$ triệu. Điều này có nghĩa là:
- Một căn nhà có giá khởi điểm là một trăm triệu đồng (ngay cả khi diện tích rất nhỏ)
- Mỗi mét vuông thêm vào sẽ làm tăng giá thêm năm triệu đồng
- Vậy một căn nhà rộng 50 mét vuông sẽ có giá: 100 + (5 × 50) = 350 triệu đồng
Hồi quy tuyến tính bội (Multiple Linear Regression)
Trong cuộc sống thực, giá nhà không chỉ phụ thuộc vào diện tích. Nó còn phụ thuộc vào nhiều thứ khác như số phòng ngủ, khoảng cách đến trung tâm thành phố, tuổi của ngôi nhà, và nhiều yếu tố khác. Khi chúng ta muốn tính đến nhiều yếu tố cùng lúc, chúng ta sử dụng hồi quy tuyến tính bội.
Công thức sẽ được mở rộng thành:
$$ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_k X_k + \epsilon $$
Bây giờ thay vì chỉ có một $X$, chúng ta có nhiều $X$ khác nhau:
- $X_1$ có thể là diện tích
- $X_2$ có thể là số phòng ngủ
- $X_3$ có thể là khoảng cách đến trung tâm
- Và cứ thế tiếp tục...
Mỗi yếu tố sẽ có hệ số riêng của nó ($\beta_1$, $\beta_2$, $\beta_3$...). Các hệ số này cho biết mỗi yếu tố ảnh hưởng đến kết quả nhiều như thế nào, khi tất cả các yếu tố khác được giữ cố định.
Ví dụ thực tế: Giả sử công thức dự đoán giá nhà của bạn là:
- Giá = 50 triệu + (5 triệu × diện tích) + (20 triệu × số phòng ngủ) - (1 triệu × khoảng cách đến trung tâm tính bằng km)
Điều này có nghĩa là:
- Mỗi mét vuông làm tăng giá năm triệu
- Mỗi phòng ngủ thêm làm tăng giá hai mươi triệu
- Mỗi km xa trung tâm làm giảm giá một triệu
2.3. Các giả định cơ bản
Để hồi quy tuyến tính hoạt động tốt và cho kết quả đáng tin cậy, dữ liệu của bạn cần thỏa mãn một số điều kiện nhất định. Hãy nghĩ về chúng như những "quy tắc chơi" mà dữ liệu cần tuân theo:
1. Tính tuyến tính - Mối quan hệ phải là đường thẳng
Điều này có nghĩa là khi một thứ tăng lên, thứ kia cũng phải tăng hoặc giảm theo một tỷ lệ không đổi. Hãy tưởng tượng bạn đang leo cầu thang - mỗi bậc thang đều có độ cao giống nhau. Đó là mối quan hệ tuyến tính. Nhưng nếu bạn leo núi, nơi mà càng lên cao càng dốc hơn, thì đó không phải là tuyến tính nữa.
Ví dụ vi phạm: Thu nhập của một người thường không tăng đều theo tuổi. Người trẻ thường tăng lương nhanh, đến trung niên ổn định, và có thể giảm khi về hưu. Đây là mối quan hệ phi tuyến, và hồi quy tuyến tính sẽ không mô tả tốt được.
2. Trung bình sai số bằng không - Không thiên vị về một phía
Điều này có nghĩa là mô hình không được "nghiêng" về một phía nào đó một cách hệ thống. Đôi khi mô hình dự đoán cao hơn thực tế, đôi khi thấp hơn, nhưng trung bình các sai lầm này phải triệt tiêu lẫn nhau.
Hãy tưởng tượng bạn đang ném phi tiêu vào bia. Nếu bạn luôn luôn ném lệch sang trái, có nghĩa là bạn có "sai lệch hệ thống". Nhưng nếu đôi khi bạn ném lệch trái, đôi khi lệch phải, và trung bình thì bạn trúng đích, thì không có sai lệch hệ thống.
3. Phương sai không đổi - Độ sai lệch không nên thay đổi
Điều này có nghĩa là mức độ "sai" của các dự đoán nên giống nhau ở mọi điểm. Bạn không muốn tình huống mô hình dự đoán rất chính xác với nhà nhỏ nhưng lại sai bét với nhà lớn.
Ví dụ minh họa: Hãy tưởng tượng bạn đang đo nhiệt độ bằng nhiệt kế. Nếu nhiệt kế này đo chính xác ở nhiệt độ thấp nhưng càng nóng càng sai nhiều, thì nó vi phạm giả định này. Một nhiệt kế tốt nên có độ sai số tương đương ở mọi nhiệt độ.
Tham khảo: Phương sai và độ lệch chuẩn
4. Độc lập - Các quan sát không ảnh hưởng lẫn nhau
Giá trị này không nên phụ thuộc vào giá trị khác trong dữ liệu. Mỗi điểm dữ liệu nên là một "sự kiện" độc lập.
Ví dụ vi phạm: Nếu bạn đo nhiệt độ mỗi phút trong một ngày, nhiệt độ ở phút này sẽ rất giống nhiệt độ ở phút tiếp theo. Chúng không độc lập với nhau. Đây là vấn đề trong dữ liệu chuỗi thời gian.
5. Phân phối chuẩn - Sai số nên theo "hình chuông"
Phần sai lệch (những lần dự đoán sai) nên phân bố theo dạng "hình chuông" đối xứng. Điều này có nghĩa là hầu hết các dự đoán sai một chút, và rất ít dự đoán sai quá nhiều.
Hãy nghĩ về điểm kiểm tra của một lớp học: Hầu hết học sinh đạt điểm trung bình, một số ít giỏi đặc biệt, và một số ít kém đặc biệt. Đây là phân phối chuẩn.
Khi những "quy tắc" này bị vi phạm, mô hình có thể cho ra kết quả sai lệch hoặc không đáng tin cậy. Vì vậy, việc kiểm tra các điều kiện này trước khi tin tưởng vào mô hình là rất quan trọng.
Tham khảo: Phân phối chuẩn
3. Công thức và lý giải
3.1. Bình phương tối thiểu thông thường (Ordinary Least Squares - OLS)
Đây là phương pháp phổ biến nhất để tìm ra đường thẳng phù hợp nhất. Tên gọi nghe có vẻ phức tạp, nhưng ý tưởng lại rất đơn giản.
Hãy tưởng tượng bạn có một tờ giấy với nhiều chấm đỏ (đại diện cho dữ liệu thực tế). Bạn muốn kẻ một đường thẳng qua những chấm đó. Nhưng kẻ đường nào? Có vô số cách kẻ! Phương pháp OLS giúp bạn chọn đường "tốt nhất".
Cách nó hoạt động như sau:
1. Với mỗi đường thẳng có thể có, bạn đo khoảng cách từ mỗi điểm dữ liệu đến đường thẳng đó (khoảng cách theo chiều dọc)
2. Bạn "bình phương" các khoảng cách này - tức là nhân chúng với chính nó. Tại sao? Bởi vì chúng ta muốn mọi khoảng cách đều là số dương (kẻo các khoảng cách dương và âm sẽ triệt tiêu nhau), và chúng ta muốn "phạt" các điểm ở xa hơn
3. Bạn cộng tất cả các "bình phương khoảng cách" này lại
4. Đường thẳng tốt nhất là đường làm cho tổng này nhỏ nhất
Công thức toán học biểu diễn ý tưởng này là:
$$ \text{RSS} = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$
Trong đó:
- $y_i$ là giá trị thực tế của điểm thứ $i$
- $\hat{y}_i$ là giá trị mà đường thẳng dự đoán cho điểm thứ $i$
- $(y_i - \hat{y}_i)$ là khoảng cách giữa giá trị thực và giá trị dự đoán
- Bình phương rồi cộng tất cả lại cho chúng ta "tổng bình phương sai lệch"
Đường thẳng tốt nhất là đường làm cho RSS này nhỏ nhất có thể.
3.2. Công thức ước lượng
Đối với hồi quy tuyến tính đơn:
Khi chỉ có một biến đầu vào, có những công thức đơn giản để tính toán. Đầu tiên, chúng ta tính độ dốc của đường thẳng:
$$ b_1 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2} $$
Công thức này trông phức tạp, nhưng ý tưởng lại đơn giản. Hãy để tôi giải thích từng phần:
- $\bar{x}$ (đọc là "x bar" hoặc "x gạch") là giá trị trung bình của tất cả các giá trị $x$. Ví dụ: nếu bạn có diện tích của 10 căn nhà, $\bar{x}$ là diện tích trung bình của chúng
- $\bar{y}$ là giá trị trung bình của tất cả các giá trị $y$ (ví dụ: giá trung bình của 10 căn nhà)
- $(x_i - \bar{x})$ đo lường một giá trị $x$ cụ thể lệch so với trung bình bao nhiêu
- $(y_i - \bar{y})$ đo lường một giá trị $y$ cụ thể lệch so với trung bình bao nhiêu
- Khi nhân hai cái này với nhau và cộng lại, chúng ta đo được "mức độ cùng biến thiên" - tức là khi $x$ tăng thì $y$ có xu hướng tăng theo không
- Chia cho tổng bình phương độ lệch của $x$ để "chuẩn hóa" con số này
Kết quả $b_1$ cho chúng ta biết: khi $x$ tăng một đơn vị, $y$ tăng $b_1$ đơn vị.
Sau khi có độ dốc $b_1$, chúng ta tính điểm cắt (điểm mà đường thẳng cắt trục dọc):
$$ b_0 = \bar{y} - b_1\bar{x} $$
Công thức này đảm bảo rằng đường thẳng đi qua điểm trung tâm của dữ liệu (điểm có tọa độ là giá trị trung bình của $x$ và $y$).
Đối với hồi quy tuyến tính bội:
Khi có nhiều biến, việc tính toán bằng tay trở nên rất phức tạp. Thực tế, chúng ta sử dụng máy tính để xử lý điều này. Máy tính sử dụng công cụ toán học gọi là "ma trận" để giải quyết vấn đề một cách hiệu quả.
Bạn không cần phải hiểu chi tiết toán học phía sau (trừ khi bạn muốn). Điều quan trọng là bạn hiểu rằng máy tính đang làm điều tương tự: tìm các hệ số sao cho tổng bình phương sai lệch là nhỏ nhất.
3.3. Đánh giá chất lượng mô hình
Sau khi xây dựng mô hình, câu hỏi quan trọng nhất là: "Mô hình này tốt không?". Có nhiều cách để trả lời câu hỏi này.
Hệ số xác định $R^2$ (R-squared)
Đây là chỉ số phổ biến nhất để đánh giá mô hình. $R^2$ cho bạn biết mô hình của bạn "giải thích" được bao nhiêu phần trăm sự thay đổi trong dữ liệu.
Công thức:
$R^2 = 1 - \frac{\text{SS}_{\text{res}}}{\text{SS}_{\text{tot}}} = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}{\sum_{i=1}^{n}(y_i - \bar{y})^2}$
Hãy để tôi giải thích bằng ngôn ngữ đơn giản:
- Phần tử số (trên) là tổng bình phương sai lệch giữa giá trị thực và giá trị dự đoán của mô hình - tức là "phần mô hình dự đoán sai"
- Phần mẫu số (dưới) là tổng bình phương sai lệch giữa giá trị thực và giá trị trung bình - tức là "tổng độ biến thiên trong dữ liệu"
- Chia hai cái này cho nhau, ta được tỷ lệ "phần dự đoán sai" so với "tổng độ biến thiên"
- Lấy 1 trừ đi cái đó, ta được tỷ lệ "phần dự đoán đúng"
Giá trị $R^2$ luôn nằm giữa 0 và 1:
- $R^2 = 0$ nghĩa là mô hình của bạn hoàn toàn vô dụng, không dự đoán được gì cả (tệ như việc bạn chỉ đoán mò)
- $R^2 = 1$ nghĩa là mô hình của bạn hoàn hảo, dự đoán chính xác một trăm phần trăm (điều này hầu như không bao giờ xảy ra trong thực tế)
- $R^2 = 0.7$ nghĩa là mô hình giải thích được bảy mươi phần trăm sự thay đổi trong dữ liệu - đây là kết quả khá tốt trong nhiều trường hợp thực tế
Tuy nhiên, cần lưu ý: $R^2$ cao không phải lúc nào cũng có nghĩa là mô hình tốt. Đôi khi mô hình "ghi nhớ" quá kỹ dữ liệu huấn luyện (hiện tượng overfitting) và sẽ hoạt động kém với dữ liệu mới.
$R^2$ hiệu chỉnh (Adjusted $R^2$)
Có một vấn đề với $R^2$ thông thường: mỗi khi bạn thêm một biến mới vào mô hình, $R^2$ luôn tăng lên (hoặc ít nhất là không giảm), ngay cả khi biến đó hoàn toàn vô nghĩa. Điều này giống như việc một học sinh được cộng điểm mỗi khi làm thêm bài tập, bất kể bài tập đó đúng hay sai.
$R^2$ hiệu chỉnh khắc phục vấn đề này bằng cách "phạt" mô hình khi bạn thêm quá nhiều biến:
$R^2_{\text{adj}} = 1 - \frac{(1-R^2)(n-1)}{n-k-1}$
Trong đó $n$ là số điểm dữ liệu và $k$ là số biến đầu vào. Nếu một biến mới không thực sự giúp ích nhiều cho mô hình, $R^2$ hiệu chỉnh có thể giảm xuống, báo hiệu cho bạn biết rằng không nên thêm biến đó.
Tham khảo thêm về chỉ số R: Corporate Finance Institute: R-Squared – Data Science
Sai số bình phương trung bình (MSE và RMSE)
Hai chỉ số này đo lường "mức độ sai trung bình" của các dự đoán:
$\text{MSE} = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2$
MSE (Mean Squared Error) tính trung bình bình phương của các sai lệch. Vì có bình phương, nó "phạt" nặng những dự đoán sai quá xa.
$\text{RMSE} = \sqrt{\text{MSE}} = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}$
RMSE (Root Mean Squared Error) là căn bậc hai của MSE. Ưu điểm của nó là có cùng đơn vị với dữ liệu gốc, nên dễ hiểu hơn.
Ví dụ: Nếu bạn dự đoán giá nhà và RMSE = 50 triệu, có nghĩa là trung bình các dự đoán của bạn sai khoảng 50 triệu đồng. Bạn có thể dễ dàng đánh giá 50 triệu là nhiều hay ít dựa trên giá nhà thực tế.
Kiểm định F (F-test)
Kiểm định F giúp trả lời câu hỏi tổng quát: "Mô hình này có thực sự hữu ích không, hay chỉ là may mắn?".
Nó kiểm tra giả thuyết:
- Giả thuyết không (H₀): Tất cả các biến đầu vào đều vô dụng, không giúp dự đoán được gì
- Giả thuyết đối (H₁): Ít nhất một biến đầu vào có ích
Nếu giá trị F lớn và p-value nhỏ (thường nhỏ hơn 0.05), chúng ta có thể tự tin rằng mô hình thực sự có ý nghĩa, không phải do ngẫu nhiên.
Hãy nghĩ về nó như một bằng chứng toán học rằng mô hình của bạn không phải là "đoán mò".
Kiểm định t (t-test)
Trong khi kiểm định F đánh giá toàn bộ mô hình, kiểm định t đánh giá từng biến riêng lẻ. Nó trả lời câu hỏi: "Biến cụ thể này có thực sự quan trọng không?".
Đối với mỗi biến đầu vào, kiểm định t kiểm tra:
- Giả thuyết không (H₀): Biến này không có tác động gì
- Giả thuyết đối (H₁): Biến này có tác động
Nếu giá trị t lớn và p-value nhỏ, có nghĩa là biến đó thực sự có đóng góp quan trọng. Nếu không, bạn có thể cân nhắc loại bỏ biến đó ra khỏi mô hình.
Link tham khảo chi tiết về các cách đánh giá: Viblo: Đánh giá model trong Machine Learning
4. Triển khai thực tế
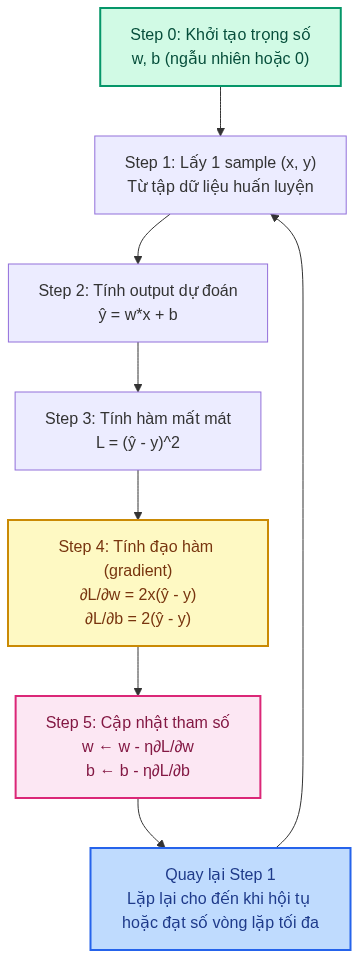
Lưu đồ thuật toán Linear Regression
4.1. Bài toán minh họa
Chúng ta sẽ xây dựng một mô hình thực tế để dự đoán lượng điện tiêu thụ dựa trên nhiệt độ. Đây là một bài toán có ý nghĩa thực tế: khi trời nóng hơn, người ta bật điều hòa nhiều hơn, do đó tiêu thụ điện tăng lên.
Dữ liệu quan sát:
| Nhiệt độ (°C) | Điện năng tiêu thụ (kWh/ngày) |
|---|---|
| 15 | 220 |
| 18 | 250 |
| 20 | 270 |
| 23 | 300 |
| 25 | 340 |
| 27 | 370 |
| 30 | 410 |
| 32 | 450 |
| 35 | 490 |
| 38 | 520 |
4.2. Quy trình thực hiện
Xây dựng mô hình hồi quy tuyến tính giống như dạy một em bé học cách ước tính. Chúng ta sẽ đi qua từng bước một cách chi tiết:
Bước 1: Khởi tạo tham số
Trước khi bắt đầu, chúng ta cần cho mô hình một "phỏng đoán ban đầu". Chúng ta có hai tham số cần khởi tạo:
- $w$ (weight - trọng số): Đây là độ dốc của đường thẳng, cho biết khi nhiệt độ tăng một độ thì điện năng tiêu thụ tăng bao nhiêu
- $b$ (bias - độ lệch): Đây là điểm khởi đầu, cho biết khi nhiệt độ bằng không thì điện năng tiêu thụ là bao nhiêu
Chúng ta thường khởi tạo $w$ với một số ngẫu nhiên rất nhỏ gần 0, và $b$ bằng 0. Tại sao lại như vậy? Vì nếu chúng ta bắt đầu với các số quá lớn, các dự đoán ban đầu sẽ sai quá xa, khiến quá trình học trở nên khó khăn. Hãy nghĩ về nó như việc điều chỉnh âm lượng - bạn luôn muốn bắt đầu từ mức thấp rồi tăng dần, thay vì bật ngay ở mức tối đa.
Bước 2: Tính giá trị dự đoán
Bây giờ với mỗi điểm dữ liệu (ví dụ: nhiệt độ 25°C), chúng ta sử dụng công thức để dự đoán điện năng tiêu thụ:
$\hat{y} = wx + b$
Ví dụ: nếu $w = 10$ và $b = 100$, và nhiệt độ $x = 25$, thì dự đoán của chúng ta là:
$\hat{y} = 10 \times 25 + 100 = 350$ kWh/ngày
Bước 3: Tính độ lỗi (Loss)
Giả sử giá trị thực tế là 340 kWh/ngày, nhưng chúng ta dự đoán 350. Chúng ta đã sai 10 kWh. Để đo lường độ sai này một cách toán học, chúng ta tính:
$L = (\hat{y} - y)^2 = (350 - 340)^2 = 100$
Tại sao lại bình phương? Có hai lý do:
1. Để tất cả các sai số đều là số dương (kẻo sai +10 và sai -10 sẽ triệt tiêu nhau)
2. Để "phạt" nặng hơn những dự đoán sai quá xa
Bước 4: Tính gradient (độ dốc của hàm lỗi)
Đây là phần hơi khó hiểu nhưng cực kỳ quan trọng. Gradient cho chúng ta biết cần phải điều chỉnh các tham số theo hướng nào và mạnh yếu ra sao.
Hãy tưởng tượng bạn đang đứng trên một ngọn đồi trong màn sương mù, không nhìn thấy gì. Bạn muốn xuống đến chân đồi (nơi độ lỗi nhỏ nhất). Bạn không biết đi về hướng nào, nhưng bạn có thể cảm nhận được độ dốc dưới chân mình. Gradient chính là "độ dốc" đó - nó chỉ cho bạn biết nên đi theo hướng nào.
Công thức tính gradient:
$$ \frac{\partial L}{\partial w} = 2x(\hat{y} - y) $$
$$ \frac{\partial L}{\partial b} = 2(\hat{y} - y) $$
Đừng lo về ký hiệu $\frac{\partial}{\partial}$ (đọc là "đạo hàm riêng"). Đơn giản nó chỉ đo lường "nếu tôi thay đổi $w$ một chút, thì độ lỗi $L$ sẽ thay đổi bao nhiêu".
Bước 5: Cập nhật tham số
Bây giờ chúng ta biết hướng cần điều chỉnh rồi, chúng ta thực hiện điều chỉnh:
$$ w \leftarrow w - \eta \frac{\partial L}{\partial w} $$
$$ b \leftarrow b - \eta \frac{\partial L}{\partial b} $$
Ký hiệu $\eta$ (đọc là "eta") gọi là "learning rate" (tốc độ học). Nó quyết định chúng ta "nhảy" một bước lớn hay nhỏ mỗi lần điều chỉnh.
- Nếu learning rate quá lớn: Chúng ta có thể "nhảy" quá đích, giống như khi bạn muốn điều chỉnh âm lượng chút xíu nhưng lại vặn quá mạnh
- Nếu learning rate quá nhỏ: Chúng ta sẽ học rất chậm, mất nhiều thời gian
Thông thường, learning rate được chọn trong khoảng 0.001 đến 0.1, tùy bài toán.
Bước 6: Lặp lại quá trình
Chúng ta không chỉ làm một lần rồi dừng. Chúng ta lặp lại quá trình này hàng trăm, thậm chí hàng nghìn lần (gọi là các "epoch"). Mỗi lần lặp, mô hình học được thêm một chút, dần dần tiến gần đến đáp án tốt nhất.
Quá trình này giống như việc bạn luyện tập một kỹ năng: lần đầu tiên bạn làm rất tệ, nhưng mỗi lần thử, bạn cải thiện một chút, cho đến khi đạt được trình độ cao.
4.3. Triển khai code Python
Link code mẫu: Link code
Import thư viện cần thiết
import numpy as np
import matplotlib.pyplot as plt
import random
Ba thư viện này giúp chúng ta:
- numpy: Xử lý các phép tính toán số học nhanh chóng
- matplotlib.pyplot: Vẽ biểu đồ để chúng ta có thể "nhìn thấy" dữ liệu và kết quả
- random: Tạo số ngẫu nhiên cho việc khởi tạo tham số ban đầu
Triển khai các hàm
# Khởi tạo tham số ban đầu
# w với giá trị ngẫu nhiên nhỏ gần 0, và b bằng 0
def initialize_params():
w = random.gauss(mu=0.0, sigma=0.01) # Số ngẫu nhiên từ phân phối chuẩn
b = 0 # Bắt đầu từ 0
return w, b
# Hàm dự đoán: tính y_hat = w*x + b
def predict(x, w, b):
return x * w + b
# Hàm tính độ lỗi: bình phương khoảng cách giữa dự đoán và thực tế
def compute_loss(y_hat, y):
return (y_hat - y) ** 2
# Hàm tính gradient theo w
# Cho biết cần thay đổi w theo hướng nào và mức độ ra sao
def compute_gradient_w(x, y, y_hat):
return 2 * x * (y_hat - y)
# Hàm tính gradient theo b
# Cho biết cần thay đổi b theo hướng nào và mức độ ra sao
def compute_gradient_b(y, y_hat):
return 2 * (y_hat - y)
# Hàm cập nhật trọng số w dựa trên gradient
def update_weight_w(w, dl_dw, lr):
return w - lr * dl_dw # Đi ngược hướng gradient để giảm lỗi
# Hàm cập nhật trọng số b dựa trên gradient
def update_weight_b(b, dl_db, lr):
return b - lr * dl_db # Đi ngược hướng gradient để giảm lỗi
# Hàm chính: huấn luyện mô hình
def implement_linear_regression(X_data, y_data, epoch_max=50, lr=0.001):
losses = [] # Danh sách lưu độ lỗi qua từng bước, để theo dõi quá trình học
w, b = initialize_params() # Khởi tạo tham số ban đầu
N = len(y_data) # Số lượng điểm dữ liệu
# Lặp qua nhiều epoch (mỗi epoch là một lần duyệt qua toàn bộ dữ liệu)
for epoch in range(epoch_max):
# Với mỗi điểm dữ liệu
for i in range(N):
x = X_data[i] # Lấy giá trị đầu vào (nhiệt độ)
y = y_data[i] # Lấy giá trị thực tế (điện năng)
# Bước 2: Dự đoán
y_hat = predict(x, w, b)
# Bước 3: Tính lỗi
loss = compute_loss(y_hat, y)
# Bước 4: Tính gradient (hướng điều chỉnh)
dl_dw = compute_gradient_w(x, y, y_hat)
dl_db = compute_gradient_b(y, y_hat)
# Bước 5: Cập nhật tham số
w = update_weight_w(w, dl_dw, lr)
b = update_weight_b(b, dl_db, lr)
# Lưu lại độ lỗi để sau này vẽ biểu đồ
losses.append(loss)
return (w, b, losses)
# Dữ liệu của chúng ta: nhiệt độ và điện năng tiêu thụ
X = [15, 18, 20, 23, 25, 27, 30, 32, 35, 38]
y = [220, 250, 270, 300, 340, 370, 410, 450, 490, 520]
# Huấn luyện mô hình
(w, b, losses) = implement_linear_regression(X, y)
# Sau khi huấn luyện, w và b chính là công thức chúng ta cần
# Bây giờ có thể dự đoán điện năng cho bất kỳ nhiệt độ nào
Sau khi chạy code này, bạn sẽ có được hai giá trị $w$ và $b$. Đó chính là công thức dự đoán của bạn! Bạn có thể dùng nó để dự đoán mức tiêu thụ điện ở bất kỳ nhiệt độ nào.
Dự đoán
# Sau khi huấn luyện, w và b chính là công thức chúng ta cần
print(f"Trọng số học được (w): {w:.4f}")
print(f"Độ chặn (b): {b:.4f}")
# Ví dụ: dự đoán điện năng tiêu thụ cho 28°C và 40°C
X_new = [28, 40]
for temp in X_new:
y_pred = predict(temp, w, b)
print(f"Nhiệt độ {temp}°C → Dự đoán điện năng: {y_pred:.2f} kWh/ngày")
# Vẽ biểu đồ kết quả
# Tạo mảng điểm dự đoán trên toàn miền nhiệt độ
X_line = np.linspace(min(X), max(X), 100)
Y_line = [predict(x, w, b) for x in X_line]
plt.figure(figsize=(8,5))
plt.scatter(X, y, color='blue', label='Dữ liệu thực tế')
plt.plot(X_line, Y_line, color='red', label='Đường hồi quy (Linear Regression)')
plt.xlabel('Nhiệt độ (°C)')
plt.ylabel('Điện năng tiêu thụ (kWh/ngày)')
plt.title('Biểu đồ Hồi quy tuyến tính dự đoán điện năng tiêu thụ')
plt.legend()
plt.grid(True)
plt.show()
Đầu ra của code dự đoán:
Trọng số học được (w): 14.4410
Độ chặn (b): -0.1435
Nhiệt độ 28°C → Dự đoán điện năng: 404.21 kWh/ngày
Nhiệt độ 40°C → Dự đoán điện năng: 577.50 kWh/ngày
Biểu đồ hiển thị có dạng dưới đây

4.4. Triển khai với Scikit-learn
Code ở trên giúp bạn hiểu cách thuật toán hoạt động từng bước một. Nhưng trong thực tế, chúng ta thường sử dụng thư viện có sẵn để tiết kiệm thời gian. Dưới đây là cách sử dụng Scikit-learn - một thư viện phổ biến nhất cho Machine Learning trong Python:
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
import numpy as np
import matplotlib.pyplot as plt
# Chuẩn bị dữ liệu
# reshape(-1, 1) chuyển dữ liệu thành dạng cột, vì sklearn yêu cầu định dạng này
X = np.array([15, 18, 20, 23, 25, 27, 30, 32, 35, 38]).reshape(-1, 1)
y = np.array([220, 250, 270, 300, 340, 370, 410, 450, 490, 520])
# Tạo mô hình và huấn luyện - chỉ cần 2 dòng!
model = LinearRegression()
model.fit(X, y) # fit = "làm khớp" mô hình với dữ liệu
# Lấy các tham số đã học được
w = model.coef_[0] # Hệ số góc (độ dốc)
b = model.intercept_ # Hệ số chặn (điểm bắt đầu)
print(f"Hệ số góc (w): {w:.2f}")
print(f"Hệ số chặn (b): {b:.2f}")
print(f"Phương trình: y = {w:.2f}x + {b:.2f}")
# Dự đoán cho tất cả các điểm dữ liệu
y_pred = model.predict(X)
# Đánh giá mô hình xem nó tốt đến đâu
r2 = r2_score(y, y_pred) # R² score: % biến thiên được giải thích
mse = mean_squared_error(y, y_pred) # Trung bình bình phương sai số
rmse = np.sqrt(mse) # Căn bậc hai của MSE
print(f"\nĐánh giá mô hình:")
print(f"R² Score: {r2:.4f}")
print(f"MSE: {mse:.2f}")
print(f"RMSE: {rmse:.2f}")
# Dự đoán cho giá trị mới chưa từng thấy
new_temp = np.array([[28], [33]]) # Nhiệt độ 28°C và 33°C
new_pred = model.predict(new_temp)
print(f"\nDự đoán điện năng tiêu thụ:")
for temp, pred in zip(new_temp.flatten(), new_pred):
print(f"Nhiệt độ {temp}°C: {pred:.2f} kWh/ngày")
# Vẽ biểu đồ để trực quan hóa kết quả
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='Dữ liệu thực tế', s=100)
plt.plot(X, y_pred, color='red', linewidth=2, label='Đường hồi quy')
plt.xlabel('Nhiệt độ (°C)', fontsize=12)
plt.ylabel('Điện năng tiêu thụ (kWh/ngày)', fontsize=12)
plt.title('Hồi quy tuyến tính: Dự đoán tiêu thụ điện theo nhiệt độ', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
Biểu đồ hiển thị có dạng dưới đây

Giải thích kết quả:
Sau khi chạy code, bạn sẽ thấy:
- Hệ số góc (w): Cho biết mỗi độ C tăng thêm sẽ làm tăng bao nhiêu kWh điện
- Hệ số chặn (b): Cho biết mức tiêu thụ điện "cơ bản" khi nhiệt độ gần bằng 0
- R² Score: Một con số từ 0 đến 1. Càng gần 1 nghĩa là mô hình càng tốt
- RMSE: Cho biết trung bình các dự đoán sai khoảng bao nhiêu kWh
Ưu điểm của Scikit-learn:
- Đơn giản: Chỉ cần vài dòng code thay vì hàng chục dòng
- Nhanh: Đã được tối ưu hóa để chạy rất nhanh, kể cả với dữ liệu lớn
- Đầy đủ: Tích hợp sẵn nhiều công cụ đánh giá và trực quan hóa
- Mở rộng dễ dàng: Có thể dễ dàng chuyển sang các mô hình phức tạp hơn như Ridge, Lasso với cú pháp tương tự
5. Kết luận và hạn chế
5.1. Ưu điểm
Hồi quy tuyến tính là một thuật toán nền tảng quan trọng trong Machine Learning với nhiều ưu điểm rõ rệt:
Đơn giản và dễ hiểu: Đây là một trong những thuật toán dễ hiểu nhất trong Machine Learning. Nó hoạt động giống như việc kẻ một đường thẳng qua các điểm dữ liệu - một ý tưởng trực quan mà ai cũng có thể nắm bắt được. Điều này làm cho nó trở thành điểm khởi đầu lý tưởng cho người mới học.
Dễ giải thích: Khi bạn có kết quả, bạn có thể giải thích nó một cách rõ ràng. Ví dụ: "Mỗi mét vuông tăng thêm làm tăng giá nhà 5 triệu đồng" là một câu mọi người đều hiểu được, không cần phải là chuyên gia toán học hay máy tính.
Tính toán nhanh: So với các thuật toán Machine Learning phức tạp khác (như mạng neural sâu), hồi quy tuyến tính chạy rất nhanh, kể cả với dữ liệu lớn.
Nền tảng vững chắc: Hiểu rõ hồi quy tuyến tính giúp bạn dễ dàng tiếp cận các mô hình nâng cao hơn. Nhiều thuật toán phức tạp thực chất là các biến thể hoặc mở rộng của hồi quy tuyến tính.
5.2. Hạn chế
Tuy nhiên, hồi quy tuyến tính không phải là "viên đạn bạc" giải quyết mọi vấn đề. Nó có những hạn chế quan trọng mà bạn cần biết:
Chỉ hoạt động với mối quan hệ đường thẳng
Đây là hạn chế lớn nhất. Mô hình giả định rằng mối quan hệ giữa đầu vào và đầu ra là một đường thẳng. Nhưng trong đời thực, nhiều quan hệ phức tạp hơn thế nhiều.
Ví dụ thực tế: Thu nhập của một người theo độ tuổi thường không phải là đường thẳng. Người trẻ thu nhập thấp, sau đó tăng nhanh khi tích lũy kinh nghiệm, ổn định ở tuổi trung niên, và có thể giảm khi về hưu. Đây là một đường cong, không phải đường thẳng. Nếu bạn ép buộc dùng đường thẳng để mô tả, kết quả sẽ rất tệ.
Dấu hiệu nhận biết: Nếu khi vẽ biểu đồ, bạn thấy các điểm tạo thành một hình cong rõ rệt (như chữ U, hay hình parabol), thì hồi quy tuyến tính không phải là lựa chọn tốt.
Rất nhạy cảm với các điểm dữ liệu lạ (outliers)
Một vài điểm dữ liệu bất thường có thể "kéo lệch" toàn bộ đường thẳng, làm cho mô hình hoạt động kém trên phần lớn dữ liệu bình thường.
Ví dụ minh họa: Tưởng tượng bạn đang phân tích mối quan hệ giữa diện tích và giá nhà. Bỗng nhiên có một căn nhà diện tích 100m² nhưng giá lên đến 50 tỷ (vì nó nằm ngay trung tâm, có view đẹp đặc biệt). Điểm dữ liệu này có thể kéo cả đường thẳng lệch đi, khiến mô hình dự đoán giá cao hơn thực tế cho tất cả các nhà khác.
Cách khắc phục: Trước khi xây dựng mô hình, hãy kiểm tra và xử lý các outliers. Đôi khi chúng là lỗi nhập liệu, đôi khi là trường hợp đặc biệt cần loại bỏ hoặc xử lý riêng.
Vấn đề đa cộng tuyến (Multicollinearity)
Đây là vấn đề phát sinh khi bạn có nhiều biến đầu vào, và một số biến có quan hệ chặt chẽ với nhau.
Ví dụ dễ hiểu: Giả sử bạn dự đoán giá nhà dựa trên: (1) diện tích tính bằng mét vuông, (2) diện tích tính bằng feet vuông. Hai biến này hoàn toàn phụ thuộc vào nhau (vì 1 mét vuông = 10.764 feet vuông). Mô hình sẽ bối rối không biết nên "tin" biến nào, dẫn đến kết quả không ổn định.
Một ví dụ khác: Thu nhập và chi tiêu của một người thường có tương quan mạnh. Nếu bạn dùng cả hai để dự đoán khả năng trả nợ, mô hình có thể hoạt động kém vì không tách bạch được tác động riêng của từng yếu tố.
Dấu hiệu nhận biết: Các hệ số hồi quy thay đổi đáng kể (thậm chí đổi dấu) khi bạn thêm hoặc bớt một biến.
Giả định về phương sai không đổi
Mô hình giả định rằng "độ sai" của dự đoán là như nhau ở mọi mức độ của biến đầu vào. Trong thực tế, điều này không phải lúc nào cũng đúng.
Ví dụ thực tế: Khi dự đoán giá nhà, bạn có thể dự đoán khá chính xác giá của những căn nhà bình dân (sai số khoảng ±50 triệu), nhưng với những biệt thự sang trọng, sai số có thể lên đến ±500 triệu hoặc hơn. Điều này vi phạm giả định "phương sai không đổi".
Hậu quả: Khi giả định này bị vi phạm, các thước đo về độ tin cậy của mô hình (như khoảng tin cậy, kiểm định thống kê) sẽ không chính xác. Bạn có thể nghĩ rằng mô hình đáng tin cậy hơn thực tế, hoặc ngược lại.
5.3. Khuyến nghị sử dụng
Khi nào nên dùng hồi quy tuyến tính:
- Mối quan hệ tuyến tính rõ ràng: Khi vẽ biểu đồ phân tán (scatter plot) và thấy các điểm tạo thành một xu hướng đường thẳng
- Cần khả năng giải thích cao: Khi bạn không chỉ muốn dự đoán mà còn muốn hiểu "tại sao" (ví dụ: báo cáo cho sếp, trình bày cho khách hàng)
- Dữ liệu sạch, ít outliers: Khi dữ liệu đã được làm sạch và không có quá nhiều điểm bất thường
- Cần tốc độ: Khi cần xây dựng và triển khai mô hình nhanh chóng
Khi nào không nên dùng:
- Mối quan hệ phi tuyến rõ rệt: Khi biểu đồ cho thấy đường cong, không phải đường thẳng
- Quá nhiều outliers: Khi dữ liệu có nhiều điểm bất thường không thể xử lý được
- Quan hệ phức tạp: Khi biến đầu ra phụ thuộc vào đầu vào theo cách phức tạp, có nhiều tương tác phi tuyến
Cách cải thiện mô hình:
Nếu bạn muốn tiếp tục sử dụng hồi quy tuyến tính nhưng gặp các vấn đề trên, có một số kỹ thuật:
- Biến đổi dữ liệu: Đôi khi lấy log, căn bậc hai, hoặc bình phương các biến có thể biến mối quan hệ phi tuyến thành tuyến tính
- Thêm các biến tương tác: Ví dụ thêm biến "diện tích × số phòng ngủ" để mô hình hóa tương tác giữa các yếu tố
- Loại bỏ outliers: Xác định và xử lý các điểm dữ liệu bất thường trước khi huấn luyện
- Regularization: Sử dụng Ridge hoặc Lasso Regression để xử lý đa cộng tuyến và overfitting
- Chuyển sang mô hình khác: Nếu các kỹ thuật trên không hiệu quả, hãy cân nhắc các mô hình phức tạp hơn như Random Forest, Gradient Boosting, hoặc Neural Networks
6. Tài liệu tham khảo
Để nghiên cứu sâu hơn về hồi quy tuyến tính và các ứng dụng của nó, bạn có thể tham khảo các nguồn sau:
Tài liệu tiếng Anh:
- Scikit-learn Documentation: Linear Regression Example - Hướng dẫn chi tiết và ví dụ thực hành với Python
- "An Introduction to Statistical Learning" by James, Witten, Hastie, Tibshirani - Một trong những sách giáo khoa tốt nhất, viết rất dễ hiểu với nhiều ví dụ và hình ảnh minh họa
- Coursera - Machine Learning by Andrew Ng - Khóa học miễn phí nổi tiếng nhất về Machine Learning, với phần giảng về hồi quy tuyến tính rất chi tiết và dễ hiểu
Lời khuyên cho người mới học:
- Thực hành, thực hành, và thực hành: Đọc lý thuyết không đủ. Hãy tự tay code, chạy trên dữ liệu thực, mắc lỗi và sửa lỗi. Đó là cách học hiệu quả nhất
- Bắt đầu từ dữ liệu nhỏ: Đừng cố giải quyết bài toán lớn ngay từ đầu. Hãy bắt đầu với 10-20 điểm dữ liệu để có thể hiểu rõ mọi thứ đang diễn ra như thế nào
- Trực quan hóa nhiều: Vẽ biểu đồ cho mọi thứ - dữ liệu gốc, đường hồi quy, phần dư (residuals). Mắt bạn có thể phát hiện những vấn đề mà con số không thể hiện
- Đừng ngại thử nghiệm: Thay đổi learning rate, số epoch, thử với dữ liệu khác nhau. Mỗi thí nghiệm là một bài học
- Tham gia cộng đồng: Tham gia các diễn đàn như Stack Overflow, Reddit r/MachineLearning, hoặc các group Facebook về Data Science. Đặt câu hỏi khi bạn gặp khó khăn
Hồi quy tuyến tính tuy đơn giản, nhưng nó là nền tảng cho toàn bộ hành trình Machine Learning của bạn. Hãy dành thời gian để thực sự hiểu rõ nó trước khi chuyển sang các thuật toán phức tạp hơn. Chúc bạn học tốt!
tôi đang tìm hiều về linear regression thì vô tình bắt gặp bài viết này, vô cùng hữu ích với 1 người mới bắt đầu tìm hiểu như tôi
Cảm ơn bạn rất nhiều <3