Tổng quan về Linear Regression
1. Giới thiệu về Linear Regression
1.1. Giới thiệu
Trong Machine Learning, khi có một bộ dữ liệu có sẵn để huấn luyện mô hình (training set), ta cố gắng tìm một giải thuật để huấn luyện với tập dữ liệu trên, mục tiêu sau cùng là có được một model (cũng có thể gọi là hypothesis). Khi đó, với mỗi đầu vào (input) đi qua model và model sẽ trả về một đầu ra (output). Một model như vậy là mục tiêu của học có giám sát (supervised learning) nhằm dự đoán giá trị đầu ra (liên tục/ rời rạc) của một bài toán.
Hồi quy tuyến tính (Linear Regression) là một phương pháp trong học có giám sát (supervised learning) nhằm mô hình hóa mối quan hệ tuyến tính giữa biến đầu vào (features) và biến đầu ra (target).
Mục tiêu là tìm bộ tham số $\theta$ sao cho sai số giữa giá trị dự đoán $\hat{y}$ và giá trị thực $y$ là nhỏ nhất.
Ví dụ 1: Chúng ta có bài toán về dự đoán giá nhà với một bộ dữ liệu training (bảng) bao gồm các cột (feature) chứa thông tin về diện tích và giá nhà. Ta cần dự đoán giá nhà (output) với mỗi input là diện tích nhà.
| Diện tích (m2) | Giá (Tỷ VND) |
|---|---|
| 100 | 1.2 |
| 160 | 1.5 |
| 200 | 2.1 |
| 250 | 2.5 |
Ta có thể quan sát sơ bộ rằng: khi diện tích nhà tăng thì giá nhà cũng tăng. Khi đó, ta có thể sử dụng 1 đường thẳng $y = ax + b$ sao cho với mỗi diện tích nhà (input), ta thế vào đường thẳng trên và sẽ tìm được giá nhà (output). Một đường thẳng như vậy là một model ta cần tìm.
Ví dụ 2: Với một bộ dữ liệu khác, vẫn là bài toán dự đoán giá nhà trên nhưng ta được cho biết thêm nhiều thông tin hơn:
| Diện tích (m2) | Số phòng ngủ | Tuổi của căn nhà | Giá |
|---|---|---|---|
| 100 | 2 | 5 | 1.2 |
| 160 | 3 | 8 | 1.5 |
| 200 | 2 | 6 | 2.1 |
| 250 | 4 | 10 | 2.5 |
Lúc này, điều ta cần tìm là một siêu mặt phẳng (hyperplane)
$y = w_1x_1 + w_2x_2 + w_3x_3 + b$, trong đó $x_1$ là diện tích, $x_2$ là số phòng ngủ, $x_3$ là tuổi của căn nhà.
Việc tìm một đường thẳng/ mặt phẳng/ siêu mặt phẳng như vậy được gọi là hồi quy tuyến tính (Linear Regression), trong đó:
-
Hồi quy: có nghĩa là dự đoán một giá trị (thường là một biến liên tục) dựa trên một/ nhiều giá trị khác. Cụ thể ở đây, ta dự đoán giá nhà ($y$) dựa trên diện tích, số phòng ngủ, tuổi của căn nhà.
-
Tuyến tính: có thể hiểu là đường thẳng hay mối quan hệ của hai biến có dạng đường thẳng. Nghĩa là khi biểu diễn các điểm này lên biểu đồ thì chúng gần như tạo thành một đường thẳng.
1.2. Thước đo sai số
Quay lại với bài toán dự đoán giá nhà, ta đã tìm được cách dự đoán giá nhà là tìm một đường thẳng/ siêu mặt phẳng cho từng bộ dữ liệu cụ thể. Vậy câu hỏi tiếp theo là làm thế nào để biết nên chọn đường thẳng/ siêu mặt phẳng nào? Hay nói cách khác là làm sao để đánh giá một đường thẳng/ siêu mặt phẳng là tốt?
Với mỗi điểm trong bộ dữ liệu, ta đưa vào phương trình đường thẳng/ siêu mặt phẳng để tìm được giá trị dự đoán ($y_{pred}$ hay $\hat{y}$). Giá trị $\hat{y} - y$ có thể sử dụng để đánh giá sai số (sự khác biệt) là nhiều hay ít giữa các đường thẳng.
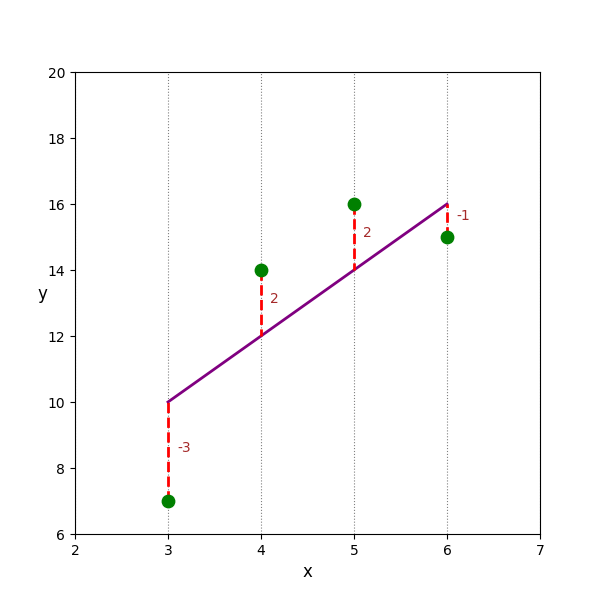
Hình 1. Minh họa sai số của Linear Regression
Tuy nhiên, có một vấn đề ở đây, với ví dụ trên ta tính được $\hat{y} - y$ lần lượt là $-3, 2, 2, -1$. Nếu ta dùng tổng 4 giá trị này để tính tổng sai số thì sai số bằng $0$, rõ ràng là không hợp lý. Vậy, cái ta cần lấy thực sự là độ lớn (magnitude) của $\hat{y} - y$, ta có thể sử dụng $|\hat{y} - y|$ (dùng trong MAE - Mean Absolute Error) hoặc $(\hat{y} - y)^2$ (dùng trong MSE - Mean Square Error). Và một điều rõ ràng rằng: với nhiều đường thẳng khác nhau, ta sẽ chọn đường thẳng có tổng sai số là nhỏ nhất.
$$MAE = \frac{1}{n} \sum_{i=1}^{n} |\hat{y}^{(i)} - y^{(i)}|$$
$$MSE = \frac{1}{n} \sum_{i=1}^{n} (\hat{y}^{(i)} - y^{(i)})^2$$
Trong đó:
- $\hat{y}^{(i)}$: giá trị dự đoán của điểm dữ liệu thứ $i$.
- $y$: giá trị dự đoán của điểm dữ liệu thứ $i$.
- $n$: số lượng điểm dữ liệu.
Ví dụ 3: Với 3 đường thẳng sau, giả sử ta chọn $(\hat{y} - y)^2$ là thước đo để tính sai số, ta thể tính được:
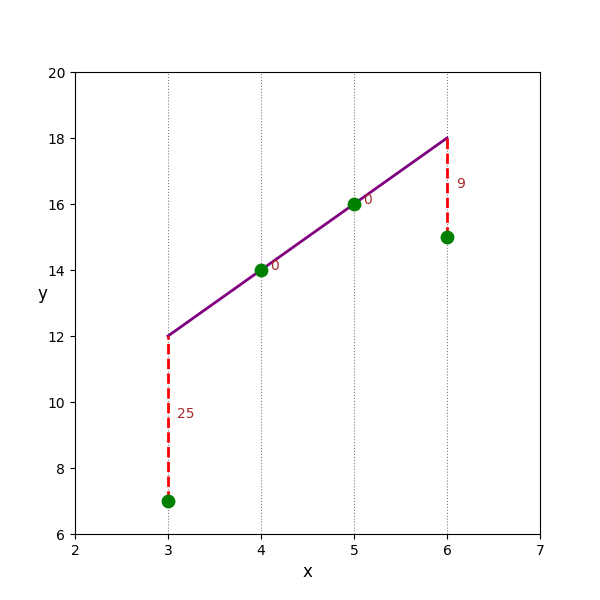
Tổng sai số của $d_1$ là: 36
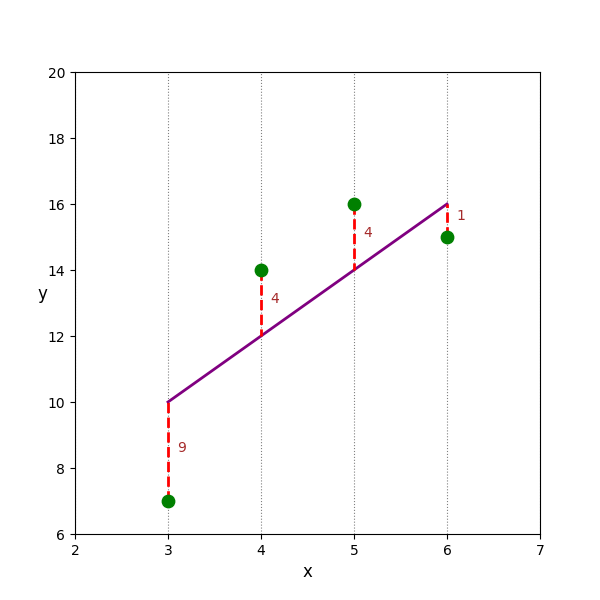
Tổng sai số của $d_2$ là: 18

Tổng sai số của $d_3$ là: 34
Hình 2. Minh họa về việc lựa chọn đường thẳng dựa trên sai số trong Linear Regression
Trong ví dụ 3, $d_2$ chính là đường thẳng tốt nhất trong 3 đường thẳng trên.
2. Giải thuật tìm hệ số tối ưu
Trước khi bàn về giải thuật tìm hệ số tối ưu, ta hãy xem xét một ví dụ sau:
Ví dụ 4: Xét hàm số $f(x) = -x^3 + 3x^2 - 1$. Ta có bảng biến thiên như sau:
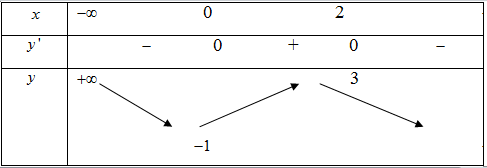
Hình 3. Bảng biến thiên của hàm số $f(x) = -x^3 + 3x^2 - 1$
Xét điểm $x_0 = 1$. Vì $x_0 \in (0;2)$ nên $f'(x_0) > 0$. Khi đó, ta có nhận xét:
-
Nếu đi cùng chiều của $f'(x_0)$ (chiều dương): $x_0$ sẽ tiến về phía cực đại ($x=2$).
-
Nếu đi ngược chiều của $f'(x_0)$ (chiều âm): $x_0$ sẽ tiến về phía cực tiểu ($x=0$).
Đây chính là ý tưởng của thuật toán Gradient Descent, được sử dụng để tìm hệ số tối ưu trong bài toán hồi quy tuyến tính. Với thuật toán này, ở mỗi bước đi ngược hướng với hướng của đạo hàm (gradient), điểm ban đầu sẽ bước một bước nhỏ hướng về điểm cực tiểu.
Phân loại bài toán trong Linear Regression
Với Linear Regression, ta có hai bài toán chính: hồi quy đơn biến và hồi quy đa biến.
Bài toán 1 (hồi quy đơn biến - univariate regression): Trong bài này, với 1 biến đầu vào $x$, ta sẽ dự đoán biến đầu ra $y$. Mục tiêu của bài toán là tìm đường thẳng tối ưu $\hat{y} = wx + b$, trong đó
- $w$: hệ số góc/ trọng số (weight),
- $b$: tung độ gốc/ độ chệch (bias)
Ta cần tìm các hệ số $w$ và $b$ tối ưu sao cho tổng sai số (còn gọi là hàm mất mát (loss function) đạt giá trị nhỏ nhất. Hàm mất mát có dạng (trường hợp ta chọn MSE là hàm mất mát):
$$L(w,b) = \sum_{i=1}^{n} (\hat{y}^{(i)} - y^{(i)})^2$$
Bài toán 2 (hồi quy đa biến - multivariate regression): ta có một bài toán tổng quát hơn: với một bộ dữ liệu đầu vào gồm nhiều biến ($x_1, x_2,..., x_n$), ta cũng cần dự đoán $y$. Mục tiêu của bài toán là tìm các hệ số $b, w_1, w_2,..., w_n$ sao cho với $\hat{y} = w_1.x_1 + w_2.x_2 + ... + w_n.x_n + b$ thì hàm mất mát đạt giá trị nhỏ nhất. Hàm mất mát có dạng tương tự bài toán hồi quy đơn biến
$$L(b, w_1, w_2,..., w_n) = \sum_{i=1}^{n} (\hat{y}^{(i)} - y^{(i)})^2$$
2.1. Cách hoạt động của Gradient Descent
Các bước của Gradient Descent: bao gồm:
-
Bước 1: Khởi tạo hệ số ban đầu cho bài toán và lựa chọn hàm mất mát $L(\theta)$.
-
Bước 2: Tính gradient: $\nabla_{\mathbf{\theta}} L(\mathbf{\theta})$
-
Bước 3: Cập nhật trọng số $\theta = \theta - \alpha \nabla_{\mathbf{\theta}} L(\mathbf{\theta})$
-
Bước 4: Lặp lại bước 2. Quá trình lặp chỉ kết thúc khi $L(\theta)$ hoặc thay đổi rất nhỏ giữa hai bước hoặc đạt ngưỡng cho trước hoặc khi đã đủ số vòng lặp.
Áp dụng cho bài toán Linear Regression
- Xét Bài toán 1:
Ở bước 2 (tính gradient), ta cần tính gradient : $\nabla_{\mathbf{\theta}} L(\mathbf{\theta}) = \begin{bmatrix} \frac{dL}{dw} \cr \frac{dL}{db} \end{bmatrix}$
Ta có thể tính trực tiếp bằng cách thay $\hat{y} = wx + b$, sau đó tính từng đạo hàm của $L$ theo $w$ và $b$.
Tuy nhiên, ta nên áp dụng cách làm tổng quát sau. Ta có $L = (\hat{y} - y)^2$ (cho mỗi điểm dữ liệu) nên ta có:
- Đạo hàm của $L$ theo $\hat{y}$:
$$\frac{dL}{d\hat{y}} = 2(\hat{y} - y)$$ - Đạo hàm của $\hat{y}$ theo $w$:
$$\frac{d\hat{y}}{dw} = x$$ - Đạo hàm của $\hat{y}$ theo $b$:
$$\frac{d\hat{y}}{db} = 1$$
Khi đó, để tính các đạo hàm trên, ta sử dụng quy tắc chuỗi (chain rule) như sau:
- Đạo hàm của $L$ theo $w$:
$$\frac{dL}{dw} = \frac{dL}{d\hat{y}}\frac{d\hat{y}}{dw} = 2(\hat{y} - y)x$$
- Đạo hàm của $L$ theo $b$:
$$\frac{dL}{db} = \frac{dL}{d\hat{y}}\frac{d\hat{y}}{db} = 2(\hat{y} - y)$$
Ở bước 3 (cập nhật trọng số), ta có trọng số mới như sau:
$$w := w - \alpha\frac{dL}{dw}$$
$$b := b - \alpha\frac{dL}{db}$$
Với $\alpha$ là tốc độ học (learning rate) để điều chỉnh tốc độ cập nhật của trọng số.
- Xét bài toán 2:
Ta sẽ thực hiện lại tương tự để thấy được sự tổng quát của chain rule.
Với
$$\hat{y} = w_1x_1 + w_2x_2 + ... + w_ix_i + ... + w_nx_n + b$$ và $$L = (\hat{y} - y)^2$$
Ta có:
$$\frac{dL}{d\hat{y}} = 2(\hat{y} - y)$$
$$\forall i = 1..n:\frac{d\hat{y}}{dw_i} = x_i$$
$$\frac{d\hat{y}}{db} = 1$$
Khi đó, gradient cần tính là:
$$\forall i = 1..n:\frac{dL}{dw_i} = \frac{dL}{d\hat{y}}\frac{d\hat{y}}{dw_i} = 2(\hat{y} - y)x_i$$
$$\frac{dL}{db} = \frac{dL}{d\hat{y}}\frac{d\hat{y}}{db} = 2(\hat{y} - y)$$
Ở bước 3 (cập nhật trọng số), ta có trọng số mới như sau:
$$\forall i = 1..n:w_i := w_i - \alpha\frac{dL}{dw_i}$$
$$b := b - \alpha\frac{dL}{db}$$
Ngoài Gradient Descent, Linear Regression còn có thể giải trực tiếp bằng công thức giải tích (Normal Equation) thông qua phương pháp đạo hàm bằng 0: $$ \theta = (X^TX)^{-1}X^Ty$$
Tuy nhiên, cách này chỉ phù hợp với dữ liệu nhỏ và khi ma trận $X^T X$ khả nghịch.
2.2. Minh họa
Quay lại với bài toán dự đoán giá nhà đơn giản (bài toán 1):
| Diện tích (m2) | Giá (Tỷ VND) |
|---|---|
| 100 | 1.2 |
| 160 | 1.5 |
| 200 | 2.1 |
| 250 | 2.5 |
Với bài toán này, ta cần tìm đường thẳng tối ưu $y = wx + b$, trong đó $y$ là giá nhà, $x$ là diện tích nhà. Hàm mất mát cần tối ưu là:
$$L = (\hat{y} - y)^2$$
Ta thực hiện từng bước của Gradient Descent như sau:
- Bước 1: Khởi tạo giá trị w = 0.005, b = 0.1
Xét điểm dữ liệu $(100, 1.2)$, ta tính được $\hat{y} = wx + b$ = 0.6
- Bước 2: Tính gradient:
$$\frac{dL}{dw} = \frac{dL}{d\hat{y}}\frac{d\hat{y}}{dw} = 2(\hat{y} - y)x = 2(0.6-1.2).100 = -120$$
$$\frac{dL}{db} = \frac{dL}{d\hat{y}}\frac{d\hat{y}}{db} = 2(\hat{y} - y) = 2(0.6-1.2)=-1.2$$
- Bước 3: Cập nhật trọng số, chọn $\alpha = 0.001$:
$$w := w - \alpha\frac{dL}{dw} = 0.005 - 0.001.(-120) = 0.125$$
$$b := b - \alpha\frac{dL}{db} = 0.1 - 0.001* (-1.2) = 0.1012$$
Tương tự, thực hiện cho các điểm dữ liệu còn lại: $(160, 1.5)$, $(200,2.1)$, $(250, 2.5)$
Đoạn code minh họa:
def predict(x, w, b):
y_pred = w*x + b
return y_pred
def compute_gradient(x, y_pred, y):
dw = 2*(y_pred-y)*x
db = 2*(y_pred-y)
return (dw,db)
def update_weight(w, b, alpha, dw, db):
w = w - alpha * dw
b = b - alpha * db
return (w,b)
2.3. Các biến thể Gradient Descent
Gradient Descent có các biến thể chính như sau:
-
Stochastic Gradient Descent (SGD): Với biến thể này, Gradient Descent sẽ dùng từng điểm dữ liệu để cập nhật trọng số. Ta có thể thấy biến thể này ở Minh họa 2.2: trọng số sẽ được cập nhật với từng điểm dữ liệu $(100, 1.2)$, $(160, 1.5)$, $(200,2.1)$, $(250, 2.5)$. Nghĩa là qua 1 epoch (vòng lặp), SGD sẽ cập nhật trọng số 4 lần với bộ dữ liệu trên. SGD sẽ giúp quá trình hội tụ diễn ra nhanh hơn, tuy nhiên khi đến gần điểm cực tiểu, SGD sẽ dao động (oscillate) quanh điểm cực tiểu thay vì hội tụ đến điểm cực tiểu.
-
Batch Gradient Descent: Với biến thể này, Gradient Descent sẽ dùng tất cả điểm dữ liệu để cập nhật trọng số. Công thức tính toán tương như SGD nhưng $\frac{dL}{dw}$ và $\frac{dL}{db}$ sẽ là trung bình cộng của $\frac{dL}{dw}$ và $\frac{dL}{db}$ của tất cả các điểm dữ liệu. Với cách hoạt động này, Batch Gradient Descent sẽ hội tụ chậm hơn nhưng quá trình hội tụ sẽ mượt (smooth) và chính xác đến điểm cực tiểu.
Quay lại với bài toán 1, với Batch Gradient Descent ta thực hiện như sau:
Bước 1: Khởi tạo giá trị w = 0.005, b = 0.1. Tính giá trị dự đoán $\hat{y}$ cho từng điểm dữ liệu.
| x | y | $\hat{y}$ |
|---|---|---|
| 100 | 1.2 | 0.6 |
| 160 | 1.5 | 0.9 |
| 200 | 2.1 | 1.1 |
| 250 | 2.5 | 1.35 |
Bước 2: Tính gradient theo công thức sau cho từng điểm dữ liệu:
$$\frac{dL}{dw} = \frac{dL}{d\hat{y}}\frac{d\hat{y}}{dw} = 2(\hat{y} - y)x$$
$$\frac{dL}{db} = \frac{dL}{d\hat{y}}\frac{d\hat{y}}{db} = 2(\hat{y} - y) $$
| x | y | $\hat{y}$ | $dL/dw$ | $dL/db$ |
|---|---|---|---|---|
| 100 | 1.2 | 0.6 | -120 | -1.2 |
| 160 | 1.5 | 0.9 | -192 | -1.2 |
| 200 | 2.1 | 1.1 | -400 | -2 |
| 250 | 2.5 | 1.35 | -575 | -2.3 |
Bước 3: Cập nhật trọng số, chọn $\alpha = 0.01$:
$$w := w - \alpha\frac{dL}{dw} = 0.005 - 0.01.\frac{(-120)+(-192)+(-400)+(-575)}{4} = 3.2225$$
$$b := b - \alpha\frac{dL}{db} = 0.1 - 0.01.\frac{(-1.2)+(-1.2)+(-2)+(-2.3)}{4} = 0.11675$$
Có thể thấy, qua mỗi epoch, Batch Gradient Descent chỉ cập nhật trọng số một lần.
- Mini-Batch Gradient Descent: là một biến thể của Gradient Descent, biến thể này sẽ dùng một số điểm dữ liệu ($m$ điểm với $1 < m < n$) thay vì tất cả ($n$ điểm) để cập nhật trọng số. Nó giúp cân bằng giữa tốc độ hội tụ của SGD và sự ổn định của Batch Gradient Descent. Qua mỗi epoch, Mini-Batch Gradient Descent sẽ cập nhật trọng số $\lfloor{n/m}\rfloor$ (phần nguyên của $n/m$) lần. Giá trị của $m$ thường được chọn là lũy thừa của $2$ trong khoảng $32 - 128$.
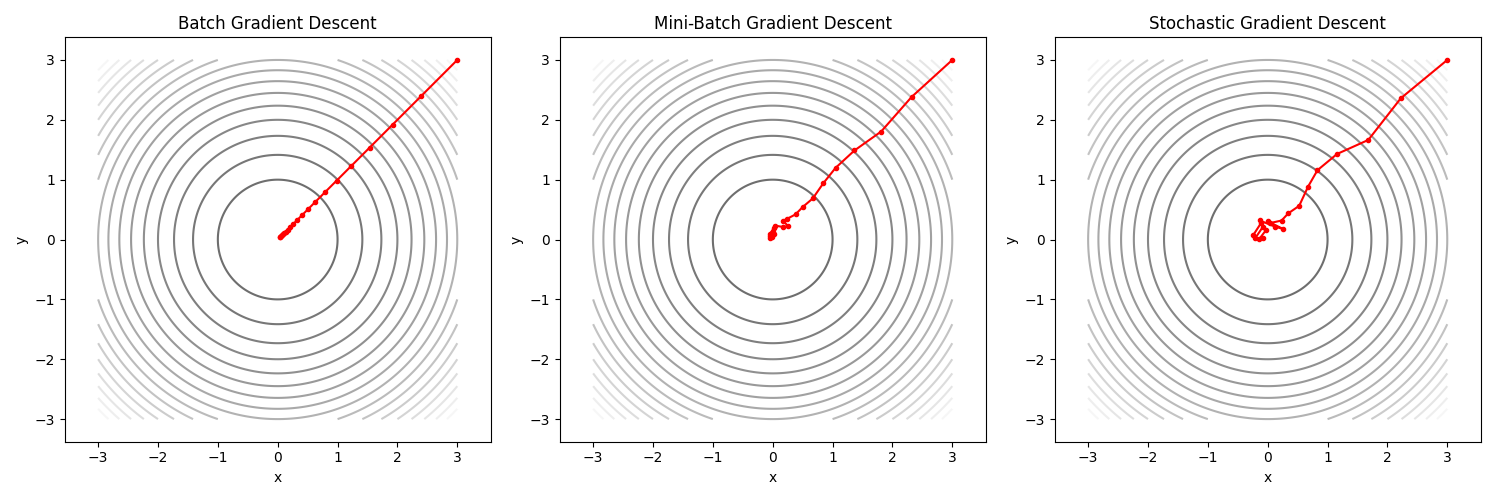
Hình 4. Minh họa về cách hội tụ của từng biến thể Gradient Descent
2.4. Một số vấn đề liên quan
Chọn Learning rate $\alpha$:
Learning rate được chọn tùy theo từng bài toán cụ thể. Giá trị của learning rate sẽ ảnh hưởng đến kết quả bài toán như sau:
-
$\alpha$ quả nhỏ: hàm mất mát hội tụ chậm hoặc không gần điểm tối ưu.
-
$\alpha$ quá lớn: dễ "vọt qua" cực tiểu, khi đó hàm mất mát chỉ dao động quanh điểm cực tiểu hoặc phân kỳ.
Trên thực tế: nên thử nghiệm $\alpha$ với nhiều giá trị (ví dụ : $10^{-3}$, $10^{-2}$, $10^{-1}$) để chọn được $\alpha$ tối ưu.
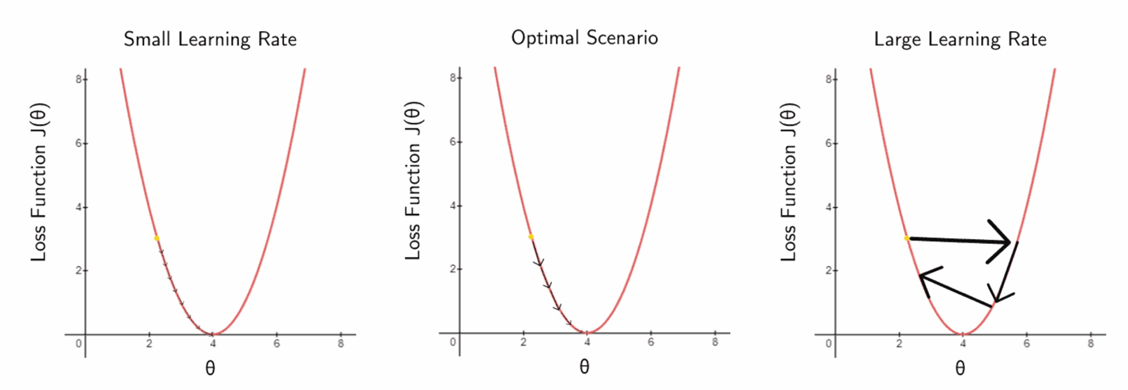
Hình 5. Minh họa về ảnh hướng của learning rate đến quá trình hội tụ của hàm mất mát
Lựa chọn hàm mất mát (loss function):
Loss function (hàm mất mát) là công cụ để đo độ sai lệch giữa giá trị dự đoán $\hat{y_i}$ và giá trị thật $y_i$. Mục tiêu của mô hình là tối thiểu hóa hàm mất mát, tức là làm cho sai số giữa dự đoán và thực tế nhỏ nhất.
Trước hết, ta xem xét hai hàm số sau: $f(x) = |x|$ và $g(x) = x^2$. Ta thấy rằng $f(x)$ và $g(x)$ đều là các hàm liên tục (continous function), $g(x)$ là hàm khả vi (differentiable function) còn $f(x)$ không khả vi (xem chi tiết tại Mục 5). Ta xem xét các khía cạnh sau:
-
Nếu dữ liệu có ngoại lai (outlier), giả sử $x$ rất lớn, khi đó $g(x)$ bị ảnh hưởng nhiều hơn do là hàm bình phương. Do đó, $g(x)$ nhạy cảm với outlier hơn $f(x)$.
-
Quá trình cập nhật trọng số: các trọng số được cập nhật ngược hướng gradient. Hãy xem xét đạo hàm của $f(x)$ và $g(x)$:
$$ f'(x) = \begin{cases} 1, & \text{nếu } x > 0 \cr -1, & \text{nếu } x < 0 \cr \text{không xác định}, & \text{nếu } x = 0 \end{cases} $$
$$g'(x) = 2x$$
Ta thấy rằng, $f'(x)$ luôn cố định còn $g'(x)$ sẽ phụ thuộc $x$. Cụ thể hơn, khi thay $x = \hat{y} - y$, qua từng epoch, quá trình hội tụ sẽ làm cho $x$ càng nhỏ dần. Nếu lựa chọn $f(x)$ làm hàm mất mát thì giá trị trọng số sẽ được cập nhật với $\alpha.f'(x)$ không đổi, điều này làm cho khi tiến gần đến điểm cực tiểu, hàm số không thể hội tụ mà chỉ dao động quanh điểm cực tiểu. Với hàm $g(x)$, khi $x$ lớn, trọng số sẽ được cập nhật nhiều, khi $x$ nhỏ, trọng số sẽ được cập nhập ít hơn nhưng dần về điểm cực trị.
Qua 2 quan sát trên, ta có các hàm mất mát sau:
MAE (Mean Absolute Error): ít ảnh hưởng bởi outlier, nhưng sẽ không thể hội tụ đến điểm cực tiểu.
MSE (Mean Square Error): ảnh hưởng mạnh bởi outlier, hội tụ dần đến điểm cực tiểu.
Huber (xem chi tiết các thiết lập tại Mục 5): Kết hợp ưu điểm của MSE và MAE:
-
Huber sẽ là MSE khi $|\hat{y} - y|$ (sai số) nhỏ (trơn, gradient ổn định).
-
Huber sẽ là MAE khi $|\hat{y} - y|$ (sai số) lớn (ít bị ảnh hưởng bởi outlier).
$$L_\delta = \begin{cases} \frac{1}{2} (\hat{y} - y)^2, & \text{nếu } |\hat{y} - y| \le \delta \cr \delta (|\hat{y} - y| - \frac{1}{2}\delta), & \text{nếu } |\hat{y} - y| > \delta \end{cases}$$
3. Tối ưu việc cài đặt (implement)
3.1. Giới thiệu về ma trận
Trước hết, ta xem xét các khái niệm liên quan sau:
Ma trận: Ma trận A cỡ $m$ x $n$ là một bảng số có $m$ hàng và $n$ cột:
$$ A = \begin{bmatrix} a_{11} & a_{12} & ... & a_{1n} \cr a_{21} & a_{22} & ... & a_{2n} \cr ... & ... & ... & ... \cr a_{m1} & a_{m2} & ... & a_{mn} \cr \end{bmatrix} = (a_{ij})_{m \times n}$$
Vector: một đại lượng có nhiều thành phần, thường được biểu diễn thành 1 hàng hoặc 1 cột. Ví dụ:
$$x = \begin{bmatrix} -1 & 2 & 3 \end{bmatrix}$$
Có thể thấy vector là một trường hợp đặc biệt của ma trận:
-
Vector hàng: ma trận $1 \times n$
-
Vector cột: ma trận $n \times 1$
Các phép toán cơ bản với ma trận:
- Phép cộng/trừ 2 ma trận:
Với 2 ma trận cùng cỡ $A$ và $B$, để thực hiện phép cộng/trừ ma trận A với ma trận B, ta cộng/trừ các phần tử tương ứng (cùng vị trí dòng, cột) với nhau. Cụ thể: $A \pm B = (a_{ij} \pm b_{ij})_{m \times n}$
Ví dụ: Cho 2 ma trận $A = \begin{bmatrix} -1 & 2 & 3 \cr 2 & -2 & 4 \end{bmatrix}$ và $B = \begin{bmatrix} 4 & -1 & -3 \cr 3 & -4 & 4 \end{bmatrix}$, ta có:
$$A+B = \begin{bmatrix} -1 + 4 & 2 + (-1) & 3 + (-3) \cr 2 + 3 & (-2) + (-4) & 4 + 4 \end{bmatrix} = \begin{bmatrix} 3 & 1 & 0 \cr 5 & -6 & 8 \end{bmatrix}$$
- Phép nhân 2 ma trận:
Cho ma trận $A = (a_{ij})_{m \times n}$ và $B = (b_{ij})_{m \times n}$.
Ma trận $A \times B = C = (c_{ij})_{ m \times p}$, trong đó phần tử $c_{ij}$ được tính bằng cách lấy tích các phần tử tương ứng của dòng $i$ của $A$ với các phần tử của cột $j$ của $B$, sau đó lấy tổng lại, nghĩa là:
$$c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + ... + a_{in}b_{nj}$$
Ví dụ: Cho ma trận $A = \begin{bmatrix} -1 & 2 & 3 \cr 2 & -2 & 4 \end{bmatrix}$ và $B = \begin{bmatrix} 4 & -1 & -3 \cr 3 & -4 & 4 \cr 1 & 2 & 1\end{bmatrix}$
Khi đó: $ A \times B = C = \begin{bmatrix} c_{11} & c_{12} & c_{13} \cr c_{21} & c_{22} & c_{23} \end{bmatrix} $, trong đó:
$$c_{11} = a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31} = -1 * 4 + 2 * 3 + 3 * 1 = 5$$
Tính tương tự cho các phần tử còn lại, ta được $C = \begin{bmatrix} 5 & -1 & 14 \cr 6 & 14 & -10 \end{bmatrix}$
Đặc biệt, với ma trận $A = (a_{ij})_{1 \times n}$ và $B = (b_{ij})_{n \times 1}$, $C = A \times B = (c_{ij})_{1 \times 1} = c_{11} $ là một số thực.
- Ma trận chuyển vị (Transpose Matrix):
Là ma trận thu được từ ma trận A bằng cách đổi các hàng thành các cột và các cột thành hàng. Ma trận chuyển vị được ký hiệu là $A^T$.
Ví dụ: Cho ma trận $ A = \begin{bmatrix} 1 & 4 & 6 \cr 2 & 5 & 3 \end{bmatrix}$. Khi đó, $A^T = \begin{bmatrix} 1 & 2 \cr 4 & 5 \cr 6 & 3 \end{bmatrix}$
- Ứng dụng của ma trận
Ta xem xét một ví dụ sau về ứng dụng ma trận. Xem xét một cửa hàng có 2 chi nhánh. Mỗi chi nhánh bán 3 mặt hàng gạo, muối và bột mì với giá lần lượt là 20, 5, 10.
| Chi nhánh 1 | Chi nhánh 2 | |
|---|---|---|
| Gạo | 5 | 7 |
| Muối | 10 | 12 |
| Bột mì | 8 | 15 |
Xét ma trận $A$ sau là số lượng sản phẩm bán được của mỗi chi nhánh:
$$A = \begin{bmatrix} 5 & 7 \cr 10 & 12 \cr 8 & 15 \end{bmatrix}$$
Bài toán 1: Hãy tính tổng số tiền kiếm được của mỗi chi nhánh.
Ta thực hiện:
$$Money = \begin{bmatrix} 20 & 5 & 10 \end{bmatrix} \times \begin{bmatrix} 5 & 7 \cr 10 & 12 \cr 8 & 15 \end{bmatrix} = \begin{bmatrix} 230 & 350 \end{bmatrix} $$
Bài toán 2: Tính tổng số lượng mỗi mặt hàng của cửa hàng.
$$Quantities = \begin{bmatrix} 5 & 7 \cr 10 & 12 \cr 8 & 15 \end{bmatrix} \times \begin{bmatrix} 1 \cr 1 \end{bmatrix} = \begin{bmatrix} 12 \cr 22 \cr23 \end{bmatrix}$$
3.2 Ứng dụng vào Linear Regression
Với bài toán Linear Regression, ta có các biểu thức sau (xem chi tiết chứng minh ở Mục 5:
- Xét trường hợp 1 điểm dữ liệu:
Ký hiệu:
$x = \begin{bmatrix} x_1 \cr x_2 \cr ... \cr x_n \end{bmatrix}_{n \times 1}$ là vector cột biểu diễn cho 1 điểm dữ liệu với $x_i$ là đặc trưng (feature) thứ $i$ của dữ liệu.
$\theta = \begin{bmatrix} \theta_1 \cr \theta_2 \cr ... \cr \theta_n \end{bmatrix}_{n \times 1}$ là vector cột biểu diễn cho các trọng số của mô hình, $w_i$ là trọng số cho đặc trưng thứ $i$.
Khi đó, Linear Regression được biểu diễn:
Bước 1: Giá trị dự đoán là: $y_{pred} = \theta^Tx = x^T\theta$.
Bước 2: Tính gradient: $L_\theta' = 2(y_{pred} - y)x$
Bước 3: Cập nhật trọng số: $\theta:=\theta-\alpha.L_\theta'$
- Xét trường hợp nhiều điểm dữ liệu:
Nếu X biểu diễn cho nhiều điểm dữ liệu, mỗi dòng tương ứng là một vector hàng biểu diễn cho một điểm dữ liệu, ta có:
$$X = \begin{bmatrix} x_1^1 & x_2^1 & ... & x_n^1 \cr x_1^2 & x_2^2 & ... & x_n^2 \cr ... & ... & ... & ... \cr x_1^m & x_2^m & ... & x_n^m\end{bmatrix}_{m \times n}$$
Khi đó, Linear Regression được biểu diễn:
Bước 1: Giá trị dự đoán là:
$$y_{pred} = \begin{bmatrix} y_{pred}^1 \cr y_{pred}^2 \cr ... \cr y_{pred}^m \end{bmatrix} = X\theta$$
Bước 2: Tính gradient:
$$L_\theta' = \begin{bmatrix} \frac{\mathrm dL}{d\theta_1} \cr \frac{\mathrm dL}{d\theta_2} \cr ... \cr \frac{\mathrm dL}{d\theta_n} \end{bmatrix} = 2X^T(y_{pred}-y)$$
Bước 3: Cập nhật trọng số:
$$\theta:=\theta-\alpha.L_\theta'$$
3.3. Cách cài đặt (implement)
- Giới thiệu về vectorzation của numpy
Với cách thức code ở mục 2.2, khi số lượng đặc trưng quá nhiều (giả sử input có 4 đặc trưng), ta cần chỉnh sửa code như sau:
def predict(x1, w1, x2, w2, x3, w3, x4, w4, b):
y_pred = w1*x1 + w2*x2 + w3*x3 + w4*x4 + b
return y_pred
def compute_gradient(x1, x2, x3, x4, y_pred, y):
dw1 = 2*(y_pred-y)*x1
dw2 = 2*(y_pred-y)*x2
dw3 = 2*(y_pred-y)*x3
dw4 = 2*(y_pred-y)*x4
db = 2*(y_pred-y)
return (dw1, dw2, dw3, dw4,db)
def update_weight(w1, w2, w3, w4, b, alpha,
dw1, dw2, dw3, dw4, db):
w1 = w1 - alpha * dw1
w2 = w2 - alpha * dw2
w3 = w3 - alpha * dw3
w4 = w4 - alpha * dw4
b = b - alpha * db
return (w1, w2, w3, w4, b)
Rõ ràng, khi số lượng đặc trưng trở nên nhiều, khi đó, ta cần phải sử dụng vòng lặp (loop) qua từng đặc trưng. Điều này không tối ưu về mặt tính toán.
Trong python, thư viện numpy có hỗ trợ cơ chế vectorization giúp thực thi toàn bộ phần tử trên mảng thay vì tuần tự. Hãy xem đoạn code sau:
# Thủ công
def predict(x, w, b, n):
y_pred = b
for i in range(n):
y += w[i]*x[i]
return y_pred
# Vectorized
def predict(x, w, b):
y_pred = x.T.dot(w) + b
return y_pred
- Thực thi các biến thể Gradient Descent
Với cách thức này, giải thuật Linear Regression sẽ được chuyển thành:
Stochastic Gradient Descent:
def predict(X, theta):
return X.dot(theta)
def compute_loss(y_pred, y):
return (y_pred - y) ** 2
def compute_gradient(y_pred, y, X):
return 2 * X * (y_pred - y)
def update_gradient(theta, gradient, lr):
theta = theta - lr * gradient
return theta
Mini-batch/ Batch Gradient Descent:
def predict(X, theta):
return X.dot(theta)
def compute_loss(y_pred, y):
N = y.shape[0]
return np.sum((y_pred - y) ** 2) / N
def compute_gradient(y_pred, y, X):
N = y.shape[0]
k = 2 * (y_pred - y)
return X.T.dot(k) / N
def update_gradient(theta, gradient, lr):
theta = theta - lr * gradient
return theta
Ghi chú: X là ma trận với mỗi dòng tương ứng với một điểm dữ liệu
4. Các vấn đề liên quan
4.1. Feature Engineering
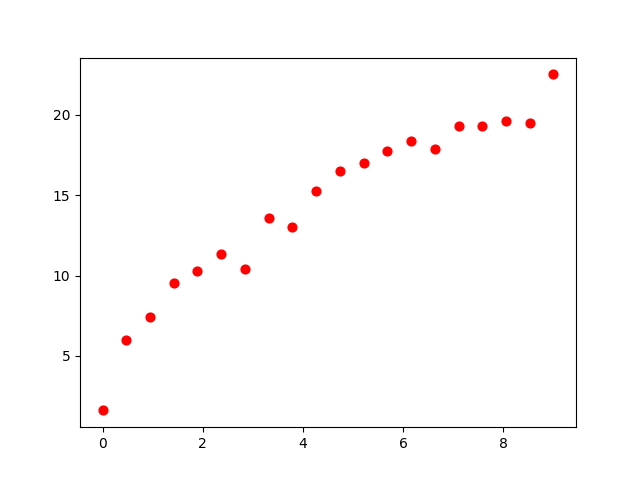
Hình 6. Minh họa về mối quan hệ phi tuyến giữa input và output
Với một số tập dữ liệu như hình, việc sử dụng một đường thẳng $y = wx+b$ sẽ không còn phù hợp, thay vào đó ta có thể bổ sung một số hàm toán học vào mô hình, chẳng hạn như các hàm bậc cao $x^2, x^3$, ..., $\sqrt{x}$, $log(x)$, ... giúp mô hình nắm bắt các quan hệ phi tuyến của input và output.
Với tập dữ liệu trên, ta có thể sử dụng một mô hình $y = w_1x + w_2\sqrt{x} + b$. Để xây dựng mô hình như vậy, ta chỉ cần bổ sung thêm 1 feature (cột trong bảng dữ liệu) $\sqrt{x}$ và áp dụng Gradient Descent để tìm các hệ số.
Tuy nhiên, khi áp dụng feature engineering, cần chú ý normalize dữ liệu để tránh việc overload (với các hàm bậc cao). Đồng thời, cần chú ý lựa chọn các hàm phù hợp. Việc lựa chọn các hàm bậc quá cao có thể làm cho mô hình bị overfitting (như hình bên dưới).
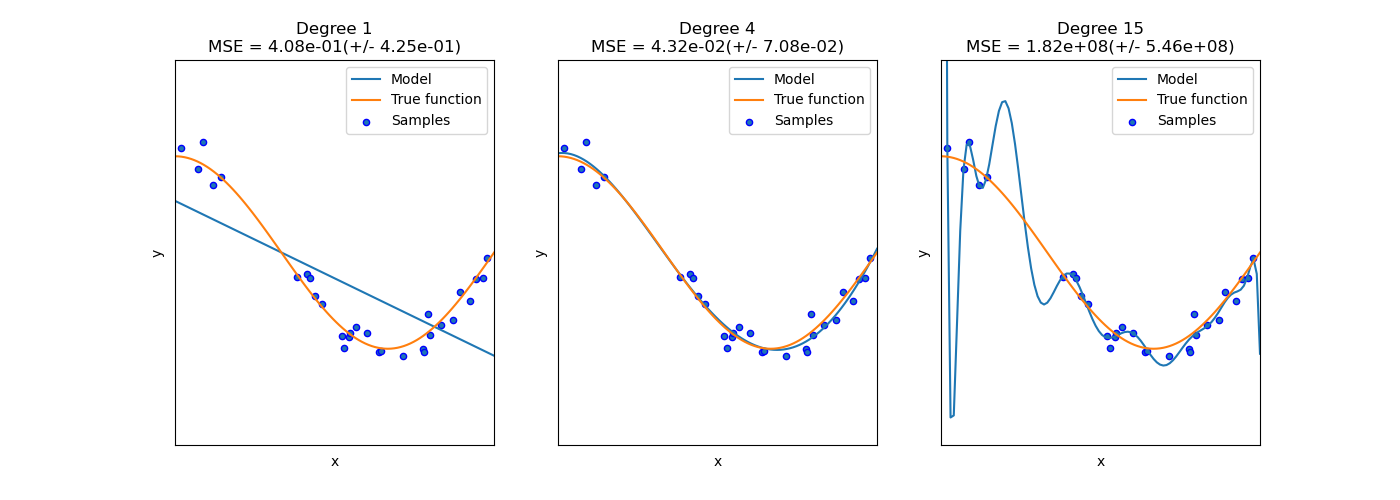
Hình 7. Minh họa về cách chọn bậc phù hợp cho hàm mũ
4.2. Locally Weighted Linear Regression
Mô hình Linear Regression truyền thống sử dụng một đường thẳng để nắm bắt mối quan hệ giữa $x$ (input) và $y$ (output), nghĩa là giả định $x$ và $y$ tuyến tính trên toàn cục. Nhưng trong nhiều trường hợp, mối quan hệ giữa $x$ và $y$ chỉ gần tuyến tính trong một vùng lân cận của $x$.
Một kỹ thuật có thể sử dụng là Locally weighted Linear Regression (LWLR). Thay vì sử dụng $\theta$ cho toàn bộ dự liệu, với mỗi điểm cần dự đoán $x_0$, LWLR sẽ điều chỉnh model tập trung nhiều vào các điểm dữ liệu gần $x_0$ (các điểm gần sẽ có weight cao hơn). Nói nôm na là với mỗi điểm $x_0$, ta sẽ fit một đường thẳng cho từng điểm.
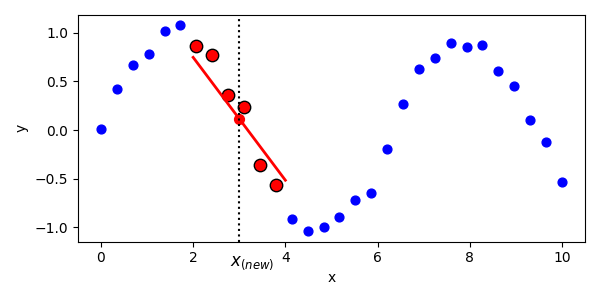
Hình 8. Minh họa về cách sử dụng Locally weighted Linear Regression
Hàm mất mát của LWLR có dạng như sau:
$$L(\theta) = \sum_{i=1}^{n}w^{(i)}(\theta^Tx^{(i)}-y^{(i)})^2$$
Trong đó:
-
x là điểm cần dự đoán
-
$w^{(i)} = exp(\frac{-(x^{(i)} - x)^2}{2\tau^2})$
Ví dụ: $x = 5.0$ và $\tau =0.5$, ta xem xét weight của 2 điểm sau:
-
$x = 4.9$: $w^{(1)} = exp(-\frac{-(4.9 - 5)^2}{2.0.5^2})= 0.9802$
-
$x = 7.0$: $x^{(2)} = exp(-\frac{-(4.9 - 5)^2}{2.0.5^2})= 0.00034$
Có thể thấy rằng, điểm $4.9$ gần với $x$ hơn nên $w^{(1)}$ đóng góp vào hàm mất mát nhiều hơn $w^{(2)}$
Giống như linear regression, nghiệm có thể tìm được bằng công thức ma trận:$$\theta=(X^TWX)^{-1}X^TWy$$
5. Giải thích các vấn đề toán học trong bài viết
Chứng minh hàm $f(x)= |x|$ không khả vi:
Ta có:
$$f(x) = \begin{cases} x, & \text{nếu } x \ge 0 \cr -x, & \text{nếu } x < 0 \end{cases}$$
Ta thấy rằng:
$$\begin{cases} \lim_{x \to 0^+} f'(x) = 1 \cr \lim_{x \to 0^-} f'(x) = -1 \end{cases}$$
Do đó, $f(x)$ không khả vi tại $x=0$.
Cách thiết lập hàm Huber:
Với hàm Huber, ta cần thiết lập một hàm tương tự MAE khi sai số lớn và tương tự MSE khi sai số nhỏ. Do đó hàm Huber có dạng:
$$L_\delta = \begin{cases} \frac{1}{2} (\hat{y} - y)^2, & \text{nếu } |\hat{y} - y| \le \delta \cr a|\hat{y} - y| + b, & \text{nếu } |\hat{y} - y| > \delta \end{cases}$$
Để được điều này, $L_\theta$ phải liên tục và khả vi. Đặt $t =\hat{y} - y$ và xét $\delta > 0$, ta có:
$$\begin{cases} \lim_{t \to \delta^-} L(t) = \lim_{t \to \delta^+} L(t) \cr \lim_{t \to \delta^-} \frac{L(t) - L(\delta)}{t - \delta} = \lim_{t \to \delta^+} \frac{L(t) - L(\delta)}{t - \delta} \end{cases}$$
$$\Leftrightarrow\begin{cases} \lim_{t \to \delta^-} \frac{1}{2} t^2 = \lim_{t \to \delta^+} a|t|+b \cr \lim_{t \to \delta^-} \frac{\frac{1}{2} t^2 - \frac{1}{2} \delta ^2}{t - \delta} = \lim_{t \to \delta^+}\frac{at+b - (a\delta+b)}{t - \delta} \end{cases}$$
$$\Leftrightarrow\begin{cases} \frac{1}{2} \delta^2 = a\delta+b \cr \delta = a\end{cases}$$
$$\Leftrightarrow\begin{cases} a = \delta \cr b=-\frac{\delta^2}{2}\end{cases}$$
Chứng minh biểu diễn ma trận trong Linear Regression
- Trường hợp 1 điểm dữ liệu
Bước 1: Tính giá trị dự đoán:
$$y_{pred} = x_1w_1 + x_2w_2 + ... + x_nw_n = \begin{bmatrix} x_1 & x_2 & ... & x_n \end{bmatrix} \times \begin{bmatrix} \theta_1 \cr \theta_2 \cr ... \cr \theta_n \end{bmatrix} = x^T\theta$$
Tương tự, ta có: $y_{pred} = \theta^Tx = x^T\theta$.
Bước 2: Tính gradient:
Ta có $$\frac{\mathrm dL}{dw_i}=2(y_{pred}-y)x_i$$
Vì vậy: $$L_\theta' = \begin{bmatrix} \frac{\mathrm dL}{dw_1} \cr \frac{\mathrm dL}{dw_2} \cr ... \cr \frac{\mathrm dL}{dw_n} \end{bmatrix} = \begin{bmatrix} 2(y_{pred}-y)x_1 \cr 2(y_{pred}-y)x_2 \cr ... \cr 2(y_{pred}-y)x_n \end{bmatrix} = 2(y_{pred} -y)\begin{bmatrix} x_1 \cr x_2 \cr ... \cr x_n \end{bmatrix} = 2(y_{pred} -y)x $$
Bước 3: Cập nhật trọng số: Với mỗi $w_i$ sẽ được cập nhật
$$w_i := w_i - \alpha \frac{\mathrm dL}{dw_i} $$
Vậy ta có thể kết hợp lại thành: $\theta := \theta - \alpha L_\theta'$
- Trường hợp nhiều điểm dữ liệu
Bước 1: Tính giá trị dự đoán:
$$ \begin{align*} Y &= \begin{bmatrix} y_{pred}^1 \cr y_{pred}^2 \cr ... \cr y_{pred}^m \end{bmatrix} = \begin{bmatrix} x_1^1w_1 + x_2^1w_2 + ... + x_n^1w_n \cr x_1^2w_1 + x_2^2w_2 + ... + x_n^2w_n \cr ... \cr x_1^mw_1 + x_2^mw_2 + ... + x_n^mw_n \end{bmatrix} \\[8pt] &= \begin{bmatrix} x_1^1 & x_2^1 & ... & x_n^1 \cr x_1^2 & x_2^2 & ... & x_n^2 \cr ... & ... & ... & ... \cr x_1^m & x_2^m & ... & x_n^m \end{bmatrix} \times \begin{bmatrix} \theta_1 \cr \theta_2 \cr ... \cr \theta_n \end{bmatrix} \\[8pt] &= X\theta \end{align*} $$
Bước 2: Tính gradient
$$
\begin{align*}
L_\theta'
&=
\begin{bmatrix}
\dfrac{\mathrm dL}{dw_1} \\[4pt]
\dfrac{\mathrm dL}{dw_2} \\[2pt]
\vdots \\[2pt]
\dfrac{\mathrm dL}{dw_n}
\end{bmatrix}
=
\begin{bmatrix}
\dfrac{1}{m}\sum_{i=1}^{m}\dfrac{\mathrm dL_i}{dw_1} \\[4pt]
\dfrac{1}{m}\sum_{i=1}^{m}\dfrac{\mathrm dL_i}{dw_2} \\[2pt]
\vdots \\[2pt]
\dfrac{1}{m}\sum_{i=1}^{m}\dfrac{\mathrm dL_i}{dw_n}
\end{bmatrix}
=
\dfrac{1}{m}
\begin{bmatrix}
\sum_{i=1}^{m} \dfrac{\mathrm dL_i}{dw_1} \\
\sum_{i=1}^{m} \dfrac{\mathrm dL_i}{dw_2} \\
\vdots \\
\sum_{i=1}^{m} \dfrac{\mathrm dL_i}{dw_n}
\end{bmatrix} \\[8pt]
&=
\frac{1}{m}
\begin{bmatrix}
2(y_{pred}^1-y^1)x_1^1 +2(y_{pred}^2-y^2)x_1^2 + ... + 2(y_{pred}^m-y^m)x_1^m \cr
2(y_{pred}^1-y^1)x_2^1 +2(y_{pred}^2-y^2)x_2^2 + ... + 2(y_{pred}^m-y^m)x_2^m \cr
... \cr
2(y_{pred}^1-y^1)x_n^1 +2(y_{pred}^2-y^2)x_n^2 + ... + 2(y_{pred}^m-y^m)x_n^m
\end{bmatrix} \\[8pt]
&=
\dfrac{2}{m}
\begin{bmatrix}
x_1^1 & x_1^2 & \cdots & x_1^m \\
x_2^1 & x_2^2 & \cdots & x_2^m \\
\vdots & \vdots & \ddots & \vdots \\
x_n^1 & x_n^2 & \cdots & x_n^m
\end{bmatrix}
\begin{bmatrix}
y_{pred}^1 - y^1 \\
y_{pred}^2 - y^2 \\
\vdots \\
y_{pred}^m - y^m
\end{bmatrix} \\[8pt]
&= \dfrac{2}{m} X^T (y_{pred} - y)
\end{align*}
$$
Bước 3: Tương tự trường hợp 1 điểm dữ liệu
6. Tài liệu tham khảo:
-
Module 5, AIO2025
-
Giáo trình Đại số tuyến tính, Đặng Văn Vinh
-
Course Stanford CS229 - Andrew Ng.
Chưa có bình luận nào. Hãy là người đầu tiên!