Giới thiệu Explainable AI (XAI)
Trong kỷ nguyên trí tuệ nhân tạo hiện đại, các mô hình học sâu (Deep Learning) và những bộ phân loại phức tạp như Random Forest hay Gradient Boosted Trees đã đạt được thành tựu vượt trội trên nhiều lĩnh vực: từ nhận dạng khuôn mặt, chẩn đoán y khoa đến phân tích dữ liệu tài chính.
Tuy nhiên, cùng với khả năng dự đoán mạnh mẽ là sự đánh đổi về tính minh bạch. Con người có thể quan sát đầu ra của mô hình, nhưng không thể biết được điều gì bên trong “bộ não” của nó dẫn đến quyết định đó. Đây chính là hiện tượng được gọi là mô hình hộp đen (black-box models).
Vấn đề này đặt ra câu hỏi quan trọng: “Chúng ta có thể tin tưởng vào một mô hình mà chính ta không hiểu rõ cách nó suy nghĩ không?” Trong các lĩnh vực nhạy cảm như y tế hay tín dụng, việc thiếu giải thích không chỉ là vấn đề kỹ thuật mà còn là rủi ro đạo đức và pháp lý.
Explainable Artificial Intelligence (XAI) ra đời để khắc phục giới hạn đó. Mục tiêu của XAI là cung cấp những phương pháp và công cụ giúp con người hiểu được cách một mô hình học máy đưa ra quyết định, hoặc ít nhất có thể xác định được “điều gì quan trọng nhất” trong quá trình suy luận của mô hình. Việc hiểu này giúp tăng độ tin cậy, hỗ trợ kiểm định sai lệch (bias), và đảm bảo rằng quyết định của AI có thể được giải thích và bảo vệ trước các yêu cầu minh bạch như “right to explanation” trong quy định GDPR của Liên minh châu Âu.
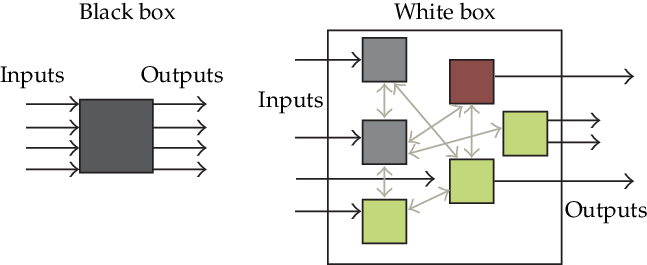
Black-box model và Transparent model
Phân loại các phương pháp Explainable AI
Các phương pháp XAI có thể được phân chia theo hai tiêu chí chính: (1) thời điểm áp dụng trong quá trình huấn luyện, và (2) phạm vi mà lời giải thích có hiệu lực.
1. Phân loại theo thời điểm áp dụng
Bảng tóm tắt sự khác biệt giữa hai nhóm Ante-hoc và Post-hoc.
| Tiêu chí | Ante-hoc (Intrinsic Explainability) | Post-hoc (Model-Agnostic Explainability) |
|---|---|---|
| Định nghĩa | Mô hình tự giải thích qua cấu trúc hoặc công thức rõ ràng. | Giải thích được sinh ra sau khi mô hình đã huấn luyện. |
| Cơ chế | Cấu trúc mô hình thể hiện mối quan hệ đặc trưng–kết quả (ví dụ: hệ số hồi quy). | Dựa trên quan sát đầu vào–đầu ra của “hộp đen”, không cần truy cập nội bộ mô hình. |
| Ví dụ điển hình | Linear Regression, Decision Tree, Rule-based Model. | LIME, SHAP, ANCHOR, Grad-CAM. |
| Ưu điểm | Minh bạch, dễ hiểu. | Áp dụng linh hoạt cho mọi loại mô hình. |
| Hạn chế | Không mô hình hóa được quan hệ phi tuyến phức tạp. | Đôi khi chỉ là “ước lượng cục bộ”, không phản ánh toàn mô hình. |
Phân loại phương pháp XAI theo thời điểm áp dụng
Các phương pháp Ante-hoc thường được sử dụng trong môi trường đòi hỏi
tính giải thích cao hơn hiệu suất, trong khi các kỹ thuật Post-hoc
ngày càng phổ biến nhờ khả năng mở rộng cho các mô hình phức tạp như
deep learning.
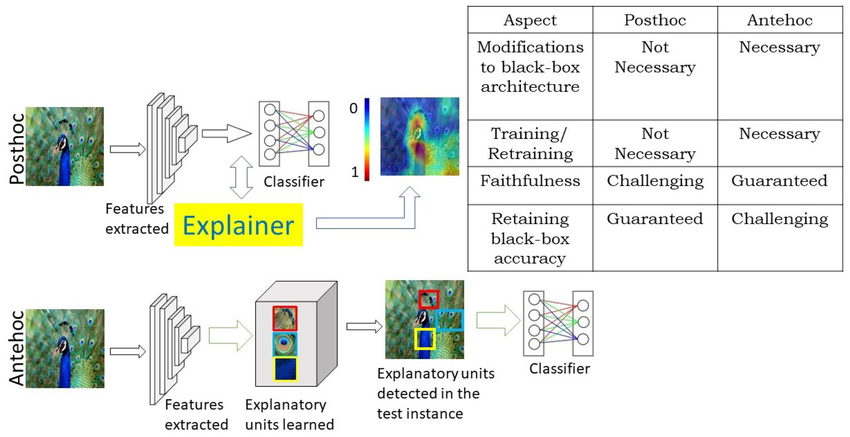
Post-hoc vs Ante-hoc
2. Phân loại theo phạm vi giải thích
Bảng minh họa sự khác biệt giữa giải thích toàn cục (global) và giải
thích cục bộ (local).
| Tiêu chí | Global Explanation | Local Explanation |
|---|---|---|
| Định nghĩa | Cung cấp cái nhìn tổng thể về hành vi của mô hình trên toàn bộ dữ liệu. | Tập trung vào giải thích cho một dự đoán cụ thể. |
| Câu hỏi đặc trưng | “Mô hình này nhìn chung coi trọng yếu tố nào nhất?” | “Tại sao mô hình đưa ra quyết định này cho mẫu này?” |
| Kỹ thuật phổ biến | Feature importance toàn cục, Partial Dependence Plot (PDP), SHAP summary. | LIME, ANCHOR, Counterfactual Explanations. |
| Ưu điểm | Giúp hiểu xu hướng chung của mô hình. | Giải thích cụ thể, dễ liên hệ thực tế. |
| Hạn chế | Có thể bỏ qua sự khác biệt giữa các cá thể. | Không khái quát được cho toàn bộ dữ liệu. |
Hai hướng này không loại trừ nhau mà bổ sung cho nhau: global giúp hiểu
tổng thể, local giúp hiểu chi tiết từng trường hợp.
Vị trí của LIME và ANCHOR trong Explainable AI
Trong bức tranh tổng thể của XAI, hai thuật toán LIME (Local
Interpretable Model-Agnostic Explanations) và ANCHOR (High-Precision Model-Agnostic Explanations) nằm tại giao điểm của hai trục: Post-hoc và Local Explanation.
Điều này có nghĩa là cả hai đều hoạt động sau khi mô hình đã huấn luyện, và mục tiêu của chúng là giải thích từng dự đoán riêng lẻ thay vì toàn bộ hành vi của mô hình. Khác biệt chủ yếu nằm ở bản chất lời giải thích:
- LIME mô tả ảnh hưởng của từng đặc trưng lên kết quả bằng cách xấp xỉ tuyến tính hành vi cục bộ của mô hình quanh điểm đang xét.
- ANCHOR diễn giải quyết định của mô hình bằng các quy tắc logic đủ mạnh để đảm bảo rằng khi các điều kiện đó đúng, mô hình hầu như sẽ không đổi kết quả.
Thuật toán LIME (Local Interpretable Model-Agnostic Explanations)
Động cơ (Motivation)
Thuật toán LIME được đề xuất bởi Ribeiro, Singh và Guestrin tại hội nghị KDD năm 2016 . Mục tiêu của họ là giải thích cục bộ (local) cách mà một mô hình phức tạp (như Random Forest, SVM, hay mạng nơ-ron sâu) đưa ra dự đoán. Thay vì tìm hiểu toàn bộ cơ chế của mô hình, LIME chỉ tập trung vào một điểm dữ liệu cụ thể, và tìm một mô hình đơn giản có thể xấp xỉ hành vi của mô hình gốc quanh điểm đó.
Một cách hình tượng, nếu ta "phóng to" một vùng nhỏ quanh điểm dữ liệu, ranh giới quyết định phức tạp của mô hình gốc có thể được xấp xỉ tuyến tính. Điều này tương tự việc tiếp tuyến mô phỏng đường cong trong giải tích (ở quy mô nhỏ, quan hệ phi tuyến trở nên tuyến tính.)
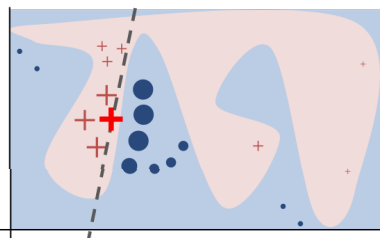
Ví dụ minh họa (toy example) để trình bày trực giác của LIME: Hàm quyết định phức tạp của mô hình hộp đen f (mà LIME không biết) được biểu diễn bằng phần nền màu xanh/hồng, và hàm này không thể được xấp xỉ tốt bằng một mô hình tuyến tính. Dấu cộng đỏ đậm là điểm dữ liệu cần được giải thích. LIME sẽ lấy mẫu nhiều điểm dữ liệu khác, dự đoán đầu ra bằng f, rồi gán trọng số cho mỗi điểm dựa trên độ gần với điểm đang được giải thích (kích thước điểm biểu diễn mức độ gần). Đường nét đứt là mô hình tuyến tính được học, nó phản ánh chính xác cục bộ (xung quanh điểm đó), nhưng không phản ánh toàn cục trên toàn bộ mô hình.
Cơ chế thuật toán
Giả sử ta có:
-
$`f`$: mô hình hộp đen cần giải thích (ví dụ CNN, SVM, RF).
-
$`x`$: điểm dữ liệu cần giải thích.
-
$`G`$: tập hợp các mô hình tuyến tính có thể dùng để xấp xỉ $`f`$.
Mục tiêu của LIME là tìm mô hình $`g \in G`$ sao cho mô hình đó vừa gần đúng hành vi của $`f`$ quanh $`x`$, vừa đủ đơn giản để con người hiểu được.
Phương trình tối ưu hóa cốt lõi:
$$
\xi(x) = \arg\min_{g \in G} \; L(f, g, \pi_x) + \Omega(g)
$$
Trong đó:
$L(f,g,\pi_x)$ là sai số giữa dự đoán của $f$ và $g$ trong vùng lân cận của $x$, có trọng số $\pi_x$.
$\pi_x(z)$ là hàm trọng số (kernel) đo mức “gần” giữa điểm $z$ và $x$, thường dùng Gaussian kernel:
$$
\pi_x(z) = \exp\left(-\frac{D(x,z)^2}{\sigma^2}\right)
$$
$\Omega(g)$ là hàm phạt độ phức tạp, đảm bảo mô hình $g$ không quá nhiều đặc trưng (thường giới hạn $`K`$ feature).
Thực tế, sai số $`L`$ được tính bằng tổng có trọng số:
$$
L(f,g,\pi_x) = \sum_{z \in Z} \pi_x(z) \left(f(z) - g(z)\right)^2
$$
với $Z$ là tập mẫu được tạo ngẫu nhiên quanh $x$ (gọi là perturbations).
| Ký hiệu | Ý nghĩa |
|---|---|
| $f$ | Mô hình hộp đen gốc (black-box model). |
| $g$ | Mô hình tuyến tính đơn giản dùng để xấp xỉ cục bộ. |
| $x$ | Điểm dữ liệu cần giải thích. |
| $Z$ | Tập các mẫu nhiễu quanh $`x`$. |
| $\pi_x(z)$ | Trọng số phản ánh độ gần của $`z`$ so với $x$. |
| $\Omega(g)$ | Mức phạt độ phức tạp của mô hình giải thích. |
| $L(f,g,\pi_x)$ | Hàm mất mát có trọng số. |
Các thành phần trong công thức LIME
Quy trình thuật toán LIME (K-LASSO Implementation)
Thuật toán LIME có thể mô tả theo các bước cụ thể như sau:
-
Tạo mẫu nhiễu: Sinh ra $`N`$ điểm dữ liệu mới bằng cách biến đổi ngẫu nhiên các đặc trưng quanh $`x`$.
-
Dự đoán bằng mô hình gốc: Với mỗi mẫu $`z_i`$, tính $`f(z_i)`$ — đầu ra của mô hình cần giải thích.
-
Tính trọng số locality: Gán trọng số $`\pi_x(z_i)`$ lớn cho các điểm gần $`x`$ hơn.
-
Chọn đặc trưng quan trọng: Áp dụng hồi quy LASSO (L1-regularization) để giữ lại $`K`$ đặc trưng có ảnh hưởng lớn nhất.
-
Huấn luyện mô hình giải thích: Xây dựng mô hình tuyến tính $`g`$ trên các mẫu đã gán trọng số.
-
Trình bày kết quả: Hiển thị các đặc trưng và hệ số trọng số của chúng dưới dạng biểu đồ hoặc bảng.
Ví dụ minh họa: LIME trên dữ liệu ảnh
Giả sử ta có mô hình ResNet50 được huấn luyện để phân loại ảnh động vật. Ta cần giải thích tại sao ảnh $`x`$ được mô hình dự đoán là “tailed frog”.
-
Ảnh $`x`$ được chia thành $`4`$ superpixels (vùng ảnh nhỏ đồng nhất).
-
LIME tạo ra hàng trăm biến thể của ảnh bằng cách bật/tắt ngẫu nhiên các vùng superpixel.
-
Mỗi biến thể $`z_i`$ được đưa qua ResNet50 để thu được xác suất $`P(f(z_i) = \text{``tailed frog''})`$.
-
Với mỗi biến thể, tính khoảng cách và trọng số $`\pi_x(z_i)`$.
-
Mô hình hồi quy tuyến tính được huấn luyện trên $`(z_i, f(z_i))`$ với trọng số $`\pi_x(z_i)`$.
-
Kết quả cho thấy các vùng quanh đầu và thân chó có hệ số dương cao nhất -> là vùng quan trọng nhất cho dự đoán “tailed frog”.


Kết quả giải thích của LIME
Triển khai LIME trong Python
Mã minh họa sau trình bày ba trường hợp sử dụng phổ biến: dữ liệu bảng, văn bản và hình ảnh. Các ví dụ này sử dụng thư viện lime phiên bản chính thức của Ribeiro et al.
# Import
from lime.lime_tabular import LimeTabularExplainer
# Create tabular explainer
explainer = LimeTabularExplainer(
training_data=X_train,
feature_names=feature_names,
class_names=class_names,
mode='classification'
)
# Explain one instance
exp = explainer.explain_instance(
data_row=X_test[5],
predict_fn=model.predict_proba,
num_features=5
)
# Result display
exp.show_in_notebook(show_table=True)
from lime.lime_text import LimeTextExplainer
# Define explainer
explainer = LimeTextExplainer(class_names=['Negative', 'Positive'])
# Choose sample
sample_text = "The movie was surprisingly good, with an amazing plot."
# Explain predictionprediction
exp = explainer.explain_instance(
text_instance=sample_text,
classifier_fn=model.predict_proba,
num_features=10
)
exp.show_in_notebook(text=True)
from lime import lime_image
from skimage.segmentation import mark_boundaries
import matplotlib.pyplot as plt
# Create LIME explainer
explainer = lime_image.LimeImageExplainer()
# Generating explanation
explanation = explainer.explain_instance(
image=image_array,
classifier_fn=model.predict,
top_labels=1,
num_samples=1000
)
# Extract most important area
temp, mask = explanation.get_image_and_mask(
label=explanation.top_labels[0],
positive_only=True,
num_features=5,
hide_rest=False
)
# Result displaydisplay
plt.imshow(mark_boundaries(temp / 255.0, mask))
plt.title("LIME explanation - important superpixels")
plt.axis('off')
plt.show()
Đánh giá và thảo luận
| Khía cạnh | Ưu điểm | Hạn chế |
|---|---|---|
| Tính tổng quát | Hoạt động trên mọi loại mô hình và dữ liệu. | Phụ thuộc vào cách sinh mẫu nhiễu. |
| Độ trực quan | Cung cấp biểu đồ trực quan, dễ hiểu. | Giải thích có thể thay đổi giữa lần chạy. |
| Tính ổn định | Cho phép kiểm tra nhanh tại nhiều điểm dữ liệu. | Không có đảm bảo về vùng bao phủ (coverage). |
| Độ chính xác | Có thể đạt độ tin cậy cao cục bộ. | Mất hiệu lực khi ra khỏi vùng lân cận. |
Tổng hợp ưu và nhược điểm của LIME
Nhìn chung, LIME là một công cụ mạnh mẽ giúp minh bạch hóa các mô hình hộp đen. Tuy nhiên, việc sinh nhiễu và giới hạn locality khiến kết quả của nó chỉ đáng tin trong vùng xung quanh điểm được giải thích.
ANCHOR, một thuật toán kế nhiệm, được phát triển để giải quyết chính hạn chế này bằng cách xác định rõ phạm vi mà giải thích còn hiệu lực.
Thuật toán ANCHOR
Động cơ (Motivation)
Mặc dù LIME giúp chúng ta hiểu được tầm quan trọng của từng đặc trưng trong dự đoán, nhưng một hạn chế lớn của LIME là nó không xác định rõ “vùng mà lời giải thích còn hiệu lực”. Nói cách khác, nếu một mẫu mới hơi khác so với mẫu được giải thích, ta không thể biết liệu giải thích của LIME có còn đúng hay không.
Để khắc phục điều đó, Ribeiro et al. (AAAI 2018) đã đề xuất ANCHOR —
một phương pháp giải thích dựa trên các quy tắc logic dạng “IF–THEN”, gọi là anchor rules. Mỗi anchor rule biểu diễn một tập điều kiện đủ sao cho nếu các điều kiện này đúng, mô hình sẽ gần như luôn đưa ra cùng một dự đoán.
Cụ thể, một quy tắc $`A`$ được coi là anchor của mẫu $`x`$ nếu:
$$
P(f(x') = f(x) \mid A(x') = 1) \geq \tau
$$
với $`\tau`$ là ngưỡng độ chính xác mong muốn (thường chọn 0.95).
Ví dụ:
IF income > 50k AND credit_score > 700 THEN prediction = Approved.
Trong ví dụ này, bất cứ người nào có thu nhập trên 50,000 USD và điểm tín dụng cao hơn 700 đều gần như chắc chắn được mô hình dự đoán là “Approved”. Không cần hiểu toàn bộ mô hình, chỉ cần quy tắc đủ mạnh để giữ nguyên dự đoán.
Công thức và định nghĩa chính
Để mô tả rõ hơn cơ chế của ANCHOR, ta cần hai khái niệm: Precision
(độ chính xác) và Coverage (độ bao phủ).
$$ \begin{align} \text{Precision: } & prec(A) = E_{x' \sim D(z|A)}[I(f(x') = f(x))] \\ \text{Coverage: } & cov(A) = P(A(x') = 1) \end{align} $$
Giải thích:
-
$`prec(A)`$ là xác suất mà mô hình $`f`$ đưa ra cùng dự đoán với $`x`$, khi tất cả điều kiện trong rule $`A`$ đều thỏa.
-
$`cov(A)`$ là xác suất (trên toàn tập dữ liệu) mà rule $`A`$ được thỏa mãn.
-
Hàm chỉ $`I(\cdot)`$ trả về 1 nếu điều kiện đúng, 0 nếu sai.
Mục tiêu của thuật toán là tối đa hóa độ bao phủ $`cov(A)`$ trong khi
vẫn đảm bảo độ chính xác $`prec(A)`$ vượt ngưỡng tin cậy $`\tau`$:
$$ \max_A \; cov(A) \quad \text{s.t.} \quad P(prec(A) \ge \tau) \ge 1 - \delta $$
Trong đó $`\delta`$ là tham số xác suất sai lệch nhỏ (ví dụ
$`\delta=0.05`$). Do không thể tính trực tiếp $`P(prec(A))`$, ANCHOR sử dụng kỹ thuật ước lượng bằng sampling kết hợp với giới hạn
Hoeffding và KL-LUCB (Kullback–Leibler Lower Upper Confidence
Bound) để đảm bảo sai số có giới hạn xác suất.
| Ký hiệu | Ý nghĩa |
|---|---|
| $`f(x)`$ | Dự đoán của mô hình tại mẫu $`x`$. |
| $`A(x)`$ | Tập điều kiện (rule) đang được xét. |
| $`\tau`$ | Ngưỡng độ chính xác mong muốn (thường 0.95). |
| $`\delta`$ | Xác suất sai lệch cho phép (ví dụ 0.05). |
| $`prec(A)`$ | Độ chính xác của rule $`A`$. |
| $`cov(A)`$ | Tỷ lệ dữ liệu thỏa mãn rule $`A`$. |
| KL-LUCB | Thuật toán tối ưu sampling dựa trên giới hạn Kullback–Leibler. |
Ký hiệu và ý nghĩa trong công thức ANCHOR
Chiến lược tìm kiếm Anchor Rule
Thuật toán ANCHOR sử dụng Beam Search để duyệt qua không gian các rule tiềm năng, kết hợp với KL-LUCB để xác định rule có độ chính xác đủ cao với ít mẫu nhất. Beam Search đảm bảo rằng chỉ giữ lại $`k`$ rule tốt nhất ở mỗi bước, giúp tránh bùng nổ tổ hợp.
Ví dụ minh họa: Titanic Dataset
Giả sử ta muốn giải thích quyết định “Survived” của mô hình phân loại trên tập Titanic.
| Rule (A) | Precision | Coverage | Valid? |
|---|---|---|---|
| Sex = female | 0.78 | 0.41 | No |
| Sex = female AND Pclass = 1 | 0.92 | 0.23 | No |
| Sex = female AND Pclass = 1 AND Age \< 30 | 0.97 | 0.18 | Yes |
Các rule ứng viên và độ chính xác tương ứng
Anchor cuối cùng được chọn là:
IF Sex = female AND Pclass = 1 AND Age < 30 THEN Survived = 1.
Điều này có nghĩa là nếu một hành khách là nữ, ở hạng nhất, và dưới 30 tuổi, mô hình dự đoán gần như chắc chắn rằng người này sống sót. Độ chính xác 0.97 thể hiện rằng 97% các mẫu thỏa rule này đều được mô hình dự đoán giống như mẫu ban đầu.
Triển khai ANCHOR trong Python
# ----------------------------------------------------------
# ANCHOR for tabular data
# ----------------------------------------------------------
from anchor import anchor_tabular
# Explainer init
explainer = anchor_tabular.AnchorTabularExplainer(
class_names = class_names,
feature_names = feature_names,
train_data = X_train
)
# Explain instance
exp = explainer.explain_instance(
data_row = X_test[0],
predict_fn = model.predict
)
# result display
print("Anchor rule:", exp.names())
print("Precision:", exp.precision())
print("Coverage:", exp.coverage())
# ----------------------------------------------------------
# ANCHOR for text
# ----------------------------------------------------------
from alibi.explainers import AnchorText
# Explainer initialization
explainer = AnchorText(predict_fn = model.predict)
# Explain instance
exp = explainer.explain_instance(
text = "I absolutely loved this movie!"
)
print("Anchor:", exp.anchor)
print("Precision:", exp.precision)
print("Coverage:", exp.coverage)
# ----------------------------------------------------------
# ANCHOR for image
# ----------------------------------------------------------
from alibi.explainers import AnchorImage
# Explainer init
explainer = AnchorImage(
predict_fn = model.predict,
segmentation_fn = 'slic'
)
# Explain instance with 95% threshold
exp = explainer.explain_instance(
image = image_array,
threshold = 0.95
)
# Result display
exp.visualise_image()
Phân tích ưu và nhược điểm
| Khía cạnh | Ưu điểm | Hạn chế |
|---|---|---|
| Dạng giải thích | Quy tắc logic IF–THEN rõ ràng, dễ hiểu. | Có thể sinh rule quá cụ thể. |
| Độ tin cậy | Có đảm bảo xác suất (confidence bound). | Độ chính xác phụ thuộc số lượng mẫu lấy. |
| Phạm vi áp dụng | Có vùng bao phủ rõ ràng (coverage). | Coverage nhỏ với rule phức tạp. |
| Hiệu năng | Ổn định hơn LIME. | Tốn thời gian sampling và ước lượng. |
Tổng hợp ưu và nhược điểm của ANCHOR
ANCHOR mang lại bước tiến lớn trong khả năng giải thích cục bộ nhờ việc định nghĩa các vùng mà lời giải thích còn hiệu lực. Khác với LIME chỉ “ước lượng tuyến tính”, ANCHOR cung cấp “điều kiện đủ” có thể kiểm chứng và tái sử dụng trong thực tế.
So sánh LIME và ANCHOR
| Tiêu chí | LIME | ANCHOR |
|---|---|---|
| Dạng giải thích | Feature weights | IF–THEN rule |
| Độ tin cậy | Trung bình | Cao (≥ τ) |
| Vùng áp dụng | Không rõ | Rõ ràng |
| Phức tạp tính toán | Thấp | Cao hơn |
| Hỗ trợ dữ liệu | Tabular, Text, Image | Tabular, Text, Image |
So sánh LIME và ANCHOR.
Kết luận
-
LIME cung cấp giải thích tuyến tính đơn giản, dễ hiểu nhưng vùng
áp dụng không rõ. -
ANCHOR mở rộng bằng các quy tắc logic có tính “điều kiện đủ”, giúp
người dùng hiểu rõ khi nào giải thích còn hiệu lực. -
Kết hợp cả hai mang lại framework XAI toàn diện: LIME cho khám phá
nhanh, ANCHOR cho xác minh chắc chắn.
Chưa có bình luận nào. Hãy là người đầu tiên!