CHƯƠNG 5: VECTORIZATION TRONG BÀI TOÁN LINEAR REGRESSION
Trong các phần trước, chúng ta đã tìm hiểu về cách mô hình Linear Regression hoạt động – từ việc dự đoán các giá trị đầu ra thông qua hàm tuyến tính đến việc đo lường sai số bằng các hàm MAE và MSE, đồng thời tìm hiểu nâng cao về hàm loss và cách để tối thiểu hóa hàm loss thông qua việc điều chỉnh các hệ số $\omega$ và b. Tuy nhiên, nếu chỉ dừng lại ở việc biểu diễn từng công thức trên giấy, việc triển khai mô hình trong thực tế – đặc biệt khi dữ liệu có hàng nghìn hoặc hàng triệu samples – sẽ trở nên rất tốn thời gian nếu chúng ta tính toán theo kiểu sample by sample. Vectorization trong Linear Regression ra đời để giải quyết vấn đề này. Trong phần này, chúng ta sẽ cùng nhau tìm hiểu chi tiết:
- Vectorization là gì? Vì sao nó cần thiết trong Linear Regression
- Cách biểu diễn mô hình và hàm loss
- Một ví dụ tính toán Vectorization thực tế.
Trong bài viết này, tôi sẽ sử dụng một số cách viết khác nhau để ký hiệu:
- x (viết thường) biểu thị cho một số
- x (viết in đậm) biểu thị cho một vector
- X (viết in đậm in hoa) biểu thị cho một ma trận
- m biểu thị cho số sample (batch size)
- n biểu thị cho số đặc trưng (feature dimension)
5.1 Khái niệm chung về Vectorization
5.1.1 Nhược điểm của Linear Regression truyền thống
Trước khi bắt đầu vào phần Vectorization, chúng ta cùng nhắc lại công thức cơ bản của Linear Regression mà các phần trên đã đề cập.
Giả sử ta có tập dữ liệu gồm m samples, n features, thì ta sẽ huấn luyện mô hình Linear Regression theo công thức quen thuộc:
$$ \hat{y}^i = \omega_1 x_1^i + \omega_2 x_2^i + \omega_3 x_3^i + \ldots + \omega_n x_n^i + b \tag{1} $$
Với:
- $x_1, x_2, \ldots, x_n$: Các features
- $\omega_1, \omega_2, \ldots, \omega_n$: Các trọng số (weights)
- $b$: Hệ số bias
Từ đây, ta bắt đầu xây dựng các công thức tính loss, tính gradient và cuối cùng là cập nhật trọng số.

Hình 5.1: Định nghĩa các công thức trong hàm Linear Regression
Sau khi xây dựng xong các công thức cần thiết, ta đưa các dữ liệu thực tế và duyệt qua từng sample trong tập dữ liệu:

Hình 5.2: Hàm Linear Regression truyền thống
Tuy nhiên, cách làm này có rất nhiều nhược điểm. Việc sử dụng hàm 'for' khiến cho mô hình chỉ có thể xử lý một sample duy nhất cho mỗi lần lặp, vì thế nếu tập dữ liệu có 10.000 hoặc 100.000 samples, thời gian huấn luyện sẽ tăng lên gấp hàng trăm lần. Ngoài ra, khi số features tăng, việc viết công thức và tính toán trở nên rối rắm và thiếu sai sót. Vì vậy, Vectorization ra đời để cải thiện các nhược điểm này.
5.1.2 Khái niệm Vectorization
Vectorization là quá trình biểu diễn các phép toán trên dữ liệu dạng vector và ma trận, thay vì xử lý từng phần tử riêng lẻ. Khi đó, toàn bộ phép tính có thể được thực hiện một cách song song và tối ưu hóa giúp chương trình chạy nhanh hơn và gọn hơn. Các thư viện như NumPy hay TensorFlow đều tối ưu hóa các phép nhân ma trận và nhân vector bằng thư viện C/C++ hoặc CUDA, cho phép mô hình có thể xử lý hàng triệu phép tính trong một lần gọi hàm. Điều này sẽ làm cho việc tính loss, gradient và cập nhật tham số trở nên nhanh chóng, chính xác và có thể mở rộng cho nhiều samples và features hơn. Phần tiếp theo sẽ đi sâu hơn vào cách thức hiện Vectorization trong Linear Regression.
5.2 Các bước thiết lập công thức
5.2.1 Vectorization 1-sample
a) Viết lại công thức dưới dạng vector
Ta giả định tập dữ liệu gồm n features, thì ta sẽ huấn luyện mô hình Linear Regression theo công thức:
$$ \hat{y} = \omega_1 x_1 + \omega_2 x_2 + \ldots + \omega_n x_n \tag{2} $$
Các biến trong công thức này hoàn toàn có thể được biểu diễn gọn gàng bằng cách nhóm tất cả các hệ số lại với nhau dưới dạng vector.
$$ \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}, \quad \boldsymbol{\omega} = \begin{bmatrix} \omega_1 \\ \omega_2 \\ \vdots \\ \omega_n \end{bmatrix} \tag{3} $$
Lúc này, công thức $\omega_1 x_1 + \omega_2 x_2 + \ldots + \omega_n x_n$ sẽ tương đương với $\boldsymbol{\omega}^T \mathbf{x}$.
Khi đó công thức dự đoán có thể được viết gọn thành tích vô hướng (dot product):
$$ \hat{y} = \boldsymbol{\omega}^T \mathbf{x} + b \tag{4} $$
Tuy nhiên công thức vẫn còn thành phần riêng lẻ ở ngoài tích vô hướng là hệ số bias. Để gộp nó vào cùng dạng vector, ta thực hiện một thủ thuật, đó là thêm hệ số bias vào đầu vector weights, và thêm phần tử 1 vào đầu vector của x để vector x và vector bias có cùng dimension. Khi này, ta định nghĩa:
$$ \mathbf{x} = \begin{bmatrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}, \quad \boldsymbol{\theta} = \begin{bmatrix} b \\ \omega_1 \\ \omega_2 \\ \vdots \\ \omega_n \end{bmatrix} \tag{5} $$
Từ đây, mô hình Linear Regression cho một sample đã trở nên đồng nhất:
$$ \hat{y} = \boldsymbol{\theta}^T \mathbf{x} \tag{6} $$
b) Công thức hàm mất mát (loss function)
Công thức tính loss function vẫn giống như trong công thức gốc:
$$ L = (\hat{y} - y)^2 \tag{7} $$
c) Công thức đạo hàm (gradient)
Trong công thức gốc, ta có các hàm tính gradient được định nghĩa là đạo hàm của hàm loss theo hệ số weight và bias:
$$ \begin{aligned} \frac{\partial L}{\partial b} &= 2(\hat{y} - y) \times 1 \\ \frac{\partial L}{\partial \omega} &= 2(\hat{y} - y) \times x \end{aligned} \tag{8} $$
Nếu đặt 2 công thức này vào cùng một vector cột, ta sẽ được vector:
$$ \begin{bmatrix} 2(\hat{y} - y) \times 1 \\ 2(\hat{y} - y) \times x \end{bmatrix} \tag{9} $$
Nhóm các thừa số chung ra ngoài, ta được:
$$ \nabla_{\boldsymbol{\theta}} L = \begin{bmatrix} \frac{\partial L}{\partial b} \\ \frac{\partial L}{\partial \boldsymbol{\omega}} \end{bmatrix} = \begin{bmatrix} 2(\hat{y} - y) \times 1 \\ 2(\hat{y} - y) \times x \end{bmatrix} = 2(\hat{y} - y) \begin{bmatrix} 1 \\ x \end{bmatrix} = 2(\hat{y} - y) \mathbf{x} $$
$$ \nabla_{\boldsymbol{\theta}} L = 2(\hat{y} - y) \mathbf{x} \tag{10} $$
d) Cập nhật các trọng số
Bước cuối cùng trong 1 chu trình của Linear Regression là cập nhật lại các trọng số $\omega$ và b. Theo cách truyền thống, các trọng số $\omega$ và b được tính như sau:
$$ \begin{aligned} b_{new} &= b_{old} - \eta \frac{\partial L}{\partial b} \\ \omega_{new} &= \omega_{old} - \eta \frac{\partial L}{\partial \omega} \end{aligned} \tag{11} $$
Đặt 2 công thức này vào 1 vector, ta có công thức cập nhật lại vector trọng số:
$$ \theta_{new} = \theta_{old} - \eta \nabla_\theta L \tag{12} $$
Sau khi đã cập nhật trọng số mới, mô hình sẽ sử dụng chúng để dự đoán cho các sample tiếp theo, mở đầu cho một chu kì mới.
5.2.2 m-sample Vectorization
Trong thực tế, mô hình không được huấn luyện trên từng sample riêng lẻ mà trên một tập gồm hàng nghìn đến hàng triệu samples. Vì thế, trong phần này chúng ta sẽ cùng mở rộng cách biểu diễn sang m-sample vectorization, nơi mọi phép tính đều được thực hiện đồng thời trên m samples trong một lần tính toán.
a) Viết lại công thức dưới dạng Vector
Trong bài toán này, x không còn là 1 vector cột n chiều nữa mà trở thành 1 ma trận. Sở dĩ có điều này vì mỗi sample x có cùng số chiều có thể viết riêng biệt như:
$$ \mathbf{x}^{(1)} = \begin{bmatrix} 1 \\ x_1^{(1)} \\ x_2^{(1)} \\ \vdots \\ x_n^{(1)} \end{bmatrix}, \quad \mathbf{x}^{(2)} = \begin{bmatrix} 1 \\ x_1^{(2)} \\ x_2^{(2)} \\ \vdots \\ x_n^{(2)} \end{bmatrix}, \quad \dots, \quad \mathbf{x}^{(m)} = \begin{bmatrix} 1 \\ x_1^{(m)} \\ x_2^{(m)} \\ \vdots \\ x_n^{(m)} \end{bmatrix} \tag{13} $$
Như vậy, ta đang có m vector cột, mỗi vector biểu diễn một sample. Thay vì dữ m vector riêng lẻ, ta có thể gom toàn bộ chúng lại thành 1 ma trận duy nhất bằng cách xếp từng vector sample thành 1 hàng của ma trận X:
$$ \mathbf{X} = \begin{bmatrix} (\mathbf{x}^{(1)})^T \\ (\mathbf{x}^{(2)})^T \\ \vdots \\ (\mathbf{x}^{(m)})^T \end{bmatrix} = \begin{bmatrix} 1 & x_1^{(1)} & x_2^{(1)} & \cdots & x_n^{(1)} \\ 1 & x_1^{(2)} & x_2^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_1^{(m)} & x_2^{(m)} & \cdots & x_n^{(m)} \end{bmatrix} \tag{14} $$
Đồng thời, dựa vào công thức của $\theta$ ở công thức số 5, ta có thể viết được phương trình cho mô hình Linear Regression với m-sample:
$$ \hat{\mathbf{y}} = \begin{bmatrix} 1 & x_1^{(1)} & x_2^{(1)} & \cdots & x_n^{(1)} \\ 1 & x_1^{(2)} & x_2^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_1^{(m)} & x_2^{(m)} & \cdots & x_n^{(m)} \end{bmatrix} \begin{bmatrix} b \\ \omega_1 \\ \omega_2 \\ \vdots \\ \omega_n \end{bmatrix} \tag{15} $$
Vector $\hat{\mathbf{Y}}$ lúc này là vector cột với kích thước $m \times 1$
Cần lưu ý rằng đây không phải công thức duy nhất trong trường hợp này. Có nhiều cách sắp xếp các phần tử của ma trận $\mathbf{X}$ và vector $\boldsymbol{\theta}$, tuy nhiên phương trình phải đảm bảo chiều của 2 phần tử để có thể tính được tích vô hướng. Ví dụ nếu ma trận $\mathbf{X}$ và vector $\boldsymbol{\theta}$ có dạng
$$ \mathbf{X} = \begin{bmatrix} x_1^{(1)} & x_1^{(2)} & x_1^{(3)} & \cdots & x_1^{(m)} \\ x_2^{(1)} & x_2^{(2)} & x_2^{(3)} & \cdots & x_2^{(m)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & 1 & \cdots & 1 \end{bmatrix}, \quad \boldsymbol{\theta} = \begin{bmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \\ \vdots \\ b \end{bmatrix} \tag{16} $$
Thì công thức của $\hat{\mathbf{Y}}$ là
$$ \hat{\mathbf{y}} = \boldsymbol{\theta}^T \mathbf{X} \tag{17} $$
Khi này, $\hat{\mathbf{Y}}$ sẽ trở thành vector hàng với kích thước $1 \times m$
b) Công thức hàm mất mát (Loss function)
Trong công thức Linear Regression truyền thống cũng như trường hợp 1-sample Vectorization, $\hat{y}$ và y là một số thực, vì vậy Loss function có thể dễ dàng tính được. Tuy nhiên trong trường hợp này, $\hat{\mathbf{Y}}$ lại là các vector cột có chiều là $(n+1) \times 1$. Vì vậy, công thức cần phải biến đổi để có thể tính toán được. Trong trường hợp này, mô hình phải tính toán trên một số lượng samples nhất định, chúng ta sẽ không muốn giá trị loss phụ thuộc vào số lượng mẫu, nên chúng ta sẽ sử dụng MSE, lấy trung bình bình phương sai số của loss. Ta có công thức tính loss function gốc được biến đổi:
$$ \begin{aligned} L &= \frac{1}{m} \sum_i (\hat{y}^{(i)} - y^{(i)})^2 \\ &= \frac{1}{m} [(\hat{y}^{(0)} - y^{(0)})^2 + (\hat{y}^{(1)} - y^{(1)})^2 + \cdots] \\ &= \frac{1}{m} \begin{bmatrix} \hat{y}^{(0)} - y^{(0)} & \hat{y}^{(1)} - y^{(1)} & \cdots \end{bmatrix} \begin{bmatrix} \hat{y}^{(0)} - y^{(0)} \\ \hat{y}^{(1)} - y^{(1)} \\ \vdots \end{bmatrix} \\ &= \frac{1}{m} (\hat{\mathbf{y}} - \mathbf{y})(\hat{\mathbf{y}} - \mathbf{y})^T \end{aligned} \tag{18} $$
c) Công thức đạo hàm (gradient)
Từ công thức số (10), chúng ta biến đổi cho phù hợp với số chiều của các phần tử.
Đặt $k = 2(\hat{\mathbf{y}} - \mathbf{y})$, lúc này k sẽ có chiều là $m \times 1$ giống với chiều của $\hat{\mathbf{y}}$. Từ đây, ta nhân vector k với ma trận $\mathbf{X}$ sử dụng element-wise multiplication:
$$ \begin{aligned} k \odot \mathbf{X} &= \begin{bmatrix} k_1 \\ k_2 \\ \vdots \\ k_m \end{bmatrix} \odot \begin{bmatrix} 1 & x_1^{(1)} & x_2^{(1)} & \cdots & x_n^{(1)} \\ 1 & x_1^{(2)} & x_2^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_1^{(m)} & x_2^{(m)} & \cdots & x_n^{(m)} \end{bmatrix} \\ &= \begin{bmatrix} k_1 & x_1^{(1)} k_1 & x_2^{(1)} k_1 & \cdots & x_n^{(1)} k_1 \\ k_2 & x_1^{(2)} k_2 & x_2^{(2)} k_2 & \cdots & x_n^{(2)} k_2 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ k_m & x_1^{(m)} k_m & x_2^{(m)} k_m & \cdots & x_n^{(m)} k_m \end{bmatrix} \end{aligned} \tag{19} $$
Nhân 1 vector hàng $1 \times m$ với ma trận trên để tổng hợp các hệ số, ta được công thức tính gradient:
$$ \nabla_\theta L = \begin{bmatrix} 1 & 1 & \cdots & 1 \end{bmatrix} (k \odot \mathbf{X}) = \begin{bmatrix} b_{grad} & \omega_{grad}^{(1)} & \cdots & \omega_{grad}^{(m)} \end{bmatrix} \tag{20} $$
Với $b_{grad}$ là hệ số cập nhật cho b, $\omega_{grad}$ là hệ số cập nhật cho $\omega$.
d) Cập nhật hệ số
Bước cuối cùng là cập nhật lại hệ số $\omega$ và b qua $\boldsymbol{\theta}$
$$ \boldsymbol{\theta}_{new} = \boldsymbol{\theta}_{old} - \eta \frac{(\nabla_\theta L)^T}{m} \tag{21} $$
Sau khi đã cập nhật các giá trị $\omega$ và b, ta quay lại bước đầu tiên, sử dụng các dữ liệu tiếp theo với các hệ số $\omega$ và b đã được cập nhật.
5.3 Ví dụ cụ thể
Sau khi đã làm rõ các công thức cũng như các bước tính toán, sau đây là một ví dụ cụ thể về bài toán Linear Regression. Ở phần này, nhóm sử dụng dữ liệu advertising.csv đã được đề cập trong bài làm ví dụ. Hình 3 cho thấy 5 samples đầu tiên của dữ liệu:
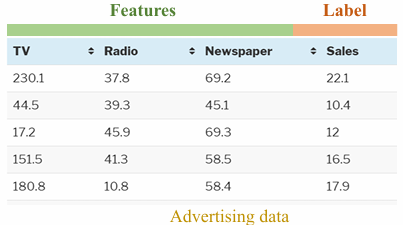
Hình 5.3: Dữ liệu cho ví dụ
Các giá trị khởi tạo ban đầu được nhóm thiết lập trước bao gồm learning rate (lr) = 0.01, $\omega = 0.1$, $b = 0$. Từ các giá trị cho trước này, ta có vector $\boldsymbol{\theta}$:
Bước 1: Tính toán $\hat{\mathbf{y}}$
Áp dụng công thức (14) tính được ma trận $\mathbf{X}$
$$ \mathbf{X} = \begin{bmatrix} 1 & 230.1 & 37.8 & 69.2 \\ 1 & 44.5 & 39.3 & 45.1 \\ 1 & 17.2 & 45.9 & 69.3 \\ 1 & 151.5 & 41.3 & 58.5 \\ 1 & 180.8 & 10.8 & 58.4 \end{bmatrix} \tag{22} $$
Có $\mathbf{X}$ và $\boldsymbol{\theta}$, ta tính được $\hat{\mathbf{y}}$ dựa vào công thức (15):
$$ \hat{\mathbf{y}} = \begin{bmatrix} 1 & 230.1 & 37.8 & 69.2 \\ 1 & 44.5 & 39.3 & 45.1 \\ 1 & 17.2 & 45.9 & 69.3 \\ 1 & 151.5 & 41.3 & 58.5 \\ 1 & 180.8 & 10.8 & 58.4 \end{bmatrix} \begin{bmatrix} 0 \\ 0.1 \\ 0.1 \\ 0.1 \end{bmatrix} = \begin{bmatrix} 33.71 \\ 12.89 \\ 13.24 \\ 25.13 \\ 24.99 \end{bmatrix} \tag{23} $$
Bước 2: Tính hàm loss
Dựa vào công thức (18), ta có hàm loss:
$$ \begin{aligned} L &= \frac{1}{m}(\hat{\mathbf{y}} - \mathbf{y})(\hat{\mathbf{y}} - \mathbf{y})^T \\ &= \frac{1}{5} \left( \begin{bmatrix} 33.71 \\ 12.89 \\ 13.24 \\ 25.13 \\ 24.99 \end{bmatrix} - \begin{bmatrix} 22.1 \\ 10.4 \\ 12 \\ 16.5 \\ 17.9 \end{bmatrix} \right) \left( \begin{bmatrix} 33.71 \\ 12.89 \\ 13.24 \\ 25.13 \\ 24.99 \end{bmatrix} - \begin{bmatrix} 22.1 \\ 10.4 \\ 12 \\ 16.5 \\ 17.9 \end{bmatrix} \right)^T \end{aligned} \tag{24} $$
Bước 3: Tính gradient
Đặt $k = 2(\hat{\mathbf{y}} - \mathbf{y})$. Ta có:
$$ k = 2\left( \begin{bmatrix} 33.71 \\ 12.89 \\ 13.24 \\ 25.13 \\ 24.99 \end{bmatrix} - \begin{bmatrix} 22.1 \\ 10.4 \\ 12 \\ 16.5 \\ 17.9 \end{bmatrix} \right) = \begin{bmatrix} 23.22 \\ 5.0 \\ 2.48 \\ 17.26 \\ 14.18 \end{bmatrix} \tag{25} $$
$$ \begin{aligned} \nabla_\theta L &= \begin{bmatrix} 1 & 1 & 1 & 1 & 1 \end{bmatrix} (k \odot \mathbf{X}) \\ &= \begin{bmatrix} 1 & 1 & 1 & 1 & 1 \end{bmatrix} \left( \begin{bmatrix} 23.22 \\ 5.0 \\ 2.48 \\ 17.26 \\ 14.18 \end{bmatrix} \odot \begin{bmatrix} 1 & 230.1 & 37.8 & 69.2 \\ 1 & 44.5 & 39.3 & 45.1 \\ 1 & 17.2 & 45.9 & 69.3 \\ 1 & 151.5 & 41.3 & 58.5 \\ 1 & 180.8 & 10.8 & 58.4 \end{bmatrix} \right) \\ &= \begin{bmatrix} 1 & 1 & 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} 23.22 & 5342.922 & 877.716 & 1606.824 \\ 5.0 & 222.5 & 196.5 & 225.5 \\ 2.48 & 42.656 & 113.832 & 171.864 \\ 17.26 & 2614.89 & 712.838 & 1009.71 \\ 14.18 & 2563.744 & 153.144 & 828.112 \end{bmatrix} \\ &= \begin{bmatrix} 62.14 & 10786.712 & 2063.03 & 3842.01 \end{bmatrix} \end{aligned} \tag{26} $$
Bước 4: Cập nhật lại các trọng số
Bước cuối cùng là cập nhật lại các trọng số:
$$ \begin{aligned} \boldsymbol{\theta}_{new} &= \boldsymbol{\theta}_{old} - \eta \frac{(\nabla_\theta L)^T}{m} \\ &= \begin{bmatrix} 0 \\ 0.1 \\ 0.1 \\ 0.1 \end{bmatrix} - \frac{0.01}{5} \begin{bmatrix} 62.14 \\ 10786.712 \\ 2063.03 \\ 3842.01 \end{bmatrix} \\ &= \begin{bmatrix} -0.1243 \\ -21.473 \\ -4.026 \\ -7.584 \end{bmatrix} \end{aligned} \tag{27} $$
Từ đây, chúng ta sẽ sử dụng giá trị $\boldsymbol{\theta}_{new}$ để tiếp tục thực hiện bài toán với 5 samples tiếp theo. Quá trình sẽ lặp lại cho đến khi lặp qua tất cả các giá trị trong bảng dữ liệu.
Chưa có bình luận nào. Hãy là người đầu tiên!