Ứng dụng Linear Regression & Chuẩn hóa dữ liệu trong Thực tế
Hồi quy tuyến tính (Linear Regression) là nền tảng của Machine Learning dự đoán giá trị liên tục. Bài viết này sẽ đi sâu vào cách xây dựng, tối ưu hóa mô hình Linear Regression một cách hiệu quả bằng kỹ thuật vectorization và các công cụ nâng cao như Chuẩn hóa dữ liệu và Regularization.
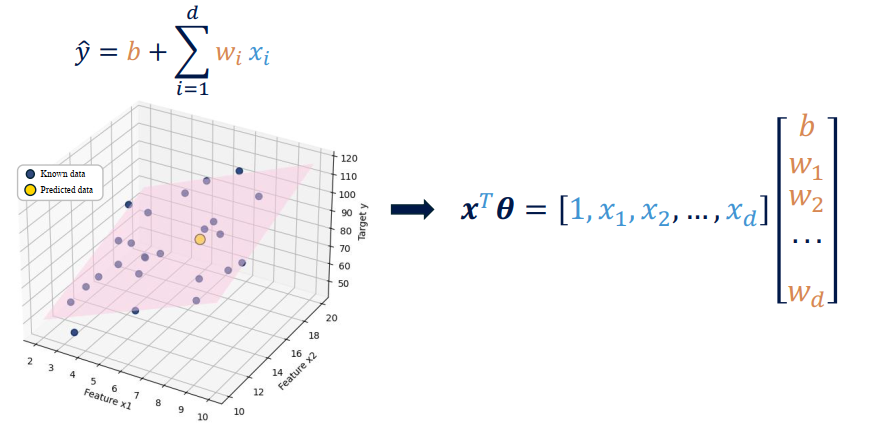
Hình 1: Minh họa mô hình hồi quy tuyến tính dưới dạng vector hóa với d đặc trưng trong không gian ba chiều [1].
I. Lý Thuyết Cơ Bản: Từ Mô Hình Đơn Giản đến Vector Hóa
1. Mô Hình Simple Linear Regression
Trong trường hợp đơn giản nhất, Linear Regression mô tả mối quan hệ giữa một biến đầu vào x và biến mục tiêu ŷ qua một đường thẳng:
$$\hat{y} = wx + b$$
Trong đó $w$ là trọng số và $b$ là bias (hệ số chặn). Bias $b$ cho phép dịch chuyển đường hồi quy để nó không bị ràng buộc đi qua gốc tọa độ.
2. Tối Ưu Hóa: Hàm Mất Mát (Loss Function)
Mục tiêu là tìm w và b sao cho tổng sai số giữa giá trị dự đoán (ŷ) và giá trị thực tế (y) là nhỏ nhất. Mean Squared Error (MSE) là hàm mất mát phổ biến nhất:
$$L(\hat{y}, y) = (\hat{y} - y)^2 \quad \text{(cho 1 mẫu)}$$
$$L(\hat{y}, y) = \frac{1}{N} \sum_{i=1}^{N} (\hat{y}^{(i)} - y^{(i)})^2 \quad \text{(cho N mẫu)}$$
3. Sức Mạnh của Vectorization (Vector Hóa)
Khi số lượng đặc trưng ($d$) tăng lên, việc viết và tính toán từng trọng số riêng lẻ là kém tối ưu. Vectorization sử dụng đại số tuyến tính để tính toán đồng thời tất cả các phép toán trên toàn bộ dữ liệu.
Tham số hợp nhất: Các trọng số ($w_i$) và bias ($b$) được gộp vào một Vector tham số θ:
$$\theta = \begin{bmatrix} b \\ w_1 \\ \vdots \\ w_d \end{bmatrix}$$
Dự đoán: Cột 1 được thêm vào ma trận đặc trưng X để nhân với bias, và dự đoán được tính bằng phép nhân ma trận-vector:
$$\hat{y} = X\theta$$
II. Tối Ưu Hóa Mô Hình Bằng Gradient Descent (GD)
Gradient Descent (GD) là cơ chế cốt lõi để cập nhật $\theta$ (gồm $w$ và $b$) theo hướng giảm Loss nhanh nhất.
1. Các Biến Thể Gradient Descent Vector Hóa
Có ba chiến lược chính để tính toán gradient và cập nhật tham số:
| Biến thể | Mẫu/Lần cập nhật | Cập nhật/Epoch | Đặc điểm |
|---|---|---|---|
| Batch GD (BGD) | $N$ (Toàn bộ dữ liệu) | 1 | Ổn định nhưng chậm, cần bộ nhớ cao |
| Mini-batch GD (MBGD) | $m$ (Mini-batch) | $N/m$ | Cân bằng giữa tốc độ và sự ổn định |
| Stochastic GD (SGD) | 1 (Mẫu ngẫu nhiên) | $N$ | Nhanh ban đầu, hội tụ nhiễu và chậm cuối cùng |
2. Công thức Gradient Vector Hóa (Batch/Mini-batch)
Trong mỗi bước lặp, gradient cho tất cả tham số θ được tính bằng ma trận:
$$\nabla_{\theta}L = \frac{2}{m} X^T (\hat{y} - y)$$
Sau đó, tham số được cập nhật:
$$\theta = \theta - \eta \nabla_{\theta}L \quad \text{($\eta$ là Learning Rate)}$$
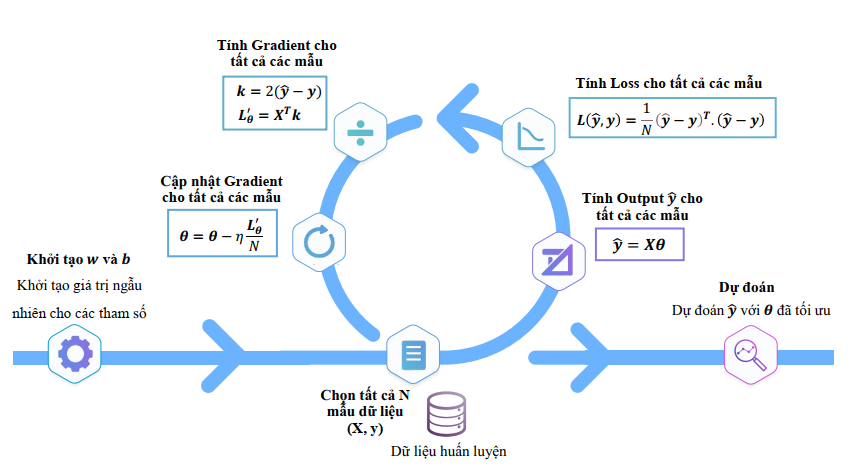
Hình 2: Pipeline tổng quát qua các bước tính toán để tối ưu hóa tham số θ (bao gồm cả trọng số w và bias b) sử dụng phương pháp vectorization [1].
3. Chi Tiết Thuật Toán Stochastic Gradient Descent (SGD)
Thuật toán SGD cập nhật tham số dựa trên từng mẫu dữ liệu một (tương ứng với $m=1$ mẫu mỗi bước).
| Bước | Mô tả | Công thức/Ký hiệu |
|---|---|---|
| Step 1 | Khởi tạo | Khởi tạo vector tham số $\theta$ (gộp $w$ và $b$) $$\theta = \begin{bmatrix} w_1 \\ \vdots \\ w_d \\ b \end{bmatrix} \in \mathbb{R}^{(d+1)}, \quad \theta \sim \mathcal{N}(0, 0.01^2 I_{d+1})$$ |
| Step 2 | Lấy một mẫu | Chọn một cặp dữ liệu duy nhất $(x, y)$ $$x = \begin{bmatrix} x_1 \\ \vdots \\ x_d \\ 1 \end{bmatrix} \in \mathbb{R}^{(d+1)}, \quad y \in \mathbb{R}$$ |
| Step 3 | Dự đoán | Tính giá trị dự đoán (Vector hóa) $$\hat{y} = x^{\top}\theta = \theta^{\top}x \in \mathbb{R}$$ |
| Step 4 | Mất mát | Tính hàm mất mát MSE cho mẫu đó $$L = (\hat{y} - y)^2$$ |
| Step 5 | Gradient | Tính vector gradient của Loss theo $\theta$ $$\nabla_{\theta}L = 2x(\hat{y} - y) \in \mathbb{R}^{(d+1)}$$ |
| Step 6 | Cập nhật | Cập nhật tham số (với learning rate $\alpha$) $$\theta \leftarrow \theta - \alpha \nabla_{\theta}L$$ |
| Lặp lại | Lặp lại từ Step 2 qua các mẫu cho đến khi hội tụ |
4. Chi Tiết Thuật Toán Mini-batch Gradient Descent (Vectorized)
| Bước | Mô tả | Chi tiết |
|---|---|---|
| Step 1 | Khởi tạo | Khởi tạo vector tham số $\theta$ $$\theta = \begin{bmatrix} w_1 \\ \vdots \\ w_d \\ b \end{bmatrix} \in \mathbb{R}^{(d+1)}, \quad \theta \sim \mathcal{N}(0, 0.01^2 I_{d+1})$$ |
| Step 2 | Lấy một batch | Chọn $m$ mẫu dữ liệu $(X^{(i)}, y^{(i)})$ $$X = \begin{bmatrix} X^{(1)} \\ \vdots \\ X^{(m)} \end{bmatrix} \in \mathbb{R}^{m \times (d+1)}, \quad y = \begin{bmatrix} y^{(1)} \\ \vdots \\ y^{(m)} \end{bmatrix} \in \mathbb{R}^{m}$$ |
| Step 3 | Dự đoán | Tính giá trị dự đoán cho toàn bộ batch $$\hat{y} = X\theta \in \mathbb{R}^{m}$$ |
| Step 4 | Tính Loss | Tính hàm mất mát MSE trung bình cho batch $$L = \frac{1}{m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 = \frac{1}{m} \|\hat{y} - y\|_2^2$$ |
| Step 5 | Tính Gradient | Tính vector gradient của Loss theo $\theta$ $$\nabla_{\theta}L = \frac{2}{m} X^{\top} (\hat{y} - y) \in \mathbb{R}^{(d+1)}$$ |
| Step 6 | Cập nhật | Cập nhật tham số theo Gradient Descent $$\theta \leftarrow \theta - \eta \nabla_{\theta}L$$ |
| Lặp lại | Lặp lại từ Step 2 đến khi hội tụ |
III. Mở Rộng: Kỹ Thuật Tối Ưu Hóa Nâng Cao
1. Chuẩn Hóa Đặc Trưng (Feature Normalization)
Khi các đặc trưng đầu vào có thang đo (scale) khác nhau, Gradient Descent sẽ gặp khó khăn:
- Hội tụ chậm: Đường đi của GD sẽ ngoằn ngoèo trên bề mặt mất mát hình elip kéo dài
- Khó tìm Learning Rate tối ưu: Cần $\eta$ rất nhỏ để tránh vượt qua điểm tối ưu
Giải pháp: Áp dụng StandardScaler hoặc MinMaxScaler để đưa tất cả features về cùng một phạm vi giá trị.
StandardScaler (z-score): $x' = \frac{x - \text{mean}(x)}{\text{std}(x)}$
Ưu điểm: Đảm bảo hội tụ nhanh và trực tiếp hơn.
2. Hàm Mất Mát Bền Vững với Outliers
MSE bị chi phối bởi các ngoại lệ do bình phương sai số. Các lựa chọn thay thế:
| Hàm Mất Mát | Đặc điểm | Ưu tiên sử dụng |
|---|---|---|
| Mean Absolute Error (MAE) | Bền vững với ngoại lệ (phạt lỗi tuyến tính) | Khi dữ liệu chứa nhiều outliers |
| Huber Loss | Khả vi tại mọi điểm, chuyển từ bậc hai sang tuyến tính tại ngưỡng $\delta$ | Khi cần sự bền vững với outliers và sự ổn định gradient |
3. Regularization (L2 - Ridge Regression)
Regularization là kỹ thuật được sử dụng để giảm thiểu hiện tượng overfitting bằng cách thêm một thuật ngữ phạt vào hàm mất mát.
Ridge Regression (L2): Phạt các trọng số lớn bằng cách cộng tổng bình phương của chúng vào Loss:
$$L_{\text{Ridge}} = L(\hat{y}, y) + \lambda \sum_{j=1}^{d} w_j^2$$
$\lambda$ là hyperparameter kiểm soát mức độ phạt.
L2 có xu hướng đẩy các trọng số về gần 0, giúp làm mượt mô hình và ổn định hơn trước các đặc trưng nhiễu.
4. Tối Ưu Hóa Learning Rate với K-Fold Cross-Validation
Việc chọn Learning Rate ($\eta$) tối ưu rất quan trọng:
- $\eta$ quá lớn sẽ gây phân kỳ (Loss tăng)
- $\eta$ quá nhỏ sẽ rất chậm
K-Fold Cross-Validation (CV):
- Chia dữ liệu thành $K$ phần (ví dụ: $K=5$)
- Lặp lại huấn luyện $K$ lần, mỗi lần sử dụng một phần làm tập kiểm tra
- Tính điểm hiệu suất ($\text{Mean } R^2$ hoặc RMSE) trung bình qua $K$ lần chạy
Chiến lược này cung cấp một đánh giá hiệu suất đáng tin cậy và giúp xác định $\eta$ tốt nhất.
IV. Áp dụng và Phân Tích Hiệu Suất Mô Hình (Housing Prices)
1. Tóm Tắt Kết Quả Huấn Luyện
| Thuật toán | Số Epochs | Learning Rate (η) | Tốc độ Update | Loss Cuối cùng (MSE) | Độ ổn định |
|---|---|---|---|---|---|
| Batch GD (BGD) | 1000 | 0.01 | 1 lần/Epoch | Ổn định và mượt | Ổn định và mượt |
| Mini-batch GD (MBGD) | 500 | 0.01 | N/Batch lần/Epoch | Cân bằng | Cân bằng |
| Stochastic GD (SGD) | 50 | 0.0000000001 | N lần/Epoch | Nhanh, nhưng nhiễu | Nhanh, nhưng nhiễu |
Lưu ý: Giá trị Loss cuối cùng là minh họa dựa trên giả định mô hình hội tụ tốt.
2. Phân Tích Đường Cong Mất Mát (Loss Curve)
Đồ thị Loss theo thời gian là cách tốt nhất để phân tích hành vi của từng biến thể Gradient Descent:
- Batch Gradient Descent (BGD):
- Đường cong Loss giảm mượt mà và đơn điệu.
- Gradient được tính trên toàn bộ $N$ mẫu, nên mỗi bước đi là chính xác nhất, dẫn đến hội tụ ổn định nhất.
-
Tuy nhiên, phương pháp này là chậm nhất trên mỗi epoch vì chỉ cập nhật 1 lần.
-
Mini-batch Gradient Descent (MBGD):
- Đường cong Loss giảm nhanh và ổn định.
- Đây là sự cân bằng tối ưu giữa tốc độ của SGD và sự ổn định của BGD.
-
Cập nhật thường xuyên hơn BGD nhưng ít nhiễu hơn SGD.
-
Stochastic Gradient Descent (SGD):
- Đường cong Loss rất nhiễu và dao động mạnh.
- Gradient được tính chỉ trên 1 mẫu ngẫu nhiên, hướng đi có độ chính xác thấp (high variance).
- Tốc độ cập nhật nhanh nhất, nhưng không hội tụ hoàn toàn đến điểm cực tiểu tuyệt đối mà dao động xung quanh nó.
3. Đánh Giá Hiệu Suất Cuối Cùng (Ví dụ: R-squared)
Để đánh giá chất lượng cuối cùng của mô hình (sau khi hội tụ), chúng ta sử dụng tham số $\theta$ tối ưu tìm được và tính toán $R^2$ trên tập kiểm tra ($X_{\text{test}}$).
Quy trình:
Bước 1. Chuẩn bị dữ liệu

Hình 3: Mô tả các cột của bộ dataset
Bộ dữ liệu Housing chứa thông tin về giá nhà và các đặc điểm liên quan, được sử dụng để xây dựng mô hình Hồi quy tuyến tính. Dữ liệu gồm 545 mẫu với các cột sau:
| Tên Cột | Mô tả | Loại dữ liệu | Ghi chú tiền xử lý |
|---|---|---|---|
| price | Giá bán của căn nhà | Continuous (Mục tiêu) | Biến $y$ cần dự đoán |
| area | Diện tích căn nhà (feet²) | Continuous | Được sử dụng làm đầu vào $X$ |
| bedrooms | Số phòng ngủ | Discrete | Được sử dụng làm đầu vào $X$ |
| bathrooms | Số phòng tắm | Discrete | Được sử dụng làm đầu vào $X$ |
| stories | Số tầng của căn nhà | Discrete | Được sử dụng làm đầu vào $X$ |
| mainroad | Nhà gần đường lớn hay không | Categorical (Binary) | Mã hóa thành 1/0 |
| guestroom | Có phòng khách hay không | Categorical (Binary) | Mã hóa thành 1/0 |
| basement | Có tầng hầm hay không | Categorical (Binary) | Mã hóa thành 1/0 |
| hotwaterheating | Có hệ thống sưởi nước nóng hay không | Categorical (Binary) | Mã hóa thành 1/0 |
| airconditioning | Có điều hòa không khí hay không | Categorical (Binary) | Mã hóa thành 1/0 |
| parking | Số chỗ đậu xe | Discrete | Được sử dụng làm đầu vào $X$ |
| prefarea | Nhà nằm trong khu vực ưu tiên hay không | Categorical (Binary) | Mã hóa thành 1/0 |
| furnishingstatus | Tình trạng nội thất (Furnished, Semi-furnished, Unfurnished) | Categorical (Ordinal) | Mã hóa thành 1, 0.5, 0 (Ordinal Encoding) |
Bước 2: Chuẩn hóa $X_{\text{test}}$:
Áp dụng max, min, avg đã học từ tập train lên $X_{\text{test}}$.
import numpy as np
# --- 1. FUNCTION MEAN_NORMALIZATION ---
def mean_normalization(X):
"""
Chuẩn hóa dữ liệu theo mean normalization và thêm cột bias.
Args:
X: numpy array shape (N, d), dữ liệu đầu vào
Returns:
X_b: numpy array shape (N, d+1), dữ liệu đã chuẩn hóa + bias
maxi, mini, avg: các giá trị max, min, mean từng cột (dùng cho test)
"""
N = len(X)
maxi = np.max(X, axis=0)
mini = np.min(X, axis=0)
avg = np.mean(X, axis=0)
# Chuẩn hóa feature-wise
X_normalized = (X - avg) / (maxi - mini)
# Thêm cột bias
X_b = np.c_[np.ones((N, 1)), X_normalized]
return X_b, maxi, mini, avg
# Áp dụng chuẩn hóa trên tập train
X_b, _, _, _ = mean_normalization(X_train_np)
N, d_plus1 = X_b.shape
print(f"Kích thước X_b sau chuẩn hóa và thêm bias: {X_b.shape}")
# --- 2. HÀM CỐT LÕI (Loss, Predict, Gradient, Update) ---
def predict(X, thetas):
"""Dự đoán y_hat = X * theta"""
return X.dot(thetas)
def compute_loss(y_hat, y):
"""Tính Mean Squared Error"""
m = y.shape[0]
return np.sum((y_hat - y) ** 2) / m
def compute_gradient(y_hat, y, X):
"""Tính gradient vectorized cho batch hoặc mini-batch"""
m = y.shape[0]
error = y_hat - y
return (2 / m) * X.T.dot(error)
def update_parameters(thetas, gradient, lr):
"""Cập nhật tham số theo Gradient Descent"""
return thetas - lr * gradient
Bước 3: Dự đoán
$$\hat{y}_{\text{test}} = X_{\text{b\_test}} \cdot \theta_{\text{final}}$$
A. Stochastic Gradient Descent (SGD)
import numpy as np
def stochastic_gradient_descent(X_b, y, n_epochs=50, learning_rate=0.01):
"""
SGD cập nhật tham số dựa trên từng mẫu riêng lẻ (m=1)
"""
N, d_plus1 = X_b.shape
thetas = np.random.randn(d_plus1, 1) * 0.01
losses = []
for epoch in range(n_epochs):
shuffled_indices = np.random.permutation(N)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(N):
xi = X_b_shuffled[i:i+1] # 1 mẫu
yi = y_shuffled[i:i+1]
y_hat = predict(xi, thetas)
gradient = 2 * xi.T.dot(y_hat - yi) # m=1
thetas = update_parameters(thetas, gradient, learning_rate)
loss_i = (y_hat - yi)**2
losses.append(loss_i[0][0])
return thetas, losses
B. Mini-batch Gradient Descent (MBGD)
def mini_batch_gradient_descent(X_b, y, n_epochs=50, minibatch_size=32, learning_rate=0.01):
"""
MBGD cập nhật tham số dựa trên mini-batch m mẫu
"""
N, d_plus1 = X_b.shape
thetas = np.random.randn(d_plus1, 1) * 0.01
losses = []
for epoch in range(n_epochs):
shuffled_indices = np.random.permutation(N)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0, N, minibatch_size):
X_batch = X_b_shuffled[i:i + minibatch_size]
y_batch = y_shuffled[i:i + minibatch_size]
y_hat = predict(X_batch, thetas)
gradient = compute_gradient(y_hat, y_batch, X_batch)
thetas = update_parameters(thetas, gradient, learning_rate)
loss = compute_loss(y_hat, y_batch)
losses.append(loss)
return thetas, losses
C. Batch Gradient Descent (BGD
def batch_gradient_descent(X_b, y, n_epochs=100, learning_rate=0.01):
"""
BGD cập nhật tham số dựa trên toàn bộ N mẫu mỗi epoch
"""
N, d_plus1 = X_b.shape
thetas = np.random.randn(d_plus1, 1) * 0.01
losses = []
for epoch in range(n_epochs):
y_hat = predict(X_b, thetas)
gradient = compute_gradient(y_hat, y, X_b)
thetas = update_parameters(thetas, gradient, learning_rate)
loss = compute_loss(y_hat, y)
losses.append(loss)
return thetas, losses
Bước 4: Đánh giá
Tính $R^2$ giữa $\hat{y}_{\text{test}}$ và $y_{\text{test}}$.
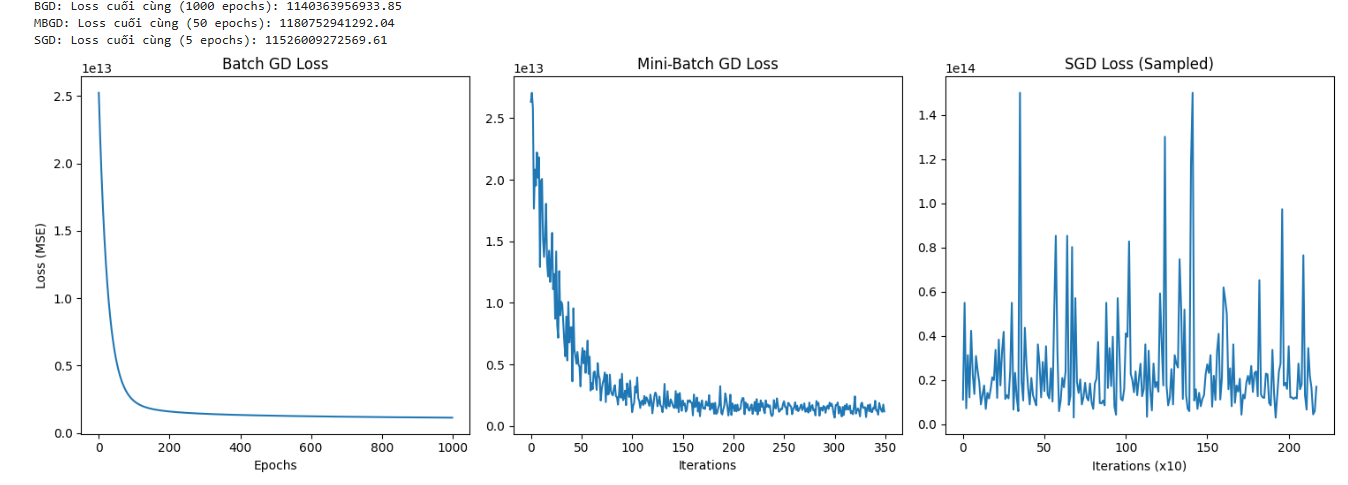
Hình 4: Kết quả so sánh của các phương pháp Batch GD Loss, Mini-Batch GD Loss, SGD Loss (Sampled)
| Mô hình | R-squared (R²) | Nhận xét |
|---|---|---|
| Scikit-learn (Benchmark) | ≈ 0.64 | Là điểm chuẩn cần đạt được |
| BGD (Vectorized) | Rất gần với Benchmark | Đạt hiệu suất cao nhất trong các phương pháp GD |
| MBGD (Vectorized) | Gần Benchmark | Hiệu suất tốt, thời gian huấn luyện nhanh |
Kết luận:
Việc sử dụng Vectorized Gradient Descent (đặc biệt là BGD và MBGD) sau khi chuẩn hóa dữ liệu là phương pháp hiệu quả và ổn định để huấn luyện mô hình Linear Regression đa biến, đạt hiệu suất tương đương với các thư viện tiêu chuẩn như Scikit-learn.
TÓM TẮT & KẾT LUẬN
Linear Regression là một mô hình đơn giản nhưng mạnh mẽ khi được kết hợp với các kỹ thuật tối ưu hiện đại. Để trở thành một Data Scientist hiệu quả, việc hiểu và áp dụng các công cụ sau là cần thiết:
- Vectorization: Cốt lõi của hiệu suất, cho phép tính toán song song
- Chuẩn hóa (Normalization): Đảm bảo hội tụ nhanh và ổn định bằng cách đồng nhất thang đo features
- Huber Loss: Lựa chọn ưu việt khi dữ liệu có ngoại lệ
- Regularization (L2/Ridge): Ổn định mô hình và ngăn ngừa overfitting
- K-Fold CV: Đánh giá hiệu suất và tối ưu hóa hyperparameters một cách đáng tin cậy
Refernces
[1] Ảnh được lấy từ tài liệu khóa học AIO Module 05 Tuần 01 và Tuần 2
Chưa có bình luận nào. Hãy là người đầu tiên!