I. A Bridge to Linear Regression
1. Tổng quan
Hồi quy tuyến tính (Linear Regression) là một trong những phương pháp học máy (Machine Learning) cơ bản và phổ biến, được áp dụng để dự đoán giá trị của một biến mục tiêu (output) từ một hoặc nhiều đặc trưng đầu vào (input).
Khi có một bảng dữ liệu với các giá trị đầu vào và các giá trị đầu ra được gắn nhãn, như số giờ học của học sinh và điểm số của họ, hay các đặc trưng của một căn hộ (như tiện nghi, khu vực, số phòng ngủ, diện tích) để dự đoán giá thuê phòng Airbnb, mục tiêu của hồi quy tuyến tính là tìm ra một mô hình phù hợp để dự đoán chính xác giá trị của biến mục tiêu.
Câu hỏi quan trọng là làm thế nào từ những dữ liệu đầu vào này, chúng ta có thể huấn luyện một mô hình sao cho nó dự đoán chính xác kết quả đầu ra. Để đánh giá mức độ tin cậy của mô hình sau khi huấn luyện, người ta sử dụng các phương pháp và chỉ số khác nhau để kiểm tra độ chính xác và hiệu quả của mô hình.
Hồi quy tuyến tính thực hiện điều này bằng cách xác định mối quan hệ tuyến tính giữa các biến đầu vào và đầu ra thông qua một hàm số có các tham số cần được tối ưu để phù hợp nhất với bộ dữ liệu. Đây là phương pháp học đơn giản nhưng mạnh mẽ, giúp các nhà phân tích và khoa học dữ liệu dễ dàng đưa ra các dự đoán có cơ sở và kiểm chứng được độ chính xác của chúng.
Phương trình cơ bản của hồi quy tuyến tính
$$ y = wx + b $$
Trong đó:
- $y$ là giá trị dự đoán (vd: điểm số)
- $x$ là biến đầu vào (vd: số giờ học)
- $w$ là hệ số góc (weight), cho biết mức độ thay đổi của $y$ sau khi $x$ thay đổi
- $b$ là hệ số chệch (bias), giá trị của y khi $x=0$
Mục tiêu của hồi quy tuyến tính là xác định các giá trị tối ưu cho các tham số $w$ và $b$ sao cho đường thẳng dự đoán khớp tốt nhất với dữ liệu thực tế. Để đạt được điều này, ta cần một phương pháp đo lường độ chính xác của mô hình, và đây chính là lúc Hàm mất mát phát huy vai trò quan trọng
💡
Hàm mất mát (Loss Function) là một công cụ phổ biến trong học máy dùng để đánh giá mức độ sai lệch giữa kết quả dự đoán của mô hình và giá trị thực tế. Cụ thể, nó đo lường tỷ lệ lỗi của mô hình thông qua việc tính toán sự khác biệt giữa giá trị dự đoán và giá trị thực. Hàm mất mát không chỉ giúp chúng ta xác định độ chính xác của mô hình mà còn là cơ sở để tối ưu hóa các tham số của mô hình, qua đó nâng cao khả năng dự đoán chính xác trong các tình huống thực tế.
Công thức tổng quát:
$$ L(w,b) = \sum_{i=1}^{n}(\hat{y} - y)^{2} $$
Trong đó:
- $\hat{y}$: giá trị dự đoán
- $y$: giá trị thực tế
- $n$: số lượng mẫu dữ liệu
2. Gradient-based Optimization
Hàm Mất Mát dưới Dạng Parabol
Trong hồi quy tuyến tính, một trong những hàm mất mát phổ biến như Mean Squared Error (MSE) có dạng đồ thị parabol khi vẽ theo các tham số $w$ và $b$.
Đặc điểm nổi bật của hàm mất mát này là:
- Điểm cực tiểu (minimum point) là điểm mà tại đó hàm mất mát đạt giá trị thấp nhất, thể hiện mô hình tối ưu nhất với sai số nhỏ nhất.
- Các giá trị ở phía trên và dưới điểm cực tiểu sẽ tương ứng với các mức sai số cao hơn, tức là mất mát lớn hơn.
💡
Điều này có nghĩa là, nếu chúng ta tìm ra được các giá trị tối ưu cho $w$ và $b$ tại điểm cực tiểu này, mô hình sẽ đạt hiệu suất tốt nhất, với sai số giữa giá trị thực tế và dự đoán thấp nhất, từ đó cung cấp những dự đoán chính xác hơn trong thực tế.
Conditions for Loss Functions
- Liên tục: Hàm số phải liên tục để đảm bảo không có sự gián đoạn trong quá trình tối ưu hóa, giúp việc tìm kiếm giá trị tối ưu diễn ra suôn sẻ.
- Tính khả vi: Hàm số phải khả vi (differentiable) tại các điểm trong không gian tham số, để có thể tính toán được gradient cho quá trình tối ưu hóa (như gradient descent).
- Có điểm cực tiểu: Hàm số cần có ít nhất một điểm cực tiểu (local minimum hoặc global minimum) để quá trình tối ưu hóa có thể tìm được giá trị tham số tối ưu.
- Có giá trị hữu hạn: Hàm mất mát phải có giá trị hữu hạn và dễ tính toán để không gặp vấn đề về số học trong quá trình tối ưu hóa.
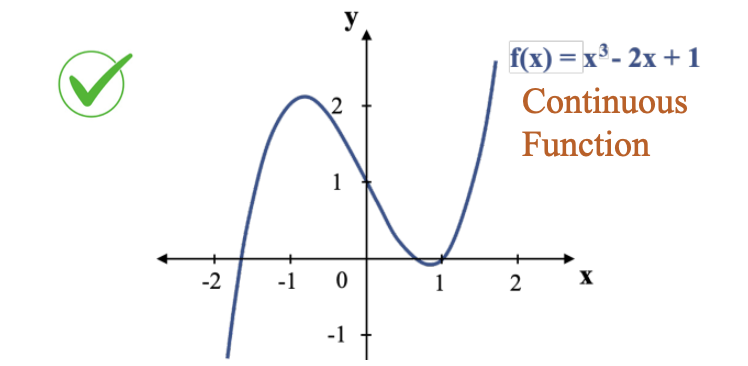
Hình 1: Minh hoạ hàm số liên tục và khả vi. Nguồn: AI Vietnam
Tính chất của đạo hàm
Để tính toán hàm mất mát, chúng ta cần sử dụng công cụ đạo hàm. Đạo hàm tại một điểm cung cấp thông tin về độ dốc của hàm tại vị trí đó.
- Nếu đạo hàm tại điểm đó dương, hàm số đang tăng.
- Nếu đạo hàm âm, hàm số đang giảm.
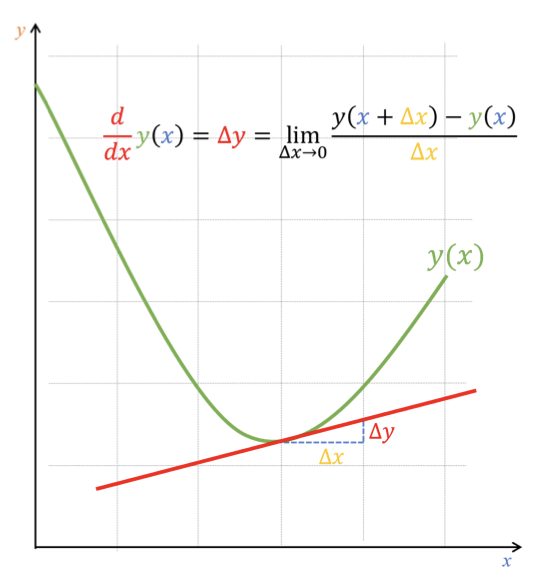
Hình 2: Đường tiếp tuyến của một hàm tại 1 điểm. Nguồn: AI Vietnam
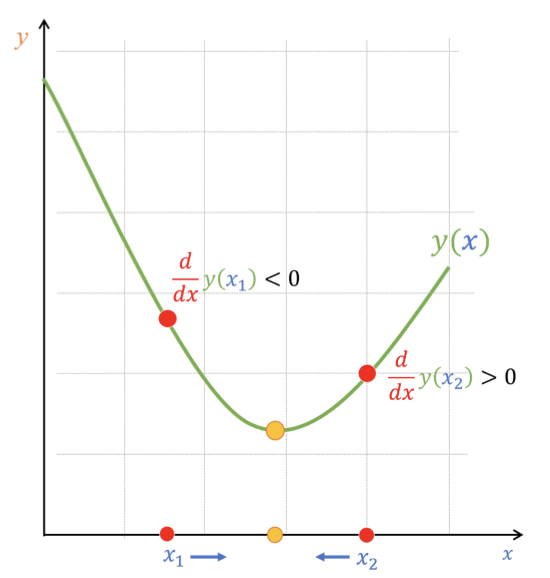
Hình 3: Giá trị đạo hàm tại các điểm khác nhau. Nguồn: AI Vietnam
Với tính chất này, ta có thể sử dụng phương pháp gradient descent (xuống dốc theo gradient) để điều chỉnh các tham số như $b$. Cụ thể, ta sẽ di chuyển ngược lại hướng đạo hàm, tiến dần về phía điểm cực tiểu.
Quá trình này tiếp tục cho đến khi các tham số $w$ và $b$ hội tụ, tức là sai số giữa giá trị dự đoán và giá trị thực tế đạt mức thấp nhất hoặc không thay đổi đáng kể qua nhiều vòng lặp.
Learning Rate
💡
Learning rate là một tham số điều chỉnh mức độ thay đổi của các tham số mô hình trong mỗi bước cập nhật. Cụ thể, khi tính toán gradient (đạo hàm) của hàm mất mát tại một điểm, learning rate quyết định kích thước bước đi mà mô hình sẽ di chuyển trong không gian tham số để giảm thiểu sai số.
Công thức cập nhật tham số:
$$ \theta_{t} = \theta_{t-1} - \eta \bigtriangledown_{\theta}L(\theta) $$
Trong đó:
- $\theta$ là tham số mô hình
- $\eta$ là lerning rate
- $\bigtriangledown_{\theta}L(\theta)$ là gradient của hàm loss đối với tham số $\theta$
Việc chọn learning rate phù hợp là một bài toán quan trọng, và trong thực tế, nó thường đòi hỏi thử nghiệm và tinh chỉnh. Thường bắt đầu với một giá trị nhỏ (ví dụ: 0.01, 0.001) và sau đó thử nghiệm với các giá trị khác nhau để tìm ra mức tối ưu.
- Learning rate quá nhỏ (0.0001): quá trình cập nhật tham số diễn ra rất chậm, khiến thời gian huấn luyện dài và mô hình có thể bị mắc kẹt ở các cực tiểu địa phương (local minimum). Với quá trình huấn luyện kéo dài, việc tính toán và cập nhật tham số sẽ tiêu tốn rất nhiều tài nguyên máy tính.
- Learning rate quá lớn (0.8-1.1): mô hình có thể vượt qua các điểm cực tiểu, khiến hàm mất mát không giảm mà dao động lên xuống. Điều này có thể dẫn đến sự không ổn định trong quá trình huấn luyện. Nếu bước đi quá lớn, gradient có thể trở nên rất lớn, làm cho mô hình cập nhật tham số quá mức khiến bước nhảy phân kỳ.
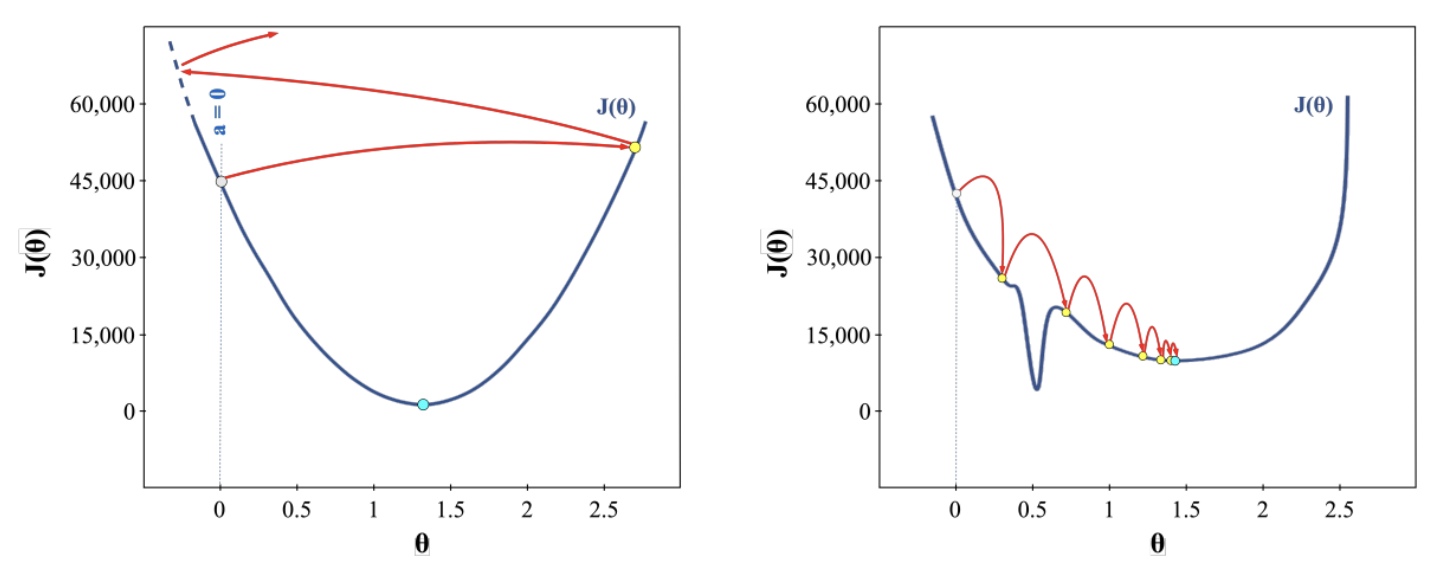
Hình 4: Minh hoạ Learning Rate trong các trường hợp. Nguồn: AI Vietnam
- Learning rate phù hợp: Giúp mô hình học nhanh chóng, ổn định và đạt được tối ưu hóa hiệu quả.
Hàm hợp và Đạo hàm của Hàm hợp
💡
Trong toán học và học máy, khi làm việc với các hàm phức tạp, chúng ta thường gặp các Hàm hợp (composite functions), tức là một hàm được tạo thành từ sự kết hợp của các hàm khác.
- Cấu trúc của Hàm hợp
- Hàm thứ nhất: $f(x) = 2x - 1$
→ Đây là hàm tuyến tính mô tả mối quan hệ giữa biến đầu vào $x$ và giá trị đầu ra $f(x)$
- Hàm thứ hai: $g(f) = (f - 3)^2$
→ Đây là hàm bậc hai với đầu và là $f$ và giá trị đầu ra là $g(f)$
- Khi kết hợp hàm thứ nhất và hàm thứ hai, ta có hàm hợp. Lúc này, $x$ tác động đến $f$ và $f$ tác động đến $g$ mô tả như sau:
$$ x \xrightarrow[]{} f(x) \xrightarrow[]{} g(f(x)) \\ g(f(x)) = (2x - 1 - 3)^2 = (2x-4)^2 $$

Hình 5: Minh hoạ hàm hợp. Nguồn: AI Vietnam
b. Tính đạo hàm Hàm hợp bằng Định lý chuỗi (Chain Value)
Khi muốn tối ưu hóa hàm $g(f(x))$, ta cần biết hàm thay đổi thế nào khi $x$ thay đổi. Tuy nhiên, vì $g$ không phụ thuộc trực tiếp vào $x$ mà thông qua $f$, ta không thể tính đạo hàm $g'(x)$ một cách trực tiếp.
Thay vào đó, ta áp dụng định lý chuỗi:
$$ \frac{\mathrm{d} }{\mathrm{d} x}g(f(x)) = \left [ \frac{\mathrm{d} }{\mathrm{d} f}g(f) \right ] \ * \left [ \frac{\mathrm{d} }{\mathrm{d} x}f(x) \ \right ] $$
Áp dụng công thức cho ví dụ trên, ta có:
$$ \frac{\mathrm{dg} }{\mathrm{d} x} = \frac{\mathrm{dg} }{\mathrm{d} f} \ \frac{\mathrm{df} }{\mathrm{d} x} = 2(f - 3)2 = 4(2x - 1 - 3) = 8x - 16 $$
Công thức này là nền tảng cho thuật toán lan truyền ngược trong các mạng nơ-ron hiện đại, nơi mà đạo hàm của hàm mất mát được lan truyền ngược qua nhiều lớp hàm hợp (layer) để cập nhật trọng số.
3. Các bước để tìm đường thẳng tối ưu
Stochastic Gradient Descent (SGD)
💡
Stochastic Gradient Descent (SGD) là một trong những phương pháp tối ưu hóa phổ biến trong học máy và học sâu. SGD là một phiên bản biến thể của thuật toán Gradient Descent, được sử dụng để tối ưu hóa các tham số của mô hình, đặc biệt trong các bài toán có dữ liệu lớn.
Trong Gradient Descent, quá trình tối ưu hóa được thực hiện bằng cách tính toán đạo hàm của hàm mất mát đối với tất cả các mẫu trong bộ dữ liệu, sau đó cập nhật tham số của mô hình dựa trên trung bình đạo hàm từ tất cả các mẫu. Tuy nhiên, việc tính toán có thể trở nên rất chậm khi bộ dữ liệu quá lớn. Để khắc phục điều này, SGD chỉ sử dụng một mẫu ngẫu nhiên trong mỗi bước tính toán để cập nhật tham số, thay vì sử dụng toàn bộ bộ dữ liệu.
Cách thức hoạt động của SGD
- Khởi tạo ngẫu nhiên hai tham số $w$ và $b$
- Với mỗi mẫu dữ liệu thứ $i$ trong bộ dữ liệu, ta áp dụng các bước tính toán sau:
- Tính toán giá trị dự đoán $\hat{y}$ cho điểm dữ liệu đầu vào $x_{i}$
$$ \hat{y_{i}} = f(x_{i}) = wx_{i} + b $$
- Tính chênh lệch giữa giá trị dự đoán và giá trị thực tế bằng hàm loss (squared error)
$$ L(\hat{y_{i}}, y_{i}) = (\hat{y_{i}} - y_{i})^2 $$
- Tính giá trị đạo hàm tại mẫu dữ liệu thứ $i$ cho hai tham số $w$ và $b$
$$ \frac{\partial L}{\partial w} = 2x_{i}(\hat{y_{i}} - y_{i}), \ \frac{\partial L}{\partial b} = 2(\hat{y_{i}} - y_{i}) $$
- Cập nhật lại giá trị mới cho hai tham số $w$ và $b$ theo công thức sau
$$ w_{new} = w_{old} - \eta \frac{\partial L}{\partial w}, \ b_{new} = b_{old} - \eta \frac{\partial L}{\partial b} $$
Với $\eta$ là learning rate, là hằng số không đổi
Lặp lại bước 2 cho đến khi xử lý hết các mẫu trong bộ dữ liệu
Vì SGD không yêu cầu tính toán gradient cho toàn bộ bộ dữ liệu trong mỗi vòng lặp, giúp giảm chi phí tính toán và tăng tốc quá trình huấn luyện, đặc biệt là khi làm việc với dữ liệu lớn. Việc cập nhật tham số dựa trên các mẫu ngẫu nhiên giúp mô hình tránh bị mắc kẹt tại các cực tiểu địa phương.
Tuy nhiên, do cập nhật tham số sau mỗi mẫu ngẫu nhiên, SGD có thể dẫn đến các cập nhật không ổn định, với độ dao động lớn trong quá trình huấn luyện. Điều này có thể làm cho quá trình tối ưu hóa không hội tụ mượt mà. Ngoài ra, cần tinh chỉnh learning rate để phù hợp với tốc độ học của mô hình.
Batch Gradient Descent (BGD)
💡
Batch Gradient Descent (BGD) là một thuật toán tối ưu hóa trong học máy, thường được sử dụng để cập nhật tham số của mô hình sao cho hàm mất mát đạt giá trị thấp nhất. BGD là phiên bản cơ bản của Gradient Descent, trong đó gradient được tính toán trên toàn bộ bộ dữ liệu thay vì một mẫu đơn lẻ hoặc một batch nhỏ như trong Stochastic Gradient Descent (SGD)
Trong khi SGD cập nhật tham số ngay sau mỗi mẫu dữ liệu, khiến quá trình huấn luyện nhanh chóng nhưng có thể gây dao động mạnh do mỗi cập nhật chỉ dựa vào một mẫu ngẫu nhiên, BGD thực hiện các cập nhật tham số một cách mượt mà hơn nhờ việc tính toán gradient trên toàn bộ bộ dữ liệu. Tuy nhiên, điều này cũng đồng nghĩa với việc BGD tốn nhiều tài nguyên tính toán và thời gian hơn, đặc biệt khi bộ dữ liệu lớn, trái ngược với SGD có thể cập nhật tham số nhanh chóng nhưng thiếu ổn định.
Cách thức hoạt động của BGD
- Pick all the N samples $x^{(i)}, y^{(i)}$ from training data
- Tính toán giá trị dự đoán $\hat{y}^{(i)}$ cho điểm dữ liệu đầu vào $x^{(i)}$
$$ \hat{y}^{(i)} = f(x^{(i)}) = wx^{(i)} + b \ for \ 0 \leq i < N $$
- Tính chênh lệch giữa giá trị dự đoán và giá trị thực tế bằng hàm loss (squared error)
$$ L = \frac{1}{N}\sum (\hat{y}^{(i)} - y^{(i)})^2 $$
- Tính giá trị đạo hàm tại mẫu dữ liệu thứ $i$ cho hai tham số $w$ và $b$
$$ \frac{\partial L}{\partial w}^{(i)} = 2x^{(i)}(\hat{y}^{(i)} - y^{(i)}), \ \frac{\partial L}{\partial b}^{(i)} = 2(\hat{y}^{(i)} - y^{(i)}) $$
- Cập nhật lại giá trị mới cho hai tham số $w$ và $b$ theo công thức sau
$$ w = w - \eta \frac{\sum _{i}\frac{\partial L}{\partial w}^{(i)}}{N}, \ b = b - \eta \frac{\sum _{i}\frac{\partial L}{\partial b}^{(i)}}{N} $$
Ưu điểm của Batch Gradient Descent:
- Tính ổn định: BGD dùng toàn bộ dữ liệu để tính gradient và cập nhật tham số, giúp quá trình cập nhật ổn định và mượt mà hơn
- Tính chính xác cao: Vì gradient được tính toán trên toàn bộ bộ dữ liệu, BGD cung cấp một hướng tối ưu chính xác hơn, giúp mô hình có xu hướng hội tụ vào cực tiểu toàn cục
Nhược điểm của BGD
- Tốn tài nguyên và thời gian
- Không thích hợp với dữ liệu lớn sẽ gặp vấn đề hiệu suất và bộ nhớ
- Khó thích ứng với dữ liệu thay đổi
4. Ví dụ minh hoạ
Stochastic Gradient Descent (SGD)
Chúng ta sẽ thử áp dụng cách triển khai phía trên để xây dựng hàm có khả năng dự đoán số điểm đạt được (Scores) dựa theo số giờ học (Study Hours) của một nhóm sinh viên qua bộ dữ liệu nhỏ theo bảng dưới đây:
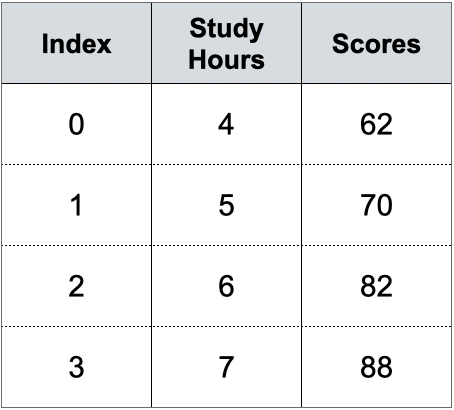
Bảng 1: Dữ liệu số giờ học
Bộ dữ liệu gồm 4 mẫu, ứng với số giờ học $(x_{i})$ sẽ có số điểm tương ứng $(y_{i})$. Ví dụ một sinh viên học 6 tiếng sẽ có điểm thi tương ứng là 82. Với bộ data này ta tiến hành áp dụng các bước tìm ra tham số tối ưu.
- Khởi tạo giá trị ngẫu nhiên cho tham số $w$ và $b$.
Giả sử $w$ = 10, $b = 5$ và hệ số học (learning rate) = 0.01. Với hai tham số như trên ta thử áp dụng công thức để tính giá trị dự đoán và tính loss để dùng cho việc so sánh giữa giá trị trước và sau khi áp dụng thuật toán, xem mức độ hiệu quả đến đâu. Đầu tiên ta dự số điểm của học sinh số 1 dựa vào số giờ học là 5:
$$ \hat{y_{1}} = wx_{1} + b = 10 \times 5 + 5 = 55 $$
Tiếp theo dựa vào công thức hàm loss để tính mức chênh lệch giữa giá trị dự đoán và giá trị thực tế, ta có công thức như sau:
$$ L(\hat{y_{1}}, y_{1}) = (\hat{y_{1}} - y_{1})^2 = (55-70)^2 = 225 $$

Hình 6: Minh hoạ bước (1)
Như vậy, có thể thấy giá trị loss tương đối cao, kết quả dự đoán của mô hình không như mong đợi. Để cải thiện việc này, chúng ta sẽ áp dụng Linear Regression, từng bước điều chỉnh tham số $w$ và $b$ sao cho phù hợp với bộ dữ liệu trên.
- Áp dụng Linear Regression, ta tiến hành duyệt qua từng mẫu trong bộ dữ liệu. Với mẫu $x_{0}$ = 4, $y_{0}$ = 62, ta tiến hành các bước tính toán:
- Output:
$$ \hat{y_{0}} = wx_{0} + b = 10 \times 4 + 5 = 45 $$
- Loss:
$$ L(\hat{y_{0}}, y_{0}) = (\hat{y_{0}} - y_{0})^2 = (45-62)^2 = 289 $$

Hình 7: Minh hoạ bước (2)
- Tính đạo hàm:
- Tham số $w$:
$$ \frac{\partial L}{\partial w} = 2x_{0}(\hat{y_{0}} - y_{0}) = 2 \times 4 \times (45-62) = -136 $$
- Tham số $b$:
$$ \frac{\partial L}{\partial b} = 2(\hat{y_{0}} - y_{0}) = 2 \times (45 - 62) = -34 $$
- Cập nhật tham số:
- Tham số $w$:
$$ w = w - \eta \frac{\partial L}{\partial w} = 10 - 0.01 \times (-136) = 11.36 $$
- Tham số $b$:
$$ b = b - \eta \frac{\partial L}{\partial b} = 5 - 0.01 \times (-34) = 5.34 $$
Sau khi cập nhật, ta thu được giá trị tham số mới là $w$ = 11.36 và $b$ = 5.34.
- Lặp lại bước (2) cho mẫu dữ liệu tiếp theo gồm có $x_{1}$ = 5, $y_{1}$ = 70 và thực hiện các bước tính toán:
- Output:
$$ \hat{y_{1}} = wx_{1} + b = 11.36 \times 5 + 5.34 = 62.14 $$
- Loss:
$$ L(\hat{y_{1}}, y_{1}) = (\hat{y_{1}} - y_{1})^2 = (62.14-70)^2 = 78.5 $$

Hình 8: Minh hoạ bước (3)
- Tính đạo hàm:
- Tham số $w$:
$$ \frac{\partial L}{\partial w} = 2x_{1}(\hat{y_{1}} - y_{1}) = 2 \times 5 \times (62.14-70) = -78.6 $$
- Tham số $b$:
$$ \frac{\partial L}{\partial b} = 2(\hat{y_{1}} - y_{1}) = 2 \times (62.14 - 70) = -15.72 $$
- Cập nhật tham số:
- Tham số $w$:
$$ w = w - \eta \frac{\partial L}{\partial w} = 11.36 - 0.01 \times (-78.6) = 12.15 $$
- Tham số $b$:
$$ b = b - \eta \frac{\partial L}{\partial b} = 5.34 - 0.01 \times (-15.72) = 5.5 $$
Sau khi cập nhật, ta thu được giá trị tham số mới là $w$ = 12.15 và $b$ = 5.5.
- Lặp lại bước (3) cho mẫu dữ liệu tiếp theo gồm có $x_{2}$ = 6, $y_{2}$ = 82 và thực hiện các bước tính toán:
- Output:
$$ \hat{y_{2}} = wx_{2} + b = 12.15 \times 6 + 5.5 = 78.4 $$
- Loss:
$$ L(\hat{y_{2}}, y_{2}) = (\hat{y_{2}} - y_{2})^2 = (78.4-82)^2 = 12.96 $$

Hình 9: Minh hoạ bước (4)
- Tính đạo hàm:
- Tham số $w$:
$$ \frac{\partial L}{\partial w} = 2x_{2}(\hat{y_{2}} - y_{2}) = 2 \times 6 \times (78.4-82) = -43.2 $$
- Tham số $b$:
$$ \frac{\partial L}{\partial b} = 2(\hat{y_{2}} - y_{2}) = 2 \times (78.4 - 82) = -7.2 $$
- Cập nhật tham số:
- Tham số $w$:
$$ w = w - \eta \frac{\partial L}{\partial w} = 12.15 - 0.01 \times (-43.2) = 12.58 $$
- Tham số $b$:
$$ b = b - \eta \frac{\partial L}{\partial b} = 5.5 - 0.01 \times (-7.2) = 5.57 $$
Sau khi cập nhật, ta thu được giá trị tham số mới là $w$ = 12.58 và $b$ = 5.57
- Lặp lại bước (3) cho mẫu dữ liệu tiếp theo gồm có $x_{3}$ = 7, $y_{3}$ = 88 và thực hiện các bước tính toán:
- Output:
$$ \hat{y_{3}} = wx_{3} + b = 12.58 \times 7 + 5.57 = 93.63 $$
- Loss:
$$ L(\hat{y_{3}}, y_{3}) = (\hat{y_{3}} - y_{3})^2 = (93.63-88)^2 = 31.7 $$

Hình 10: Minh hoạ bước (5)
- Tính đạo hàm:
- Tham số $w$:
$$ \frac{\partial L}{\partial w} = 2x_{3}(\hat{y_{3}} - y_{3}) = 2 \times 7 \times (93.63-88) = 78.82 $$
- Tham số $b$:
$$ \frac{\partial L}{\partial b} = 2(\hat{y_{3}} - y_{3}) = 2 \times (93.63-88) = 11.26 $$
- Cập nhật tham số:
- Tham số $w$:
$$ w = w - \eta \frac{\partial L}{\partial w} = 12.58 - 0.01 \times (78.82) = 11.8 $$
- Tham số $b$:
$$ b = b - \eta \frac{\partial L}{\partial b} = 5.57 - 0.01 \times (11.26) = 5.45 $$
Sau khi cập nhật, ta thu được giá trị tham số mới là $w$ = 11.8 và $b$ = 5.45
- Sau khi duyệt qua tất cả các mẫu dữ liệu, tham số $w$ và $b$ đã được điều chỉnh lại phù hợp hơn với bộ dữ liệu. Để kiểm chứng mức độ hiệu quả của mô hình, ta sẽ dự đoán lại số điểm đạt được với số giờ học của sinh viên. Với sinh viên ở vị trí thứ nhất, có số giờ học $x_{1} = 5$ và $y_{1} = 70$
Before
$w = 10$
$b = 5$
$\hat{y_{1}} = wx_{1} + b = 55$
$loss = (\hat{y_{1}} - y_{1})^2 = 225$
After
$w = 11.8$
$b = 5$.45
$\hat{y_{1}} = wx_{1} + b = 64.45$
$loss = (\hat{y_{1}} - y_{1})^2 = 30.8$
Quan sát kết quả trước và sau khi chạy mô hình ta có thể thấy giá trị dự đoán đã tiến gần hơn đến giá trị thực tế. Giá trị loss cũng cải thiện đáng kể (30.8 < 225), điều này cho thấy mô hình đã được học, các tham số được điều chỉnh để phù hợp hơn với bộ dữ liệu huấn luyện và có thể đưa ra dự đoán hợp lý hơn.
Đồ thị biểu diễn

Hình 11: Đồ thị biểu diễn Stochastic Gradient Descent
Batch Gradient Descent (BGD)
Step by step ta sẽ mô tả các bước thực hành Batch Gradient Descent cho dữ liệu advertising.csv
- Import thư viện
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import random
- Đọc dữ liệu và chuẩn bị dữ liệu
data_set = pd.read_csv("advertising.csv")
X = data_set.iloc[:, :1]
y = data_set.iloc[:, -1:]
- Chia dữ liệu thành tập huấn luyện và kiểm tra
X_train, X_test, y_train, y_test
= train_test_split(X, y, train_size=0.8, random_state=42)
- Dữ liệu được chia thành 80% cho huấn luyện và 20% cho kiểm tra.
random_state=42giúp tái tạo kết quả chia tập dữ liệu mỗi lần chạy.
4. Chuẩn hoá dữ liệu
X_min = X_train.min(axis = 0)
X_max = X_train.max(axis = 0)
X_train = (X_train - X_min) / (X_max - X_min)
X_test = (X_test - X_min) / (X_max - X_min)
- Chuẩn hóa dữ liệu để các giá trị đầu vào XXX nằm trong khoảng từ 0 đến 1, giúp tối ưu hóa quá trình huấn luyện.
- Các giá trị tối thiểu và tối đa của X_train được tính và dùng để chuẩn hóa cả X_train và X_test.
5. Define các hàm tính toán
# Dự đoán giá trị đầu ra
def predict(X, w, b):
return w * X + b
#Tính loss giữa dự đoán và giá trị thực tế
def compute_loss(y_hat, y):
return (y_hat - y)**2
#Tính loss bình phương trung bình (Mean Squared Error - MSE)
def compute_MSE(y_hat, y):
return (y_hat - y)**2
# Tính loss tuyệt đối trung bình (Mean Absolute Error - MAE)
def compute_MAE(y_hat, y):
return abs(y_hat - y)
# Tính gradient đối với tham số
def compute_gradient(X, y_hat, y):
dw = 2 * X * (y_hat - y)
db = 2 * (y_hat - y)
return dw, db
# Cập nhật tham số
def update_weights(w, b, dw, db, lr):
w_new = w - lr * dw
b_new = b - lr * db
return w_new, b_new
- Khởi tạo các tham số và cấu hình
epochs = 250
lr = 0.001
w = 0.0
b = 0.0
N = len(X_train)
loss_history = []
mse_history = []
mae_history = []
- epochs = 250: Số vòng lặp huấn luyện (epochs) cho mô hình
- Learning rate = 0.001
- $w$ và $b$: Khởi tạo các tham số của mô hình (trọng số và bias) bằng 0
- N = len(X_train): Số lượng mẫu trong tập huấn luyện
- Vòng lặp huấn luyện
for epoch in range(epochs):
loss_sample = []
MSE_sample = 0
MAE_sample = 0
for i in range(N):
y_hat = predict(X_train[i], w, b)
loss = compute_loss(y_hat, y_train[i])
loss_sample.append(loss)
mse = compute_MSE(y_hat, y_train[i])
MSE_sample += mse
mae = compute_MAE(y_hat, y_train[i])
MAE_sample += mae
d_w, d_b = compute_gradient(X_train[i], y_hat, y_train[i])
w, b = update_weights(w, b, d_w, d_b, lr)
avg_loss = sum(loss_sample) / len(loss_sample)
avg_mse = MSE_sample / N
avg_mae = MAE_sample / N
loss_history.append(avg_loss)
mse_history.append(avg_mse)
mae_history.append(avg_mae)
print(f"Epoch {epoch}: loss={avg_loss:.4f}, MSE={avg_mse:.4f}, MAE={avg_mae:.4f}")
- Chuyển đổi X_train và y_train thành mảng 1D
X_train = np.array(X_train).flatten()
y_train = np.array(y_train).flatten()
print(f"After flatten - X_train: {X_train.shape}, y_train: {y_train.shape}")
- Vẽ đồ thị
plt.figure(figsize=(8, 8))
# Đồ thị 1: Loss
plt.subplot(2, 2, 1)
plt.plot(loss_history, 'b-')
plt.title('Training Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.grid(True)
# Đồ thị 2: Loss mini
plt.subplot(2, 2, 2)
plt.plot(loss_history, 'b-')
plt.title('Training range Loss (0, 30)')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.grid(True)
plt.ylim(0, 30)
# Đồ thị 3: MSE
plt.subplot(2, 2, 3)
plt.plot(mse_history, 'r-')
plt.title('MSE')
plt.xlabel('Epoch')
plt.ylabel('MSE')
plt.grid(True)
# Đồ thị 4: MAE
plt.subplot(2, 2, 4)
plt.plot(mae_history, 'g-')
plt.title('MAE')
plt.xlabel('Epoch')
plt.ylabel('MAE')
plt.grid(True)
plt.tight_layout()
plt.show()
print(f" Final parameters: w = {w}, b = {b}")
- Kết quả

Hình 12: Đồ thị kết quả bài toán ứng dụng Batch Gradient Descent
Chưa có bình luận nào. Hãy là người đầu tiên!