Bài viết này tiếp nối bài viết "Sales Prediction P5.1 (P1)" ứng dụng các mô hình Linear để dự đoán giá nhà.
Phần II. Triển khai mô hình và phân tích kết quả
1. Triển khai mô hình
Hệ thống triển khai các mô hình hồi quy khác nhau trên tập dữ liệu train:
1. Linear Regression: Mô hình cơ bản
2. Ridge Regression: Giảm độ phức tạp bằng cách hạn chế độ lớn của hệ số
3. Lasso Regression: Tự động chọn đặc trưng quan trọng
4. Elastic Net: Kết hợp Ridge và Lasso
5. Huber Regression: Chịu được dữ liệu bất thường
6. Quantile Regression: Dự đoán theo phân vị (trung vị, 75%, 25%)
7. RANSAC Regression: Loại bỏ tự động các điểm ngoại lai
8. Theil-Sen Regression: Ước lượng mạnh mẽ với nhiều dữ liệu bất thường
1.1. Mô hình cơ bản và có regularization
1.1.1. Linear Regression
Linear Regression là mô hình hồi quy cơ bản, giả định mối quan hệ tuyến tính giữa biến độc lập $(X)$ và biến phụ thuộc $(y)$. Mục tiêu là tìm vector trọng số w và hệ số chặn b sao cho sai số bình phương giữa giá trị dự đoán và giá trị thực là nhỏ nhất. Hàm mất mát phổ biến là Least Squares (OLS):
$$\min_{w}||\hat y-y||^2_2=\min_{w}||(Xw+b)-y||^2_2$$
Ưu điểm:
- Đơn giản, dễ hiểu, dễ diễn giải mô hình
- Tốc độ huấn luyện nhanh, phù hợp với dữ liệu lớn có ít nhiễu
Nhược điểm:
- Rất nhạy cảm với outliers
- Giả định quan hệ tuyến tính và phân phối chuẩn thường không chính xác trong thực tế
Phù hợp sử dụng khi dữ liệu có mối quan hệ tuyến tính rõ ràng, ít nhiễu
1.1.2. Ridge Regression (L2 Regularization)
Ridge Regression giải quyết một số vấn đề của Linear Regression bằng cách thêm một thành phần phạt (L2 penalty) với kích thước của các hệ số vào hàm mất mát:
$$\min_{w}||\hat y-y||^2_2+\alpha||w||^2_2$$
Áp dụng đoạn code sau để minh họa ảnh hưởng của hệ số alpha
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
# Generate some sample data
np.random.seed(0)
n_samples, n_features = 50, 10
X = np.random.randn(n_samples, n_features)
y = np.random.randn(n_samples)
# Define a range of alpha values
alphas = np.logspace(-6, 6, 200)
# Fit Ridge models for each alpha
coefs = []
for a in alphas:
ridge = Ridge(alpha=a, fit_intercept=False) # Ridge model
ridge.fit(X, y)
coefs.append(ridge.coef_)
# Plot the coefficients
plt.figure(figsize=(10, 6))
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
plt.xlabel('alpha')
plt.ylabel('coefficients')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()

Hình 1. Tham số alpha tác động đến các trọng số trong mô hình Ridge
Kết quả thu được cho thấy hệ số $\alpha$ điều khiển mức độ của các trọng số, giá trị của $\alpha$ càng lớn thì mức độ co càng nhiều và gần 0 nhưng không loại bỏ chúng hoàn toàn. Ridge có xu hướng thu nhỏ các hệ số. Điều này làm giảm phương sai (variance), ngăn overfitting và hiệu quả trước hiện tượng collinearity.
Ưu điểm:
- Giảm overfitting trong dữ liệu có nhiều biến độc lập.
- Hoạt động tốt khi các biến có collinearity cao.
Nhược điểm:
- Không thực hiện chọn đặc trưng (feature selection).
- Việc chọn hệ số điều chỉnh $\alpha$ cần cẩn thận.
- Vẫn bị ảnh hưởng bởi ngoại lệ, mặc dù ít hơn Linear Regression.
Phù hợp khi dữ liệu có collinearity cao
1.1.3. Lasso Regression (L1 Regularization)
Lasso Regression giải quyết một số vấn đề của Linear Regression bằng cách thêm một thành phần phạt norm 1 (L1 penalty) với kích thước của các hệ số vào hàm mất mát:
$$ \min_{w}\frac{1}{2n_{samples}}||\hat y-y||^2_2+\alpha||w||_1 $$
Áp dụng data giống như với Ridge ở trên:
coefs_lasso = []
for a in alphas:
lasso = Lasso(alpha=a, fit_intercept=False, max_iter=10000) # Lasso model
lasso.fit(X, y)
coefs_lasso.append(lasso.coef_)
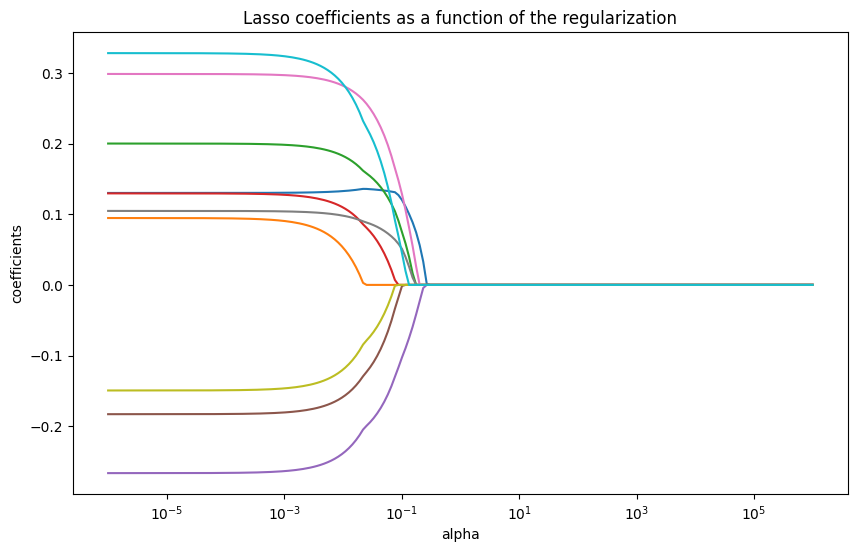
Hình 2. Tham số alpha tác động đến các trọng số trong mô hình Lasso
Kết quả cho thấy khi hệ số $\alpha$ tăng lên, nhiều hệ số L1 penalty khiến một số trọng số bị triệt tiêu về 0 hoàn toàn. Điều này làm cho Lasso hữu ích cho việc lựa chọn đặc trưng (feature selection), vì nó loại bỏ các đặc trưng ít quan trọng bằng cách đặt hệ số của chúng về 0.
Ưu điểm:
- Giảm overfitting hiệu quả.
- Chọn lọc đặc trưng tự động, giảm số chiều của mô hình.
- Dễ diễn giải vì nhiều hệ số trở thành 0.
Nhược điểm:
- Không ổn định khi có nhiều biến tương quan mạnh — có thể chọn một biến ngẫu nhiên trong nhóm tương quan.
- Khó tối ưu khi số đặc trưng lớn hơn số mẫu (p > n).
- Vẫn nhạy cảm với outlier.
Phù hợp khi dữ liệu có nhiều biến nhưng chỉ một phần nhỏ thực sự quan trọng
1.1.4. Elastic Net Regression
Elastic Net kết hợp ưu điểm của Lasso (L1) và Ridge (L2) bằng cách thêm cả hai loại phạt:
$$ \min_{w}\frac{1}{2n_{samples}}||\hat y-y||^2_2+\alpha\rho||w||_1+\alpha\frac{1-\rho}{2}||w||^2_2 $$
Áp dụng data giống như với Ridge ở trên và l1_ratio $(\rho)$ lần lượt là 0.01, 0.5:
l1_ratio = 0.01
coefs_elastic = []
for a in alphas:
elastic_net = ElasticNet(alpha=a, l1_ratio=l1_ratio, fit_intercept=False, max_iter=10000)
elastic_net.fit(X, y)
coefs_elastic.append(elastic_net.coef_)
ax.plot(alphas, coefs_elastic)
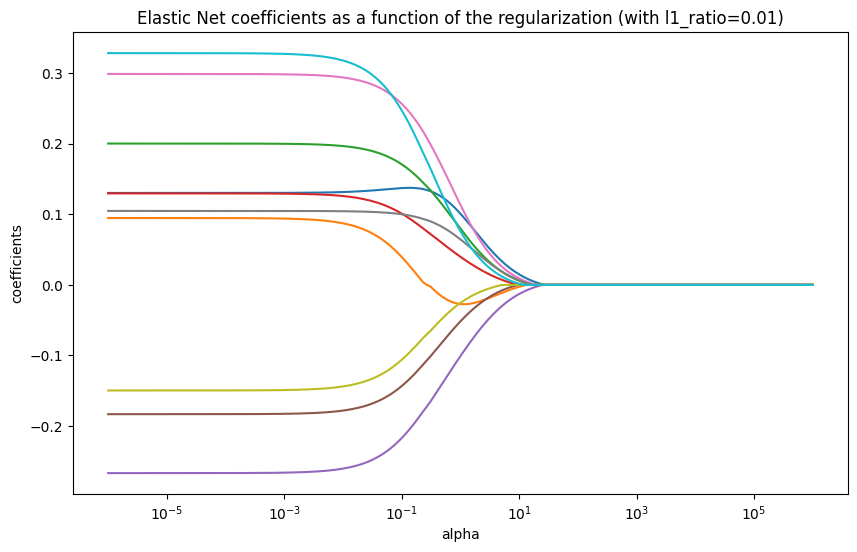
Hình 3. Tham số alpha tác động đến các tham số trong mô hình Elastic Net với l1_ratio=0.01
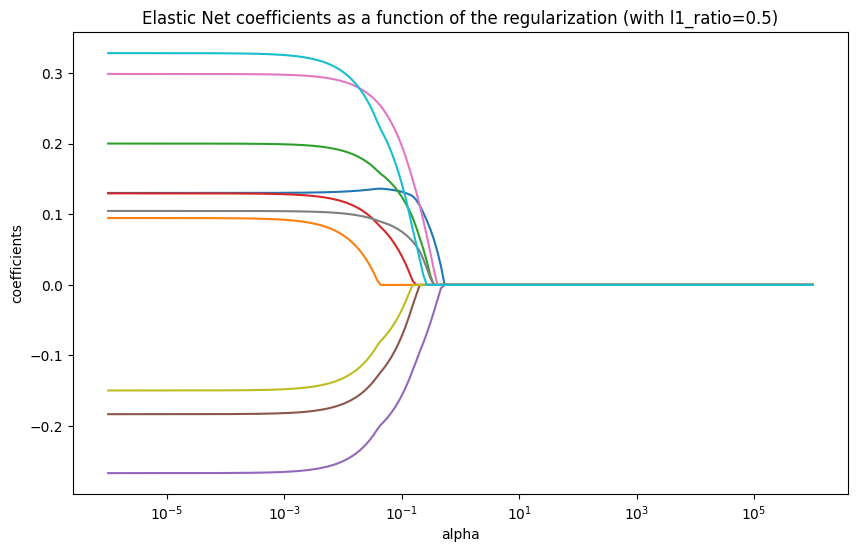
Hình 4. Tham số alpha tác động đến các tham số trong mô hình Elastic Net với l1_ratio=0.5
Kết quả cho thấy sự kết hợp của hành vi của Ridge và Lasso. Tùy thuộc vào tỷ lệ pha trộn $(\rho)$, Elastic Net có thể hoạt động giống Lasso (khi $\rho$ gần 1) hoặc giống Ridge (khi $\rho$ gần 0). Nó có thể nhóm các đặc trưng tương quan lại với nhau và đặt hệ số của chúng về 0 cùng nhau.
Ưu điểm:
- Giải quyết vấn đề của Lasso khi có các biến tương quan mạnh.
- Cung cấp khả năng chọn đặc trưng, nhưng vẫn ổn định như Ridge.
- Phù hợp cho high-dimensional data (p >> n).
Nhược điểm:
- Cần tinh chỉnh hai tham số (α, λ).
- Không kháng ngoại lệ.
Phù hợp khi:
- Dữ liệu có nhiều đặc trưng tương quan
- Cần mô hình vừa chọn đặc trưng vừa ổn định
- Áp dụng cho bài toán high-dimensional regression
1.2. Mô hình chịu nhiễu và ngoại lệ tốt
1.2.1. Huber Regression
Huber Regression sử dụng huber loss là sự kết hợp giữa MSE (ở vùng lỗi nhỏ) và MAE (ở vùng lỗi lớn). Điều này giúp mô hình có hàm loss khả vi tại mọi điểm và mượt ở vùng trung tâm (như MSE) nhưng kháng được nhiễu ở vùng ngoại biên (như MAE).
$$ L_{\delta}(a) =\begin{cases}\frac{1}{2} a^2, & \text{if } |a| \le \delta \\\delta \left( |a| - \frac{1}{2}\delta \right), & \text{otherwise}\end{cases} $$
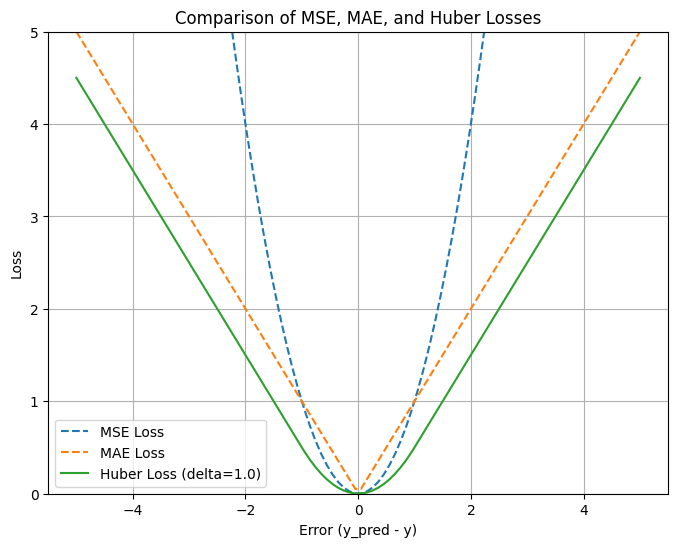
Hình 5. Hàm Huber loss
Đoạn code sau chứng minh khả năng chịu nhiễu tốt hơn của Huber Regression so với Ridge
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_regression
from sklearn.linear_model import HuberRegressor, Ridge
# Generate toy data.
rng = np.random.RandomState(0)
X, y = make_regression(
n_samples=20, n_features=1, random_state=0, noise=4.0, bias=100.0
)
# Add four strong outliers to the dataset.
X_outliers = rng.normal(0, 0.5, size=(4, 1))
y_outliers = rng.normal(0, 2.0, size=4)
X_outliers[:2, :] += X.max() + X.mean() / 4.0
X_outliers[2:, :] += X.min() - X.mean() / 4.0
y_outliers[:2] += y.min() - y.mean() / 4.0
y_outliers[2:] += y.max() + y.mean() / 4.0
X = np.vstack((X, X_outliers))
y = np.concatenate((y, y_outliers))
plt.plot(X, y, "b.")
# Fit the huber regressor over a series of epsilon values.
colors = ["r-", "b-", "y-", "m-"]
x = np.linspace(X.min(), X.max(), 7)
epsilon_values = [1, 1.5]
for k, epsilon in enumerate(epsilon_values):
huber = HuberRegressor(alpha=0.0, epsilon=epsilon)
huber.fit(X, y)
coef_ = huber.coef_ * x + huber.intercept_
plt.plot(x, coef_, colors[k], label="huber loss, %s" % epsilon)
# Fit a ridge regressor to compare it to huber regressor.
ridge = Ridge(alpha=0.0, random_state=0)
ridge.fit(X, y)
coef_ridge = ridge.coef_
coef_ = ridge.coef_ * x + ridge.intercept_
plt.plot(x, coef_, "g-", label="ridge regression")
plt.title("Comparison of HuberRegressor vs Ridge")
plt.xlabel("X")
plt.ylabel("y")
plt.legend(loc=0)
plt.show()
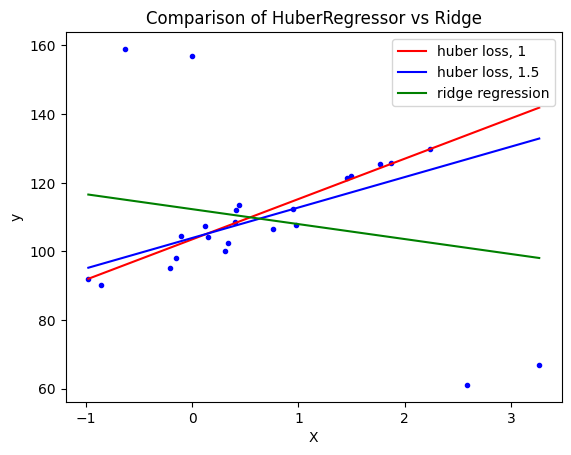
Hình 6. Ảnh hưởng của outlier lên mô hình Huber và Ridge regression
Ưu điểm:
- Ổn định hơn Linear Regression khi có outlier.
- Giữ tính liên tục và khả vi, dễ tối ưu bằng gradient descent.
- Không quá cứng nhắc như MAE (L1) nên hội tụ nhanh hơn.
Nhược điểm:
- Cần chọn tham số ngưỡng $\delta$ hợp lý.
- Không loại bỏ hoàn toàn ảnh hưởng của outlier cực mạnh.
- Kém hiệu quả nếu dữ liệu cực kỳ nhiễu.
Phù hợp khi:
- Dữ liệu có một vài outlier nhưng không quá nhiều.
- Muốn có mô hình cân bằng giữa ổn định và mượt mà.
1.2.2. RANSAC Regression
RANSAC (RANdom SAmple Consensus) là thuật toán robust regression dựa trên ý tưởng chọn mẫu con ngẫu nhiên để fit mô hình, sau đó đánh giá số lượng inlier phù hợp với mô hình đó. Quá trình lặp lại nhiều lần, chọn mô hình có nhiều inlier nhất.
Đoạn code sau chứng minh khả năng chịu nhiễu của RANSAC Regression so với Linear Regression
import numpy as np
from matplotlib import pyplot as plt
from sklearn import datasets, linear_model
n_samples = 1000
n_outliers = 50
X, y, coef = datasets.make_regression(
n_samples=n_samples,
n_features=1,
n_informative=1,
noise=10,
coef=True,
random_state=0,
)
# Add outlier data
np.random.seed(0)
X[:n_outliers] = 3 + 0.5 * np.random.normal(size=(n_outliers, 1))
y[:n_outliers] = -3 + 10 * np.random.normal(size=n_outliers)
# Fit line using all data
lr = linear_model.LinearRegression()
lr.fit(X, y)
# Robustly fit linear model with RANSAC algorithm
ransac = linear_model.RANSACRegressor()
ransac.fit(X, y)
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)
# Predict data of estimated models
line_X = np.arange(X.min(), X.max())[:, np.newaxis]
line_y = lr.predict(line_X)
line_y_ransac = ransac.predict(line_X)
# Compare estimated coefficients
print("Estimated coefficients (true, linear regression, RANSAC):")
print(coef, lr.coef_, ransac.estimator_.coef_)
lw = 2
plt.scatter(
X[inlier_mask], y[inlier_mask], color="yellowgreen", marker=".", label="Inliers"
)
plt.scatter(
X[outlier_mask], y[outlier_mask], color="gold", marker=".", label="Outliers"
)
plt.plot(line_X, line_y, color="navy", linewidth=lw, label="Linear regressor")
plt.plot(
line_X,
line_y_ransac,
color="cornflowerblue",
linewidth=lw,
label="RANSAC regressor",
)
plt.legend(loc="lower right")
plt.xlabel("Input")
plt.ylabel("Response")
plt.show()
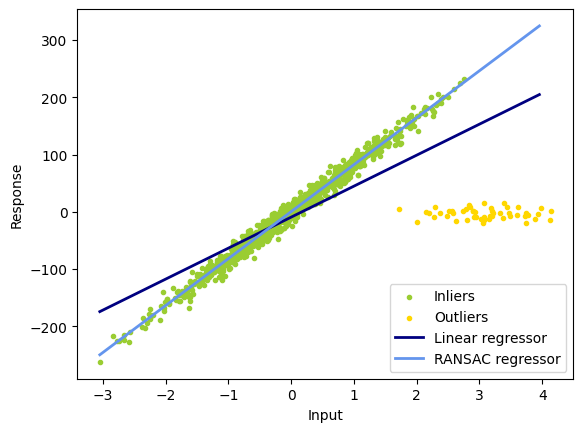
Hình 7. Ảnh hưởng của outlier lên mô hình RANSAC và Linear regression
Ưu điểm:
- Rất mạnh trong môi trường có nhiều outlier (50% outliers vẫn OK)
- Không bị ảnh hưởng bởi các điểm dữ liệu sai lệch nặng.
- Dễ áp dụng với các mô hình tuyến tính và phi tuyến.
Nhược điểm:
- Ngẫu nhiên → kết quả không ổn định nếu số vòng lặp nhỏ.
- Cần chọn ngưỡng inlier hợp lý.
- Không hoạt động tốt nếu tỷ lệ outlier quá cao.
Phù hợp khi dữ liệu chứa nhiều nhiễu, điểm lỗi, hoặc giá trị đo sai.
1.2.3. Theil-Sen Regression
Theil-Sen Regression ước lượng hệ số hồi quy bằng median của tất cả các slope giữa các cặp điểm dữ liệu.
Ưu điểm:
- Rất robust với outlier và dữ liệu không chuẩn.
- Không yêu cầu giả định phân phối chuẩn.
- Dễ hiểu, không cần tham số điều chỉnh.
Nhược điểm:
- Tốc độ chậm khi số lượng mẫu lớn (O(n²) cặp điểm).
- Không mở rộng tốt cho nhiều biến độc lập.
- Không thích hợp với dữ liệu có quan hệ phi tuyến.
Phù hợp khi:
- Dữ liệu có ít đặc trưng.
- Có một số outlier nhưng vẫn cần mô hình tuyến tính đơn giản.
1.2.4. Huber Regression vs RANSAC vs Theil Sen
- Huber Regression chạy nhanh hơn RANSAC và Theil Sen trừ khi số lượng samples lớn hơn rất nhiều so với số lượng features, điều này là bởi RANSAC và Theil Sen fit trên các tập dữ liệu con.
- RANSAC nhanh hơn Theil Sen và scale tốt hơn với số lượng samples lớn
- RANSAC tốt hơn với nhiễu nặng theo $y$
- Theil Sen tốt hơn với dữ liệu nhiễu vừa phải theo $X$, nhưng có thể không hiệu quả với dữ liệu có nhiều chiều
1.3. Quantile Regression
Quantile Regression tối ưu hàm loss
$$ \min_{w} \frac{1}{n_{\text{samples}}} \sum_{i} PB_{q}(y_i - X_i w) + \alpha \|w\|_{1}. $$
trong đó $\alpha||w||_1$là phần phạt L1 và hàm pinball loss
$$ pinball(y_i,\hat y_i)=PB_q(y_i-\hat y_i) = q \max(y_i-\hat y_i, 0) + (1 - q)\max(\hat y_i-y_i, 0)= \begin{cases}q(y_i-\hat y_i), & y_i-\hat y_i > 0, \\0, & y_i-\hat y_i = 0, \\(q - 1)(y_i-\hat y_i), & y_i-\hat y_i < 0.\end{cases} $$
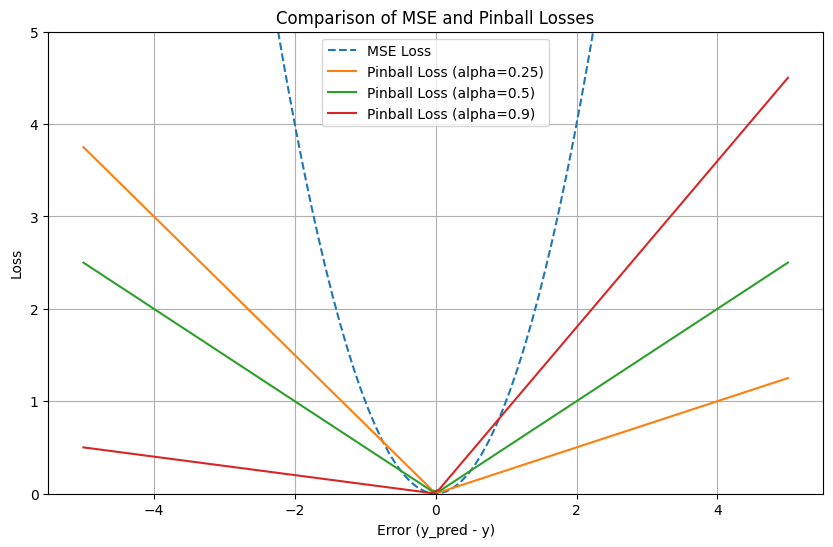
Hình 8. Pinball loss
Dễ thấy rằng pinball loss có vẻ giống MAE, đó là bởi MAE là một trường hợp đặc biệt của pinball loss khi tham số $\alpha=0.5$, lúc này pinball loss phạt lỗi âm và lỗi dương với cùng một mức độ. Sự khác biệt thực sự của Pinball Loss so với MAE nằm ở chỗ bạn có thể thay đổi giá trị $\alpha$ để phạt lỗi dương và lỗi âm không đối xứng, điều mà MAE không làm được.
Ưu điểm:
- Không giả định phân phối chuẩn của phần dư.
- Mô hình hóa được sự bất đối xứng trong dữ liệu.
- Dự đoán dải phân vị thay vì chỉ trung bình. Trong bài này là có thể dự đoán khoảng giá thay vì chỉ điểm giá.
Nhược điểm:
- Tính toán phức tạp hơn least squares (OLS).
- Có thể không ổn định ở phân vị rất cao hoặc rất thấp.
- Diễn giải khó hơn Linear Regression.
Phù hợp khi dữ liệu có phân phối lệch
1.4. Triển khai mô hình
Các mô hình sử dụng trong project
models = {
'linear': LinearRegression(),
'ridge': Ridge(random_state=self.random_state),
'lasso': Lasso(random_state=self.random_state),
'elastic_net': ElasticNet(random_state=self.random_state),
'huber': HuberRegressor(),
'quantile_median': QuantileRegressor(quantile=0.5),
'quantile_75': QuantileRegressor(quantile=0.75),
'quantile_25': QuantileRegressor(quantile=0.25),
'ransac': RANSACRegressor(random_state=self.random_state),
'theil_sen': TheilSenRegressor(random_state=self.random_state)
}
Việc tìm các tham số tối ưu cho từng mô hình được thực hiện với GridSearch hoặc RandomizedSearch với các tham số:
'elastic_net': {
'alpha': np.logspace(-4, 2, 50), # Log scale: 0.0001 to 100
'l1_ratio': np.linspace(0.1, 0.9, 9), # Fine-tuned range
'max_iter': [1000, 2000, 5000],
'tol': [1e-4, 1e-5]
},
'ridge': {
'alpha': np.logspace(-4, 4, 50), # Log scale: 0.0001 to 10000
'max_iter': [1000, 2000, 5000],
'tol': [1e-4, 1e-5]
},
'lasso': {
'alpha': np.logspace(-4, 2, 50), # Log scale: 0.0001 to 100
'max_iter': [1000, 2000, 5000],
'tol': [1e-4, 1e-5]
},
'huber': {
'epsilon': [1.1, 1.35, 1.5, 2.0], # Robustness parameter
'alpha': np.logspace(-4, 2, 20),
'max_iter': [100, 200, 300]
},
'quantile': {
'quantile': [0.1, 0.25, 0.5, 0.75, 0.9], # Different quantiles
'alpha': np.logspace(-4, 2, 20),
'solver': ['highs', 'highs-ds', 'highs-ipm']
},
'ransac': {
'min_samples': [0.5, 0.6, 0.7, 0.8],
'residual_threshold': [None, 1.0, 2.0, 3.0],
'max_trials': [50, 100, 200]
}
2. Kết quả
2.1. Metrics
Kết quả được đánh giá dựa trên:
- MSE
- RMSE
- MAE
- R2
- CV_MSE
2.2. Kết quả
Bảng sau tóm tắt hiệu suất của từng mô hình sử dụng trong project với các metrics bao gồm MSE, RMSE, MAE, R² và cross-validation MSE.
| Model | MSE | RMSE | MAE | R² | CV MSE |
|---|---|---|---|---|---|
| huber | 1,250,758,077.89 | 35,366.06 | 16,170.74 | 0.7549 | 512,672,736.61 |
| elastic_net | 1,332,676,361.19 | 36,505.84 | 16,534.30 | 0.7389 | 522,642,259.86 |
| ridge | 1,335,785,358.49 | 36,548.40 | 16,533.05 | 0.7383 | 523,164,468.95 |
| ransac | 1,827,564,734.65 | 42,750.03 | 17,411.01 | 0.6419 | 670,594,395.57 |
| lasso | 1,985,283,139.61 | 44,556.52 | 16,692.98 | 0.6110 | 597,484,136.61 |
| linear | 2,237,525,422.85 | 47,302.49 | 17,611.20 | 0.5616 | 681,024,769.13 |
| theil_sen | 3,526,083,860.69 | 59,380.84 | 26,530.84 | 0.3091 | 2,689,159,802.76 |
| quantile_median | 5,375,160,579.53 | 73,315.49 | 54,235.21 | -0.0533 | 4,562,841,702.57 |
| quantile_75 | 6,128,144,635.09 | 78,282.47 | 66,526.91 | -0.2008 | 5,627,763,875.05 |
| quantile_25 | 7,503,083,635.09 | 86,620.34 | 61,664.18 | -0.4702 | 6,460,699,272.02 |
Bảng 1. Performance của các mô hình
- RMSE, MSE, MAE, CV MSE: bé hơn là tốt hơn.
- R^2: xấp xỉ 1 là tốt hơn.
2.3. Giải thích kết quả
2.3.1. Permutation Importance
Phương pháp này đánh giá tầm quan trọng của từng đặc trưng bằng cách:
- Ghi lại độ chính xác ban đầu của mô hình
- Xáo trộn ngẫu nhiên một đặc trưng
- Đo sự giảm sút độ chính xác
- Nếu độ chính xác giảm nhiều → đặc trưng đó quan trọng
perm_importance = permutation_importance(
model, X_test, y_test,
n_repeats=10, # Lặp lại 10 lần để có độ tin cậy
random_state=42
)
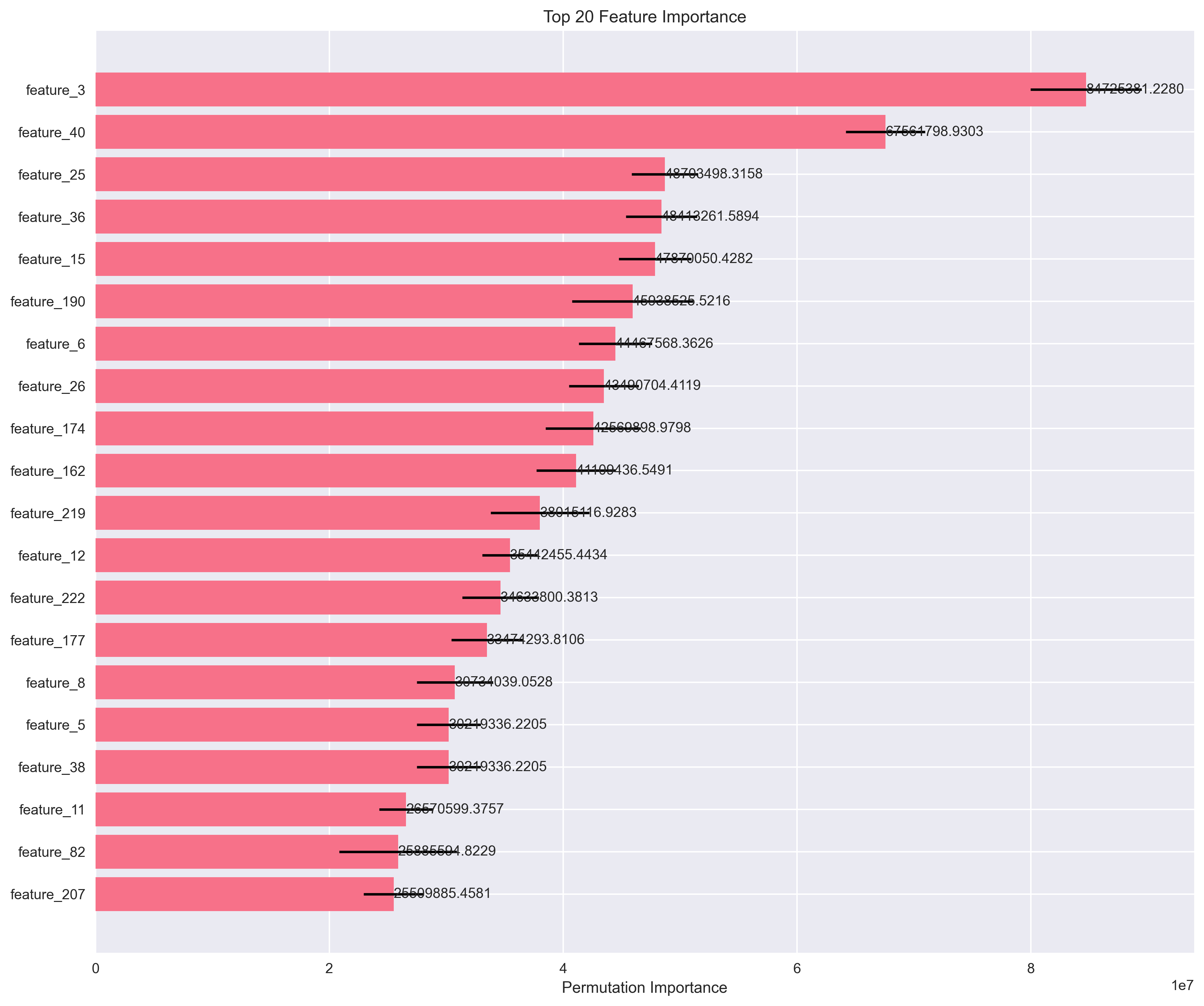
Hình 9. Top 20 features quan trọng suy ra với Permutation Importance
2.3.2. SHAP Values
SHAP (SHapley Additive exPlanations) giải thích từng dự đoán bằng cách tính đóng góp của từng đặc trưng:
explainer = shap.LinearExplainer(model, X_train)
shap_values = explainer.shap_values(X_test)
Lợi ích: Giúp hiểu tại sao mô hình đưa ra một dự đoán cụ thể.
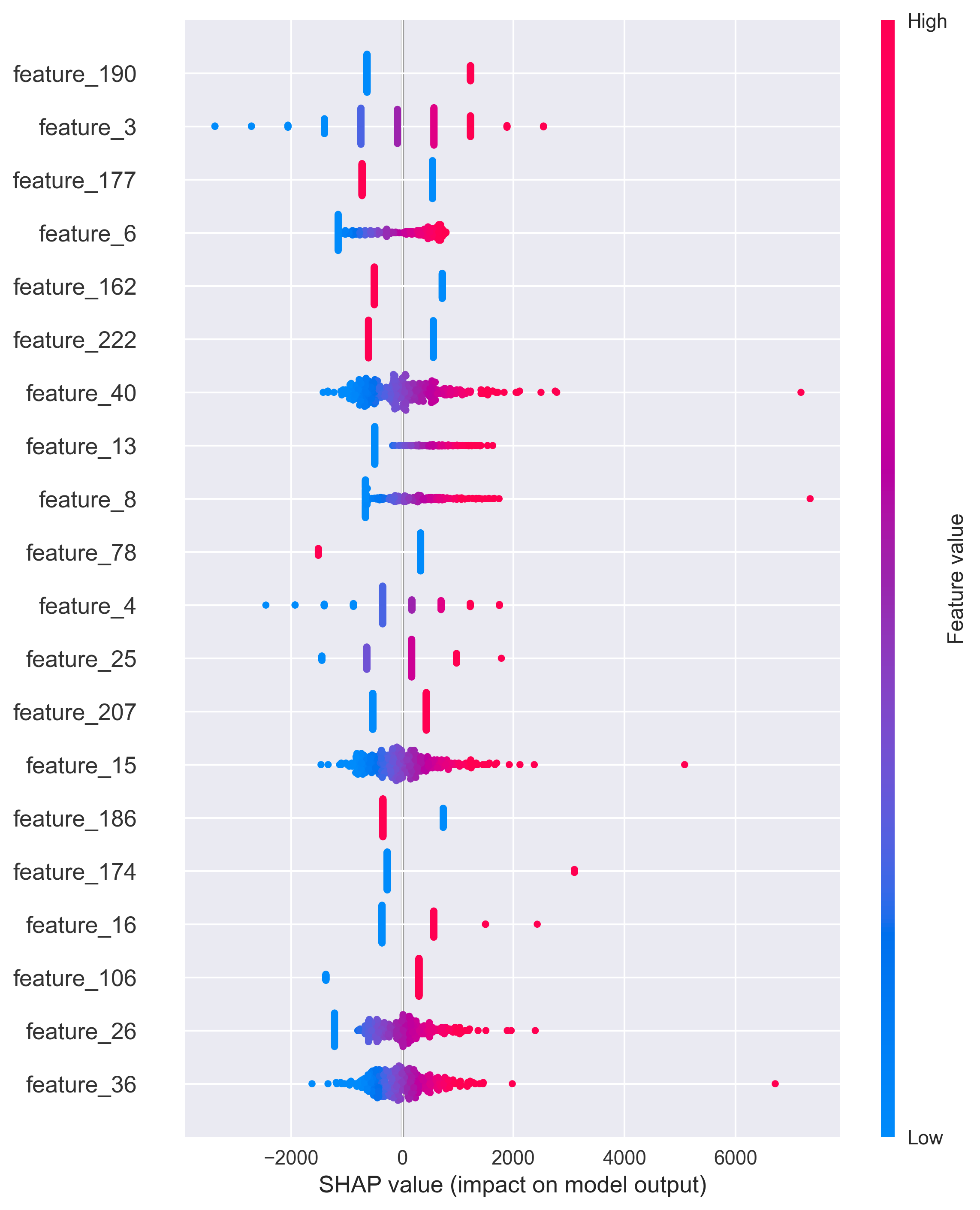
Hình 10. Giải thích mô hình với SHAP
2.3.3. Partial Dependence Plots
Phương pháp này cho thấy mối quan hệ giữa một đặc trưng và kết quả dự đoán:
pdp_result = partial_dependence(
model, X_train, [feature_index],
kind='average' # Giá trị trung bình
)
2.4. Phân tích tại sao kết quả không tốt hơn kết quả tham chiếu
Thực nghiệm cho kết quả không tốt hơn ví dụ ban đầu, điều này là do:
-
Số lượng đặc trưng quá lớn
Khi sử dụng polynomial features (bậc 2), số đặc trưng tăng từ khoảng 80 lên 1,097. Điều này gây ra vấn đề được gọi là "lời nguyền của chiều cao" (curse of dimensionality):
- Với 1,078 mẫu huấn luyện và 1,097 đặc trưng: Tỷ lệ gần 1:1
- Hậu quả: Mô hình dễ "học thuộc" dữ liệu (overfitting) thay vì học được các mẫu tổng quát
- Kết quả: Hoạt động tốt trên tập huấn luyện nhưng kém trên tập kiểm tra mới
Trong các kết quả tham chiếu, số đặc trưng chỉ khoảng 100-200 (không dùng polynomial hoặc dùng ít hơn). Với tỷ lệ mẫu:đặc trưng tốt hơn (5:1 đến 10:1), mô hình học ổn định hơn và không bị overfitting.
-
Tác động của Domain Feature Engineering
Mặc dù các đặc trưng domain (TotalSF, QualityArea, ...) có ý nghĩa, việc thêm chúng có thể:
- Thay đổi phân phối dữ liệu: Các đặc trưng mới có thể có phân phối khác với đặc trưng gốc
- Tạo tương quan: Một số đặc trưng mới có thể tương quan cao với đặc trưng cũ, gây redundancy
- Ảnh hưởng đến scaling: Các đặc trưng có scale khác nhau có thể làm lệch kết quả
3. Hyperparameter Tuning chưa đủ Tối ưu
Với n_iter=50 trong RandomizedSearchCV, hệ thống chỉ thử 50 kết hợp ngẫu nhiên trong không gian tham số rất lớn:
- Elastic Net: 50 alpha values × 9 l1_ratio values = 450 combinations
- Chỉ thử 50: Có thể bỏ lỡ các kết hợp tối ưu
4. Phương pháp Scaling
Hệ thống hiện tại sử dụng MinMaxScaler trong preprocessing và StandardScaler trong model.py, có thể gây double scaling hoặc mâu thuẫn.
Tác động: Scaling hai lần có thể làm méo phân phối dữ liệu và giảm hiệu suất.
2.5. Gợi ý cải thiện
- Giảm Số lượng Đặc trưng
- Loại bỏ polynomial features
- Feature selection: lựa chọn các đặc trưng quan trọng
- Tối ưu hóa hyperparameter
- Tăng số lần thử: thời gian training sẽ tăng, nhưng chất lượng mô hình tốt hơn
- Tinh chỉnh Phạm vi Alpha cho từng Model
grids = {
'ridge': {
'alpha': np.logspace(0, 5, 100), # Tăng từ (-4, 4) lên (0, 5)
# Alpha từ 1 đến 100,000 thay vì 0.0001 đến 10,000
},
'lasso': {
'alpha': np.logspace(-1, 4, 100), # Tăng từ (-4, 2) lên (-1, 4)
# Alpha từ 0.1 đến 10,000 thay vì 0.0001 đến 100
}
}
Với nhiều đặc trưng, cần regularization mạnh hơn để kiểm soát overfitting.
- Điều chỉnh preprocessing
- Chỉ sử dụng một phương pháp scaling
3. Tài liệu tham khảo
AI Viet Nam
scikit-learn: https://scikit-learn.org/stable/modules/linear_model.html
Chưa có bình luận nào. Hãy là người đầu tiên!