Xây dựng Mô hình Hồi quy Tuyến tính từ đầu: Lý thuyết, Code và Thực hành
Tóm tắt
Bài viết này trình bày một tổng quan về mô hình hồi quy tuyến tính (Linear Regression), một trong những thuật toán cơ bản và quan trọng nhất trong học máy. Nội dung tập trung vào nguyên lý hoạt động của hồi quy tuyến tính, vai trò của hàm mất mát, các phương pháp tối ưu dựa trên Gradient Descent, cùng những chủ đề mở rộng như hồi quy đa biến, chuẩn hóa đặc trưng và ảnh hưởng của tốc độ học (learning rate) đến quá trình hội tụ. Mục tiêu của bài viết là cung cấp cái nhìn hệ thống về toàn bộ pipeline huấn luyện mô hình hồi quy, từ lý thuyết đến thực tiễn.
1. Giới thiệu
Học máy (Machine Learning) là một nhánh của Trí tuệ Nhân tạo (AI), cho phép hệ thống học từ dữ liệu và đưa ra dự đoán cho các tình huống mới.
Các phương pháp học máy được chia thành hai nhóm chính:
- Học không giám sát (Unsupervised Learning): Mô hình phát hiện cấu trúc tiềm ẩn trong dữ liệu không có nhãn.
- Học có giám sát (Supervised Learning): Mô hình học từ các cặp dữ liệu đầu vào và đầu ra để dự đoán kết quả cho dữ liệu mới.
Hồi quy tuyến tính thuộc nhóm học có giám sát và được sử dụng khi biến mục tiêu là giá trị liên tục, chẳng hạn như dự đoán giá nhà, doanh thu quảng cáo, hay nhiệt độ trong tương lai.
2. Cơ sở của Hồi quy tuyến tính
Mô hình hồi quy tuyến tính mô tả mối quan hệ tuyến tính giữa biến độc lập $x$ và biến phụ thuộc $y$ dưới dạng:
$$ \hat{y} = wx + b $$
trong đó $w$ là hệ số trọng số (độ dốc) và $b$ là hệ số chệch (bias).
Hàm mất mát thường được sử dụng để đo lường sai số là Mean Squared Error (MSE):
$$ L = \frac{1}{N}\sum_{i=1}^{N}(y^{(i)} - \hat{y}^{(i)})^2 $$
3. Vectorization trong Linear Regression
Khi dữ liệu có kích thước lớn, việc sử dụng vòng lặp để tính gradient trở nên chậm. Kỹ thuật Vectorization tận dụng phép nhân ma trận để tính toán đồng thời nhiều mẫu, giúp tăng tốc đáng kể.
$$ \hat{y} = X\theta, \quad L = \frac{1}{m}\|X\theta - y\|^2 $$
Gradient vector hóa:
$$ \nabla_\theta L = \frac{2}{m}X^T(X\theta - y) $$
4. Thuật toán Gradient Descent
Để tối thiểu hóa hàm mất mát $L$, ta sử dụng thuật toán Gradient Descent nhằm điều chỉnh các tham số theo hướng giảm của gradient:
$$ \theta \leftarrow \theta - \eta \nabla_{\theta}L $$
với $\eta$ là tốc độ học (learning rate).
4.1 Stochastic Gradient Descent
Stochastic Gradient Descent (SGD) là một biến thể của thuật toán Gradient Descent, trong đó việc cập nhật tham số được thực hiện sau mỗi mẫu dữ liệu đơn lẻ thay vì sử dụng toàn bộ tập huấn luyện. Điều này giúp mô hình cập nhật nhanh hơn, nhưng đồng thời làm cho quá trình hội tụ dao động nhiều hơn so với Batch Gradient Descent.
Các bước thực hiện Stochastic Gradient Descent:
- Chọn ngẫu nhiên một mẫu $(x, y)$ từ tập dữ liệu huấn luyện.
- Tính giá trị dự đoán $\hat{y} = wx + b$
- Tính hàm mất mát: $L = (\hat{y} - y)^2$
- Tính gradient:
$$ \frac{\partial L}{\partial w} = 2x(\hat{y} - y), \quad \frac{\partial L}{\partial b} = 2(\hat{y} - y) $$ - Cập nhật tham số:
$$ w = w - \eta \frac{\partial L}{\partial w}, \quad b = b - \eta \frac{\partial L}{\partial b} $$
4.2 Mini-batch Gradient Descent
Mini-batch Gradient Descent (MBGD) là sự kết hợp giữa Batch Gradient Descent và Stochastic Gradient Descent. Thay vì cập nhật sau mỗi mẫu (SGD) hoặc sau toàn bộ tập dữ liệu (Batch GD), MBGD cập nhật tham số sau mỗi nhóm nhỏ (mini-batch) gồm $m$ mẫu:
$$ \hat{y} = X\theta, \quad L = \frac{1}{m}(\hat{y}-y)^T(\hat{y}-y), \quad \nabla_\theta L = \frac{2}{m}X^T(\hat{y}-y) $$
Cập nhật tham số:
$$ \theta = \theta - \eta \nabla_\theta L $$
MBGD giúp giảm phương sai của gradient, cân bằng giữa tốc độ hội tụ và độ ổn định, đặc biệt phù hợp với dữ liệu lớn.
4.3 Batch Gradient Descent
Batch Gradient Descent (BGD) sử dụng toàn bộ tập dữ liệu huấn luyện để tính gradient:
$$ L = \frac{1}{N}\sum_{i=1}^N (y^{(i)} - \hat{y}^{(i)})^2, \quad \nabla_\theta L = \frac{2}{N}X^T(X\theta - y) $$
$$ \theta = \theta - \eta \nabla_\theta L $$
Phương pháp này cho kết quả hội tụ mượt và chính xác, nhưng yêu cầu tài nguyên tính toán và bộ nhớ lớn.
4.4 So sánh các phương pháp Gradient Descent
| Đặc điểm | SGD | Mini-batch GD | Batch GD |
|---|---|---|---|
| Số mẫu mỗi lần cập nhật | 1 | $m$ (16–256) | $N$ (toàn bộ) |
| Số lần cập nhật mỗi epoch | $N$ | $N/m$ | 1 |
| Tốc độ hội tụ | Nhanh ban đầu, chậm dần | Cân bằng | Ổn định, chậm |
| Độ chính xác của gradient | Cao (nhiễu) | Trung bình | Chính xác |
| Yêu cầu bộ nhớ | Thấp | Vừa | Cao |
4.5 Hồi quy tuyến tính với nhiều đặc trưng
Khi dữ liệu gồm nhiều đặc trưng $(x_1, x_2, ..., x_n)$, mô hình mở rộng thành:
$$ \hat{y} = \theta_0 + \theta_1x_1 + \cdots + \theta_nx_n = X\theta $$
với:
$$ X = \begin{bmatrix} 1 & x_1^{(1)} & \cdots & x_n^{(1)} \\ 1 & x_1^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_1^{(N)} & \cdots & x_n^{(N)} \\ \end{bmatrix}, \quad \theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix}, \quad y = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(N)} \end{bmatrix} $$
5. K-Fold Cross Validation
K-Fold Cross Validation chia dữ liệu thành $K$ phần bằng nhau, mỗi lần dùng $K-1$ phần để huấn luyện và 1 phần để kiểm thử. Lặp lại $K$ lần, giá trị trung bình của các kết quả phản ánh độ ổn định mô hình:
$$ R^2_{mean} = \frac{1}{K} \sum_{k=1}^{K} R^2_k $$
Phương pháp này giúp đánh giá mô hình khách quan và tránh hiện tượng overfitting.
6. Tốc độ học (Learning Rate)
Tốc độ học $\eta$ quyết định độ lớn của bước cập nhật:
$$ \theta = \theta - \eta \nabla_\theta L $$
Giá trị $\eta$ quá nhỏ khiến hội tụ chậm, trong khi quá lớn làm mô hình dao động hoặc phân kỳ.
| Learning Rate | Triệu chứng | Hậu quả |
|---|---|---|
| $\eta = 0.00001$ | Giảm rất chậm | Có thể không hội tụ |
| $\eta = 0.5$ | Dao động quanh cực tiểu | Hội tụ không ổn định |
| $\eta = 1.0$ | Mất ổn định, giá trị NaN | Phân kỳ |
| $\eta = 0.01$ | Giảm mượt, ổn định | Tối ưu |
7. Chuẩn hóa và Tỷ lệ hóa đặc trưng
Khi các đặc trưng có thang giá trị khác nhau (ví dụ: diện tích từ 0–5000, số phòng từ 1–5), Gradient Descent có thể hội tụ chậm hoặc dao động. Hai phương pháp phổ biến để khắc phục là:
-
Min-Max Scaling:
$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$ -
Standardization:
$$ x' = \frac{x - \mu}{\sigma} $$
$$ \mu = \frac{1}{N} \sum_i x_i $$
$$ \sigma = \sqrt{ \frac{1}{N} \sum_i (x_i - \mu)^2 } $$
Việc chuẩn hóa giúp gradient ổn định hơn và cải thiện tốc độ hội tụ.
8. Implementation
Phần này trình bày quá trình triển khai (Implementation) mô hình hồi quy tuyến tính theo quy trình pipeline chuẩn trong học máy. Toàn bộ quá trình được chia thành hai giai đoạn chính: Huấn luyện (Training) và Kiểm thử (Testing). Mục tiêu là xây dựng mô hình dự đoán chính xác giá trị đầu ra dựa trên dữ liệu đầu vào, đồng thời tối ưu tham số $w, b$ bằng Gradient Descent.
8.1 Pipeline huấn luyện
Một pipeline huấn luyện cơ bản bao gồm:
- Chuẩn bị dữ liệu đầu vào và nhãn mục tiêu.
- Chia tập dữ liệu thành tập huấn luyện và kiểm thử.
- Huấn luyện mô hình bằng Gradient Descent.
- Kiểm thử mô hình trên dữ liệu chưa thấy để đánh giá hiệu năng.
8.2 MinMax Scaler và Standardization Scaler
8.2.1 MinMax Scaler
Xây dựng phương trình MinMax scaling:
def min_max_scaling(X):
mins=[]
maxs=[]
X_scaled=[]
for feature in X:
min_val = min(feature)
max_val = max(feature)
mins.append(min_val)
maxs.append(max_val)
scaled_feature=[]
for x in feature:
scaled_x = (x - min_val/(max-min_val))
scaled_feature.append(scaled_x)
X_scaled.append(scaled_feature)
return mins, maxs, X_scaled
def inverse_min_max_scaling(mins, maxs, X_scaled):
X_recovered = []
for i in range(len(X_scaled)):
feature = X_scaled[i]
min_val = mins[i]
max_val = maxs[i]
recovered_feature = []
for x in feature:
original_x = x*(max_val-min_val) + min_val
recovered_feature.append(original_x)
X_recovered.append(recovered_feature)
return X_recovered
8.2.2 Standardization Scaler
Xây dựng standardization scaler:
def z_score_scaling(X):
means=[]
stds=[]
X_scaled=[]
for feature in X:
mean_val = sum(feature)/len(feature)
means.append(mean_val)
std_val = sum((x - mean_val)**2 for x in feature) / len(feature) - 1)) ** 0.5
stds.append(std_val)
scaled_feature=[]
for x in feature:
scaled_x = (x - mean_val/std_val)
scaled_feature.append(scaled_x)
X_scaled.append(scaled_feature)
return means, stds, X_scaled
def inverse_z_score_scaling(means, stds, X_scaled):
X_recovered = []
for i in range(len(X_scaled)):
feature = X_scaled[i]
mean_val = means[i]
std_val = stds[i]
recovered_feature = []
for x in feature:
original_x = x*std_val + mean_val
recovered_feature.append(original_x)
X_recovered.append(recovered_feature)
return X_recovered
Kết quả của quy trình triển khai cho thấy cách hồi quy tuyến tính được huấn luyện thông qua việc giảm dần sai số, thể hiện sự hội tụ của mô hình tới nghiệm tối ưu của hàm mất mát.
8.3 Thực hành với tệp dữ liệu Advertising
Trong phần này, chúng ta sẽ thực hành sử dụng mô hình hồi quy tuyến tính với tệp dữ liệu Advertising.
8.3.1 Sử dụng Stochastic Gradient Descent thông thường
Chuẩn bị dataset
Tải về và giải nén dữ liệu:
# Dataset
!gdown 1x3OX304PO-bonyooK4FKcRhyrTmT4kif
!unzip advertising.zip
Ta sẽ được bộ dữ liệu với format như sau:
| TV | Radio | Newspaper | Sales |
|---|---|---|---|
| 230.1 | 37.8 | 69.2 | 22.1 |
| 44.5 | 39.3 | 45.1 | 10.4 |
| 17.2 | 45.9 | 69.3 | 12.0 |
| 151.5 | 41.3 | 58.5 | 16.5 |
| 180.8 | 10.8 | 58.4 | 17.9 |
| 8.7 | 48.9 | 75.0 | 7.2 |
| 57.5 | 32.8 | 23.5 | 11.8 |
| 120.2 | 19.6 | 11.6 | 13.2 |
| 8.6 | 2.1 | 1.0 | 4.8 |
| 199.8 | 2.6 | 21.2 | 15.6 |
Bảng 8.1: Một phần dữ liệu từ advertising.csv
Lưu dữ liệu vào các biến tương ứng:
def prepare_data(file_name):
data = np.genfromtxt(file_name, delimiter=',', skip_header=1).tolist()
N = len(data)
# Get TV data
tv_data = get_column(data,)
# Get Radio data
radio_data = get_column(data,1)
# Get Newspaper data
newspaper_data = get_column(data,2)
# Get Sales data
sales_data = get_column(data,3)
# Build X input and y output for training
X = [tv_data, radio_data, newspaper_data]
y = sales_data
return X,y
X,y = prepare_data('../content/advertising.csv')
Xây dựng các hàm dự đoán, hàm mất mát, tính đạo hàm:
# Predict
def predict(x1, x2, x3, w1, w2, w3, b):
y_hat = w1*x1 + w2*x2 + w3*x3 + b
return y_hat
# Compute Loss
def compute_loss(y_hat,y):
loss = (y_hat-y)**2
return loss
# Compute Gradient
def compute_gradient_wi(y_hat,y,xi):
dwi = 2*xi*(y_hat-y)
return dwi
def compute_gradient_b(y_hat,y):
db = 2*(y_hat-y)
return db
Cập nhật các trọng số sau khi thực hiện tính toán:
# Update weights
def update_weights_wi(wi,b,dwi,db,lr):
wi = wi - lr*dwi
return wi
def update_weight_b(b, db, lr):
b = b - lr*db
return b
Xây dựng phương trình Linear Regression:
def linear_regression(X_data, y_data, epochs=50, lr=1e-5):
# Initialization
losses = []
w1, w2, w3, b = 0.001, 0.007, -0.002, 0.001
N = len(y)
for epoch in range(epochs):
for i in range(N):
x1 = X_data[0][i]
x2 = X_data[1][i]
x3 = X_data[2][i]
y = y_data[i]
# Predict
y_hat = predict(x1, x2, x3, w1, w2, w3, b)
# Loss
loss = compute_loss(y_hat, y)
# Gradient
d_w1 = compute_gradient_wi(y_hat, y, x1)
d_w2 = compute_gradient_wi(y_hat, y, x2)
d_w3 = compute_gradient_wi(y_hat, y, x3)
d_b = compute_gradient_b(y_hat, y)
# Update
w1 = update_weight_wi(w1, d_w1, lr)
w2 = update_weight_wi(w2, d_w2, lr)
w3 = update_weight_wi(w3, d_w3, lr)
b = update_weight_b(b, db, lr)
# Log
losses.append(loss)
return (w1, w2, w3, b, losses)
Thực hiện cập nhật trọng số:
w1, w2, w3, b, losses = linear_regression(X_data=X, y_data=y, epochs=1, lr=1e-7)
import matplotlib.pyplot as plt
import random
plt.plot(losses[:200])
plt.xlabel('#iteration')
plt.ylabel('Loss')
plt.show()
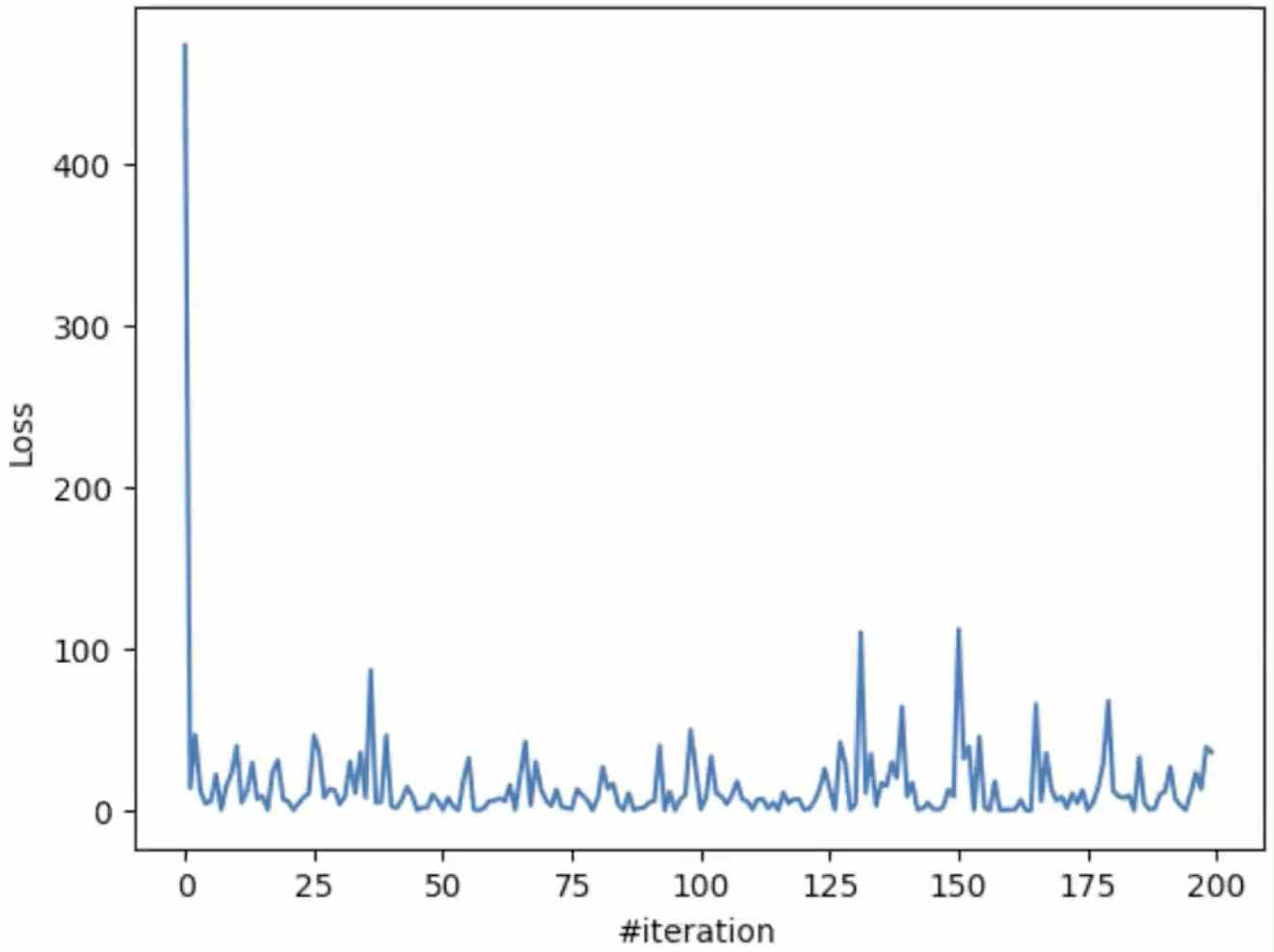
Hình 8.1: Biểu đồ loss của mô hình dự đoán
8.3.2 Sử dụng các phương pháp Gradient Descent Vectorization
Cập nhật dữ liệu:
data = genfromtxt('../content/advertising.csv', delimiter=',', skip_header=1)
N = data.shape[0]
X = data[:,:3]
y = data[:,3:]
Chuẩn hóa dữ liệu bằng phương pháp Mean Normalization:
# Normalize input data by using mean normalizaton
def mean_normalization(X):
N = len(X)
maxi = np.max(X)
mini = np.min(X)
avg = np.mean(X)
X = (X-avg) / (maxi-mini)
X_b = np.c_[np.ones((N, 1)), X]
return X_b, maxi, mini, avg
Stochastic Gradient Descent
Phương trình Stochastic Gradient Descent:
def stochastic_gradient_descent(X_b, y, n_epochs=50, learning_rate=0.01):
N, d_plus1 = X_b.shape
# Step 1: Init parameters
thetas = np.asarray([[1.16270837], [-0.81960489],
[1.39501033], [0.29763545]])
thetas_path = [thetas.copy()]
losses = []
# Step 2-6: SGD loop
for epoch in range(n_epochs):
for i in range(N):
random_index = i
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
# Step 3: prediction
oi = xi.dot(thetas) # scalar (1,1)
# Step 4: MSE loss for 1 sample
li = (oi - yi)**2
# Step 5: gradient
gradients = 2*(oi - yi)*xi.T
# Step 6: update
thetas = thetas - learning_rate*gradients
# log
thetas_path.append(thetas.copy())
losses.append(li[0][0])
return thetas_path, losses
Trực quan hóa losses sau khi thực hiện training sau 50 epochs:
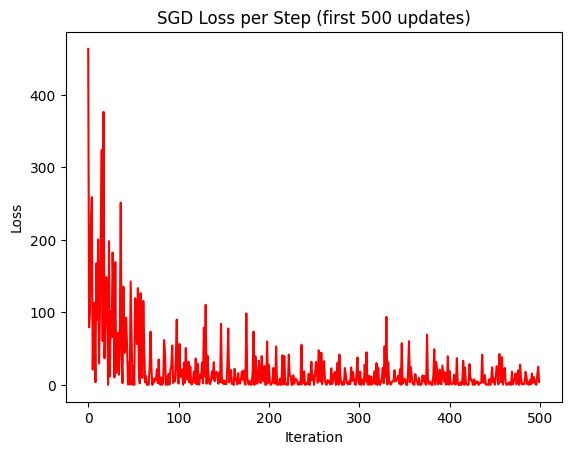
Hình 8.2: Biểu đồ loss của mô hình SGD
Mini-batch Gradient Descent
Phương trình Mini-batch Gradient Descent:
def mini_batch_gradient_descent(X_b, y, n_epochs=50, minibatch_size=20, learning_rate=0.01):
N, d_plus1 = X_b.shape
# Step 1: Init parameters
thetas = np.asarray([[1.16270837], [-0.81960489],
[1.39501033], [0.29763545]])
thetas_path = [thetas.copy()]
losses = []
for epoch in range(n_epochs):
# shuffle data
shuffled_indices = np.random.permutation(N)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0, N, minibatch_size):
xi = X_b_shuffled[i:i+minibatch_size] # (m, d+1)
yi = y_shuffled[i:i+minibatch_size] # (m, 1)
# Step 3: prediction
output = xi.dot(thetas) # (m,1)
# Step 4: MSE loss for minibatch
loss = np.mean((output - yi)**2)
# Step 5: gradient for minibatch
gradients = (2/minibatch_size) * xi.T.dot(output - yi) # (d+1,1)
# Step 6: update
thetas = thetas - learning_rate*gradients
# log
thetas_path.append(thetas.copy())
losses.append(loss)
return thetas_path, losses
Trực quan hóa losses sau khi thực hiện training sau 50 epochs và mini batch size 20 với learning rate = 0.01:
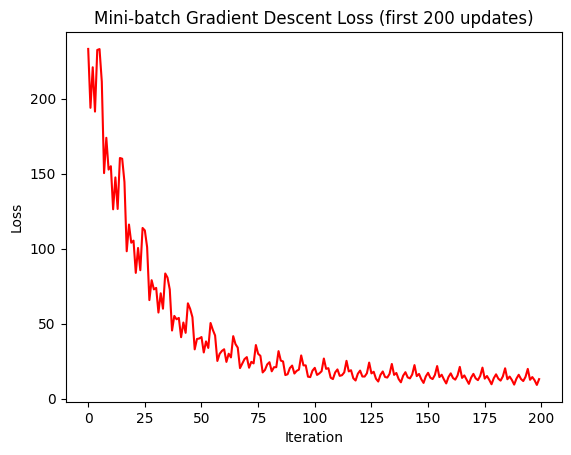
Hình 8.3: Biểu đồ loss của mô hình Mini-Batch Gradient Descent
Batch Gradient Descent
Phương trình Batch Gradient Descent:
def batch_gradient_descent(X_b, y, n_epochs=100, learning_rate=0.01):
N, d_plus1 = X_b.shape
# Step 1: Init parameters
thetas = np.asarray([[1.16270837], [-0.81960489], [1.39501033], [0.29763545]])
thetas_path = [thetas.copy()]
losses = []
for epoch in range(n_epochs):
# Step 3: prediction
output = X_b.dot(thetas) # (N,1)
# Step 4: MSE loss
loss = np.mean((output - y)**2)
# Step 5: gradient
gradients = (2/N) * X_b.T.dot(output - y)
# Step 6: update parameters
thetas = thetas - learning_rate * gradients
# log
thetas_path.append(thetas.copy())
losses.append(loss)
return thetas_path, losses
Trực quan hóa losses sau khi thực hiện training sau 100 epochs với learning rate = 0.01:

Hình 8.4: Biểu đồ loss của mô hình Batch Gradient Descent
8.4 Thực hành với tệp dữ liệu Bitcoin
Trong phần này, chúng ta sẽ thực hành sử dụng mô hình hồi quy tuyến tính với tệp dữ liệu Bitcoin Prices.
Cho tệp dữ liệu Bitcoin với format như sau:
| unix | date | symbol | open | high | low | close | Volume BTC | Volume USD |
|---|---|---|---|---|---|---|---|---|
| 1646092800 | 2022-03-01 00:00:00 | BTC/USD | 43221.71 | 43626.49 | 43185.48 | 43185.48 | 49.006289 | 2.116360e+06 |
| 1646006400 | 2022-02-28 00:00:00 | BTC/USD | 37717.10 | 44256.08 | 37468.99 | 43178.98 | 3160.618070 | 1.364723e+08 |
| 1645920000 | 2022-02-27 00:00:00 | BTC/USD | 39146.66 | 39886.92 | 37015.74 | 37712.68 | 1701.817043 | 6.418008e+07 |
| 1645833600 | 2022-02-26 00:00:00 | BTC/USD | 39242.64 | 40330.99 | 38600.00 | 39146.66 | 912.724087 | 3.573010e+07 |
| 1645747200 | 2022-02-25 00:00:00 | BTC/USD | 38360.93 | 39727.97 | 38027.61 | 39231.64 | 2202.851827 | 8.642149e+07 |
Bảng 8.2: Một phần dữ liệu giá Bitcoin (BTC/USD)
Biểu đồ closing price của bitcoin trong một số năm:
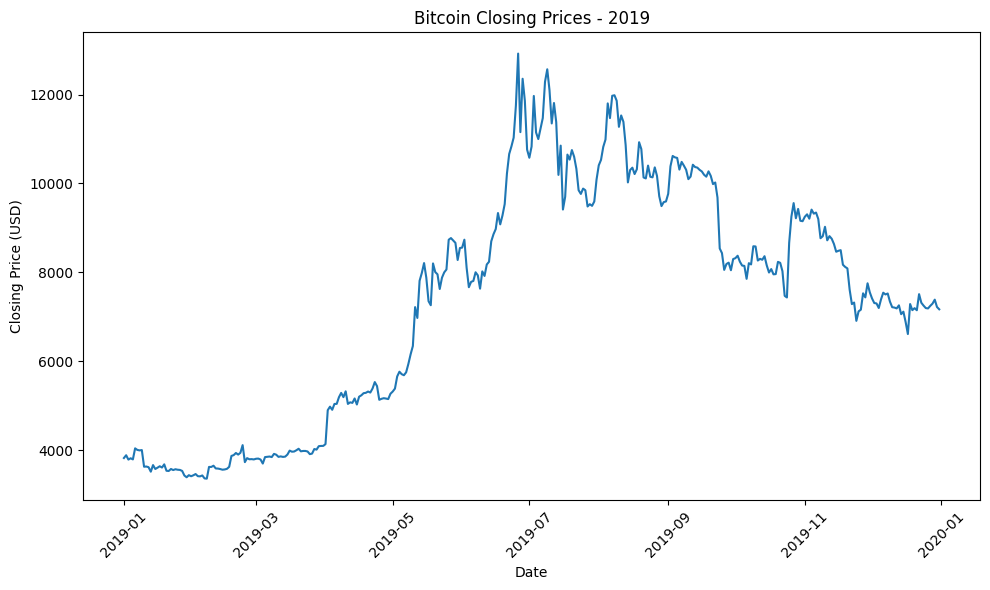
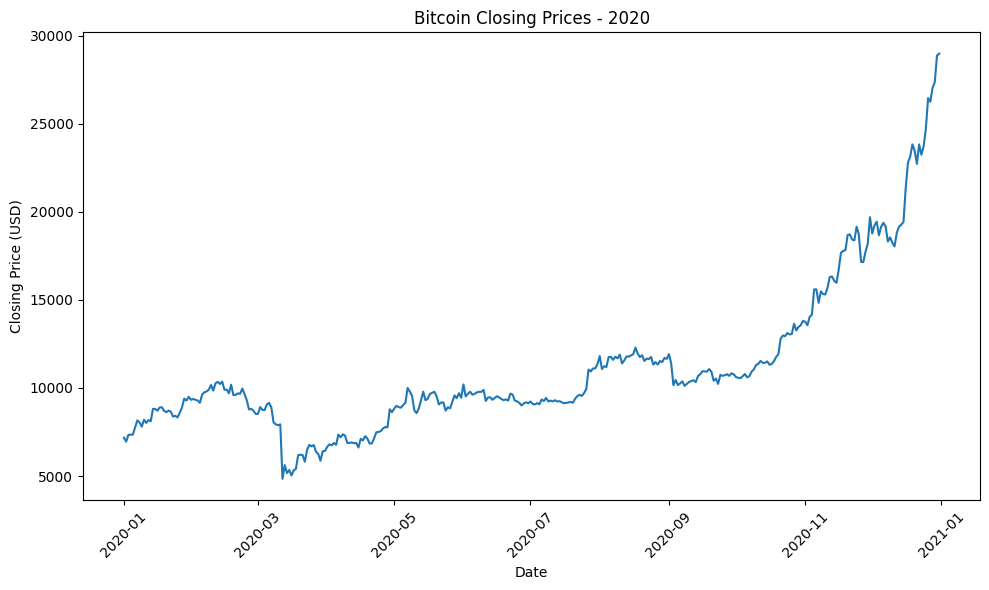
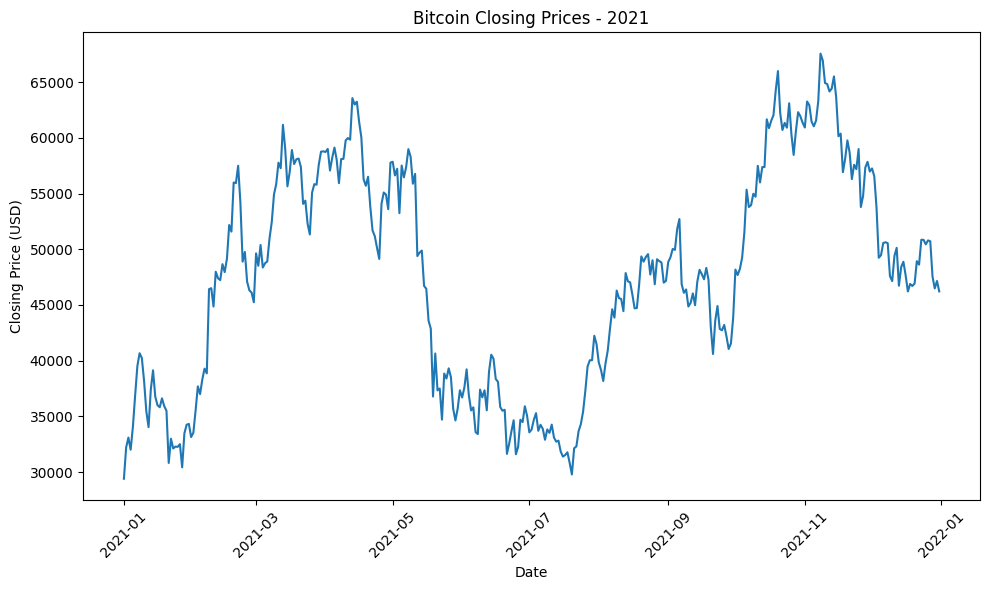
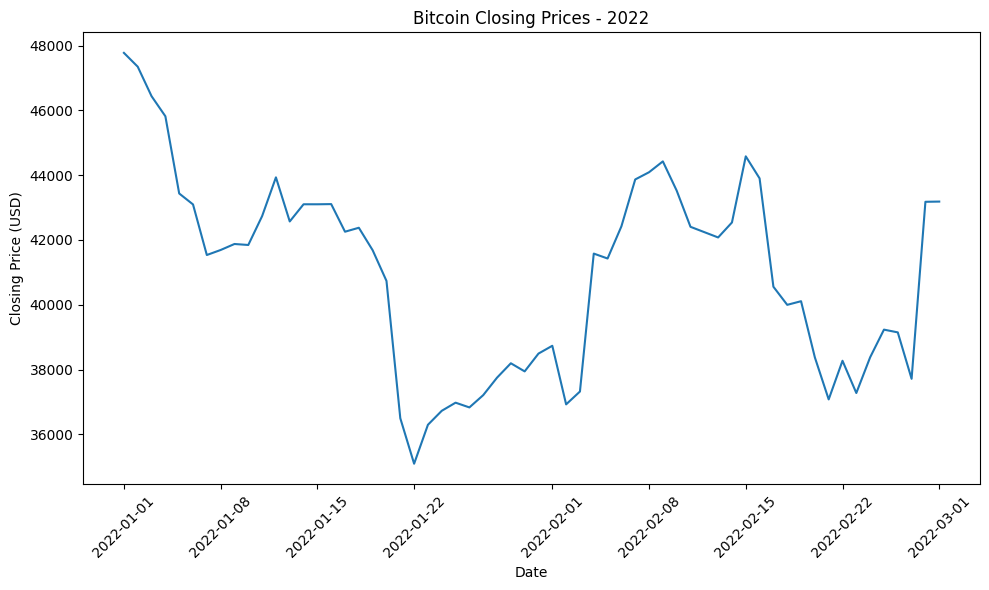
Hình 8.5: Tổng hợp biểu đồ giá đóng Bitcoin qua một số năm
Biểu đồ nến của bitcoin qua các năm:

Hình 8.6: Biểu đồ nến của BTC qua các năm
8.4.1 Linear Regression Vectorized
Cập nhật các phương trình linear regression theo phương pháp vector hóa:
def predict(X, w, b):
return X.dot(w) + b
def linear_regression_vectorized(X, y, learning_rate=0.01, num_iterations=200):
"""
Args:
X: Feature matrix (numpy array).
y: Target variable (numpy array).
learning_rate: Learning rate for gradient descent.
num_iterations: Number of iterations for gradient descent.
Returns:
w: Optimal weight vector.
b: Optimal bias term.
"""
n_samples, n_features = X.shape
w = np.zeros(n_features) # Initialize weights
b = 0 # Initialize bias
losses = []
for _ in range(num_iterations):
y_hat = predict(X, w, b) # Make predictions
dw, db, cost = gradient(y_hat, y, X) # Calculate gradients
w, b = update_weight(w, b, learning_rate, dw, db) # Update weights and bias
losses.append(cost)
return w, b, losses
def gradient(y_hat, y, x):
loss = y_hat-y
dw = x.T.dot(loss)/len(y)
db = np.sum(loss)/len(y)
cost = np.sum(loss**2)/(2*len(y))
return (dw,db, cost)
def update_weight(w,b,lr,dw,db):
w_new = w - lr*dw
b_new = b - lr*db
return (w_new, b_new)
Chuẩn hóa Data
Chia dataset thành 2 cặp training và testing:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42, shuffle=True
)
Chuẩn hóa dataset sử dụng phương pháp Standard Scaler:
from sklearn.preprocessing import StandardScaler
scalar = StandardScaler()
X_train_scaled = scalar.fit_transform(X_train)
X_test_scaled = scalar.transform(X_test)
Nạp data sau khi chuẩn hóa vào phương trình để huấn luyện mô hình:
w, b, losses = linear_regression_vectorized(
X_train_scaled, y_train, learning_rate=0.1, num_iterations=200
)
Trực quan hóa loss sau khi training:
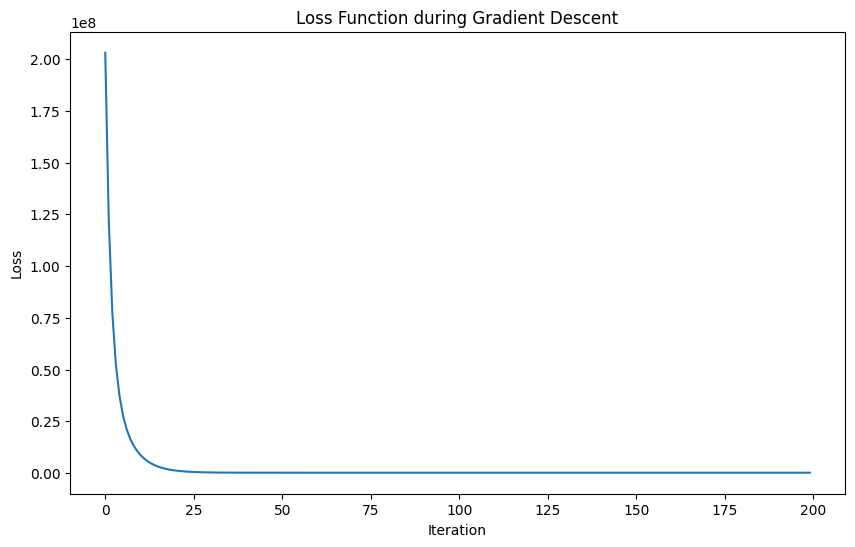
Hình 8.7: Biểu đồ loss của mô hình
8.4.2 Cross Validation Technique
Sử dụng phương pháp K-Fold Cross Validation để đánh giá độ ổn định của mô hình:
from sklearn.model_selection import KFold, TimeSeriesSplit
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
def cross_validate_model(X, y, learning_rate=0.01, num_iterations=200, n_splits=5):
cv = KFold(n_splits=n_splits, shuffle=True, random_state=42)
cv_scores = {
'rmse': [], 'mae': [], 'r2': []
}
for fold, (train_idx, val_idx) in enumerate(cv.split(X), 1):
X_train_cv, X_val_cv = X[train_idx], X[val_idx]
y_train_cv, y_val_cv = y[train_idx], y[val_idx]
# Train model
w, b, _ = linear_regression_vectorized(X_train_cv, y_train_cv,
learning_rate, num_iterations)
# Validate
y_pred_cv = predict(X_val_cv, w, b)
# Metrics
cv_scores['rmse'].append(np.sqrt(mean_squared_error(y_val_cv, y_pred_cv)))
cv_scores['mae'].append(mean_absolute_error(y_val_cv, y_pred_cv))
cv_scores['r2'].append(r2_score(y_val_cv, y_pred_cv))
print(f"Fold {fold}: RMSE={cv_scores['rmse'][-1]:.4f}, "
f"MAE={cv_scores['mae'][-1]:.4f}, R2={cv_scores['r2'][-1]:.4f}")
# Average scores
print(f"\nAverage CV Scores:")
print(f"RMSE: {np.mean(cv_scores['rmse']):.4f} (+/- {np.std(cv_scores['rmse']):.4f})")
print(f"MAE: {np.mean(cv_scores['mae']):.4f} (+/- {np.std(cv_scores['mae']):.4f})")
print(f"R2: {np.mean(cv_scores['r2']):.4f} (+/- {np.std(cv_scores['r2']):.4f})")
return cv_scores
8.5 Tìm tốc độ học tối ưu bằng Cross Validation
Để đảm bảo quá trình huấn luyện mô hình Gradient Descent đạt hiệu quả cao, việc lựa chọn tốc độ học (learning rate) phù hợp là rất quan trọng. Giá trị $\eta$ quá nhỏ sẽ khiến quá trình hội tụ chậm, trong khi quá lớn có thể làm mô hình dao động hoặc phân kỳ.
Để tìm được learning rate tốt nhất, ta cần thực hiện những bước sau:
-
Khởi tạo danh sách các giá trị learning rate cần thử nghiệm:
Nếu không được chỉ định, danh sách mặc định gồm: $[0.001, 0.01, 0.1, 0.5, 1.0]$. -
Khởi tạo biến lưu kết quả:
Biếnresultsdùng để lưu trung bình và độ lệch chuẩn của các chỉ số $R^2$ và RMSE cho từng giá trị learning rate. -
Thực hiện K-Fold Cross Validation:
Với mỗi giá trị $\eta$, dữ liệu được chia thành $k$ phần (mặc định $k=5$). Mỗi lần, mô hình được huấn luyện trên $k-1$ phần và kiểm thử trên phần còn lại. Quá trình này được lặp lại $k$ lần để tính trung bình chỉ số $R^2$ và RMSE. -
Đánh giá và chọn tốc độ học tối ưu:
Giá trị learning rate có điểm $R^2$ trung bình cao nhất được chọn làm $\eta^*$ (learning rate tối ưu). -
Hiển thị kết quả tóm tắt:
Bảng tổng hợp thể hiện hiệu suất trung bình ($R^2$, RMSE) của từng learning rate, giúp người dùng so sánh và trực quan hóa lựa chọn.
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np
def find_best_learning_rate(X, y, lr_candidates=None, num_iterations=200, n_splits=5):
if lr_candidates is None:
lr_candidates = [0.001, 0.01, 0.1, 0.5, 1.0]
best_lr = None
best_score = -float('inf')
results = {}
print("="*50)
print("Finding Best Learning Rate with Cross-Validation")
print("="*50)
for lr in lr_candidates:
print(f"\nTesting Learning Rate: {lr}")
print("-"*30)
# Use Cross validation for this learning rate
cv_scores = cross_validate_model(X, y, lr, num_iterations, n_splits)
# Use R2 as main metric for comparison
mean_r2 = np.mean(cv_scores['r2'])
results[lr] = {
'mean_r2': mean_r2,
'std_r2': np.std(cv_scores['r2']),
'mean_rmse': np.mean(cv_scores['rmse'])
}
# Update best learning rate
if mean_r2 > best_score:
best_score = mean_r2
best_lr = lr
# Summary
print("\n" + "="*50)
print("SUMMARY - Learning Rate Comparison")
print("="*50)
for lr, scores in results.items():
print(f"LR={lr:6.4f}: R2={scores['mean_r2']:.4f} (+/- {scores['std_r2']:.4f}), "
f"RMSE={scores['mean_rmse']:.4f}")
print(f"\nBest Learning Rate: {best_lr}")
print(f"Best R2 Score: {results[best_lr]['mean_r2']:.4f}")
return best_lr, results
Cách tiếp cận này giúp tự động lựa chọn tốc độ học phù hợp nhất với dữ liệu và mô hình, đảm bảo cân bằng giữa tốc độ hội tụ và độ ổn định trong quá trình huấn luyện.
9. Kết luận
Qua bài viết này, chúng ta đã đi qua toàn bộ hành trình từ nền tảng lý thuyết đến thực hành của Hồi quy tuyến tính (Linear Regression) – một trong những thuật toán cốt lõi và dễ hiểu nhất trong học máy.
-
Từ việc xây dựng phương trình mô hình, định nghĩa hàm mất mát, cho đến việc tối ưu tham số bằng Gradient Descent và các biến thể của nó (SGD, Mini-Batch, Batch GD), người học có thể thấy được cơ chế học của mô hình tuyến tính một cách rõ ràng và trực quan.
-
Phần mở rộng về Vectorization đã cho thấy sức mạnh của đại số tuyến tính trong việc tối ưu tốc độ tính toán, giúp mô hình xử lý hiệu quả hơn khi làm việc với dữ liệu lớn. Kết hợp cùng các kỹ thuật như chuẩn hóa dữ liệu, Cross Validation, và tối ưu tốc độ học, bài viết đã mô phỏng quy trình huấn luyện hiện đại trong học máy thực tiễn.
-
Thông qua hai bài thực hành – dự đoán
Salestừ dữ liệuAdvertisingvà dự đoánBitcoin Prices– ta thấy rõ khả năng áp dụng linh hoạt của hồi quy tuyến tính trong nhiều bối cảnh khác nhau. Việc so sánh các phương pháp Gradient Descent, trực quan hóa hàm mất mát và phân tích tác động của tốc độ học giúp người học hiểu sâu hơn về hành vi hội tụ của mô hình. -
Mặc dù đơn giản, hồi quy tuyến tính vẫn là nền tảng vững chắc để tiếp cận các mô hình phức tạp hơn như Neural Networks. Không chỉ là một công cụ dự đoán, mà còn là chìa khóa giúp mở ra tư duy tối ưu hóa – một kỹ năng cốt lõi trong toàn bộ lĩnh vực học máy và khoa học dữ liệu.
Hết
Chưa có bình luận nào. Hãy là người đầu tiên!