PROJECT 5.1: HOUSE PRICING PREDITION
Nhóm CONQ007
Mở đầu
Với mục tiêu là dự đoán giá nhà là, blog này sẽ phân tích dữ liệu và xây dựng mô hình dự đoán, với trọng tâm là giải thích rõ ràng các khái niệm toán học thông qua ví dụ cụ thể.
Blog sẽ tập trung các vấn đền:
* Xử lý dữ liệu nâng cao: Phát hiện outliers bằng PCA + Isolation Forest, xử lý missing values, và feature engineering thông minh
* Nền tảng toán học: Eigenvalues/eigenvectors, covariance matrix, PCA - từ lý thuyết đến ứng dụng thực tế
* Thuật toán Machine Learning hữu ích: Elastic Net Regression (kết hợp L1 & L2) và CatBoost với Ordered Target Statistics.
1. Khảo sát dữ liệu
1.1 Đánh giá ban đầu
Sau khi download tập dataset của House Pricing, chúng ta kiểm tra data types của dữ liệu và số lượng giá trị bị thiếu trong dữ liệu:
print("\nData types summary:")
display(df.dtypes.value_counts())
print("\nNumber of nulls per column (top 30):")
display(df.isnull().sum().sort_values(ascending=False).head(30))
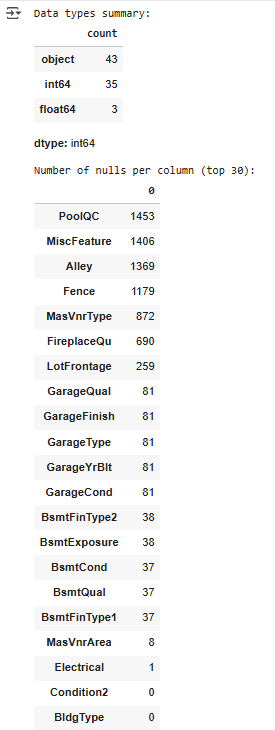
Kết quả đánh giá dữ liệu ban đầu
Từ kết quả này, ta có thể rút ra rằng:
- Có 43 categorical features
- Có 35 numerical features dạng số nguyên (năm xây dựng, số phòng)
- Có 3 numerical features dạng số thực (diện tích)
- PoolQC, MiscFeature, Alley, Fence, MasVnrType, FireplaceQu thuộc vào nhóm có giá trị null cao nhất, cần phải loại bỏ hoặc có các phương pháp xử lý về sau
1.2 Thống kê dữ liệu tổng quan
Tiếp theo, chúng ta sẽ hiển thị 5 dòng đầu tiên của tập dữ liệu kèm theo thống kê mô tả.
target = "SalePrice"
print(f"Dataset shape: {df.shape}")
display(df.head())
display(df.describe(include='all').T)
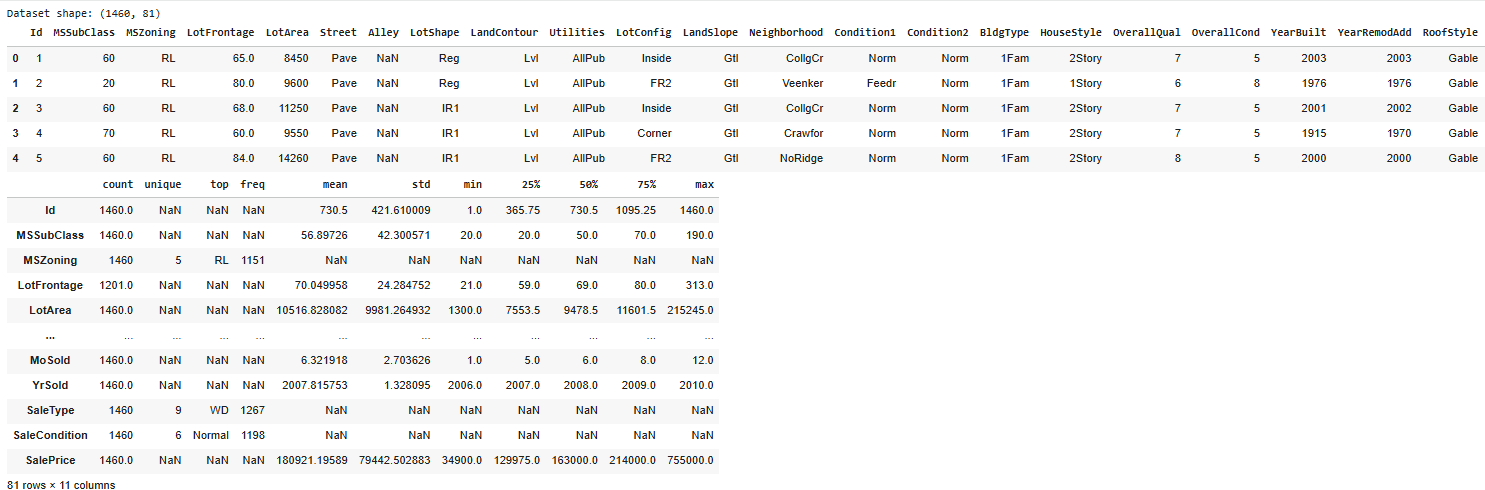
Thống kê chi tiết dữ liệu
Từ kết quả này, chúng ta có thể rút ra một số kết luận:
- Một số features có phân phối lệch phải (right-skewed), như SalePrice, MoSold, LotArea, khi mà giá trị mean>median(50%)
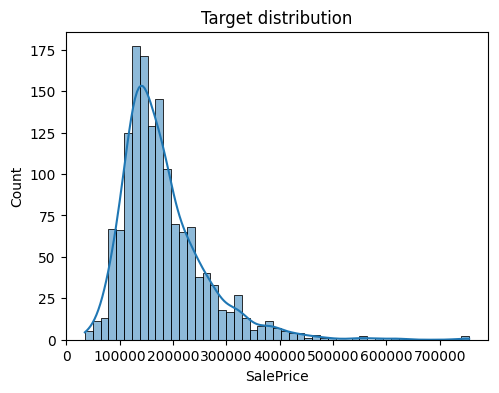
Biểu đồ lệch phải mạnh của SalePrice
- Một số features có các giá trị outliers rất lớn, ví dụ như LotArea, giá trị Q3 chỉ có 11,651.5 trong khi giá trị max của feature này là 215,245 , gấp xấp xỉ 18 lần. Các giá trị này cần có cách xử lý phù hợp để tránh gây nhiễu cho mô hình
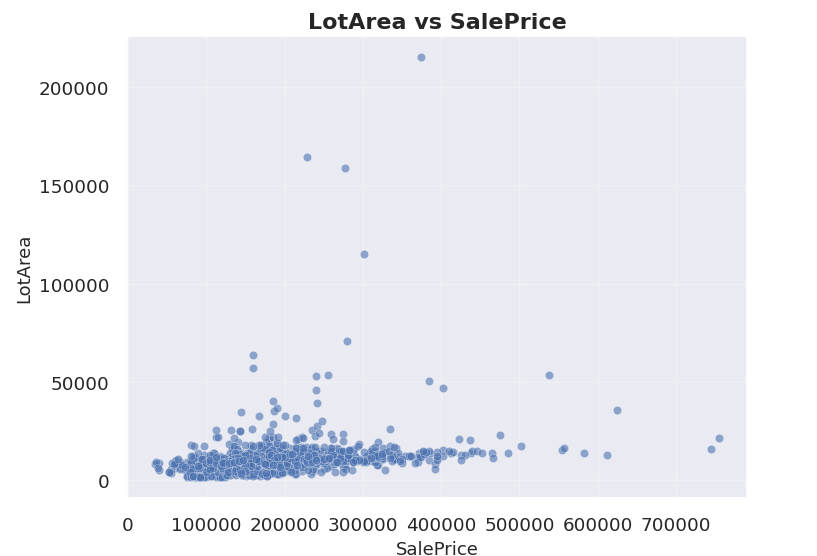
Biểu đồ giá trị của LotArea với rất nhiều outliers
1.3 Đánh giá sự tương quan giữa các dữ liệu
Để kiểm tra mức độ tương quan giữa các features, chúng ta sử dụng Missingness Matrix và Missingness Correlation Heatmap
msno.heatmap(df, figsize=(10,6))
plt.title("Missingness correlation heatmap")
plt.show()
Ta được kết quả là đồ thị
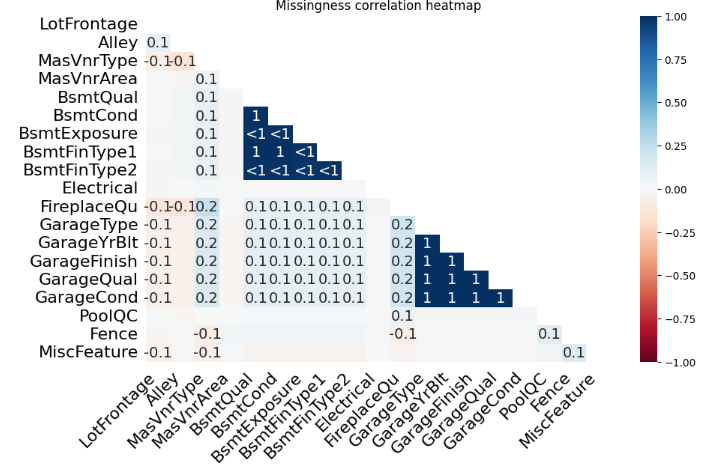
Missingness Correlation Heatmap
Biểu đồ Missingness Correlation Heatmap hiển thị sự tương quan giữa việc bị thiếu dữ liệu của các cột. Các giá trị nằm trong khoảng [-1,1]
- Nhóm 1: Hai cột thường thiếu cùng nhau
- 0: Không liên quan
- -1: Khi cột này thiếu, cột kia luôn có dữ liệu
Từ dữ liệu này, ta có thể thấy được sự tương quan giữa một số nhóm features nhất định.
- Nhóm Basement(BsmtQual, BsmtCond, BsmtExposure, BsmtFinType1, BsmtFinType2) có hệ số +1. Lí do là vì nếu nhà không có tầng hầm thì toàn bộ thông tin về tầng hầm đều không có.
- Nhóm Garage(GarageType, GarageFinish, GarageQual, GarageCond, GarageYrBlt) cũng có hệ số +1, vì nếu nhà không có garage thì mọi chỉ số liên quan đến garage đềukhoong có
- Một số features như PoolQC, Fence, MiscFeature có tương quan thấp (0.1 hoặc 0) với hầu hết các feature khác, cho thấy việc thiếu giá trị ở features này không gắn liền với các features khác
1.4 Đánh giá mức độ lệch và bất thường trong phân phối dữ liệu
Chúng ta sẽ sử dụng một số hàm để đo độ lệch và độ nhọn của phân phối, cũng như sử dụng kiểm định Shapiro-Wilk để áp dụng lên 20 biến đầu tiên trong tập dữ liệu xem biến nào không tuân theo phân phối chuẩn
# --- Numeric summary & distribution diagnostics ---
num_cols = df.select_dtypes(include=[np.number]).drop(columns=['Id', target], errors='ignore')
stats = pd.DataFrame({
'missing_%': df[num_cols.columns].isnull().mean()*100,
'skew': num_cols.skew(),
'kurtosis': num_cols.kurt()
}).sort_values('skew', key=lambda s: s.abs(), ascending=False)
display(stats.head(15))
# --- Normality check (Shapiro-Wilk on sample) ---
from scipy.stats import shapiro
normality = {}
for col in num_cols.columns[:20]:
try:
stat, p = shapiro(num_cols[col].dropna().sample(min(5000, num_cols[col].notna().sum()), random_state=RANDOM_SEED))
normality[col] = p
except Exception:
pass
normality = pd.Series(normality, name='p_value').sort_values()
print("Variables deviating from normality (p<0.05):")
display(normality[normality<0.05].head(10))
Ta được kết quả sau:
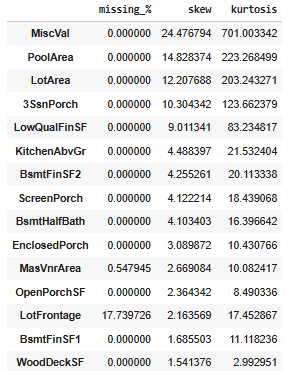
Biểu đồ thể hiện giá trị skew và kurtosis
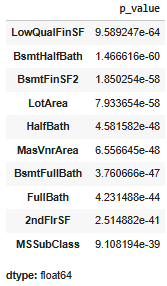
Biểu đồ Shatosis
Các kết quả thống kê này cho thấy:
- Có một số features có độ lệch phải rất lớn (skew>1), đặc biệt là các features liên quan đến diện tích hoặc tiện ích (PoolArea, LotArea, Porch, Deck, ...). Các features này có outlier và phân phối không chuẩn, do phần lớn các giá trị = 0 hoặc nhỏ, chỉ có một số ít giá trị cực lớn kéo trung bình lên. Cần sử dụng 1 số phương pháp như log để giảm độ lệch, cũng như một số phương pháp để giảm ảnh hưởng gây ra bởi outliers, những phương pháp này sẽ được nêu ở các phần tiếp theo
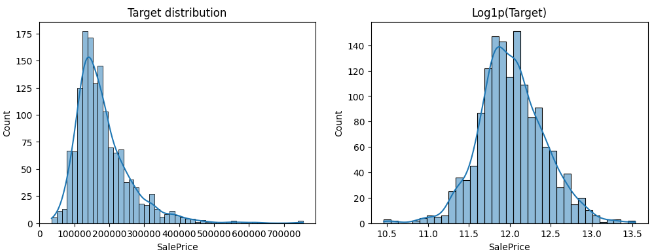
SalePrice trước và sau khi sử dụng log
- Mục tiêu của biểu đồ Shatosis là xem biến nào không tuân theo phân phối chuẩn. Nếu giá trị (p_value<0.05) , đây là phân phối không chuẩn. Vì thế từ dữ liệu có được, ta thấy rằng tất cả các feature được liệt kê đều không phải tuân theo phân phối chuẩn.>
1.5 Đánh giá mức độ tương quan giữa các features
Bước tiếp theo trong quá trình đánh giá dữ liệu là phải thể hiện được mức độ tương quan giữa các features
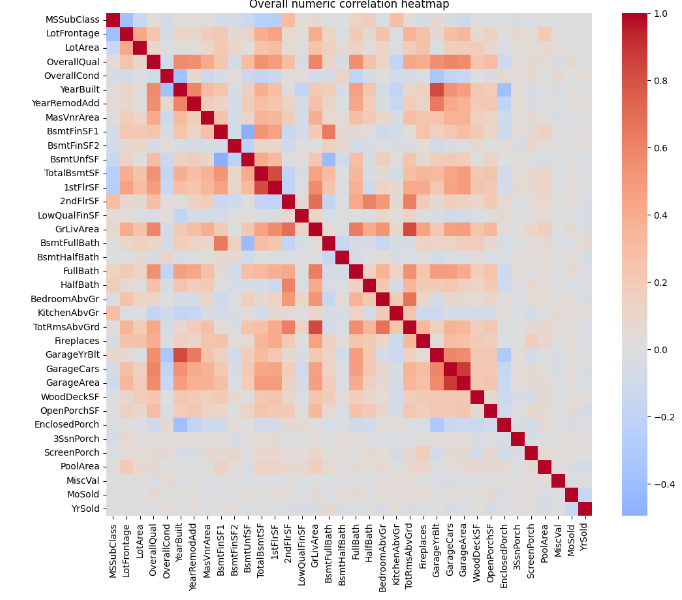
Heatmap mức độ tương quan giữa các features
Dựa vào biểu đồ, ta có thể đưa ra một số đánh giá liên quan đến dữ liệu:
- Một số nhóm features có tương quan cao cùng nhau như 1stFlrSF và TotalBsmtSF (các biến cùng đo diện tích/tổng diện tích), GarageCars và GarageArea (Số xe trong garage tỉ lệ thuận với diện tích garage), ...
- Một vài features có tương quan âm nhẹ như MSSubClass tương quan âm với OverallQual, YearBuilt, GrLivArea, nghĩa là các nhà cũ thì thường là xây lâu năm đi kèm chất lượng thấp và diện tích nhỏ
- Nhiều cặp features như PoolArea, MiscVal, MoSold, YrSold gần như không liên quan gì đến các features còn lại, do đây là những yếu tố ít ảnh hưởng đến giá bán
1.6 Đánh giá về mức độ quan trọng của từng feature trong tập dữ liệu
Với dữ liệu dạng categorical, chúng ta sẽ đánh giá dựa trên Mutual Information Regression, còn dữ liệu dạng numerical sẽ được đánh giá dựa trên Spearman Rank Corelation
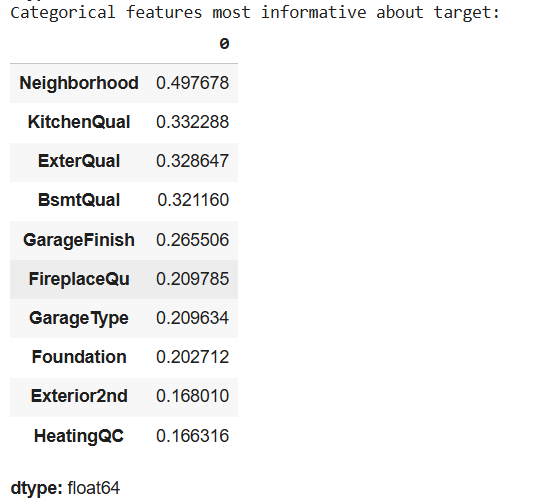
Đánh giá mức độ quan trọng các biến categorical
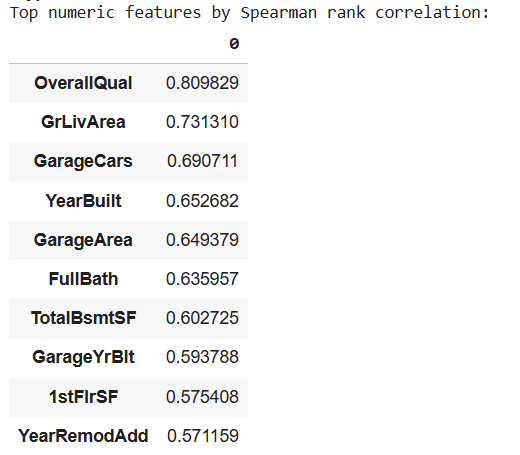
Đánh giá mức độ quan trọng các biến numerical
Từ các kết quả này, chúng ta có thể đưa ra một số đánh giá về tầm quan trọng của các features:
- Với Categorical features, các features liên quan đến chất lượng, vật liệu và vị trí như Neighborhood, KitchenQual hay ExterQual sẽ là những yếu tố định giá mạnh nhất, ảnh hưởng khá lớn đến giá nhà, vì chất lượng của khu dân cư, khu bếp hay độ hoàn thiện bên ngoài sẽ là các yếu tố rất quan trọng trong việc chọn nhà
- Với Numerical features, các features liên quan đến chất lượng, diện tích và năm xây nhà có tương quan mạnh nhất với giá nhà. Các features này mang quan hệ dương tuyến tính và đơn điệu, phù hợp với cả mô hình Linear Regression lẫn các mô hình phi tuyến tính như Lasso, Ridge, Gradient Boosting.
1.7 Đánh giá tính ổn định và sự đồng nhất của dữ liệu
Vì trong project này sử dụng các mô hình hồi quy tuyến tính nên chúng ta cần phải đánh giá sự đồng nhất của dữ liệu. Nếu dữ liệu không đồng nhất (ví dụ với giá nhà nhỏ, chênh lệch giá nhỏ, và giá nhà lớn thì chênh lệch giá lớn) khi này khoảng tin cậy không còn được chính xác.
Project này sử dụng phương pháp kiểm định Goldfeld-Quandt. Nếu giá trị p>0.05 thì phương sai là đồng nhất, từ đấy mô hình hồi quy tuyến tính có thể được áp dụng an toàn.
from statsmodels.stats.diagnostic import het_goldfeldquandt
for col in spearman_corr.head(3).index:
y_clean = df[target]
x_clean = df[[col]] # ✅ wrap in double brackets -> DataFrame (2D)
# Drop missing rows synchronously
mask = y_clean.notna() & x_clean[col].notna()
res = het_goldfeldquandt(y_clean[mask], x_clean[mask], alternative='two-sided')
print(f"Homoscedasticity test for {col}: p={res[1]:.4f}")
Ta thu được kết quả
Homoscedasticity test for OverallQual: p=0.2370
Homoscedasticity test for GrLivArea: p=0.3173
Homoscedasticity test for GarageCars: p=0.3699
Từ đây ta xác định rằng một số biến quan trọng như OverallQual, GrLivArea và GarageCars vẫn thỏa mãn giả định phương sai đồng nhất.
2. Handle outliers bằng các phương pháp PCA + IsolationForest
2.1. Trị riêng và vector riêng (Eigenvalue and Eigenvector)
Cho một ma trận vuông $A \in \mathbb{R}^{n \times n}$.
Một vector riêng (eigenvector) $\mathbf{v} \neq \mathbf{0}$ và một trị riêng (eigenvalue) $\lambda \in \mathbb{R}$ được định nghĩa là cặp thỏa mãn:
$$ A\mathbf{v} = \lambda \mathbf{v} $$
Trong đó:
- $A$ là ma trận vuông cần xét.
- $\mathbf{v}$ là vector riêng (eigenvector) tương ứng với trị riêng $\lambda$.
- $\lambda$ là trị riêng (eigenvalue) của ma trận $A$.
Nói cách khác, khi ma trận $A$ tác động lên vector $\mathbf{v}$, nó không làm thay đổi hướng của $\mathbf{v}$ mà chỉ phóng đại hoặc thu nhỏ nó theo hệ số $\lambda$.
Nếu $\lambda > 1$, vector bị phóng đại; nếu $0 < \lambda < 1$, vector bị thu nhỏ; còn nếu $\lambda < 0$, hướng của vector bị đảo ngược.
2.1.1 Cách tìm Trị riêng (Eigenvalues)
Để tìm các trị riêng, chúng ta cần giải phương trình $A\mathbf{v} = \lambda \mathbf{v}$.
- Chuyển vế: $A\mathbf{v} - \lambda \mathbf{v} = \mathbf{0}$
- Để thực hiện phép trừ, ta nhân $\lambda$ với ma trận đơn vị $I$: $A\mathbf{v} - \lambda I \mathbf{v} = \mathbf{0}$
- Đặt $\mathbf{v}$ làm nhân tử chung: $(A - \lambda I)\mathbf{v} = \mathbf{0}$
Phương trình này có ý nghĩa rất quan trọng. Nó nói rằng vector riêng $\mathbf{v}$ (là một vector $\neq \mathbf{0}$) nằm trong không gian rỗng (nullspace) của ma trận $(A - \lambda I)$.
Một hệ phương trình $(A - \lambda I)\mathbf{v} = \mathbf{0}$ chỉ có nghiệm $\mathbf{v} \neq \mathbf{0}$ khi và chỉ khi ma trận $(A - \lambda I)$ là ma trận suy biến (singular), tức là định thức (determinant) của nó phải bằng 0.
Phương trình đặc trưng (Characteristic Equation):
$$ > \det(A - \lambda I) = 0 > $$
Giải phương trình này (một phương trình đa thức theo $\lambda$) sẽ cho chúng ta tất cả các trị riêng $\lambda$.
2.1.2 Ví dụ với ma trận 2x2 (Kiến thức THPT)
Chúng ta hãy sử dụng một ma trận 2x2 cơ bản:
$$ A = \begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} $$
Bước 1: Thiết lập $(A - \lambda I)$
$$ A - \lambda I = \begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 4 - \lambda & 1 \\ 2 & 3 - \lambda \end{bmatrix} $$
Bước 2: Tính $\det(A - \lambda I)$ và cho bằng 0
Đối với ma trận 2x2 $\begin{bmatrix} a & b \\ c & d \end{bmatrix}$, định thức (theo kiến thức THPT) là $ad - bc$.
$$ \det(A - \lambda I) = (4 - \lambda)(3 - \lambda) - (1)(2) = 0 $$
Bước 3: Giải phương trình đặc trưng
$$ (12 - 4\lambda - 3\lambda + \lambda^2) - 2 = 0 $$
$$ \lambda^2 - 7\lambda + 10 = 0 $$
Phân tích thành nhân tử:
$$ (\lambda - 2)(\lambda - 5) = 0 $$
Kết quả là ta có hai trị riêng:
- $\lambda_1 = 2$
- $\lambda_2 = 5$
2.1.3 Cách tìm Vector riêng (Eigenvectors)
Với mỗi trị riêng $\lambda$ tìm được, chúng ta thay nó trở lại phương trình $(A - \lambda I)\mathbf{v} = \mathbf{0}$ và giải tìm vector $\mathbf{v} = \begin{bmatrix} x \\ y \end{bmatrix}$.
a) Trường hợp 1: $\lambda_1 = 2$
Ta giải phương trình $(A - 2I)\mathbf{v}_1 = \mathbf{0}$:
$$ \begin{bmatrix} 4 - 2 & 1 \\ 2 & 3 - 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \implies \begin{bmatrix} 2 & 1 \\ 2 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
Cả hai hàng đều cho cùng một phương trình: $2x + y = 0 \implies y = -2x$.
- Nếu ta chọn $x = 1$, thì $y = -2$. Ta được $\mathbf{v}_1 = \begin{bmatrix} 1 \\ -2 \end{bmatrix}$.
b) Trường hợp 2: $\lambda_2 = 5$
Ta giải phương trình $(A - 5I)\mathbf{v}_2 = \mathbf{0}$:
$$ \begin{bmatrix} 4 - 5 & 1 \\ 2 & 3 - 5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \implies \begin{bmatrix} -1 & 1 \\ 2 & -2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
Cả hai hàng đều cho cùng một phương trình: $-x + y = 0 \implies x = y$.
- Nếu ta chọn $x = 1$, thì $y = 1$. Ta được $\mathbf{v}_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$.
2.1.4 Ma trận lớn hơn và Phép khai triển Cofactor
Quy trình trên áp dụng cho mọi kích thước ma trận. Điểm khác biệt duy nhất là cách tính định thức.
Đối với ma trận $3 \times 3$ hoặc lớn hơn, bạn không thể dùng ad-bc. Bạn phải dùng phép khai triển cofactor (Cofactor Expansion) để tính $\det(A - \lambda I)$.
Ví dụ, khai triển theo hàng 1 của ma trận $3 \times 3$ $B$:
$$ \det(B) = b_{11}C_{11} - b_{12}C_{12} + b_{13}C_{13} $$
Trong đó $C_{ij}$ là định thức của ma trận con (ma trận 2x2) sau khi đã loại bỏ hàng $i$ và cột $j$.
Việc này sẽ tạo ra một phương trình đa thức bậc 3 (cho ma trận 3x3), bậc 4 (cho ma trận 4x4)..., và việc giải phương trình này để tìm $\lambda$ có thể phức tạp.
2.1.5 Đặc điểm của $(A - \lambda I)$ và các trường hợp đặc biệt
Ma trận $B = (A - \lambda I)$ là chìa khóa. Việc $\det(B) = 0$ có nghĩa là:
- $B$ suy biến (singular).
- Các hàng (và các cột) của $B$ phụ thuộc tuyến tính (linearly dependent). Đây là lý do tại sao trong ví dụ 2x2, hai phương trình tìm $x, y$ luôn giống hệt nhau (ví dụ: $2x+y=0$ và $2x+y=0$).
- $B$ có một không gian rỗng (nullspace) không tầm thường (chứa nhiều vector hơn là chỉ vector 0). Vector riêng $\mathbf{v}$ chính là một vector (khác 0) bất kỳ trong không gian rỗng đó.
Bảng các trường hợp đặc biệt:
| Loại Ma trận | Đặc điểm | Trị riêng ($\lambda$) | Vector riêng ($\mathbf{v}$) |
|---|---|---|---|
| Ma trận suy biến | $\det(A) = 0$ | Luôn có ít nhất một $\lambda = 0$ | Vector $\mathbf{v}$ trong không gian rỗng của $A$ (tức là $A\mathbf{v} = 0\mathbf{v}$). |
| Ma trận chiếu (Projection) | $P^2 = P$ | Chỉ có thể là $\lambda = 1$ hoặc $\lambda = 0$ | $\mathbf{v}$ (với $\lambda=1$): các vector nằm trên không gian chiếu. $\mathbf{v}$ (với $\lambda=0$): các vector trực giao với không gian chiếu. |
| Ma trận đơn vị $I$ | $I\mathbf{v} = \mathbf{v}$ | Chỉ có $\lambda = 1$ (với bội $n$) | Mọi vector $\mathbf{v} \neq \mathbf{0}$ đều là vector riêng. |
| Ma trận tam giác | Các phần tử bên dưới (hoặc trên) đường chéo chính bằng 0 | Các trị riêng chính là các phần tử nằm trên đường chéo chính. | (Phải tính toán, không đơn giản) |
Ví dụ 1: Phóng đại (Expansion)
Xét ma trận: $A = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}$
Ma trận này có thể được viết là $A = 2 \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = 2I$.
Hãy xem điều gì xảy ra khi nó tác động lên một vector $\mathbf{v} = \begin{bmatrix} x \\ y \end{bmatrix}$ bất kỳ:
$$ A\mathbf{v} = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2x \\ 2y \end{bmatrix} = 2 \begin{bmatrix} x \\ y \end{bmatrix} = 2\mathbf{v} $$
Phương trình $A\mathbf{v} = 2\mathbf{v}$ luôn đúng với mọi vector $\mathbf{v}$.
- Trị riêng (Eigenvalue) là $\lambda = 2$.
- Vector riêng (Eigenvector) là tất cả mọi vector $\mathbf{v} \neq \mathbf{0}$.
Phép biến đổi này chỉ đơn giản là phóng to mọi vector trong không gian lên 2 lần mà không làm thay đổi hướng của bất kỳ vector nào.
Ví dụ 2: Thu nhỏ (Compression)
Tương tự, xét ma trận $A = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix}$.
Ma trận này là $A = 0.5 \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = 0.5I$.
Khi tác động lên một vector $\mathbf{v} = \begin{bmatrix} x \\ y \end{bmatrix}$ bất kỳ:
$$ A\mathbf{v} = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0.5x \\ 0.5y \end{bmatrix} = 0.5 \begin{bmatrix} x \\ y \end{bmatrix} = 0.5\mathbf{v} $$
Phương trình $A\mathbf{v} = 0.5\mathbf{v}$ cũng luôn đúng với mọi vector $\mathbf{v}$.
- Trị riêng (Eigenvalue) là $\lambda = 0.5$.
- Vector riêng (Eigenvector) là tất cả mọi vector $\mathbf{v} \neq \mathbf{0}$.
Phép biến đổi này thu nhỏ mọi vector lại còn một nửa.
Kết luận: Đối với các ma trận có dạng $k \cdot I$ (một hằng số $k$ nhân với ma trận đơn vị $I$), chúng có một trị riêng duy nhất là $\lambda = k$ và mọi vector (khác 0) trong không gian đều là vector riêng của chúng.
2.2 Phương sai (Variance) và Ma trận Hiệp phương sai (Covariance Matrix)
Trong khi trị riêng (eigenvalues) cho chúng ta biết về hệ số co giãn, ma trận hiệp phương sai cho chúng ta biết về hình dạng và hướng của dữ liệu.
2.2.1 Phương sai (Variance) là gì?
Phương sai (ký hiệu $\sigma^2$ hoặc $\text{Var}(X)$) là một đại lượng đo lường mức độ phân tán của một tập hợp dữ liệu (một biến) so với giá trị trung bình của nó.
- Phương sai nhỏ: Các điểm dữ liệu có xu hướng tụ tập rất gần giá trị trung bình.
- Phương sai lớn: Các điểm dữ liệu trải rộng ra xa giá trị trung bình.
Công thức (cho mẫu):
Giả sử ta có một biến $X$ với $n$ điểm dữ liệu $x_1, x_2, \dots, x_n$.
1. Tính giá trị trung bình (mean) $\mu_x$:
$$
\mu_x = \frac{1}{n} \sum_{i=1}^{n} x_i
$$
- Tính phương sai $\text{Var}(X)$:
$$ \text{Var}(X) = \sigma_x^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \mu_x)^2 $$
(Chúng ta thường chia cho $n-1$ thay vì $n$ để ước lượng phương sai của tổng thể từ dữ liệu mẫu).
2.2.2 Hiệp phương sai (Covariance) là gì?
Hiệp phương sai (ký hiệu $\sigma_{xy}$ hoặc $\text{Cov}(X, Y)$) đo lường mối quan hệ tuyến tính giữa hai biến $X$ và $Y$. Nó cho biết chúng thay đổi cùng nhau như thế nào.
- $\text{Cov}(X, Y) > 0$ (Dương): Khi $X$ tăng, $Y$ cũng có xu hướng tăng. Chúng đồng biến.
- $\text{Cov}(X, Y) < 0$ (Âm): Khi $X$ tăng, $Y$ có xu hướng giảm. Chúng nghịch biến.
- $\text{Cov}(X, Y) \approx 0$ (Bằng 0): Không có mối quan hệ tuyến tính rõ rệt giữa $X$ và $Y$.
Công thức (cho mẫu):
Giả sử ta có $n$ cặp dữ liệu $(x_i, y_i)$.
1. Tính trung bình $\mu_x$ và $\mu_y$.
2. Tính hiệp phương sai $\text{Cov}(X, Y)$:
$$
\text{Cov}(X, Y) = \sigma_{xy} = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \mu_x)(y_i - \mu_y)
$$
2.2.3 Ma trận Hiệp phương sai (Covariance Matrix)
Ma trận hiệp phương sai (ký hiệu $\Sigma$) là một ma trận vuông tổng hợp tất cả phương sai và hiệp phương sai của một tập dữ liệu nhiều chiều.
Nó mô tả hình dạng (shape) và hướng (orientation) của "đám mây" điểm dữ liệu (data cloud).
- Các phần tử trên đường chéo chính: Là phương sai của từng biến. Chúng cho biết dữ liệu trải rộng bao nhiêu theo mỗi trục (ví dụ: trục X, trục Y).
- Các phần tử ngoài đường chéo chính: Là hiệp phương sai giữa các cặp biến. Chúng cho biết dữ liệu có xu hướng "nghiêng" hay không.
Đối với tập dữ liệu 2 chiều (với 2 biến $X$ và $Y$):
$$ \Sigma = \begin{bmatrix} \text{Var}(X) & \text{Cov}(X, Y) \\ \text{Cov}(Y, X) & \text{Var}(Y) \end{bmatrix} $$=$$ \begin{bmatrix} \sigma_x^2 & \sigma_{xy} \\ \sigma_{yx} & \sigma_y^2 \end{bmatrix} $$
Lưu ý: Ma trận này luôn đối xứng, vì $\text{Cov}(X, Y) = \text{Cov}(Y, X)$.
2.2.4 Ví dụ cụ thể (2D)
Giả sử chúng ta có dữ liệu về chiều cao (X) và cân nặng (Y) của 3 người:
| Người | Chiều cao (X) (m) | Cân nặng (Y) (kg) |
|---|---|---|
| 1 | 1.6 | 50 |
| 2 | 1.7 | 65 |
| 3 | 1.8 | 70 |
2.2.4.1) Giá trị trung bình (inline)
- $\mu_x = \frac{1.6 + 1.7 + 1.8}{3} = 1.7\ \mathrm{m}$
- $\mu_y = \frac{50 + 65 + 70}{3} = 61.67\ \mathrm{kg}$
2.2.4.2) Phương sai (inline + block)
- $\mathrm{Var}(X) = \dfrac{(1.6-1.7)^2 + (1.7-1.7)^2 + (1.8-1.7)^2}{3-1}$
$$ \mathrm{Var}(X) = \frac{(-0.1)^2 + 0^2 + (0.1)^2}{2} = \frac{0.01 + 0.01}{2} = \mathbf{0.01} $$
- $\mathrm{Var}(Y) = \dfrac{(50-61.67)^2 + (65-61.67)^2 + (70-61.67)^2}{3-1}$
$$ \mathrm{Var}(Y) = \frac{(-11.67)^2 + (3.33)^2 + (8.33)^2}{2} = \frac{136.19 + 11.09 + 69.39}{2} = \mathbf{108.34} $$
2.2.4.3) Hiệp phương sai (inline + block)
- $\mathrm{Cov}(X,Y) = \dfrac{(1.6-1.7)(50-61.67) + (1.7-1.7)(65-61.67) + (1.8-1.7)(70-61.67)}{3-1}$
$$ \mathrm{Cov}(X,Y) = \frac{(-0.1)(-11.67) + (0)(3.33) + (0.1)(8.33)}{2} = \frac{1.167 + 0 + 0.833}{2} = \frac{2}{2} = \mathbf{1.0} $$
2.2.4.4) Ma trận hiệp phương sai (block duy nhất)
$$ \Sigma = \begin{bmatrix} \mathrm{Var}(X) & \mathrm{Cov}(X,Y) \\ \mathrm{Cov}(Y,X) & \mathrm{Var}(Y) \end{bmatrix} = \begin{bmatrix} 0.01 & 1.0 \\ 1.0 & 108.34 \end{bmatrix} $$
Phân tích (inline)
- $\mathrm{Var}(X)=0.01$: phương sai chiều cao nhỏ (quanh $1.7\ \mathrm{m}$).
- $\mathrm{Var}(Y)=108.34$: phương sai cân nặng lớn hơn.
- $\mathrm{Cov}(X,Y)=1.0$: hiệp phương sai dương → cao hơn thường nặng hơn.
2.2.5 Công thức Vector hóa (Vectorized Formula) cho Ma trận Hiệp phương sai
Việc tính toán ma trận hiệp phương sai bằng cách lặp qua từng cặp điểm dữ liệu (như ví dụ trên) có thể rất chậm với các bộ dữ liệu lớn. Trong thực tế, chúng ta sử dụng các phép toán ma trận (Đại số tuyến tính) để tính toán nhanh hơn.
Phương pháp này được gọi là "vector hóa". Các bước tính toán như sau:
1. Biểu diễn dữ liệu dưới dạng Ma trận $X$
Giả sử chúng ta có $n$ mẫu (hàng) và $d$ đặc trưng (cột). Trong ví dụ trước, $n=3$ và $d=2$.
$$ X = \begin{bmatrix} 1.6 & 50 \\ 1.7 & 65 \\ 1.8 & 70 \end{bmatrix} $$
2. Tính Vector trung bình $\boldsymbol{\mu}$
Tính giá trị trung bình cho từng cột (từng đặc trưng).
$$ \boldsymbol{\mu} = \begin{bmatrix} \mu_x \\ \mu_y \end{bmatrix} = \begin{bmatrix} 1.7 \\ 61.67 \end{bmatrix} $$
3. "Tâm hóa" dữ liệu (Data Centering)
Trừ vector trung bình $\boldsymbol{\mu}$ từ mỗi hàng của $X$. Kết quả là ma trận $X_{\text{centered}}$ (còn gọi là $B$), trong đó trung bình của mỗi cột là 0.
-
Tạo một ma trận trung bình $M$ bằng cách lặp lại vector $\boldsymbol{\mu}$ cho $n$ hàng:
$$ M = \begin{bmatrix} 1.7 & 61.67 \\ 1.7 & 61.67 \\ 1.7 & 61.67 \end{bmatrix} $$ -
Trừ $M$ khỏi $X$:
$$ X_{\text{centered}} = X - M = \begin{bmatrix} 1.6 - 1.7 & 50 - 61.67 \\ 1.7 - 1.7 & 65 - 61.67 \\ 1.8 - 1.7 & 70 - 61.67 \end{bmatrix} $$=$$ \begin{bmatrix} -0.1 & -11.67 \\ 0 & 3.33 \\ 0.1 & 8.33 \end{bmatrix} $$
4. Công thức Vector hóa
Công thức ma trận cho ma trận hiệp phương sai (mẫu) là:
$$ \Sigma = \frac{1}{n-1} (X_{\text{centered}})^T (X_{\text{centered}}) $$
Trong đó $(X_{\text{centered}})^T$ là ma trận chuyển vị của $X_{\text{centered}}$.
2.2.6 Áp dụng công thức Vector hóa
-
$$(X_{\text{centered}})^T = \begin{bmatrix} -0.1 & 0 & 0.1 \\ -11.67 & 3.33 & 8.33 \end{bmatrix}$$
-
$$X_{\text{centered}} = \begin{bmatrix} -0.1 & -11.67 \\ 0 & 3.33 \\ 0.1 & 8.33 \end{bmatrix}$$
-
Nhân ma trận $(X_{\text{centered}})^T (X_{\text{centered}})$ (kết quả là ma trận $2 \times 2$):
$$ \begin{bmatrix} (-0.1)^2 + 0^2 + (0.1)^2 & (-0.1)(-11.67) + (0)(3.33) + (0.1)(8.33) \\ (-11.67)(-0.1) + (3.33)(0) + (8.33)(0.1) & (-11.67)^2 + (3.33)^2 + (8.33)^2 \end{bmatrix} $$
$$ = \begin{bmatrix} 0.02 & 2.0 \\ 2.0 & 216.67 \end{bmatrix} $$
- Chia cho $(n-1)$ (với $n=3$, nên $n-1=2$):
$$ \Sigma = \frac{1}{2} \begin{bmatrix} 0.02 & 2.0 \\ 2.0 & 216.67 \end{bmatrix} $$=$$ \begin{bmatrix} 0.01 & 1.0 \\ 1.0 & 108.335 \end{bmatrix} $$
Kết quả này hoàn toàn trùng khớp với ma trận $\begin{bmatrix} 0.01 & 1.0 \\ 1.0 & 108.34 \end{bmatrix}$ mà chúng ta đã tính toán ở phần trước (sự khác biệt nhỏ là do làm tròn).

Hình ảnh sau khi scale data gốc về với mean -> Ta có thể thấy data sau khi scale sẽ tạo thành một đám mây dữ liệu như đã đề cập ở trên
2.3 Phân tích Thành phần Chính (Principal Component Analysis - PCA)
Chúng ta đã thấy ma trận hiệp phương sai $\Sigma$ mô tả hình dạng và hướng của đám mây dữ liệu. Bây giờ, chúng ta sẽ sử dụng chính thông tin đó để giảm chiều dữ liệu (dimensionality reduction).
PCA là một kỹ thuật tìm một hệ tọa độ mới (một tập hợp các trục mới) để biểu diễn lại dữ liệu.
-
Mục tiêu của PCA là tìm ra các "thành phần chính" (các trục mới) mà ở đó dữ liệu có phương sai lớn nhất.
-
Nó cho phép chúng ta nén dữ liệu bằng cách loại bỏ các trục (thành phần) chứa ít thông tin (phương sai thấp).
2.3.1 Mối liên hệ Thần kỳ: PCA và Eigenvectors
Đây là điểm kết nối tất cả các khái niệm lại với nhau:
Các Thành phần Chính (Principal Components) chính là các Vector riêng (Eigenvectors) của Ma trận Hiệp phương sai $\Sigma$.
-
Vector riêng (Eigenvector) của $\Sigma$ cho ta hướng của trục mới.
-
Trị riêng (Eigenvalue) tương ứng cho ta biết lượng phương sai (tầm quan trọng) của trục đó.
Cụ thể:
-
Thành phần chính 1 (PC1): Là vector riêng ứng với trị riêng lớn nhất. Đây là hướng mà dữ liệu trải dài nhiều nhất (phương sai lớn nhất).
-
Thành phần chính 2 (PC2): Là vector riêng ứng với trị riêng lớn thứ hai, và luôn trực giao (vuông góc) với PC1. Đây là hướng có phương sai lớn thứ nhì.
-
... và cứ thế cho các chiều dữ liệu cao hơn.
2.3.2 Các bước thực hiện PCA
Sử dụng lại ví dụ về chiều cao và cân nặng của chúng ta.
Bước 1: Chuẩn bị dữ liệu
- Chúng ta đã có dữ liệu đã được "tâm hóa" (centered):
$$X_{\text{centered}} = \begin{bmatrix} -0.1 & -11.67 \\ 0 & 3.33 \\ 0.1 & 8.33 \end{bmatrix}$$
Bước 2: Tính Ma trận Hiệp phương sai ($\Sigma$)
- Chúng ta cũng đã tính được:
$$\Sigma = \begin{bmatrix} 0.01 & 1.0 \\ 1.0 & 108.34 \end{bmatrix}$$
Bước 3: Tìm Trị riêng (Eigenvalues) và Vector riêng (Eigenvectors) của $\Sigma$
-
Bây giờ, chúng ta tìm trị riêng $\lambda$ và vector riêng $\mathbf{v}$ cho ma trận $\Sigma$ này.
-
Ta giải phương trình đặc trưng $\det(\Sigma - \lambda I) = 0$:
$$\det \left( \begin{bmatrix} 0.01 - \lambda & 1.0 \\ 1.0 & 108.34 - \lambda \end{bmatrix} \right) = 0$$
-
$(0.01 - \lambda)(108.34 - \lambda) - (1.0)(1.0) = 0$
-
$\lambda^2 - 108.35\lambda + 1.0834 - 1.0 = 0$
-
$\lambda^2 - 108.35\lambda + 0.0834 = 0$
-
Giải phương trình bậc hai này, ta được 2 trị riêng:
-
$\lambda_1 \approx 108.349$
-
$\lambda_2 \approx 0.00077$
-
Tìm 2 vector riêng tương ứng (bằng cách giải $(\Sigma - \lambda I)\mathbf{v} = 0$):
-
$\mathbf{v}_1 \approx \begin{bmatrix} 0.0092 \\ 0.9999 \end{bmatrix}$ (Đây là PC1)
-
$\mathbf{v}_2 \approx \begin{bmatrix} -0.9999 \\ 0.0092 \end{bmatrix}$ (Đây là PC2)
Bước 4: Phân tích và Giảm chiều
-
Tổng phương sai = $\lambda_1 + \lambda_2 \approx 108.35$.
-
Tỷ lệ phương sai mà PC1 giải thích:
$\frac{\lambda_1}{\lambda_1 + \lambda_2} = \frac{108.349}{108.35} \approx 0.9999$ (tức 99.99%!) -
Tỷ lệ phương sai mà PC2 giải thích:
$\frac{\lambda_2}{\lambda_1 + \lambda_2} = \frac{0.00077}{108.35} \approx 0.00007$ (tức 0.007%)
Kết luận:
-
PC1 ($\mathbf{v}_1$) giải thích gần như toàn bộ sự biến thiên trong dữ liệu. PC1 gần như song song với trục Y (cân nặng), điều này hợp lý vì phương sai của cân nặng ($\sigma_y^2=108.34$) lớn hơn rất nhiều so với chiều cao ($\sigma_x^2=0.01$).
-
PC2 ($\mathbf{v}_2$) giải thích cực kỳ ít thông tin.
-
Do đó, chúng ta có thể giảm chiều dữ liệu từ 2D xuống 1D bằng cách chỉ giữ lại PC1.
Bước 5: Chiếu dữ liệu (Transform Data)
- Chúng ta tạo ma trận $W$ từ vector riêng ta muốn giữ (chỉ PC1):
$$W = \mathbf{v}_1 = \begin{bmatrix} 0.0092 \\ 0.9999 \end{bmatrix}$$
- Nhân dữ liệu đã tâm hóa $X_{\text{centered}}$ (kích thước $3 \times 2$) với $W$ (kích thước $2 \times 1$):
$$X_{\text{new}} = X_{\text{centered}} \cdot W$$ $$X_{\text{new}} = \begin{bmatrix} -0.1 & -11.67 \\ 0 & 3.33 \\ 0.1 & 8.33 \end{bmatrix} \begin{bmatrix} 0.0092 \\ 0.9999 \end{bmatrix} $$=$$ \begin{bmatrix} (-0.1)(0.0092) + (-11.67)(0.9999) \\ (0)(0.0092) + (3.33)(0.9999) \\ (0.1)(0.0092) + (8.33)(0.9999) \end{bmatrix} \approx \begin{bmatrix} -11.67 \\ 3.33 \\ 8.33 \end{bmatrix}$$
- Dữ liệu 2D (chiều cao, cân nặng) của chúng ta giờ đã được nén thành dữ liệu 1D, trong khi vẫn giữ được 99.99% thông tin cốt lõi!

Giải thích ngắn gọn về hình ảnh:
Hình ảnh này cho thấy mối liên hệ trực tiếp giữa ma trận hiệp phương sai và PCA:
- Biểu đồ bên phải (Covariance Matrix):
-
Đây là ma trận hiệp phương sai $\Sigma$ của dữ liệu.
-
Giá trị
Cov(X, Y) = 3.26(hiệp phương sai) là số dương, cho thấy X và Y có xu hướng tăng cùng nhau. Đây là lý do tại sao đám mây dữ liệu (bên trái) bị "nghiêng" theo hướng đi lên.
- Biểu đồ bên trái (PCA Visualization):
-
Đây chính là đám mây dữ liệu.
-
PC1 (mũi tên xanh lá): Là vector riêng của ma trận hiệp phương sai (bên phải) ứng với trị riêng lớn nhất. Nó chỉ ra hướng mà dữ liệu có nhiều thông tin nhất (phương sai lớn nhất).
-
PC2 (mũi tên cam): Là vector riêng thứ hai, luôn vuông góc với PC1. Nó nắm bắt phần thông tin còn lại.
Tóm lại: PCA đã tìm ra các vector riêng (PC1, PC2) của ma trận hiệp phương sai để cho chúng ta một hệ tọa độ mới (các mũi tên) mô tả dữ liệu tốt hơn là các trục X, Y ban đầu.
2.4 Xử lý Outlier bằng phương pháp Hybrid (Kết hợp IsolationForest và PCA)
Chúng ta đã tìm hiểu rất kỹ về PCA (Phân tích Thành phần Chính) và cách nó giúp chúng ta tìm ra hình dạng và cấu trúc cốt lõi của dữ liệu thông qua các vector riêng (mục 3.9). Giờ đây, chúng ta sẽ tận dụng sức mạnh đó và kết hợp với một phương pháp mạnh mẽ khác là IsolationForest để tạo ra một hệ thống phát hiện outlier cực kỳ hiệu quả.
2.4.1. Tại sao lại cần phương pháp Hybrid?
Không có một thuật toán phát hiện outlier nào là hoàn hảo cho mọi loại dữ liệu. Mỗi phương pháp có một góc nhìn khác nhau về sự bất thường.
Isolation Forest (IF)
- Hoạt động tốt với dữ liệu phi tuyến (non-linear) và không yêu cầu dữ liệu phải tuân theo một phân phối cụ thể (non-parametric).
- Isolation Forest hoạt động bằng cách cô lập các điểm dữ liệu: những điểm bị cô lập nhanh hơn (qua ít lần chia hơn) thì càng có khả năng là outlier.
Điểm mạnh:
- Hiệu quả trong việc phát hiện các điểm bất thường toàn cục (global outliers) — nằm xa so với mọi cụm dữ liệu.
Điểm yếu:
- Có thể nhầm lẫn các điểm nằm ở rìa cụm dữ liệu là bất thường.
- Không nhạy với các điểm phá vỡ mối tương quan giữa các biến.
Ví dụ: Một người cao 2m (bất thường) và nặng 100kg (bất thường) có thể là hợp lý. Nhưng một người cao 2m và nặng 40kg vi phạm mối quan hệ chiều cao–cân nặng. IF có thể bỏ sót trường hợp này.
PCA–Mahalanobis
- PCA tìm ra các thành phần chính (vector riêng của ma trận hiệp phương sai), mô tả hình dạng và hướng của dữ liệu.
- Khoảng cách Mahalanobis đo xem một điểm nằm xa trung tâm dữ liệu bao nhiêu, có tính đến tương quan giữa các biến.
Điểm mạnh:
- Nhạy với các điểm vi phạm cấu trúc tương quan của dữ liệu.
Điểm yếu:
- Giả định mối quan hệ tuyến tính và nhạy cảm với các outlier cực đoan (mà chính nó đang cố phát hiện).
2.4.2. Sức mạnh của sự kết hợp — Logic AND
Phương pháp hybrid không chỉ chạy hai thuật toán song song mà còn kết hợp kết quả một cách thông minh để đạt độ chính xác và tính bảo thủ cao.
Hai “giám khảo” của chúng ta là:
- Isolation Forest: “Điểm này có dễ bị cô lập không?” → phát hiện bất thường phi tuyến / toàn cục.
- PCA–Mahalanobis: “Điểm này có vi phạm cấu trúc tương quan không?” → phát hiện bất thường tuyến tính / cấu trúc.
Quyết định Hybrid:
Chỉ coi một điểm là outlier nếu cả hai giám khảo đồng ý:
python outlier = iso_mask & mahal_mask
Lợi ích:
- Giảm False Positives: Một điểm trông “lạ” với IF nhưng vẫn phù hợp cấu trúc PCA thì sẽ được giữ lại.
- Tận dụng thế mạnh của cả hai: IF lọc điểm “lạ” toàn cục, PCA–Mahalanobis xác minh mối tương quan vi phạm.
Kết quả là ta chỉ giữ lại những điểm thực sự bất thường và đáng tin cậy nhất.
2.4.3. Winsorization — Làm mượt dữ liệu có phân phối lệch mạnh
Trước khi phát hiện ngoại lệ, cần đảm bảo các đặc trưng có phân phối lệch mạnh (highly skewed) không ảnh hưởng đến mô hình.
Phương pháp Winsorization cắt ngưỡng các giá trị cực trị, thay thế bằng giá trị biên (quantile) 1% và 99%.
from scipy.stats.mstats import winsorize
def winsorize_series(s, lower_pct=0.01, upper_pct=0.99):
arr = s.copy().astype(float)
low = arr.quantile(lower_pct)
high = arr.quantile(upper_pct)
return arr.clip(lower=low, upper=high)
Phương pháp này giúp ổn định dữ liệu, giảm tác động của các điểm cực trị trước khi phát hiện outliers.
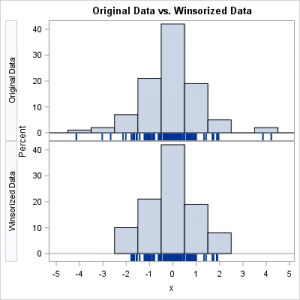
2.4.4. Phát hiện ngoại lệ bằng mô hình lai (Hybrid Outlier Detection)
Phương pháp lai này kết hợp IsolationForest và PCA–Mahalanobis để tận dụng ưu điểm của cả hai.
- Isolation Forest: dựa trên ý tưởng cô lập điểm bất thường bằng cây nhị phân.
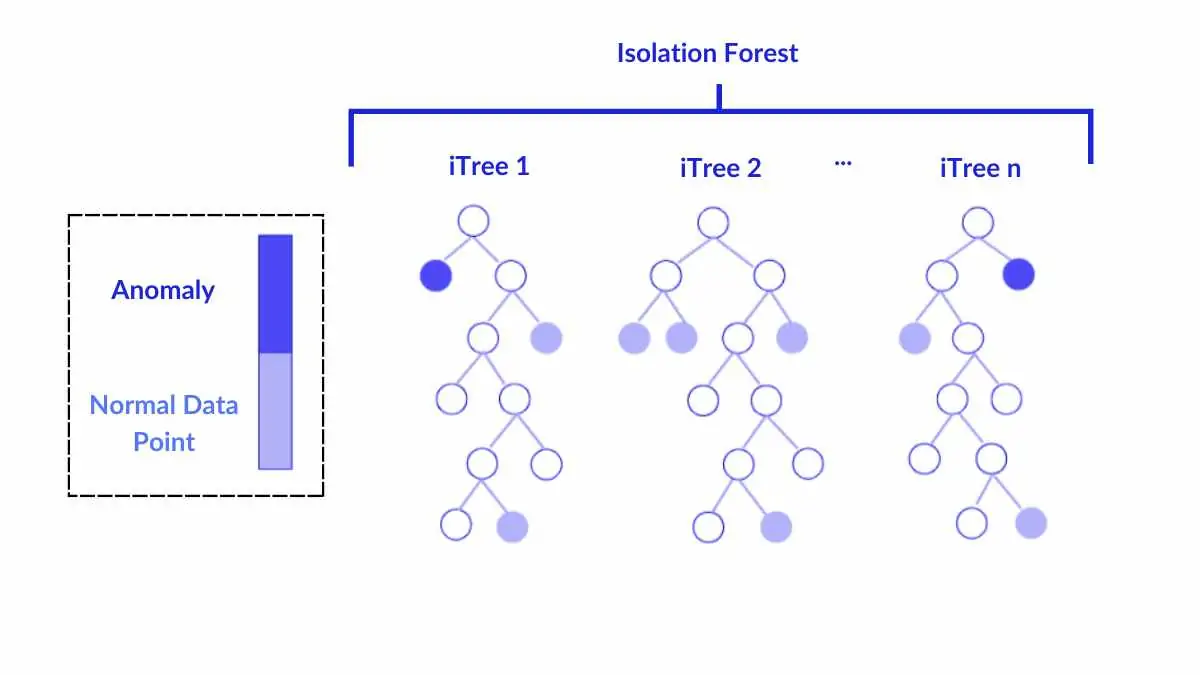
- PCA–Mahalanobis: đo khoảng cách dữ liệu so với phân phối tổng thể sau khi giảm chiều bằng PCA.
Các bước chính trong hàm hybrid_outlier_mask:
- Imputation (thay giá trị thiếu) bằng trung vị.
- Chạy IsolationForest để gắn nhãn bất thường
(-1). - Thực hiện PCA (giữ
pca_var% phương sai), tính khoảng cách Mahalanobis cho từng điểm. - Xác định mask dữ liệu hợp lệ — chỉ loại bỏ điểm bị cả hai phương pháp đánh dấu.
def hybrid_outlier_mask(X_numeric, contamination=0.03, pca_var=0.95):
si = SimpleImputer(strategy='median')
Xf = si.fit_transform(X_numeric)
# Isolation Forest
iso = IsolationForest(contamination=contamination, random_state=RANDOM_SEED)
iso_mask = iso.fit_predict(Xf) == -1
# PCA + Mahalanobis Distance
pca = PCA(n_components=pca_var, random_state=RANDOM_SEED)
pcs = pca.fit_transform(StandardScaler().fit_transform(Xf))
cov = np.cov(pcs, rowvar=False)
inv_cov = np.linalg.pinv(cov)
mean_vec = pcs.mean(axis=0)
dists = np.sqrt(np.sum((pcs - mean_vec) @ inv_cov * (pcs - mean_vec), axis=1))
mahal_mask = dists > np.percentile(dists, 100*(1-contamination))
# Giữ lại điểm hợp lệ (not flagged by both)
keep = ~(iso_mask & mahal_mask)
return keep
Khi áp dụng:
keep_mask = hybrid_outlier_mask(df_wins[num_cols], contamination=0.03)
print("Kept fraction:", float(keep_mask.mean()))
2.4.5. Cách sử dụng trong thực tế
- Bước 1: Chạy Winsorization để giảm ảnh hưởng của phân phối lệch.
- Bước 2: Dùng hàm
hybrid_outlier_mask()để loại bỏ các điểm cực trị bất thường. - Bước 3: Lưu lại mask và tạo DataFrame sạch:
df_final = df_wins[keep_mask]
✅ Tóm tắt
| Phương pháp | Mạnh ở đâu | Yếu ở đâu | Vai trò trong Hybrid |
|---|---|---|---|
| IsolationForest | Phát hiện outliers phi tuyến, toàn cục | Dễ nhầm cluster nhỏ | Phát hiện điểm “lạ” ban đầu |
| PCA–Mahalanobis | Phát hiện outliers tuyến tính, tương quan | Không bắt phi tuyến | Xác thực cấu trúc dữ liệu |
Kết hợp cả hai = Cân bằng giữa độ nhạy và độ tin cậy
3. Các bước tiền xử lý và chọn đặc trưng khác
Trong bất kỳ dự án học máy nào, tiền xử lý dữ liệu (data preprocessing) là bước quan trọng quyết định chất lượng đầu vào cho mô hình.
Quy trình được áp dụng trong dự án này được thiết kế theo thứ tự logic từ làm sạch đến chuẩn hoá, đảm bảo rằng dữ liệu:
1. Được chia tách hợp lý cho huấn luyện và đánh giá (train/test split).
2. Không còn giá trị bị thiếu (missing).
3. Các biến phân loại được mã hoá phù hợp (Target Encoding).
4. Đặc trưng số có thể biểu diễn được mối quan hệ phi tuyến (Polynomial Features).
5. Cuối cùng, tất cả đặc trưng đều được chuẩn hoá về cùng thang đo (Scaling).
Mục tiêu của chuỗi bước này là tạo ra một pipeline có tính tổng quát cao, giảm overfitting, và tối ưu hiệu suất mô hình hồi quy.
3.1 Chia dữ liệu Train/Test
Khi huấn luyện mô hình, nếu ta dùng toàn bộ dữ liệu để học và đánh giá cùng lúc, mô hình có thể nhớ luôn dữ liệu (overfitting).
Do đó, ta tách dữ liệu thành hai phần:
| Tập | Tỉ lệ | Mục tiêu |
|---|---|---|
| Train | ~75% | Dùng để huấn luyện mô hình |
| Test | ~25% | Dùng để đánh giá khả năng tổng quát |
train_test_split() trong sklearn chia ngẫu nhiên, nhưng có thể cố định bằng random_state để kết quả tái lập.
from sklearn.model_selection import train_test_split
train_df, test_df = train_test_split(df_clean, test_size=0.25, random_state=42)

Hình 1: Histogram so sánh phân phối
SalePricegiữa train/test
3.2 Xử lý giá trị khuyết (Missing Values)
Khi một biến có giá trị bị thiếu, mô hình học máy không thể xử lý NaN.
Có hai hướng tiếp cận chính:
- Điền giá trị (Imputation) – thay thế giá trị thiếu bằng một đại diện thống kê (mean/median/mode).
- Tạo nhãn “không có” – dùng cho dữ liệu phân loại để giữ nguyên thông tin “bị thiếu”.
Ví dụ minh họa:
| Feature | Giá trị gốc | Cách điền median | Cách điền “none” |
|---|---|---|---|
| LotFrontage | NaN | 70.0 | – |
| Alley | NaN | – | "none" |

Hình 2: Heatmap tỉ lệ thiếu trước và sau khi xử lý
Dự án chia hai loại đặc trưng:
- Biến phân loại (categorical): điền "none" để biểu thị “không có giá trị”.
x_train[cat_cols] = train_df[cat_cols].fillna("none")
x_test[cat_cols] = test_df[cat_cols].fillna("none")
- Biến số (numerical): điền bằng trung vị (median) để tránh bị ảnh hưởng bởi ngoại lệ.
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy='median')
X_train_encoded[num_cols] = imputer.fit_transform(x_train[num_cols])
X_test_encoded[num_cols] = imputer.transform(x_test[num_cols])
Tại sao dùng median?
Vì median không bị ảnh hưởng bởi giá trị ngoại lệ (outlier), đảm bảo dữ liệu ổn định hơn mean.
3.3 Mã hoá Target Encoding
3.3.1 Trực giác và cơ chế
Giả sử ta có đặc trưng phân loại “Neighborhood” (khu vực nhà ở), và biến mục tiêu “SalePrice”.
* One-Hot Encoding biến mỗi khu vực thành 1 cột (A, B, C --> 3 cột).
--> Làm tăng số chiều dữ liệu và không phản ánh mức giá thực tế.
* Label Encoding gán số 1, 2, 3 tùy ý.
--> Tạo thứ bậc giả giữa nhãn.
Target Encoding thay giá trị của từng nhóm bằng trung bình giá nhà của nhóm đó, phản ánh được mối liên hệ thực giữa nhãn và target. Công thức:$$ \text{TE}(x_i) = \mathbb{E}[y | X = x_i] $$

Hình 3: Biểu đồ cột minh hoạ giá trị target mean theo từng hạng mục (ví dụ “Neighborhood”).
Tuy nhiên, với nhóm ít dữ liệu (ví dụ chỉ có 1 căn nhà), trung bình đó không đáng tin cậy --> dễ overfit. Khi đó ta dùng hệ số smoothing:
$$
\text{TE}(x_i) = \frac{n_i \cdot \bar{y}*{x_i} + m \cdot \bar{y}*{global}}{n_i + m}
$$
- $ n_i $: số mẫu trong nhóm
- $ \bar{y}_{x_i} $: giá trị trung bình của nhóm
- $ \bar{y}_{global} $: trung bình toàn bộ
- $ m $: tham số làm mượt (nhóm nhỏ bị kéo về trung bình chung nhiều hơn)
3.3.2 Cách thực hiện trong dự án
from category_encoders import TargetEncoder
target_encoder = TargetEncoder(
cols=cat_cols,
smoothing=1.0,
min_samples_leaf=1,
handle_unknown='value',
handle_missing='value'
)
X_train_encoded = target_encoder.fit_transform(x_train, y_train)
X_test_encoded = target_encoder.transform(x_test)
Tham số smoothing=1.0 điều chỉnh mức độ “kéo trung bình” của nhóm nhỏ về trung bình toàn cục, giúp tránh overfitting với các nhóm có ít mẫu.
3.4 Tạo đặc trưng đa thức (Polynomial Features)
3.4.1 Trực giác và cơ chế
Mô hình tuyến tính chỉ học được quan hệ $y = a·x + b$. Nhưng nếu quan hệ thực sự là phi tuyến (nonlinear) như $ y = 3x^2 + 5x + 2 $, mô hình tuyến tính sẽ không thể học tốt.
Giải pháp là tạo thêm biến bậc cao như $ x^2, x^3, x_1 \times x_2 $ để mở rộng không gian đặc trưng. Cơ chế hoạt động:
- Với 2 đặc trưng $ [x_1, x_2] $, bậc 2 sẽ sinh ra:
$$ [x_1, x_2, x_1^2, x_2^2, x_1 x_2] $$ - Nhờ vậy, mô hình tuyến tính có thể học quan hệ cong, tương tác giữa biến.
3.4.2 Cách thực hiện trong dự án
Dự án chọn 10 đặc trưng số có tương quan cao nhất với SalePrice, sau đó áp dụng PolynomialFeatures(degree=2):
from sklearn.preprocessing import PolynomialFeatures
correlations = x_train[num_cols].corrwith(pd.Series(y_train)).abs()
top_features = correlations.nlargest(10).index.tolist()
poly = PolynomialFeatures(degree=2, include_bias=False)
X_train_poly = poly.fit_transform(x_train[top_features])
X_test_poly = poly.transform(x_test[top_features])
Kết quả: dữ liệu chứa các đặc trưng mới như x1², x2², x1*x2, … → tăng khả năng biểu diễn phi tuyến mà không cần dùng mô hình quá phức tạp.

Hình 4: Mối tương quan giữa đặc trưng gốc và đặc trưng tạo thêm.
3.5 Chuẩn hoá đặc trưng (Feature Scaling)
3.5.1 Cơ chế
Khi các đặc trưng có đơn vị khác nhau (m², năm, số phòng,…), các thuật toán dùng khoảng cách (như Ridge, Lasso, hoặc Gradient Boosting) sẽ ưu tiên đặc trưng có độ lớn lớn hơn, gây sai lệch. StandardScaler chuẩn hoá mỗi đặc trưng:
$$
z = \frac{x - \mu}{\sigma}
$$
Trong đó:
* $ \mu $: giá trị trung bình
* $ \sigma $: độ lệch chuẩn
--> Sau khi chuẩn hoá: trung bình = 0, phương sai = 1.
3.5.2 Cách thực hiện trong dự án
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train_poly)
X_test_scaled = scaler.transform(X_test_poly)
Sau bước này, dữ liệu đã được chuẩn bị hoàn chỉnh để huấn luyện mô hình hồi quy tuyến tính và phi tuyến (Ridge, Lasso, ElasticNet, RandomForest, GradientBoosting...).

Hình 5: So sánh phân phối trước/sau chuẩn hoá
3.6 Tổng kết:
Quy trình tiền xử lý này đảm bảo dữ liệu:
- Không còn giá trị thiếu,
- Các đặc trưng phân loại được mã hoá tối ưu,
- Thông tin phi tuyến được bổ sung bằng đặc trưng đa thức,
- Và tất cả đặc trưng đều có thang đo thống nhất.
Nhờ vậy, mô hình đạt được hiệu suất ổn định, giảm overfitting và tăng khả năng tổng quát khi dự đoán giá nhà.
4. Một số khái niệm của mô hình
4.1 Elastic Net
4.1.1. Định nghĩa
Regularization là 1 kỹ thuật sử dụng trong machine learning để giảm overfitting và tăng khả năng khái quát hoá. Bằng cách thêm hệ số phạt (penalty) vào hàm loss, mô hình sẽ phải giữ cho các trọng số nhỏ hoặc triệt tiêu bớt các trọng số không quan trọng.
Trong thống kê vàtrong mô hình hồi quy tuyến tính (linear regression), elastic net là 1 phương pháp kết hợp cả 2 kỹ thuật:
- phương pháp L1 (Lasso): khuyến khích nhiều hệ số hồi quy bằng 0 → chọn lọc đặc trưng (feature selection).
- phương pháp L2(Ridge): thu nhỏ tất cả các hệ số về gần 0 → ổn định mô hình và xử lý đa cộng tuyến.
Elasitc net đặc biệt hữu ích trong trường hợp dataset có nhiều features và các features có hiện tượng đa cộng tuyến (multicollinearity) vì trong những trường hợp này Lasso có xu hướng chọn ngẫu nhiên một trong các đặc trưng tương quan, còn Elastic Net thì giữ lại và chia sẻ trọng số giữa chúng.
4.1.2 Công thức
$$
\hat{\beta}
= \underset{\beta}{\operatorname{argmin}}
\left(
\frac{1}{N}\|y - X\beta\|^{2}
+ \lambda_{2}\|\beta\|^{2}
+ \lambda_{1}\|\beta\|_{1}
\right)
$$
Trong đó:
$\hat{\beta}$: giá trị tối ưu của vector hệ số hồi quy.
$\frac{1}{N}\|y - X\beta\|^{2}$: MSE
$\lambda_{1}\|\beta\|_{1}$: thành phần Lasso
$\lambda_{2}\|\beta\|^{2}$: thành phần Ridge
Tuy nhiên công thức này có đến 2 hyperparameters cần optimized, không thuận tiện cho việc tuning nên có thể tái tham số hoá bằng việc: $$ \lambda_1 = \alpha \lambda, \quad \lambda_2 = (1 - \alpha)\lambda $$
Trong đó:
-
$ \lambda > 0 $: cường độ tổng của regularization (độ mạnh phạt)
- Khi $ \lambda $ nhỏ gần bằng 0:
- Không có regularization nào được áp dụng
- Mô hình chỉ tối thiểu hóa sai số dự đoán (giống hồi quy tuyến tính thông thường)
- Các hệ số $ \beta$ có thể tăng rất lớn, dẫn đến overfitting nếu mô hình quá phức tạp.
- Khi $ \lambda $ lớn:
- Thành phần phạt chiếm ưu thế, làm cho các hệ số $ \beta_j $ bị thu nhỏ mạnh về 0.
- Điều này giúp giảm overfitting, nhưng nếu quá mạnh sẽ làm mô hình mất thông tin quan trọng
- Khi $ \lambda $ nhỏ gần bằng 0:
-
$ \alpha \in [0, 1] $: tỉ lệ giữa L1 và L2
vì vậy công thức của elastic nét trong các mô hình tính toán là:
$$
\hat{\beta}
= \underset{\beta}{\operatorname{argmin}}
\left[
\frac{1}{2N}\|y - X\beta\|^2
+ \lambda \left(
\alpha \|\beta\|_1
+ \frac{1 - \alpha}{2}\|\beta\|_2^2
\right)
\right]
$$
4.1.3 Ý nghĩa của elastic net
Giảm đa cộng tuyến: kết hợp L2 giúp ổn định ước lượng khi các feature tương quan mạnh.
Chọn lọc đặc trưng: thành phần L1 giúp loại bỏ các biến không quan trọng, làm mô hình gọn nhẹ.
Cân bằng bias–variance: cho phép điều chỉnh linh hoạt giữa độ phức tạp và khả năng tổng quát.
Ứng dụng rộng: thường được dùng trong bài toán có nhiều biến độc lập, dữ liệu nhiễu, hoặc bài toán sinh học, tài chính có tương quan mạnh giữa các yếu tố.
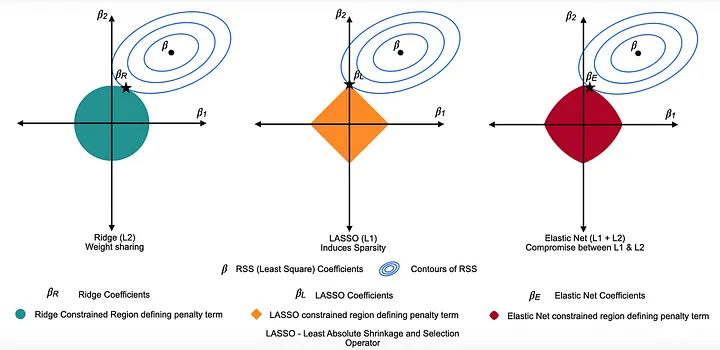
So sánh Lasso, Ridge và Elastic net
4.2 So sánh Lasso, Ridge và Elastic Net Regression
| Đặc điểm | Lasso Regression | Ridge Regression | Elastic Net Regression |
|---|---|---|---|
| Loại Regularization (Penalty Type) | L1 Penalty: sử dụng giá trị tuyệt đối của hệ số. | L2 Penalty: sử dụng bình phương của hệ số. | Kết hợp L1 + L2 Penalty: sử dụng đồng thời trị tuyệt đối và bình phương. |
| Ảnh hưởng đến hệ số (Effect on Coefficients) | Loại bỏ hoàn toàn các đặc trưng không quan trọng bằng cách đưa hệ số về 0. | Thu nhỏ tất cả hệ số nhưng không đưa về 0. | Vừa loại bỏ một số đặc trưng, vừa thu nhỏ các đặc trưng khác (cân bằng giữa L1 và L2). |
| Trường hợp sử dụng tốt nhất (Best Use Case) | Khi cần loại bỏ đặc trưng không liên quan. | Khi tất cả đặc trưng đều quan trọng, nhưng cần giảm ảnh hưởng của chúng. | Khi các đặc trưng có tương quan cao và cần vừa chọn lọc, vừa ổn định. |
| Siêu tham số (Hyperparameters) | α (alpha): kiểm soát độ mạnh regularization. α lớn → thu nhỏ mạnh hơn. | α (alpha): tương tự Lasso, điều chỉnh độ mạnh của regularization. | α + L1_ratio (hoặc λ, α): hai tham số. α điều chỉnh tổng thể, L1_ratio cân bằng giữa Lasso và Ridge. |
| Độ chệch & phương sai (Bias and Variance) | Độ chệch cao, phương sai thấp. | Độ chệch thấp, phương sai cao. | Cân bằng giữa độ chệch và phương sai. |
| Ưu điểm (Strengths) | Tự động chọn lọc đặc trưng quan trọng (feature selection). | Hoạt động tốt khi các đặc trưng liên quan nhau, không nên loại bỏ hoàn toàn. | Kết hợp được khả năng chọn lọc của Lasso và tính ổn định của Ridge. |
| Nhược điểm (Weaknesses) | Có thể loại bỏ nhầm đặc trưng quan trọng nếu không tinh chỉnh kỹ. | Giữ lại tất cả đặc trưng, có thể gây nhiễu khi dữ liệu nhiều đặc trưng vô ích. | Khó tinh chỉnh hơn do có hai siêu tham số. |
| Ví dụ minh họa (Example) | Giả sử ta có 100 đặc trưng dự đoán giá nhà. Nó sẽ đưa các đặc trưng không liên quan (như màu sơn nhà) về 0. | Cũng với 100 đặc trưng, nó sẽ giảm ảnh hưởng của từng đặc trưng, nhưng không loại bỏ đặc trưng nào. | Nếu có hai đặc trưng tương quan cao (như diện tích và số phòng), nó sẽ loại bớt một và thu nhỏ giá trị của đặc trưng còn lại. |
4.3 CatBoost
4.3.1 Giới thiệu
Trong các mô hình Gradient Boosting Decision Tree như XGBoost hay LightGBM, người dùng thường phải xử lý thủ công các biến phân loại bằng cách one-hot, label, hoặc target encoding. Các kỹ thuật này dễ gây data leakage, làm tăng số chiều dữ liệu và đòi hỏi nhiều công đoạn tiền xử lý.
CatBoost (Categorical Boosting), được phát triển bởi Yandex năm 2017, ra đời để giải quyết trực tiếp những hạn chế đó. Nó cung cấp cơ chế mã hóa biến phân loại tự động, đồng thời sử dụng Ordered Boosting để tránh rò rỉ thông tin trong quá trình huấn luyện.
CatBoost vì vậy trở thành một giải pháp boosting ổn định và dễ dùng hơn, hiệu quả với dữ liệu chứa nhiều biến phân loại hoặc phân bố không đồng đều.
4.3.2 Bản chất của CatBoost
CatBoost là một thuật toán Gradient Boosting trên cây quyết định (Decision Tree), tương tự như XGBoost và LightGBM, nhưng khác biệt ở cách huấn luyện và cách xử lý biến phân loại.
Cụ thể:
- CatBoost sử dụng cơ chế Ordered Boosting để giảm overfitting.
- CatBoost tự động mã hoá biến phân loại bằng Target Statistics, nhưng theo thứ tự học (ordered encoding) để tránh data leakage.
- Có thể xem CatBoost là boosting kết hợp với target encoding an toàn — đây là lý do tên gọi “Categorical + Boosting”.
4.3.3 Cơ chế hoạt động của CatBoost
a. Gradient Boosting cơ bản
Giống như các mô hình boosting khác, CatBoost huấn luyện nhiều cây quyết định nối tiếp nhau.
Mỗi cây mới học từ phần sai số (residual) của các cây trước:
$$ F_t(x) = F_{t-1}(x) + \eta \cdot h_t(x) $$
Trong đó:
- $F_t(x)$: mô hình sau bước boosting thứ $t$
- $h_t(x)$: cây được huấn luyện ở bước $t$
- $\eta$: tốc độ học (learning rate)
b. Ordered Target Statistics
Thay vì one-hot hoặc label encoding, CatBoost mã hoá biến phân loại bằng mean target, nhưng được tính theo thứ tự ngẫu nhiên cố định (ordered permutation) để tránh data leakage:
$$ \mathrm{Enc}(x_i)=\frac{\sum_{j\lt i} y_j + a\,\bar{y}}{N_{x_i}^{(j\lt i)} + a} $$
Trong đó:
- $j < i$: chỉ dùng các mẫu đứng trước trong thứ tự học
- $a$: hệ số làm mượt (smoothing parameter)
- $\bar{y}$: giá trị trung bình của toàn bộ target
Điều này tương tự phần Target Encode phía trên, nhưng tránh được leakage bằng việc không dùng chính nhãn của giá trị encode và các nhãn tương lai mà chỉ dùng các nhãn trước đó.
c. Ordered Boosting
Ở XGBoost hoặc LightGBM, mô hình tính gradient bằng toàn bộ dữ liệu → có thể gây data leakage giữa các mẫu.
CatBoost giải quyết bằng Ordered Boosting:
- Mỗi mẫu chỉ cập nhật gradient dựa trên các mô hình trước đó trong thứ tự permutation.
- Điều này đảm bảo gradient được ước lượng không thiên vị (unbiased) → mô hình ổn định hơn.
d. Ưu điểm chính
| Tính năng | Mô tả ngắn gọn |
|---|---|
| Xử lý biến phân loại tự động | Không cần one-hot hoặc label encoding. |
| Tránh overfitting | Nhờ Ordered Boosting và Ordered Encoding. |
| Ít cần tuning | Tham số mặc định hoạt động tốt trên nhiều loại dữ liệu. |
| Hỗ trợ GPU và đa luồng | Tăng tốc huấn luyện đáng kể. |
| Tự xử lý missing values | Không cần fillna thủ công. |
e. Nhược điểm
| Vấn đề | Giải thích |
|---|---|
| Tốn bộ nhớ hơn | Cần lưu nhiều permutation để thực hiện ordered encoding. |
| Huấn luyện chậm hơn XGBoost | Đặc biệt khi dữ liệu rất lớn. |
| Cần shuffle dữ liệu | Vì thứ tự học ảnh hưởng trực tiếp đến quá trình encoding. |
4.4 Tối ưu hóa siêu tham số với Optuna
4.4.1 Giới thiệu về Optuna
Optuna là một framework tối ưu hóa siêu tham số mã nguồn mở. Khác với Grid Search hoặc Random Search, Optuna sử dụng thuật toán Tree-structured Parzen Estimator (TPE) để tìm kiếm thông minh, học từ các thử nghiệm trước đó.
Ưu điểm chính:
- Tìm kiếm thích ứng dựa trên lịch sử thử nghiệm
- Pruning tự động các trial kém hiệu quả
- Định nghĩa không gian tìm kiếm linh hoạt
- Nhanh hơn Grid Search đáng kể
4.4.2 Cơ chế TPE (Tree-structured Parzen Estimator)
TPE xây dựng hai mô hình xác suất:
$$ p(\mathbf{x}|y) = \begin{cases} \ell(\mathbf{x}) & \text{if } y < y^* \text{ (cấu hình tốt)} \\ g(\mathbf{x}) & \text{if } y \geq y^* \text{ (cấu hình xấu)} \end{cases} $$
TPE chọn cấu hình tiếp theo bằng cách tối đa hóa $\ell(\mathbf{x})/g(\mathbf{x})$, ưu tiên các vùng có khả năng cho kết quả tốt.
4.4.3 Áp dụng trong dự án
a. Định nghĩa không gian tìm kiếm
Mỗi mô hình có không gian siêu tham số riêng:
ElasticNet:
model = ElasticNet(
alpha=trial.suggest_float('alpha', 1e-3, 10.0, log=True), # log scale
l1_ratio=trial.suggest_float('l1_ratio', 0.0, 1.0) # linear scale
)
GradientBoosting:
model = GradientBoostingRegressor(
n_estimators=trial.suggest_int('n_estimators', 100, 500),
learning_rate=trial.suggest_float('learning_rate', 0.01, 0.3),
max_depth=trial.suggest_int('max_depth', 2, 8),
subsample=trial.suggest_float('subsample', 0.5, 1.0)
)
b. Objective Function
def objective(trial, model_name):
# Khởi tạo mô hình với siêu tham số từ trial
model.fit(X_train_encoded, y_train)
y_pred = model.predict(X_test_encoded)
r2 = r2_score(y_test, y_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
trial.set_user_attr("rmse", rmse) # Lưu metric phụ
return r2 # Maximize R²
c. Quá trình tối ưu
for model_name in models.keys():
study = optuna.create_study(direction="maximize")
study.optimize(lambda trial: objective(trial, model_name),
n_trials=30)
Quy trình:
1. 5-10 thử nghiệm đầu ngẫu nhiên (warm-up)
2. Áp dụng TPE để tìm kiếm thông minh
3. Cập nhật mô hình xác suất liên tục
4.4.4 So sánh với các phương pháp khác
| Phương pháp | Số thử nghiệm | Hiệu quả |
|---|---|---|
| Grid Search | $k_1 \times k_2 \times ... \times k_n$ | Đầy đủ nhưng rất chậm |
| Random Search | ~100 | Tốt với không gian lớn |
| Optuna (TPE) | ~30 | Rất tốt, học từ lịch sử |
Ví dụ: ElasticNet có 2 siêu tham số với 10 giá trị mỗi tham số:
- Grid Search: $10 \times 10 = 100$ thử nghiệm
- Optuna: chỉ cần 30 thử nghiệm nhờ TPE
4.4.5 Kết quả
Output mẫu sau khi tối ưu:
best_r2 best_rmse
GradientBoosting 0.916228 20295.968433
RandomForest 0.907131 21369.567067
Ridge 0.905876 21513.460095
ElasticNet 0.905799 21522.262927
Lasso 0.899695 22208.696372
Cat Boost 0.930966 18424.310375
GradientBoosting 0.927131 18929.2119
XG Boost 0.925846 19095.331406
Light GBM 0.924782 19231.844782
RandomForest 0.913844 20582.783236
Chưa có bình luận nào. Hãy là người đầu tiên!