PROJECT 5.1: DỰ ĐOÁN GIÁ NHÀ BẰNG LINEAR REGRESSION
Tóm tắt
Bài nghiên cứu trình bày việc xây dựng mô hình dự đoán giá nhà dựa trên tập dữ liệu “House Prices: Advanced Regression Techniques”. Ba mô hình hồi quy được sử dụng gồm: Linear Regression, Ridge Regression và Lasso Regression. Sau quá trình tiền xử lý dữ liệu và tối ưu tham số, kết quả cho thấy mô hình Ridge và Lasso có khả năng giảm overfitting và đạt độ chính xác cao hơn mô hình tuyến tính cơ bản. Bài toán thể hiện ứng dụng của các kỹ thuật hồi quy tuyến tính trong dự đoán giá trị liên tục và minh họa quy trình xây dựng mô hình học máy hoàn chỉnh.
1. Giới thiệu
Dự đoán giá nhà là một bài toán phổ biến trong lĩnh vực khoa học dữ liệu và kinh tế học, đóng vai trò quan trọng trong việc định giá bất động sản, đầu tư và quy hoạch đô thị.
Nghiên cứu này hướng đến việc áp dụng các phương pháp hồi quy tuyến tính và biến thể của nó nhằm xây dựng mô hình dự đoán giá nhà chính xác và ổn định.
Mục tiêu chính:
- Hiểu rõ mối quan hệ giữa các thuộc tính (ví dụ: diện tích, số phòng, chất lượng xây dựng) và giá nhà.
- So sánh hiệu năng của các mô hình hồi quy khác nhau.
- Đưa ra đánh giá thực nghiệm và kết luận về mô hình phù hợp nhất
- So sánh hiệu năng của các mô hình hồi quy với các mô hình khác
2. Phương pháp
A. Dataset
- Bộ dữ liệu được lấy từ Kaggle: House Prices – Advanced Regression Techniques, gồm ~1,460 mẫu và hơn 80 đặc trưng mô tả thông tin nhà ở.
- Biến mục tiêu: SalePrice.
- Các đặc trưng bao gồm: diện tích (GrLivArea), chất lượng (OverallQual), năm xây (YearBuilt), số phòng (TotRmsAbvGrd),.....
B. Tiền xử lý dữ liệu
-
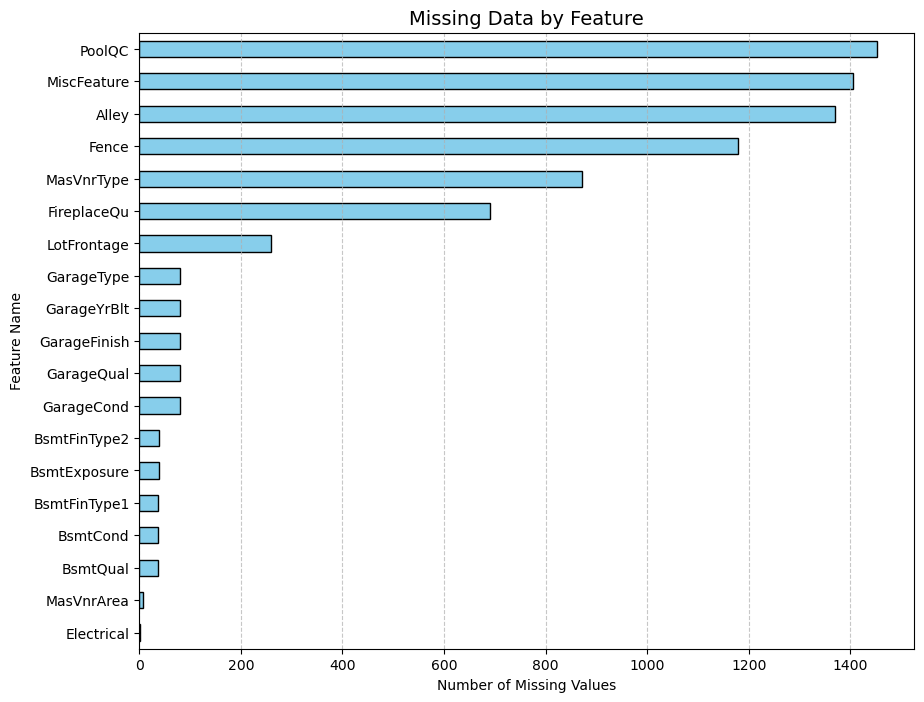
i. Xử lý giá trị bị thiếu: Đầu tiên, kiểm tra số lượng giá trị bị thiếu bằng biểu đồ cột nằm ngang. Những cột có trên 50% giá trị thiếu như:
-
Alley
-
PoolQC
-
Fence
-
MiscFeature
-
Ý nghĩa: Nguyên nhân là các cột này chứa quá nhiều giá trị rỗng, nếu cố gắng điền vào sẽ gây sai lệch thống kê và làm giảm chất lượng mô hình.
house_df = house_df.drop(["Id","Alley","PoolQC","Fence","MiscFeature",], axis=1)
- Các cột dữ liệu phân loại (categorical features) có giá trị bị thiếu (NaN), thì thay thế nó bằng chuỗi "none"
train_df[cat_cols] = train_df[cat_cols].fillna("none")
test_df[cat_cols] = test_df[cat_cols].fillna("none")
- ii. Kiểm tra tương quan (Correlation Analysis):
Trước khi chuẩn hóa, ta phân tích mối tương quan giữa các biến số bằng heatmap:
plt.figure(figsize=(30, 9))
sns.heatmap(
house_df.corr(numeric_only=True),
cmap="coolwarm",
linewidths=0.5,
center=0,
cbar_kws={"shrink": 0.8}
)
plt.title("Correlation Heatmap of Numerical Features", fontsize=16, pad=15)
plt.show()
Ý nghĩa: Qua đó nhận biết các đặc trưng có ảnh hưởng mạnh đến giá nhà như:
- OverallQual (chất lượng tổng thể)
- GrLivArea (diện tích sàn sinh hoạt)
- GarageCars (số lượng chỗ để xe)
C. Chuẩn hóa dữ liệu (Normalization)
Để đảm bảo tất cả các đặc trưng có cùng thang đo, quá trình chuẩn hóa dữ liệu được áp dụng.
Điều này đặc biệt quan trọng với các mô hình hồi quy, vì các giá trị lớn hơn có thể chi phối quá trình học, gây sai lệch trọng số.
- Lý do cần chuẩn hóa:
- Các đặc trưng như GrLivArea (có thể đến hàng nghìn) và OverallQual (thang điểm 1–10) có độ chênh lệch lớn.
- Nếu không chuẩn hóa, mô hình có xu hướng “ưu tiên” những biến có giá trị lớn, khiến kết quả dự đoán thiếu chính xác.
- Phương pháp sử dụng:
Ta áp dụng Min-Max Normalization, đưa toàn bộ giá trị của mỗi đặc trưng về khoảng [0, 1] theo công thức:
$$ X' = \frac{X - X_{\min}}{X_{\max} - X_{\min}} $$
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
train_num_features = scaler.fit_transform(train_df[num_cols])
test_num_features = scaler.transform(test_df[num_cols])
Đối với một số mô hình hồi quy tuyến tính, cũng có thể dùng Standardization (Z-score normalization):
$$ X' = \frac{X - \mu}{\sigma} $$
giúp dữ liệu có trung bình 0 và độ lệch chuẩn 1.
- Kết quả sau chuẩn hóa::
- Các đặc trưng số đều nằm trong cùng khoảng giá trị, giúp thuật toán học máy hội tụ nhanh hơn.
- Giảm thiểu rủi ro sai lệch do đơn vị đo khác nhau ($m^2$, năm, số lượng,…).
- Cải thiện độ ổn định và độ chính xác của mô hình.
D. Xây dựng các mô hình
models = {
# --- Tuyến tính & regularization ---
"LinearRegression": LinearRegression(),
"Ridge": Ridge(alpha=10.0),
"Lasso": Lasso(alpha=0.0005, max_iter=10000),
"ElasticNet": ElasticNet(alpha=0.0005, l1_ratio=0.5, max_iter=10000),
"BayesianRidge": BayesianRidge(),
"SGDRegressor": SGDRegressor(random_state=42, max_iter=2000, tol=1e-3),
"PassiveAggressive":PassiveAggressiveRegressor(random_state=42, max_iter=1000, tol=1e-3),
# --- Robust ---
"Huber": HuberRegressor(),
"RANSAC": RANSACRegressor(random_state=42),
# --- KNN ---
"KNN_k5": KNeighborsRegressor(n_neighbors=5),
# --- Tree/Ensemble/Boosting ---
"DecisionTree": DecisionTreeRegressor(random_state=42),
"RandomForest": RandomForestRegressor(n_estimators=500, random_state=42, n_jobs=-1),
"GradientBoosting": GradientBoostingRegressor(random_state=42),
"AdaBoost": AdaBoostRegressor(random_state=42),
}
Linear Regression
Nguyên lý:
Mô hình giả định mối quan hệ tuyến tính giữa biến độc lập $X$ và biến phụ thuộc $y$.
$$ \hat{y} = w_0 + w_1x_1 + w_2x_2 + \ldots + w_nx_n = Xw + b $$
Trọng số $w$ được ước lượng bằng cách tối thiểu hóa tổng bình phương sai số (OLS):
$$ (y - \hat{y})^2 $$
Ưu điểm: Đơn giản, dễ hiểu, huấn luyện nhanh.
Hạn chế: Nhạy cảm với ngoại lai và chỉ mô hình hóa quan hệ tuyến tính.
Trong dự án: Được dùng làm baseline để so sánh với các mô hình phức tạp hơn.
Ridge Regression
Nguyên lý:
Là phiên bản mở rộng của Linear Regression với chuẩn L2 để chống overfitting:
$$ J(w) = \sum_{i=1}^{m} (y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{n} w_j^2 $$
Ưu điểm: Ổn định hơn khi có đa cộng tuyến.
Hạn chế: Không loại bỏ đặc trưng (chỉ làm nhỏ hệ số).
Trong dự án: Dùng để ổn định mô hình tuyến tính và xử lý hiện tượng overfitting.
Lasso Regression
Nguyên lý:
Thêm chuẩn L1 vào hàm mất mát, giúp triệt tiêu các hệ số nhỏ:
$$
J(w) = \sum_{i=1}^{m} (y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{n} |w_j|
$$
Ưu điểm: Có khả năng chọn lọc đặc trưng tự động.
Hạn chế: Không ổn định khi nhiều đặc trưng tương quan cao.
Trong dự án: Dùng để giảm chiều dữ liệu và loại bỏ đặc trưng kém quan trọng.
ElasticNet Regression
Nguyên lý:
Kết hợp ưu điểm của Lasso (L1) và Ridge (L2):
$$ \min_w ||y - Xw||^2 + \alpha \left[ \rho ||w||_1 + (1 - \rho) ||w||^2 \right] $$
Ưu điểm: Cân bằng giữa chọn lọc đặc trưng và ổn định mô hình.
Hạn chế: Cần tinh chỉnh hai siêu tham số $\alpha$ và $\rho$.
Trong dự án: Dùng để cải thiện hiệu quả của hồi quy tuyến tính.
Bayesian Ridge Regression
Nguyên lý:
Áp dụng suy luận Bayes để tìm phân phối hậu nghiệm của trọng số $w$:
$$
p(w|X, y, \alpha, \lambda) \propto p(y|X, w, \alpha) \cdot p(w|\lambda)
$$
Giúp mô hình hóa sự không chắc chắn trong ước lượng.
Ưu điểm: Giảm overfitting, cung cấp phân bố xác suất cho dự đoán.
Hạn chế: Phức tạp hơn hồi quy thường, giả định Gaussian.
Trong dự án: Dùng để ước lượng tin cậy của dự đoán giá nhà.
SGD Regressor
Nguyên lý:
Cập nhật trọng số theo Stochastic Gradient Descent:
$$
w_{t+1} = w_t - \eta \nabla L(w_t)
$$
với $\eta$ là tốc độ học (learning rate).
Ưu điểm: Nhanh, phù hợp dữ liệu lớn.
Hạn chế: Dễ dao động, phụ thuộc vào learning rate.
Trong dự án: Dùng để thử nghiệm mô hình tuyến tính huấn luyện nhanh.
Passive Aggressive Regressor
Nguyên lý:
Cập nhật trọng số chỉ khi sai số vượt ngưỡng:
$$
w_{t+1} = w_t + \tau_t y_t x_t, \quad \text{với } \tau_t = \frac{\max(0, 1 - y_t w_t^T x_t)}{||x_t||^2}
$$
Giúp cân bằng giữa “Passive” (đúng thì giữ nguyên) và “Aggressive” (sai thì cập nhật mạnh).
Ưu điểm: Học online nhanh, không cần huấn luyện lại toàn bộ.
Hạn chế: Dễ bị nhiễu nếu dữ liệu không ổn định.
Trong dự án: Dùng để thử nghiệm khả năng học trực tuyến.
Huber Regressor
Nguyên lý:
Hàm mất mát kết hợp giữa MSE và MAE:
$$
L_\delta(a) =
\begin{cases}
\frac{1}{2}a^2, & |a| \le \delta \\
\delta(|a| - \frac{1}{2}\delta), & |a| > \delta
\end{cases}
$$
Giúp giảm ảnh hưởng của outlier.
Ưu điểm: Ổn định với dữ liệu có nhiễu.
Hạn chế: Cần chọn ngưỡng $\delta$ phù hợp.
Trong dự án: Dùng để giảm tác động của giá nhà bất thường.
RANSAC Regressor
Nguyên lý:
Chọn ngẫu nhiên tập con dữ liệu "inlier" và khớp mô hình nhiều lần, chọn mô hình tốt nhất theo tiêu chí sai số:
$$ \text{Model}^* = \arg\min_M \sum_{i \in \text{inliers}} |y_i - f_M(x_i)| $$
Ưu điểm: Rất mạnh khi dữ liệu chứa nhiều outlier.
Hạn chế: Tốn thời gian nếu dữ liệu lớn.
Trong dự án: Dùng để tăng tính robust cho mô hình hồi quy.
KNN Regressor (k=5)
Nguyên lý:
Dự đoán giá trị đầu ra bằng trung bình của $k$ láng giềng gần nhất:
$$ \hat{y}(x) = \frac{1}{k} \sum_{i \in \mathcal{N}_k(x)} y_i $$
Ưu điểm: Không cần giả định về mối quan hệ giữa biến.
Hạn chế: Tính toán chậm khi dữ liệu lớn, nhạy với outlier.
Trong dự án: Dùng để so sánh mô hình phi tuyến.
Decision Tree Regressor
Nguyên lý:
Phân chia dữ liệu dựa trên đặc trưng để giảm tổng phương sai:
$$ \text{Var}_{\text{split}} = \text{Var}_{\text{parent}} - (w_L \text{Var}_L + w_R \text{Var}_R) $$
Ưu điểm: Dễ diễn giải, biểu diễn được quan hệ phi tuyến.
Hạn chế: Dễ overfit nếu không giới hạn độ sâu.
Trong dự án: Dùng làm nền tảng cho các mô hình ensemble.
Random Forest Regressor
Nguyên lý:
Kết hợp nhiều cây quyết định huấn luyện trên các mẫu bootstrap, dự đoán trung bình:
$$ \hat{y} = \frac{1}{T} \sum_{t=1}^T f_t(x) $$
Ưu điểm: Giảm phương sai, ổn định hơn Decision Tree.
Hạn chế: Ít khả năng diễn giải.
Trong dự án: Là mô hình ensemble mạnh, được dùng để tăng độ chính xác.
Gradient Boosting Regressor
Nguyên lý:
Huấn luyện các cây nối tiếp nhau, mỗi cây học phần sai số còn lại:
$$
F_m(x) = F_{m-1}(x) + \eta h_m(x)
$$
với $h_m(x)$ là cây mới học residual.
Ưu điểm: Hiệu năng cao, nắm bắt tốt quan hệ phi tuyến.
Hạn chế: Dễ overfit, cần tuning cẩn thận.
Trong dự án: Dùng để nâng cao độ chính xác mô hình dự đoán giá nhà.
AdaBoost Regressor
Nguyên lý:
Kết hợp các mô hình yếu bằng cách gán trọng số cao hơn cho các mẫu bị dự đoán sai:
$$
F(x) = \sum_{m=1}^M \alpha_m h_m(x)
$$
với $\alpha_m$ là trọng số tỉ lệ với độ chính xác của mô hình $h_m$.
Ưu điểm: Dễ triển khai, hiệu quả trên dữ liệu nhỏ.
Hạn chế: Nhạy cảm với nhiễu và outlier.
Trong dự án: Dùng để đánh giá hiệu quả của boosting đơn giản.
E. Các chức năng mở rộng
- Bảng tóm tắt các chức năng mở rộng:
| STT | Xử lý | Baseline | Advanced |
|---|---|---|---|
| 1 | Xử lý missing data | Xoá các cột bị có tỉ lệ missing > 50%, các dữ liệu NaN thay = "none" | KNNImputer |
| 2 | Huấn luyện dữ liệu | Train bình thường | Cross-Validation |
| 3 | Xử lý outlier | Không có xử lý | Winsorization |
- KNNImputer: là phương pháp điền giá trị bị thiếu dựa trên k láng giềng gần nhất trong không gian đặc trưng.
Giá trị bị thiếu của một mẫu được thay thế bằng trung bình có trọng số của các giá trị tương ứng từ các mẫu gần nhất:
$$
\hat{x}_i = \frac{\sum_{j \in \mathcal{N}_k(i)} w_{ij} x_j}{\sum_{j \in \mathcal{N}_k(i)} w_{ij}}
$$
Trong đó $\mathcal{N}_k(i)$ là tập các láng giềng gần nhất, và $w_{ij}$ là trọng số tỉ lệ nghịch với khoảng cách giữa mẫu $i$ và $j$.
Phương pháp này giúp bảo toàn mối quan hệ giữa các biến, chính xác hơn so với việc điền bằng trung bình hoặc trung vị.
from sklearn.impute import KNNImputer
# Check missing values
missing_before = train_df[num_cols].isnull().sum()
missing_before = missing_before[missing_before > 0]
if len(missing_before) > 0:
print(f"{len(missing_before)} numeric columns with missing values:")
for col, count in list(missing_before.items())[:5]:
print(f" • {col}: {count} missing ({count/len(train_df)*100:.2f}%)")
knn_imputer = KNNImputer(n_neighbors=5, weights='distance')
train_df[num_cols] = knn_imputer.fit_transform(train_df[num_cols])
test_df[num_cols] = knn_imputer.transform(test_df[num_cols])
print(f"Applying KNNImputer (n_neighbors=5) to handle missing values")
else:
print("No missing values in numeric columns")
- Cross-Validation: là kỹ thuật đánh giá độ tổng quát của mô hình học máy bằng cách chia dữ liệu thành nhiều phần (folds).
Trong k-fold cross-validation, dữ liệu được chia thành $k$ phần bằng nhau; mô hình được huấn luyện trên $k-1$ phần và kiểm thử trên phần còn lại.
Quy trình lặp lại $k$ lần, và kết quả trung bình được dùng để đánh giá hiệu năng mô hình:
$$
CV_{score} = \frac{1}{k} \sum_{i=1}^{k} MSE_i
$$
Phương pháp này giúp giảm bias và variance trong quá trình đánh giá, đảm bảo mô hình hoạt động ổn định trên dữ liệu mới.
# Cross-Validate trên X_train
cv_res = cross_validate(
model, X_train, y_train,
cv=cv, scoring=scoring,
n_jobs=-1, return_train_score=False
)
- Winsorization: Winsorization là kỹ thuật giảm ảnh hưởng của các giá trị ngoại lai (outliers) bằng cách cắt ngưỡng dữ liệu tại hai đầu phân phối.
Các giá trị vượt quá ngưỡng được thay thế bằng giá trị tại ngưỡng đó:
$$
x_i' =
\begin{cases}
L_p, & x_i < L_p \\
x_i, & L_p \le x_i \le U_p \\
U_p, & x_i > U_p
\end{cases}
$$
trong đó $L_p$ và $U_p$ lần lượt là ngưỡng phần trăm thấp và cao (ví dụ 1% và 99%).
Kỹ thuật này giúp ổn định mô hình hồi quy và giảm sai lệch do outlier mà không cần loại bỏ dữ liệu.
#Winsorization (limits in percentile 1% and 99%)
from scipy.stats.mstats import winsorize
limits = (0.01, 0.01) # Winsorize 1% ở mỗi đuôi
for col in num_cols:
if train_df[col].notna().sum() > 0:
train_values = train_df[col].dropna().values
winsorized_train = winsorize(train_values, limits=limits)
train_df.loc[train_df[col].notna(), col] = winsorized_train
lower_bound = winsorized_train.min()
upper_bound = winsorized_train.max()
test_df[col] = test_df[col].clip(lower=lower_bound, upper=upper_bound)
print(f"Winsorization (limits={limits}) for {len(num_cols)} numeric columns")
F. Chỉ số đánh giá mô hình
- Sai số trung bình bình phương gốc (RMSE)
$$ \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} $$
- Đo lường sai số dự đoán trung bình theo đơn vị gốc (USD).
- Giá trị càng nhỏ càng tốt.
- Nhạy với các sai số lớn do bình phương.
- Hệ số xác định (R²)
$$ R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2} $$
- Biểu thị tỷ lệ phương sai của biến mục tiêu được mô hình giải thích.
- $R^2 \in (-\infty, 1]$, với $R^2 = 1$ là dự đoán hoàn hảo.
- Dùng để so sánh độ phù hợp giữa các mô hình.
Cả hai chỉ số được tính trên tập huấn luyện và tập kiểm tra để phát hiện hiện tượng quá khớp (overfitting).
3. Thực nghiệm và đánh giá
A. Kết quả đánh giá trên tập Train/Test
Sau quá trình huấn luyện các mô hình, kết quả được tổng hợp và sắp xếp theo Test R² (từ cao xuống thấp):
| STT | Mô hình | Train RMSE | Test RMSE | Train R² | Test R² | Thời gian (s) |
|---|---|---|---|---|---|---|
| 1 | XGBRegressor | 367.85 | 23,616.63 | 0.9999 | 0.9204 | 4.20 |
| 2 | GradientBoosting | 13,533.89 | 25,858.11 | 0.9698 | 0.9046 | 0.94 |
| 3 | LGBMRegressor | 2,682.46 | 27,076.11 | 0.9988 | 0.8953 | 1.18 |
| 4 | RandomForest | 11,684.36 | 27,964.15 | 0.9775 | 0.8884 | 15.92 |
| 5 | Huber | 25,651.25 | 27,974.45 | 0.8916 | 0.8883 | 0.20 |
| 6 | ElasticNet | 20,813.54 | 28,674.14 | 0.9286 | 0.8826 | 1.03 |
| 7 | BayesianRidge | 22,871.74 | 28,734.52 | 0.9138 | 0.8821 | 0.06 |
| 8 | Ridge | 24,285.71 | 29,223.02 | 0.9029 | 0.8781 | 0.03 |
| 9 | SGDRegressor | 24,049.51 | 29,282.60 | 0.9047 | 0.8776 | 0.18 |
| 10 | PassiveAggressive | 27,394.74 | 29,525.55 | 0.8764 | 0.8756 | 1.24 |
| 11 | Lasso | 20,487.71 | 29,826.90 | 0.9309 | 0.8730 | 4.66 |
| 12 | LinearRegression | 20,487.71 | 30,004.15 | 0.9309 | 0.8715 | 0.04 |
| 13 | AdaBoost | 27,529.05 | 32,772.05 | 0.8752 | 0.8467 | 0.50 |
| 14 | RANSAC | 28,819.86 | 35,630.74 | 0.8632 | 0.8188 | 1.61 |
| 15 | KNN_k5 | 32,293.15 | 38,011.24 | 0.8282 | 0.7937 | 0.09 |
| 16 | DecisionTree | 0.00 | 43,397.15 | 1.0000 | 0.7312 | 0.08 |
Nhận xét:
- Mô hình tốt nhất: XGBRegressor đạt Test R² = 0.9204 với RMSE = 23,616.63 USD, nhưng có dấu hiệu overfitting (Train R² = 0.9999).
- Mô hình hồi quy tuyến tính: Ridge, Lasso, và LinearRegression có Test R² tương đối thấp (0.87–0.88), nhưng ít overfitting hơn.
- Mô hình ensemble: GradientBoosting và RandomForest cho kết quả tốt (R² > 0.88), cân bằng giữa độ chính xác và độ ổn định.
B. Kết quả Cross-Validation
Để đánh giá độ tổng quát của mô hình, kỹ thuật Cross-Validation được áp dụng. Kết quả được sắp xếp theo CV_RMSE_mean (từ thấp đến cao):
| STT | Mô hình | CV RMSE (mean) | CV RMSE (std) | CV R² (mean) | CV R² (std) | Holdout RMSE | Holdout R² |
|---|---|---|---|---|---|---|---|
| 1 | Huber | 28,306.08 | 4,338.06 | 0.8624 | 0.0459 | 27,974.45 | 0.8883 |
| 2 | Ridge | 29,462.67 | 3,973.64 | 0.8517 | 0.0454 | 29,223.02 | 0.8781 |
| 3 | PassiveAggressive | 29,565.41 | 4,001.48 | 0.8514 | 0.0418 | 29,525.55 | 0.8756 |
| 4 | SGDRegressor | 29,517.54 | 3,988.82 | 0.8505 | 0.0482 | 29,282.60 | 0.8776 |
| 5 | BayesianRidge | 29,657.29 | 4,064.82 | 0.8492 | 0.0483 | 28,734.52 | 0.8821 |
| 6 | GradientBoosting | 29,597.78 | 5,164.13 | 0.8472 | 0.0631 | 25,858.11 | 0.9046 |
| 7 | XGBRegressor | 29,930.64 | 5,692.36 | 0.8438 | 0.0680 | 23,616.63 | 0.9204 |
| 8 | LGBMRegressor | 30,767.00 | 3,323.81 | 0.8398 | 0.0390 | 27,076.11 | 0.8953 |
| 9 | RandomForest | 31,623.49 | 4,035.35 | 0.8285 | 0.0538 | 27,964.15 | 0.8884 |
| 10 | ElasticNet | 32,007.65 | 4,728.04 | 0.8240 | 0.0591 | 28,674.14 | 0.8826 |
| 11 | LinearRegression | 34,922.74 | 5,501.81 | 0.7909 | 0.0688 | 30,004.15 | 0.8715 |
| 12 | Lasso | 35,211.06 | 5,752.42 | 0.7880 | 0.0677 | 29,826.90 | 0.8730 |
| 13 | AdaBoost | 37,693.90 | 3,374.86 | 0.7594 | 0.0587 | 32,772.05 | 0.8467 |
| 14 | KNN_k5 | 40,323.29 | 4,591.93 | 0.7285 | 0.0470 | 38,011.24 | 0.7937 |
| 15 | DecisionTree | 50,880.14 | 8,183.08 | 0.5450 | 0.1758 | 43,397.15 | 0.7312 |
Nhận xét:
- Huber Regressor cho CV R² trung bình cao nhất (0.8624) và độ lệch chuẩn thấp, thể hiện tính ổn định tốt.
- Ridge Regression đạt CV R² = 0.8517, có độ ổn định cao và ít biến thiên (std = 0.0454).
- LinearRegression và Lasso có độ lệch chuẩn cao hơn trong CV, cho thấy nhạy cảm với sự thay đổi của dữ liệu.
- DecisionTree có độ lệch chuẩn rất cao (0.1758), chứng tỏ mô hình không ổn định và dễ overfitting.
C. So sánh mô hình hồi quy tuyến tính với tham số tối ưu
Sau khi tối ưu tham số cho các mô hình hồi quy tuyến tính cơ bản:
| Mô hình | Train RMSE | Test RMSE | Train R² | Test R² |
|---|---|---|---|---|
| Ridge (α=5.0) | 19,575.33 | 27,772.39 | 0.9369 | 0.8899 |
| Lasso (α=0.0005) | 11,107.64 | 52,705.82 | 0.9797 | 0.6035 |
| LinearRegression | 9,545.51 | 55,032.36 | 0.9850 | 0.5677 |
Nhận xét:
- Ridge Regression với α=5.0 cho kết quả tốt nhất trong nhóm mô hình tuyến tính, với Test R² = 0.8899 và Test RMSE = 27,772.39 USD.
- Lasso và LinearRegression có hiện tượng overfitting nghiêm trọng: Train R² rất cao (>0.97) nhưng Test R² thấp (<0.61).
- Ridge Regression cho thấy khả năng giảm overfitting hiệu quả nhờ regularization L2.
D. Phân tích Overfitting
Để phát hiện overfitting, ta so sánh chênh lệch giữa Train R² và Test R²:
Mô hình có overfitting nghiêm trọng:
- DecisionTree: Train R² = 1.0000, Test R² = 0.7312 (chênh lệch = 0.2688)
- XGBRegressor: Train R² = 0.9999, Test R² = 0.9204 (chênh lệch = 0.0795)
- LGBMRegressor: Train R² = 0.9988, Test R² = 0.8953 (chênh lệch = 0.1035)
- LinearRegression (chưa tối ưu): Train R² = 0.9850, Test R² = 0.5677 (chênh lệch = 0.4173)
Mô hình cân bằng:
- Huber: Train R² = 0.8916, Test R² = 0.8883 (chênh lệch = 0.0033)
- Ridge (α=5.0): Train R² = 0.9369, Test R² = 0.8899 (chênh lệch = 0.0470)
- BayesianRidge: Train R² = 0.9138, Test R² = 0.8821 (chênh lệch = 0.0317)
E. So sánh thời gian huấn luyện
Các mô hình được so sánh về thời gian huấn luyện:
- Nhanh nhất: Ridge (0.03s), BayesianRidge (0.06s), KNN_k5 (0.09s), Huber (0.20s)
- Trung bình: SGDRegressor (0.18s), PassiveAggressive (1.24s), ElasticNet (1.03s)
- Chậm nhất: RandomForest (15.92s), Lasso (4.66s), XGBRegressor (4.20s)
4. Kết luận
Tóm tắt kết quả
Qua quá trình thực nghiệm trên tập dữ liệu "House Prices: Advanced Regression Techniques", nghiên cứu đã so sánh 16 mô hình hồi quy khác nhau, từ các mô hình tuyến tính đơn giản đến các mô hình ensemble phức tạp.
Kết quả chính
-
Mô hình tốt nhất về độ chính xác: XGBRegressor đạt Test R² = 0.9204 và Test RMSE = 23,616.63 USD. Tuy nhiên, mô hình này có dấu hiệu overfitting với Train R² = 0.9999.
-
Mô hình cân bằng tốt: GradientBoosting và RandomForest cho kết quả tốt (Test R² > 0.88) với độ ổn định cao và ít overfitting hơn so với XGBRegressor.
-
Mô hình hồi quy tuyến tính tối ưu: Ridge Regression với α=5.0 đạt Test R² = 0.8899, thể hiện khả năng giảm overfitting hiệu quả và ổn định hơn so với LinearRegression và Lasso.
-
Mô hình ổn định nhất: Huber Regressor đạt CV R² trung bình cao nhất (0.8624) với độ lệch chuẩn thấp, chứng tỏ tính ổn định tốt khi áp dụng trên dữ liệu mới.
Nhận định về các mô hình
Mô hình hồi quy tuyến tính:
- Ridge Regression cho thấy hiệu quả trong việc giảm overfitting và ổn định mô hình.
- Lasso Regression có khả năng chọn lọc đặc trưng, nhưng trong trường hợp này dễ overfitting khi tham số không được tối ưu.
- LinearRegression cơ bản dễ bị overfitting khi dữ liệu phức tạp, cần regularization để cải thiện.
Mô hình ensemble:
- GradientBoosting và RandomForest là lựa chọn tốt cho bài toán dự đoán giá nhà, cân bằng giữa độ chính xác và tính ổn định.
- XGBRegressor cho kết quả tốt nhất nhưng cần cẩn thận với overfitting.
Mô hình robust:
- Huber Regressor thể hiện khả năng chống nhiễu tốt và ổn định trong cross-validation.
Đóng góp của nghiên cứu
-
So sánh toàn diện: Nghiên cứu đã so sánh nhiều mô hình hồi quy từ đơn giản đến phức tạp, cung cấp cái nhìn tổng quan về hiệu năng của từng phương pháp.
-
Phân tích overfitting: Nghiên cứu chỉ ra rõ ràng sự khác biệt giữa Train R² và Test R², giúp nhận diện các mô hình dễ bị overfitting.
-
Đánh giá bằng Cross-Validation: Việc sử dụng Cross-Validation cho phép đánh giá độ tổng quát của mô hình một cách chính xác hơn.
-
Tối ưu tham số: Việc tối ưu tham số cho Ridge và Lasso cho thấy tầm quan trọng của regularization trong việc cải thiện hiệu năng mô hình.
Hướng phát triển
-
Tinh chỉnh tham số: Có thể áp dụng Grid Search hoặc Random Search để tối ưu thêm các tham số của các mô hình ensemble như XGBRegressor, GradientBoosting.
-
Feature Engineering: Nghiên cứu thêm về feature engineering, tạo các đặc trưng mới từ dữ liệu hiện có để cải thiện độ chính xác.
-
Stacking/Blending: Có thể kết hợp nhiều mô hình tốt nhất (như Ridge, GradientBoosting, RandomForest) bằng kỹ thuật stacking để nâng cao hiệu năng.
-
Xử lý dữ liệu nâng cao: Áp dụng các kỹ thuật xử lý dữ liệu nâng cao như KNNImputer và Winsorization một cách hệ thống hơn để cải thiện chất lượng dữ liệu đầu vào.
Kết luận cuối cùng
Nghiên cứu đã chứng minh rằng Ridge Regression là lựa chọn tốt cho bài toán dự đoán giá nhà khi cân nhắc giữa độ chính xác, tính ổn định và khả năng chống overfitting. Mặc dù các mô hình ensemble như XGBRegressor và GradientBoosting cho độ chính xác cao hơn, nhưng chúng đòi hỏi nhiều tinh chỉnh và có nguy cơ overfitting cao hơn. Huber Regressor là lựa chọn tốt khi cần tính ổn định cao trên dữ liệu mới.
Kết quả nghiên cứu cho thấy tầm quan trọng của việc:
- Áp dụng regularization (Ridge, Lasso) để giảm overfitting
- Sử dụng Cross-Validation để đánh giá độ tổng quát của mô hình
- So sánh nhiều mô hình để chọn ra phương pháp phù hợp nhất
- Cân nhắc giữa độ chính xác và tính ổn định trong thực tế ứng dụng
Chưa có bình luận nào. Hãy là người đầu tiên!