Giải Mã Sức Mạnh Tối Ưu Hóa: Loss Functions, Vectorization và Regularization Trong Hồi Quy Tuyến Tính
Hồi quy Tuyến tính (Linear Regression) không chỉ là một phương trình đơn giản. Nó là nền tảng cho các mô hình phức tạp hơn, nơi việc lựa chọn hàm mất mát và kỹ thuật tối ưu hóa đóng vai trò then chốt. Bài viết này sẽ phân tích chi tiết các hàm mất mát nâng cao, cách mô hình mở rộng sang đa biến và kỹ thuật Chính quy hóa (Regularization) để khắc phục vấn đề vô số nghiệm và Overfitting.
I. Nền Tảng: Mô Hình Đơn Biến và Quá Trình Huấn Luyện.
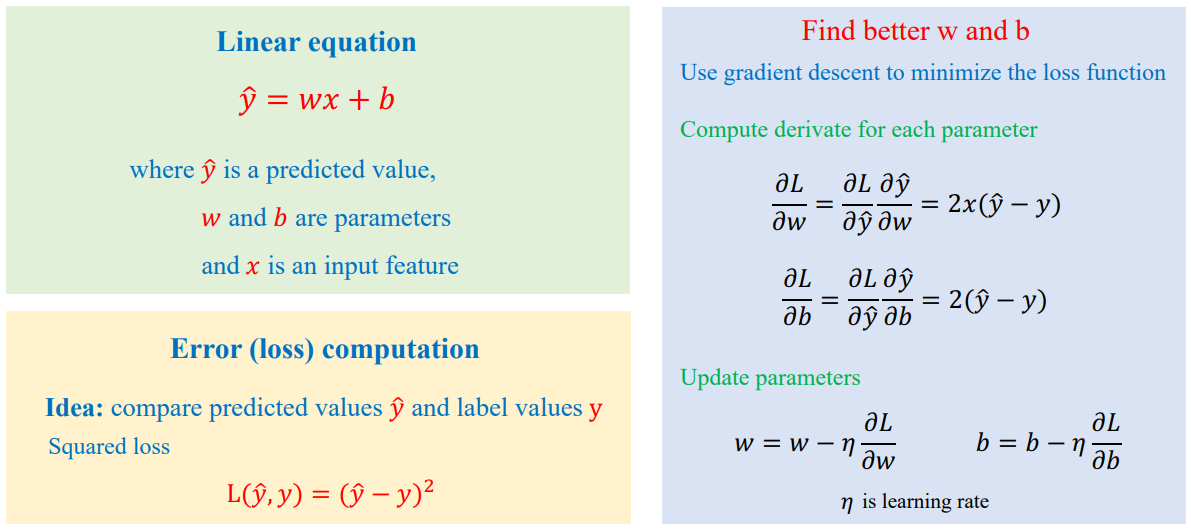
Mục tiêu cốt lõi của Hồi quy Tuyến tính là tìm ra bộ tham số (w và b) để giá trị dự đoán ($\hat{y}$) gần giá trị thực tế (y) nhất, mô tả mối quan hệ giữa x và y.
Mô hình tuyến tính cơ bản:
$$
\hat{y} = wx + b
$$
Quá trình huấn luyện sử dụng thuật toán Gradient Descent để giảm thiểu hàm mất mát:
$$ L(\hat{y}, y) $$
Quy trình lặp lại gồm 5 bước cốt lõi:
- Chọn một mẫu (x,y) từ dữ liệu huấn luyện
- Tính giá trị dự đoán $\hat{y}$
- Tính Loss L
- Tính đạo hàm của Loss theo từng tham số:
$$ \frac{\partial L}{\partial w}, \quad \frac{\partial L}{\partial b} $$
- Cập nhật tham số:
$$ w = w - \eta \frac{\partial L}{\partial w}, \quad b = b - \eta \frac{\partial L}{\partial b}, \quad \eta \text{ là tốc độ học} $$
Sơ Đồ Quy Trình Huấn Luyện
II. Phân Tích Các Hàm Mất Mát (Loss Functions)
1. Mean Squared Error (MSE) / Squared Loss
MSE là hàm mất mát phổ biến nhất, dựa trên hàm cơ sở $f(x) = x^2$ với đạo hàm $f'(x) = 2x$.
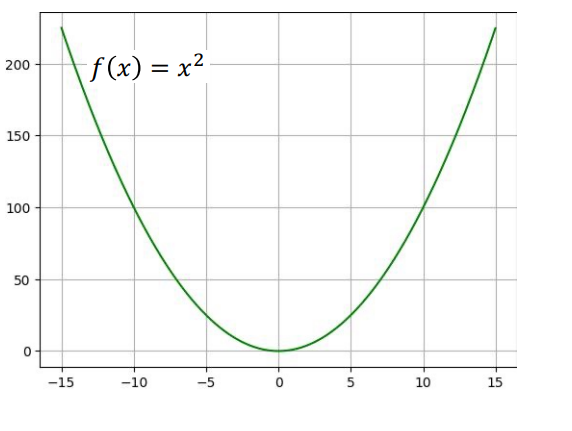
Công thức (cho 1 mẫu):
$$L(\hat{y}, y) = (\hat{y} - y)^2$$
Đạo hàm (theo w):
$$\frac{\partial L}{\partial w} = 2x(\hat{y} - y)$$
Ưu điểm & Nhược điểm:
✅ Tối ưu Vùng Bên Trong:
Khi lỗi $(\hat{y} - y)$ nhỏ (tham số gần điểm tối ưu), giá trị đạo hàm $\eta f'(x)$ sẽ giảm dần. Điều này khiến MSE rất phù hợp để tối ưu khi sử dụng tốc độ học cố định.
❌ Nhạy cảm với Outliers:
Do có phép bình phương, MSE khuếch đại sai số rất mạnh. Nếu x=10 là một outlier, $g(10) \gg f(10)$ và Loss sẽ bị phạt nặng nề (ví dụ: $10^2 = 100$). MSE không tốt hơn MAE khi tồn tại dữ liệu nhiễu, đặc biệt khi miền giá trị x lớn.
2. Mean Absolute Error (MAE) / L1 Loss
MAE dựa trên giá trị tuyệt đối, $f(x) = |x|$.

Công thức (cho 1 mẫu):
$$L(\hat{y}, y) = |\hat{y} - y|$$
Đạo hàm (theo w):
$$\frac{\partial L}{\partial w} = x \frac{|\hat{y} - y|}{(\hat{y} - y)}$$
Ưu điểm & Nhược điểm:
Chống chịu Outliers:
MAE ít nhạy cảm với dữ liệu nhiễu hơn so với MSE vì nó chỉ phạt lỗi theo giá trị tuyệt đối. MAE là lựa chọn hàng đầu khi dữ liệu có nhiều nhiễu.
Vấn đề Differentiability:
Đạo hàm của MAE (khi lỗi khác 0) luôn là hằng số ($\pm 1$). Hàm này không khả vi tại điểm sai số bằng 0 và có thể khiến thuật toán nhảy qua nhảy lại, khó hội tụ khi gần điểm tối ưu nếu sử dụng tốc độ học cố định.
3. Huber Loss: Giải Pháp Khả Vi Toàn Cục
Huber Loss được xây dựng để tận dụng ưu điểm của MSE (cho lỗi nhỏ) và MAE (cho lỗi lớn), đồng thời đảm bảo hàm số liên tục và khả vi trên toàn miền.
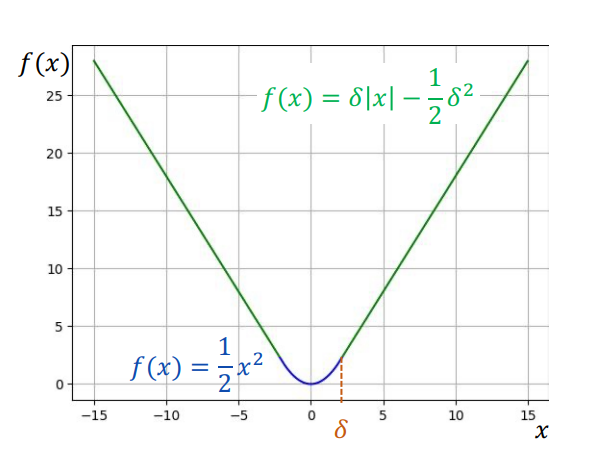
Yêu cầu Khả vi:
Để Gradient-based Optimization hoạt động hiệu quả, hàm mất mát phải liên tục và khả vi tại mọi vị trí, bao gồm điểm chuyển đổi.
Huber Loss sử dụng ngưỡng δ (delta) để chuyển đổi:
$$L(\hat{y}, y) = \begin{cases}
\frac{1}{2}(\hat{y} - y)^2 & \text{for } |\hat{y} - y| \leq \delta \\
\delta|\hat{y} - y| - \frac{1}{2}\delta^2 & \text{otherwise}
\end{cases}$$
Vai trò của δ:
- δ càng nhỏ: Huber Loss càng tiến về MAE
- δ càng lớn: Huber Loss càng tiến về MSE
Huber Loss đảm bảo tính liên tục và khả vi bằng cách điều chỉnh hệ số của nhánh tuyến tính (δ và $-\frac{1}{2}\delta^2$) sao cho đạo hàm bên trái và bên phải tại điểm δ bằng nhau.
Đạo hàm của Huber Loss:
$$\frac{\partial L}{\partial w} = \begin{cases} x(\hat{y} - y) & \text{for } |\hat{y} - y| \leq \delta \\ x \cdot \delta \cdot \text{sign}(\hat{y} - y) & \text{otherwise} \end{cases}$$
Ưu điểm của Huber Loss:
- Khả vi toàn cục: Không có điểm không khả vi như MAE
- Robust với outliers: Ít nhạy cảm với outliers hơn MSE
- Smooth optimization: Gradient descent hội tụ ổn định hơn MAE
- Flexible: Có thể điều chỉnh δ để cân bằng giữa MSE và MAE
Bảng So Sánh Loss Functions
| Loss Function | Differentiability | Robust to Outliers | Convergence | Use Case |
|---|---|---|---|---|
| MSE | ✅ Smooth everywhere | ❌ Sensitive | ✅ Fast near optimum | Clean data, small errors |
| MAE | ❌ Not differentiable at 0 | ✅ Robust | ❌ Oscillates near optimum | Noisy data, outliers |
| Huber | ✅ Smooth everywhere | ✅ Robust | ✅ Stable | Mixed data, balanced approach |
III. Mô Hình Đa Biến (Vectorization) và Chính Quy Hóa
Trong môi trường thực tế, mô hình phải xử lý nhiều features (đa biến), ví dụ như dự đoán Sales từ TV, Radio, Newspaper.
1. Vectorization và Mô Hình Đa Biến
Mô hình tuyến tính mở rộng:
$$\hat{y} = w_1 x_1 + w_2 x_2 + w_3 x_3 + b$$
Mô hình này có N features sẽ có N+1 tham số ($w_i$ và b).
Quá trình huấn luyện đòi hỏi tính đạo hàm riêng cho từng trọng số $w_i$.
Ví dụ sử dụng MSE:
$$\frac{\partial L}{\partial w_i} = 2x_i (\hat{y} - y)$$
2. Chính Quy Hóa (Regularization) - Giải Quyết Vấn Đề Vô Số Nghiệm
Khi các features đầu vào có mối quan hệ tương đồng (ví dụ: $x_2$ luôn bằng 9 lần $x_1$), mô hình có thể dẫn đến hiện tượng vô số lời giải (vô số nghiệm) cho các tham số $w_i$. Điều này là nguyên nhân chính gây ra Overfitting (ví dụ: train 99%, test 40%).
Mục tiêu: Khi có vô số nghiệm, người ta mong muốn các trọng số $w_i$ phải nhỏ.
Ridge Regression (L2 Regularization):
Để ràng buộc các trọng số, chúng ta thêm một thuật ngữ hình phạt (penalty term) vào hàm mất mát gốc (ví dụ MSE):
$$L(w_1, w_2, b) = (\hat{y} - y)^2 + \lambda(w_1^2 + w_2^2)$$
(Đây là ví dụ cho mô hình hai biến $w_1, w_2$).
Cập nhật Tham số với L2:
Thuật ngữ chính quy hóa làm thay đổi đạo hàm và do đó thay đổi cách cập nhật trọng số:
$$\frac{\partial L}{\partial w_i} = 2x_i (\hat{y} - y) + 2\lambda w_i$$
Vai trò của λ:
λ là siêu tham số kiểm soát mức độ mạnh mẽ của hình phạt.
Quy ước: Việc sử dụng $\lambda/M$ (với M là số lượng mẫu) thay vì chỉ λ trong thuật ngữ điều chuẩn giúp thành phần này không bị ảnh hưởng bởi kích thước tập dữ liệu huấn luyện, từ đó giúp quá trình tìm kiếm siêu tham số λ ổn định hơn.
L1 Regularization (Lasso):
$$L(w_1, w_2, b) = (\hat{y} - y)^2 + \lambda(|w_1| + |w_2|)$$
Đặc điểm của L1:
- Feature Selection: L1 có thể đưa một số trọng số về 0, thực hiện feature selection tự động
- Sparse solutions: Tạo ra các giải pháp thưa (sparse)
- Non-differentiable: Cần sử dụng subgradient tại điểm 0
Elastic Net:
Kết hợp cả L1 và L2:
$$L(w_1, w_2, b) = (\hat{y} - y)^2 + \lambda_1(|w_1| + |w_2|) + \lambda_2(w_1^2 + w_2^2)$$
Bảng So Sánh Regularization Methods
| Method | Formula | Feature Selection | Sparse Solution | Differentiable |
|---|---|---|---|---|
| L1 (Lasso) | $\lambda \sum |w_i|$ | ✅ Yes | ✅ Yes | ❌ No (at 0) |
| L2 (Ridge) | $\lambda \sum w_i^2$ | ❌ No | ❌ No | ✅ Yes |
| Elastic Net | $\lambda_1 \sum |w_i| + \lambda_2 \sum w_i^2$ | ✅ Yes | ✅ Yes | ❌ No (at 0) |
IV. Chuẩn Hóa Dữ Liệu và Nguy Cơ Data Leakage
Chuẩn hóa dữ liệu (Normalization) là bước quan trọng để đưa các features về cùng một phạm vi giá trị, giúp Gradient Descent hội tụ nhanh và hiệu quả hơn.
⚠️ Cảnh báo Data Leakage:
Nguyên tắc VÀNG: Tuyệt đối KHÔNG được chuẩn hóa dữ liệu trước khi chia thành tập Huấn luyện (Train) và Kiểm tra (Test).
Lý do: Công thức chuẩn hóa (thường sử dụng Min/Max) sẽ vô tình lấy thông tin của tập Test set nếu áp dụng cho toàn bộ dữ liệu trước khi chia. Điều này được gọi là Rò rỉ Dữ liệu (Data Leakage), khiến kết quả đánh giá mô hình không phản ánh đúng khả năng tổng quát hóa trên dữ liệu hoàn toàn mới.
Quy trình Chuẩn Hóa Đúng:
- Chia dữ liệu: Train/Test split trước
- Tính thống kê: Chỉ sử dụng Train set để tính mean, std
- Chuẩn hóa: Áp dụng cùng thống kê cho cả Train và Test
- Validation: Sử dụng Train set để tìm hyperparameters
Các Phương Pháp Chuẩn Hóa:
1. Standardization (Z-score normalization):
$$x_{norm} = \frac{x - \mu}{\sigma}$$
Trong đó:
- $\mu$: mean của feature
- $\sigma$: standard deviation của feature
2. Min-Max Scaling:
$$x_{norm} = \frac{x - x_{min}}{x_{max} - x_{min}}$$
3. Robust Scaling:
$$x_{norm} = \frac{x - \text{median}}{IQR}$$
Trong đó IQR là Interquartile Range.
V. So Sánh Hiệu Suất Các Loss Functions
Khi Nào Sử Dụng Loss Function Nào:
MSE - Mean Squared Error:
- Khi nào: Dữ liệu sạch, ít outliers, cần hội tụ nhanh
- Ưu điểm: Smooth, differentiable, fast convergence
- Nhược điểm: Sensitive to outliers
MAE - Mean Absolute Error:
- Khi nào: Dữ liệu nhiều outliers, cần robust estimation
- Ưu điểm: Robust, less sensitive to outliers
- Nhược điểm: Non-differentiable at 0, slow convergence
Huber Loss:
- Khi nào: Dữ liệu mixed, cần balance giữa MSE và MAE
- Ưu điểm: Best of both worlds, smooth optimization
- Nhược điểm: Cần tune hyperparameter δ
VI. Advanced Topics: Subgradient và Optimization
Subgradient cho MAE:
Khi $|\hat{y} - y| = 0$, MAE không khả vi. Chúng ta sử dụng subgradient:
$$\frac{\partial L}{\partial w} = x \cdot \text{sign}(\hat{y} - y)$$
Trong đó:
$$\text{sign}(x) = \begin{cases}
1 & \text{if } x > 0 \\
0 & \text{if } x = 0 \\
-1 & \text{if } x < 0
\end{cases}$$
Convergence Analysis:
MSE Convergence:
- Rate: $O(1/t)$ với t là số iterations
- Condition: Learning rate $\eta < \frac{1}{L}$ với L là Lipschitz constant
MAE Convergence:
- Rate: $O(1/\sqrt{t})$ (slower than MSE)
- Condition: Subgradient method cần learning rate schedule
Huber Convergence:
- Rate: $O(1/t)$ (similar to MSE)
- Condition: $\eta < \frac{1}{L}$ với L phụ thuộc vào δ
VII. Practical Implementation Guidelines
1. Loss Function Selection:
if data_has_outliers:
if need_differentiable:
USE Huber Loss
else:
USE MAE
else:
USE MSE
2. Regularization Strategy:
if features_correlated:
if need_feature_selection:
USE L1 (Lasso)
else:
USE L2 (Ridge)
else:
USE Elastic Net
3. Hyperparameter Tuning:
Huber Loss δ:
- Start with: δ = 1.0
- Range: [0.1, 10.0]
- Method: Grid search hoặc Bayesian optimization
Regularization λ:
- Start with: λ = 0.01
- Range: [0.001, 1.0]
- Method: Cross-validation
VIII. Kết luận & Lời khuyên thực tiễn
Điểm mấu chốt:
- Lựa chọn hàm mất mát: Phụ thuộc vào đặc tính dữ liệu và mục tiêu tối ưu hóa
- Chính quy hóa(Regularization): Cần thiết để tránh overfitting và xử lý tình trạng đa cộng tuyến
- Tiền xử lý dữ liệu: Chuẩn hóa đúng quy trình để tránh rò rỉ dữ liệu
- Tối ưu siêu tham số: Áp dụng quy trình bài bản để tìm bộ tham số tối ưu
Lời khuyên thực tiễn
- Theo dõi hội tụ để phát hiện sớm các vấn đề tối ưu hóa
- Dùng chính quy hóa khi số lượng đặc trưng lớn hoặc có tương quan cao
- Ngăn rò rỉ dữ liệu trong toàn bộ quy trình tiền xử lý
- Ghi chép siêu tham số và lý do lựa chọn để dễ tái lập kết quả
Refernces
[1] Ảnh được lấy từ tài liệu khóa học AIO Module 05 Tuần 2 AIO 2025
Tags: machine-learning, linear-regression, loss-functions, regularization, optimization, gradient-descent, data-preprocessing, mathematical-optimization, statistical-learning, feature-engineering
Chưa có bình luận nào. Hãy là người đầu tiên!