Giới thiệu về Mean Squared Error (MSE)
Mean Squared Error (MSE - Sai số toàn phương trung bình) là một trong những hàm mất mát phổ biến nhất trong các bài toán hồi quy. Nó đo lường sự khác biệt giữa giá trị dự đoán ($`\hat{y}`$) và giá trị thực tế ($`y`$) bằng cách lấy trung bình của bình phương các sai số.
Công thức cho một mẫu dữ liệu:
$$
L_{MSE} = (\hat{y} - y)^2
$$
Trong đó $`\hat{y} = wx + b`$.
Mục tiêu của việc huấn luyện mô hình là tìm ra các tham số $`w`$ và $`b`$ để tối thiểu hóa hàm mất mát này. Để làm điều đó, chúng ta sử dụng thuật toán Gradient Descent, yêu cầu tính toán đạo hàm của hàm mất mát theo từng tham số.
Đạo hàm của MSE
Sử dụng quy tắc chuỗi (chain rule), ta có:
$$
\frac{\partial L}{\partial w} = \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial w} = 2(\hat{y} - y) \cdot x
$$
$$
\frac{\partial L}{\partial b} = \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial b} = 2(\hat{y} - y) \cdot 1
$$
Minh họa bằng hình ảnh
Hàm mất mát MSE có dạng một đường cong Parabol, với điểm cực tiểu toàn cục là nơi sai số bằng 0.
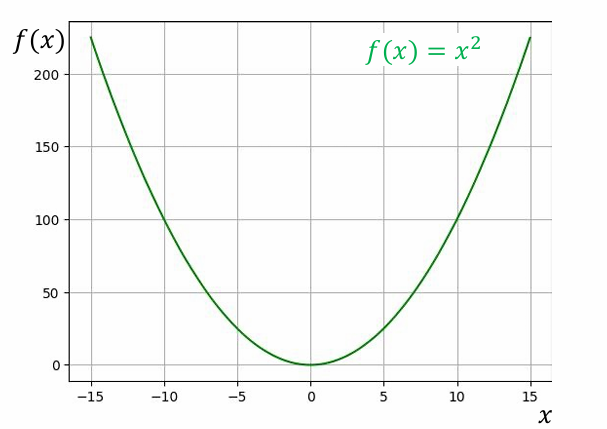
Đồ thị của hàm mất mát MSE
Ví dụ về mã nguồn
Dưới đây là đoạn code Python minh họa cách tính MSE và đạo hàm của nó.
def predict(x, w, b):
return w * x + b
def mse_loss(y_hat, y):
return (y_hat - y)**2
def mse_gradient(x, y_hat, y):
# Dao ham theo w
dl_dw = 2 * x * (y_hat - y)
# Dao ham theo b
dl_db = 2 * (y_hat - y)
return dl_dw, dl_db
# Du lieu mau
x_sample, y_sample = 6.7, 9.1
w_init, b_init = -0.34, 0.04
# Tinh toan
y_pred = predict(x_sample, w_init, b_init)
loss = mse_loss(y_pred, y_sample)
dw, db = mse_gradient(x_sample, y_pred, y_sample)
print(f"Du doan: {y_pred:.2f}")
print(f"Mat mat MSE: {loss:.2f}")
print(f"Dao ham theo w: {dw:.2f}, Dao ham theo b: {db:.2f}")
Giới thiệu về Mean Absolute Error (MAE)
Mean Absolute Error (MAE - Sai số tuyệt đối trung bình) là một hàm mất
mát khác, đo lường sai số bằng cách lấy trung bình của giá trị tuyệt đối
của các sai số.
Công thức cho một mẫu dữ liệu:
$$
L_{MAE} = |\hat{y} - y|
$$
MAE ít nhạy cảm với các điểm dữ liệu ngoại lai (outliers) hơn so với MSE.
Đạo hàm của MAE
Đạo hàm của hàm giá trị tuyệt đối là hàm dấu (sign function):
$$
\frac{\partial L}{\partial w} = x \cdot \text{sign}(\hat{y} - y)
$$
$$
\frac{\partial L}{\partial b} = \text{sign}(\hat{y} - y)
$$
Trong đó, $`\text{sign}(z)`$ là 1 nếu $`z > 0`$, -1 nếu $`z < 0`$, và không xác định tại $`z=0`$. Trong thực tế, ta có thể quy ước giá trị tại 0 là 0 hoặc bỏ qua.
Minh họa bằng hình ảnh
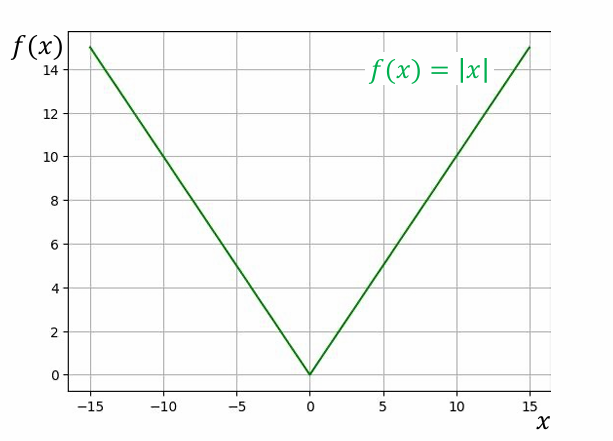
Đồ thị của hàm mất mát MAE
Ví dụ về mã nguồn
import numpy as np
def mae_loss(y_hat, y):
return abs(y_hat - y)
def mae_gradient(x, y_hat, y):
# Dao ham theo w
dl_dw = x * np.sign(y_hat - y)
# Dao ham theo b
dl_db = np.sign(y_hat - y)
return dl_dw, dl_db
# Su dung lai du lieu mau
y_pred = predict(x_sample, w_init, b_init)
loss_mae = mae_loss(y_pred, y_sample)
dw_mae, db_mae = mae_gradient(x_sample, y_pred, y_sample)
print(f"Du doan: {y_pred:.2f}")
print(f"Mat mat MAE: {loss_mae:.2f}")
print(f"Dao ham theo w: {dw_mae:.2f}, Dao ham theo b: {db_mae:.2f}")
So sánh MSE và MAE
-
Độ nhạy với Outlier: MSE bình phương sai số, nên các lỗi lớn (thường do outlier) bị trừng phạt nặng hơn nhiều so với MAE. Điều này làm cho MAE mạnh mẽ hơn (robust) khi dữ liệu có outlier.
-
Tính ổn định của Gradient: Gradient của MSE giảm dần khi tiến gần đến điểm cực tiểu, giúp cho việc hội tụ mượt mà hơn. Ngược lại, gradient của MAE có độ lớn không đổi, có thể gây ra hiện tượng "vượt qua" điểm tối ưu nếu tốc độ học (learning rate) không được điều chỉnh cẩn thận.
-
Tính duy nhất của điểm cực tiểu: Hàm MSE là hàm lồi và có đạo hàm mượt, đảm bảo có một điểm cực tiểu duy nhất. MAE cũng lồi nhưng không có đạo hàm trơn tru tại điểm 0.
Ví dụ trực quan về Outlier
Hãy xem xét một tập dữ liệu nhỏ với một điểm ngoại lai (outlier).
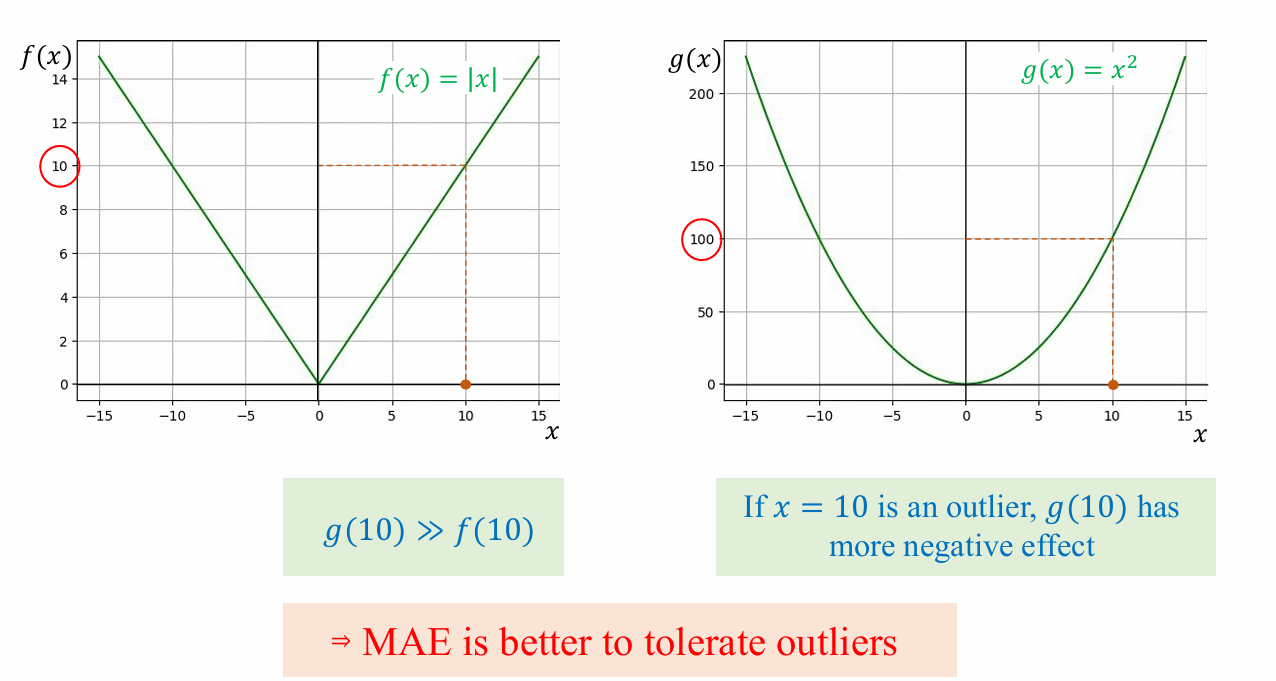
So sánh 2 hàm loss khi có outliers
Do MSE trừng phạt các lỗi lớn một cách nặng nề, đường hồi quy sẽ cố gắng "dịch chuyển" về phía điểm ngoại lai để giảm thiểu sai số bình phương khổng lồ đó. Ngược lại, MAE chỉ tính giá trị tuyệt đối, nên đường hồi quy ít bị ảnh hưởng hơn.
import numpy as np
import matplotlib.pyplot as plt
y_true = np.array([2, 3, 4, 5, 6])
y_pred = np.array([2.1, 3.2, 3.9, 5.3, 6.1])
y_true_outlier = np.array([2, 3, 4, 5, 20])
y_pred_outlier = np.array([2.1, 3.2, 3.9, 5.3, 6.1])
mse_normal = np.mean((y_pred - y_true)**2)
mae_normal = np.mean(np.abs(y_pred - y_true))
mse_outlier = np.mean((y_pred_outlier - y_true_outlier)**2)
mae_outlier = np.mean(np.abs(y_pred_outlier - y_true_outlier))
print(f"--- Without Outlier ---")
print(f"MSE: {mse_normal:.2f}, MAE: {mae_normal:.2f}")
print(f"\n--- Outlier ---")
print(f"MSE: {mse_outlier:.2f}")
print(f"MAE: {mae_outlier:.2f}")
labels = ['MSE', 'MAE']
no_outlier_losses = [mse_normal, mae_normal]
with_outlier_losses = [mse_outlier, mae_outlier]
x = np.arange(len(labels))
width = 0.35
fig, ax = plt.subplots(figsize=(10, 6))
rects1 = ax.bar(x - width/2, no_outlier_losses, width, label='Without Outlier', color='skyblue')
rects2 = ax.bar(x + width/2, with_outlier_losses, width, label=' Outlier', color='salmon')
ax.set_ylabel('(Loss)')
ax.set_title(' MSE and MAE', fontsize=16, pad=20)
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
ax.bar_label(rects1, padding=3, fmt='%.2f')
ax.bar_label(rects2, padding=3, fmt='%.2f')
fig.tight_layout()
plt.show()
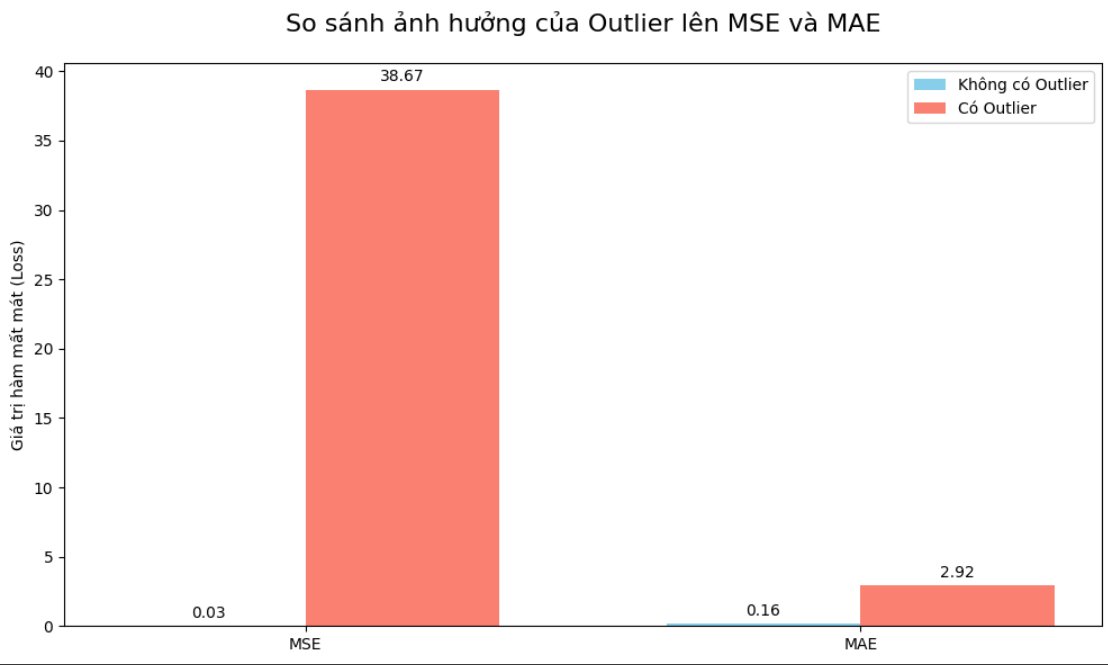
Có và không có outliers
Hàm Huber Loss
Huber Loss là một hàm mất mát kết hợp những ưu điểm của cả MSE và MAE.Nó hoạt động giống như MSE khi sai số nhỏ và giống như MAE khi sai số lớn.
Công thức của Huber Loss:
$$
L_{\delta}(y, \hat{y}) =
\begin{cases}
\frac{1}{2}(y - \hat{y})^2 & \text{cho } |y - \hat{y}| \le \delta \\
\delta |y - \hat{y}| - \frac{1}{2}\delta^2 & \text{còn lại}
\end{cases}
$$
Tham số $`\delta`$ là một siêu tham số (hyperparameter) quyết định ngưỡng chuyển đổi giữa hai chế độ.
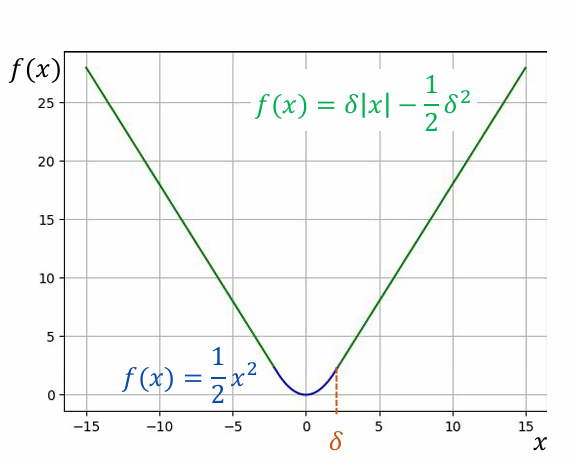
Một dạng của huber loss
Chuẩn hóa (Normalization) và Chính quy hóa (Regularization)
Chuẩn hóa Dữ liệu (Data Normalization/Scaling)
Chuẩn hóa dữ liệu là quá trình đưa tất cả các đặc trưng về một thang đo tương tự nhau. Điều này làm cho bề mặt hàm mất mát trở nên đối xứng hơn (gần với hình tròn), giúp Gradient Descent hội tụ nhanh hơn và ổn định hơn.
Có hai phương pháp chuẩn hóa phổ biến:
Min-Max Scaling
Phương pháp này đưa tất cả các giá trị về một khoảng xác định, thường là [0, 1].
$$
x' = \frac{x - x_{min}}{x_{max} - x_{min}}
$$
Nó hữu ích khi chúng ta biết chắc chắn về giới hạn trên và dưới của dữ liệu. Tuy nhiên, nó khá nhạy cảm với các điểm ngoại lai (outliers).
Standardization (Z-score Normalization)
Phương pháp này biến đổi dữ liệu sao cho nó có giá trị trung bình (mean) là 0 và độ lệch chuẩn (standard deviation) là 1.
$$
x' = \frac{x - \mu}{\sigma}
$$
Trong đó $`\mu`$ là trung bình và $`\sigma`$ là độ lệch chuẩn của đặc trưng. Phương pháp này ít bị ảnh hưởng bởi outlier hơn Min-Max Scaling và thường được ưa chuộng hơn trong nhiều thuật toán Machine Learning.
import numpy as np
data = np.array([10, 20, 30, 40, 100]) # Co mot outlier la 100
# Min-Max Scaling
min_val = np.min(data)
max_val = np.max(data)
min_max_scaled = (data - min_val) / (max_val - min_val)
# Standardization
mean_val = np.mean(data)
std_val = np.std(data)
standardized = (data - mean_val) / std_val
print("Du lieu goc:", data)
print("Sau Min-Max Scaling:", np.round(min_max_scaled, 2))
print("Sau Standardization:", np.round(standardized, 2))
Chính quy hóa (Regularization)
Chính quy hóa là một tập hợp các kỹ thuật được sử dụng để chống lại hiện tượng overfitting (mô hình quá khớp). Overfitting xảy ra khi mô hình học thuộc lòng cả những chi tiết và nhiễu trong dữ liệu huấn luyện, thay vì học quy luật tổng quát. Kết quả là mô hình hoạt động rất tốt trên dữ liệu huấn luyện nhưng lại kém hiệu quả trên dữ liệu mới.
Chính quy hóa hoạt động bằng cách thêm một "thành phần phạt" (penalty term) vào hàm mất mát. Thành phần này phạt các mô hình phức tạp (thường là các mô hình có trọng số $`w`$ lớn). Điều này buộc mô hình phải giữ các trọng số ở mức nhỏ, tạo ra một mô hình đơn giản hơn và có khả năng tổng quát hóa tốt hơn. Đây là một cách để quản lý sự đánh đổi giữa độ chệch và phương sai (bias-variance tradeoff).
L2 Regularization (Ridge Regression)
Đây là phương pháp chính quy hóa phổ biến nhất. Nó thêm vào hàm mất mát tổng bình phương của các trọng số.
$$
L_{Ridge} = \text{Loss}_{Original} + \lambda \sum_{i=1}^{n} w_i^2
$$
Trong đó $`\lambda`$ (lambda) là siêu tham số chính quy hóa, kiểm soát mức độ phạt.
-
Khi $`\lambda = 0`$, không có chính quy hóa.
-
Khi $`\lambda`$ tăng, các trọng số sẽ bị "kéo" về gần 0 hơn.
Đạo hàm theo $`w_i`$ cũng được cập nhật:
$$
\frac{\partial L}{\partial w_i} = \frac{\partial L_{Original}}{\partial w_i} + 2\lambda w_i
$$
L2 có xu hướng làm cho các trọng số nhỏ một cách đồng đều nhưng hiếm khi bằng 0.
L1 Regularization (Lasso Regression)
L1 thêm vào hàm mất mát tổng giá trị tuyệt đối của các trọng số.
$$
L_{Lasso} = \text{Loss}_{Original} + \lambda \sum_{i=1}^{n} |w_i|
$$
Một đặc điểm quan trọng của L1 là nó có thể làm cho một số trọng số bằng chính xác 0. Điều này có nghĩa là L1 có thể thực hiện lựa chọn đặc trưng (feature selection), loại bỏ các đặc trưng không quan trọng ra khỏi mô hình.
Ví dụ về mã nguồn
Đoạn code dưới đây minh họa cách bước cập nhật trọng số thay đổi khi có L2 regularization.
# Thong so
learning_rate = 0.01
lambda_val = 0.1
w = 2.0 # Trong so ban dau
# Du lieu
x, y = 1.5, 2.5
# Tinh toan gradient cho MSE
y_hat = w * x
gradient_mse = 2 * x * (y_hat - y)
# Tinh toan gradient cho L2
gradient_l2 = 2 * lambda_val * w
# Tong gradient
total_gradient = gradient_mse + gradient_l2
# Cap nhat trong so
w_updated = w - learning_rate * total_gradient
print(f"Gradient tu MSE: {gradient_mse:.2f}")
print(f"Gradient tu L2: {gradient_l2:.2f}")
print(f"Trong so w truoc khi cap nhat: {w:.2f}")
print(f"Trong so w sau khi cap nhat: {w_updated:.4f}")
Chưa có bình luận nào. Hãy là người đầu tiên!