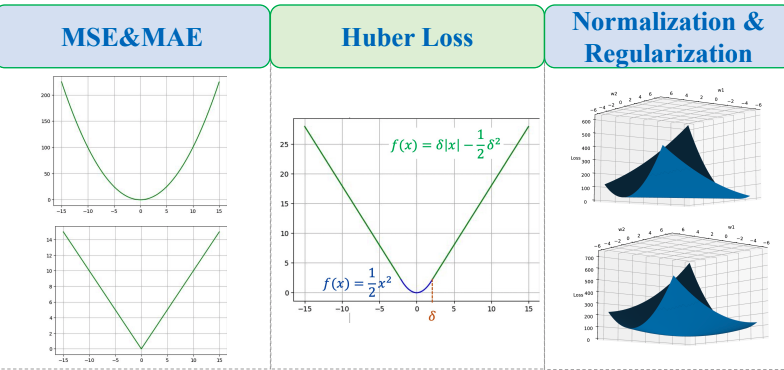
1. Tổng quan về Loss Function
Loss function hay còn gọi là hàm mất mát, thể hiện một mối quan hệ giữa $\hat{y}$ (là kết quả dự đoán của model) và $y$ (là giá trị thực tế). Loss function trả về một số thực không âm. Loss function giống như một cơ chế phạt (giá trị hàm Loss) model mỗi khi dự đoán sai; mức phạt tỉ lệ thuận với độ nghiêm trọng của sai sót. Trong mọi bài toán supervised learning, mục tiêu của ta là giảm thiểu tổng mức phạt phải đóng. Ở trường hợp lý tưởng, khi $\hat{y} = y$, loss function đạt giá trị cực tiểu bằng $0$.
Loss function kí hiệu là $L$ là thành phần cốt lõi của evaluation function và objective function. Cụ thể, trong công thức thường gặp:
$$
\mathcal{L}_D(f_w)=\frac{1}{|D|}\sum_{(x,y)\in D} L\big(f_w(x),\,y\big)
$$
-- hàm $L$ chính là loss function.
| Ký hiệu | Ý nghĩa | Mô tả chi tiết |
|---|---|---|
| $\mathcal{L}_D(f_w)$ | Giá trị trung bình của hàm mất mát (Loss tổng) | Giá trị mất mát trung bình trên toàn bộ tập dữ liệu D. |
| $D$ | Tập dữ liệu huấn luyện | Bao gồm các cặp $(x, y)$. |
| $\|D\|$ | Kích thước của tập dữ liệu | Số mẫu trong $D$. |
| $f_w(x)$ | Giá trị dự đoán của mô hình | Kết quả mô hình dự đoán cho đầu vào $x$. |
| $L(f_w(x),\,y$ | Hàm mất mát (Loss function) | Đo độ sai lệch giữa dự đoán và giá trị thật. |
1.1. Hai dạng bài supervised learning cơ bản
Ta phân chia các dạng bài supervised learning dựa vào tính chất của $y$. Để đơn giản, ta xét các bài toán mà $y$ có thể biểu diễn được bằng một con số.
Khi $y$ là một số thực dao động trong khoảng $(-\infty, \infty)$, ta được một bài toán regression. Ví dụ như ta cần tiên đoán giá cổ phiếu, giá xăng, giá vàng vào ngày mai.
Khi $y$ là một đại lượng rời rạc chỉ nhận giá trị trong một tập label hữu hạn rời rạc nào đó, ta được bài toán classification. Ví dụ, khi ta cần nhận dạng tên một người từ một tấm ảnh chân dung, cho dù có hàng tỉ cái tên trên thế giới thì tập hợp này vẫn là rời rạc hữu hạn. Vì thế, bài toán này vẫn được quy vào dạng classification.
1.2. Xây dựng hàm Loss Function:
Vì loss function đo đạc chênh lệch giữa $\hat{y}$ và $y$, nên không lạ gì nếu ta nghĩ ngay đến việc lấy hiệu giữa chúng:
$$ L(\hat{y}, y) = \hat{y} - y $$
Tuy nhiên hàm này lại không thỏa mãn tính chất không âm của một loss function. Ta có thể sửa nó lại một chút để thỏa mãn tính chất này. Ví dụ như lấy giá trị tuyệt đối của hiệu:
$$ L(\hat{y}, y) = |\hat{y} - y| $$
Loss function này không âm nhưng lại không thuận tiện trong việc cực tiểu hóa, bởi vì đạo hàm của nó không liên tục (nhớ là đạo hàm của $f(x) = |x|$ bị đứt quãng tại $x = 0$)
và thường các phương pháp cực tiểu hóa hàm số thông dụng đòi hỏi phải tính được đạo hàm. Một cách khác đó là lấy bình phương của hiệu:
$$ L(\hat{y}, y) = \frac{1}{2} (\hat{y} - y)^2 $$
Khi tính đạo hàm theo $\hat{y}$, ta được
$$
\nabla L = \frac{1}{2} \times 2 \times (\hat{y} - y) = \hat{y} - y
$$
Có thể thấy rằng hằng số $\frac{1}{2}$ được thêm vào chỉ để cho công thức đạo hàm được đẹp hơn, không có hằng số phụ. Loss function này được gọi là square loss. Square loss có thể được sử dụng cho cả regression và classification, nhưng thực tế thì nó thường được dùng cho regression hơn.
Đối với binary classification, ta có một cách tiếp cận khác để xây dựng loss function. Nhắc lại là đối với dạng bài này, thì nếu model trả về $\hat{y} < 0$ tức là thích đáp án -1 hơn, trả về $\hat{y} \ge 0$ tức là thích đáp án +1 hơn.
Một cách rất tự nhiên, ta thấy rằng loss function của binary classification cần phải đạt được một số tiêu chí sau:
-
Phải phạt mô hình nhiều hơn khi dự đoán sai:
- Khi mô hình dự đoán sai dấu (tức $y$ và $\hat{y}$ trái dấu), hàm mất mát cần trả về giá trị lớn.
- Ngược lại, khi mô hình dự đoán đúng dấu (tức $y$ và $\hat{y}$ cùng dấu), loss nên trả về giá trị nhỏ.
- Mục tiêu: mô hình càng sai → phạt càng nặng (tăng Loss).
-
Càng “tự tin” đúng thì càng được thưởng, càng “tự tin” sai thì phạt nặng hơn:
- Giá trị tuyệt đối $|\hat{y}|$ biểu thị mức độ tự tin của mô hình với dự đoán đó.
- $|\hat{y}|$ lớn → mô hình rất chắc chắn với kết quả mình chọn.
- $|\hat{y}|$ nhỏ → mô hình còn lưỡng lự.
- Nếu $y$ và $\hat{y}$ cùng dấu → mô hình dự đoán đúng, nên khi $|\hat{y}|$ càng lớn thì loss càng nhỏ (được thưởng nhiều hơn).
- Nếu $y$ và $\hat{y}$ trái dấu → mô hình dự đoán sai, mà $|\hat{y}|$ càng lớn thì nghĩa là mô hình càng tự tin sai, nên cần phạt nặng hơn để nó học lại.
- Giá trị tuyệt đối $|\hat{y}|$ biểu thị mức độ tự tin của mô hình với dự đoán đó.
Một cách tổng quát, đối với binary classification thì các loss function thường có dạng như sau:
$$ L(\hat{y}, y) = f(y \cdot \hat{y}) $$
trong đó $f$ là một hàm không âm và không tăng.
2. Các loại Loss Function phổ biến trong Linear Regression
Việc lựa chọn Loss Function đóng vai trò trung tâm trong huấn luyện mô hình Linear Regression và các bài toán Deep Learning. Loss function giúp mô hình đo lường mức độ sai lệch giữa giá trị dự đoán $\hat{y}$ và giá trị thực tế $y$, từ đó điều chỉnh trọng số để giảm sai số qua từng vòng lặp huấn luyện.
Ký hiệu chung
- $y$: giá trị thực tế
- $\hat{y}$: giá trị dự đoán
- $r = \hat{y} − y $: sai số (residual)
- $y$: số lượng mẫu dữ liệu
2.1. Mean Squared Error (MSE)
2.1.1. Khái niệm - MSE là gì? Tại sao ta cần nó?
Mean Squared Error (MSE) là loại loss function phổ biến nhất trong Linear Regression. Nó xuất hiện trong mọi mô hình hồi quy, mọi slide giảng dạy - và được gọi vui là “loss function đầu đời”.
MSE đo sai số trung bình bình phương giữa giá trị dự đoán và giá trị thực tế.
$$ MSE = \frac{1}{N}\sum_{i=1}^{N} (ŷᵢ - yᵢ)^2 $$
Giả sử bạn muốn dạy một mô hình dự đoán giá nhà.
Bạn đưa vào 3 căn nhà, và mô hình trả lời như sau:
| Nhà | Giá thật (triệu) | Dự đoán (triệu) | Sai số |
|---|---|---|---|
| 1 | 500 | 480 | -20 |
| 2 | 800 | 820 | +20 |
| 3 | 1000 | 1200 | +200 |
Bây giờ bạn muốn biết: “Mô hình của tôi sai trung bình bao nhiêu?”
- Vấn đề là nếu chỉ cộng các sai số lại, số dương và âm triệt tiêu nhau. Vì vậy ta bình phương chúng — để mọi sai số đều trở thành dương, và phạt mạnh lỗi lớn hơn lỗi nhỏ.
- Trong ví dụ trên, MSE ≈ 13600 — con số này không có ý nghĩa trực tiếp (vì đơn vị bị bình phương), nhưng nó giúp ta so sánh các mô hình với nhau: MSE càng nhỏ → mô hình càng chính xác.
Insight:
MSE không chỉ “đếm lỗi”, mà còn phóng đại lỗi lớn — điều này vừa là ưu điểm khi tối ưu, vừa là nhược điểm khi đánh giá.
2.1.2. Nhược điểm của MSE - MSE tệ khi đánh giá
Hãy nhớ:
MSE đo bình phương lỗi trung bình — tức là nó phạt lỗi lớn cực kỳ mạnh.
Nếu một điểm dữ liệu bị dự đoán lệch gấp 10 lần, MSE sẽ coi nó nghiêm trọng gấp $10^2 = 100$ lần!
Những “tật xấu” của MSE khi đánh giá
| Nhược điểm | Giải thích |
|---|---|
| Đơn vị sai lệch | Nếu dữ liệu là “triệu USD”, MSE lại ra “triệu² USD²” — không ai hiểu nổi mô hình “sai bao nhiêu tiền”. |
| Nhạy với outlier | Một vài điểm ngoại lai có thể “bóp méo” toàn bộ kết quả. |
| Khó diễn giải | Người đọc muốn biết “trung bình mô hình sai bao nhiêu”, nhưng MSE không cho ta cảm giác đó. |
Vì vậy, nhiều người chọn đối thủ dễ chịu hơn:
- MAE (Mean Absolute Error):
$$ \text{MAE} = \frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y}_i| $$ - hoặc MAD (Mean Absolute Deviation) — khái niệm tương tự MAE, nhưng dùng để mô tả độ lệch của dữ liệu khỏi trung bình.
Minh họa: MSE bị kéo bởi outlier
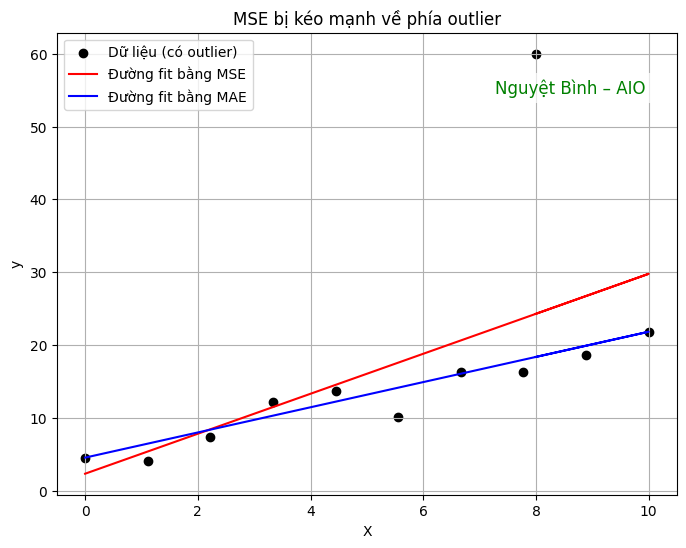
Khi có một điểm dữ liệu quá xa (outlier), MSE sẽ cố gắng giảm lỗi cho điểm đó,
dẫn đến đường hồi quy bị “nghiêng” về phía outlier — mô hình tổng thể trở nên kém chính xác hơn.
Kết luận: MSE bình phương sai số, do đó phạt nặng các điểm dữ liệu có sai số lớn (outlier)
2.1.3. Ưu điểm của MSE - MSE "lên ngôi" khi tối ưu
Sở hữu những nhược điểm như trên, vậy tại sao MSE vẫn là “đứa con cưng” của machine learning?
Bởi vì:
MSE không “thông minh” — mà nó “ngoan ngoãn với toán học.”
Khi huấn luyện, ta cần đạo hàm để biết hướng giảm lỗi. Lúc này, MSE cho kết quả cực kỳ gọn gàng:
$$
\frac{\partial \text{MSE}}{\partial \hat{y}_i} = -\frac{2}{n}(y_i - \hat{y}_i)
$$
Đạo hàm của MSE mượt mà và liên tục, không có trị tuyệt đối hay điểm gấp khúc như MAE, nên gradient descent đi theo hướng giảm lỗi ổn định và dễ hội tụ.

Kết luận: Hàm loss mượt và khả vi toàn miền, giúp việc tối ưu bằng Gradient Descent diễn ra ổn định và nhanh chóng.
Trong Deep Learning, MSE được sử dụng phổ biến cho các bài toán hồi quy liên tục (continuous regression) — ví dụ: dự đoán giá nhà, nhiệt độ, hoặc giá cổ phiếu.
2.1.4. Liên hệ với xác suất thống kê
Nếu giả định nhiễu trong dữ liệu tuân theo phân phối chuẩn (Gaussian), thì việc cực đại hóa xác suất (Maximum Likelihood Estimation) sẽ tương đương với tối thiểu hóa MSE.
Khi đó, mô hình học giá trị trung bình có điều kiện (conditional mean) của biến mục tiêu.
2.1.5. Đạo hàm (cho mô hình tuyến tính)
Vào đầu thế kỷ 19, hai nhà toán học Legendre và Gauss lần đầu sử dụng bình phương sai số để mô tả mô hình hồi quy tuyến tính.
Không phải vì họ “nghĩ nó đúng hơn”, mà vì dễ tính hơn.
Từ đó đến nay, MSE trở thành chuẩn mực — không phải vì hoàn hảo,
mà vì nó là sự thỏa hiệp hoàn hảo giữa toán học và thực dụng.
Cách MSE “dạy” mô hình học
Giả sử ta có mô hình tuyến tính đơn giản:
$$
\hat{y}_i = w x_i + b
$$
Ở mỗi vòng lặp (iteration), mô hình cập nhật trọng số theo hướng giảm MSE:
$$ \begin{aligned} w_{\text{new}} &= w_{\text{old}} - \eta \frac{\partial \text{MSE}}{\partial w} \\ b_{\text{new}} &= b_{\text{old}} - \eta \frac{\partial \text{MSE}}{\partial b} \end{aligned} $$
với $\eta$ là learning rate (tốc độ học).
Ta có thể tính các đạo hàm:
$$
\begin{aligned}
\frac{\partial \text{MSE}}{\partial w} &= -\frac{2}{n}\sum_{i=1}^{n} x_i (y_i - \hat{y}_i) \\
\frac{\partial \text{MSE}}{\partial b} &= -\frac{2}{n}\sum_{i=1}^{n} (y_i - \hat{y}_i)
\end{aligned}
$$
Gradient của MSE cho bạn biết hướng tăng lỗi. Để giảm MSE, mô hình đi ngược hướng gradient. Qua mỗi vòng lặp, trọng số $w$ và $b$ di chuyển một chút → đường dự đoán dần khớp dữ liệu thật.
Mini code block Python/NumPy để minh hoạ MSE giảm dần:
import numpy as np
# Dữ liệu đơn giản
X = np.array([1, 2, 3])
y = np.array([2, 4, 6])
w, b = 0.0, 0.0
lr = 0.1 # learning rate
for epoch in range(10):
y_pred = w * X + b
mse = np.mean((y - y_pred) ** 2)
dw = -2 * np.mean(X * (y - y_pred))
db = -2 * np.mean(y - y_pred)
w -= lr * dw
b -= lr * db
print(f"Epoch {epoch+1}: MSE={mse:.3f}")
Output mô phỏng:
Epoch 1: MSE=18.667
Epoch 2: MSE=0.296
Epoch 3: MSE=0.073
Epoch 4: MSE=0.067
Epoch 5: MSE=0.064
Epoch 6: MSE=0.061
Epoch 7: MSE=0.058
Epoch 8: MSE=0.055
Epoch 9: MSE=0.053
Epoch 10: MSE=0.050
2.1.6. Kết Luận
Qua câu chuyện về MSE, ta rút ra vài điểm chính:
- MSE phóng đại lỗi lớn, điều này vừa giúp mô hình học nhanh khi tối ưu, vừa gây nhạy cảm với outlier khi đánh giá.
- Khi đánh giá mô hình, metric khác như MAE hoặc MAD có thể trực quan hơn.
- Khi huấn luyện, MSE vẫn là sự lựa chọn kinh điển vì tính toán gọn, đạo hàm mượt, gradient descent dễ hội tụ.
- Gradient của MSE cho mô hình biết hướng giảm lỗi, giúp đường dự đoán dần khớp với dữ liệu thật.
Notice:
MSE không phải luôn hoàn hảo, nhưng là minh chứng cho sự thỏa hiệp giữa toán học và thực dụng — dễ hiểu, dễ tính, và vẫn hữu ích trong hầu hết các bài toán hồi quy.
Fun fact:Khoảng năm 1801, nhà toán học Carl Friedrich Gauss đã sử dụng phương pháp này để dự đoán quỹ đạo của tiểu hành tinh Ceres - và ông đoán chính xác đến mức giới khoa học lúc đó ngỡ ngàng.
2.2. Mean Absolute Error (MAE)
2.2.1. Khái niệm
Mean Absolute Error (MAE) đo sai số trung bình tuyệt đối giữa giá trị dự đoán và thực tế.
Không giống MSE, MAE không bình phương sai số, nên mọi sai lệch được tính công bằng.
$$ MAE = \frac{1}{N}\sum_{i=1}^{N} |ŷᵢ - yᵢ| $$
2.2.2 Trực giác và ý nghĩa
Ưu điểm:
- Đơn giản, dễ hiểu và dễ tính toán.
- Không bị ảnh hưởng mạnh bởi outlier, giúp mô hình ổn định hơn khi dữ liệu chứa nhiễu.
Nhược điểm:
-
Không phân biệt mức độ nghiêm trọng của sai số:
MAE coi mọi sai số đều như nhau, trong khi một số ứng dụng cần phạt nặng sai số lớn (ví dụ trong y tế hoặc dự báo an toàn). -
Không khả vi tại điểm 0:
Do hàm giá trị tuyệt đối $|x|$ có “góc nhọn” tại $x = 0$, đạo hàm của MAE không tồn tại tại điểm sai số bằng 0, gây khó khăn khi tối ưu bằng Gradient Descent truyền thống. -
Giải pháp:
- Sử dụng subgradient (đạo hàm mở rộng) hoặc hàm xấp xỉ trơn như Huber Loss để thay thế.
- Ví dụ: Huber Loss hoạt động như MSE với sai số nhỏ và như MAE với sai số lớn — giúp khả vi và ổn định hơn khi huấn luyện.
2.2.3. Cách tính MAE
Bước 1:
Tính sai số tuyệt đối cho từng điểm dữ liệu:
$|y_i - \hat{y}_i|$
Bước 2:
Cộng tất cả các sai số tuyệt đối.
Bước 3:
Chia tổng sai số cho số lượng mẫu $n$ để thu được giá trị MAE trung bình.
Ví dụ minh họa:
| Giá trị thực tế $y$ | Dự đoán ($\hat{y}$) | Sai số tuyệt đối |
|---|---|---|
| 5 | 4.5 | 0.5 |
| 7 | 6.2 | 0.8 |
| 3 | 2.5 | 0.5 |
$$ MAE = \frac{0.5 + 0.8 + 0.5}{3} = 0.6 $$
Tính bằng Python (sklearn):
from sklearn.metrics import mean_absolute_error
y_true = [5, 7, 3]
y_pred = [4.5, 6.2, 2.5]
mae = mean_absolute_error(y_true, y_pred)
print("MAE:", mae)
2.3. Huber Loss (Smooth L1)
2.3.1. Khái niệm
Huber Loss kết hợp ưu điểm của MSE và MAE,sử dụng siêu tham số δ để xác định khi nào dùng MSE và khi nào dùng MAE:
Lý do tạo ra:
| Hàm mất mát | Ưu điểm | Nhược điểm |
|---|---|---|
| MAE | Ít bị ảnh hưởng bởi outlier | Không có đạo hàm tại mọi điểm → khó tối ưu |
| MSE | Có đạo hàm mượt → hội tụ tốt | Rất nhạy với outlier do bình phương sai số |
Công thức:
$$ L(\hat{y}, y) = \begin{cases} \frac{1}{2}(\hat{y} - y)^2 & \text{for } |\hat{y} - y| \le \delta \\ \delta |\hat{y} - y| - \frac{1}{2}\delta^2 & \text{otherwise} \end{cases} $$
Trong đó:
- $\delta$ (delta) là một siêu tham số (hyperparameter) mà bạn có thể điều chỉnh.
Cách hoạt động:
Huber Loss sẽ đặt ra 1 ngưỡng delta sau đó so sánh sai số với delta:
- Lớn hơn: hoạt động giống MAE (trị tuyệt đối để tránh outlier ảnh hưởng quá mạnh).
- Nhỏ hơn: hoạt động giống MSE (bình phương, mượt để tối ưu).
2.3.2. Đặc điểm và ứng dụng
- Huber Loss mượt quanh 0, nên dễ tối ưu bằng gradient descent.
- Giới hạn ảnh hưởng của outlier khi sai số lớn hơn δ.
- Trong thư viện
scikit-learn,HuberRegressorsử dụng tham sốepsilon(≈ δ) để điều chỉnh độ nhạy.
Trong Deep Learning, Huber còn được gọi là Smooth L1 Loss, thường thấy trong các mô hình như YOLO, Faster R-CNN để giảm tác động của các lỗi quá lớn khi huấn luyện.
2.3.3. Ví dụ minh họa
Với δ = 1:
| Sai số $r$ | Huber Loss |
|---|---|
| 0.5 | 0.125 |
| 2 | 1.5 |
Huber hoạt động như MSE khi sai số nhỏ và như MAE khi sai số lớn — giúp mô hình cân bằng giữa độ chính xác và tính ổn định.
2.4. Log-Cosh Loss (Đọc thêm)
Log-Cosh Loss là một lựa chọn thay thế mềm mại hơn cho MSE và MAE:
$$ LogCosh = \frac{1}{N}\sum_{i=1}^{N} \log(\cosh(ŷᵢ - yᵢ)) $$
-
Khi $r$ nhỏ: $\log(\cosh(r)) \approx \tfrac{1}{2}r^2$ (giống MSE)
-
Khi $r$ lớn: $\log(\cosh(r)) \approx |r| - \log(2)$ (giống MAE)
Log-Cosh mượt toàn miền và ít bị outlier ảnh hưởng, nhưng hiếm khi cần thiết trong các bài toán cơ bản.
2.5. So sánh tổng hợp
| Tiêu chí | MSE | MAE | Huber Loss | Log-Cosh |
|---|---|---|---|---|
| Độ trơn | Mượt toàn miền | Không khả vi tại 0 | Mượt quanh 0, tuyến tính xa 0 | Mượt toàn miền |
| Nhạy cảm outlier | Cao | Thấp | Trung bình | Thấp |
| Giả định nhiễu | Gaussian | Laplace | Trung gian | Gần Gaussian |
| Mục tiêu thống kê | Mean | Median | Mean–Median | Mean (mượt) |
| Khi nên dùng | Dữ liệu sạch | Có nhiều outlier | Có nhiễu vừa phải | Cần mượt & ổn định |
2.6. Ví dụ minh họa so sánh
Giả sử y = 100:
| $\hat{y}$ | Sai số $r$ | MSE | MAE | Huber ($\delta = 1$) | Log-Cosh |
|---|---|---|---|---|---|
| 102 | +2 | 4 | 2 | 1.5 | ≈1.32 |
| 90 | −10 | 100 | 10 | 9.5 | ≈8.6 |
Khi sai số lớn, MSE tăng rất mạnh trong khi các hàm khác tăng chậm hơn — minh họa khả năng chống outlier của MAE, Huber, và Log-Cosh.
2.7. Minh họa đồ thị Loss Function
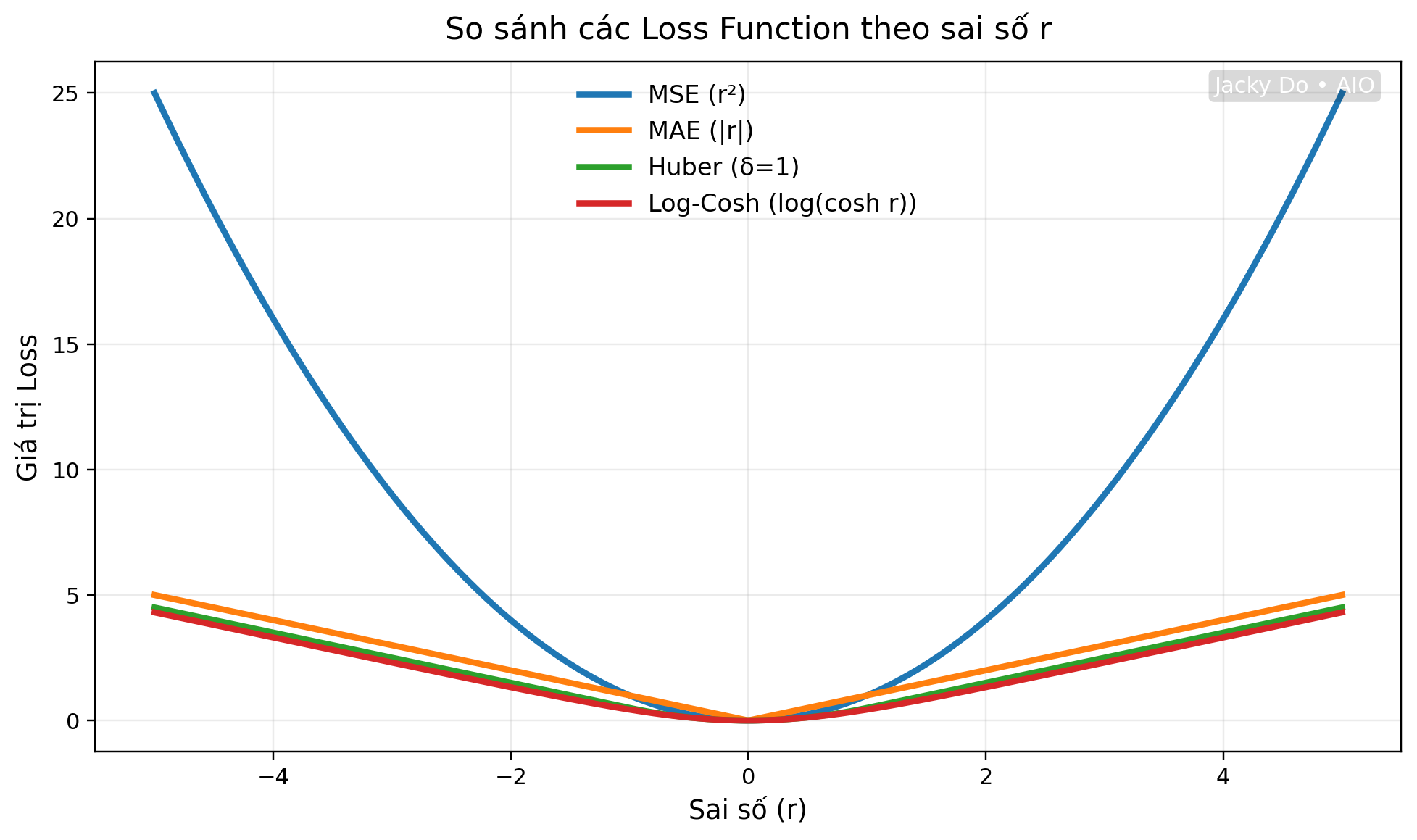
Hình ở trên thể hiện mối quan hệ giữa giá trị sai số $r$ (trục hoành) và giá trị $loss$ (trục tung) của 4 hàm phổ biến:
- MSE: đường cong parabol tăng nhanh
- MAE: đường thẳng hình chữ V
- Huber: kết hợp giữa parabol và tuyến tính
- Log-Cosh: cong mượt nằm giữa MSE và MAE
2.8. Kết luận
- MSE: phù hợp cho dữ liệu sạch, gradient mượt, hội tụ nhanh.
- MAE: phù hợp khi có outlier, phản ánh độ sai lệch trung bình thực tế.
- Huber: cân bằng giữa MSE và MAE, mượt mà và ổn định.
- Log-Cosh: mượt toàn miền, ít bị ảnh hưởng bởi nhiễu, thường dùng trong một số mô hình Deep Learning.
3. Mối Liên Hệ Giữa L1 và L2 Regularization
Như ở phần trên đã trình bày, trong trường hợp Overfiting, hàm Loss sẽ cố gắng giảm lỗi trên tập huấn luyện, Loss càng nhỏ càng tốt (trên train dataset).
Để làm được điều đó, đôi khi mô hình sẽ:
-
“Phóng đại” ảnh hưởng của một số đặc trưng lên kết quả, tức là cho các trọng số $𝑤_i$ có giá trị rất lớn (dương hoặc âm). Hậu quả của điều này là mô hình nhớ dữ liệu huấn luyện quá kỹ, khiến cho khi gặp dữ liệu mới (chưa thấy bao giờ), dự đoán bị rối và không ổn định. Biểu hiện thường thấy là sai số trên train dataset nhỏ nhưng sai số trên validation/test dataset rất lớn.
-
Cả L1 (Lasso) và L2 (Ridge) Regularization là hai kỹ thuật cơ bản trong Machine Learning, dùng để giải quyết vấn đề Overfitting bằng cách thêm một khoản chi phí (penalty term) vào hàm mất mát (loss function) của mô hình.
3.1. Mối Liên Hệ Chung (Mục Đích)
- Mối liên hệ cơ bản nhất là chúng đều sửa đổi hàm mất mát gốc theo cùng một công thức:
$$\text{Loss}_{\text{Mới}} = \text{Loss}_{\text{Gốc}} + \lambda \cdot (\text{Chi phí Regularization})$$
-
Loss Gốc: Là hàm mất mát thông thường (ví dụ: MSE - Mean Squared Error trong hồi quy).
-
Chi phí Regularization: Là hình phạt dựa trên độ lớn của các hệ số $w$ (trọng số) của mô hình.
-
$\lambda$ (Lambda): Là hệ số điều chỉnh (Hyperparameter), kiểm soát mức độ mạnh mẽ của hình phạt.
-
Mục tiêu chung: Ngăn các hệ số (weights) trở nên quá lớn, từ đó làm cho mô hình tổng quát hóa tốt hơn với dữ liệu chưa từng thấy.
3.2. Sự Khác Biệt Cốt Lõi (Công thức và Tác dụng)
Sự khác biệt giữa L1 và L2 nằm ở cách chúng tính chi phí hình phạt, dẫn đến các hậu quả khác nhau đối với các hệ số của mô hình.
3.2.1. L2 Regularization (Ridge)
L2 Regularization tính chi phí dựa trên tổng bình phương của các hệ số:
$$\text{Loss L2} = \lambda \sum_{j=1}^{p} w_j^2$$
| Đặc điểm L2 | Giải thích |
|---|---|
| Tác dụng chính | Thu nhỏ (Shrinkage). L2 buộc tất cả các hệ số phải thu nhỏ về gần 0. |
| Lựa chọn đặc trưng | Không. L2 giữ lại tất cả các đặc trưng (hệ số gần 0 nhưng hiếm khi bằng 0 tuyệt đối). |
| Minh họa Hình học | Vùng giới hạn là hình tròn (hoặc siêu cầu). |
3.2.2. L1 Regularization (Lasso)
L1 Regularization tính chi phí dựa trên tổng giá trị tuyệt đối (chuẩn L1) của các hệ số:
$$\text{Loss L1} = \lambda \sum_{j=1}^{p} |w_j|$$
| Đặc điểm L1 | Giải thích |
|---|---|
| Tác dụng chính | Sự thưa thớt (Sparsity). L1 có xu hướng đẩy một số hệ số về 0 tuyệt đối. |
| Lựa chọn đặc trưng | Có. L1 tự động loại bỏ các đặc trưng ít quan trọng bằng cách đặt hệ số của chúng bằng 0 (Feature Selection). |
| Minh họa Hình học | Vùng giới hạn là hình thoi (hoặc hình vuông/bát diện). |
3.3. Giải thích Hình học (Visualizing the Constraint)
Sự khác biệt rõ rệt nhất giữa L1 và L2 nằm ở hình học của chúng, nơi hàm mất mát gốc (thường được biểu diễn bằng các đường đồng mức hình elip) gặp vùng giới hạn (constraint region) của Regularization. Điểm tiếp xúc chính là nghiệm tối ưu của mô hình.
Hình học L1 (Vùng giới hạn hình thoi)
-
Vùng giới hạn L1 là một hình thoi (hoặc hình vuông/bát diện trong 2D/3D).
-
Hình thoi có các góc nhọn nằm trên các trục tọa độ.
-
Đường contour của hàm mất mát rất dễ tiếp xúc với vùng giới hạn này tại một trong các góc nhọn (ví dụ: góc nằm trên trục $w_1$ hoặc $w_2$).
-
Khi điểm tiếp xúc xảy ra ở góc, giá trị của hệ số tương ứng với trục còn lại sẽ bằng 0 tuyệt đối, qua đó thực hiện chức năng lựa chọn đặc trưng (Feature Selection).
3.4. Sự Kết Hợp: Elastic Net
Mối liên hệ giữa L1 và L2 được củng cố bằng sự tồn tại của Elastic Net, một kỹ thuật kết hợp cả hai hình phạt để tận dụng ưu điểm của cả hai:
$$\text{Loss}_{\text{Elastic Net}} = \text{Loss}_{\text{Gốc}} + \lambda_1 \sum_{j=1}^{p} |w_j| + \lambda_2 \sum_{j=1}^{p} w_j^2$$
Elastic Net có khả năng:
-
Thu nhỏ các hệ số (nhờ L2).
-
Thực hiện lựa chọn đặc trưng bằng cách đặt một số hệ số bằng 0 (nhờ L1).
-
Hoạt động tốt hơn L1 khi có các đặc trưng tương quan cao (correlated features).
Khi so sánh hiệu quả giữa hai phương pháp regularization L1 và L2, có thể nhận thấy rằng mỗi phương pháp đều mang lại những ưu điểm và hạn chế riêng trong việc xử lý và tối ưu hóa mô hình. L1 (Lasso) thường được ưa chuộng trong các bài toán cần giảm thiểu số lượng biến, trong khi L2 (Ridge) thường cho phép giữ lại tất cả các biến nhưng với trọng số nhỏ hơn.
3.5. So sánh hiệu quả giữa L1 và L2
-
L1 tạo ra các mô hình thưa thớt, loại bỏ các biến không quan trọng. L2 giữ lại tất cả các biến, giúp cải thiện độ ổn định của mô hình. L1 có khả năng chọn biến tốt hơn trong những trường hợp có nhiều biến tương quan. L2 thường hoạt động hiệu quả hơn khi các biến có tương quan cao. L1 có thể tạo ra các mô hình đơn giản hơn nhờ vào việc loại bỏ hoàn toàn các biến không cần thiết. Việc lựa chọn giữa L1 và L2 phụ thuộc vào mục tiêu cụ thể và tính chất của dữ liệu trong mô hình.
-
Trong thực tế, việc áp dụng L1 và L2 regularization rất phổ biến trong nhiều lĩnh vực khác nhau, từ tài chính đến y tế và công nghệ thông tin. L1 regularization, hay còn gọi là Lasso, thường được sử dụng trong các bài toán phân loại và hồi quy khi cần lựa chọn biến, nhờ tính chất làm giảm bớt số lượng yếu tố đầu vào mà vẫn giữ được hiệu suất mô hình. Điều này đặc biệt hữu ích trong các lĩnh vực như phân tích tài chính, nơi chỉ một số ít yếu tố có thể ảnh hưởng đến kết quả. Ví dụ: Một công ty bảo hiểm muốn dự đoán chi phí bồi thường từ hàng trăm yếu tố, trong trường hợp này áp dụng L1 Regularization có thể giúp giảm 40% số biến (features), tăng độ chính xác dự đoán.
-
Ngược lại, L2 regularization, hay còn gọi là Ridge, thường được ưa chuộng trong các mô hình yêu cầu độ chính xác cao và ổn định hơn, như trong các bài toán dự đoán trong y tế. L2 giúp giảm thiểu hiện tượng đa cộng tuyến và cải thiện khả năng tổng quát của mô hình bằng cách phân bổ trọng số đều hơn cho các biến.
4. Tối ưu hóa hàm Loss trong bài toán Hồi quy Tuyến tính
Tối ưu hoá hàm loss trong bài toán hồi quy tuyến tính (linear regression) chủ yếu tập trung vào việc cải thiện độ chính xác của mô hình và giảm sai số dự đoán. Các phương pháp tối ưu hoá trong linear regression thường liên quan đến việc tối ưu hoá hàm loss function (thường là Mean Squared Error - MSE). Dưới đây là một số cách cụ thể để tối ưu hoá hàm loss trong hồi quy tuyến tính:
4.1 Sử dụng Gradient Descent
Đây là một trong những kỹ thuật tối ưu hóa phổ biến để tìm các tham số (trọng số) sao cho hàm loss đạt giá trị thấp nhất.
- Batch Gradient Descent:
Cập nhật trọng số sau khi tính toán gradient của toàn bộ tập huấn luyện. Tuy nhiên, cách này có thể tốn thời gian khi dữ liệu lớn. Công thức cập nhật trong Batch Gradient Descent:
$$ \theta = \theta - \eta \nabla_\theta J(\theta) $$
- Stochastic Gradient Descent (SGD):
Cập nhật trọng số theo từng mẫu (sample). Công thức cập nhật trong SGD:
$$ \theta = \theta - \eta \nabla_\theta J(\theta; x^{(i)}, y^{(i)}) $$
Mặc dù cách này có thể khá nhiễu, nhưng nó giúp cải thiện hiệu suất tính toán khi làm việc với tập dữ liệu lớn.
- Mini-Batch Gradient Descent:
Kết hợp giữa SGD và Batch Gradient Descent. Thay vì sử dụng toàn bộ dữ liệu như trong BGD, hoặc chỉ dùng một mẫu như trong SGD, Mini-Batch sử dụng một nhóm con nhỏ các mẫu dữ liệu (ví dụ 32, 64, 128 mẫu mỗi nhóm) tại mỗi bước. Ưu điểm của Mini-Batch Gradient Descent là tăng tốc huấn luyện so với BGD vì không phải tính toán trên toàn bộ dữ liệu, ổn định hơn SGD vì không có dao động lớn giữa các cập nhật và các phép toán trên mini-batch có thể tận dụng hiệu quả các GPU.
4.2 Tuning Learning Rate
Learning rate là một tham số quan trọng trong tối ưu hóa. Nếu learning rate quá nhỏ, việc tối ưu hóa sẽ rất chậm. Nếu quá lớn, mô hình có thể không hội tụ hoặc thậm chí sẽ không ổn định.
-
Learning Rate Scheduling:
Điều chỉnh learning rate theo thời gian để giúp quá trình huấn luyện trở nên hiệu quả hơn. -
Adaptive Learning Rates:
Sử dụng các thuật toán tối ưu như Adam hay RMSprop để tự động điều chỉnh learning rate trong suốt quá trình huấn luyện.
4.3 Regularization
Regularization là một cách để tránh overfitting trong mô hình hồi quy tuyến tính. Nếu chỉ sử dụng MSE mà không có regularization, mô hình có thể học được các trọng số rất lớn hoặc không phù hợp với dữ liệu, dẫn đến overfitting.
- L2 Regularization (Ridge Regression):
Thêm một yếu tố vào hàm loss tỷ lệ với bình phương của trọng số để giảm các trọng số quá lớn. Công thức hàm loss trở thành:
$$ \text{Loss} = \text{MSE} + \lambda \sum_{i=1}^{n} w_i^2 $$
Trong đó, $\lambda$ là hệ số regularization, giúp điều chỉnh mức độ regularization.
- L1 Regularization (Lasso Regression):
Thêm một yếu tố vào hàm loss tỷ lệ với giá trị tuyệt đối của trọng số. Điều này có thể dẫn đến việc một số trọng số trở thành 0, giúp thực hiện feature selection.
$$ \text{Loss} = \text{MSE} + \lambda \sum_{i=1}^{n} |w_i| $$
- Elastic Net:
Kết hợp cả L1 và L2 regularization, tạo ra một sự kết hợp tốt giữa Ridge và Lasso.
4.4 Feature Scaling
Để tối ưu hóa hàm loss hiệu quả, các đặc trưng đầu vào cần được chuẩn hóa hoặc chuẩn hóa (scaling). Nếu các đặc trưng có giá trị quá khác biệt về độ lớn, gradient sẽ không được tính đồng đều, gây khó khăn cho việc tối ưu hóa.
-
Standardization (Chuẩn hóa):
Thay đổi các giá trị đặc trưng sao cho chúng có giá trị trung bình là 0 và độ lệch chuẩn là 1. -
Normalization (Chuẩn hóa theo tỉ lệ):
Chuyển các giá trị về khoảng [0, 1] hoặc [-1, 1] bằng cách trừ đi giá trị tối thiểu và chia cho khoảng giá trị.
Lợi ích: Giúp gradient descent hội tụ nhanh hơn và hiệu quả hơn.
4.5 Tối ưu hóa Hệ số Regularization (Lambda)
Đối với Ridge và Lasso, bạn cần chọn giá trị tối ưu cho hệ số regularization $\lambda$. Điều này có thể được thực hiện thông qua:
-
Cross-validation:
Chia dữ liệu thành các phần và kiểm tra giá trị của $\lambda$ cho từng phần. Lựa chọn giá trị $\lambda$ tạo ra mô hình có hiệu suất tốt nhất trên dữ liệu kiểm tra. -
Grid Search:
Thử nhiều giá trị khác nhau của $\lambda$ để tìm giá trị tối ưu.
Lợi ích: Giúp cân bằng giữa bias và variance.
4.6 Dữ liệu và Outliers
Kiểm tra và xử lý dữ liệu không hợp lệ (outliers) cũng rất quan trọng trong hồi quy tuyến tính:
-
Loại bỏ outliers:
Những điểm dữ liệu xa rời khỏi phần lớn các điểm còn lại có thể làm sai lệch các tham số hồi quy, gây ra giá trị hàm loss không chính xác. -
Chuyển đổi log:
Đôi khi áp dụng log transformation cho các biến có sự phân phối không chuẩn (skewed distribution) có thể giúp cải thiện hiệu suất mô hình.
5. Kết luận
Qua toàn bộ nội dung, ta có thể tóm tắt ngắn gọn như sau:
- Loss Function là trái tim của mọi mô hình học có giám sát (supervised learning), giúp định lượng “mức độ sai” giữa dự đoán và thực tế, từ đó hướng dẫn mô hình học tốt hơn qua từng vòng tối ưu.
- Việc lựa chọn đúng hàm Loss ảnh hưởng trực tiếp đến hiệu quả huấn luyện:
- MSE phù hợp khi dữ liệu sạch, gradient mượt, hội tụ nhanh.
- MAE bền vững với outlier, phản ánh sai số trung bình thực tế.
- Huber cân bằng giữa MSE và MAE, vừa ổn định vừa khả vi.
- Log-Cosh mượt toàn miền, dùng khi cần tính ổn định cao.
- Các kỹ thuật Regularization (L1, L2, Elastic Net) bổ sung thêm “hình phạt” vào Loss để tránh overfitting, giúp mô hình tổng quát hóa tốt hơn.
- Quá trình tối ưu hóa hàm Loss (bằng Gradient Descent và các biến thể) chính là quá trình “dạy” mô hình học từ sai số — điều chỉnh trọng số từng chút một để tiệm cận giá trị tối ưu.
💡 Tóm lại:
Loss Function không chỉ đo lường sai số, mà còn là “bản đồ dẫn đường” cho toàn bộ quá trình huấn luyện mô hình.
Hiểu rõ bản chất và lựa chọn đúng hàm Loss chính là bước đầu tiên để làm chủ mọi thuật toán học máy.
Chưa có bình luận nào. Hãy là người đầu tiên!