1. Linear Regression And Loss Funcion
Linear Regression — mô hình đơn giản nhất trong Machine Learning, nhưng lại chứa đựng triết lý sâu sắc nhất: làm thế nào để máy móc học được từ sai lầm?
1.1. Mô hình tuyến tính
- Giả định : quan hệ giữa đầu vào và đầu ra xấp xỉ tuyến tính..

Mục tiêu là tìm tham số w, b (hoặc vector θ) sao cho mô hình dự đoán gần sát giá trị thật nhất theo một thước đo lỗi (loss function).
1.2. Loss Function — Hàm quan trọng như thế nào?
Loss Function là trái tim của học có giám sát: nó định nghĩa “thế nào là tốt/xấu”. Chọn loss khác nhau sẽ dẫn đến hành vi tối ưu khác nhau, đặc biệt khi dữ liệu có nhiễu/outlier.
- Tối ưu: tìm
$$\theta^* = \arg\min_{\theta} \mathcal{L}(y, \hat{y}(X;\theta))$$ -
Tối ưu hóa dựa trên gradient: cần loss khả vi (hoặc gần-khả-vi) để cập nhật theo hướng giảm dốc.
-
Tối ưu hóa tiến hóa (Genetic Algorithsm ): xem loss như “độ thích nghi”, không cần đạo hàm, phù hợp bề mặt lỗi gập ghềnh/không trơn.
2. Gradient-based Optimization
Ý tưởng cốt lõi của Gradient Descent (GD): xuất phát từ tham số khởi tạo, lặp lại bước đi ngắn theo hướng Ngược với đạo hàm để hạ loss:
- Cập nhật: $\theta \leftarrow \theta - \eta \nabla_{\theta} \mathcal{L}$
- $\eta$ là learning rate (quá lớn dễ “nổ”, quá nhỏ hội tụ chậm).
- Kỹ thuật hữu ích: chuẩn hóa đặc trưng, clipping gradient, early stopping.
2.1 MSE (Mean Squared Error)
Công thức: $\mathrm{MSE} = \frac{1}{n}\sum_i (y_i - \hat{y}_i)^2$
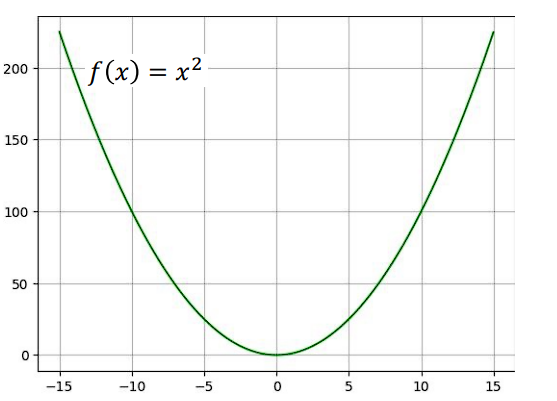
Tính chất:
- Trơn, khả vi khắp nơi, nhạy với outliers (vì bình phương phóng đại sai lệch lớn).
- Phù hợp khi nhiễu Gaussian
Gradient (đơn biến):
$$\frac{\partial \mathcal{L}}{\partial w} = -\frac{2}{n}\sum (y -\hat{y})x,\quad\frac{\partial \mathcal{L}}{\partial b} = -\frac{2}{n}\sum (y -\hat{y}$$
2.2 MAE (Mean Absolute Error)
Công thức : $\mathrm{MAE} = \frac{1}{n}\sum_i |y_i - \hat{y}_i|$
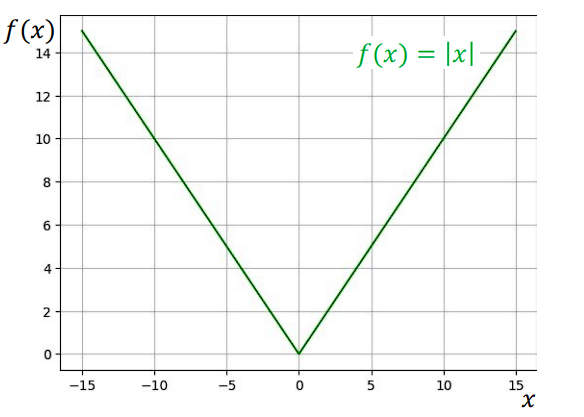
Tính chất:
- Không bình phương sai số → ít nhạy với outliers hơn MSE.
- Không khả vi tại 0, vì giá trị tuyệt đối có “góc nhọn”.
Gradient dựa trên dấu sai số:
$$
\frac{\partial \mathcal{L}}{\partial \hat{y}_i} =
\begin{cases}
-1, & y_i - \hat{y}_i > 0 \\
1, & y_i - \hat{y}_i < 0 \\
0, & y_i - \hat{y}_i = 0
\end{cases}
$$
2.3 Huber Loss
Ý tưởng: kết hợp ưu điểm của MSE (trơn gần 0) và MAE (bền vững xa 0).
Công thức với ngưỡng :
$$\text{Let } e = y - \hat{y}. \\
L_{\delta}(e) =
\begin{cases}
\tfrac{1}{2} e^2, & |e| \le \delta,\\[6pt]
\delta\big(|e| - \tfrac{1}{2}\delta\big), & |e| > \delta.
\end{cases}$$
Gradient theo $\hat{y}$ :
$$
\frac{\partial L_{\delta}}{\partial \hat{y}} =
\begin{cases}
-\,e, & |e| \le \delta,\\[4pt]
-\,\delta\,\operatorname{sign}(e), & |e| > \delta,
\end{cases}
\quad\text{với } e=y-\hat{y}.
$$
2.4 Khi nào nên dùng các hàm Loss
| Hàm Loss | Khi nào nên dùng |
|---|---|
| MSE (Mean Squared Error) | Khi dữ liệu sạch, nhiễu phân phối chuẩn (Gaussian), không có outlier lớn. |
| MAE (Mean Absolute Error) | Khi dữ liệu có nhiều outliers, muốn mô hình bền vững hơn với sai số lớn. |
| Huber Loss | Khi nghi ngờ có outliers nhưng vẫn muốn gradient mượt để hội tụ ổn định. |
3. Evolutionary Optimization
3.1. Ý tưởng cốt lõi và ưu/nhược điểm của GA
Genetic Algorithm (GA) là thuật toán tìm kiếm toàn cục mô phỏng quá trình tiến hóa tự nhiên, gồm các giai đoạn:
population → selection → crossover → mutation → elitism.
GA không cần đạo hàm, chỉ yêu cầu một hàm đánh giá (fitness) cho mỗi cá thể θ.
Các thành phần chính
- Fitness:$f(θ)=L(y,y^(X;θ))f(\theta) = \mathcal{L}(y, \hat{y}(X; \theta))f(θ)=L(y,y^(X;θ))$ — càng thấp càng tốt.
- Selection: Ưu tiên cá thể có fitness tốt hơn để lai ghép.
- Crossover:Trộn tham số giữa “bố mẹ” để tạo “con” mới.
- Mutation:Biến dị nhỏ để khám phá thêm không gian tham số.
- Elitism: Giữ lại một số cá thể tốt nhất qua thế hệ để tránh mất nghiệm tốt.
Ưu điểm và Nhược điểm
| Ưu điểm | Nhược điểm |
|---|---|
| - Không cần gradient. - Hoạt động tốt với loss không trơn (MAE, Quantile, v.v.). - Ít nhạy với khởi tạo ban đầu. - Khám phá không gian nghiệm tốt (tránh local minima). | - Chậm hơn Gradient Descent. - Cần tinh chỉnh hyperparameter (population size, mutation rate, số thế hệ). |
Độ phức tạp tính toán:
-
Population size: P
-
Số thế hệ: G
-
Số chiều tham số: d
Chi phí xấp xỉ:
$$O(P×G×d)$$
3.2. GA cho MSE, MAE, Huber
Trong project này, Genetic Algorithm (GA) được áp dụng cho ba hàm loss nhằm tối ưu tham số θ\thetaθ:
3.3. Kết luận về GA
GA là bộ tối ưu độc lập (black-box):$θ∈Θminf(θ)$
Chỉ cần một hàm fitness $f(θ)$; không yêu cầu gradient hay tính lồi/trơn.
→ Có thể áp dụng GA cho mọi dạng bài toán:
$$minθ∈Θf(θ)\min_{\theta \in \Theta} f(\theta)$$
từ loss khả vi / không khả vi đến bài toán rời rạc / tổ hợp.
- Cách dùng trong thực tế:
- Dùng GA thuần cho mục tiêu khó đạo hàm hoặc có nhiều cực trị.
- Dùng Hybrid (GA → GD/Adam) để tận dụng khả năng tìm nghiệm toàn cục của GA và tốc độ hội tụ của Gradient Descent.
Trong project:
GA được áp dụng cho MSE / MAE / Huber, và biến thể Hybrid GA→GD cho kết quả ổn định nhất khi dữ liệu có outliers.
4. So sánh hai phương pháp
| Khía cạnh | Gradient Descent (GD) | Genetic Algorithm (GA) |
|---|---|---|
| Yêu cầu đạo hàm | Cần đạo hàm hoặc gần-khả-vi | Không cần đạo hàm |
| Tốc độ hội tụ | Nhanh (tìm kiếm cục bộ – local search) | Chậm hơn (tìm kiếm toàn cục – global search) |
| Nhạy khởi tạo | Nhạy cảm với điểm bắt đầu | Ít nhạy hơn |
| Outliers / Loss không trơn | Nhạy cảm (MSE); Huber/MAE cải thiện phần nào | Xử lý tự nhiên, không cần gradient |
| Bề mặt nhiều local minima | Dễ mắc kẹt | Khám phá tốt hơn, có khả năng thoát bẫy cục bộ |
| Tính lồi của hàm mất mát | Tận dụng tốt khi loss lồi / “đẹp”; cần điểm khởi tạo tốt | Không yêu cầu lồi; hoạt động kiểu black-box |
| Khả năng song song hóa | Trung bình (song song theo batch) | Cao – mỗi cá thể đánh giá độc lập |
Nhận xét
-
Gradient Descent (GD): nhanh, hiệu quả khi loss trơn và khả vi, phù hợp các bài toán học có cấu trúc rõ ràng.
-
Genetic Algorithm (GA): mạnh ở tìm kiếm toàn cục, đặc biệt khi loss phi tuyến, nhiều bẫy cục bộ hoặc khó đạo hàm.
👉 Kết hợp (Hybrid GA + GD) thường mang lại kết quả tối ưu:
GA giúp tìm khởi tạo tốt, GD tiếp tục tinh chỉnh chính xác và nhanh chóng.
5. Hybrid Genetic Algorithsm + Gradient Descent — optimized
Kết hợp “tìm đường” toàn cục của Genetic Algorithsm với “chạy nhanh” cục bộ của Gradient Descent
- Genetic Algorithsm: tìm điểm khởi tạo tốt θ_GA ở vùng tiềm năng.
- Gradient Descent: fine-tune từ θ_GA để đạt cực trị gần nhất với tốc độ cao.

Lợi ích:
- Tránh local minima nhờ GA, đồng thời giữ tốc độ mượt mà của GD.
- Ổn định hơn trước outliers (chọn Huber/MAE) mà vẫn tối ưu mượt.
- Thực nghiệm thường cho kết quả tốt hoặc rất tốt mà ít chi phí tinh >chỉnh hơn so với chỉ dùng một phương pháp
5.1 Hybrid với MSE, MAE, Huber
Trong project, Hybrid được chạy cho cả 3 loss:
Hybrid + MSE:GA tìm θ tốt, GD mài giũa chính xác (nhanh, trơn).
Hybrid + MAE:GA vượt qua điểm gấp khúc, GD tinh chỉnh quanh nghiệm bền vững.
Hybrid + Huber:thường ổn định nhất khi dữ liệu có outliers vừa phải.
Kết quả tiêu biểu từ demo:
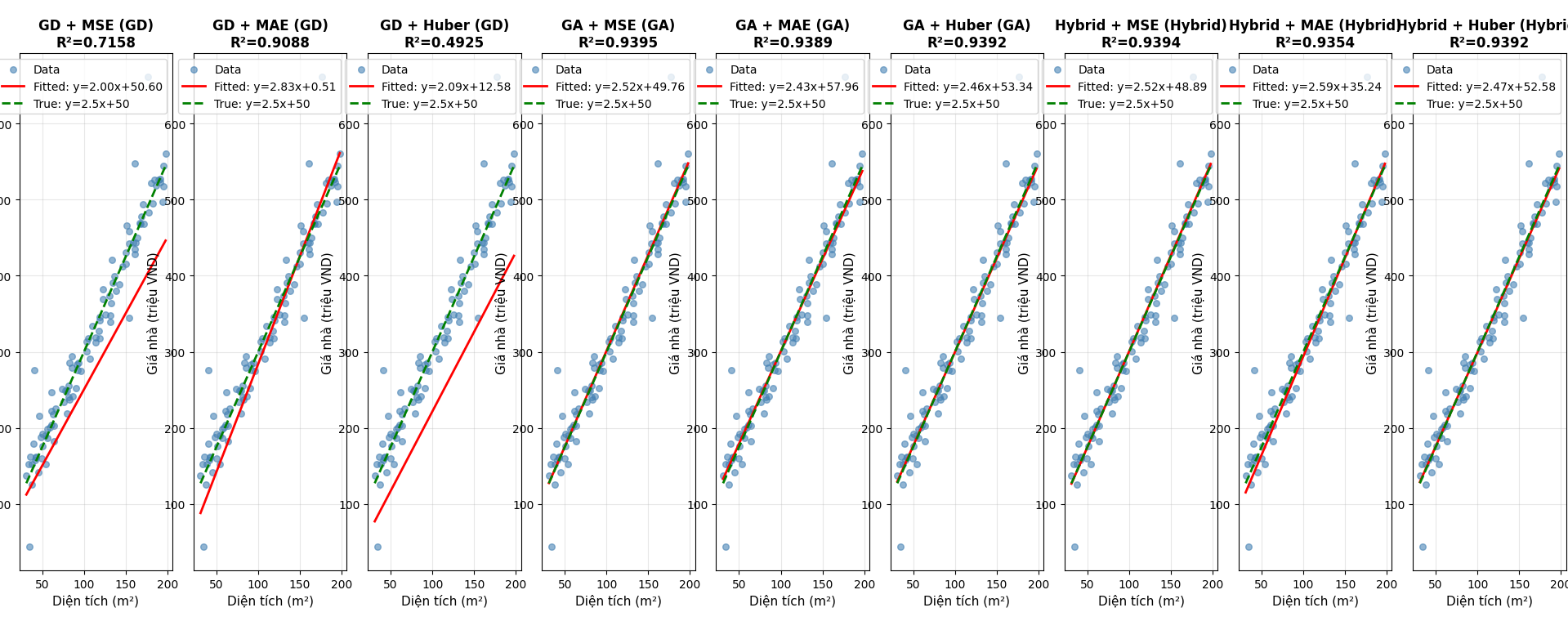
Synthetic data (y = 2.5x + 50 + noise, 5% outliers)
| Model | Method | R² | Ghi chú |
| -------------- | ------ | ----- | ----------------------------- |
| GD + MSE | GD | 0.716 | Nhạy outliers, cần LR phù hợp |
| GD + MAE | GD | 0.909 | Bền vững, hội tụ chậm hơn |
| GD + Huber | GD | 0.493 | Cần tinh chỉnh δ/LR |
| GA + MSE | GA | 0.940 | Tốt, không cần gradient |
| GA + MAE | GA | 0.937 | Ổn trên outliers |
| GA + Huber | GA | 0.937 | Cân bằng |
| Hybrid + MSE | Hybrid | 0.940 | GA khởi tạo, GD tinh chỉnh |
| Hybrid + MAE | Hybrid | 0.939 | Ổn định |
| Hybrid + Huber | Hybrid | 0.939 | Ổn định
Kết luận :
Hybrid Gradient Descent → Genetic Algorithsm có lợi thế thực nghiệm (empirically observed) trên dữ liệu phức tạp:
- GA tends to tìm khởi tạo tốt nhờ tìm kiếm toàn cục, vượt qua bẫy cục bộ và vùng loss không trơn.
- GD tends to fine‑tune nhanh và chính xác quanh khởi tạo đó.
- In our experiments, Hybrid đạt R² cao, tham số gần ground truth, và loss thấp/ổn định so với phương án đơn lẻ.
So sánh ngắn gọn:- Gradient Descent : nhanh trên loss trơn nhưng nhạy LR/khởi tạo; dễ local minima.
- Genetic Algorithsm: robust, gradient‑free; tinh chỉnh chậm.
- Hybrid: kết hợp “tìm đường” + “chạy nhanh đến đích”>
code demo : https://github.com/PhucVinhDEV/Loss-Func-LinearRegression
Tài liệu tham khảo:
Genetic Algorithms, With Inheritance, Versus Gradient Optimizers, And GA/Gradient Hybrids
Chưa có bình luận nào. Hãy là người đầu tiên!