I. Giới thiệu chung
Linear Regression là thuật toán nền tảng trong Machine Learning, được sử dụng để mô hình hóa mối quan hệ tuyến tính giữa các đặc trưng (features) và biến mục tiêu (label). Bài viết này sẽ tổng hợp các khía cạnh quan trọng nhất của mô hình này: từ công thức cơ bản, các hàm mất mát, đến kỹ thuật tối ưu hóa và vector hóa.
II. Cơ sở lý thuyết và mô hình toán học
1. Khái niệm
Linear Regression tìm cách vẽ một đường thẳng (hoặc siêu phẳng trong không gian đa chiều) khớp nhất với dữ liệu, nhằm mục đích dự đoán giá trị của biến mục tiêu ($\hat{y}$) dựa trên các biến đầu vào ($x$).
2. Mô hình
a. Hồi quy tuyến tính đơn (Simple Linear Regression)
Chỉ sử dụng một đặc trưng ($x$): $\hat{y} = \omega x + b$. Trong đó:
- $\hat{y}$: Giá trị dự đoán.
- $\omega$: Trọng số (weight) hay độ dốc của đường thẳng.
- $b$: Sai số (bias) hay điểm cắt trục tung.
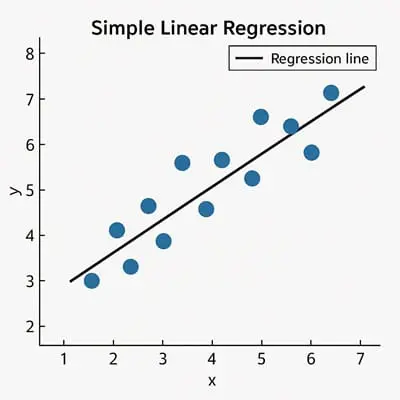
Hình 1. Minh họa mô hình hồi quy tuyến tính
b. Hồi quy tuyến tính đa biến (Multiple Linear Regression)
Sử dụng nhiều đặc trưng $(x_1, x_2, ..., x_n)$:
$$\hat{y} = \omega_1x_1 + \omega_2x_2 + ... + \omega_nx_n + b$$
Trong đó:
- $\hat{y}$: Giá trị dự đoán.
- $\omega_i$: Trọng số (weight) tương ứng với đặc trưng thứ $i$.
- $b$: Sai số (bias).
Ví dụ:
| Dữ liệu | Đặc trưng ($x$) | Nhãn ($y$) |
|---|---|---|
| Giá nhà | area |
price |
| Quảng cáo | TV, Radio, Newspaper |
Sales |
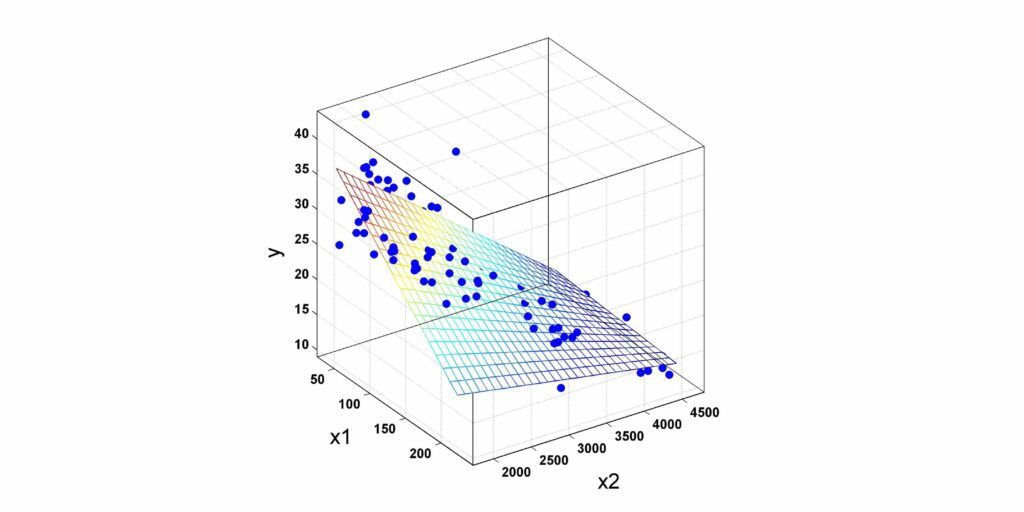
Hình 2. Mô hình hồi quy tuyến tính 2 biến
III. Các hàm mất mát (Loss Function)
Hàm mất mát L đo lường mức độ sai lệch giữa giá trị dữ đoán ($\hat{y}$) và giá trị thực tế ($y$). Mục tiêu là tối thiểu hóa hàm mất mát này.
1. Mean Squared Error (MSE) - Sai số bình phương trung bình
MSE là hàm mất mát phổ biến nhất, tính tổng bình phương của các sai số, sau đó lấy trung bình.
-
Công thức (cho $N$ mẫu):
$$L = \frac{1}{N}\sum_{i=1}^N (\hat{y}_i - y_i)^2$$ -
Trong đó:
- $L$: Giá trị hàm loss cho tất cả sample.
- $\hat{y}_i$: Giá trị dự đoán cho sample thứ $i$.
- $y_i$: Giá trị thực tế của sample thứ $i$.
-
Đặc điểm:
- Là hàm lồi (convex) và khả vi (differentiable) trên toàn miền, rất lý tưởng cho Gradient Descent.
- Nhạy cảm với Outlier (điểm ngoại lai): Do có phép bình phương, các lỗi lớn (gây ra bởi outlier) sẽ bị phóng đại, khiến mô hình cố gắng điều chỉnh để giảm thiểu ảnh hưởng của chúng.
2. Mean Absolute Error (MAE) - Sai số tuyệt đối trung bình
MAE là hàm mất mát tính tổng trị tuyệt đối của các sai số, sau đó lấy trung bình.
-
Công thức (cho $N$ mẫu):
$$L = \frac{1}{N}\sum_{i=1}^N |\hat{y}_i - y_i|$$ -
Trong đó:
- $L$: Giá trị hàm loss cho tất cả sample.
- $\hat{y}_i$: Giá trị dự đoán cho sample thứ $i$.
- $y_i$: Giá trị thực tế của sample thứ $i$.
-
Đặc điểm:
- Ít nhạy cảm với Outlier: Chỉ xem xét độ lớn tuyệt đối của lỗi, vì vậy không bị ảnh hưởng mạnh bởi các điểm ngoại lai như MSE.
- Vấn đề về đạo hàm: Không khả vi tại $\hat{y}=y$, điều này có thể gây khó khăn cho thuật toán Gradient Descent tại điểm cực tiểu.
3. Huber Loss
Huber Loss là sự kết hợp giữa MSE và MAE, mang lại sự cân bằng giữa tính khả vi và khả năng chống chịu outlier.
-
Công thức:
$$ L(\hat{y}, y) = \begin{cases} \frac{1}{2}(\hat{y} - y)^2, & \text{với } |\hat{y} - y| \le \delta \\ \delta |\hat{y} - y| - \frac{1}{2}\delta^2, & \text{còn lại} \end{cases} $$ -
Trong đó:
- $L$: Giá trị hàm loss cho tất cả sample.
- $\hat{y}_i$: Giá trị dự đoán cho sample thứ $i$.
- $y_i$: Giá trị thực tế của sample thứ $i$.
- $\delta$: Hằng số được định nghĩa trước để tối ưu hàm loss cho phù hợp
-
Khi lỗi nhỏ (trong khoảng $-\delta$ đến $\delta$), nó sử dụng MSE.
- Khi lỗi lớn (ngoài khoảng $-\delta$ đến $\delta$), nó sử dụng MAE.
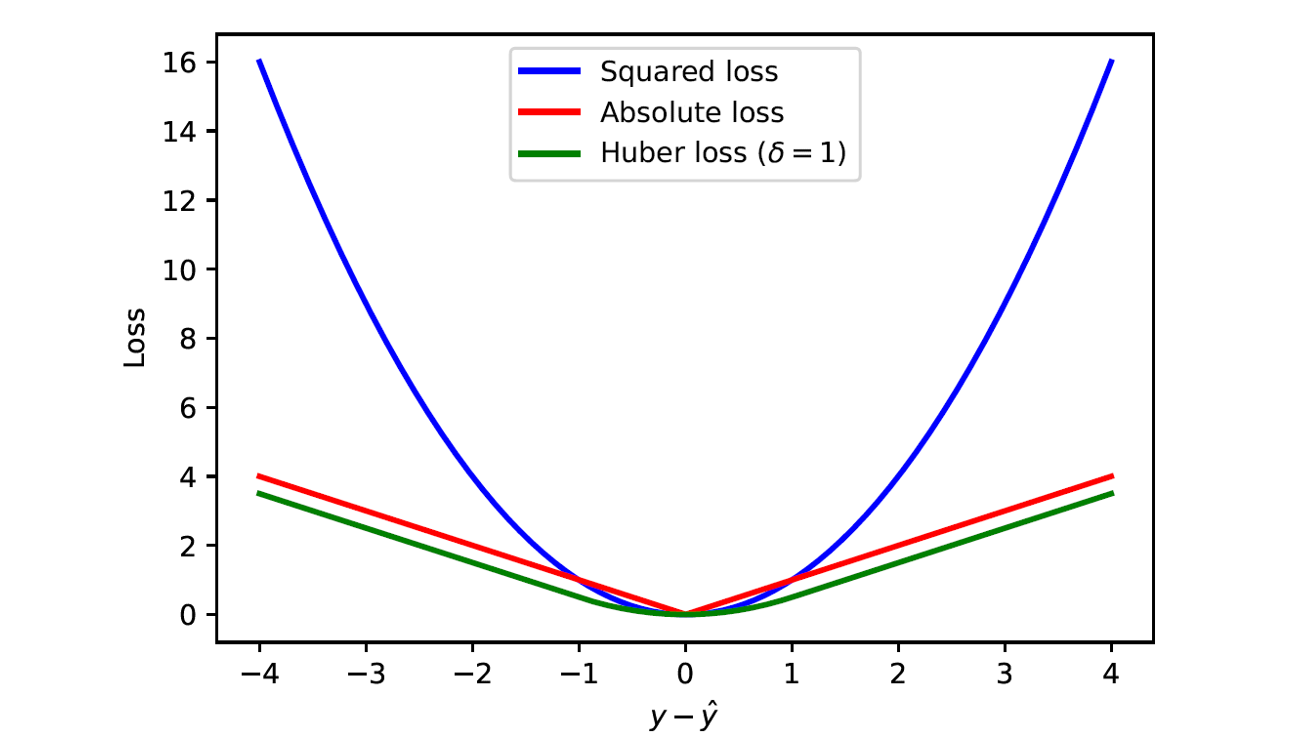
Hình 3. Loss functions
IV. Tối ưu hóa bằng Gradient Descent
Gradient Descent là thuật toán tối ưu hóa được sử dụng để tìm bộ tham số $(\omega, b)$ tối ưu bằng cách đi theo hướng ngược lại với gradient (đạo hàm) của hàm mất mát.
1. Quy tắc cập nhật tham số
Các tham số được cập nhật sau mỗi bước theo công thức:
$$\theta_{new}=\theta_{old}-\eta \cdot \nabla_{\theta} L$$
- $\theta$: Đại diện cho tham số ($\omega$ hoặc $b$).
- $\eta$: Tốc độ học (Learning rate), xác định kích thước bước nhảy.
- $\cdot \nabla_{\theta} L$: Gradient (Đạo hàm) của hàm mất mát theo tham số $\theta$.
2. Tính Gradient (với MSE)
Đạo hàm cho một mẫu $(\hat{y}, y)$:
- Theo $\omega$: $$\frac{\partial L}{\partial w} = 2x(\hat{y} - y)$$
- $\frac{\partial L}{\partial w}$: Đạo hàm của hàm loss $L$ theo $\omega$.
- $x$: Biến đặc trưng đầu vào.
- $y$: Giá trị thực tế.
- $\hat{y}$: Giá trị dự đoán.
<br>
-
Theo $b$: $$\frac{\partial L}{\partial b} = 2(\hat{y} - y)$$
- $\frac{\partial L}{\partial b}$: Đạo hàm của hàm loss $L$ theo $b$.
- $y$: Giá trị thực tế.
- $\hat{y}$: Giá trị dự đoán.
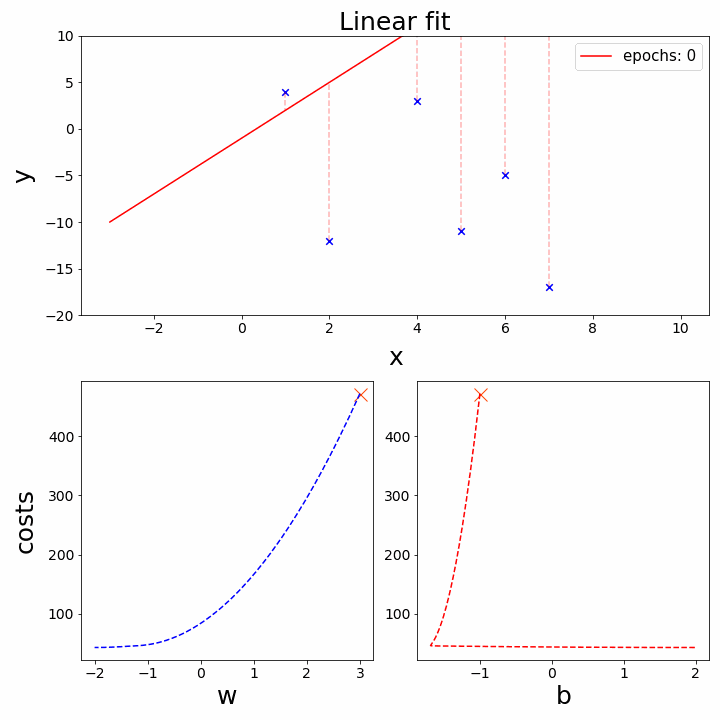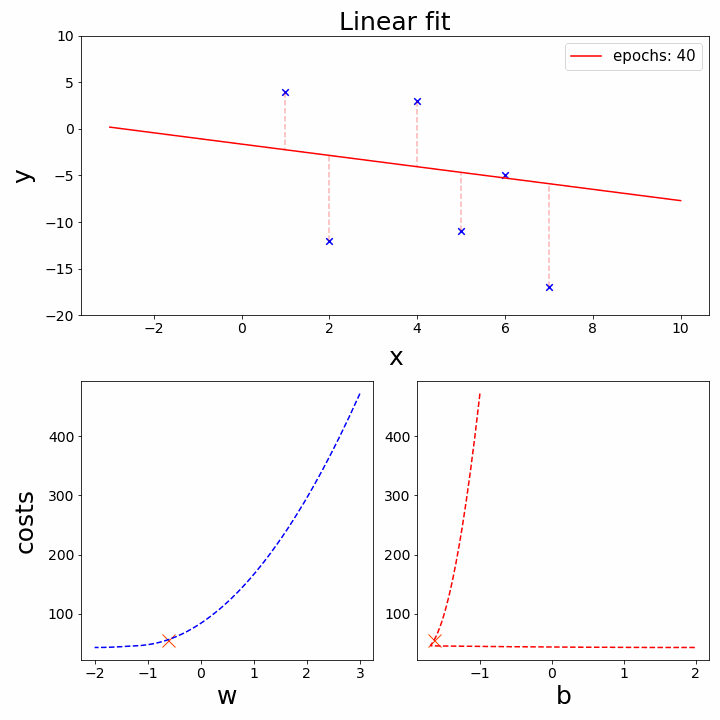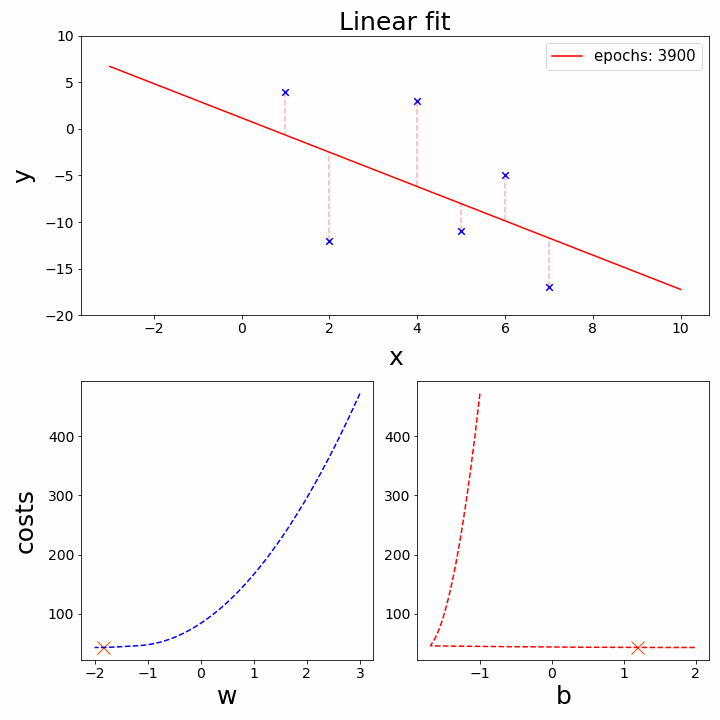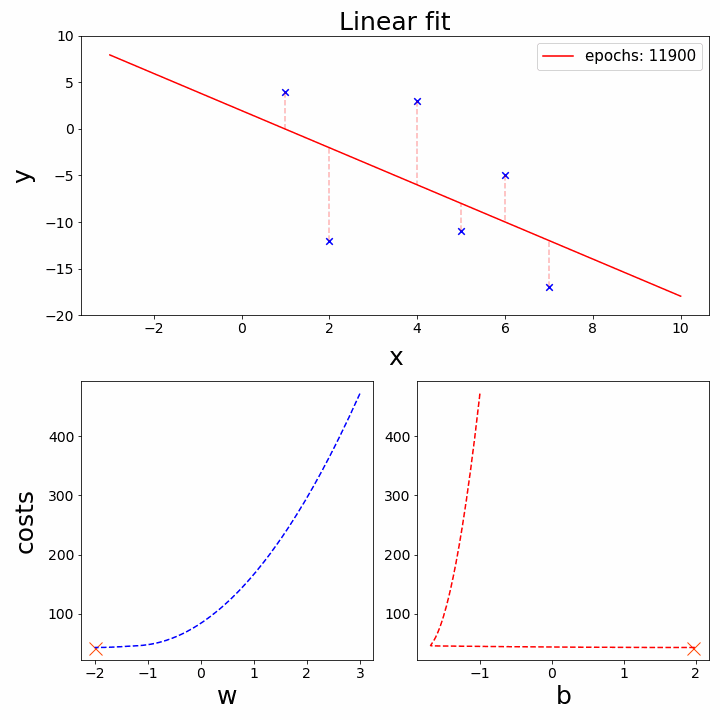
Hình 4. Gradient Descent
3. Các phương pháp huấn luyện
| Phương pháp | Cập nhật tham số | Lợi ích |
|---|---|---|
| Batch Gradient Descent | Toàn bộ $N$ mẫu dữ liệu | Đường đi Gradient ổn định, đảm bảo hội tụ về cực tiểu toàn cục |
| Mini-batch Gradient Descent | Một lô nhỏ ($m$ mẫu) | Cân bằng giữa hiệu quả tính toán (Vectorization) và tốc độ hội tụ (ít mẫu). |
| Stochastic Gradient Descent (SGD) | Mỗi một mẫu dữ liệu ($m = 1$) | Cập nhật nhanh, thoát khỏi cực tiểu cục bộ (ít khi xảy ra trong Linear Regression) nhưng đường bị nhiễu. |
V. Vectorization
Vectorization là việc sử dụng các phép toán đại số tuyến tính (ma trận, vector) thay vì vòng lặp, giúp tận dụng tối đa khả năng xử lý song song của CPU/GPU, làm tăng tốc độ huấn luyện.
1. Biểu diễn dữ liệu và tham số
Ta sử dụng ma trận để gom tất cả các đặc trưng và tham số lại:
-
Vector tham số ($\theta$) (vector cột, $n+1$ chiều):
$$ \theta = \begin{bmatrix} b \\ w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix} $$- $\omega_i$: Trọng số tương ứng với đặc trưng thứ $i$.
- $b$: Sai số (bias).
-
Ma trận đặc trưng ($X$) (ma trận $N\times (n + 1)$):
$$ X = \begin{bmatrix} 1 & x_1^{(1)} & x_2^{(1)} & \dots & x_n^{(1)} \\ 1 & x_1^{(2)} & x_2^{(2)} & \dots & x_n^{(2)} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & x_1^{(N)} & x_2^{(N)} & \dots & x_n^{(N)} \end{bmatrix} $$ -
$N$ là số lượng mẫu.
- $n$ là số lượng đặc trưng.
- Cột đầu tiên là cột số $1$ (dành cho bias $b$).
- $x_i^{(j)}$: Giá trị đặc trưng thứ $i$ của sample thứ $j$.
2. Công thức vector hóa
a. Tính đầu ra ($\hat{Y}$)
$$\hat{Y}=X\theta$$
- $\hat{Y}$: Ma trận đầu ra dự đoán.
- $X$: Ma trận đầu vào gồm các giá trị của biến đặc trưng.
- $\theta$: Ma trận trọng số $\omega$ và bias $b$.
b. Tính Gradient ($\nabla_{\theta} L$)
-
Với MSE:
$$\nabla_{\theta} L=X^T(\hat{Y} - Y)$$ -
$Y$: Ma trận đầu ra thực tế.
- $\hat{Y}$: Ma trận đầu ra dự đoán.
- $X$: Ma trận đầu vào gồm các giá trị của biến đặc trưng.
- $\theta$: Ma trận trọng số $\omega$ và bias $b$.
VI. Các kỹ thuật nâng cao
1. Data Normalization (Chuẩn hóa dữ liệu)
Chuẩn hóa là cần thiết khi các đặc trưng có phạm vi giá trị (scale) khác nhau (ví dụ: age từ 1-100 và area từ 10-10000).
- Mục đích: Đảm bảo tất cả các đặc trưng đóng góp như nhau vào quá trình tối ưu hóa và giúp Gradient Descent hội tụ nhanh hơn.
-
Công thức (Min-Max hoặc Z-Score):
$$x_{norm} = \frac{x-x_{min}}{x_{max} - x_{min}}$$ hoặc $$x_{norm}=\frac{x-\mu}{\sigma}$$ -
Trong đó:
- $x_{norm}$: Giá trị chuẩn hóa của $x$.
- $x_{min}$: Giá trị $min$ của $x$.
- $x_{max}$: Giá trị $max$ của $x$.
- $\mu$: Giá trị trung bình tổng thể.
- $\sigma$: Độ lệch chuẩn.
2. Regularization (Chuẩn hóa tham số)
Regularization là kỹ thuật thêm một phần phạt vào hàm mất mát để kiểm soát độ lớn của các trọng số ($\omega$), từ đó ngăn chặn overfitting (quá khớp) trên dữ liệu huấn luyện.
L2 Regularization (Ridge Regression)
Thêm tổng bình phương của các trọng số ($\omega_i$) vào hàm mất mát
- Hàm mất mát mới:
$$ L_{L2}=\frac{1}{N}\sum_{i=1}^N (\hat{y}_i-y_i)^2+\lambda \sum_{j=1}^n \omega_j^2$$- $\lambda$: Tham số chuẩn hóa, điều chỉnh mức độ phạt.
- $\hat{y}_i$: Giá trị dự đoán của sample thứ $i$.
- $y_i$: Giá trị thực tế của sample thứ $i$.
- $\omega_j$: Trọng số của biến đặc trưng đầu vào thứ $j$.
- Cập nhật tham số (với MSE): Đạo hàm theo $\omega$ sẽ thêm một lượng $2\lambda\omega$:
$$\frac{\partial L}{\partial w_j} = \frac{1}{N}\sum_{i=1}^N 2x_j^{(i)} (\hat{y}^{(i)} - y^{(i)}) + 2\lambda\omega_j$$- $\lambda$: Tham số chuẩn hóa, điều chỉnh mức độ phạt.
- $\hat{y}_i$: Giá trị dự đoán của sample thứ $i$.
- $y_i$: Giá trị thực tế của sample thứ $i$.
- $\omega_j$: Trọng số của biến đặc trưng đầu vào thứ $j$.
- $\frac{\partial L}{\partial w_j}$: Đạo hàm của hàm loss $L$ theo $\omega_j$.
- $x_j^{(i)}$: Giá trị đầu vào của biến đặc trưng thứ $j$ trong sample thứ $i$.
- Mục tiêu: Giảm độ lớn của các trọng số về gần $0$ (nhưng không hoàn toàn bằng $0$).
VII. Kết luận
Linear Regression là một mô hình đơn giản nhưng cực kỳ mạnh mẽ, đóng vai trò là khối xây dựng cơ bản trong Machine Learning. Việc nắm vững các khái niệm về hàm mất mát (MSE, MAE, Huber), quá trình tối ưu hóa bằng Gradient Descent, và đặc biệt là kỹ thuật Vectorization là chìa khóa để triển khai mô hình hiệu quả trên thực tế.
Các kỹ thuật nâng cao như Normalization và Regularization đảm bảo mô hình không chỉ chính xác mà còn mạnh mẽ và có khả năng khái quát hóa tốt trên dữ liệu mới. Linear Regression không chỉ là một thuật toán dự đoán, mà còn là một minh chứng tuyệt vời cho cách Đại số Tuyến tính và Giải tích kết hợp để giải quyết các vấn đề thế giới thực.
Chưa có bình luận nào. Hãy là người đầu tiên!