Machine Learning (ML)
Machine Learning (ML) là lĩnh vực thuộc Trí tuệ nhân tạo (AI), tập trung vào việc giúp máy tính học từ dữ liệu và cải thiện hiệu suất mà không cần lập trình trực tiếp.
ML được chia thành bốn nhóm chính:
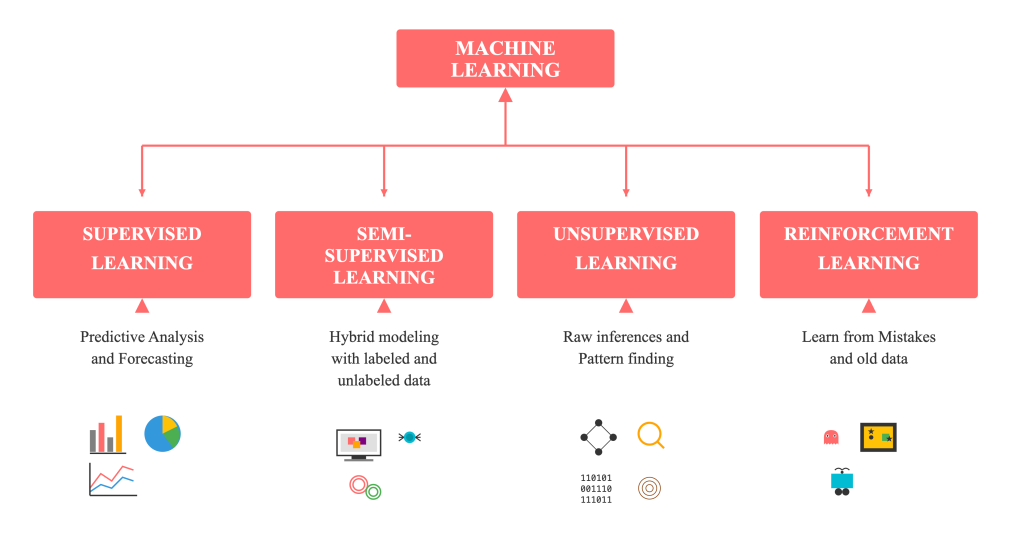
Hình 1: Mô tả các nhóm trong Machine Learning [1] - Module 05 Exercise
- Supervised Learning: Học có giám sát – dự đoán giá trị hoặc phân loại dữ liệu dựa trên dữ liệu gắn nhãn.
- Semi-supervised Learning: Kết hợp giữa dữ liệu có nhãn và chưa có nhãn.
- Unsupervised Learning: Học không giám sát – tìm mẫu hoặc cấu trúc ẩn trong dữ liệu.
- Reinforcement Learning: Học thông qua phản hồi và phần thưởng từ môi trường.
Trong đó, Linear Regression là một mô hình cơ bản của Supervised Learning, được sử dụng để dự đoán giá trị liên tục (như lương, doanh thu, giá nhà). Mô hình hoạt động dựa trên việc tìm ra mối quan hệ tuyến tính giữa các biến đầu vào và đầu ra, tối ưu tham số bằng Gradient Descent.
Linear Regression Exercise & Data Normalization
I. Lý thuyết cơ bản
1. Giới thiệu về Machine Learning và Hồi quy
Hồi quy tuyến tính (Linear Regression) là một phương pháp cổ điển bắt nguồn từ phương pháp bình phương tối thiểu.
Nó thuộc lĩnh vực Machine Learning (Học máy) – một nhánh của Trí tuệ Nhân tạo (AI) tập trung vào việc sử dụng dữ liệu và thuật toán để mô phỏng cách con người học và dần dần cải thiện độ chính xác.
Linear Regression được sử dụng để giải quyết bài toán Hồi quy (Regression) — nhiệm vụ dự đoán một giá trị liên tục (continuous value) dựa trên các đầu vào cho trước.
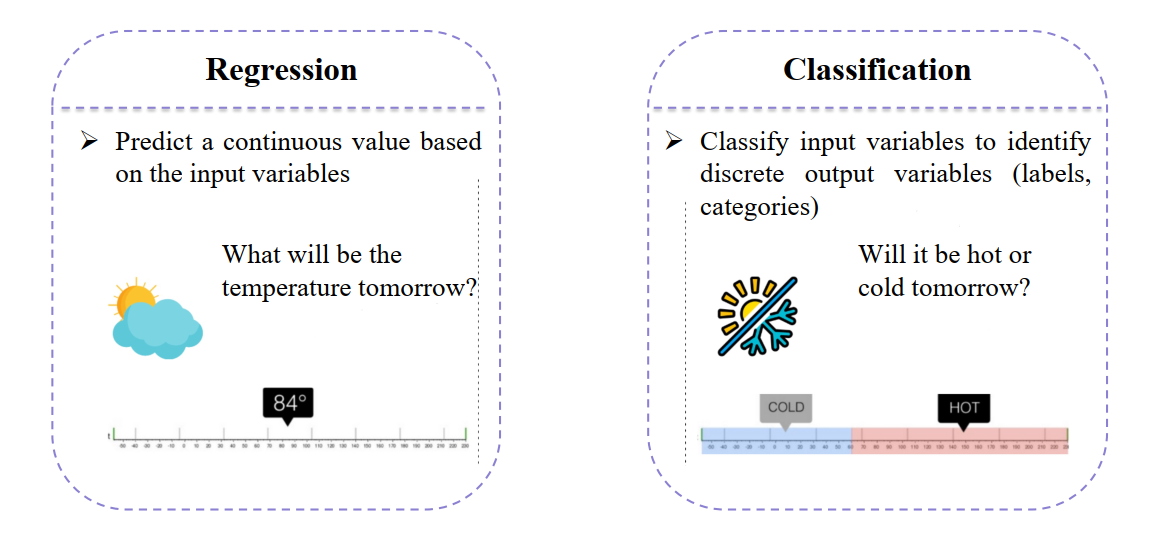
Hình 2: So sánh giữa regression và classification [1]
Regression cho giá trị số, còn Classification cho nhãn hoặc loại. Điều này trái ngược với bài toán Phân loại (Classification), nơi mục tiêu là dự đoán một giá trị rời rạc (phân loại).
2. Mô hình Simple Linear Regression
Simple Linear Regression tập trung vào việc dự đoán giá trị đầu ra (y) – ví dụ: tiền lương, dựa trên một biến đầu vào duy nhất (x) – ví dụ: số năm kinh nghiệm.
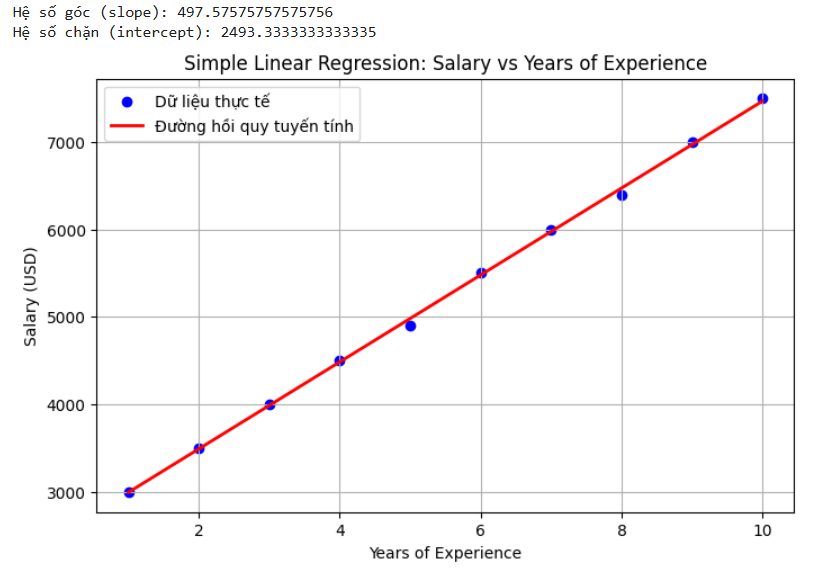
Hình 3: Mô tả dự đoán tiền lương dựa vào số năm kinh nghiệm [1]
Mô hình Linear Regression đã học được mối quan hệ tuyến tính giữa số năm kinh nghiệm (x) và mức lương (y).
- x: Biến độc lập – thể hiện số năm làm việc
- y: Biến phụ thuộc – biểu thị mức lương dự đoán
- Mục tiêu là tìm ra đường thẳng phù hợp nhất với sự phân bố của dữ liệu. Phương trình đường thẳng dự đoán:
$$\hat{y}_i = f(x_i) = w \cdot x_i + b$$
Trong đó:
- x: Biến đầu vào (số năm kinh nghiệm)
- y: Biến đầu ra (tiền lương)
- ŷᵢ: Giá trị dự đoán tại mẫu (x_i)
- w: Hệ số góc / trọng số (weight) của mô hình — thay đổi w làm thay đổi độ nghiêng của đường thẳng
- b: Tung độ gốc / độ chệch (bias) của mô hình — thay đổi b sẽ dịch chuyển đường thẳng song song theo trục tung
Bảng 1: Mở rộng các ký hiệu toán học
| Ký hiệu | Ý nghĩa |
|---|---|
| x, y | Biến đầu vào (số năm kinh nghiệm) và đầu ra (tiền lương). |
| (xᵢ, yᵢ) | Mẫu dữ liệu thứ i trong bài. |
| $\hat{y}_i$ | Dự đoán tại $x_i$: $\hat{y}_i = f(x_i) = w x_i + b$ |
| $f(x)$ | Hàm dự đoán tuyến tính: $f(x) = w x + b$ |
| w | Hệ số góc / trọng số (weight) của mô hình. |
| b | Tung độ gốc / độ chệch (bias) của mô hình. |
| $L_i$ | Mất mát từng mẫu: $L_i = (\hat{y}_i - y_i)^2$ |
| $L(\hat{y}_i, y_i)$ | Viết tường minh hàm mất mát theo cặp $(\hat{y}_i, y_i)$. |
| $\frac{∂L}{∂w}$, $\frac{∂L}{∂b}$ | Đạo hàm riêng của loss theo w và b (dùng để cập nhật). |
| η | Learning rate (hệ số học) trong bước cập nhật. |
II. Tối ưu hóa mô hình bằng Gradient Descent
1. Khái niệm: Đường thẳng tối ưu & Hàm mất mát (Loss Function)
- Mỗi cặp tham số ((w, b)) xác định một đường thẳng dự đoán $\hat{y} = w x + b$.
- Đường thẳng tối ưu là đường làm cho tổng khoảng cách (sai số) giữa các điểm dữ liệu thực tế và giá trị dự đoán là nhỏ nhất.
Sai số (Error) của một mẫu: Là chênh lệch giữa giá trị dự đoán (ŷ) và giá trị thực tế (y).
$$\text{error}_i = \hat{y}_i - y_i$$
Hàm mất mát (Squared Error) cho một mẫu:
$$L_i = (\hat{y}_i - y_i)^2$$
Mean Squared Error (MSE) cho toàn bộ tập (N) mẫu:
$$ \text{MSE} = L(w,b) = \frac{1}{N}\sum_{i=1}^{N} (\hat{y}_i - y_i)^2\quad\text{với}\quad \hat{y}_i = w x_i + b $$
Mục tiêu: tìm ((w,b)) sao cho (L(w,b)) nhỏ nhất.
2. Cơ chế tối ưu hóa bằng đạo hàm và Gradient Descent
a) Ý tưởng đạo hàm
- Đạo hàm cho biết hướng và độ dốc của hàm mất mát theo từng tham số.Gradient Descent sẽ di chuyển tham số (x) theo hướng ngược chiều với đạo hàm để giảm giá trị hàm mất mát.
- Mỗi lần lặp, thuật toán di chuyển ngược hướng với đạo hàm để tiến gần đến điểm có giá trị Loss nhỏ nhất.
- Nếu đạo hàm dương → hàm tăng theo chiều dương → ta giảm tham số theo chiều âm (ngược gradient).
- Nếu đạo hàm âm → hàm giảm theo chiều âm → ta tăng tham số theo chiều dương.
- Bảng 2: Mô tả nguyên lý đạo hàm
| Trường hợp | Ký hiệu | Ý nghĩa | Hành động |
|---|---|---|---|
| Đạo hàm dương | $\displaystyle \frac{d}{dx}f(x) > 0$ | Hàm đang tăng | 🔻 Di chuyển $x$ sang trái để giảm $f(x)$ |
| Đạo hàm âm | $\displaystyle \frac{d}{dx}f(x) < 0$ | Hàm đang giảm | 🔺 Di chuyển $x$ sang phải để giảm $f(x)$ |
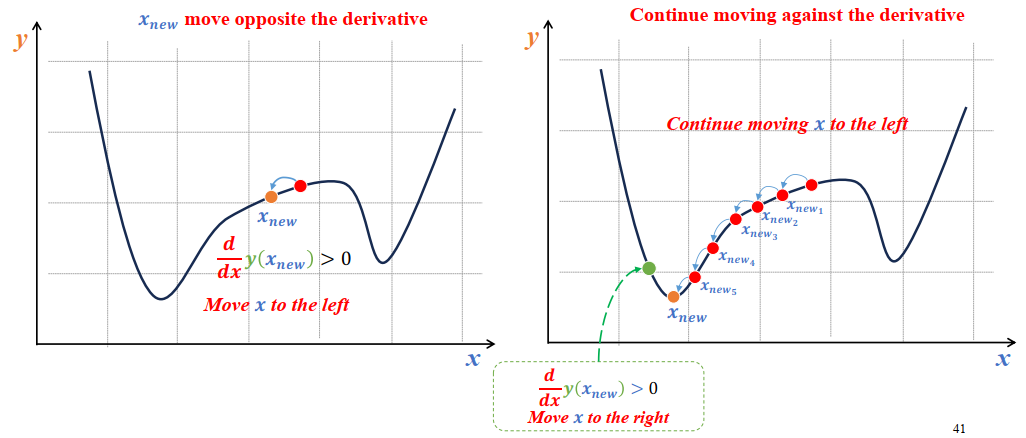
Hình 4: Minh họa quá trình Gradient Descent tìm điểm cực tiểu của hàm mất mát [1].
Công thức cập nhật Gradient Descent
$$x_{\text{new}} = x_{\text{old}} - \eta \frac{d}{dx}f(x_{\text{old}})$$
Trong đó:
- $x_{\text{new}}$: Giá trị mới của tham số (sau khi cập nhật).
- $x_{\text{old}}$: Giá trị hiện tại của tham số.
- $\eta$: Learning rate — hệ số học điều chỉnh tốc độ di chuyển.
Note:
Gradient Descent giúp mô hình từng bước tiến gần đến điểm cực tiểu toàn cục, nơi hàm mất mát (Loss) đạt giá trị nhỏ nhất, bằng cách di chuyển ngược hướng gradient qua từng vòng lặp huấn luyện.
b) Đạo hàm riêng (gradients)
- Với một mẫu (sử dụng $L_i$:
$$\frac{\partial L_i}{\partial w} = 2 x_i (\hat{y}_i - y_i)\qquad\frac{\partial L_i}{\partial b} = 2 (\hat{y}_i - y_i)$$
- Với toàn tập (MSE, trung bình trên N mẫu):
$$\frac{\partial L}{\partial w} = \frac{2}{N} \sum_{i=1}^{N} x_i (\hat{y}_i - y_i) $$
$$\frac{\partial L}{\partial b} = \frac{2}{N} \sum_{i=1}^{N} (\hat{y}_i - y_i)$$
Ghi chú: hệ số 2 có thể được bỏ bằng cách định nghĩa hàm mất mát khác (ví dụ 1/2 MSE). Kết quả cập nhật sẽ tương đương sau điều chỉnh learning rate.
c) Quy tắc cập nhật (Gradient Descent)
- Learning rate $\eta$:
$$ w = w - \eta \ \frac{\partial L}{\partial w}$$
$$ b = b - \eta \ \frac{\partial L}{\partial b}$$
- Cập nhật lặp đi lặp lại cho đến khi hội tụ (loss không còn giảm nhiều) hoặc đạt số epoch tối đa.
d) Quy trình Tổng quát (Pipeline)
Quy trình huấn luyện Simple Linear Regression có thể tóm tắt qua 5 bước chính như sau:
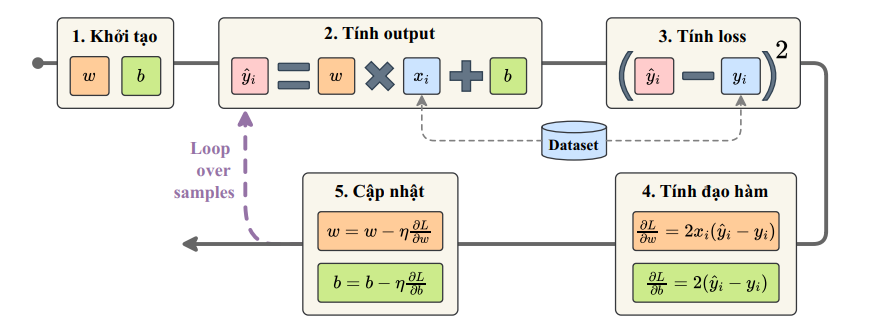
Hình 5: Pipeline của quá trình huấn luyện Linear Regression [1]
| Bước | Mô tả |
|---|---|
| 1️ Khởi tạo | Chọn giá trị ban đầu ngẫu nhiên cho $w$ (trọng số) và $b$ (bias). |
| 2️ Tính Output (Forward Pass) | Dự đoán giá trị: $\hat{y}_i = w \cdot x_i + b$ |
| 3️ Tính Loss (Sai số) | Đo sai số giữa dự đoán và giá trị thật: $L = (\hat{y}_i - y_i)^2$ |
| 4️ Tính Đạo hàm (Gradient) | Xác định hướng điều chỉnh: $\frac{\partial L}{\partial w} = 2x_i(\hat{y}_i - y_i)$, $\frac{\partial L}{\partial b} = 2(\hat{y}_i - y_i)$ |
| 5 Cập nhật Tham số (Update Step) | Cập nhật theo Gradient Descent: $w = w - \eta \frac{\partial L}{\partial w}$, $b = b - \eta \frac{\partial L}{\partial b}$ |
🔁 Lặp lại (Loop over samples):
Các bước từ 2 → 5 được lặp lại nhiều lần cho đến khi mô hình hội tụ (Loss đạt cực tiểu).
💡 Tóm lại:
Pipeline này giúp mô hình học được mối quan hệ tuyến tính giữa đầu vào (x) và đầu ra (y) bằng cách điều chỉnh dần w và b sao cho hàm mất mát nhỏ nhất.
3. Các biến thể Gradient Descent và mô hình đa biến
| Phương pháp | Mô tả | Ưu điểm | Nhược điểm |
|---|---|---|---|
| Batch Gradient Descent (BGD) | Tính gradient trên toàn bộ tập dữ liệu, sau đó cập nhật 1 lần mỗi epoch. | - Gradient chính xác - Ổn định khi hội tụ |
- Tốn thời gian khi tập dữ liệu lớn - Yêu cầu nhiều bộ nhớ |
| Stochastic Gradient Descent (SGD) | Cập nhật sau mỗi mẫu (i), dùng $\frac{\partial L_i}{\partial \theta}$. | - Nhanh, ít tốn bộ nhớ - Có thể thoát khỏi cực tiểu cục bộ |
- Gradient nhiễu (noisy) - Hội tụ dao động quanh cực tiểu |
| Mini-batch Gradient Descent | Cập nhật theo nhóm nhỏ (m) mẫu (ví dụ 16, 32, 64). | - Ổn định hơn SGD - Hiệu quả hơn BGD - Tối ưu GPU tốt hơn |
- Cần chọn kích thước batch phù hợp - Vẫn có dao động nhẹ |
Note: Multiple Linear Regression (Hồi quy tuyến tính đa biến)
Khi có nhiều biến đầu vào $(x_1, x_2, x_3, \dots, x_n)$, mô hình hồi quy tuyến tính được mở rộng như sau:
$$\hat{y} = w_1 x_1 + w_2 x_2 + \dots + w_n x_n + b$$
a) Đạo hàm riêng cho từng biến:
$$\frac{\partial L}{\partial w_j} = \frac{2}{N} \sum_{i=1}^{N} x_{ij}(\hat{y}_i - y_i)$$
$$\frac{\partial L}{\partial b} = \frac{2}{N} \sum_{i=1}^{N} (\hat{y}_i - y_i)$$
b) Cập nhật tham số:
$$w_j^{(new)} = w_j^{(old)} - \eta \frac{\partial L}{\partial w_j}$$
$$b^{(new)} = b^{(old)} - \eta \frac{\partial L}{\partial b}$$
c) Chuẩn hóa đặc trưng:
Feature Scaling giúp mô hình hội tụ nhanh hơn khi các đặc trưng (features) có phạm vi giá trị khác nhau.
Bảng 3: So sánh phương pháp Min-Max scaling và Z-score
| Phương pháp | Công thức | Giải thích |
|---|---|---|
| Min-Max Scaling | $$x' = \frac{x - x_{min}}{x_{max} - x_{min}}$$ | Chuẩn hóa giá trị về khoảng ([0, 1]). Thường dùng cho dữ liệu không có ngoại lệ lớn. |
| Z-score Scaling (Standardization) | $$ x' = \frac{x - \mu}{\sigma} $$ | Chuyển dữ liệu sao cho trung bình bằng 0, độ lệch chuẩn bằng 1. Hiệu quả khi dữ liệu có giá trị lệch lớn (outliers). |
⚙️ Lưu ý:
- Feature Scaling đặc biệt quan trọng với các thuật toán dựa trên Gradient Descent.
- Nếu không chuẩn hóa, biến có giá trị lớn sẽ chi phối hướng tối ưu, làm mô hình hội tụ chậm hoặc không ổn định.
TÓM TẮT
Báo cáo này trình bày toàn bộ quy trình từ cơ sở lý thuyết về Machine Learning đến xây dựng mô hình Linear Regression và tối ưu bằng Gradient Descent.
Cụ thể, nội dung bao gồm:
- Giới thiệu tổng quan về Machine Learning và vai trò của hồi quy tuyến tính trong học có giám sát.
- Trình bày phương trình hồi quy tuyến tính đơn và đa biến, kèm hàm mất mát (MSE) và ý nghĩa tham số.
- Phân tích chi tiết thuật toán Gradient Descent, bao gồm công thức đạo hàm, quy trình cập nhật trọng số và các biến thể như BGD, SGD, Mini-batch GD.
- Giới thiệu kỹ thuật chuẩn hóa đặc trưng (Feature Scaling) giúp mô hình hội tụ nhanh và ổn định hơn.
- Tổng kết vai trò của Linear Regression như một mô hình nền tảng cho các phương pháp học sâu và dự đoán dữ liệu trong thực tế.
Reference
[1] Ảnh được lấy từ tài liệu khóa học AIO Module 05 Tuần 01 và 02.
Chưa có bình luận nào. Hãy là người đầu tiên!