Simple Regression và phương trình đường thẳng tối ưu
Các bài toán dạng bảng thường gặp:
- Dự đoán tiền lương dựa trên kinh nghiệm làm việc
- Dự đoán giá đất dựa trên diện tích
- Dự đoán tổng doanh số (Sales) dựa trên chi phí quảng cáo (TV, Radio, Báo)
Các bài toán trên có thể được mô hình hóa bằng phương trình đường thẳng:
$$
y = wx + b
$$

Hình 1: Minh hoạ 1 đường thẳng bất kỳ trên toạ độ
Trong đó:
- $`y`$: giá trị cần dự đoán
- $`x`$: đặc trưng đầu vào (feature)
- $`w`$: hệ số góc (slope)
- $`b`$: hệ số chặn (intercept)
Mục tiêu: Tìm giá trị tối ưu của $`w`$ và $`b`$ sao cho đường thẳng khớp với dữ liệu tốt nhất, tức là tổng sai số giữa các điểm dữ liệu và đường thẳng là nhỏ nhất.
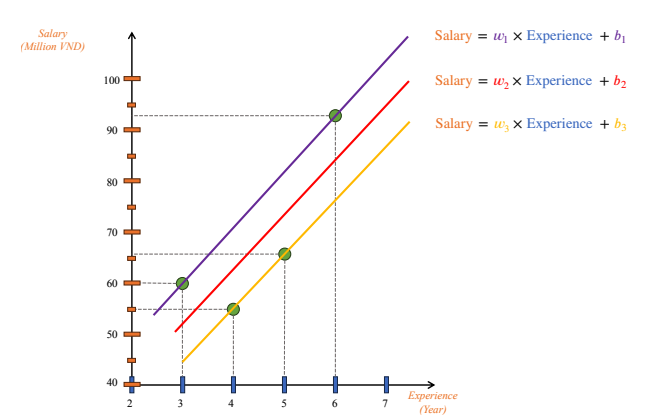
Hình 2: Minh hoạ các đường thẳng khác nhau với các giá trị w và b khác nhau
Hàm mất mát
Giả sử phương trình tối ưu là $`y = wx + b`$ $`\Leftrightarrow`$ tổngkhoảng cách giữa các điểm và đường thẳng phải là nhỏ nhất, hay đường thẳng FIT NHẤT vào bộ dữ liệu này = hàm Loss giữa các điểm và đường thẳng phải đạt giá trị MIN.
Với giá trị $`w_1, b_1`$ khởi tạo ngẫu nhiên $`\rightarrow`$ phương trình ban đầu:
$$
\hat{y} = w_1 x + b_1
$$
⇒ di chuyển $`w_1, b_1`$ dần dần sao cho đạt giá trị$`w, b`$ tối ưu.

Hình 3: Khoảng cách giữa các điểm với đường thẳng theo trục Oy
Với mỗi điểm dữ liệu $`(x_i, y_i)`$, hàm mất mát được định nghĩa là:
$$
\mathcal{L}_i = \left(wx_i + b - y_i\right)^2
$$
Đồ thị của $`\mathcal{L}_i`$ theo $`w`$ hoặc $`b`$ có dạng parabol, nênmục tiêu là di chuyển trong không gian $`(w, b)`$ đến điểm cực tiểu củaparabol — tức là điểm $`(w, b)`$ tối ưu.
⇒ Di chuyển bằng cách NGƯỢC HƯỚNG ĐẠO HÀM (gradient-based optimization)
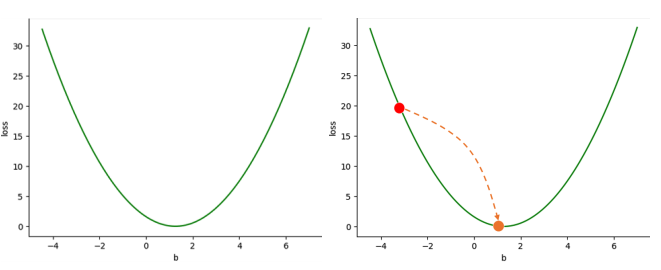
Hình 4: Di chuyển điểm (w,b) đến điểm cực tiểu trong hàm mất mát
Cập nhật tham số bằng Gradient Descent
Ta di chuyển ngược hướng đạo hàm (gradient) của hàm mất mát để tiến dần về điểm cực tiểu.
Công thức cập nhật:
$$
\begin{aligned}
w &= w - \alpha \cdot \frac{\partial \mathcal{L}}{\partial w} \\
b &= b - \alpha \cdot \frac{\partial \mathcal{L}}{\partial b}
\end{aligned}
$$
Với hàm MSE (Mean Squared Error):
$$ \mathcal{L} = \left(y - (wx + b)\right)^2 $$
Đạo hàm:
$$ \begin{aligned} \frac{\partial \mathcal{L}}{\partial w} &= 2(\hat{y} - y) \cdot x \\ \frac{\partial \mathcal{L}}{\partial b} &= 2(\hat{y} - y) \end{aligned} $$
Công thức cập nhật:
$$ \begin{aligned} w &= w - \alpha \cdot 2(\hat{y} - y) \cdot x \\ b &= b - \alpha \cdot 2(\hat{y} - y) \end{aligned} $$

Hình 5: Di chuyển điểm ngược hướng đạo hàm với learning rate để tới điểm tối ưu
Ghi chú: Learning rate ($`\alpha`$) cần chọn phù hợp. Nếu $`\alpha`$quá lớn, thuật toán dao động không hội tụ; nếu quá nhỏ, quá trình học sẽ rất chậm.

Hình 6: Quy trình tổng quát để tìm được tham số w và b tối ưu
#compute y_hat
def predict(x,w,b):
return x*w+b
#compute gradient
def gradient(y_hat,y,x):
dw = 2*(y_hat-y)*x
db = 2*(y_hat-y)
return (dw,db)
#update weight
def update_weight(w,b,lr,dw,db):
w_new = w - lr*dw
b_new = b-lr*db
return (w_new,b_new)
Ví dụ: Linear Regression đơn giản
Cho bảng dữ liệu diện tích đất và giá đất tương ứng:
| Diện tích đất (m2) | Giá (triệu VND) |
|---|---|
| 56 | 45 |
| 45 | 23 |
| 234 | 199 |
| 113 | 123 |
| 542 | 448 |
| 351 | 367 |
Ta muốn tìm mối quan hệ tuyến tính giữa diện tích (x) và giá đất (y):
$$ y = w \cdot x + b $$
Bước 1. Khởi tạo tham số:
$$
w = 2,\quad b = 5
$$
Bước 2. Dự đoán giá trị:
Với điểm ((x_1, y_1) = (56, 45)):
$$
\hat{y}_1 = w \cdot x_1 + b = 2 \cdot 56 + 5 = 117
$$
Bước 3. Tính hàm mất mát (Loss):
$$
L = (\hat{y}_1 - y_1)^2 = (117 - 45)^2 = 5184
$$
Bước 4. Tính đạo hàm (Gradient):
$$
\frac{\partial L}{\partial w} = 2x_1(\hat{y}_1 - y_1) = 2 \cdot 56 \cdot 72 = 8064
$$
$$
\frac{\partial L}{\partial b} = 2(\hat{y}_1 - y_1) = 144
$$
Bước 5. Cập nhật tham số (với tốc độ học $ \eta = 0.01 \ldots $):
$$
\begin{aligned}
w_{\text{new}} &= w - \eta \cdot \frac{\partial L}{\partial w}
= 2 - 0.01 \cdot 8064 = -78.64 \\
b_{\text{new}} &= b - \eta \cdot \frac{\partial L}{\partial b}
= 5 - 0.01 \cdot 144 = 3.56
\end{aligned}
$$
Bước 6. Lặp lại: Tiếp tục tính cho các điểm $(x_2, y_2), (x_3, y_3), \ldots$.
Sau nhiều lần cập nhật, các giá trị $w$ và $b$ sẽ hội tụ, cho ra đường thẳng khớp dữ liệu nhất.
Trực quan bằng code:
w = 2.0
b = 5.0
lr = 1e-5
epochs = 5
area = np.array([56, 45, 234, 113, 542, 351], dtype=float)
price = np.array([45, 23, 199, 123, 448, 367], dtype=float)
for _ in range (epochs):
for i in range(len(area)):
x = area[i]
y = price[i]
y_hat = predict(x,w,b)
(dw,db) = gradient(y_hat,y, x)
(w,b)= update_weight(w,b,lr,dw,db)

Hình 7: Các đường thẳng sau từng lần cập nhập epoch
Mini-Batch Gradient Descent
Khi tập dữ liệu có nhiều mẫu, thay vì cập nhật $`w, b`$ sau từng điểm,ta tính trung bình loss trên một mini-batch.
- Với tập dữ liệu có $`N`$ mẫu và mini-batch gồm $`m`$ mẫu ($`1 < m < N`$):
- Mỗi lần cập nhật là 1 mini-batch update
- Sau khi đi qua toàn bộ dữ liệu ($`N/m`$ mini-batch), ta hoàn thành 1 epoch

Hình 8: Quy trình thực hiện mini-batch với m samples
Ưu điểm:
- Giảm thời gian tính toán mỗi bước
- Giới thiệu nhiễu ngẫu nhiên giúp tránh cực tiểu cục bộ
- Tăng tốc độ hội tụ trong thực tế
Tóm tắt quy trình Linear Regression với Gradient Descent
- Khởi tạo ngẫu nhiên $`w, b`$
- Dự đoán giá trị $`\hat{y} = wx + b`$
- Tính hàm mất mát $`\mathcal{L} = (y - \hat{y})^2`$
- Tính đạo hàm $`\frac{\partial \mathcal{L}}{\partial w}, \frac{\partial \mathcal{L}}{\partial b}`$
- Cập nhật tham số theo gradient descent
- Lặp lại qua nhiều epoch cho đến khi hội tụ (Loss không giảm đáng kể)
Chưa có bình luận nào. Hãy là người đầu tiên!