Hiểu về Vector hóa trong Hồi quy Tuyến tính

1. Giới thiệu: Từ Công Thức Quen Thuộc Đến Nền Tảng Deep Learning
Hãy cùng xem xét biểu thức quen thuộc này:
$$\hat{y} = ax + b \tag{1}$$
Đây chính là công thức cơ bản nhất của hồi quy tuyến tính. Tùy vào cách hiểu về $a$, $x$, $b$, và các phép toán $+$, $\cdot$, biểu thức "$ax + b$" có thể vừa là mô hình machine learning đầu tiên sinh viên gặp, vừa là thành phần chính của neural network xử lý hàng triệu tham số.
Sự chuyển đổi từ dạng cơ bản sang hiện đại được định hình bởi hai nguyên lý toán học:
Khái quát hóa - mở rộng ý nghĩa của các ký hiệu đơn giản như $+$ và $\cdot$ để làm được nhiều việc hơn.
Trừu tượng hóa - biến các biểu thức phức tạp trở lại thành dạng đơn giản $a$, $b$, và $x$.
Hai quá trình này cho phép chúng ta coi hàm số như vector, dùng ma trận như số mũ, và xây dựng các cấu trúc toán học phức tạp từ những viên gạch đơn giản.
Bài viết này sẽ khám phá cách công thức (1) dạy ta về vector hóa - không chỉ giúp code chạy nhanh hơn hàng nghìn lần, mà còn là nền tảng để hiểu kiến trúc deep learning hiện đại.
2. Từ Một Điểm Đến Một Đám Mây Điểm: Vấn Đề Cơ Bản
Bài toán cơ bản của machine learning: dự đoán một biến từ một biến khác. Về mặt toán học, ta cần tìm hàm số $y = h(x)$ mô tả mối quan hệ giữa biến dự báo $x$ và biến mục tiêu $y$.
Ý tưởng đơn giản nhất? Giả định mối quan hệ này là tuyến tính và sử dụng công thức (1). Nếu $x$ là biến dự báo và $a$ định lượng ảnh hưởng của nó lên $y$, thì phép nhân "$\cdot$" tính tổng đóng góp của $x$ vào $y$. Hay, ta đang cố fit 1 đường thẳng vào một đám mây điểm.

Khi mới học hồi quy tuyến tính, nhiều người thường triển khai thuật toán bằng vòng lặp - tính từng bước, từng mẫu một. Cách này dễ hiểu nhưng lại có nhiều vấn đề về hiệu suất và khả năng mở rộng.
Vậy làm sao công thức (1) trở thành building block của neural networks? Câu trả lời nằm ở vector hóa - bước nhảy từ mặt phẳng vào không gian nhiều chiều.
3. Bước Vào Không Gian Nhiều Chiều
3.1. Từ Một Biến Đến Nhiều Biến
Mô hình (1) không đủ tốt trong hầu hết trường hợp thực tế. Lý do? Nó không xử lý được nhiều biến dự báo. Trong thực tế, dữ liệu thường có nhiều mẫu, mỗi mẫu không chỉ có một đặc trưng $x$ đơn lẻ mà có cả một bộ: $x_1, x_2, \dots, x_d$.
Lấy ví dụ dự đoán giá bất động sản. Giá nhà không chỉ phụ thuộc vào một yếu tố mà bị ảnh hưởng bởi vị trí, diện tích, số phòng, tuổi nhà, v.v. Thay vì một $x$ cô đơn, ta có cả một chuỗi: $x_1, x_2, \ldots, x_d$.
Mô hình hồi quy tuyến tính dự đoán $\hat{y}$ bằng cách tính tổ hợp tuyến tính của các đặc trưng. Vì mỗi biến có ảnh hưởng khác nhau, ta tính riêng hiệu ứng $w_i x_i$ cho từng đặc trưng, rồi cộng chúng lại:
$$\hat{y} = w_1 x_1 + w_2 x_2 + \cdots + w_d x_d + b \tag{2}$$
Sau khi khái quát hóa mô hình từ một sang nhiều biến, đến lúc trừu tượng hóa.
3.2. Vector Xuất Hiện
Về mặt toán học, ta lưu biến dự báo trong một vector:
$$\mathbf{x} = \begin{bmatrix} x_1 \ x_2 \ \vdots \ x_d \end{bmatrix} \tag{3}$$
và vector trọng số:
$$\mathbf{w} = \begin{bmatrix} w_1 \ w_2 \ \vdots \ w_d \end{bmatrix} \tag{4}$$
Định nghĩa phép nhân "$\cdot$" giữa hai vector bằng tích vô hướng (dot product):
$$\mathbf{w} \cdot \mathbf{x} = w_1 x_1 + w_2 x_2 + \cdots + w_d x_d \tag{5}$$
Khi đó mô hình có dạng đẹp đẽ:
$$\hat{y} = \mathbf{w}^\top \mathbf{x} + b \tag{6}$$
Nhìn kỹ lại - biểu thức này giống hệt công thức (1)! Chỉ khác là toán tử nhân đã được nạp chồng (overloaded). Việc khái quát hóa "$\cdot$" vẫn giữ nguyên ý nghĩa: nếu $x$ là biến dự báo và $a$ định lượng ảnh hưởng, thì "$\cdot$" tính tổng đóng góp vào $y$.
Kết quả là tích vô hướng - viên đá góc của toán học với nhiều tính chất hữu ích và diễn giải hình học sâu sắc.
Quá trình gom nhiều scalar thành một vector này chính là vector hóa (vectorization).
4. Vector Hóa: Hai Mặt Của Đồng Xu
Vector hóa có hai lớp ý nghĩa khác nhau: một về toán học, một về tính toán. Phần trên ta đã thấy khía cạnh toán học - nạp chồng các ký hiệu để làm nhiều việc hơn.
Nhưng còn một khía cạnh khác quan trọng không kém - lý do vector hóa trở thành cốt lõi của deep learning hiện đại.
4.1. Tại Sao Vector Hóa Lại Quan Trọng?
Code được vector hóa nhanh hơn cực kỳ nhiều so với vòng lặp vì hai lý do:
-
Song song hóa - CPU và GPU hiện đại thực hiện nhiều phép toán cùng lúc
-
Bộ nhớ liên tục - các phần tử được lưu kế tiếp nhau, giảm thời gian truy cập
Code vector hóa làm machine learning khả thi.
Giải pháp? Tận dụng các phép tính vector/matrix đã được tối ưu trong NumPy, PyTorch thay vì tự viết vòng lặp Python.
5. Từ Vòng Lặp Đến Vector Hóa: Khác Biệt Ra Sao?
Để thấy rõ sự khác biệt, hãy xem cách dự đoán $\hat{y}$.
Giả sử có:
-
Ma trận đặc trưng $X$ kích thước $n \times d$ (mỗi trong $n$ hàng là một mẫu với $d$ đặc trưng)
-
Vector trọng số $\mathbf{w}$ kích thước $d \times 1$
-
Bias $b$ là số vô hướng
Mục tiêu: tính vector dự đoán $\hat{\mathbf{y}}$ kích thước $n \times 1$ cho toàn bộ $n$ mẫu.
5.1. Cách 1 – Vòng Lặp Thủ Công (Không Vector Hóa)
Cách truyền thống: lấy từng mẫu, tính $\hat{y}$ bằng cách nhân từng đặc trưng với trọng số tương ứng rồi cộng dồn:
# Giả sử X có shape (n, d), w có shape (d,), b là số
y_hat = np.zeros(n)
for i in range(n): # lặp qua từng mẫu
y_pred_i = b # khởi tạo với bias
for j in range(d): # lặp qua từng đặc trưng
y_pred_i += X[i, j] * w[j] # cộng dồn w_j * x_ij
y_hat[i] = y_pred_i # lưu dự đoán
Cách này dễ hiểu - bám sát định nghĩa toán $\hat{y}^{(i)} = \sum_{j} w_j x_{ij} + b$. Nhưng nhược điểm? Chậm và code dài dòng.
Với Python, vòng lặp chạy chậm vì thông dịch viên phải xử lý từng phần tử một. Cộng hai vector 10,000 phần tử bằng vòng lặp có thể mất 5 giây, trong khi NumPy chỉ tốn 0.0004 giây – nhanh hơn gấp hàng nghìn lần!
5.2. Cách 2 – Vector Hóa Với Phép Nhân Ma Trận
Thay vì tự lặp, dùng trực tiếp phép nhân ma trận đã được tối ưu. Công thức vector cho toàn bộ batch:
$$\hat{\mathbf{y}} = X \mathbf{w} + b \tag{7}$$
Trong NumPy, chỉ cần một dòng:
y_hat = X.dot(w) + b # hoặc X @ w + b
Đoạn code này tương đương hoàn toàn với vòng lặp, nhưng ngắn gọn và nhanh hơn rất nhiều. NumPy (hay PyTorch, TensorFlow) đã tối ưu phép nhân ma trận bằng C/C++ và tận dụng vector hóa ở mức CPU/GPU.
Bonus: code ngắn cũng giảm bug - không sợ cộng nhầm chỉ số hay quên cập nhật biến trong vòng lặp.
5.3. Một Mẫu vs Nhiều Mẫu
Với một mẫu đơn $\mathbf{x}$, công thức dự đoán là công thức (6). Nếu chỉ có một mẫu, vector hóa hay không cũng không khác biệt nhiều.
Nhưng với nhiều mẫu? Nếu áp dụng công thức từng mẫu tuần tự thì chi phí tỉ lệ thuận với số mẫu.
Thay vào đó, xếp tất cả mẫu thành ma trận $X$ và tính công thức (7) chỉ với một phép nhân. Thư viện tự động thực hiện song song - CPU tính nhiều phép nhân cùng lúc, hoặc GPU xử lý hàng loạt cực nhanh.
Với vector hóa, xử lý cả batch gần như nhanh bằng xử lý một mẫu. Nếu mỗi mẫu tốn 1 đơn vị thời gian, thì $n$ mẫu tuần tự tốn $n$ đơn vị. Nhưng vector hóa có thể chỉ tốn ~1 đơn vị cho cả batch!
Đó chính là sức mạnh vector hóa: tận dụng tính toán song song và tối ưu đại số tuyến tính.
6. Tính Loss Cho Cả Batch
Sau khi có dự đoán $\hat{\mathbf{y}}$, bước tiếp theo là tính độ sai lệch so với nhãn thực. Hàm mất mát phổ biến cho hồi quy là Mean Squared Error (MSE) - trung bình bình phương sai số.
Với mẫu $i$, nếu $\hat{y}^{(i)}$ là dự đoán và $y^{(i)}$ là nhãn thật:
$$\ell^{(i)} = \frac{1}{2}(\hat{y}^{(i)} - y^{(i)})^2 \tag{8}$$
Hệ số $\frac{1}{2}$ không ảnh hưởng nhiều nhưng tiện cho việc đạo hàm (triệt tiêu với mũ 2). Loss cho toàn bộ $n$ mẫu:
$$L(\mathbf{w}, b) = \frac{1}{n}\sum_{i=1}^n \frac{1}{2}\big(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\big)^2 \tag{9}$$
Viết gọn bằng vector: tính vector sai số $\mathbf{e} = \hat{\mathbf{y}} - \mathbf{y}$, thì:
$$L = \frac{1}{2n}|\mathbf{e}|^2 \tag{10}$$
6.1. Vector Hóa Việc Tính Loss
Với NumPy, thay vì lặp qua từng phần tử để bình phương rồi cộng, ta tính toàn bộ trong một lần:
loss = np.mean((y_hat - y)**2) / 2
Phép tính y_hat - y trả về vector sai số, sau đó bình phương và lấy trung bình cho kết quả theo công thức (10). Tất cả đều thực hiện dưới dạng vector mà không cần vòng lặp Python.
7. Gradient Descent: Làm Sao Cập Nhật Tham Số?
Câu hỏi quan trọng: làm sao cập nhật $\mathbf{w}, b$ để giảm loss?
Dùng gradient descent - thuật toán đi xuống theo đạo hàm. Ý tưởng đơn giản: tính gradient của hàm loss theo tham số, rồi điều chỉnh tham số ngược hướng gradient (hướng giảm loss).
Với hàm loss MSE, công thức đạo hàm dạng vector:
$$\nabla_{\mathbf{w}}L(\mathbf{w},b) = \frac{1}{n} X^\top (\hat{\mathbf{y}} - \mathbf{y}) \tag{11}$$
$$\nabla_{b}L(\mathbf{w},b) = \frac{1}{n} \sum_{i=1}^n (\hat{y}^{(i)} - y^{(i)}) \tag{12}$$
Kết quả khá đẹp: gradient theo $\mathbf{w}$ là tích $X^\top$ với vector sai số, còn gradient theo $b$ là trung bình các sai số.
Dựa vào gradient, gradient descent cập nhật:
$$\mathbf{w} := \mathbf{w} - \eta \nabla_{\mathbf{w}}L \tag{13}$$
$$b := b - \eta \nabla_{b}L \tag{14}$$
trong đó $\eta$ là learning rate - hệ số nhỏ quyết định bước nhảy mỗi lần cập nhật. Quá trình này lặp lại qua nhiều epoch.
7.1. Triển Khai Vector Hóa
Với vòng lặp: lặp qua từng mẫu, tính gradient từ mẫu đó rồi cộng dồn. Phải dùng hai tầng vòng lặp - code dài và dễ sai.
Với vector hóa: tận dụng công thức matrix. Tính vector sai số $\mathbf{e} = \hat{\mathbf{y}} - \mathbf{y}$ cho cả batch, rồi:
# Giả sử đã có y_hat từ bước dự đoán
e = y_hat - y # vector sai số
grad_w = X.T.dot(e) / len(X) # gradient theo w
grad_b = np.mean(e) # gradient theo b
# Cập nhật
w = w - lr * grad_w
b = b - lr * grad_b
Chỉ vài dòng đã xong việc mà vòng lặp phải viết rất dài. Quan trọng hơn: chạy nhanh hơn nhiều nhờ phép nhân ma trận được tối ưu.
8. Từ Vector-Scalar Đến Vector-Vector
8.1. Nhiều Biến Mục Tiêu
Cho đến giờ, input là vector $\mathbf{x}$ nhưng output vẫn là scalar $\hat{y}$. Liệu đã đủ?
Chưa đâu! Thực tế thường có nhiều biến mục tiêu. Ví dụ dự đoán sản xuất của vi sinh vật - không chỉ ethanol mà còn hàng trăm metabolite khác. Thay vì một $y$ đơn lẻ, ta có: $y_1, y_2, \ldots, y_m$.
Đang chuyển từ mô hình vector-scalar sang vector-vector.
Nghĩ hàm vector-vector $\mathbf{h}$ như một vector của các hàm vector-scalar. Nếu mỗi hàm là tuyến tính:
$$\mathbf{h}(\mathbf{x}) = \begin{bmatrix} \mathbf{w}_1^\top \mathbf{x} + b_1 \ \mathbf{w}_2^\top \mathbf{x} + b_2 \ \vdots \ \mathbf{w}_m^\top \mathbf{x} + b_m \end{bmatrix} \tag{15}$$
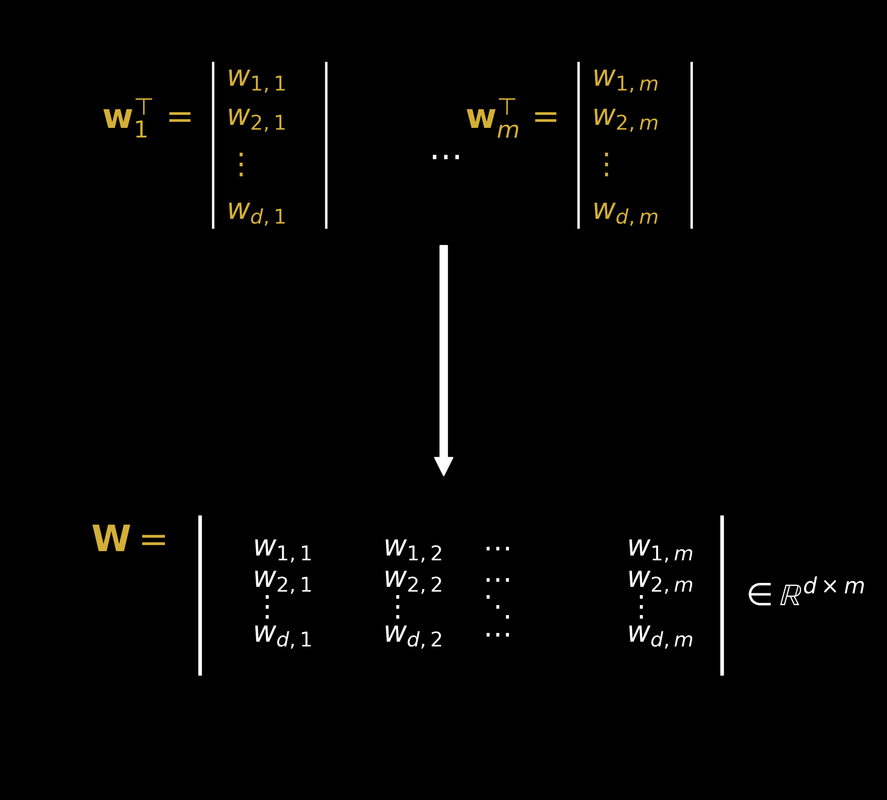
8.2. Ma Trận Trọng Số
Cách đơn giản hóa? Nối các $\mathbf{w}_j^\top$ thành ma trận trọng số $W$:
$$W = \begin{bmatrix} \mathbf{w}_1^\top \ \mathbf{w}_2^\top \ \vdots \ \mathbf{w}_m^\top \end{bmatrix} \tag{16}$$
Mô hình trở thành:
$$\mathbf{h}(\mathbf{x}) = W\mathbf{x} + \mathbf{b} \tag{17}$$
Nhìn lại công thức (1) - chúng gần như giống nhau! Nhưng phiên bản vector hóa xử lý được:
-
Nhiều đặc trưng đầu vào ($d$ chiều)
-
Nhiều đầu ra ($m$ chiều)
-
Tất cả với một công thức đơn giản
9. Xử Lý Cả Batch Cùng Lúc
9.1. Ma Trận Dữ Liệu
Bước cuối cùng để đạt dạng hoàn chỉnh.
Dữ liệu thường đến theo batch - chuỗi mẫu $\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n$ xếp chồng thành ma trận $X$:
$$X = \begin{bmatrix} \mathbf{x}_1^\top \ \mathbf{x}_2^\top \ \vdots \ \mathbf{x}_n^\top \end{bmatrix} \tag{18}$$
Ma trận $n \times d$ với $n$ mẫu, mỗi mẫu $d$ đặc trưng.
9.2. Broadcasting
Áp dụng $\mathbf{h}$ cho toàn bộ $X$:
$$\mathbf{h}(X) = XW^\top + \mathbf{b} \tag{19}$$
Vector $\mathbf{b}$ tự động "mở rộng" để khớp với từng hàng của ma trận - gọi là broadcasting. Trong NumPy, điều này được tích hợp sẵn.
import numpy as np
def h(X, A, b):
return X @ A + b
X = np.array([[1, 2, 3],
[4, 5, 6]])
A = np.array([[0.1, 0.2],
[0.3, 0.4],
[0.5, 0.6]])
b = np.array([-1, 1])
h(X, A, b)
# Out[4]: array([[1.2, 3.8],
# [3.9, 7.4]])
Với ký hiệu thông dụng trong deep learning:
$$\hat{Y} = XW + \mathbf{b} \tag{20}$$
trong đó $W$ kích thước $d \times m$, $X$ kích thước $n \times d$, $\hat{Y}$ kích thước $n \times m$.
9.3. Code Minh Họa
import numpy as np
# Tạo dữ liệu
n_samples = 1000 # số mẫu
n_features = 100 # số đặc trưng
n_outputs = 10 # số đầu ra
X = np.random.randn(n_samples, n_features)
W = np.random.randn(n_features, n_outputs)
b = np.random.randn(n_outputs)
# CHỈ MỘT DÒNG!
Y_hat = X @ W + b
print(f"X: {X.shape}") # (1000, 100)
print(f"W: {W.shape}") # (100, 10)
print(f"b: {b.shape}") # (10,)
print(f"Y_hat: {Y.shape}") # (1000, 10)
Vậy là hoàn thành vòng khái quát hóa và trừu tượng hóa! Đã đạt được:
-
Xử lý nhiều đặc trưng và nhiều mục tiêu
-
Không có độ phức tạp thêm trong mô hình
-
Triển khai song song batch với cấu trúc dữ liệu hiệu quả
Nếu quen neural networks, công thức (20) chính là linear layer (fully connected layer) - một trong những building block phổ biến nhất.
10. Thực Hành: Huấn Luyện Mô Hình
Tóm tắt các bước huấn luyện và thấy rõ lợi ích vector hóa.
Giả sử có $n$ mẫu, batch kích thước $B$. Thuật toán (mini-batch SGD) lặp qua nhiều epoch:
-
Khởi tạo $\mathbf{w}, b$ (thường random nhỏ)
-
Với mỗi batch:
-
Lấy batch $X$ (shape $B \times d$) và nhãn $\mathbf{y}$ (shape $B \times 1$)
-
Dự đoán: $\hat{\mathbf{y}} = X \mathbf{w} + b$
-
Loss: $L = \frac{1}{2B}|\hat{\mathbf{y}} - \mathbf{y}|^2$
-
Gradient:
grad_w = X.T @ (y_hat - y) / B,grad_b = np.mean(y_hat - y) -
Cập nhật:
w -= lr * grad_w,b -= lr * grad_b
- Lặp cho batch tiếp theo
Điểm mấu chốt: không hề có vòng lặp for duyệt qua từng mẫu hay đặc trưng. Mọi phép tính đã "gói" thành tensor và giao cho thư viện xử lý. Nhờ đó thuật toán chạy nhanh và tận dụng phần cứng tốt.
11. So Sánh Hiệu Suất Thực Tế
Xem sự khác biệt qua ví dụ cụ thể:
import numpy as np
import time
def non_vectorized_linear_regression(X, y, learning_rate=0.01, epochs=100):
"""Linear regression KHÔNG vector hóa"""
n_samples, n_features = X.shape
weights = np.zeros(n_features)
bias = 0
losses = []
start_time = time.time()
for epoch in range(epochs):
total_loss = 0
grad_weights = np.zeros(n_features)
grad_bias = 0
# Duyệt từng sample
for i in range(n_samples):
# Tính prediction cho MỖI sample
prediction = bias
for j in range(n_features):
prediction += weights[j] * X[i, j]
error = prediction - y[i]
total_loss += error ** 2
# Tính gradients
for j in range(n_features):
grad_weights[j] += 2 * X[i, j] * error
grad_bias += 2 * error
# Average gradients
grad_weights /= n_samples
grad_bias /= n_samples
losses.append(total_loss / n_samples)
# Update
for j in range(n_features):
weights[j] -= learning_rate * grad_weights[j]
bias -= learning_rate * grad_bias
return weights, bias, losses, time.time() - start_time
def vectorized_linear_regression(X, y, learning_rate=0.01, epochs=100):
"""Linear regression ĐƯỢC vector hóa"""
n_samples, n_features = X.shape
weights = np.zeros(n_features)
bias = 0
losses = []
start_time = time.time()
for epoch in range(epochs):
# TẤT CẢ samples cùng lúc
predictions = X @ weights + bias
errors = predictions - y
loss = np.mean(errors ** 2)
losses.append(loss)
# Gradients cho TẤT CẢ samples
grad_weights = (2 / n_samples) * (X.T @ errors)
grad_bias = (2 / n_samples) * np.sum(errors)
# Update
weights -= learning_rate * grad_weights
bias -= learning_rate * grad_bias
return weights, bias, losses, time.time() - start_time
# Test
np.random.seed(42)
n_samples = 1000
n_features = 100
X = np.random.randn(n_samples, n_features)
true_weights = np.random.randn(n_features)
y = X @ true_weights + 2.5 + 0.1 * np.random.randn(n_samples)
# So sánh
print("Training NON-vectorized...")
w1, b1, losses1, time1 = non_vectorized_linear_regression(X, y, epochs=50)
print("Training VECTORIZED...")
w2, b2, losses2, time2 = vectorized_linear_regression(X, y, epochs=50)
print(f"\\n{'='*60}")
print(f"KẾT QUẢ:")
print(f"{'='*60}")
print(f"Thời gian không vector hóa: {time1:.4f} giây")
print(f"Thời gian vector hóa: {time2:.4f} giây")
print(f"Tăng tốc: {time1/time2:.2f}x NHANH HƠN!")
print(f"{'='*60}")
Kết quả điển hình trên máy tính thường:
============================================================
KẾT QUẢ:
============================================================
Thời gian không vector hóa: 3.1283 giây
Thời gian vector hóa: 0.0032 giây
Tăng tốc: 982.27x NHANH HƠN!
============================================================
Sự khác biệt hơn 950 lần! Con số này còn lớn hơn nếu:
-
Số mẫu ($n$) tăng
-
Số đặc trưng ($d$) tăng
-
Dùng GPU thay vì CPU
12. Gradient Descent Vector Hóa: Đi Sâu Hơn
Xem chi tiết toán học đằng sau gradient descent vector hóa. Hàm loss từ công thức (9), viết dạng vector với $\hat{\mathbf{y}} = X\mathbf{w} + b$:
$$L(\mathbf{w}) = \frac{1}{n}(X\mathbf{w} + b - \mathbf{y})^\top(X\mathbf{w} + b - \mathbf{y}) \tag{21}$$
Gradient:
$$\nabla_{\mathbf{w}} L(\mathbf{w}) = \frac{2}{n} X^\top(X\mathbf{w} + b - \mathbf{y}) \tag{22}$$
12.1. Code Hoàn Chỉnh
def vectorized_gradient_descent(X, y, learning_rate=0.01, epochs=1000, tolerance=1e-6):
"""
Gradient descent vector hóa hoàn chỉnh với kiểm tra hội tụ
"""
m, n = X.shape
# Thêm cột 1 cho bias
X_b = np.c_[np.ones((m, 1)), X]
w_b = np.zeros(n + 1) # Bao gồm cả bias
losses = []
for epoch in range(epochs):
# Predictions - VECTORIZED
predictions = X_b @ w_b
# Loss - VECTORIZED
loss = np.mean((predictions - y) ** 2)
losses.append(loss)
# Gradient - VECTORIZED
gradients = (2/m) * X_b.T @ (predictions - y)
gradient_norm = np.linalg.norm(gradients)
# Update - VECTORIZED
w_b -= learning_rate * gradients
# Kiểm tra hội tụ
if gradient_norm < tolerance:
print(f"Hội tụ sau {epoch} epochs (gradient norm: {gradient_norm:.2e})")
break
if epoch % 100 == 0:
print(f"Epoch {epoch}: Loss = {loss:.6f}, Gradient norm = {gradient_norm:.6f}")
return w_b[1:], w_b[0], losses
# Ridge Regression với L2 regularization
def ridge_regression_vectorized(X, y, alpha=0.1, learning_rate=0.01, epochs=1000):
"""
Ridge regression vector hóa
Loss: L = MSE + alpha * ||w||^2
"""
m, n = X.shape
X_b = np.c_[np.ones((m, 1)), X]
w_b = np.zeros(n + 1)
losses = []
for epoch in range(epochs):
predictions = X_b @ w_b
error = predictions - y
# Loss với L2 regularization
mse_loss = np.mean(error ** 2)
reg_loss = alpha * np.sum(w_b[1:] ** 2) # Không regularize bias
total_loss = mse_loss + reg_loss
losses.append(total_loss)
# Gradient
grad_mse = (2/m) * X_b.T @ error
grad_reg = np.r_[0, 2 * alpha * w_b[1:]] # Bias không bị regularize
gradients = grad_mse + grad_reg
w_b -= learning_rate * gradients
return w_b[1:], w_b[0], losses
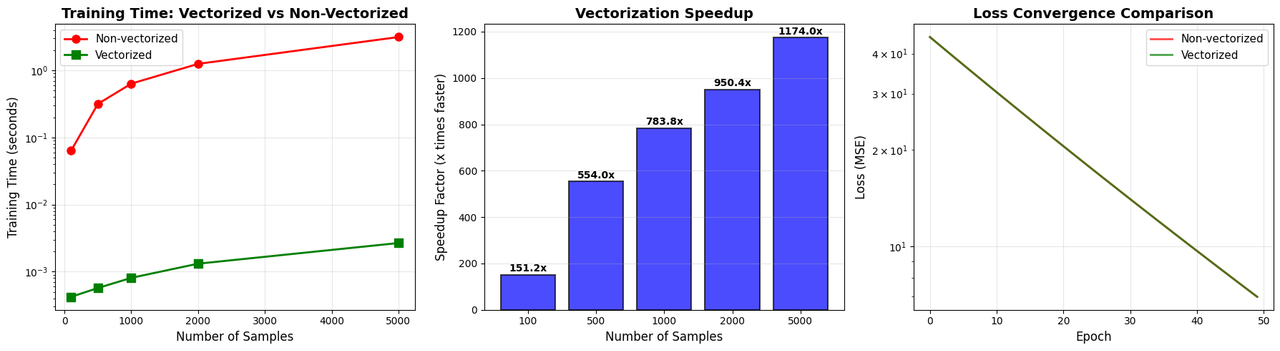
13. Minh Họa Sức Mạnh Vector Hóa
Tạo visualization để thấy rõ ưu thế:
import matplotlib.pyplot as plt
def benchmark_vectorization(n_samples_list, n_features=50, epochs=10):
"""
Benchmark hiệu suất với các kích thước dữ liệu khác nhau
"""
results = {
'n_samples': [],
'non_vec_time': [],
'vec_time': [],
'speedup': []
}
for n_samples in n_samples_list:
print(f"\\nTest với {n_samples} mẫu...")
# Tạo dữ liệu
X = np.random.randn(n_samples, n_features)
true_w = np.random.randn(n_features)
y = X @ true_w + np.random.randn(n_samples) * 0.1
# So sánh
_, _, _, time_non_vec = non_vectorized_linear_regression(X, y, epochs=epochs)
_, _, _, time_vec = vectorized_linear_regression(X, y, epochs=epochs)
results['n_samples'].append(n_samples)
results['non_vec_time'].append(time_non_vec)
results['vec_time'].append(time_vec)
results['speedup'].append(time_non_vec / time_vec)
print(f" Không vector hóa: {time_non_vec:.4f}s")
print(f" Vector hóa: {time_vec:.4f}s")
print(f" Tăng tốc: {time_non_vec/time_vec:.2f}x")
return results
# Chạy benchmark
n_samples_list = [100, 500, 1000, 2000, 5000]
results = benchmark_vectorization(n_samples_list, n_features=50, epochs=20)
# Visualization
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
# Plot 1: So sánh thời gian
axes[0].plot(results['n_samples'], results['non_vec_time'],
marker='o', linewidth=2, markersize=8,
label='Không vector hóa', color='red')
axes[0].plot(results['n_samples'], results['vec_time'],
marker='s', linewidth=2, markersize=8,
label='Vector hóa', color='green')
axes[0].set_xlabel('Số mẫu', fontsize=12)
axes[0].set_ylabel('Thời gian huấn luyện (giây)', fontsize=12)
axes[0].set_title('So Sánh Thời Gian Huấn Luyện', fontsize=14, fontweight='bold')
axes[0].legend(fontsize=11)
axes[0].grid(True, alpha=0.3)
axes[0].set_yscale('log')
# Plot 2: Tốc độ tăng
axes[1].bar(range(len(results['n_samples'])), results['speedup'],
color='blue', alpha=0.7, edgecolor='black', linewidth=1.5)
axes[1].set_xlabel('Số mẫu', fontsize=12)
axes[1].set_ylabel('Hệ số tăng tốc (lần)', fontsize=12)
axes[1].set_title('Tăng Tốc Nhờ Vector Hóa', fontsize=14, fontweight='bold')
axes[1].set_xticks(range(len(results['n_samples'])))
axes[1].set_xticklabels(results['n_samples'])
axes[1].grid(True, alpha=0.3, axis='y')
for i, speedup in enumerate(results['speedup']):
axes[1].text(i, speedup + 5, f'{speedup:.1f}x',
ha='center', va='bottom', fontweight='bold', fontsize=10)
# Plot 3: Hội tụ loss
np.random.seed(42)
X_demo = np.random.randn(1000, 50)
y_demo = X_demo @ np.random.randn(50) + np.random.randn(1000) * 0.1
_, _, losses_non_vec, _ = non_vectorized_linear_regression(X_demo, y_demo, epochs=50)
_, _, losses_vec, _ = vectorized_linear_regression(X_demo, y_demo, epochs=50)
axes[2].plot(losses_non_vec, label='Không vector hóa',
color='red', alpha=0.7, linewidth=2)
axes[2].plot(losses_vec, label='Vector hóa',
color='green', alpha=0.7, linewidth=2)
axes[2].set_xlabel('Epoch', fontsize=12)
axes[2].set_ylabel('Loss (MSE)', fontsize=12)
axes[2].set_title('Quá Trình Hội Tụ', fontsize=14, fontweight='bold')
axes[2].legend(fontsize=11)
axes[2].grid(True, alpha=0.3)
axes[2].set_yscale('log')
plt.tight_layout()
plt.savefig('vectorization_comparison.png', dpi=300, bbox_inches='tight')
plt.show()
print("\\n" + "="*70)
print("TÓM TẮT: TẠI SAO VECTOR HÓA QUAN TRỌNG")
print("="*70)
print(f"Tăng tốc trung bình: {np.mean(results['speedup']):.2f}x")
print(f"Tăng tốc tối đa: {np.max(results['speedup']):.2f}x")
print(f"Tăng tốc tối thiểu: {np.min(results['speedup']):.2f}x")
print("="*70)
14. Kết Luận
Vậy là chúng ta đã đi hết hành trình từ công thức đơn giản $ax + b$ đến vector hóa hoàn chỉnh trong machine learning.
Những Điểm Quan Trọng
Vector hóa về toán học: Cho phép khái quát từ công thức đơn giản thành các phép toán ma trận phức tạp, xử lý nhiều đặc trưng và nhiều mục tiêu cùng lúc.
Vector hóa về tính toán: Tăng tốc độ lên hàng nghìn lần nhờ song song hóa và tối ưu bộ nhớ.
Nền tảng Deep Learning: Mọi kiến trúc neural network hiện đại đều xây trên các phép toán ma trận được vector hóa.
Vector hóa không chỉ là kỹ thuật tối ưu - nó là ngôn ngữ cốt lõi của machine learning hiện đại. Từ công thức (1) đơn giản đến công thức (20) xử lý batch, chúng ta đã thấy cách toán học và lập trình kết hợp để tạo nên sức mạnh.
Khi viết code machine learning, hãy luôn nghĩ: "Mình có thể vector hóa phần này không?" Câu trả lời thường là có, và lợi ích luôn đáng giá.
Tham Khảo
[1] Book, Mathematics for Machine Learning by Marc Peter Deisenroth, A Aldo Faisal, and Cheng Soon Ong
[2] Notes, CS229 lecture notes by Stanford
[3] Course, Machine Learning course by Stanford on Coursera
[4] Course, Mathematics for Machine Learning by Imperial College London on Coursera
[5] Notes, Computing Neural Network Gradients by Kevin Vlark
Chưa có bình luận nào. Hãy là người đầu tiên!