Hàm Mất Mát (loss function) là một trong những thành phần quan trọng nhất trong machine learning — nó đóng vai trò như trái tim trong quá trình huấn luyện. Đúng như tên gọi, nó đo lường mức độ “thua lỗ” hoặc sai lệch của mô hình dự đoán. Về mặt toán học, nó định lượng độ sai lệch giữa dự đoán của mô hình và giá trị thực tế.
Để hiểu khái niệm về sự mất mát (loss), hãy tưởng tượng bạn đang chơi bắn cung. Mục tiêu là bắn trúng tâm màu vàng – đây đại diện cho dự đoán chính xác.Và thay vì đo lường mức độ bắn trúng mục tiêu , thì chúng ta đo lường mức độ nó trượt mục tiêu – và gọi đó là Mất Mát.
Trong bắn cung, bia sẽ được chia thành 4 lớp màu. Và khi bắn trúng màu :
🟡 Vàng (tâm bia): Cú bắn xuất sắc
🔴 Đỏ: Gần tâm bia, rất tốt
🔵 Xanh dương: Xa so với tâm
⚫ Đen: Gần như ra khỏi bia
Đây là cách chúng ta diễn giải “Mất Mát”:
- 🎯 Trúng vàng: Không trượt → Mất mát = 0 (Hoàn hảo)
- 🔴 Trúng đỏ: Gần mục tiêu → Mất mát thấp (Tốt)
- 🔵⚫ Trúng xanh lam hoặc đen: Xa mục tiêu → Mất mát cao (Tệ)
Từ giá trị “Mất Mát” này, cung thủ biết cách điều chỉnh cú bắn tiếp theo để đến gần tâm màu vàng hơn.
Đây chính xác là cách một Hàm Mất Mát hướng dẫn một mô hình học máy.
Trong Machine Learning
Một hàm Mất Mát nhận vào giá trị và trả về mức phạt (penalty):
-
Input: Giá trị thật $Y_{true}$ và dự đoán của mô hình ($Y_{pred}$)
-
Output: Một con số duy nhất (sai số / loss) thể hiện mức độ sai lệch
Mục tiêu cốt lõi của Hàm Mất Mát là hướng dẫn mô hình học trong quá trình huấn luyện. Sau đó sẽ “nói” với mô hình: “Sai ở mức này nè nha.”
Tiếp theo, mô hình sẽ sử dụng điểm số này để điều chỉnh các tham số nội bộ (trọng số và độ lệch) nhằm giảm sự mất mát trong các lần lặp tiếp theo – dần dần cải thiện độ chính xác và tiến gần hơn đến mức mất mát bằng không (loss = 0)
Vòng lặp huấn luyện của hàm loss hoạt động như thế nào
Hàm loss nằm ở trung tâm của vòng lặp học liên tục, gồm các bước sau:
Bước 1 - Thực hiện dự đoán: Mô hình nhận một đầu vào (input), có thể là hình ảnh, câu văn, hay một con số, và tạo ra một đầu ra (output) — đây được gọi là dự đoán.
Bước 2 - Tính toán Mất Mát: Hàm Mất Mát sẽ so sánh dự đoán của mô hình với giá trị thật và tính xem mô hình sai lệch bao nhiêu. Sai lệch đó được gọi là Mất Mát.
Bước 3 - Tính Gradient: Sử dụng thuật toán như lan truyền ngược (backpropagation) (trong mạng nơ-ron), mô hình sẽ tính toán gradient — cho biết mỗi tham số (trọng số/độ lệch) đã góp phần bao nhiêu vào lỗi vừa rồi.
⇒ Nói đơn giản: đây là bước tìm truy tìm trách nhiệm tạo ra lỗi tại phần nào của mô hình.
Bước 4 - Cập nhật tham số : Một bộ tối ưu hóa như Gradient Descent sử dụng các gradient để điều chỉnh tham số của mô hình theo cách giúp giảm Mất Mát trong lần dự đoán tiếp theo.
⇒ Giống như học từ sai lầm và chỉnh lại mục tiêu cho chính xác hơn.
Bước 5 - Lặp lại quá trình : Vòng lặp này sẽ được lặp đi lặp lại hàng nghìn hoặc thậm chí hàng triệu lần trên nhiều ví dụ huấn luyện – liên tục giảm Mất Mát –cho đến khi mô hình đạt độ chính xác tốt nhất có thể.
Các Loại Hàm Mất Mát Thường Gặp
Các hàm Mất Mát được phân loại rộng rãi dựa trên các tính chất toán học của chúng – điều này quyết định liệu chúng có phù hợp để huấn luyện (tối ưu hóa) hay chỉ để đánh giá.
Hàm Mất Mát Gián Đoạn/ Không Liên Tục (Discontinuous Loss Functions)
Một hàm mất mát Gián Đoạn là hàm mà giá trị Mất Mát nhảy đột ngột thay vì thay đổi một cách từ tốn.
Hãy tưởng tượng nó giống như dùng thang máy đi thẳng từ tầng trệt lên tầng 3 – mà không cần bước qua tầng 1 hoặc tầng 2 một cách từ từ. Tương tự, các hàm Mất Mát Gián Đoạn nhảy tức thì giữa các giá trị mà không có sự chuyển tiếp dần dần.
Những hàm này lý tưởng để đo lường độ chính xác, nhưng không phù hợp để huấn luyện vì chúng không khả vi – tức là không thể tính gradient để tối ưu cho mô hình.
1. Mất Mát 0–1 (Zero-One Loss)
- Dùng trong: Phân loại nhị phân (binary) hoặc đa lớp (multiclass)
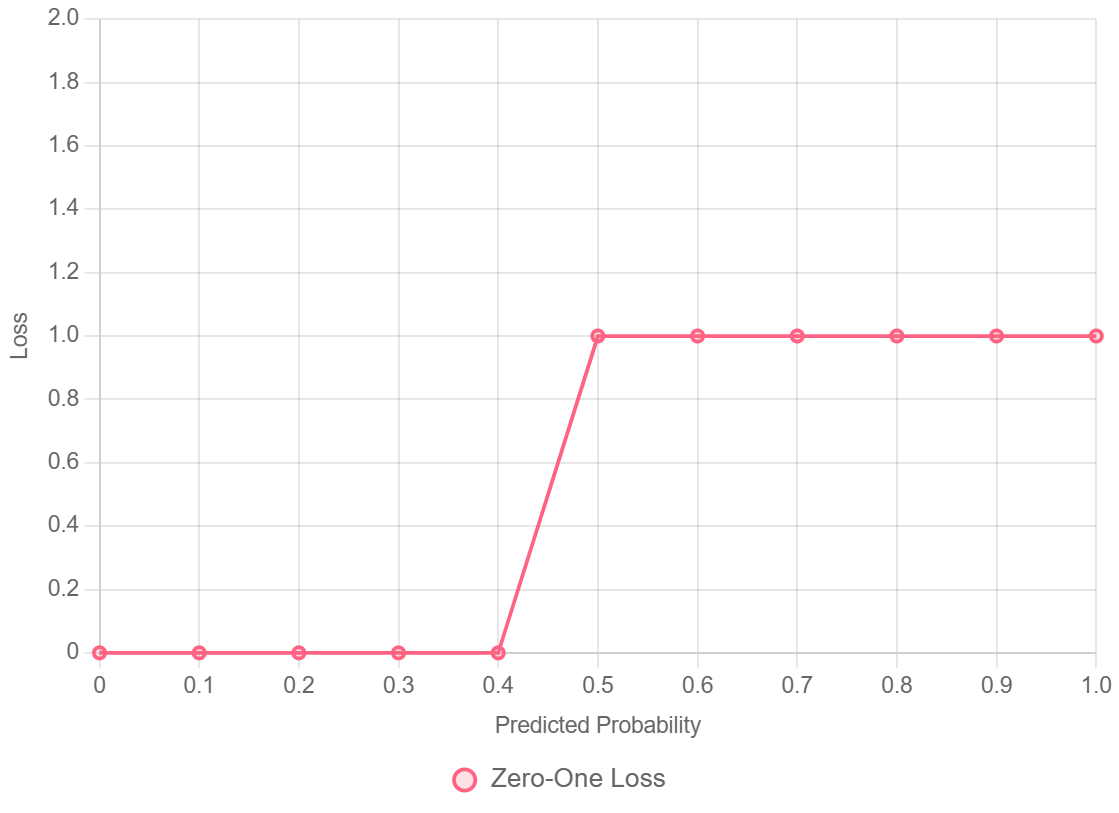
-
Công thức:
$$L(y, \hat{y}) = \begin{cases} 0 & \text{nếu } y = \hat{y} \\ 1 & \text{nếu } y \neq \hat{y} \end{cases}$$
Trong đó:
$L(y, \hat{y})$ là Hàm Mất Mát (Loss Function) dùng để đo lường mức độ sai lầm của mô hình.
$y$ là Giá trị Thực ($Y_{true}$) dùng để nhãn hoặc giá trị mục tiêu chính xác của dữ liệu.
$\hat{y}$ là dự đoán ($Y_{pred}$) Giá trị mà mô hình học máy dự đoán được.
$\begin{cases} \dots \end{cases}$ là Hàm Điều kiện dùng để xác định giá trị của $L$ dựa trên điều kiện bên trong.
$0$(Loss = 0) nghĩa là mô hình dự đoán hoàn toàn chính xác ($y = \hat{y}$).
$1$(Loss = 1) nghĩa là mô hình dự đoán sai ($y \neq \hat{y}$). -
Vì sao được phân loại là Gián Đoạn? -> Mất mát nhảy tức thì từ 0 lên 1 – giống như chỉ có một bước đi
- Đặc tính: Không lồi (non-convex), không khả vi $\rightarrow$ không thể tối ưu hóa bằng gradient descent.
- Ứng dụng: Chỉ được sử dụng làm metric đánh giá (độ chính xác/tỷ lệ lỗi), không dùng để huấn luyện.
2. Mất Mát Hinge (Hinge Loss)
(Về mặt kỹ thuật là liên tục, nhưng có một điểm gấp khúc không khả vi sắc nét.)
- Dùng trong: Máy Vectơ Hỗ trợ (SVM), bộ phân loại dựa trên lề (margin-based classifiers).
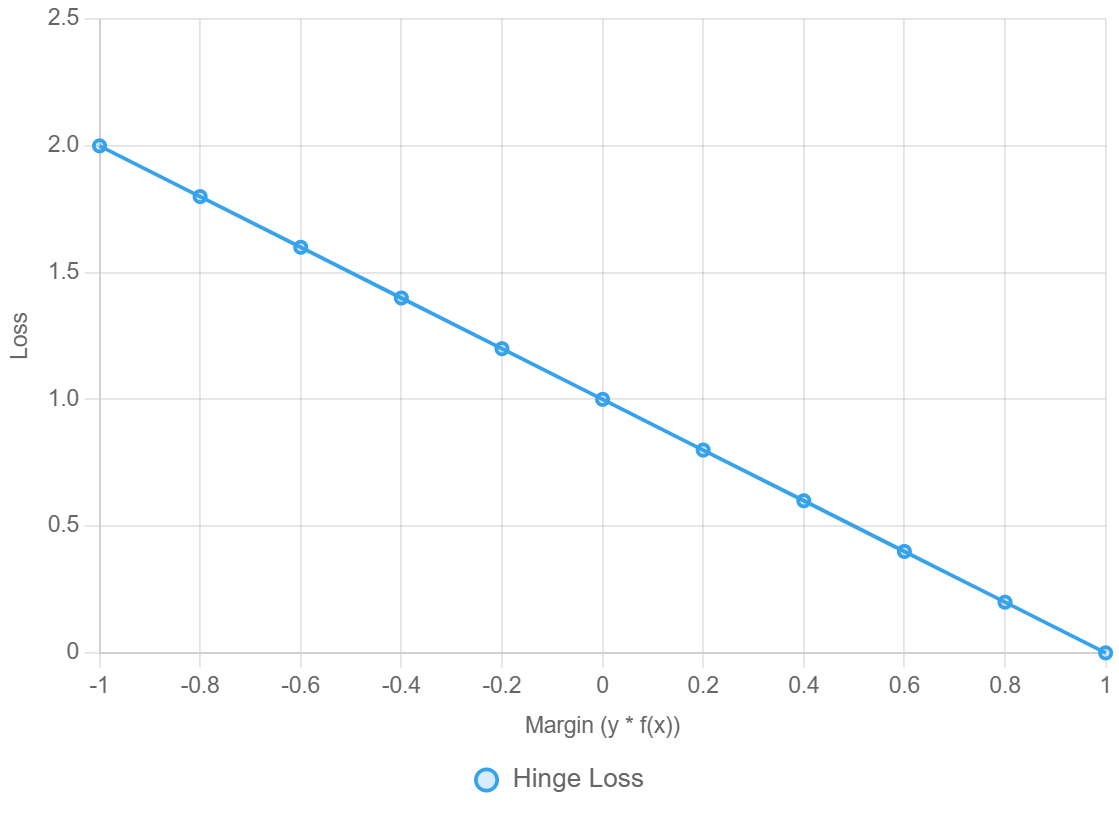
-
Công thức:
$$L(y, \hat{y}) = \max(0, 1 - y\hat{y})$$
Trong đó :
$L(y, \hat{y})$ là Hàm Mất Mát (Loss Function) dùng để đo lường mức độ sai lầm của mô hình.
$y$ là giá trị Thực ($Y_{true}$) nghĩa là nhãn lớp thực tế.
$\hat{y}$ là dự đoán (Decision Function Output) nghĩa là đầu ra của hàm quyết định của mô hình (ví dụ: $w \cdot x + b$), có thể là một số thực bất kỳ, thể hiện mức độ tự tin và lớp dự đoán của mô hình.
$\max(A, B)$ là Hàm Lấy Giá Trị Lớn Nhất nghĩa là sẽ trả về giá trị lớn nhất giữa A và B.
$1 - y\hat{y}$ là lề An Toàn nghĩa là giá trị này cho biết mô hình tự tin đúng hay sai, và khoảng cách từ dự đoán đến "lề an toàn" (margin). -
Ý tưởng chính: Không có Mất Mát nếu mô hình dự đoán đúng một cách tự tin – nhưng phạt những dự đoán thiếu tự tin, giới thiệu một lề an toàn.
- Vì sao được phân loại là Gián đoạn?
Có một điểm không khả vi tại $1 - y\hat{y} = 0$.
3. Mất Mát Ramp (Clipped Hinge Loss)
- Dùng trong: Phân loại mạnh mẽ (robust classification) (ví dụ: SVM kháng nhiễu).
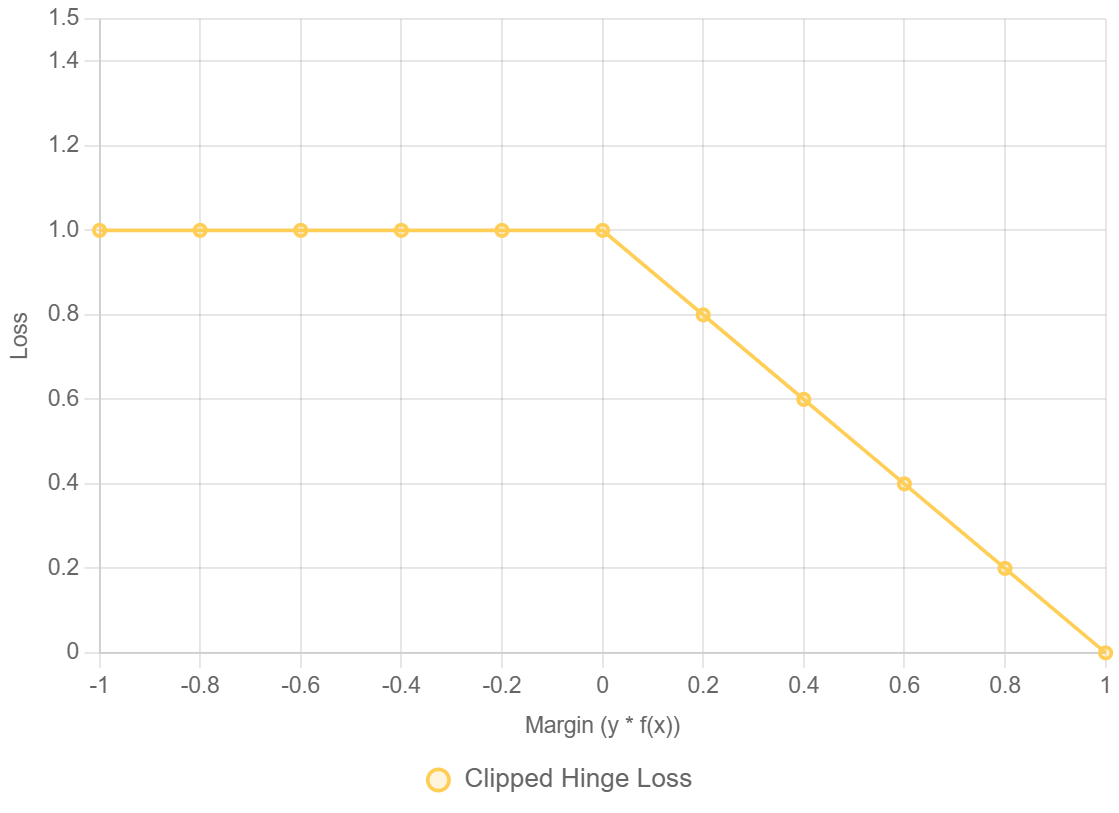
- Công thức:
$$L(y, \hat{y}) = \max(0, \min(1, 1 - y\hat{y}))$$
Trong đó :
$L(y, \hat{y})$: Là Hàm Mất Mát (Loss Function), đo lường lỗi.
$y$: Là Giá trị Thực ($Y_{true}$), thường là $+1$ hoặc $-1$ trong phân loại nhị phân.
$\hat{y}$: Là Dự đoán (Decision Function Output) của mô hình, thể hiện mức độ tự tin.
$1 - y\hat{y}$: Là Margin (Lề) hoặc phần mất mát tiềm năng, tương tự như trong Hinge Loss.
$\min(1, 1 - y\hat{y})$: Giá trị mất mát không bao giờ vượt quá 1. Đây là phần "Clipped" (bị cắt) trong tên gọi Clipped Hinge Loss. - Tại sao bị giới hạn/gián đoạn?
Mất mát bị giới hạn ở 1, không như Hinge Loss có thể tiếp tục tăng – điều này làm cho nó ít nhạy cảm với các giá trị ngoại lai (outliers). - Ứng dụng: Dùng khi ưu tiên độ ổn định và chống nhiễu hơn là nhạy cảm cao
4. Hàm Mất Mát Dựa Trên Ngưỡng/Bước Nhảy (Step / Threshold-Based Losses)
- Dùng trong: Reinforcement learning, các hệ thống yêu cầu an toàn tuyệt đối
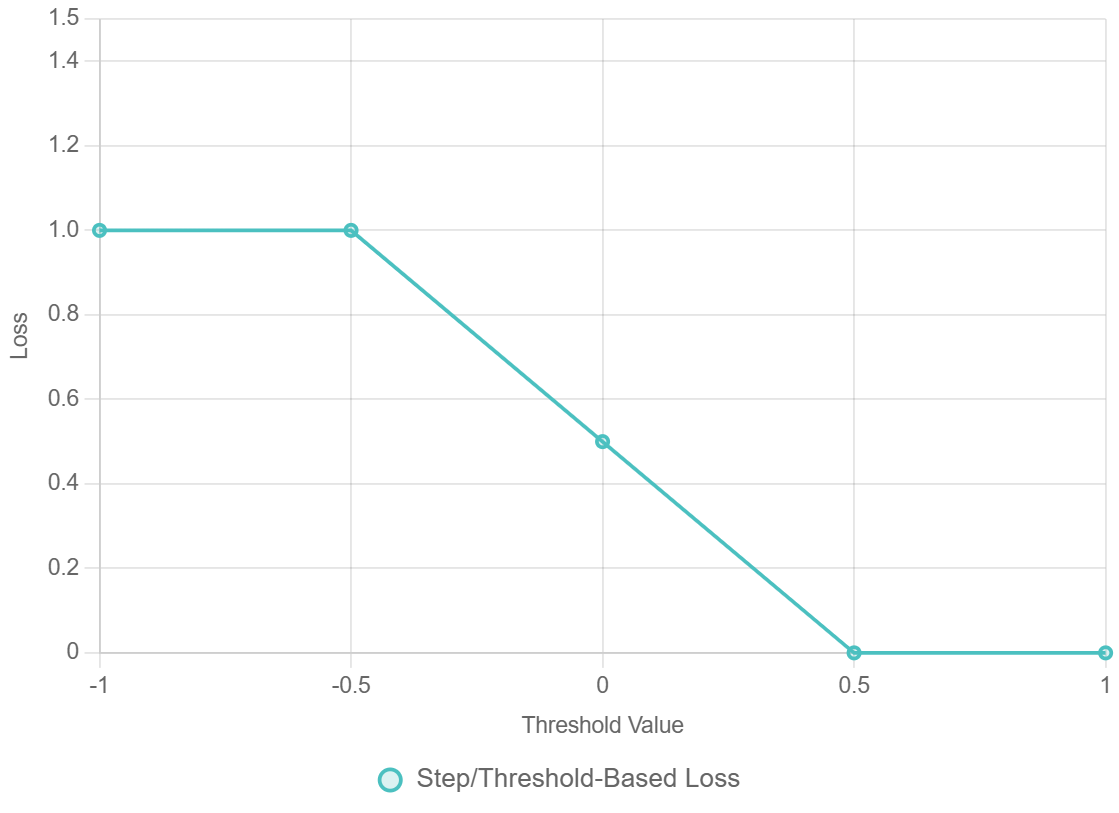
- Công thức:
$$L = \begin{cases} 0 & \text{Nếu an toàn} \\ 1 \text{ hoặc } \infty & \text{nếu ngưỡng an toàn bị vi phạm} \end{cases}$$
Trong đó :
$L$: Là Hàm Mất Mát (Loss Function) hoặc giá trị hình phạt.
$\begin{cases} \dots \end{cases}$: Là Hàm Điều kiện, xác định mức mất mát dựa trên trạng thái của hệ thống.
$0$: Là mức Không có Mất Mát (Loss = 0).
$\text{Nếu an toàn}$: Xảy ra khi hệ thống hoặc tác nhân (agent) đang ở trong trạng thái an toàn hoặc đáp ứng tất cả các điều kiện ràng buộc.
$1 \text{ hoặc } \infty$: Là mức Mất Mát Cao (High Loss) hoặc Vô Cùng (Infinite Loss). - Ví dụ: Nếu robot bước ra khỏi vùng an toàn → bị phạt ngay lập tức mức rất lớn
- Được ứng dụng phổ biến trong AI để đảm bảo an toàn và tránh rủi ro
Hàm mất mát liên tục (Continuous Loss Function)
Hàm mất mát liên tục là một hàm toán học chạy trơn tru dùng để đo lường mức độ sai lệch giữa dự đoán của mô hình và giá trị thực tế — thay đổi một cách dần dần, không có bước nhảy đột ngột khi dự đoán thay đổi.
Hãy tưởng tượng giống đi bộ từ tầng trệt lên tầng 3 bằng cầu thang, từng bước một — chứ không phải bị dịch chuyển tức thời từ tầng trệt lên thẳng tầng 3. Chính sự trơn tru này giúp ta có thể tính được gradient và tối ưu mô hình bằng gradient descent.
1. Sai Số Bình Phương Trung Bình (Mean Squared Error - MSE)
MSE là hàm Mất Mát phổ biến nhất được sử dụng cho các bài toán hồi quy (dự đoán các giá trị số liên tục).
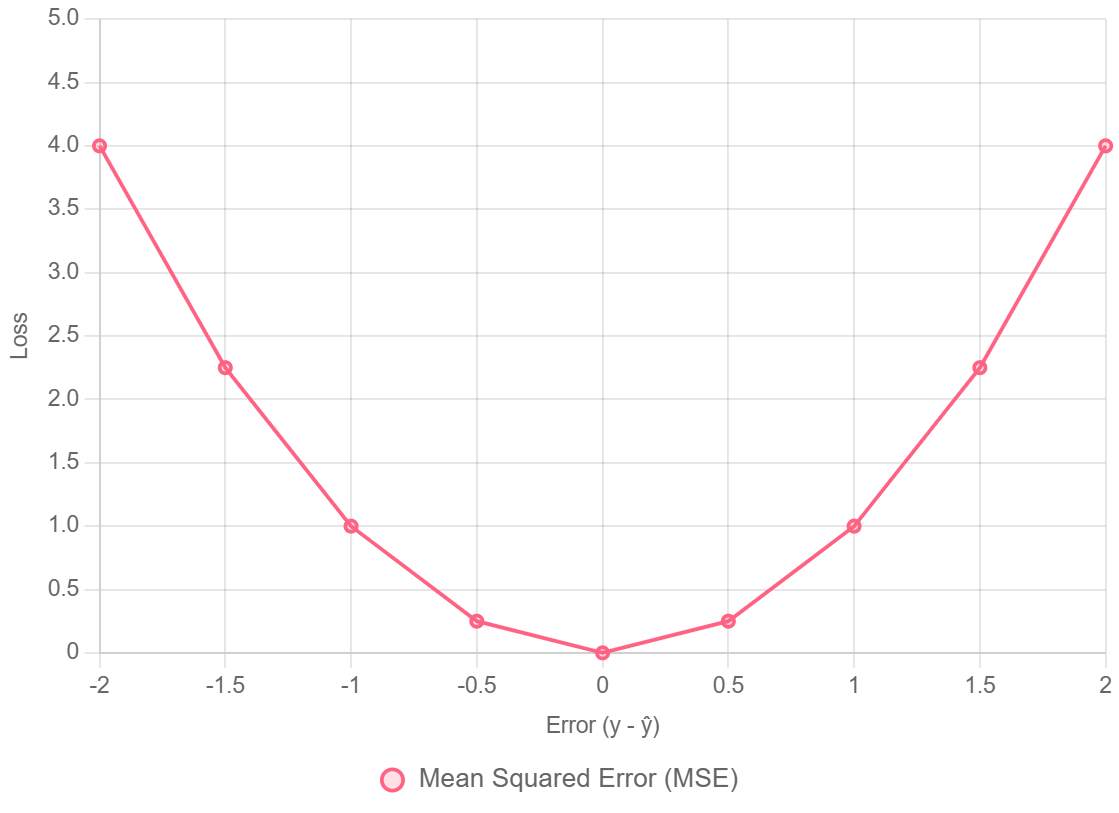
- Công thức:
$$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2$$
Trong đó:
$\text{MSE}$: Là Sai số Bình phương Trung bình (Mean Squared Error), giá trị mất mát mà mô hình cần tối thiểu hóa.
$\frac{1}{n}$: Là phép tính trung bình (Mean), chia tổng sai số cho số lượng điểm dữ liệu ($n$).
$\sum_{i=1}^{n}$: Là ký hiệu tổng (Summation), tính tổng các giá trị từ điểm dữ liệu đầu tiên ($i=1$) đến điểm dữ liệu cuối cùng ($n$).
$Y_i$: Là Giá trị Thực ($Y_{true}$) của điểm dữ liệu thứ $i$.
$\hat{Y}_i$: Là Dự đoán ($Y_{pred}$) của mô hình cho điểm dữ liệu thứ $i$.
$(Y_i - \hat{Y}_i)$: Là Sai số (Error) hoặc phần dư (Residual), là sự khác biệt giữa giá trị thực và giá trị dự đoán.
$(\dots)^2$: Là phép Bình phương sai số. - Tại sao bình phương sai số?
Nhấn mạnh các lỗi lớn $\rightarrow$ lỗi lớn bị phạt nặng hơn.
Khả vi và lồi (convex) $\rightarrow$ lý tưởng cho gradient descent, đảm bảo có cực tiểu toàn cục (đối với mô hình tuyến tính).
Đơn vị bị bình phương $\rightarrow$ nên $\text{RMSE} = \sqrt{\text{MSE}}$ thường được ưa chuộng hơn để dễ diễn giải - Hạn chế: Rất nhạy cảm với các giá trị ngoại lai (outlier).
2. Sai Số Tuyệt Đối Trung Bình (Mean Absolute Error - MAE)
MAE là một hàm Mất Mát hồi quy khác được dùng trong bài toán hồi quy, nhưng có khả năng giả quyết đối với các giá trị ngoại lai (outlier) tốt hơn.
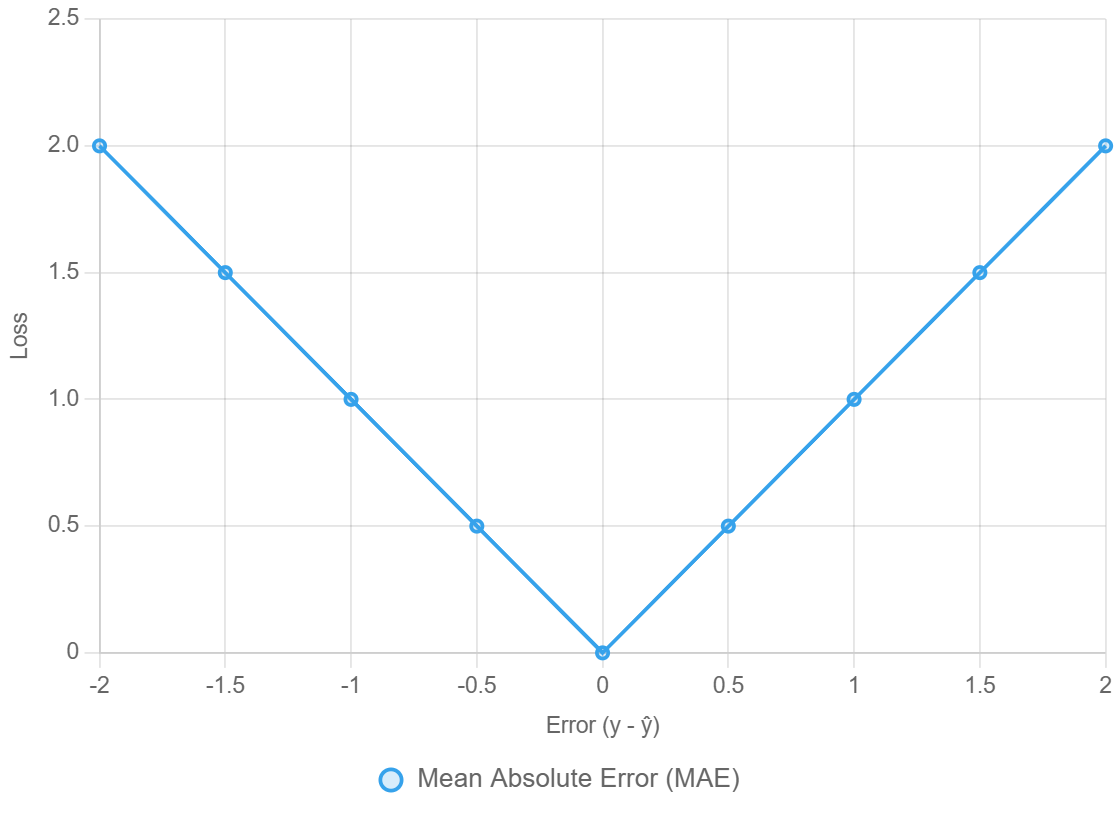
- Công thức:
$$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |Y_i - \hat{Y}_i|$$
Trong đó :
$\text{MAE}$: Là Sai số Tuyệt đối Trung bình (Mean Absolute Error), giá trị mất mát mà mô hình cần tối thiểu hóa.
$\frac{1}{n}$: Là phép tính trung bình (Mean), chia tổng sai số cho số lượng điểm dữ liệu ($n$).
$\sum_{i=1}^{n}$: Là ký hiệu tổng (Summation), tính tổng các giá trị tuyệt đối của sai số từ điểm dữ liệu đầu tiên ($i=1$) đến điểm dữ liệu cuối cùng ($n$).
$Y_i$: Là Giá trị Thực ($Y_{true}$) của điểm dữ liệu thứ $i$.
$\hat{Y}_i$: Là Dự đoán ($Y_{pred}$) của mô hình cho điểm dữ liệu thứ $i$.
$(Y_i - \hat{Y}_i)$: Là Sai số (Error) hoặc phần dư (Residual), là sự khác biệt giữa giá trị thực và giá trị dự đoán.
$|\dots|$: Là phép lấy Giá trị Tuyệt đối (Absolute value) của sai số. - Đặc điểm chính:
Phạt sai số một cách tuyến tính $\rightarrow$ lỗi lớn không bị thổi phồng như trong MSE.
Liên tục nhưng không khả vi tại 0 $\rightarrow$ tạo ra một “kink” (điểm gấp khúc); subgradients được sử dụng trong thực tế.
Rất dễ diễn giải $\rightarrow$ đơn vị giống như biến mục tiêu.
3. Huber Loss (Sự kết hợp)
Huber Loss được thiết kế để giải quyết một mâu thuẫn cơ bản trong bài toán hồi quy:
- MSE chính xác nhưng quá nhạy cảm với outlier (chỉ 1 giá trị cực đoan cũng có thể chi phối toàn bộ loss).
- MAE chống chịu tốt với outlier, nhưng khó tối ưu hơn (không khả vi tại 0 và hội tụ chậm hơn).
Huber Loss kết hợp điểm mạnh của cả hai:
- Hành xử giống MSE khi lỗi nhỏ → chính xác, mượt mà, học nhanh
- Hành xử giống MAE khi lỗi lớn → ổn định, giảm ảnh hưởng của nhiễu cực đoan
Ví dụ : Bạn có 1 lượng dự liệu, thì 95% dữ liệu là sạch và 5% là nhiễu (outliers), Huber Loss sẽ tập trung học từ 95% dữ liệu sạch, đồng thời nhẹ nhàng bỏ qua phần nhiễu. Vì thế, nó rất phổ biến trong tài chính, xe tự lái, dự báo time-series, và môi trường cảm biến nhiễu.
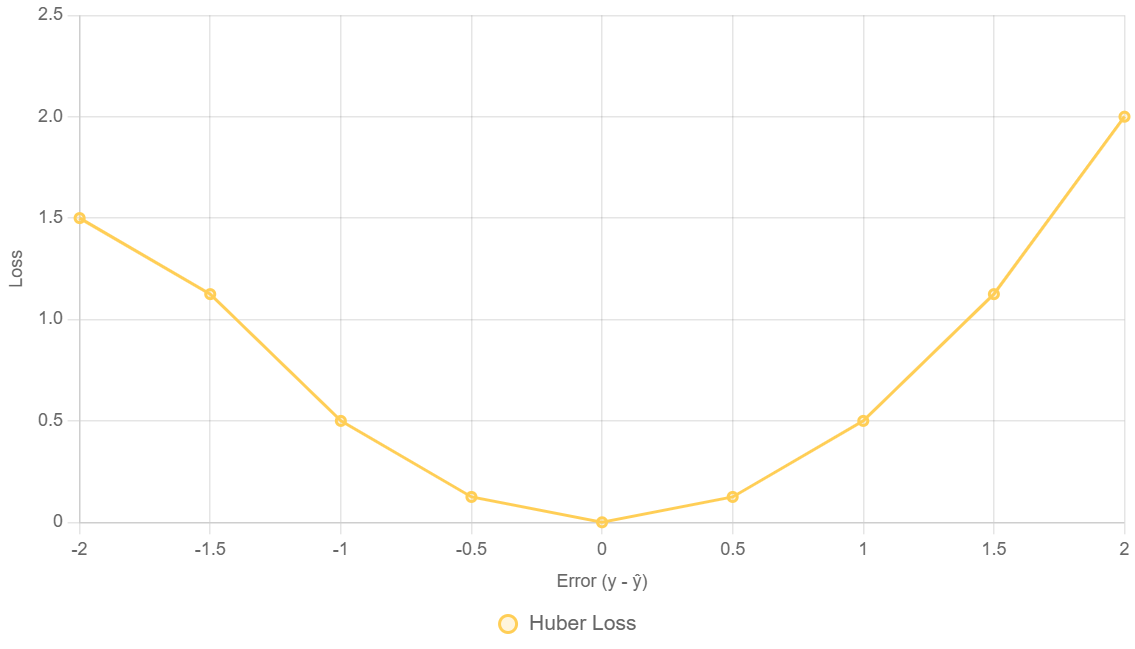
Định nghĩa toán học
Huber Loss được định nghĩa như sau:
$$L(\hat{y}, y) =
\begin{cases}
\frac{1}{2}(\hat{y} - y)^2, & \text{nếu } |\hat{y} - y| \leq \delta \\
\delta|\hat{y} - y| - \frac{1}{2}\delta^2, & \text{ngược lại}
\end{cases}
$$
Trong đó
$L(\hat{y}, y)$: Là Hàm Mất Mát Huber (Huber Loss), giá trị lỗi mà mô hình cần tối thiểu hóa.
$y$: Là Giá trị Thực ($Y_{true}$) của dữ liệu.
$\hat{y}$: Là Dự đoán ($Y_{pred}$) của mô hình.
$\delta$ (delta): là một ngưỡng có thể điều chỉnh.Hàm này liên tục và khả vi (differentiable) ở mọi nơi, ngay cả tại ranh giới. $\delta$ là siêu tham số (hyperparameter) cần được tinh chỉnh.
$|\hat{y} - y|$: Là Sai số tuyệt đối (Absolute Error), khoảng cách giữa dự đoán và giá trị thực.
$\frac{1}{2}(\hat{y} - y)^2$: Đây là công thức của một nửa MSE (Sai số Bình phương Trung bình).Nó được áp dụng nếu sai số tuyệt đối $(\text{nếu } |\hat{y} - y|)$ nhỏ hơn hoặc bằng $\delta$. Với mục đích khi sai số nhỏ, Huber Loss hoạt động như MSE, cung cấp bề mặt tối ưu hóa trơn tru và hội tụ nhanh chóng.
$\delta|\hat{y} - y| - \frac{1}{2}\delta^2$: Đây là công thức có tính chất tuyến tính (linear) với sai số tuyệt đối, tương tự như MAE (Sai số Tuyệt đối Trung bình).Nó được áp dụng ngược lại (nếu $|\hat{y} - y| > \delta$), tức là khi sai số lớn hơn ngưỡng. Với mục đích là khi sai số lớn (thường là ngoại lai), Huber Loss chuyển sang chế độ phạt tuyến tính, giúp mô hình hạn chế bị ảnh hưởng bởi các điểm dữ liệu nhiễu/ngoại lai.
Đạo hàm (dùng cho Gradient Descent)
Đặt $\hat{y} = w x + b$.
Đạo hàm theo $w$ :
$$\frac{\partial L}{\partial w} =\begin{cases}x(\hat{y} - y), & \text{nếu } |\hat{y} - y| \leq \delta \\\delta x \frac{(\hat{y} - y)}{|\hat{y} - y|}, & \text{ngược lại}\end{cases}$$
- $\frac{\partial L}{\partial w}$: là Đạo hàm riêng (Partial Derivative) của Hàm Mất Mát $L$ theo tham số trọng số $w$. Đạo hàm này cho biết mức độ thay đổi của mất mát khi trọng số $w$ thay đổi, được dùng để cập nhật $w$ trong thuật toán Gradient Descent.
- $L$: Là Hàm Mất Mát Huber.$w$: Là Trọng số (Weight) của mô hình (trong trường hợp mô hình tuyến tính:
- $\hat{y} = wx + b$).$\delta$: Là Ngưỡng (Threshold) có thể điều chỉnh của Huber Loss, xác định ranh giới giữa hai chế độ phạt.
- $x$: Là Giá trị đầu vào (Input Feature) tương ứng với trọng số $w$.$y$: Là Giá trị Thực ($Y_{true}$).
- $\hat{y}$: Là Dự đoán ($Y_{pred}$) của mô hình.
- $x(\hat{y} - y)$:Đây là công thức đạo hàm riêng của MSE (Sai số Bình phương Trung bình).Nó được áp dụng nếu sai số tuyệt đối $|\hat{y} - y|$ nhỏ hơn hoặc bằng $\delta$ (sai số nhỏ).Mục đích là khi sai số nhỏ, việc cập nhật trọng số hoạt động giống như MSE, tận dụng tính chất dốc và trơn tru để hội tụ nhanh.
- $\delta x \frac{(\hat{y} - y)}{|\hat{y} - y|}$:Đây là công thức đạo hàm riêng của phần phạt tuyến tính (MAE), được điều chỉnh bởi $\delta$. Lưu ý rằng $\frac{(\hat{y} - y)}{|\hat{y} - y|}$ chính là hàm dấu ($\text{sgn}(\hat{y} - y)$), nhận giá trị $+1$ nếu $\hat{y} > y$ và $-1$ nếu $\hat{y} < y$.Nó được áp dụng ngược lại (nếu $|\hat{y} - y| > \delta$) (sai số lớn, thường là ngoại lai).Mục đích là để đảm bảo rằng mức độ cập nhật trọng số (gradient) là một hằng số ($\delta \cdot x$) theo hướng của sai số, giúp mô hình không phản ứng thái quá với các ngoại lai.
Đạo hàm theo $b$ :
$$\frac{\partial L}{\partial b} =\begin{cases}(\hat{y} - y), & \text{nếu } |\hat{y} - y| \leq \delta \\\delta \frac{(\hat{y} - y)}{|\hat{y} - y|}, & \text{ngược lại}\end{cases}$$
- $\frac{\partial L}{\partial b}$: Là Đạo hàm riêng (Partial Derivative) của Hàm Mất Mát $L$ theo tham số độ lệch $b$ (hay Bias). Đạo hàm này cho biết mức độ thay đổi của mất mát khi độ lệch $b$ thay đổi, được dùng để cập nhật $b$ trong thuật toán Gradient Descent.
- $L$: Là Hàm Mất Mát Huber.$b$: Là Độ lệch (Bias) của mô hình (trong trường hợp mô hình tuyến tính: $\hat{y} = wx + b$).$\delta$: Là Ngưỡng (Threshold) có thể điều chỉnh của Huber Loss.
- $y$: Là Giá trị Thực ($Y_{true}$).$\hat{y}$: Là Dự đoán ($Y_{pred}$) của mô hình.
- $(\hat{y} - y)$:Đây là công thức đạo hàm riêng của MSE (Sai số Bình phương Trung bình) theo $b$.Nó được áp dụng nếu sai số tuyệt đối $|\hat{y} - y|$ nhỏ hơn hoặc bằng $\delta$ (sai số nhỏ).Mục đích là để khi sai số nhỏ, việc cập nhật độ lệch hoạt động giống như MSE, tận dụng tính chất dốc và trơn tru để hội tụ nhanh.
- $\delta \frac{(\hat{y} - y)}{|\hat{y} - y|}$:Đây là công thức đạo hàm riêng của phần phạt tuyến tính (MAE), được điều chỉnh bởi $\delta$. Biểu thức $\frac{(\hat{y} - y)}{|\hat{y} - y|}$ chính là hàm dấu ($\text{sgn}(\hat{y} - y)$), nhận giá trị $+1$ hoặc $-1$.Nó được áp dụng ngược lại (nếu $|\hat{y} - y| > \delta$) (sai số lớn, thường là ngoại lai).Mục đích là để đảm bảo rằng mức độ cập nhật độ lệch (gradient) là một hằng số ($\delta$ hoặc $-\delta$) theo hướng của sai số, giúp mô hình không phản ứng thái quá với các ngoại lai và giữ sự ổn định trong huấn luyện.
Các đạo hàm này sau đó được sử dụng trong việc cập nhật tham số:
$$w := w - \eta \frac{\partial L}{\partial w}$$
- $w$: Là Trọng số (Weight) hiện tại của mô hình.
- $\eta$ (eta): Là Tốc độ Học (Learning Rate). Đây là một siêu tham số (hyperparameter) quyết định kích thước của bước nhảy mà mô hình thực hiện để di chuyển xuống gradient.
-$\frac{\partial L}{\partial w}$: Là Đạo hàm riêng (Gradient) của Hàm Mất Mát ($L$) theo trọng số $w$. Nó chỉ ra hướng dốc nhất mà mất mát đang tăng lên.
$$b := b - \eta \frac{\partial L}{\partial b}$$
- $b$: Là Độ lệch (Bias) hiện tại của mô hình.
- $\eta$ (eta): Là Tốc độ Học (Learning Rate). Đây là một siêu tham số (hyperparameter) quyết định kích thước của bước nhảy mà mô hình thực hiện để di chuyển xuống gradient.
- $\frac{\partial L}{\partial b}$: Là Đạo hàm riêng (Gradient) của Hàm Mất Mát ($L$) theo độ lệch $b$.
Ưu điểm của Huber Loss
| Ưu điểm | Giải thích |
|---|---|
| ✅ Chống outlier tốt | Xử lý dữ liệu nhiễu tốt hơn MSE rất nhiều |
| ✅ Trơn tru & khả vi hoàn toàn | Tối ưu tốt hơn MAE |
| ✅ Tốc độ hội tụ nhanh | Gradient lớn hơn khi lỗi nhỏ |
| ✅ Được dùng rộng rãi trong thực tế | Dùng mặc định trong TensorFlow RobustRegression & Google Vision models |
Lưu ý: Tuy nhiên, siêu tham số $\delta$ phải được điều chỉnh cẩn thận
- Nếu quá nhỏ $\rightarrow$ hoạt động như MAE;
- Còn quá lớn $\rightarrow$ hoạt động như MSE.
Sử dụng Huber Loss vào lúc nào?
- Khi dữ liệu có thể chứa ngoại lai hoặc nhiễu.
- Khi muốn có được sự kết hợp tốt nhất giữa độ chính xác(MSE) và sự ổn định(MAE).
- Nếu MSE đang phản ứng thái quá hoặc không ổn định.
Như vậy
Huber Loss là một cải tiến tinh tế và thực tế so với cả MSE và MAE. Nó cung cấp một bề mặt tối ưu hóa trơn tru đồng thời vẫn chịu được dữ liệu nhiễu, làm cho nó trở thành lựa chọn hàng đầu cho các bài toán hồi quy trong thực tế.
So sánh MSE vs MAE vs Huber Loss
| Loss Function | Cách hoạt động | Độ nhạy với Outlier | Độ mượt / Khả vi | Tốc độ hội tụ | Trường hợp phù hợp nhất |
|---|---|---|---|---|---|
| MSE (Mean Squared Error) | Bình phương sai số → phạt cực mạnh với lỗi lớn | ❌ Rất nhạy cảm (outlier chi phối toàn bộ Mất Mát) | ✅ Rất mượt & khả vi hoàn toàn | ✅ Nhanh khi dữ liệu sạch | Dữ liệu sạch, bài toán hồi quy cơ bản |
| MAE (Mean Absolute Error) | Phạt tuyến tính → mọi lỗi đều như nhau | ✅ Chống chịu tốt với outlier | ⚠ Không khả vi tại 0 → tối ưu chậm hơn | ❌ Hội tụ chậm, bước nhảy không ổn định | Dữ liệu nhiễu, cần đo theo median |
| Huber Loss | MSE khi lỗi nhỏ, MAE khi lỗi lớn | ✅ Cân bằng tốt — kiểm soát outlier hiệu quả | ✅ Khả vi hoàn toàn | ✅ Nhanh hơn MAE, an toàn hơn MSE | Dữ liệu thực tế có một chút nhiễu |
Sự Khác Biệt Chính Giữa Hàm Mất Mát Liên Tục và Mất Mát Gián Đoạn
Sự khác biệt chính nằm ở cách giá trị Mất Mát thay đổi khi dự đoán thay đổi, và những điều có thể ảnh hưởng đến việc huấn luyện mô hình học máy (machine learning).
| Mất Mát Liên Tục | Mất Mát Gián Đoạn | |
|---|---|---|
| Hành vi | Thay đổi mượt, từ từ — dự đoán thay đổi nhỏ → Mất Mát thay đổi nhỏ | Có bước nhảy đột ngột — thay đổi dự đoán rất nhỏ → Mất Mát nhảy mạnh |
| Ví dụ dễ hiểu | Đi bộ lên cầu thang, cảm nhận từng bước | Đi thang máy, nhảy thẳng từ tầng trệt đến tầng 3, không đi qua tầng 1,2 |
| Phương diện Toán Học | Thường khả vi (hoặc ít nhất là khả vi hầu hết mọi nơi) -> gradient tồn tại và ổn định. | Đạo hàm có thể không tồn tại tại các điểm nhảy (gradient không xác định) -> khó tối ưu, thường phi tuyến & hỗn loạn |
Ảnh hưởng thực tế đến việc tối ưu
Hàm Mất Mát Liên Tục
- Có thể được tối ưu hóa bằng các phương pháp dựa trên gradient tiêu chuẩn (SGD, Adam, v.v.).
- Huấn luyện ổn định, được sử dụng rộng rãi trong mạng nơ-ron và machine learning
=> Đối với việc huấn luyện mô hình : có thể giúp cập nhật tham số 1 cách ổn định, tạo dự đoán.
Hàm Mất Mát Gián Đoạn
- Thường chỉ được sử dụng cho đánh giá (ví dụ: độ chính xác, mất mát 0–1).
- Không thể tối ưu hóa trực tiếp bằng gradient descent — yêu cầu các phương pháp thay thế như:
Mất mát thay thế trơn tru (Smooth surrogate losses) (ví dụ: cross-entropy thay vì 0–1 loss).
Phương pháp subgradient (cho các điểm gấp khúc như MAE hoặc hinge loss).
Tối ưu hóa chuyên biệt (ví dụ: lập trình số nguyên, thuật toán tiến hóa).
=> Đối với việc huấn luyện mô hình : dễ nhảy loạn, khó hội tụ -> tránh sử dụng trong huấn luyện
Chưa có bình luận nào. Hãy là người đầu tiên!