I. Giới thiệu
Giải thuật Di truyền (Genetic Algorithm - GA) là một trong những kỹ thuật tìm kiếm và tối ưu hóa siêu kinh điển (metaheuristic), lấy cảm hứng sâu sắc từ quy trình chọn lọc tự nhiên và di truyền sinh học. Nền tảng của GA được đặt bởi John Holland tại Đại học Michigan vào những năm 1960 và 1970. GA thuộc lớp lớn hơn là Thuật toán Tiến hóa (Evolutionary Algorithms - EA), cùng với Chiến lược Tiến hóa (Evolution Strategies) và Lập trình Tiến hóa (Evolutionary Programming).
Hình 1. Minh họa bốn giai đoạn cốt lõi: Biến dị (chim mẹ nuôi con với sự đa dạng), Chọn lọc tự nhiên (chỉ những cá thể thích nghi sống sót), Sinh sản (tạo thế hệ mới với biến dị), và Di truyền (truyền đặc tính cho thế hệ sau).
Động lực học thuật chính đằng sau sự phát triển của GA là nhu cầu tìm kiếm một phương pháp tối ưu hóa toàn cục (global search) không cần đạo hàm. Khác với các phương pháp dựa trên đạo hàm (như Gradient Descent) vốn đòi hỏi hàm mục tiêu phải khả vi và dễ mắc kẹt tại cực tiểu cục bộ (local minima), GA tiếp cận không gian tìm kiếm bằng cách duy trì một quần thể giải pháp đa dạng. Bằng cách mô phỏng các lực lượng tiến hóa như chọn lọc, lai ghép (recombination) và đột biến (mutation).
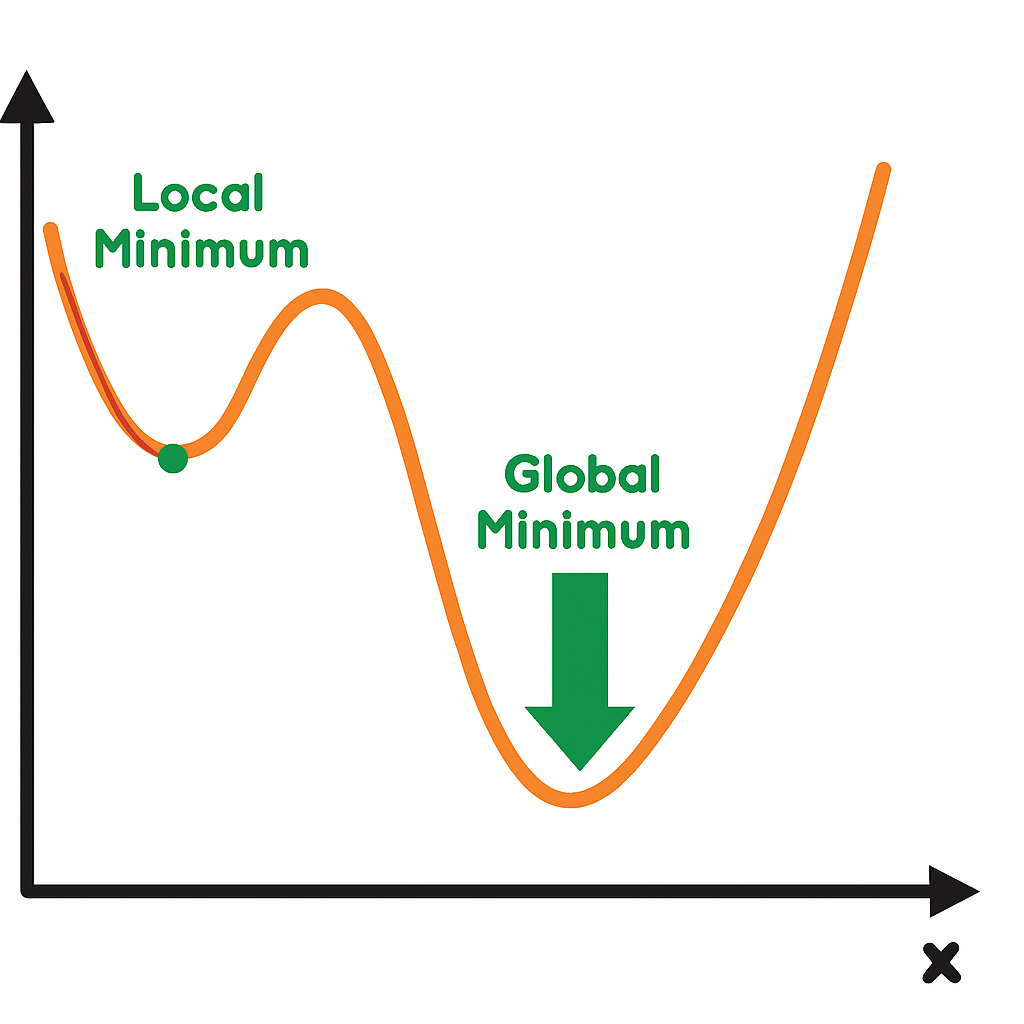
Hình 2. Minh họa thách thức của gradient descent: thuật toán có thể "kẹt" ở cực tiểu cục bộ (local minimum), bỏ lỡ cực tiểu toàn cục (global minimum) trong không gian tìm kiếm phức tạp. Genetic algorithm ra đời để khắc phục, bằng cách mô phỏng tiến hóa tự nhiên, khám phá đa dạng và hội tụ tối ưu toàn cục.
GA có khả năng khám phá rộng rãi không gian giải pháp, giúp nó vượt trội trong các bài toán có hàm mục tiêu đa đỉnh (multimodal) hoặc bị che mờ bởi nhiễu.
II. Khái niệm Cơ bản về Giải thuật Di truyền
1. Phân loại và Cấu trúc Thuật toán Tiến hóa
Trong lĩnh vực Tối ưu hóa Tính toán, GA được định nghĩa qua ba thành phần cơ bản của quá trình tiến hóa:
-
Cá thể (Individual) hoặc Nhiễm sắc thể (Chromosome): Đây là một giải pháp cho bài toán tối ưu hóa. Nhiễm sắc thể biểu diễn các tham số cần tối ưu hóa, thường được mã hóa dưới dạng chuỗi bit nhị phân (GA truyền thống) hoặc vector số thực (Real-Coded GA).
-
Gen (Gene): Là đơn vị thông tin cơ bản trên nhiễm sắc thể.
-
Độ Thích nghi (Fitness): Là thước đo định lượng chất lượng của cá thể. Hàm fitness được thiết kế để đánh giá mức độ tốt của giải pháp ứng viên trong việc giải quyết bài toán.
Trong các bài toán tối thiểu hóa chi phí (cost minimization), hàm fitness thường là nghịch đảo của hàm chi phí hoặc hàm lỗi. Mục tiêu của GA là tối đa hóa hàm fitness.
2. Chu trình cơ bản của GA
Quá trình vận hành của GA là một vòng lặp tiến hóa liên tục, diễn ra qua các bước sau:
-
Bước 1: Khởi tạo (Initialization): Tạo ra một dân số (population) ban đầu của các nhiễm sắc thể một cách ngẫu nhiên. Kích thước dân số $N$ là tham số quan trọng, ảnh hưởng đến khả năng tìm kiếm toàn cục của thuật toán.
-
Bước 2: Đánh giá (Evaluation): Tính toán độ thích nghi (fitness) của mỗi cá thể trong dân số bằng cách sử dụng hàm mục tiêu của bài toán.
-
Bước 3: Chọn lọc (Selection): Chọn lọc các cá thể có độ thích nghi cao (fittest individuals) để trở thành cha mẹ cho thế hệ tiếp theo. Các phương pháp chọn lọc phổ biến bao gồm Roulette Wheel, Rank Selection, và Tournament Selection.
-
Bước 4: Tái tạo (Reproduction): Áp dụng các toán tử di truyền lên các cha mẹ đã chọn để tạo ra thế hệ con cái (offspring).
- Lai ghép (Crossover): Kết hợp vật chất di truyền của hai cha mẹ để tạo ra một hoặc nhiều con cái mới.
- Đột biến (Mutation): Thay đổi ngẫu nhiên một số gen của con cái để đưa vào sự đa dạng.

Hình 3. Hình minh họa hai cơ chế chính: Crossover (lai chéo) - hai nhiễm sắc thể cha trao đổi đoạn gen tại điểm cắt, sinh ra thế hệ con mới đa dạng; Mutation (đột biến) - thay đổi ngẫu nhiên bit.
-
Bước 5: Thay thế (Replacement): Thay thế dân số cũ bằng thế hệ con cái mới được tạo ra. Quá trình này có thể là thay thế toàn bộ (Generational GA) hoặc thay thế một phần (Steady-State GA).
-
Bước 6: Kết thúc (Termination): Lặp lại các bước 2 đến 5 cho đến khi đạt được tiêu chí dừng đã định trước (ví dụ: đạt số lượng thế hệ tối đa, hoặc khi độ thích nghi của cá thể tốt nhất không còn cải thiện đáng kể).
Hình 4. Hình flowchart minh họa quy trình lặp lại của GA
III. Từ Mã hóa Nhị phân cổ điển đến Mô hình Giá trị Thực
1. Hạn chế của mã hoá nhị phân (Binary-Coded GA)
Lý thuyết GA ban đầu của John Holland được xây dựng dựa trên mô hình các nhiễm sắc thể được mã hóa dưới dạng chuỗi nhị phân (Binary-Coded GA). Tuy nhiên, khi GA được áp dụng vào các bài toán tối ưu hóa tham số liên tục, mô hình nhị phân đã bộc lộ những hạn chế đáng kể.
Hiệu ứng Vách đá Hamming (Hamming Cliff Effect)
Vấn đề này xảy ra khi một thay đổi nhỏ trong giá trị thực đòi hỏi một số lượng lớn các bit phải thay đổi trong mã nhị phân tương ứng.
Ví dụ, ta có cá thể có giá trị là $15_{\text{dec}} = 01111_{\text{bin}}$, để đột biến cá thể này sang giá trị $16_{\text{dec}} = 10000_{\text{bin}}$ thì ta phải thay đổi 5 bit đồng thời. Trong GA, các toán tử Đột biến và Lai ghép chỉ thay đổi một hoặc hai bit. Khả năng thay đổi 5 bit cùng lúc là rất thấp, tạo ra một "vách đá" Hamming trong không gian tìm kiếm. Điều này cản trở khả năng tinh chỉnh dần dần (gradual search) của thuật toán.
Điều này dẫn đến hai vấn đề lớn:
* Lai ghép (crossover): Lai ghép các chuỗi nhị phân có thể tạo ra các cá thể con rất khác biệt so với bố mẹ, ngay cả khi sử dụng lai ghép 1 điểm. Điều này làm mất đi sự kế thừa "tốt" từ bố mẹ.
- Đột biến (Mutation): Đảo 1 bit có thể khiến giá trị thay đổi rất mạnh — đặc biệt là bit có trọng số cao (MSB). Điều này đôi khi sẽ làm cho bước nhảy ngẫu nhiên lớn, vô tình bỏ qua các điểm tối ưu toàn cục.
Hạn chế về độ dài nhiễm sắc thể và không gian tìm kiếm
Đối với các bài toán có nhiều biến, mỗi biến cần một chuỗi bit dài để mã hóa, dẫn đến một nhiễm sắc thể tổng thể rất dài. Điều này làm tăng đáng kể không gian tìm kiếm, khiến thuật toán chậm hòi tụ và đòi hỏi nhiều thế hệ hơn để tìm ra lời giải tốt.
2. Di truyền mã hoá thực (Real-Coded GA)
Để vượt qua những hạn chế này, đặc biệt trong các bài toán tối ưu hóa tham số liên tục, Real-Coded Genetic Algorithm (GA mã hóa giá trị thực) biểu diễn các nhiễm sắc thể (cá thể) trực tiếp bằng các giá trị số thực thay vì chuỗi nhị phân. Điều này có nghĩa là mỗi "gen" trong nhiễm sắc thể tương ứng trực tiếp với một biến thiết kế trong bài toán tối ưu.
Ví dụ: Nếu bạn đang tối ưu một hàm với hai biến $x_1=15.78,$ và $x_2=3.14$ là số thực, một cá thể trong Real-Coded Genetic Algorithm (RCGA) có thể được biểu diễn trực tiếp là một cặp số thực $(x_1, x_2)$ hay $(15.78, 3.14)$.
Sự khác biệt lớn nhất giữa RCGA và Binary-Coded GA nằm ở các toán tử Lai ghép (Crossover) và Đột biến (Mutation), vốn phải được thiết kế lại để hoạt động với số thực:
Lai ghép (Crossover)
Lai ghép số thực thường tạo ra các cá thể con nằm trong hoặc gần lân cận của các cá thể cha mẹ:
-
Simulated Binary Crossover - SBX: Là một trong những toán tử phổ biến nhất, được thiết kế để mô phỏng đặc tính tìm kiếm của lai ghép một điểm trong GA nhị phân, tạo ra các cá thể con phân bố xung quanh cha mẹ.
-
Blend Crossover - BLX-$\alpha$: Tạo ra các cá thể con được chọn ngẫu nhiên trong một khoảng không gian mở rộng (hoặc thu hẹp) xung quanh hai cá thể cha mẹ.
Đột biến (Mutation)
Thay vì ngẫu nhiên thay đổi giá trị 1 nhiễm sắc thể của một gen trong mã hoá nhị phân thì RCGA điều chỉnh ngẫu nhiên giá trị của gen đó, có ba loại đột biến phổ biến trong RCGA:
-
Đột biến đồng nhất (Uniform Mutation): Thay thế giá trị gen bằng một số ngẫu nhiên trong phạm vi biến đó.
-
Đột biến theo Phân phối Gaussian (Normally Distributed Mutation): Cộng thêm một lượng ngẫu nhiên theo phân phối chuẩn (Gaussian) vào giá trị gen hiện tại. Đây là một phương pháp "tinh chỉnh" cục bộ hiệu quả.
-
Đột biến không đồng nhất (Non-Uniform Mutation): Độ lớn của sự đột biến giảm dần theo số thế hệ, giúp thuật toán tập trung tìm kiếm tinh tế hơn khi tiến gần đến lời giải tối ưu.
IV. Tối Ưu Hóa hàm liên tục với giải thuật di truyền.
Trong phần này, mình sẽ sử dụng Thuật toán Di truyền (Genetic Algorithm - GA): GA Mã hóa Nhị phân (Binary-Coded GA) và GA Mã hóa Số thực (Real-Coded GA) để tìm tối ưu hóa hàm số mục tiêu $f(x)$ trên miền $[0, 1]$.
$$ f(x) = x \cdot \sin(50 \pi x) + 1 $$
def objective_function(x):
"""f(x) = x * sin(10 * π * x) + 1, domain [0, 1]"""
return x * np.sin(50 * np.pi * x) + 1
Trước khi đi vào từng bước chi tiết của giải thuật di truyền, mình sẽ sử dụng một số hàm phổ biến sau:
def real_to_binary(x, n_bits=20):
"""Convert real value in [0, 1] to binary string"""
max_val = 2**n_bits - 1
decimal = int(x * max_val)
return format(decimal, f'0{n_bits}b')
# real_to_binary(10, n_bits=10)
# 10011111110110
def binary_to_real(binary_string, n_bits=20):
"""Convert binary string to real value in [0, 1]"""
decimal = int(binary_string, 2)
max_val = 2**n_bits - 1
return decimal / max_val
# binary_to_real("10011111110110", n_bits=10)
# 10.0
Hai hàm trên dùng để chuyển đổi giá trị số thực $x$ trở lại thành chuỗi nhị phân và ngược lại, n_bits thể hiện độ dài của chuỗi kết quả nhị phân.
1. Binary-Coded GA
Đầu tiên, chúng ta sẽ tạo ra một tập hợp các cá thể ngẫu nhiên ban đầu, mỗi cá thể là một chuỗi nhị phân dài $n\_bits$.
def initialize_binary_population(pop_size, n_bits=20):
"""Initialize random binary population"""
return [''.join(np.random.choice(['0', '1'], n_bits)) for _ in range(pop_size)]
Tiếp theo, chúng ta lựa chọn các cá thể bố mẹ tốt hơn từ quần thể hiện tại dựa trên giá trị độ thích nghi (fitness) của chúng, sử dụng phương pháp Tournament Selection.
def tournament_selection(population, fitness, k=3):
"""Tournament selection (k=3)"""
selected = []
for _ in range(len(population)):
tournament_idx = np.random.choice(len(population), k, replace=False)
tournament_fitness = [fitness[i] for i in tournament_idx]
winner_idx = tournament_idx[np.argmax(tournament_fitness)]
selected.append(population[winner_idx])
return selected
Kế đến, chúng ta lai ghép, tạo ra hai cá thể con từ hai cá thể bố mẹ bằng cách hoán đổi bit tại các vị trí ngẫu nhiên theo một xác suất nhất định (lai ghép đồng nhất).
def uniform_crossover(parent1, parent2, prob=0.8):
"""Uniform binary crossover"""
if np.random.random() > prob:
return parent1, parent2
n_bits = len(parent1)
mask = np.random.randint(0, 2, n_bits)
child1 = ''.join([parent1[i] if mask[i] == 0 else parent2[i] for i in range(n_bits)])
child2 = ''.join([parent2[i] if mask[i] == 0 else parent1[i] for i in range(n_bits)])
return child1, child2
Cuối cùng, chúng ta đột biến, thay đổi ngẫu nhiên một bit (0 thành 1 hoặc ngược lại) trong chuỗi nhị phân của một cá thể với một xác suất nhỏ.
def bit_flip_mutation(individual, prob=0.01):
"""Bit-flip mutation (prob per bit)"""
mutated = list(individual)
for i in range(len(mutated)):
if np.random.random() < prob:
mutated[i] = '1' if mutated[i] == '0' else '0'
return ''.join(mutated)
Toàn bộ quá trình trên được lặp đi lặp lại để tạo ra được thế hệ tốt nhất, trong bài toán của chúng ta là tìm được giá trị cực đại của hàm mục tiêu $f(x)$.
def binary_ga(pop_size=100, generations=100, n_bits=20, cross_prob=0.8, mut_prob=0.01):
"""Run binary-coded genetic algorithm"""
print("\n" + "="*60)
print("BINARY-CODED GA")
print("="*60)
start_time = time.time()
# Initialize
population = initialize_binary_population(pop_size, n_bits)
best_fitness_history = []
avg_fitness_history = []
best_individual = None
best_fitness = -np.inf
converged_gen = -1
for gen in range(generations):
# Decode and evaluate
real_values = [binary_to_real(ind, n_bits) for ind in population]
fitness = [objective_function(x) for x in real_values]
# Track statistics
gen_best_idx = np.argmax(fitness)
gen_best_fitness = fitness[gen_best_idx]
avg_fitness = np.mean(fitness)
if gen_best_fitness > best_fitness:
best_fitness = gen_best_fitness
best_individual = real_values[gen_best_idx]
converged_gen = gen
best_fitness_history.append(best_fitness)
avg_fitness_history.append(avg_fitness)
if gen % 10 == 0:
print(f"Gen {gen:3d}: Best={best_fitness:.6f}, Avg={avg_fitness:.6f}, x={best_individual:.6f}")
# Elitism: preserve top 5%
elite_size = max(1, int(0.05 * pop_size))
elite_idx = np.argsort(fitness)[-elite_size:]
elites = [population[i] for i in elite_idx]
# Selection
selected = tournament_selection(population, fitness)
# Crossover
offspring = []
for i in range(0, len(selected), 2):
if i + 1 < len(selected):
child1, child2 = uniform_crossover(selected[i], selected[i+1], cross_prob)
offspring.extend([child1, child2])
else:
offspring.append(selected[i])
# Mutation
offspring = [bit_flip_mutation(ind, mut_prob) for ind in offspring]
# Replace population with offspring + elites
population = offspring[:pop_size - elite_size] + elites
runtime = time.time() - start_time
print(f"\nFinal Best: x={best_individual:.6f}, f(x)={best_fitness:.6f}")
print(f"Converged at generation: {converged_gen}")
print(f"Runtime: {runtime:.4f}s")
# Get final population stats
final_real = [binary_to_real(ind, n_bits) for ind in population]
final_fitness = [objective_function(x) for x in final_real]
return {
'best_x': best_individual,
'best_fitness': best_fitness,
'best_history': best_fitness_history,
'avg_history': avg_fitness_history,
'converged_gen': converged_gen,
'runtime': runtime,
'final_population': final_real,
'final_fitness': final_fitness
}
2. Real-Coded GA
Tương tự như trên, ta cũng sẽ thực hiện qua các bước Khởi tạo quần thể -> Chọn lọc -> Lai ghép -> Đột biến. Tuy nhiên, lần này mã hoá/giải mã giá trị $x$, chúng ta sẽ sử dụng trực tiếp $x$ dưới dạng số thực.
RCGA sẽ có sự khác nhau về lai ghép và đột biến. Cụ thể, ở đây mình sử dụng phương pháp Simulated Binary Crossover cho lai ghép và Polynomial Mutation cho đột biến.
def initialize_real_population(pop_size):
"""Initialize random real-valued population in [0, 1]"""
return np.random.random(pop_size)
def sbx_crossover(parent1, parent2, prob=0.8, eta=20):
"""Simulated Binary Crossover (SBX)"""
if np.random.random() > prob:
return parent1, parent2
u = np.random.random()
if u <= 0.5:
beta = (2 * u) ** (1 / (eta + 1))
else:
beta = (1 / (2 * (1 - u))) ** (1 / (eta + 1))
child1 = 0.5 * ((1 + beta) * parent1 + (1 - beta) * parent2)
child2 = 0.5 * ((1 - beta) * parent1 + (1 + beta) * parent2)
# Clip to [0, 1]
child1 = np.clip(child1, 0, 1)
child2 = np.clip(child2, 0, 1)
return child1, child2
def polynomial_mutation(individual, prob=0.1, eta=20):
"""Polynomial mutation"""
if np.random.random() > prob:
return individual
u = np.random.random()
if u < 0.5:
delta = (2 * u) ** (1 / (eta + 1)) - 1
else:
delta = 1 - (2 * (1 - u)) ** (1 / (eta + 1))
mutated = individual + delta
return np.clip(mutated, 0, 1)
Chúng ta cũng sẽ đưa toàn bộ quá trình vào một vòng lặp nhằm tạo ra được thế hệ tốt nhất.
def real_ga(pop_size=100, generations=100, cross_prob=0.8, mut_prob=0.1):
"""Run real-coded genetic algorithm"""
print("\n" + "="*60)
print("REAL-CODED GA")
print("="*60)
start_time = time.time()
# Initialize
population = initialize_real_population(pop_size)
best_fitness_history = []
avg_fitness_history = []
best_individual = None
best_fitness = -np.inf
converged_gen = -1
for gen in range(generations):
# Evaluate
fitness = np.array([objective_function(x) for x in population])
# Track statistics
gen_best_idx = np.argmax(fitness)
gen_best_fitness = fitness[gen_best_idx]
avg_fitness = np.mean(fitness)
if gen_best_fitness > best_fitness:
best_fitness = gen_best_fitness
best_individual = float(population[gen_best_idx]) # ensure Python float
converged_gen = gen
best_fitness_history.append(best_fitness)
avg_fitness_history.append(avg_fitness)
if gen % 10 == 0:
print(f"Gen {gen:3d}: Best={best_fitness:.6f}, Avg={avg_fitness:.6f}, x={best_individual:.6f}")
# Elitism: preserve top 5%
elite_size = max(1, int(0.05 * pop_size))
elite_idx = np.argsort(fitness)[-elite_size:]
elites = population[elite_idx] # numpy array
# Selection (tournament)
selected = []
for _ in range(pop_size):
tournament_idx = np.random.choice(pop_size, 3, replace=False)
winner_idx = tournament_idx[np.argmax(fitness[tournament_idx])]
selected.append(float(population[winner_idx]))
# Crossover
offspring = []
for i in range(0, len(selected), 2):
if i + 1 < len(selected):
child1, child2 = sbx_crossover(selected[i], selected[i+1], cross_prob)
offspring.extend([float(child1), float(child2)])
else:
offspring.append(float(selected[i]))
# Mutation
offspring = [float(polynomial_mutation(ind, mut_prob)) for ind in offspring]
# Replace population with offspring + elites
# Fix: offspring is a Python list, elites is a numpy array -> convert elites to list then combine
needed = pop_size - elite_size
new_pop_list = offspring[:needed] + elites.tolist()
population = np.array(new_pop_list)
runtime = time.time() - start_time
print(f"\nFinal Best: x={best_individual:.6f}, f(x)={best_fitness:.6f}")
print(f"Converged at generation: {converged_gen}")
print(f"Runtime: {runtime:.4f}s")
# Get final population stats
final_fitness = [objective_function(x) for x in population]
return {
'best_x': best_individual,
'best_fitness': best_fitness,
'best_history': best_fitness_history,
'avg_history': avg_fitness_history,
'converged_gen': converged_gen,
'runtime': runtime,
'final_population': population,
'final_fitness': final_fitness
}
Trực quan hoá kết quả và nhận xét
Sau khi đã xây dựng được hai giải thuật di truyền, chúng ta chạy đoạn mã nguồn sau để tối ưu hoá hàm mục tiêu, ở đây mình cố tình chọn n_bits thấp để thấy được sự chênh lệch của 2 giải thuật.
binary_results = binary_ga(pop_size=100, generations=100, n_bits=5,
cross_prob=0.8, mut_prob=0.01)
real_results = real_ga(pop_size=100, generations=100,
cross_prob=0.8, mut_prob=0.1)
Các bạn có thể chạy đoạn mã nguồn sau để so sánh kết quả:
def visualize_results(binary_results, real_results):
"""Create comprehensive visualization comparing both GAs"""
fig = plt.figure(figsize=(16, 10))
# 1. Objective Function Landscape
ax1 = plt.subplot(2, 2, 1)
x_range = np.linspace(0, 1, 1000)
y_range = objective_function(x_range)
ax1.plot(x_range, y_range, 'b-', linewidth=2, label='f(x)')
# Mark GA solutions
ax1.plot(binary_results['best_x'], binary_results['best_fitness'],
'ro', markersize=12, label=f"Binary GA: x={binary_results['best_x']:.4f}")
ax1.plot(real_results['best_x'], real_results['best_fitness'],
'gs', markersize=12, label=f"Real GA: x={real_results['best_x']:.4f}")
# Mark global maximum (approximate)
global_max_idx = np.argmax(y_range)
ax1.plot(x_range[global_max_idx], y_range[global_max_idx],
'k*', markersize=15, label=f"Global max ≈{x_range[global_max_idx]:.4f}")
ax1.set_xlabel('x', fontsize=12)
ax1.set_ylabel('f(x)', fontsize=12)
ax1.set_title('Objective Function Landscape', fontsize=14, fontweight='bold')
ax1.legend()
ax1.grid(True, alpha=0.3)
# 2. Convergence: Best Fitness
ax2 = plt.subplot(2, 2, 2)
ax2.plot(binary_results['best_history'], 'r-', linewidth=2, label='Binary GA')
ax2.plot(real_results['best_history'], 'g-', linewidth=2, label='Real GA')
ax2.set_xlabel('Generation', fontsize=12)
ax2.set_ylabel('Best Fitness', fontsize=12)
ax2.set_title('Best Fitness Convergence', fontsize=14, fontweight='bold')
ax2.legend()
ax2.grid(True, alpha=0.3)
# 3. Convergence: Average Fitness
ax3 = plt.subplot(2, 2, 3)
ax3.plot(binary_results['avg_history'], 'r--', linewidth=2, label='Binary GA (avg)')
ax3.plot(real_results['avg_history'], 'g--', linewidth=2, label='Real GA (avg)')
ax3.set_xlabel('Generation', fontsize=12)
ax3.set_ylabel('Average Fitness', fontsize=12)
ax3.set_title('Average Fitness Convergence', fontsize=14, fontweight='bold')
ax3.legend()
ax3.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('ga_comparison.png', dpi=150, bbox_inches='tight')
print("\n✓ Visualization saved as 'ga_comparison.png'")
plt.show()
def print_analysis(binary_results, real_results):
"""Print detailed textual analysis"""
print("\n" + "="*60)
print("ANALYSIS & COMPARISON")
print("="*60)
print("\n1. CONVERGENCE SPEED:")
print(f" Binary GA converged at generation {binary_results['converged_gen']}")
print(f" Real GA converged at generation {real_results['converged_gen']}")
if real_results['converged_gen'] < binary_results['converged_gen']:
print(" → Real GA converged faster")
else:
print(" → Binary GA converged faster")
print("\n2. FINAL ACCURACY:")
print(f" Binary GA: f(x) = {binary_results['best_fitness']:.8f}")
print(f" Real GA: f(x) = {real_results['best_fitness']:.8f}")
print(f" Difference: {abs(real_results['best_fitness'] - binary_results['best_fitness']):.8f}")
print("\n3. COMPUTATIONAL EFFICIENCY:")
print(f" Binary GA runtime: {binary_results['runtime']:.4f}s")
print(f" Real GA runtime: {real_results['runtime']:.4f}s")
# Visualize and compare
visualize_results(binary_results, real_results)
# Print analysis
print_analysis(binary_results, real_results)
Trực quan hoá kết quả lên đồ thị ta thấy có:
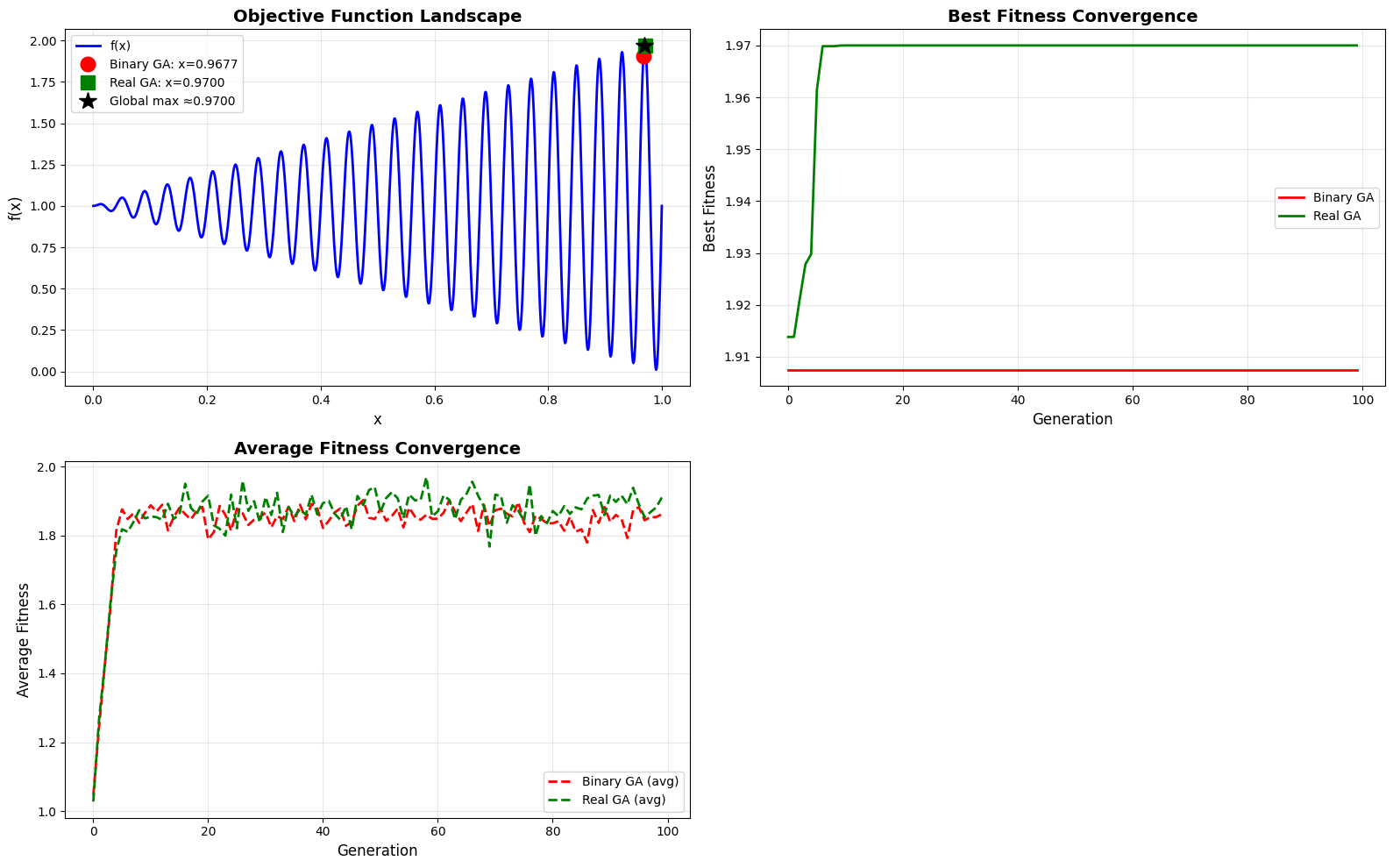
Hình 5. Kêt quả thu được sau khi di truyền qua 100 thế hệ.
-
Đối với đồ thị thứ nhất: Real GA đã tìm ra nghiệm gần cực đại toàn cục hơn hẳn so với Binary GA, thể hiện bằng việc ngôi sao xanh lá nằm gần đỉnh của đồ thị hơn.
-
Đối với đồ thị thứ hai: Real GA cho thấy khả năng khai thác (exploitation) mạnh mẽ và hiệu quả hơn trong việc tìm kiếm đỉnh cục bộ/toàn cục. Binary GA bị mắc kẹt ở một mức tối ưu cục bộ thấp hơn.
-
Đối với đồ thị thứ ba: Cả hai thuật toán đều cho thấy độ thích nghi trung bình tăng nhanh chóng trong 10-20 thế hệ đầu, cho thấy quần thể đã di chuyển từ các vùng giá trị thấp lên các vùng có giá trị cao. Tuy nhiên, Real GA (Đường Đứt Xanh Lá) duy trì độ thích nghi trung bình cao hơn so với Binary GA (Đường Đứt Đỏ) trong suốt quá trình chạy.
Như vậy, đối với bài toán tối ưu hóa hàm liên tục như thế này, Real-Coded GA vượt trội hoàn toàn so với Binary-Coded GA khi Binary GA được cấu hình với độ phân giải thấp. Để Binary GA cạnh tranh được, cần phải tăng $n\_bits$ lên ít nhất 20 hoặc cao hơn.
Bây giờ ta sẽ thử thay đổi thông số n_bits=20 để xem kết quả như thế nào nhé
binary_results = binary_ga(pop_size=100, generations=100, n_bits=5,
cross_prob=0.8, mut_prob=0.01)
real_results = real_ga(pop_size=100, generations=100,
cross_prob=0.8, mut_prob=0.1)
Kết quả thu được:
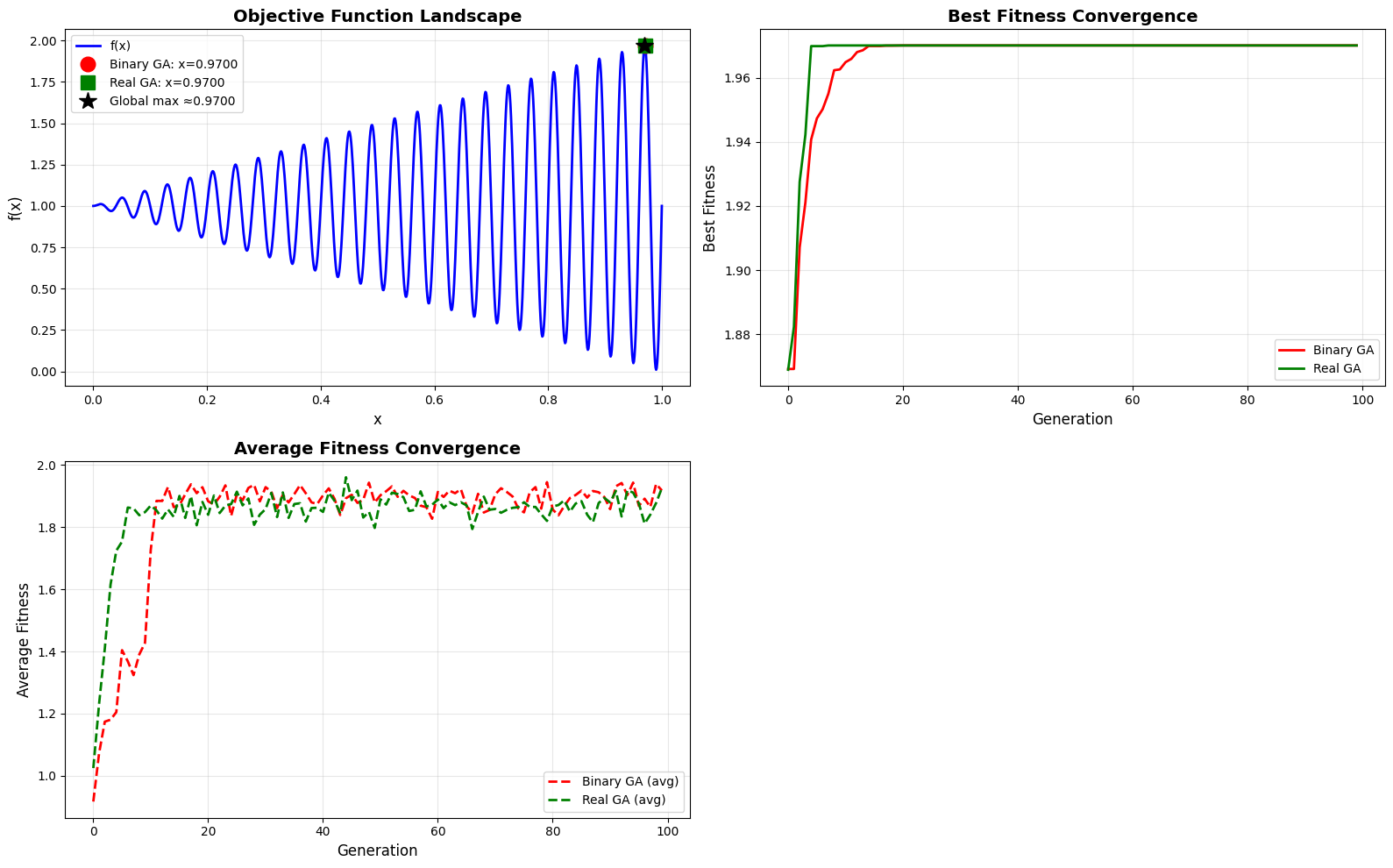
Hình 6. Kêt quả thu được sau khi tăng chuỗi độ dài nhị phân lên 20.
Binary GA đã có thể tìm ra nghiệm gần cực đại toàn cục chứng tỏ rằng nó đã mượt mà hơn trong viêc tìm kiếm đỉnh cục bộ/toàn cục, không bị kẹt một mức tối ưu cục bộ thấp hơn nữa. Tuy nhiên, việc tăng số lượng n_bits=20 chắc chắn sẽ làm tăng đáng kể không gian tìm kiếm, khiến thuật toán chậm hòi tụ.
Tài liệu Tham khảo
-
Sudhoff, S. D. (2009). Lecture 4: Real-Coded Genetic Algorithms. Purdue University.
-
Eshelman, L. J., & Schaffer, J. D. (1993). Real-coded genetic algorithms and interval schemata. Theoretical Computer Science.
Chưa có bình luận nào. Hãy là người đầu tiên!