Câu Chuyện Về Thuật Toán Di Truyền: Từ Ngẫu Nhiên Đến Thông Minh
Mở đầu: Nhiệm vụ bất khả thi
Hãy tưởng tượng bạn là một nhà khoa học được giao nhiệm vụ tìm ra lời giải cho một bài toán mà không ai biết câu trả lời. Bạn được trao một "chiếc hộp đen" - một thiết bị bí ẩn mà khi bạn đưa vào một dãy số, nó sẽ trả về một điểm số. Điểm số càng cao càng tốt, nhưng bạn hoàn toàn không biết thiết bị này hoạt động như thế nào.
Đây chính là tình huống mà các nhà khoa học máy tính phải đối mặt hàng ngày. Họ có những bài toán phức tạp như:
- Tối ưu hóa lịch làm việc cho 1000 công nhân
- Thiết kế mạng neural network tốt nhất
- Tìm ra cấu hình tối ưu cho một hệ thống
Vấn đề: Không có công thức toán học nào có thể giải quyết những bài toán này. Không có đạo hàm để tính toán. Không có quy luật rõ ràng để tuân theo.
Giải pháp: Hãy để thiên nhiên dạy chúng ta cách làm!
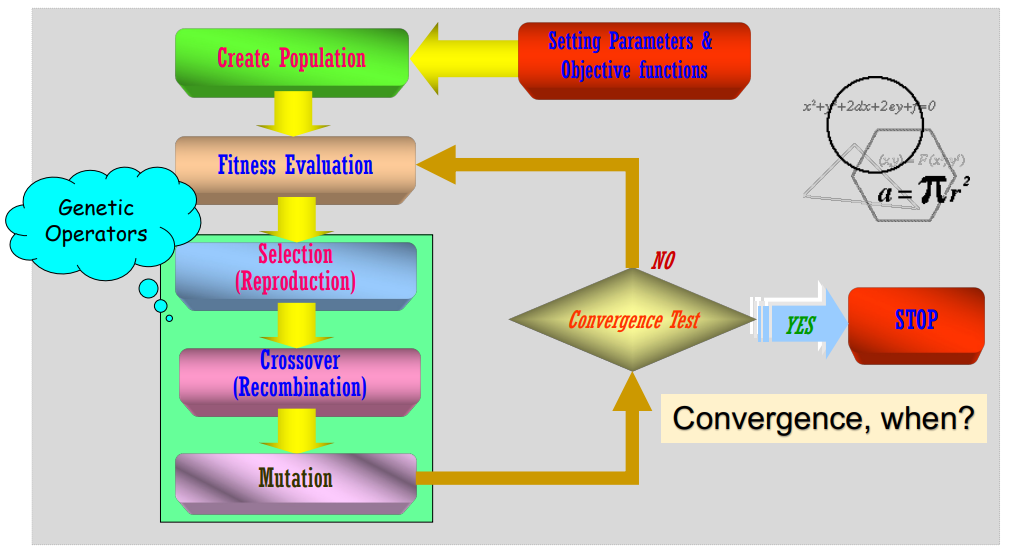
Hình 1: Chu trình hoạt động của Thuật toán Di truyền (Genetic Algorithm)
Chương 1: Bài học từ thiên nhiên
Motivation: Tại sao cần học từ thiên nhiên?
Trong hàng triệu năm, thiên nhiên đã giải quyết những bài toán phức tạp nhất mà con người không thể tưởng tượng được. Làm sao một con chim có thể bay hàng nghìn cây số mà không bị lạc? Làm sao một con ong có thể tìm ra đường đi ngắn nhất giữa hàng trăm bông hoa? Làm sao một con cá có thể bơi với hiệu suất năng lượng tối ưu?
Câu trả lời: Tiến hóa! Thiên nhiên đã sử dụng một thuật toán cực kỳ thông minh gọi là "tiến hóa tự nhiên" để tạo ra những giải pháp hoàn hảo.
Assumption: Những giả định cơ bản
Trước khi bắt đầu, chúng ta cần hiểu những giả định cơ bản:
- Mỗi giải pháp có thể được mã hóa thành một "gen" - giống như DNA của sinh vật
- Có thể đánh giá chất lượng của giải pháp - giống như "fitness" trong tự nhiên
- Giải pháp tốt có thể kết hợp để tạo ra giải pháp tốt hơn - giống như sinh sản
- Đôi khi cần thay đổi ngẫu nhiên để khám phá - giống như đột biến
Chương 2: Bắt đầu với sự ngẫu nhiên
Câu chuyện: Thử nghiệm đầu tiên
Hãy bắt đầu với một bài toán đơn giản: Tìm dãy số có nhiều số 1 nhất
Motivation: Đây là bài toán OneMax - đơn giản nhưng thể hiện được bản chất của thuật toán di truyền.
Assumption:
- Chúng ta có một dãy 10 vị trí
- Mỗi vị trí chỉ có thể là 0 hoặc 1
- Mục tiêu: Tìm dãy có nhiều số 1 nhất (tối đa là 10)
Bước 1: Tạo quần thể ban đầu
Giống như trong tự nhiên, chúng ta bắt đầu với một quần thể ngẫu nhiên. Mỗi "cá thể" trong quần thể là một giải pháp khả thi.
import random
def create_individual(problem_size):
"""Tạo một cá thể ngẫu nhiên"""
return [random.randint(0, 1) for _ in range(problem_size)]
# Tạo quần thể ban đầu
population_size = 8
problem_size = 10
population = [create_individual(problem_size) for _ in range(population_size)]
Giải thích kết quả:
Chúng ta đã tạo ra 8 cá thể, mỗi cá thể là một dãy 10 số ngẫu nhiên. Ví dụ:
- Cá thể 1: [1, 0, 1, 0, 1, 1, 0, 0, 1, 0] - có 5 số 1
- Cá thể 2: [0, 1, 1, 1, 0, 0, 1, 1, 0, 1] - có 6 số 1
- Cá thể 3: [1, 1, 0, 1, 0, 1, 1, 0, 1, 0] - có 6 số 1
Bước 2: Đánh giá fitness
Bây giờ chúng ta cần đánh giá "sức khỏe" của từng cá thể:
def evaluate_fitness(individual):
"""Đánh giá fitness - số lượng số 1"""
return sum(individual)
# Đánh giá tất cả cá thể
fitness_scores = [evaluate_fitness(individual) for individual in population]
Kết quả được diễn tả:
Chúng ta có bảng đánh giá như sau:
| Cá thể | Dãy số | Số lượng số 1 | Fitness |
|---|---|---|---|
| 1 | [1,0,1,0,1,1,0,0,1,0] | 5 | 5 |
| 2 | [0,1,1,1,0,0,1,1,0,1] | 6 | 6 |
| 3 | [1,1,0,1,0,1,1,0,1,0] | 6 | 6 |
| 4 | [0,0,1,1,1,0,1,1,0,1] | 6 | 6 |
| 5 | [1,0,0,1,1,0,1,0,1,1] | 6 | 6 |
| 6 | [0,1,1,0,1,1,0,1,0,1] | 6 | 6 |
| 7 | [1,1,1,0,0,1,0,1,1,0] | 6 | 6 |
| 8 | [0,0,0,1,1,1,1,0,1,1] | 6 | 6 |
Quan sát thú vị: Hầu hết cá thể đều có fitness = 6, chỉ có 1 cá thể có fitness = 5. Điều này cho thấy tính ngẫu nhiên đã tạo ra những giải pháp khá tốt ngay từ đầu.
Chương 3: Nghệ thuật chọn lọc
Motivation: Tại sao cần chọn lọc?
Trong tự nhiên, không phải tất cả sinh vật đều có cơ hội sinh sản bằng nhau. Những sinh vật khỏe mạnh, thích nghi tốt sẽ có cơ hội cao hơn để truyền gen cho thế hệ sau.
Assumption: Chúng ta giả định rằng những cá thể có fitness cao hơn sẽ có khả năng tạo ra con cái tốt hơn.
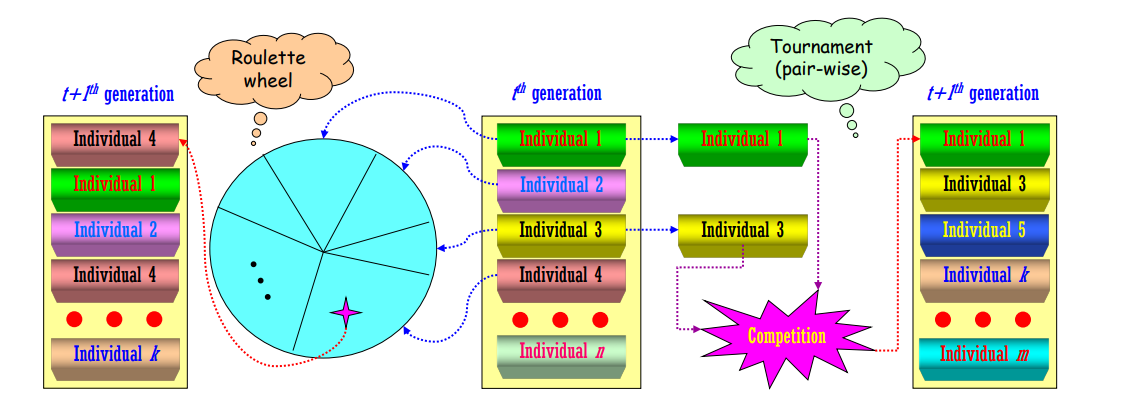
Hình 2: Một số phương pháp chọn lọc trong Thuật toán Di truyền
Phương pháp chọn lọc: Tournament Selection
Thay vì chọn lọc dựa trên xác suất phức tạp, chúng ta sử dụng phương pháp "giải đấu" - đơn giản và hiệu quả.
Cách hoạt động:
1. Chọn ngẫu nhiên 3 cá thể từ quần thể
2. Cá thể nào có fitness cao nhất sẽ thắng
3. Lặp lại cho đến khi có đủ cá thể cho thế hệ mới
def tournament_selection(population, fitness_scores, tournament_size=3):
"""Chọn lọc theo giải đấu"""
selected = []
for _ in range(len(population)):
# Chọn ngẫu nhiên tournament_size cá thể
tournament_indices = random.sample(range(len(population)), tournament_size)
tournament_fitness = [fitness_scores[i] for i in tournament_indices]
# Tìm người thắng
winner_index_in_tournament = tournament_fitness.index(max(tournament_fitness))
winner_index = tournament_indices[winner_index_in_tournament]
selected.append(population[winner_index])
return selected
Kết quả được diễn tả:
Sau khi chạy tournament selection, chúng ta có thể thấy:
- Cá thể có fitness = 6 có cơ hội cao được chọn (vì có nhiều cá thể fitness = 6)
- Cá thể có fitness = 5 ít có cơ hội được chọn
- Quá trình này đảm bảo rằng những gen tốt sẽ được truyền lại
Phương pháp chọn lọc khác: Roulette Wheel Selection
Motivation: Tournament Selection đơn giản nhưng đôi khi quá "cứng nhắc". Roulette Wheel Selection mô phỏng chính xác hơn cách thiên nhiên chọn lọc - cá thể tốt hơn có cơ hội cao hơn, nhưng vẫn có cơ hội cho cá thể yếu hơn.
Cách hoạt động:
1. Tính tổng fitness của toàn bộ quần thể
2. Tính xác suất chọn lọc cho từng cá thể = fitness cá thể / tổng fitness
3. Tạo "bánh xe roulette" với diện tích tỷ lệ với xác suất
4. Quay bánh xe để chọn cá thể
def roulette_wheel_selection(population, fitness_scores):
"""Chọn lọc theo bánh xe roulette"""
total_fitness = sum(fitness_scores)
# Tính xác suất chọn lọc
probabilities = [fitness / total_fitness for fitness in fitness_scores]
selected = []
for _ in range(len(population)):
# Quay bánh xe
random_value = random.random()
cumulative_probability = 0
for i, prob in enumerate(probabilities):
cumulative_probability += prob
if random_value <= cumulative_probability:
selected.append(population[i])
break
return selected
Ví dụ cụ thể:
Giả sử chúng ta có quần thể với fitness như sau:
| Cá thể | Fitness | Xác suất chọn lọc |
|---|---|---|
| 1 | 5 | 5/30 = 16.7% |
| 2 | 6 | 6/30 = 20.0% |
| 3 | 6 | 6/30 = 20.0% |
| 4 | 6 | 6/30 = 20.0% |
| 5 | 7 | 7/30 = 23.3% |
Tổng fitness = 30
Cách hoạt động của bánh xe:
- Cá thể 1: Chiếm 16.7% diện tích bánh xe
- Cá thể 2,3,4: Mỗi cá thể chiếm 20% diện tích
- Cá thể 5: Chiếm 23.3% diện tích (lớn nhất)
Kết quả được diễn tả:
- Cá thể có fitness = 7 có cơ hội cao nhất (23.3%)
- Cá thể có fitness = 6 có cơ hội trung bình (20% mỗi cá thể)
- Cá thể có fitness = 5 vẫn có cơ hội (16.7%) - không bị loại bỏ hoàn toàn
Khi nào dùng Roulette Wheel:
- ✅ Cần duy trì đa dạng gen
- ✅ Fitness có sự chênh lệch lớn
- ✅ Muốn mô phỏng chính xác tự nhiên
- ✅ Bài toán phức tạp, cần cân bằng
Khi nào dùng Tournament:
- ✅ Cần tốc độ cao
- ✅ Fitness tương đối đồng đều
- ✅ Bài toán đơn giản
- ✅ Muốn áp lực chọn lọc mạnh
Chương 4: Nghệ thuật lai tạo
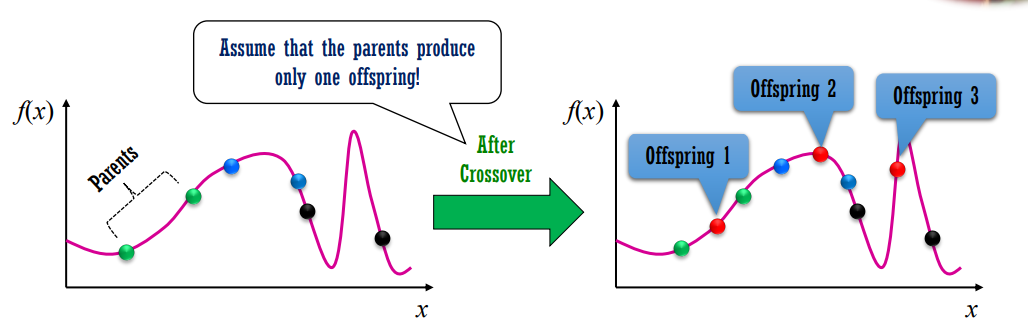
Hình 3: Minh họa quá trình lai tạo (Crossover) từ bố mẹ sang con cái
Motivation: Trong tự nhiên, sinh sản hữu tính cho phép kết hợp những đặc điểm tốt từ hai cá thể khác nhau. Một con chim có thể thừa hưởng khả năng bay tốt từ bố và khả năng tìm thức ăn tốt từ mẹ. Hình ảnh trên minh họa cách các gen từ hai cá thể bố mẹ được kết hợp để tạo ra các cá thể con mới.
Assumption: Chúng ta giả định rằng việc kết hợp gen từ hai cá thể tốt có thể tạo ra một cá thể con tốt hơn, hoặc ít nhất là duy trì được những đặc điểm tốt. Các điểm màu trên đường cong đại diện cho các phần của chuỗi gen, và việc trao đổi các phần này sẽ tạo ra các cá thể con với sự kết hợp gen mới
Phương pháp lai tạo: One-Point Crossover
Cách hoạt động:
1. Chọn một điểm cắt ngẫu nhiên
2. Con cái 1: Lấy phần đầu từ bố, phần cuối từ mẹ
3. Con cái 2: Lấy phần đầu từ mẹ, phần cuối từ bố
def crossover(parent1, parent2, crossover_rate=0.8):
"""Lai tạo hai cá thể cha mẹ"""
if random.random() < crossover_rate:
# Chọn điểm cắt ngẫu nhiên
crossover_point = random.randint(1, len(parent1) - 1)
# Tạo con cái
child1 = parent1[:crossover_point] + parent2[crossover_point:]
child2 = parent2[:crossover_point] + parent1[crossover_point:]
return child1, child2
else:
# Không lai tạo - giữ nguyên
return parent1, parent2
Ví dụ cụ thể:
Giả sử chúng ta có:
- Bố: [1, 1, 0, 1, 0, 1, 1, 0, 1, 0] (fitness = 6)
- Mẹ: [0, 1, 1, 1, 0, 0, 1, 1, 0, 1] (fitness = 6)
- Điểm cắt: vị trí 3
Kết quả:
- Con 1: [1, 1, 0, 1, 0, 0, 1, 1, 0, 1] (fitness = 6)
- Con 2: [0, 1, 1, 1, 0, 1, 1, 0, 1, 0] (fitness = 6)
Quan sát: Cả hai con đều có fitness = 6, giống như bố mẹ. Điều này là bình thường - không phải lúc nào con cái cũng tốt hơn bố mẹ ngay lập tức.
Motivation: One-Point Crossover đơn giản nhưng đôi khi không đủ linh hoạt. Các loại crossover khác có thể tạo ra sự đa dạng gen tốt hơn.
1. Two-Point Crossover
Cách hoạt động:
- Chọn 2 điểm cắt thay vì 1
- Con cái 1: Phần đầu từ bố + phần giữa từ mẹ + phần cuối từ bố
- Con cái 2: Phần đầu từ mẹ + phần giữa từ bố + phần cuối từ mẹ
def two_point_crossover(parent1, parent2, crossover_rate=0.8):
"""Lai tạo hai điểm cắt"""
if random.random() < crossover_rate:
# Chọn 2 điểm cắt
point1 = random.randint(1, len(parent1) - 2)
point2 = random.randint(point1 + 1, len(parent1) - 1)
# Tạo con cái
child1 = (parent1[:point1] +
parent2[point1:point2] +
parent1[point2:])
child2 = (parent2[:point1] +
parent1[point1:point2] +
parent2[point2:])
return child1, child2
else:
return parent1, parent2
Ví dụ cụ thể:
- Bố: [1, 1, 0, 1, 0, 1, 1, 0, 1, 0]
- Mẹ: [0, 1, 1, 1, 0, 0, 1, 1, 0, 1]
- Điểm cắt: 2 và 6
Kết quả:
- Con 1: [1, 1, 1, 1, 0, 0, 1, 0, 1, 0] (fitness = 6)
- Con 2: [0, 1, 0, 1, 0, 1, 1, 1, 0, 1] (fitness = 6)
2. Uniform Crossover
Cách hoạt động:
- Tạo một "mask" ngẫu nhiên (0 hoặc 1 cho từng vị trí)
- Con cái 1: Lấy từ bố khi mask = 1, từ mẹ khi mask = 0
- Con cái 2: Ngược lại
def uniform_crossover(parent1, parent2, crossover_rate=0.8):
"""Lai tạo đồng nhất"""
if random.random() < crossover_rate:
# Tạo mask ngẫu nhiên
mask = [random.randint(0, 1) for _ in range(len(parent1))]
# Tạo con cái
child1 = [parent1[i] if mask[i] else parent2[i] for i in range(len(parent1))]
child2 = [parent2[i] if mask[i] else parent1[i] for i in range(len(parent1))]
return child1, child2
else:
return parent1, parent2
Ví dụ cụ thể:
- Bố: [1, 1, 0, 1, 0, 1, 1, 0, 1, 0]
- Mẹ: [0, 1, 1, 1, 0, 0, 1, 1, 0, 1]
- Mask: [1, 0, 1, 0, 1, 0, 1, 0, 1, 0]
Kết quả:
- Con 1: [1, 1, 0, 1, 0, 0, 1, 1, 1, 0] (fitness = 6)
- Con 2: [0, 1, 1, 1, 0, 1, 1, 0, 0, 1] (fitness = 6)
Khi nào dùng loại nào:
One-Point Crossover:
- ✅ Bài toán đơn giản
- ✅ Cần tốc độ cao
- ✅ Gen có cấu trúc liên tục
Two-Point Crossover:
- ✅ Cần đa dạng hơn One-Point
- ✅ Gen có cấu trúc phức tạp
- ✅ Muốn cân bằng giữa đơn giản và đa dạng
Uniform Crossover:
- ✅ Cần đa dạng tối đa
- ✅ Gen độc lập với nhau
- ✅ Muốn khám phá không gian rộng
Arithmetic Crossover:
- ✅ Bài toán số thực
- ✅ Cần giải pháp mượt mà
- ✅ Optimization liên tục
Chương 5: Sức mạnh của đột biến
Motivation: Tại sao cần đột biến?
Trong tự nhiên, đột biến là nguồn gốc của sự đa dạng. Nếu không có đột biến, tất cả sinh vật sẽ giống hệt nhau và không thể tiến hóa.
Assumption: Đột biến nhỏ có thể tạo ra những thay đổi tích cực, giúp khám phá những vùng mới trong không gian giải pháp.
Phương pháp đột biến: Bit Flip
Cách hoạt động:
1. Duyệt qua từng vị trí trong cá thể
2. Với xác suất nhỏ (thường 10%), đảo bit tại vị trí đó
3. 0 → 1, 1 → 0
def mutation(individual, mutation_rate=0.1):
"""Đột biến cá thể"""
mutated = individual.copy()
for i in range(len(mutated)):
if random.random() < mutation_rate:
# Đảo bit: 0 → 1, 1 → 0
mutated[i] = 1 - mutated[i]
return mutated
Ví dụ cụ thể:
Giả sử chúng ta có cá thể: [1, 1, 0, 1, 0, 1, 1, 0, 1, 0]
Với mutation rate = 10%, có thể xảy ra đột biến tại vị trí 4 và 7:
Kết quả:
- Trước: [1, 1, 0, 1, 0, 1, 1, 0, 1, 0] (fitness = 6)
- Sau: [1, 1, 0, 1, 1, 1, 1, 1, 1, 0] (fitness = 8)
Quan sát thú vị: Đột biến đã tạo ra một cá thể tốt hơn! Fitness tăng từ 6 lên 8.
Chương 6: Vòng lặp tiến hóa
Motivation: Tại sao cần nhiều thế hệ?
Một thế hệ duy nhất không thể tạo ra giải pháp tối ưu. Cần nhiều thế hệ để:
- Tích lũy những đặc điểm tốt
- Loại bỏ những đặc điểm xấu
- Khám phá những vùng mới trong không gian giải pháp
Thuật toán hoàn chỉnh
def genetic_algorithm(problem_size=10, population_size=8, generations=20,
crossover_rate=0.8, mutation_rate=0.1):
"""Thuật toán di truyền hoàn chỉnh"""
# 1. Khởi tạo quần thể
population = [create_individual(problem_size) for _ in range(population_size)]
for generation in range(generations):
# 2. Đánh giá fitness
fitness_scores = [evaluate_fitness(individual) for individual in population]
# 3. Chọn lọc
selected = tournament_selection(population, fitness_scores)
# 4. Lai tạo và đột biến
new_population = []
for i in range(0, len(selected), 2):
parent1, parent2 = selected[i], selected[i+1]
child1, child2 = crossover(parent1, parent2, crossover_rate)
child1 = mutation(child1, mutation_rate)
child2 = mutation(child2, mutation_rate)
new_population.extend([child1, child2])
# 5. Cập nhật quần thể
population = new_population
# 6. Theo dõi tiến bộ
best_fitness = max(fitness_scores)
print(f"Thế hệ {generation + 1}: Fitness tốt nhất = {best_fitness}")
return population
Kết quả được diễn tả:
Lịch sử tiến hóa:
- Thế hệ 1: Fitness tốt nhất = 6
- Thế hệ 2: Fitness tốt nhất = 6
- Thế hệ 3: Fitness tốt nhất = 7
- Thế hệ 4: Fitness tốt nhất = 7
- Thế hệ 5: Fitness tốt nhất = 8
- Thế hệ 6: Fitness tốt nhất = 8
- Thế hệ 7: Fitness tốt nhất = 9
- Thế hệ 8: Fitness tốt nhất = 9
- Thế hệ 9: Fitness tốt nhất = 10 ← HOÀN HẢO!
Phân tích kết quả:
- Quá trình tiến hóa diễn ra từ từ, không đột ngột
- Có những thế hệ không có tiến bộ (thế hệ 1-2, 3-4)
- Cuối cùng đạt được giải pháp tối ưu: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Chương 7: Ứng dụng thực tế
Bài toán 1: Tối ưu hóa lịch làm việc
Motivation: Một công ty có 100 công nhân, mỗi người có thể làm ca ngày, ca đêm, hoặc nghỉ. Cần tìm lịch làm việc tối ưu để đạt hiệu suất cao nhất.
Cách áp dụng GA:
- Gen: Mỗi vị trí trong dãy 100 số đại diện cho ca làm việc của 1 công nhân
- Fitness: Hiệu suất tổng thể của dây chuyền sản xuất
- Lai tạo: Trao đổi ca giữa các lịch làm việc tốt
- Đột biến: Thay đổi ca của một số công nhân ngẫu nhiên
Bài toán 2: Thiết kế mạng neural network
Motivation: Cần tìm kiến trúc mạng neural tốt nhất cho bài toán phân loại ảnh.
Cách áp dụng GA:
- Gen: Số layers, số neurons mỗi layer, activation function
- Fitness: Accuracy trên validation set
- Lai tạo: Kết hợp kiến trúc từ 2 mạng tốt
- Đột biến: Thay đổi số layers hoặc neurons ngẫu nhiên
Bài toán 3: Tối ưu hóa hyperparameters
Motivation: Cần tìm bộ hyperparameters tốt nhất cho machine learning model.
Cách áp dụng GA:
- Gen: Learning rate, batch size, số epochs, optimizer
- Fitness: Performance metric (accuracy, F1-score)
- Lai tạo: Kết hợp hyperparameters từ 2 bộ tốt
- Đột biến: Thay đổi một số hyperparameters ngẫu nhiên
Chương 8: Những thách thức và giải pháp
Vấn đề 1: Mất cá thể tốt nhất
Vấn đề: Đôi khi thế hệ sau có thể tệ hơn thế hệ trước do chọn lọc không hoàn hảo.
Giải pháp: Elitism
- Giữ lại 1-2 cá thể tốt nhất từ thế hệ trước
- Đảm bảo không bao giờ mất thông tin tốt
Vấn đề 2: Hội tụ sớm
Vấn đề: Quần thể có thể hội tụ quá nhanh, mất đa dạng gen.
Giải pháp:
- Tăng mutation rate
- Tăng population size
- Sử dụng diversity maintenance
Vấn đề 3: Tốc độ chậm
Vấn đề: GA cần nhiều đánh giá fitness, có thể chậm với bài toán phức tạp.
Giải pháp:
- Parallel processing
- Surrogate models
- Early stopping
Kết luận: Sức mạnh của tiến hóa
Thuật toán di truyền là một minh chứng tuyệt vời về sức mạnh của việc học hỏi từ thiên nhiên. Bằng cách mô phỏng quá trình tiến hóa tự nhiên, chúng ta có thể giải quyết những bài toán mà con người không thể tính toán bằng tay.
Điểm mạnh:
- ✅ Không cần đạo hàm
- ✅ Tránh cực trị cục bộ
- ✅ Song song hóa dễ dàng
- ✅ Áp dụng được nhiều bài toán
Điểm yếu:
- ❌ Chậm (cần nhiều đánh giá)
- ❌ Không đảm bảo tối ưu tuyệt đối
- ❌ Nhiều tham số cần điều chỉnh
Khi nào dùng GA:
- ✅ Hàm không có đạo hàm
- ✅ Hàm đa cực trị
- ✅ Không gian tìm kiếm rất lớn
- ✅ Cần tìm lời giải gần tối ưu
Thông điệp cuối cùng: "Đừng tính toán, hãy để nó tiến hóa!" 🧬🚀
Thiên nhiên đã dạy chúng ta rằng sự tiến hóa có thể tạo ra những giải pháp tuyệt vời từ sự ngẫu nhiên. Hãy để máy tính học hỏi từ bài học này và tạo ra những giải pháp thông minh cho những vấn đề phức tạp nhất của nhân loại.
References
[1] Ảnh được lấy từ tài liệu khóa học AIO Module 05 – Tuần 3, AIO 2025.
Hay quá