1. Mở đầu – Vì sao gọi là “thuật toán di truyền”?
Trong tự nhiên, các loài sinh vật tiến hóa qua nhiều thế hệ nhờ cơ chế chọn lọc tự nhiên: những cá thể có đặc điểm thích nghi tốt hơn sẽ có khả năng sinh tồn và truyền lại gene của mình cho thế hệ sau.
Genetic Algorithm (GA) – thuật toán di truyền – được xây dựng dựa trên cùng nguyên lý đó, nhưng thay vì sinh vật, nó tiến hóa các lời giải cho một bài toán tối ưu.
Trong ngữ cảnh tính toán, mỗi cá thể (individual) biểu diễn một lời giải khả dĩ, được mã hóa thành chuỗi gene (genome) – thường là chuỗi nhị phân, vector thực, hoặc cấu trúc hỗn hợp tùy theo bài toán.
Mức độ “tốt” của một lời giải được đánh giá bằng hàm thích nghi (fitness function), ký hiệu là: $f_i = Fitness(x_i)$
Các cá thể có giá trị fitness cao hơn được chọn lọc để “sinh sản”, thông qua hai quá trình chính:
- Lai ghép (Crossover): kết hợp thông tin di truyền giữa hai cá thể.
- Đột biến (Mutation): thay đổi ngẫu nhiên một phần gene nhằm duy trì đa dạng.
Quá trình này tạo ra thế hệ mới với những đặc điểm được kết hợp và biến đổi, giúp quần thể dần tiến hóa về phía lời giải tối ưu.
Không giống như những phương pháp giải tích truyền thống (ví dụ Gradient Descent) cần đạo hàm hoặc hàm liên tục, GA hoạt động hoàn toàn dựa trên nguyên tắc tìm kiếm ngẫu nhiên có hướng (stochastic search), cho phép áp dụng trong nhiều bài toán phức tạp, rời rạc hoặc phi tuyến.
Tuy nhiên, chính tính “ngẫu nhiên” này cũng là con dao hai lưỡi. GA có thể dễ dàng hội tụ sớm vào lời giải cục bộ nếu các bước tiến hóa không được cân bằng hợp lý giữa khai thác (exploitation) và khai phá (exploration).
Vấn đề này – cách duy trì sự cân bằng tiến hóa – sẽ là trọng tâm của bài viết.

Hình 1. Mô tả quá trình Genetic Algorithm.
2. Tổng quan ngắn gọn về Genetic Algorithm
Genetic Algorithm (GA) là một phương pháp tối ưu hóa lấy cảm hứng từ quá trình tiến hóa sinh học.
GA hoạt động bằng cách mô phỏng sự chọn lọc tự nhiên, lai ghép và đột biến để cải thiện quần thể các lời giải theo thời gian.
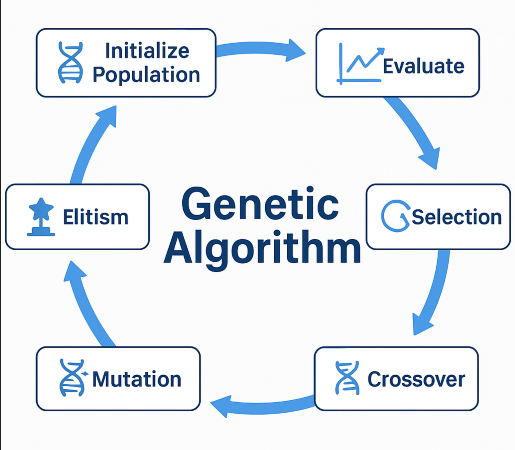
Hình 2. Sơ đồ vòng lặp tiến hóa trong Genetic Algorithm.
2.1 Chu trình tiến hóa cơ bản
Một vòng tiến hóa (generation) của GA bao gồm bốn bước chính:
-
Khởi tạo quần thể (Initialization)
- Tạo ngẫu nhiên $N$ cá thể.
- Mỗi cá thể biểu diễn một lời giải được mã hóa dưới dạng chuỗi gene (bit, số thực, hoặc vector). -
Đánh giá độ thích nghi (Fitness Evaluation)
- Tính giá trị fitness của mỗi cá thể bằng hàm đánh giá $f(x)$, thể hiện mức độ "tốt" của lời giải.
$$ f_i = Fitness(x_i) $$
-
Tiến hóa quần thể (Evolution Step)
Bao gồm ba phép toán chính:
- Selection: Chọn cá thể tốt để sinh sản.
- Crossover: Lai ghép hai cá thể cha mẹ để tạo thế hệ con.
- Mutation: Đột biến ngẫu nhiên trên các gene để duy trì đa dạng. -
Elitism (nếu có)
- Giữ lại một hoặc vài cá thể tốt nhất để đảm bảo kết quả không kém hơn thế hệ trước. -
Lặp lại quá trình cho đến khi thỏa mãn điều kiện dừng (đạt fitness mục tiêu hoặc số thế hệ tối đa).
2.2 Biểu diễn mô hình toán học
Quá trình tiến hóa của GA có thể được khái quát bằng phương trình:
$$ P_{t+1} = G(P_t) $$
Trong đó:
- $P_t$: quần thể tại thế hệ $t$
- $G$: toán tử tiến hóa bao gồm selection, crossover, mutation
Mục tiêu của thuật toán là tối đa hóa hàm fitness $f(x)$ hoặc tối thiểu hóa hàm chi phí $J(x)$ trên không gian tìm kiếm.
2.3 Pseudocode tổng quát
Initialize population P(0)
Evaluate fitness of each individual in P(0)
t = 0
while not termination_condition:
Select parents from P(t)
Apply crossover to create offspring
Apply mutation to offspring
Evaluate fitness of offspring
Form new population P(t+1) with elitism
t = t + 1
return best individual
2.4 Ví dụ minh họa: Bài toán One-Max
Bài toán One-Max yêu cầu tìm chuỗi nhị phân có tổng số bit 1 là lớn nhất.
Đây là ví dụ đơn giản nhưng thể hiện đầy đủ nguyên lý hoạt động của GA.
import random
# Parameters - Các tham số cấu hình thuật toán
POP_SIZE = 20 # Kích thước quần thể (số cá thể)
GENES = 10 # Số gene trong mỗi cá thể (độ dài chuỗi nhị phân)
MUT_RATE = 0.01 # Tỷ lệ đột biến (1%)
GENERATIONS = 50 # Số thế hệ tối đa
def fitness(ind):
"""
Hàm đánh giá độ thích nghi của một cá thể
- Input: ind - danh sách các bit (0 hoặc 1)
- Output: tổng số bit 1 trong chuỗi (càng nhiều càng tốt)
- Mục đích: đo lường chất lượng của lời giải
"""
return sum(ind) # maximize number of 1s
def mutate(ind):
"""
Hàm đột biến - thay đổi ngẫu nhiên một số gene
- Input: ind - cá thể cần đột biến
- Output: cá thể sau khi đột biến
- Cơ chế: với xác suất MUT_RATE, đảo bit (0->1, 1->0)
- Mục đích: duy trì đa dạng di truyền, tránh hội tụ sớm
"""
return [1 - g if random.random() < MUT_RATE else g for g in ind]
def crossover(p1, p2):
"""
Hàm lai ghép - tạo cá thể con từ hai cá thể cha mẹ
- Input: p1, p2 - hai cá thể cha mẹ
- Output: cá thể con
- Cơ chế: chọn điểm cắt ngẫu nhiên, ghép nửa đầu của p1 với nửa sau của p2
- Mục đích: kết hợp đặc tính tốt của cả hai cha mẹ
"""
point = random.randint(1, GENES - 1) # Chọn điểm cắt ngẫu nhiên
return p1[:point] + p2[point:] # Ghép nửa đầu p1 + nửa sau p2
# Khởi tạo quần thể ban đầu
# Tạo POP_SIZE cá thể, mỗi cá thể có GENES bit ngẫu nhiên (0 hoặc 1)
population = [[random.randint(0, 1) for _ in range(GENES)] for _ in range(POP_SIZE)]
# Vòng lặp tiến hóa chính
for gen in range(GENERATIONS):
# Sắp xếp quần thể theo độ thích nghi giảm dần (cá thể tốt nhất ở đầu)
population = sorted(population, key=fitness, reverse=True)
# Elitism: giữ lại 2 cá thể tốt nhất cho thế hệ tiếp theo
next_gen = population[:2] # elitism
# Tạo các cá thể mới cho đến khi đủ POP_SIZE
while len(next_gen) < POP_SIZE:
# Selection: chọn 2 cha mẹ từ top 10 cá thể tốt nhất
p1, p2 = random.sample(population[:10], 2)
# Tạo cá thể con: lai ghép rồi đột biến
child = mutate(crossover(p1, p2))
next_gen.append(child)
# Cập nhật quần thể cho thế hệ tiếp theo
population = next_gen
# Tìm và in ra cá thể tốt nhất cuối cùng
best = max(population, key=fitness)
print("Best:", best, "Fitness:", fitness(best))
2.5 Ý nghĩa và hạn chế
| Ưu điểm | Hạn chế |
|---|---|
| Không yêu cầu đạo hàm hoặc tính liên tục | Tốc độ chậm với hàm fitness phức tạp |
| Khả năng thoát khỏi local optimum | Dễ hội tụ sớm nếu đa dạng giảm |
| Dễ song song hóa, mở rộng nhiều ứng dụng | Cần tinh chỉnh nhiều tham số |
| --- |
3. Trái tim của Genetic Algorithm – Cân bằng giữa Khai phá và Khai thác
Một trong những yếu tố quyết định sự thành công của Genetic Algorithm không nằm ở bản thân các phép toán di truyền, mà ở cách chúng được điều chỉnh để đạt cân bằng giữa khai phá (exploration) và khai thác (exploitation).
3.1 Khai phá và Khai thác là gì?
-
Khai phá (Exploration):
Là khả năng của thuật toán trong việc tìm kiếm và khám phá các vùng mới trong không gian lời giải.
GA thực hiện khai phá chủ yếu thông qua đột biến (mutation) và chọn lọc mềm (low selection pressure). -
Khai thác (Exploitation):
Là việc đào sâu các vùng đã biết có lời giải tốt, giúp hội tụ nhanh hơn đến cực trị.
GA khai thác thông qua chọn lọc mạnh (high selection pressure) và tần suất lai ghép cao (crossover rate).
Cân bằng giữa hai yếu tố này là cốt lõi của quá trình tiến hóa hiệu quả.
Nếu khai thác quá mạnh, quần thể dễ hội tụ sớm (mất đa dạng).
Nếu khai phá quá mức, thuật toán trở nên ngẫu nhiên và mất phương hướng.
3.2 Minh họa toán học
Sự tiến hóa của quần thể có thể được xem như quá trình tối ưu hóa kỳ vọng:
$$ E[f(P_{t+1})] = (1 - \mu) \cdot E[f(\text{offspring from crossover})] + \mu \cdot E[f(\text{mutated individuals})] $$
Trong đó:
- $\mu$: xác suất đột biến (mutation rate)
- $E[f(P_{t+1})]$: giá trị fitness trung bình của thế hệ tiếp theo
Giá trị $\mu$ càng lớn thì yếu tố khai phá càng mạnh, nhưng độ ổn định của tiến hóa giảm.
Khi $\mu$ nhỏ, GA tập trung vào khai thác — tiến hóa nhanh nhưng dễ rơi vào cực trị cục bộ.
3.3 Biểu hiện mất cân bằng trong thực tế
| Tình huống | Dấu hiệu | Nguyên nhân chính | Hệ quả |
|---|---|---|---|
| Hội tụ sớm | Best fitness không tăng, quần thể giống hệt nhau | Chọn lọc mạnh, mutation thấp | Mất đa dạng, kẹt ở local optimum |
| Tiến hóa chậm | Fitness tăng rất chậm, dao động mạnh | Mutation cao, crossover yếu | Không tập trung khai thác |
| Tiến hóa ổn định | Fitness tăng đều, đa dạng duy trì vừa đủ | Tỷ lệ cân bằng crossover–mutation | Cải thiện dần đến nghiệm tối ưu |
3.4 Cách duy trì cân bằng hiệu quả
-
Điều chỉnh áp lực chọn lọc (Selection Pressure)
- Tournament size nhỏ (2–3) → tăng đa dạng.
- Tournament size lớn (≥5) → hội tụ nhanh hơn nhưng dễ kẹt cục bộ. -
Tùy biến tỉ lệ đột biến (Adaptive Mutation)
- Tăng mutation khi quần thể mất đa dạng.
- Giảm mutation khi fitness đang cải thiện ổn định.
Ví dụ:
$$
\text{mutation\_rate}(t) = \mu_0 \times \left(1 - \frac{\text{diversity}(t)}{\text{diversity}(0)}\right)
$$
-
Giới hạn elitism hợp lý
- Giữ lại 1–2 cá thể tốt nhất để đảm bảo ổn định.
- Không nên quá 5% quần thể, tránh "đóng băng gene trội". -
Theo dõi chỉ số đa dạng (Diversity Index)
- Đo khoảng cách Hamming trung bình giữa các cá thể.
- Khi chỉ số này < 0.1 → cần tăng mutation hoặc khởi tạo lại một phần quần thể.
Hình 3. Exploration–Exploitation balance
4. Bốn nút điều khiển quyết định sức mạnh của Genetic Algorithm
Genetic Algorithm được xem như một hệ thống tiến hóa nhân tạo.
Bốn thành phần: Selection, Crossover, Mutation và Elitism đóng vai trò như các "nút điều khiển" định hình cách quần thể phát triển qua từng thế hệ.
Việc hiểu rõ và tinh chỉnh chúng là yếu tố quyết định để GA đạt hiệu quả tối ưu.
4.1 Selection – Áp lực chọn lọc
Selection là bước chọn ra các cá thể cha mẹ có khả năng sinh ra thế hệ con tốt hơn.
Mục tiêu là ưu tiên cá thể tốt nhưng vẫn duy trì đa dạng di truyền.
Một số chiến lược phổ biến:
| Phương pháp | Cách hoạt động | Ưu điểm | Hạn chế |
|---|---|---|---|
| Roulette Wheel | Xác suất chọn tỷ lệ với fitness | Giữ đa dạng tốt | Dễ bị chi phối bởi cá thể mạnh |
| Tournament | Chọn ngẫu nhiên $k$ cá thể, lấy tốt nhất | Dễ điều chỉnh áp lực chọn lọc | Khi $k$ lớn dễ mất đa dạng |
| Rank Selection | Xếp hạng cá thể, chọn theo xác suất | Ổn định, giảm chênh lệch fitness | Cần sắp xếp toàn bộ quần thể |
Công thức xác suất chọn trong Roulette:
$$ p_i = \frac{f_i}{\sum_{j=1}^{N} f_j} $$
Khi $p_i$ quá cao cho một cá thể, quần thể sẽ nhanh chóng hội tụ – dấu hiệu của áp lực chọn lọc mạnh.
4.2 Crossover – Khai thác thông tin di truyền
Crossover (lai ghép) là cơ chế kết hợp gene từ hai cá thể cha mẹ để tạo ra cá thể con, với mục tiêu tái tổ hợp thông tin tốt.
Đây là bước quan trọng nhất trong việc khai thác (exploitation) tri thức sẵn có.
Các dạng lai ghép phổ biến:
| Kiểu Crossover | Mô tả | Khi nên dùng |
|---|---|---|
| 1-Point | Chọn ngẫu nhiên 1 vị trí cắt, trao đổi phần còn lại | Khi gene có ý nghĩa tuần tự |
| 2-Point | Cắt tại 2 điểm, trao đổi đoạn giữa | Khi muốn kết hợp mạnh mẽ hơn |
| Uniform | Trao đổi từng gene với xác suất p |
Khi gene độc lập hoặc phi tuyến |
Xác suất lai ghép (crossover rate) thường trong khoảng:
$$ 0.6 \leq p_c \leq 0.9 $$
Ví dụ minh họa bằng code Python:
def crossover(p1, p2):
"""
Hàm lai ghép 1-điểm
- Input: p1, p2 - hai cá thể cha mẹ
- Output: cá thể con
"""
point = random.randint(1, len(p1) - 1)
return p1[:point] + p2[point:]
4.3 Mutation – Khai phá không gian tìm kiếm
Mutation là cơ chế thay đổi ngẫu nhiên một phần nhỏ trong gene của cá thể con.
Nó đóng vai trò khai phá (exploration), giúp GA tránh hội tụ sớm.
Ví dụ: lật bit trong chuỗi nhị phân hoặc thêm nhiễu Gaussian trong không gian thực.
$$ x_i' = x_i + N(0, \sigma^2) $$
Tỷ lệ đột biến nhỏ nhưng rất quan trọng:
$$ 10^{-3} \leq p_m \leq 10^{-1} $$
- Nếu $p_m$ quá thấp → kẹt ở cực trị cục bộ.
- Nếu $p_m$ quá cao → tiến hóa trở thành tìm kiếm ngẫu nhiên.
Ví dụ code:
def mutate(ind):
"""
Hàm đột biến cho chuỗi nhị phân
- Input: ind - cá thể cần đột biến
- Output: cá thể sau đột biến
"""
return [1 - g if random.random() < 0.01 else g for g in ind]
4.4 Elitism – Giữ lại gene tốt nhất
Elitism là cơ chế sao chép trực tiếp một số cá thể có fitness cao nhất vào thế hệ kế tiếp mà không thay đổi.
Điều này đảm bảo chất lượng trung bình không giảm qua các thế hệ.
Công thức biểu diễn quá trình elitism:
$$ P_{t+1} = E(P_t, n_e) \cup G(P_t) $$
Trong đó:
- $E(P_t, n_e)$: tập hợp $n_e$ cá thể tốt nhất được giữ lại
- $G(P_t)$: tập hợp cá thể sinh ra từ các phép lai ghép và đột biến
Lưu ý:
- $n_e$ quá lớn → quần thể mất đa dạng, hội tụ sớm.
- $n_e = 1–2$ cá thể (5–10% quần thể) thường là lựa chọn hợp lý.
4.5 Tổng hợp: bốn nút điều khiển và vai trò
| Thành phần | Vai trò chính | Tác động khi tăng | Tác động khi giảm |
|---|---|---|---|
| Selection Pressure | Định hướng tiến hóa | Hội tụ nhanh, dễ kẹt cục bộ | Tăng đa dạng, tiến hóa chậm |
| Crossover Rate | Khai thác thông tin tốt | Kết hợp mạnh, dễ "nhiễu" gene | Mất khả năng trộn gene |
| Mutation Rate | Duy trì đa dạng | Khai phá mạnh, dễ loạn | Nhanh kẹt cục bộ |
| Elitism | Ổn định kết quả | Giữ ổn định, dễ đóng băng | Giảm chất lượng trung bình |
5. Khi Genetic Algorithm bị "kẹt" – Nguyên nhân và cách cứu vãn
Giống như sinh học, một quần thể "thiếu đột biến" hoặc "độc gene" sẽ dần suy yếu.
Trong Genetic Algorithm (GA), tình huống tương tự xảy ra khi quần thể mất đa dạng, khiến tiến hóa dừng lại ở một nghiệm cục bộ thay vì tiếp tục cải thiện.
5.1 Biểu hiện của hiện tượng "kẹt"
Một số dấu hiệu cho thấy GA đang rơi vào trạng thái hội tụ sớm (premature convergence):
| Dấu hiệu | Mô tả |
|---|---|
| Best fitness không tăng qua nhiều thế hệ | Quần thể ngừng tiến hóa |
| Các cá thể trở nên giống nhau gần hoàn toàn | Đa dạng di truyền mất |
| Fitness trung bình ≈ Fitness tốt nhất | Áp lực chọn lọc quá mạnh |
| Nhiều phép lai ghép tạo ra con giống cha mẹ | Mất khả năng khai phá |
5.2 Nguyên nhân phổ biến
-
Áp lực chọn lọc quá cao (Selection Pressure lớn)
- Tournament size quá lớn, hoặc roulette tập trung vào cá thể mạnh nhất.
- Dẫn đến "độc quyền gene" – chỉ một vài lời giải chi phối toàn bộ quần thể. -
Tỷ lệ đột biến quá thấp (Low Mutation Rate)
- Không đủ biến động để tạo cá thể mới.
- Quần thể bị mắc kẹt quanh một điểm trong không gian tìm kiếm. -
Elitism quá mạnh
- Giữ lại quá nhiều cá thể tốt → "đóng băng" tiến hóa.
- Không gian tìm kiếm bị co lại quanh một vùng nhỏ. -
Không có tái khởi tạo (No Restart Mechanism)
- GA không thể tự "phá vỡ cân bằng" khi bị kẹt, dẫn đến dừng sớm.
5.3 Đo lường mức độ đa dạng quần thể
Để phát hiện hội tụ sớm, ta có thể đo mức độ đa dạng di truyền.
Một cách đơn giản là tính khoảng cách Hamming trung bình giữa các cá thể:
$$ D_t = \frac{2}{N(N-1)} \sum_{i=1}^{N-1} \sum_{j=i+1}^{N} d_H(x_i, x_j) $$
Nếu $D_t$ giảm nhanh về gần 0, quần thể đang mất đa dạng.
Khi đó, cần can thiệp bằng các chiến lược tăng khai phá.
5.4 Các chiến lược "cứu vãn" khi GA bị kẹt
(1) Adaptive Mutation – Đột biến thích nghi
Tăng tạm thời tỷ lệ đột biến khi đa dạng giảm:
$$ p_m(t) = p_{m0} \times \left(1 + \alpha \cdot \left(1 - \frac{D_t}{D_0}\right)\right) $$
Trong đó:
- $p_{m0}$: mutation ban đầu
- $D_t$: độ đa dạng hiện tại
- $α$: hệ số điều chỉnh (0.5–1.5)
Cách này giúp quần thể "làm mới" khi đang bị đồng hóa.
(2) Local Restart – Tái khởi tạo cục bộ
Khi quần thể hội tụ sớm, giữ lại một phần nhỏ cá thể tốt nhất, tái khởi tạo phần còn lại ngẫu nhiên:
def local_restart(population, elite_size=5):
"""
Tái khởi tạo cục bộ khi quần thể bị kẹt
- Input: population - quần thể hiện tại
- Output: quần thể mới với một phần elite + cá thể ngẫu nhiên
"""
# Giữ lại elite_size cá thể tốt nhất
elite = sorted(population, key=fitness, reverse=True)[:elite_size]
# Tạo cá thể mới ngẫu nhiên
new_individuals = [[random.randint(0, 1) for _ in range(GENES)]
for _ in range(POP_SIZE - elite_size)]
return elite + new_individuals
Cách này duy trì "trí nhớ" tốt trong khi bơm thêm gene mới.
(3) Niching hoặc Sharing – Duy trì nhiều ổ lời giải
Giải pháp cao cấp hơn là phân cụm quần thể thành các "ổ sinh thái" (niche).
Mỗi niche tập trung tối ưu ở một vùng khác nhau trong không gian tìm kiếm.
Phương pháp này giúp GA tìm nhiều nghiệm tối ưu cục bộ cùng lúc, tránh hội tụ toàn cục.
(4) Giới hạn số lần chọn cá thể (Selection Cap)
Giảm khả năng cá thể mạnh được chọn liên tục:
$$ P_{select}(i) = \min(p_i, p_{max}) $$
-> Điều này tránh việc "gene trội" lặp đi lặp lại, cho phép cá thể yếu hơn vẫn có cơ hội đóng góp.
6. Thử nghiệm thực tế: One-Max và Sphere
Phần này minh họa cách Genetic Algorithm (GA) vận hành trên hai bài toán kinh điển:
1. One-Max (nhị phân) – mục tiêu: đếm số bit 1, càng nhiều 1 càng tốt.
2. Sphere (liên tục) – mục tiêu: tối thiểu hóa tổng bình phương, càng gần 0 càng tốt.
Lý do chọn hai bài toán này:
- Chúng đơn giản, dễ hiểu trực quan.
- Chúng cho phép quan sát rõ hiệu ứng của các tham số GA (selection, mutation, elitism).
- Một bài toán là dạng tối đa hóa rời rạc, bài còn lại là tối thiểu hóa liên tục → đủ đa dạng cho người đọc.
6.1 Bài toán One-Max
Mô tả bài toán
Cho một chuỗi nhị phân độ dài $L$, ví dụ $1011010110$.
Hàm thích nghi (fitness) là tổng số bit bằng 1:
$$ f(x) = \sum_{k=1}^{L} x_k $$
Mục tiêu: tìm được cá thể có $f(x) = L$, tức là toàn bit 1.
Vì sao One-Max hữu ích?
- Fitness đơn giản, dễ quan sát.
- Dùng tốt để giải thích hiện tượng hội tụ sớm, đa dạng di truyền, và tác dụng của mutation.
Code minh họa GA giải One-Max
import random
# Hyperparameters
POP_SIZE = 20 # kích thước quần thể
GENES = 20 # độ dài chuỗi nhị phân
MUT_RATE = 0.01 # xác suất đột biến mỗi gene
GENERATIONS = 50 # số thế hệ lặp
def fitness(ind):
# số bit 1
return sum(ind)
def mutate(ind):
# lật bit với xác suất MUT_RATE
return [1 - g if random.random() < MUT_RATE else g for g in ind]
def crossover(p1, p2):
# 1-point crossover
point = random.randint(1, GENES - 1)
return p1[:point] + p2[point:]
# khởi tạo quần thể ngẫu nhiên
population = [[random.randint(0, 1) for _ in range(GENES)] for _ in range(POP_SIZE)]
history_best = []
history_avg = []
for gen in range(GENERATIONS):
# sắp theo fitness giảm dần
population = sorted(population, key=fitness, reverse=True)
# log lại tiến trình
best_fit = fitness(population[0])
avg_fit = sum(fitness(ind) for ind in population) / POP_SIZE
history_best.append(best_fit)
history_avg.append(avg_fit)
# elitism: giữ nguyên top 2
next_gen = population[:2]
# chọn cha mẹ trong top 10 rồi sinh con
while len(next_gen) < POP_SIZE:
p1, p2 = random.sample(population[:10], 2)
child = mutate(crossover(p1, p2))
next_gen.append(child)
population = next_gen
print("Best individual:", population[0])
print("Best fitness:", fitness(population[0]))
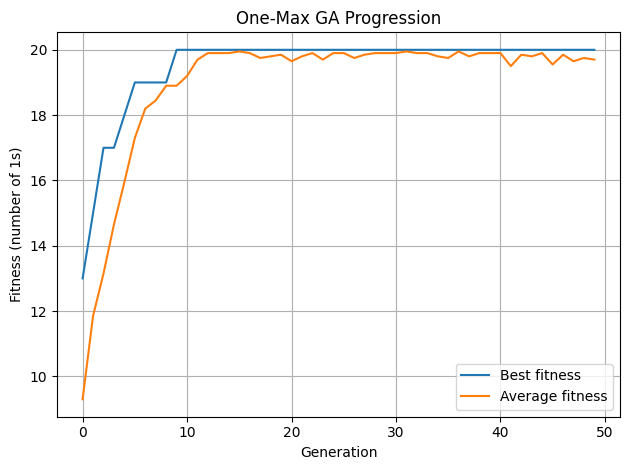
Hình 4. One-Max: Tiến trình tiến hóa qua các thế hệ
6.2 Bài toán Sphere
Mô tả bài toán
Với một vector thực $x \in \mathbb{R}^d$, hàm mục tiêu là:
$$ J(x) = \sum_{k=1}^{d} x_k^2 $$
Mục tiêu là tối thiểu hóa $J(x)$.
Nghiệm tối ưu toàn cục là $x = (0, 0, \ldots, 0)$.
Đây là ví dụ kinh điển dùng để đánh giá các thuật toán tối ưu liên tục.
Chuyển đổi thành bài toán tối đa hóa
Khác với One-Max (tối đa hóa), Sphere là tối thiểu hóa – vì vậy ta dùng fitness = -J(x) để biến nó thành bài toán tối đa hóa (vì GA thường chọn cá thể có fitness cao hơn).
$$ f(x) = -\sum_{k=1}^{d} x_k^2 $$
Cá thể nào có vector gần gốc (càng nhỏ về độ dài) thì có fitness càng lớn.
GA cho bài toán liên tục
Khác với bài toán nhị phân, ở đây:
- Gene không còn là bit 0/1, mà là số thực.
- Đột biến không phải lật bit nữa, mà là thêm nhiễu Gaussian nhỏ.
import random
import math
# Hyperparameters
POP_SIZE = 30
DIM = 5 # số chiều của vector
MUT_STD = 0.1 # độ lệch chuẩn cho đột biến Gaussian
GENERATIONS = 60
def random_vector():
# khởi tạo mỗi chiều trong [-5, 5]
return [random.uniform(-5, 5) for _ in range(DIM)]
def objective(x):
# J(x) = sum x_k^2 (cần MINIMIZE)
return sum(v*v for v in x)
def fitness(x):
# fitness = -J(x) (cần MAXIMIZE)
return -objective(x)
def crossover_real(a, b):
# uniform crossover theo từng gene
child = []
for va, vb in zip(a, b):
child.append(random.choice([va, vb]))
return child
def mutate_real(x):
# thêm nhiễu Gaussian ~ N(0, MUT_STD^2)
return [v + random.gauss(0, MUT_STD) for v in x]
# khởi tạo quần thể
population = [random_vector() for _ in range(POP_SIZE)]
history_bestJ = []
history_avgJ = []
for gen in range(GENERATIONS):
# sắp theo fitness giảm dần (tức J nhỏ nhất lên đầu)
population = sorted(population, key=fitness, reverse=True)
best = population[0]
best_J = objective(best)
avg_J = sum(objective(ind) for ind in population) / POP_SIZE
history_bestJ.append(best_J)
history_avgJ.append(avg_J)
# elitism
next_gen = population[:2]
# chọn cha mẹ trong top 10
while len(next_gen) < POP_SIZE:
p1, p2 = random.sample(population[:10], 2)
child = mutate_real(crossover_real(p1, p2))
next_gen.append(child)
population = next_gen
print("Best vector:", best)
print("Objective J(x):", best_J)
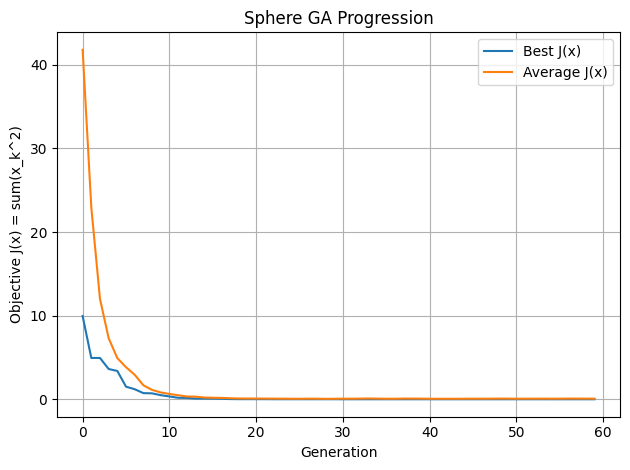
Hình 5. Sphere: Quá trình giảm giá trị hàm mục tiêu
6.3 Những điều thú vị cần nhấn mạnh
Tác động của mutation rate (tỷ lệ đột biến)
- Nếu tăng MUT_RATE ở One-Max lên quá cao (ví dụ 0.2), quần thể sẽ hỗn loạn → fitness trung bình dao động mạnh, khó leo lên tối ưu.
- Nếu giảm quá thấp (ví dụ 0.0001), hầu như không có bit mới → rất dễ bị kẹt.
Vai trò của elitism
- Trong cả hai ví dụ, ta đều giữ lại top 1–2 cá thể không đụng tới.
- Điều này giúp đảm bảo tiến trình không thụt lùi giữa các thế hệ.
- Nhưng nếu giữ lại quá nhiều (ví dụ top 10 trong quần thể 20), đa dạng sẽ biến mất rất nhanh.
Sự khác biệt giữa tìm kiếm nhị phân và liên tục
- Với One-Max, đột biến = lật bit.
- Với Sphere, đột biến = thêm nhiễu Gaussian.
- → GA không chỉ áp dụng cho biến nhị phân, mà còn áp dụng được cho không gian thực.
6.4 Kết luận cho phần thực nghiệm
GA không phải thuật toán phép màu. Nó là quá trình tiến hóa có kiểm soát.
Có thể đánh giá và chẩn đoán GA bằng các số liệu cụ thể: fitness tốt nhất, fitness trung bình, giá trị mục tiêu, độ đa dạng quần thể.
Các tham số như tỉ lệ đột biến, mức elitism, cách chọn lọc… ảnh hưởng rất rõ đến đường học qua thời gian.
7. Bài học rút ra – Nghệ thuật chứ không chỉ là công thức
Genetic Algorithm (GA) là một trong những ví dụ điển hình cho việc “tối ưu hóa không phải là tính toán thuần túy, mà là một quá trình tiến hóa có định hướng”.
Sau khi quan sát qua các phần trên, có thể rút ra một số bài học cốt lõi cả về nguyên lý lẫn thực hành.
7.1 Bản chất tiến hóa – Không tìm lời giải hoàn hảo, mà tìm lời giải thích nghi
GA không đảm bảo tìm nghiệm toàn cục, mà tìm nghiệm tốt nhất có thể dựa trên lịch sử tiến hóa.
Điểm mạnh của GA là khả năng thích nghi dần dần, chứ không phải nhảy cóc đến optimum.
Sự tiến hóa này có thể được mô hình hóa đơn giản:
$$ P_{t+1} = G(P_t) $$
trong đó hàm ( G ) không cố định mà thay đổi theo quần thể, nghĩa là quá trình tiến hóa tự điều chỉnh — điều khiến GA trở thành thuật toán "sống động" hơn hầu hết các phương pháp tối ưu khác.
7.2 Cân bằng giữa cấu trúc và ngẫu nhiên
- Cấu trúc (Structure): do crossover, elitism và selection cung cấp — hướng quá trình tìm kiếm.
- Ngẫu nhiên (Randomness): đến từ mutation — đảm bảo không gian lời giải được khám phá đầy đủ.
Một GA hiệu quả là sự pha trộn tinh tế giữa trật tự và hỗn loạn.
Nếu quá trật tự → hội tụ sớm; nếu quá hỗn loạn → tìm kiếm vô định hướng.
Vì vậy, người thiết kế phải “cảm nhận” được ranh giới này qua quan sát thực nghiệm.
7.3 GA không chỉ là công thức, mà là một hệ sinh thái tham số
Mỗi thành phần trong GA đều có thể ví như một “sinh vật” trong hệ sinh thái:
- Selection quyết định ai được sống sót.
- Crossover quyết định cách gene lan truyền.
- Mutation tạo ra đột biến – nguồn năng lượng đổi mới.
- Elitism bảo tồn tinh hoa để tránh thoái hóa.
Không có “cấu hình đúng” cho mọi bài toán, mà chỉ có cấu hình phù hợp cho từng không gian tìm kiếm.
Thực hành GA là một quá trình điều chỉnh liên tục – không khác gì sinh học thực sự.
7.4 GA thành công khi đạt ba trạng thái
| Trạng thái | Ý nghĩa | Cách nhận biết |
|---|---|---|
| Đa dạng duy trì ổn định | Quần thể không đồng nhất hoàn toàn | Các cá thể khác nhau đáng kể trong không gian tìm kiếm |
| Fitness trung bình tăng đều | Hướng tiến hóa đang có lợi | Biểu đồ trung bình tăng ổn định, không gián đoạn dài |
| Hội tụ có kiểm soát | GA đạt nghiệm tốt và giữ được độ biến động nhỏ | Fitness tốt nhất tiến gần optimum, không dao động mạnh |
Nếu chỉ thỏa hai trong ba điều kiện, GA sẽ hoặc dừng sớm, hoặc lan man, hoặc dao động mãi mà không hội tụ.
7.5 Tư duy “nghệ thuật” khi vận hành GA
-
Quan sát thay vì chỉ điều chỉnh
Mỗi thay đổi về mutation hay selection đều để lại “dấu vết” trong biểu đồ fitness.
Việc quan sát đồ thị và hành vi quần thể giúp hiểu bản chất tiến hóa hơn là chỉ điều chỉnh mù quáng. -
Thiết kế fitness function tốt hơn là tinh chỉnh tham số
Một hàm fitness phản ánh đúng mục tiêu thực tế quan trọng hơn việc tìm tỷ lệ crossover tối ưu. -
Đa dạng hóa thay vì tối ưu hóa cục bộ
Khi quần thể phong phú, GA luôn có đường lùi. Khi mất đa dạng, GA rơi vào “ngõ cụt”.
7.6 Kết luận chung
Genetic Algorithm không phải chỉ là “một công thức tìm kiếm ngẫu nhiên”, mà là một mô hình thu nhỏ của tiến hóa.
Sức mạnh của nó đến từ việc dung hòa giữa trật tự và ngẫu nhiên, giữa khai thác và khai phá.
Người làm khoa học dữ liệu hay kỹ sư tối ưu hóa giỏi sẽ không chỉ chạy GA như một công cụ, mà sẽ hiểu cách “nuôi dưỡng” nó — quan sát, điều chỉnh, và duy trì sự tiến hóa theo thời gian.
Khi đó, GA không còn là một thuật toán, mà là một nghệ thuật của sự thích nghi.
Tài liệu tham khảo
-
Mitchell, M. (1998). An Introduction to Genetic Algorithms. MIT Press.
Cuốn sách nền tảng trình bày toàn bộ cơ chế tiến hóa nhân tạo: selection, crossover, mutation, elitism, và hiện tượng hội tụ sớm. -
Herrera-Poyatos, A., & Herrera, F. (2017). Genetic and Memetic Algorithm with Diversity Equilibrium based on Greedy Diversification. arXiv preprint arXiv:1702.03594.
Trình bày cơ chế cân bằng giữa exploration và exploitation trong GA thông qua việc duy trì đa dạng quần thể, rất phù hợp với phần 3 và 5 của blog. -
Majeed, S., & Zhang, S. (2019). Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review. Information, 10(12), 390. https://doi.org/10.3390/info10120390
Bài tổng quan chi tiết về ảnh hưởng của tỷ lệ mutation và crossover đến hiệu suất thuật toán, hỗ trợ phần 4 (bốn nút điều khiển GA) và phần 8 (checklist tham số). -
Ahmad, M. W., & Islam, T. (2016). Crossover and Mutation Operators of Genetic Algorithms. International Journal of Machine Learning, 7(2), 121–129. PDF
Phân tích vai trò của crossover và mutation operators, giải thích cách chúng ảnh hưởng đến khai phá và khai thác trong quá trình tiến hóa. -
De Jong, K. A. (1975). Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. dissertation, University of Michigan.
Công trình học thuật đầu tiên phân tích định lượng hành vi của GA: tốc độ hội tụ, ảnh hưởng của kích thước quần thể và mutation rate – nền tảng cho hầu hết lý thuyết GA hiện nay.
Chưa có bình luận nào. Hãy là người đầu tiên!