Explainable AI
ANCHOR
1. Động lực - Tại sao chúng ta cần có XAI?
1.1 Blackbox models
- Trong AI ngày nay, để có thể đạt được những kết quả tốt, chúng ta thường sử dụng những mô hình rất phức tạp như là neural networks, random forest,… Và những mô hình này thường không tường minh về cách đưa ra dự đoán của mình.
-
Ví dụ:
-
Model dự đoán là: “Bức ảnh này là con mèo.”

-
Nhưng mà khi ta hỏi: “Tại sao bạn lại nói bức ảnh này là con mèo?”
→ Thì model sẽ không giải thích được - do đó nó chính là một blackbox model.
-
1.2 XAI
- XAI được sử dụng để diễn giải những dự đoán của blackbox models cho con người dễ hiểu và có thể tin cậy được vào dự đoán đó của AI.
- Có nhiều cách người ta sử dụng để giải thích model:
- LIME: sử dụng những model đơn giản để giải thích.
- ANCHOR: tìm ra những điều kiện mà nếu được thoả bởi datapoint thì gần như chắc chắn là model của mình sẽ predict ra một label nhất định.
2. Ý tưởng chính - ANCHOR là gì?
2.1 Định nghĩa
- ANCHOR là một tập hợp của 1 hoặc nhiều điều kiện mà khi những điều kiện này được thoả thì kết quả dự đoán của model hầu như không thay đổi.
-
Ví dụ trong data dạng bảng:
- “Lương trên 10 triệu và là nam”
→ Model gần như lúc nào cũng dự đoán là “Cho vay”
2.2 Tại sao nó được gọi là ANCHOR?
-
Đơn giản vì đây là những điều kiện mà sẽ không thay đổi cho dù những features khác có thay đổi như thể nào. Miễn là điều kiện ANCHOR được thoả thì model sẽ hầu như dự đoán một kết quả nhất định.

→ Như trong ví dụ trên, những vùng được tô vàng chính là ANCHOR để model xác định bức ảnh này là con mèo
3. Cách để đo lường chất lượng của ANCHOR
3.1 Precision (Độ chính xác)
- Precision đo lường mức độ chính xác của ANCHOR này. Nó sẽ trả lời câu hỏi như là: “Nếu điều kiện ANCHOR được thoả, bao nhiều phần trăm thì model sẽ predict đúng cái label đó.
$$ {prec}(A) = \frac{\text{(samples thoả mãn A và có cùng label)}}{\text{(samples thoả mãn A)}} $$
-
Ví dụ:
90% số người có feature như sau : “> $100k and Age < 30” đều được dự đoán là “High credit score”.
→ Precision = 0.9
3.2 Coverage (Độ phủ)
- Coverage đo lường mức độ bao quát mà ANCHOR này có thể ứng dụng trên toàn bộ dataset.
$$ \text{cov}(A) = \frac{\text{(samples thoả mãn A)}}{\text{(tất cả samples)}} $$
-
Ví dụ:
Trong toàn bộ dataset thì có 5% người có điều kiện là: “> $100k and Age < 30” thì chỉ số coverage của ANCHOR đó sẽ là 5%.
3.3 Confidence score (Độ tự tin của ANCHOR)
- Lý do mà chúng ta phải cần có confidence score liên quan tới cách mà precision được tính toán và chúng ta sẽ thảo luận ở phần 4. Về lý thuyết, confidence score là mức độ chắc chắn của chúng ta đối với độ chính xác (precision) của cái ANCHOR này. Nói cách khác, nó giúp cho chúng ta có thể nói rằng ANCHOR này có thể tổng quát được với dữ liệu thực tế thông qua xác suất thống kê.
$$ P(\text{true precision} \ge {p_{lb}} ) \ge 1 - \delta $$
- $\text{true precision}$: độ chính xác thực tế của anchor A mà chúng ta không thể tính toán chính xác được
- $p_{lb}$: cận dưới của true precision (đôi khi cận dưới cũng có thể được kí hiệu là $\tau$)
-
$\delta$: error rate, sai số chấp nhận được (thường là 0.05)
→ Diễn giải từ công thức thì ta có thể nói một cách như sau:
“Chúng ta có thể chắc chắn 95% (1 - $\delta$ ) là độ chính xác thực tế sẽ lớn hơn $\tau$ chấp nhận được”
4. Làm sao để tính toán những chỉ số trên?
Bước 1: Bắt đầu với input
- Sử dụng model để predict một datapoint và chúng ta muốn giải thích model này dựa trên datapoint đó.
- Quan sát tất cả các features của data:
- Nếu là data dạng bảng thì các features sẽ là các đặc trưng trong bảng đó
- Nếu là data dạng ảnh thì từ một bức ảnh, chúng ta phân nó ra thành các vùng super-pixels và mỗi vùng super-pixel sẽ là một feature với giá trị nhị phân (bật hoặc tắt).
Bước 2: Tạo ra những ANCHOR thí sinh
- Chúng ta sẽ bắt đầu với một tập ANCHOR rỗng
- Qua mỗi vòng lặp chúng ta sẽ thêm một features vào ANCHOR:
- “Income > 100k”
- “Age < 30”
- etc…
- Mỗi tổ hợp mới sẽ là một ANCHOR thí sinh
-
Ví dụ:
[Rỗng]
→ [[”Income > 100k”],[”Age < 30”],[”Sex = Male”]]
→ [[”Income > 100k”, ”Age < 30”],[”Income > 100k”, ”Sex = Male”],[”Age < 30”, ”Income > 100k”],…]
(Mỗi [] là một ANCHOR thí sinh)
Bước 3: Tạo ra những datapoint cục bộ
- Mục đích chính của việc tạo ra dữ liệu cục bộ là để tính toán precision. Vì ANCHOR tập trung vào việc giải thích một datapoint cụ thể, chứ không phải toàn bộ dataset, nên để kiểm tra một anchor có phù hợp để giải thích cho datapoint đó hay không, chúng ta phải tạo ra những dữ liệu cục bộ xung quanh datapoint đó.
- Vì số lượng dữ liệu cục bộ là hữu hạn và được sinh ra nhân tạo, chúng ta cần đảm bảo rằng những dữ liệu này đủ đại diện để phản ánh prediction của model trên datapoint ban đầu. Do đó, cần sử dụng confidence score, như đã trình bày ở phần 3.3, để đánh giá độ tin cậy của precision ước lượng từ dữ liệu cục bộ.
- Vậy thì số lượng datapoint bao nhiêu là đủ?
Hoeffding nói rằng là:
$$ P\big(|\hat{p} - p| \geq \varepsilon \big) \leq 2 e^{-2 n \varepsilon^2} $$
- $\hat{p}$: observed precision
- $p$: true precision
- $\epsilon$: sai số cho phép giữa observed và true precision
- $n$: số lượng sample
Với $n$ là số lượng samples và $\epsilon$ là sai số cho phép giữ precision cục bộ và precision thực tế (không thể tính toán được). Ta quan sát được rằng với số lượng sample càng lớn thì xác suất mà độ lệch của precision, lớn hơn $\epsilon$ càng nhỏ.
- Ban đầu chúng ta đang muốn: (xem lại phần 3.3)
$$ P(p \ge {p_{lb}} ) \ge 1 - \delta $$
Áp dụng Hoeffding vào bất phương trình trên, ta có thể nghĩ rằng cận dưới $p_{lb}$ được tính bởi việc lấy $\hat{p}$ trừ đi một số lượng error $\epsilon$ (tại vì true precision đang nằm trong khoảng $[\hat{p}−ε,\hat{p}+ε]$ dựa theo hoeffding). Ta có thể ghi lại bất phương trình như sau:
$$ P(p \ge \hat{p} - \epsilon ) \ge 1 - \delta $$
Cho dù Hoeffding sử dụng trị tuyệt đối nhưng chúng ta chỉ đang xét trường hợp mà precision observed trừ epsilon luôn bé hơn precision thực tế. Như vậy thì chúng ta sẽ luôn chắc chắn rằng precision thực tế sẽ lớn hơn một con số tính toán được. Thay đổi chiều của bất phương trình ta sẽ được một bất phương trình tương đương với lại Hoeffding:
$$ P(p \leq \hat{p} - \epsilon ) \leq \delta $$
Vậy thì ta quan sát được là:
$$ \delta = 2 e^{-2 n \varepsilon^2} $$
Suy ra:
$$ n = \frac{\ln(2/\delta)}{2 \varepsilon^2} $$
Và đây chính là cách chúng ta tính toán được số lượng samples cần sinh ra để thoả được error-rate $\delta$ và $\epsilon$.
Lưu ý: Những datapoints được tạo ra đều phải thoả mãn điều kiện của ANCHOR
Bước 4: Tính precision và coverage
- Precision đều được tính toán trên những datapoints mới được tạo ra từ bước 3. Sử dụng model gốc để predict những datapoints mới đó và chúng ta sẽ tính được precision dựa trên phần trăm datapoint có cùng label.
-
Coverage:
- Trong data dạng bảng thì việc tính toán có vẻ khá đơn giản, chúng ta chỉ cần tính toán phần trăm rows mang những đặc trưng của ANCHOR trên tổng toàn bộ dataset.
- Đối với data hình ảnh thì sẽ phức tạp hơn. Theo lý thuyết thì chúng ta phải tìm kiếm những hình ảnh mà mang những đặc trưng, sắc độ, chỉ số RGB của vùng super-pixel mà chúng ta xác định là ANCHOR để tính phần trăm của nó trong toàn bộ dataset. Thực tế thì chúng ta có rất nhiều cách nhưng đều phải xem xét thêm về mặt lợi và hại trước khi áp dụng chúng, đây là một số ví dụ:
Phương pháp Mô tả Đo lường cái gì Ưu điểm Nhược điểm Tương đồng superpixel So sánh các vùng màu/sắc thái Tái xuất hiện trực quan Trực quan, dễ hiểu Tốn nhiều tính toán Bao phủ không gian đặc trưng (feature-space) So sánh embedding của CNN Tái xuất hiện ngữ nghĩa Chịu nhiễu tốt Cần embedding tốt Bao phủ kích hoạt mô hình (model-activation) So sánh bản đồ activation/attention Tái xuất hiện cách suy luận của mô hình Nhận biết mô hình Khó tính toán Bao phủ xác suất (probabilistic coverage) Ước lượng xác suất của vùng anchor Tần suất thống kê Rõ ràng về mặt lý thuyết Cần biết phân phối đặc trưng
Bước 5: Sử dụng KL-LUCB để đảm bảo confidence score
- Hãy xem một số công thức:
$$ \mathrm{KL}(\hat{p} \,\|\, q) = \hat{p} \ln \frac{\hat{p}}{q} + (1-\hat{p}) \ln \frac{1-\hat{p}}{1-q} $$
- $\hat{p}$: một số tỉ lệ nào đó (0,1)
- $q$: một số tỉ lệ nào đó (0,1)
→ Công thức này cho chúng ta biết là $\hat{p}$ và $q$ sẽ càng khác nhau khi mà giá trị càng lớn.
$$ \mathrm{KL}(\hat{p} \,\|\, p_{\mathrm{lb}}) = \frac{\log \frac{2}{\delta}}{n} $$
- $\hat{p}$: true precision
- $p_{lb}$: cận dưới của true precision
- $n$: số lượng sample
- $\delta$: error rate (xem lại phần 3.3)
→ Đây là công thức tính Mục tiêu hay còn gọi là giá trị khác biệt mong muống giữa $\hat{p}$ và $p_{lb}$
- Đầu tiên chúng ta sẽ tính $\mathrm{KL}(\hat{p} \,\|\, p_{\mathrm{lb}})$ bằng cách thay thế các giá trị số lượng samples và $\delta$ mong muốn vào.
- Hiện tại chúng ta đang có observed precision $\hat{p}$, một giá trị target của $\mathrm{KL}(\hat{p} \,\|\, p_{\mathrm{lb}})$ mà ta mong muốn nó bằng hoặc là nhỏ hơn. Vì giá trị của $p_{lb}$ có những đặc tính sau:
- Nằm trong khoảng từ 0 đến $\hat{p}$
- Có giá trị đơn điệu với $\mathrm{KL}(\hat{p} \,\|\, p_{\mathrm{lb}})$. Có nghĩa là khi giá trị $p_{lb}$ càng tăng (nhưng mà vẫn nhỏ hơn $\hat{p}$) thì giá trị của $\mathrm{KL}(\hat{p} \,\|\, p_{\mathrm{lb}})$ càng nhỏ.
Với những tính chất và giá trị trên, chúng ta thay thế từng giá trị của $p_{lb}$ vào công thức số 1 của bước 5 theo thuật toán binary search để tìm ra được precision lower bound phù hợp nhất.
import math
def kl(p, q):
if q in [0, 1]:
return float('inf')
if p == 0:
return math.log(1 / (1 - q))
if p == 1:
return math.log(1 / q)
return p * math.log(p / q) + (1 - p) * math.log((1 - p) / (1 - q))
def kl_bounds(phat, n, delta, tol=1e-6):
target = math.log(2 / delta) / n
# Lower bound
low, high = 0.0, phat
print("Low: ")
while high - low > tol:
mid = (low + high) / 2
print(low, high, mid)
if kl(phat, mid) > target:
low = mid
else:
high = mid
pL = low
# Upper bound
low, high = phat, 1.0
print("High: ")
while high - low > tol:
print(low, high, mid)
mid = (low + high) / 2
if kl(phat, mid) > target:
high = mid
else:
low = mid
pU = high
return pL, pU
phat, n, delta = 0.8, 100, 0.05
print(kl_bounds(phat, n, delta))
Bước 6: Beam search
- Hãy nhớ lại bước 2, mỗi lần chúng ta bắt đầu vòng lặp, chúng ta sẽ kết hợp các đặc tính để tạo ra những ANCHOR thí sinh. Nếu chúng ta tính toán hết tất cả trường hợp thì số lượng sẽ trở nên khổng lồ theo cấp số nhân. Do đó, chúng ta cần áp dụng một thuật toán để có thể hiệu quả tìm ra những tổ hợp ANCHOR tốt nhất.
- Đó chính là Beam search. Ở mỗi vòng lặp chúng ta áp dụng Beam search để chỉ giữ lại top K ANCHOR có thông số tốt nhất.
- Một trong những cách để đánh giá ANCHOR là:
- Lower bound precision cao (phải lớn hơn ngưỡng $\tau$)
- Coverage cao
- Trong một vòng lặp beam, các điều kiện dừng là đánh giá xong hết tất cả ANCHOR thí sinh trong beam đó
- Sau đó chúng ta lại bắt đầu vòng lặp (beam) tiếp theo ở Bước 2.
- Lưu ý: top K ANCHOR của beam này được lưu lại để chọn lọc trong bước cuối.
Bước 7: Lựa chọn ANCHOR cuối cùng
-
Điệu kiện dừng của thuật toán:
- Tất cả các beam đã hoàn tất vòng lặp
- Tức là không còn anchor nào khả thi để mở rộng thêm predicate mới.
- Hoặc tất cả anchor trong beam đều đã đạt $precision \ge \tau$ và bạn đã chọn anchor có coverage cao nhất.
- Hoặc vượt giới hạn tính toán
- Giới hạn số mẫu perturbation tối đa, hoặc số vòng lặp tối đa.
- Nếu vượt quá mà chưa tìm được ANCHOR hoàn hảo → chọn ANCHOR tốt nhất hiện tại (ghi nhận xác suất $P(\text{prec}(A) ≥ \tau)$).
TÓM TẮT TOÀN BỘ QUÁ TRÌNH
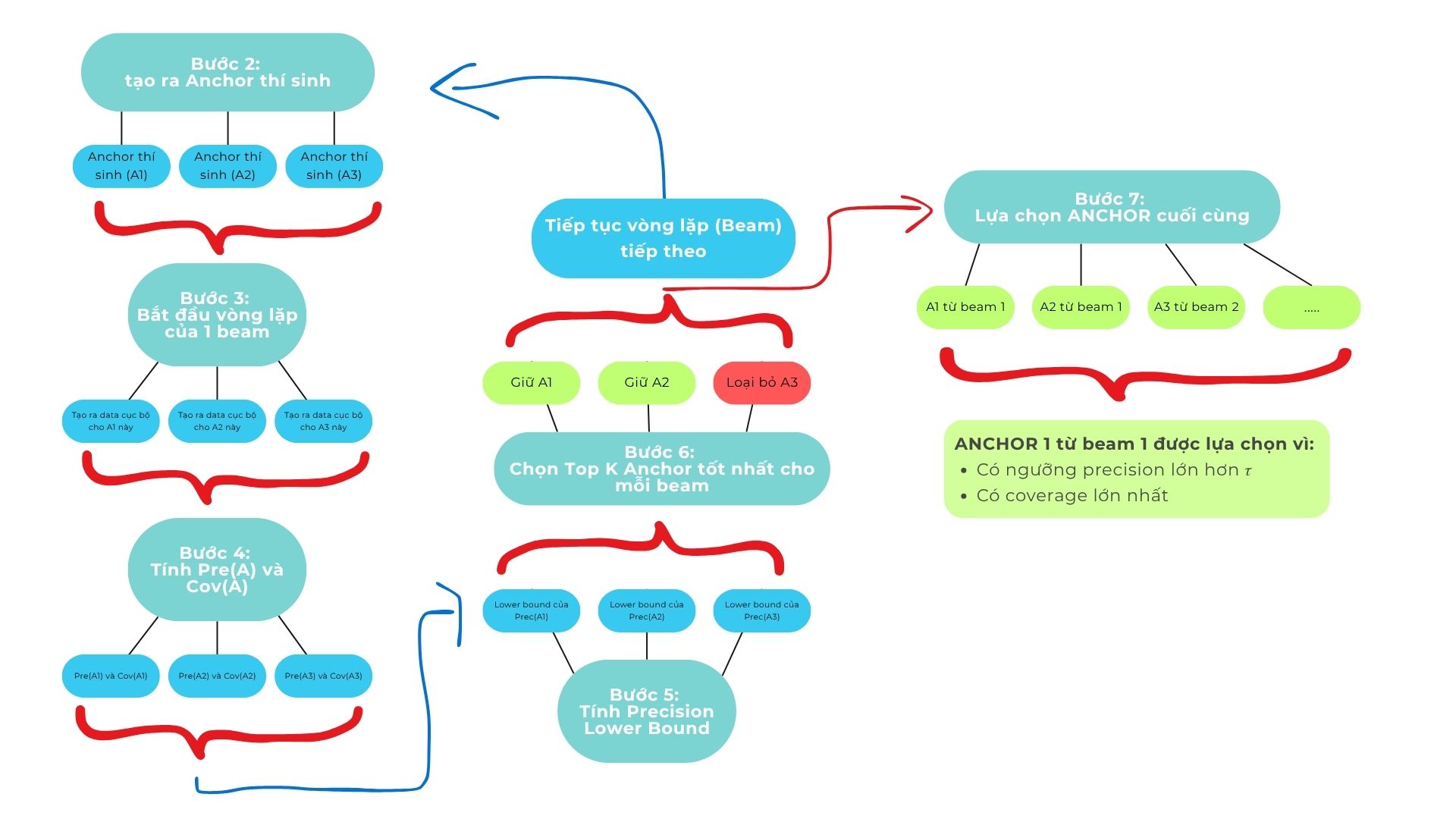
- Tất cả các beam đã hoàn tất vòng lặp
5. Tại sao ANCHOR hoạt động được?
5.1 Local behavior
- Tập trung vào dự đoán của một ảnh cục bộ.
- Nó sẽ trả lời câu hỏi là: “Điều kiện nào sẽ phải giữ để cho model luôn predict datapoint này như vậy?”
5.2 Logical explanations
- ANCHORS áp dụng định luật nếu-thì nên dễ hiểu cho con người:
→ Nếu điều kiện này thoả → thì model sẽ predict X
5.3 Chứng minh bởi xác suất thống kê
- Bằng việc sử dụng KL-LUCB, ANCHOR giúp cho thuật toán trở nên đáng tin cậy trong thực tế
- Có nghĩa là nó sẽ không chỉ là những giải thích dự đoán một cách ăn may của thuật toán mà đã được chứng mình một cách toán học.
LIME (XAI)
1. LIME là gì?
LIME (Local Interpretable Model-agnostic Explanations) là một phương pháp giải thích model (XAI) thuộc nhóm local post-hoc, nghĩa là LIME sẽ thực hiện giải thích một dự đoán cụ thể của mô hình sau khi train, thay vì dựa trên cấu trúc hay cách hoạt động của mô hình.
2. Động lực của LIME
Một mô hình AI vừa báo: “Bệnh nhân A — rủi ro nhập viện trong 30 ngày: 87%.”
Đây là một con số lớn, nhưng bác sĩ hỏi: Tại sao lại là 87% cho đúng bệnh nhân này? Thay vì cố gắng “giải mã” toàn bộ mạng nơ-ron phức tạp, ta làm một việc đơn giản và thực dụng: tạo vài kịch bản gần giống bệnh nhân A (ví dụ: thay đổi nhẹ creatinine, SpO₂, hay thuốc đang dùng), hỏi mô hình phản ứng thế nào, rồi tóm tắt bằng một mô hình rất đơn giản chỉ với 2–3 yếu tố chính. Kết quả trả về không phải là một giải thích chung chung mà là câu trả lời cụ thể cho bệnh nhân A: “Ở điểm này, suy thận (creatinine cao) đóng góp lớn nhất; cải thiện oxy có thể giúp một chút.”
Đó chính là tinh thần của LIME: xấp xỉ cục bộ, câu trả lời dễ hiểu, có thể hành động ngay.
3. Mục tiêu của LIME
LIME được sử dụng để giải thích một datapoint cụ thể từ 1 model phức tạp bằng cách lựa chọn model đơn giản hơn và xấp xỉ hành vi của mô hình gốc trong phạm vi lân cận của datapoint đó. Để làm được như vậy, LIME cần tối ưu hàm Loss sau:
$\underset{g \in G}{argmin} \ L(f,g,\pi_{{x_i}'}) + \Omega (g)$
với
- $f$: mô hình gốc (phức tạp) đang cần được phân tích
- $g$: mô hình đơn giản hơn được LIME dùng để giải thích datapoint
- $G$$:$ tập hợp các model đơn giản (linear regression, tree, rule-based,…)
- $L(f, g, \pi_{{x_i}'})$: hàm loss có trọng số
- $\Omega(g)$: penalty cho độ phức tạp mô hình $g$
Một chút góc nhìn về hàm “loss” này mà LIME cần minimize:
- Ta muốn hành vi của $g$ giống với model gốc $f$ nhất có thể.
- Các sample sẽ contribute khác nhau vào hàm loss tùy thuộc vào khoảng cách của nó với datapoint gốc (bàn thêm vào phần Cơ chế hoạt động).
- $\Omega(g)$ sẽ phạt nhiều cho các model $g$ phức tạp, vì càng nếu model giải thích càng phức tạp thì khả năng interpret của model sẽ bị ảnh hưởng.
-
Đối với Weighted Linear Regression sử dụng LASSO, $\Omega(g)$ = $\lambda ||w||_1$ , với $\lambda$ là hyperparameter để tuning sức ảnh hưởng của regularization, còn $||w||_1$ là số lượng weights trong model. Nếu model sử dụng quá nhiều weight (tương ứng với feature) để giải thích, lời giải thích sẽ trở nên mơ hồ. Ví dụ, nếu bạn giải thích quyết định mua bánh kem của bạn, mà trong đó chứa:
- 22% vì hôm nay sinh nhật
- 10% vì hôm nay trời đẹp
- 7% vì hôm qua bạn không đi học
- 5% vì ngày mai là chủ nhật
- …………
Các lí do (feature) càng nhỏ thì càng không liên quan, nhưng nó được train chung với các feature quan trọng, điều này có thể gây nhiễu, ảnh hưởng xấu đến quá trình training và kết quả.
⇒ Ta cần giới hạn độ phức tạp (số lượng weights đối với Linear Regression, Tree Depth đối với Tree…) để tập trung nhiều hơn vào các feature quan trọng.
4. Chi tiết về Cơ chế hoạt động của LIME
Chúng ta đã biết được rằng LIME được sử dụng sau khi train, và chỉ được áp dụng để giải thích một dự đoán cụ thể. LIME sử dụng default model là Weighted Linear Regression, vì vậy trong bài này, chúng mình sẽ phân tích sâu cách LIME ứng dụng kĩ thuật này.
Đối với LIME, ta sẽ thực hiện khác nhau một chút cho 2 loại data:
- Tabular Data (Data dạng bảng)
- Non-tabular Data (Hình ảnh, Text,….)
Gọi $x_{current}$ là sample hiện tại được dự đoán bởi model $f$ Cơ chế hoạt động của LIME là:
4.1. Tạo các mẫu dữ liệu lân cận $X'$ (Perturbation)
- Mục tiêu: LIME muốn “hiểu” hành vi mô hình ggg cục bộ quanh điểm $x_{current}$. Vì $g$ có thể rất phi tuyến, ta không thể dùng một mô hình tuyến tính đơn giản toàn cục — nhưng ta có thể xấp xỉ $g$ ở vùng rất gần điểm cần giải thích bằng một mô hình tuyến tính.
- Cách làm thông thường: tạo tập $X'=\{x'_i\}$ bằng cách thêm nhiễu (perturbation) vào mỗi đặc trưng của $x_{current}$. Lý do:
- Nếu nhiễu quá lớn, các mẫu không còn đại diện vùng cục bộ → mô hình tuyến tính học được có thể phản ánh hành vi toàn cục, không phải cục bộ.
- Nếu nhiễu quá nhỏ, dữ liệu không có đủ phương sai để ước lượng hệ số; phương pháp sẽ bị nhiễu ngẫu nhiên (noisy).
Ví dụ cho 2 loại data:
-
Tabular Data:
-
Numerical (Data dạng số):
-
Lấy giá trị của feature gốc rồi cộng thêm nhiễu Gaussian (phân phối chuẩn).
$x_i' = x_{current} + \mathcal{N}(0, \sigma^2)$
với $x_i’$: mẫu lân cận với $x_{current}$
$\mathcal{N}(0, \sigma^2)$: 1 số random được generated theo phân phối chuẩn với mean = 0, và std = $\sigma$
- $\sigma$ thường được chọn dựa trên độ lệch chuẩn của feature đó trong tập huấn luyện (để phản ánh mức biến thiên tự nhiên).
- Categorical (Data dạng phân loại):
- Chọn ngẫu nhiên giá trị khác cùng feature, theo tần suất xuất hiện trong tập huấn luyện. (nghĩa là ta sẽ chọn lại các feature cho 1 sample $x_i’$, lựa chọn này sẽ weightedly random với các categorical value có tần suất xuất hiện trong tập huấn luyện cao hơn sẽ được đánh trọng số khi random cao hơn ⇒ dễ xuất hiện hơn).
- Có thể thêm xác suất giữ nguyên feature gốc cao hơn (nghĩa là có thể đánh trọng số cho các categorical value của $x_{current}$ cao hơn ⇒ Các mẫu $x_i’$ sẽ dễ giống với $x_{current}$ hơn).
- Non-tabular Data:
-
Đối với Non-tabular Data, ta sẽ chuyển data từ nhiều dạng như ảnh, text,… về dạng binary vector theo cơ chế bật/tắt feature. Các feature có thể là:
- Một vùng (superpixel) trong ảnh
- Một từ trong một câu
- ……..
Xét 2 trường hợp ảnh và text:
-
Ảnh: Đối với ảnh khi các feature được phân ra làm $n$ vùng (superpixel), nghĩa là ta đang cho rằng ảnh đang có n feature. Để tạo nhiễu, ta có thể bật/tắt các vùng (tô đen hoặc xám ảnh đó khi tắt, và để hình gốc cho vùng đó khi bật) và tạo nhiều phiên bản như thế.
Nghĩa là ban đầu $x_{current}$ là [1,1,1,1,1] (nếu chua ảnh ra làm 5 vùng/features (superpixel)), để tạo nhiễu, ta có thể tạo:
- [1,0,1,0,1]: vùng 2 và 4 sẽ bị tô đen
- [0,0,0,0,1]: chỉ có vùng 5 là không bị tô đen
⇒ Nếu xét 1 ảnh chia làm $n$ vùng (superpixel), ta có thể tạo được $2^n - 1$ nhiễu (không tính ảnh gốc).
⇒ Ta tạo nhiễu cho ảnh $x_{current}$ bằng cách bật/tắt một số vùng trong ảnh
-
Text: Ta cũng làm như đối với ảnh, tuy nhiên với text, các features sẽ là các từ trong câu. Để tạo nhiễu, ta sẽ bật/tắt các từ trong câu và tạo nhiều phiên bản như thế.
⇒ Đối với non-tabular data: ta sẽ chuyển các dạng data đó về dạng binary vectors (có thể gọi là không gian binary).
-
4.2. Dự đoán dùng mô hình gốc $f$
Dùng mô hình gốc $f$ để thực hiện dự đoán cho từng ${x_i}'$ trong $X’$ và ra được tập $y_i’$
4.3. Tính khoảng cách giữa từng sample ${x_i}’$ trong $X’$
Nếu ta chỉ ngẫu nhiên tạo ra $x_i’$ và tất cả các $x_i’$ đều contribute bằng nhau vào LIME, vấn đề lớn nhất chính là các mẫu $x_i’$ có độ sai khác lớn so với $x_{current}$ (xa mẫu gốc) cũng contribute ngang với các mẫu $x_i’$ gần mẫu gốc hơn.
⇒ Vì vậy ta cần tính khoảng cách $dist_i$ giữa từng mẫu $x_i’$ với $x_{current}$ trước khi tính trọng số cho từng mẫu $x_i’$.
Các distance metric thường được sử dụng:
- Tabular Data:
- Numerical Data: Euclidean Distance (L2 Distance)
- Categorical Data:
- Không One-Hot Encoding: Hamming Distance
- Có One-Hot Encoding: L2 Distance,…
- Cả Numerical và Categorical Data: Gower Distance
- Non-tabular Data: 1 − Cosine Similarity (tuy nhiên, đối với Text thì Cosine_Similarity được tính trên Tf-Idf vector, không phải binary vector như dữ liệu Ảnh)
4.4. Tính trọng số cho từng ${x_i}’$ trong $X’$
Ta đã có $dist_i$ là khoảng cách giữa $x_i’$ và mẫu gốc $x_{current}$. Bây giờ ta cần tính trọng số cho từng mẫu $x_i’$ bằng công thức sau:
$w_i = exp(-\frac{{dist_i}^2}{{kernel\_width}^2})$
| kernel_width nhỏ | kernel_width lớn |
|---|---|
| vùng ảnh hưởng rất hẹp, chỉ những điểm cực gần ($x_{current}$) mới có trọng số đáng kể | vùng ảnh hưởng rộng, nhiều điểm xa vẫn có trọng số đáng kể |
| rất “local” (giải thích cực cục bộ, nhạy với nhiễu) | khá “global” (giải thích ít đặc trưng cho điểm hiện tại) |
⇒ Phân tích: ta có thể thấy rằng kernel_width điều khiển độ “mượt” của vùng lân cận mà LIME xem là "có liên quan".
Ví dụ, khi $kernel\_width= 0.25$, đây là biểu đồ với trục x là $dist_i$ và trục y là giá trị $w_i$ tương ứng:

Các bạn có thể thấy, biểu đồ hàm trọng số theo khoảng cách có dạng "chuông" khá nhọn: trọng số tại khoảng cách 0 bằng 1, và giảm rất nhanh khi khoảng cách tăng lên. Điều này có nghĩa là các điểm $x_i$ rất gần $x_{\text{current}}$ sẽ được gán trọng số lớn, trong khi các điểm xa hơn hầu như không đóng góp (trọng số rất nhỏ).
Ngoài ra, đối với $kernel\_width = 0.75$ như hình dưới đây, "cái chuông" rộng hơn, tức là các điểm ở xa vẫn giữ trọng số đáng kể, nên ảnh hưởng của nhiều điểm xung quanh được “làm mượt” hơn.
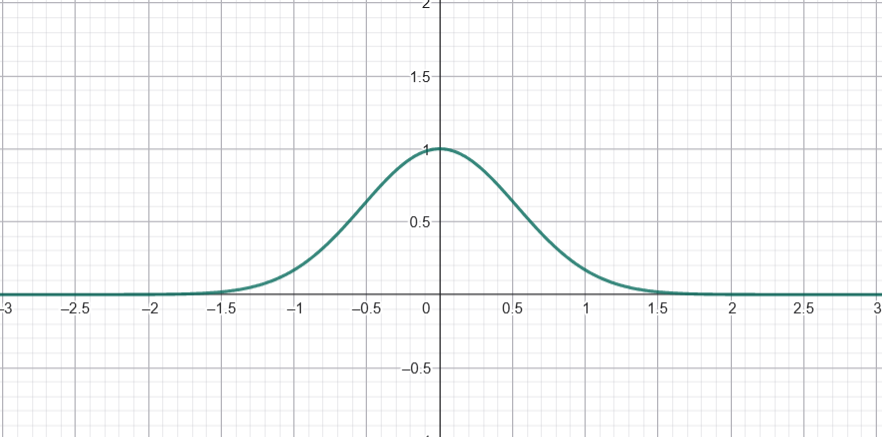
⇒ Kernel_width nhỏ → mô hình nhạy với điểm gần (ít làm mượt, có thể overfit local noise); Kernel_width lớn → làm mượt mạnh hơn (giảm variance, có thể underfit).
Ta sẽ dùng đến $w_i$ khi bắt đầu fit model đơn giản vào các mẫu $x_i’$. Cách chọn kernel_width:
| Loại dữ liệu | Distance | Khoảng giá trị distance | kernel_width khuyến nghị | Ghi chú |
|---|---|---|---|---|
| Numerical (tabular) | Euclidean (sau khi scale) | $≈ [0, \sqrt{d}]$ | $0.75 * \sqrt{d}$ hoặc dựa percentile | càng nhỏ → local hơn |
| Categorical (tabular) | Hamming / Gower | $[0, 1]$ | $0.25–0.75$ | thường 0.5 |
| Text | 1 − Cosine similarity | $[0, 2]$ (thường $< 0.5$) | $0.25–0.5$ | chọn nhỏ để local |
| Image | 1 − Cosine giữa mask | $[0, 1]$ | $0.25–0.5$ | tùy số superpixel |
Giải thích:
-
Text và Image đều dùng 1 - Cosine_Similarity, tuy nhiên vì Text khi vectorised (bằng tf-idf…) có thể âm, vậy nên Cosine_Similarity có range là [-1,1]
⇒ Range của 1 - Cosine_Similarity là [0,2].
-
Dữ liệu Ảnh chỉ có vector dương (binary vector), vì vậy range của 1 - Cosine_Similarity đối với dữ liệu Ảnh là [0,1].
4.5. Lựa chọn ra $k$ đặc trưng quan trọng nhất để mô hình giải thích sử dụng Weighted LASSO Regression (Feature Selection)
Sau khi đã đánh trọng số $w_i$ cho tất cả mẫu $x_i’$, ta cần lựa chọn ra một lượng $k$ các đặc trưng (feature) quan trọng nhất trong quyết định của mô hình $g$.
⇒ Áp dụng Weighted LASSO Regression.
Weighted LASSO Regression: kĩ thuật này cũng tương tự với Linear Regression, nhưng thay vì Linear Regression muốn tối ưu hàm loss này:
$\underset{\beta }{min}\underset{i}\sum_{}^{}({y_i}' - {{X_i}'}^T\beta )$
thì Weighted LASSO Regression muốn tối ưu hàm loss sau:
$\underset{\beta }{min}\underset{j}{\sum{}}w_i({y_i}' - {{X_i}'}^T\beta ) + \lambda \underset{j}{\sum{}}{|\beta _j|}$
với
- $w_i$: trọng số dựa trên khoảng giữa từng sample $x_i’$ với mẫu gốc $x_{current}$
- $y_i'$: label của $x_i’$ predict bởi model gốc $f$
- $\beta$: vector weights (tương ứng với các feature trong model Linear Regression) với $\beta_j$ là weight (feature) thứ $j$ trong tổng $k$ features được chọn để train Linear Regression
Vì có thêm Penalty là $\underset{j}{\sum{}}{|\beta _j|}$, là tổng độ lớn của các feature, ta có thể loại bỏ các feature ít quan trọng bằng cách tiếp tục tăng $\lambda$ đến khi giữ lại được $k$ features mong muốn.
Góc nhìn:
- Feature ít quan trọng
- Nếu feature j gần như không giúp giảm MSE:
- Sai số tăng khi $\beta_j$ = 0 → nhỏ
- Penalization term: $\lambda|\beta_j|$ → nhỏ
- Tối ưu: $\beta_j$ → 0 (đơn giản nhất, ít ảnh hưởng lỗi)
- Nếu feature j gần như không giúp giảm MSE:
- Feature quan trọng
- Nếu feature j giúp giảm MSE mạnh:
- Giữ $\beta_j$ = 0 → MSE tăng lớn
- Penalization: $\lambda|\beta_j|$→ tăng, nhưng ít hơn so với lợi ích giảm MSE
- Tối ưu: $\beta_j$ ≠ 0, để tổng loss (MSE + $\lambda$Regularization) nhỏ nhất
- Nếu feature j giúp giảm MSE mạnh:
⇒ Đây là cơ chế đảm bảo feature quan trọng không bị “ép về 0”.
Chúng ta không dùng Ridge Regression ở đây (dù cho cả 2 phương pháp đều hướng đến việc đánh penalty cho độ lớn của weights) vì chỉ có LASSO mới có khả năng đưa các $\beta_j$ không quan trọng về 0, trong khi đối với RIDGE, $\beta_j$ chỉ có thể tiến về 0, không thể bằng 0.
⇒ Ta train mô hình Weighted LASSO Regression qua tập $X’$, tuning $\lambda$ đến khi thu được $k$ features quan trọng nhất.
4.6. Fit 1 model Weighted Linear Regression (có thể kết hợp Ridge Regularization) sử dụng $k$ features vừa chọn
Lúc này, ta sẽ bắt đầu fit $X’$ vào mô hình Weighted Linear Regression và tối ưu hàm loss:
$\underset{\beta }{min}\underset{i}\sum_{}^{}w_i(y_i - {X_i}^T\beta )$
hoặc có thể áp dụng thêm Ridge Regularization:
$\underset{\beta }{min}\underset{j}{\sum{}}w_i(y_i - {X_i}^T\beta ) + \lambda \underset{j}{\sum{}}{|\beta _j|^2}$
4.7. Các Weights tương ứng với $k$ features được chọn sẽ được sử dụng để giải thích kết quả của $x_{current}$
Sau khi train xong ta sẽ thu được tập các $\beta_j$ tương ứng với các features, $\beta_j$ càng lớn chứng tỏ mô hình dựa càng nhiều vào $\beta_j$ khi predict $x_{current}$.
Chưa có bình luận nào. Hãy là người đầu tiên!