Excerise on Genetic Algorithm
Genetic Algorithm là phương pháp tối ưu hoá theo quần thể lời giải, trong đó mỗi thế hệ sẽ thực hiện các bước tính toán gồm: fitness, selection, crossover và mutation. Bài blog sẽ review lại pipeline của GA và ứng dụng trong 2 bài tập: 1.onemax vs trap, 2.linear regression với mục tiêu là kết nối tất cả thành một pipeline cài đặt code hoàn chỉnh để giải một số bài toán học máy cơ bản.
Review Genetic Algoritm (GA)
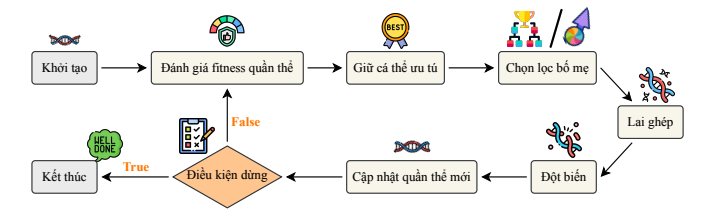
Hình 1: Pipeline tổng quát các bước trong GA
Bước 1: Khởi tạo
- Khởi tạo thư viện: Numpy, random, matplotlib, scikit-learn,...
- Đặt seed (generate_seed) để các kết quả trong random có thể tái tạo được
- Tạo quần thể: kích thước chromosome (chrom), số lượng chrom trong quần thể. Trong blog này quần thể sẽ tạo ở dạng array 2D(matrix) và chrom ở dạng array 1D (vector)
#Import thư viện (thêm vào nếu cần)
import numpy as np
import random
import matplotlib.pyplot as plt
#set random_state để có thể tái lập kết quả
random_state = 42
def generate_seed(seed = random_state):
random.seed(seed )
np.random.seed(seed)
generate_seed()
#khoi tao quan the
def generate_population(pop_size:int ,chrom_len: int):
Bắt đầu vòng lặp thế hệ (generation)
Bước 2: Đánh giá fitness quần thể + giữ cá thể ưu tú
- Định nghĩa và tính fitness_fn cho quần thể tuỳ vào mục đích bài toán (thay dổi theo mỗi bài)
- Sắp xếp quần thể theo fitness_fn theo thứ tự giảm dần và giữ lại các chrom thuộc elitism (hyperparameters, thường là 2). Các elite này sẽ được thêm vào quần thể mới
def fitness_fn(population,...):
#chon ra elitism:
def elitism_keeping(population, fitness, elite):
order = sorted(range(len(population)), key =lambda i: fitness[i], reverse = True)
elites = [population[i].copy()for i in order[:elite]]
elites_fit = [fitness[i] for i in order[:elite]]
return elites, elites_fit
Bước 3: Tạo các chrom con từ chrom bố mẹ (selection, crossover, mutation)
1. Selection:
Có 2 cách lựa chọn chrom bố mẹ từ quần thể được thường áp dụng: tournament selection và proportional selection
- Tournament selection: Như thể thức của 1 giải đấu - cơ chế này sẽ chọn ngẫu nhiên k giá trị (hyperparameter) rồi từ đó so sánh fitnes_fn trong k giá trị đó để lựa chọn chrom có fitness_fn cao nhất
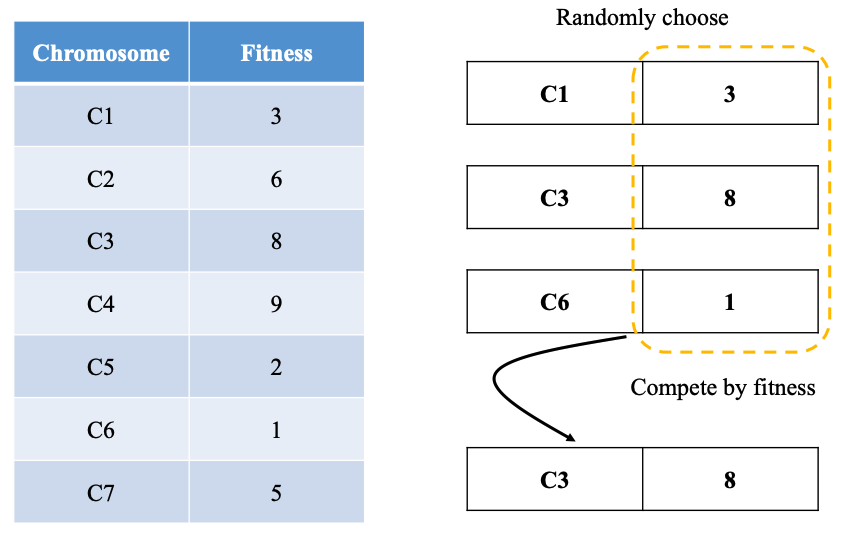
Hình 2: Minh hoạ cơ chế Tournament selection
def tournament_selection(population, fitness_score, k=2):
idx = np.random.choice(len(population), size = k, replace = False)
best_idx = max(idx, key = lambda i: fitness_score[i])
return population[best_idx].copy()
- Proportional selection (Roulette selection): Tương tự 1 vòng quay ngẫu nhiên, trong đó các thành phần của vòng quay được chia tỷ lệ theo độ lớn của fitness_fn. Quay và chọn 1 giá trị ngẫu nhiên từ 1 vòng quay đó.
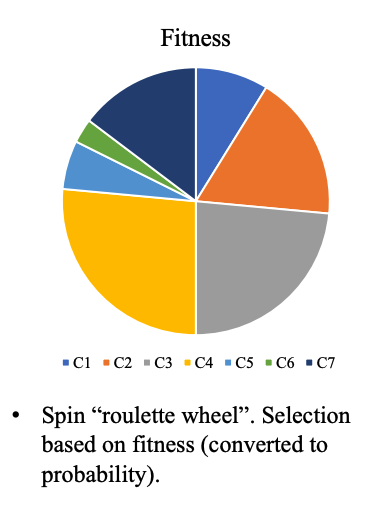
Hình 3: Minh hoạ cơ chế Proportional selection
def proportional_selection(population, fitness_score):
weights = fitness_score / np.sum(fitness_score)
idx = np.random.choice(len(population), p = weights)
return population[idx].copy()
def parent_selection(type, population, fitness_score):
if type == "tournament":
return tournament_selection(population,fitness_score)
else:
return proportional_selection(population, fitness_score)
2. Crossover (lai tạo)
Từ selection sẽ chọn ra 2 chrom bố mẹ để tiến hành bước crossover. Các kỹ thuật crossover bao gồm: single-point crossover, n-points crossover, và uniform crossover.
Bài viết này sẽ nói về uniform crossover:
- mỗi phần tử trong chrom sẽ được random 1 giá trị thuộc [0,1]. Nếu giá trị này bé hơn crossover_rate thì sẽ tiến hành hoán đổi phần tử tại vị trí này giữa 2 chrom bố mẹ.
- giá trị crossover_rate được trước (hyperparameter). Để tiến hành thúc đẩy lại tạo, tạo nên thế hệ con đa dạng hơn nên crossover_rate thường cao (0.9; 0.95)
Việc tạo thế hệ con đa dạng nhằm mục đích tối ưu hoá nguồn gen của bố mẹ, đạt được mục đích của bài toán.
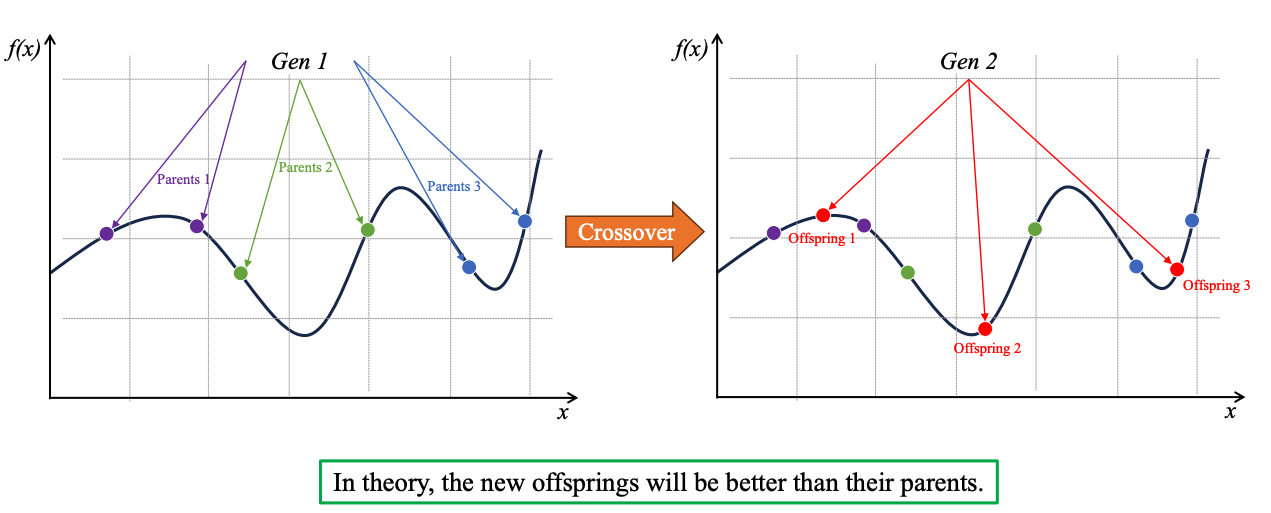
Minh hoạ cơ chế Crossover
def uniform_crossover(parent1, parent2, rate):
mask = np.random.rand(len(parent1)) < rate
c1, c2 = parent1.copy(), parent2.copy()
c1[mask], c2[mask] = parent2[mask], parent1[mask]
return (c1,c2)
3. Mutation (đột biến)
Mutation (đột biến) nhằm giúp đa dạng hoá bộ gen hơn nữa (nằm ngoài giới hạn của bố mẹ) và giúp bài toán thoát khỏi tối ưu cục bố, hướng đến tối ưu toàn cục.
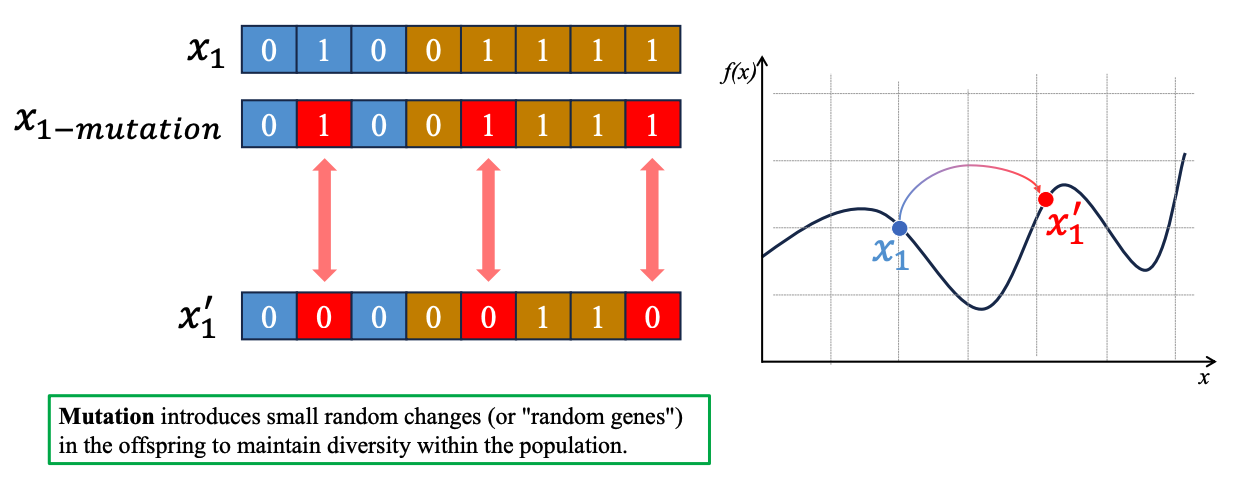
Hình 4: Trong bài toán tìm max, giá trị x1 sẽ có xu hướng dịch chuyển về bên trái để hướng đến tối ưu cục bộ, bằng cách mutation từ giá trị x1 -> x1', giá trị x1' sẽ dịch chuyển về bên phải, hướng đến tối ưu toàn cục
- Tiến hành random 1 giá trị thuộc [0,1] với mỗi phần tử trong chrom. Nếu giá trị này nhỏ hơn mutation_rate sẽ tiến hành mutate phần tử này.
- Trong di truyền học, tỷ lệ đột biến thường thấp để tránh những đột biến dị dạng và bảo vệ kiểu hình bình thường. Tương tự trong GA, mutation_rate thường thấp (0.05, 0.1, 0.2) để tránh việc biến bài toán thành random, dù có mục đích là tối ưu toàn cục. (Bài báo 1, Bài báo 2)
def mutation(population, rate): #tuỳ từng bài toán có cơ chế muation khác nhau
Bước 4: Cập nhật quần thể mới và điều kiện dừng
- Quần thể mới bao gồm: chrom elite, chrom con sau khi select, crossover, mutate từ chrom bố mẹ.
- Liên tục tạo các chrom con đến khi nào số lượng cá thể chrom đạt được mục tiêu ban đầu.
- Tạo được quần thể mới = kết thúc 1 vòng lặp (thế hệ). Lưu trữ kết quả thế hệ này (history).
-> tiếp tục đến vòng lặp tiếp theo (số lượng vòng lặp - thế hệ cho trước).
#Evolutionary algorithm
def evolve_ga(chrom_size, pop_size, fitness_type, selection_type, generations, elitism, crossover_rate, mutation_rate, seed = random_state):
generate_seed(seed)
population = generate_population(pop_size,chrom_size)
best_per_gen = []
for gen in range(generations):
#compute fitness for all the population
fitness_scores = np.array([compute_fitness(fitness_type,chrom) for chrom in population])
#keeping the best score
best_idx = int(np.argmax(fitness_scores))
best_per_gen.append(fitness_scores[best_idx])
#keeping the elites
elites, elites_fit = elitism_keeping(population, fitness_scores, elitism)
#creating new population:
new_pop = elites
while len(new_pop) < pop_size:
parent1 = parent_selection(selection_type, population, fitness_scores)
parent2 = parent_selection(selection_type, population, fitness_scores)
c1,c2 = uniform_crossover(parent1, parent2, crossover_rate)
c1 = bitflip_mutation(c1, mutation_rate)
if len(new_pop) < pop_size:
new_pop.append(c1)
c2 = bitflip_mutation(c2, mutation_rate)
if len(new_pop) < pop_size:
new_pop.append(c2)
population = new_pop
final_fitness = [compute_fitness(fitness_type, ind) for ind in population]
best_idx = int(np.argmax(final_fitness))
best_ind = population[best_idx]
return best_ind, best_per_gen, compute_fitness(fitness_type, best_ind)
Exercise 1: Onemax vs Trap fitness
Từ pipeline trên, áp dụng vào bài toán so sánh onemax fitness và trap fitness:
Tổng quan bài toán:
| Bài | Mục tiêu | Biểu diễn | Hàm Fitness |
|---|---|---|---|
| 1 | Tối đa hoá số bit 1 | Chuỗi nhị phân | Tổng số bit 1 hoặc trap theo block |
với 1 chromosome có dạng 𝑥 = $𝑥1, 𝑥2, … , 𝑥n$ , 𝑥 ∈ {0, 1}:
#khoi tao quan the
def generate_population(pop_size:int ,chrom_len: int):
return [np.random.randint(0,2, size = chrom_len) for _ in range(pop_size)]
- Hàm onemax:
$$ f(x) = \sum_{i=1}^{n} x_i $$
def onemax_fitness(chrom):
return np.sum(chrom)
- Hàm trap:
$$ f_{\text{trap}}(x) = \begin{cases} b, & \text{nếu } \sum_{i=1}^{b} x_i = b \\ b - 1 - \sum_{i=1}^{b} x_i, & \text{ngược lại} \end{cases} $$
def trap_fitness(chrom):
n = len(chrom)
score = np.sum(chrom)
return n if n == score else (n-1-score)
- Công thức mutation: swap giá trị 0 <-> 1 nếu nhỏ hơn mutation rate
#bitflip mutation definition
def bitflip_mutation(chrom, rate):
chrom = chrom.copy()
mask = np.random.rand(len(chrom)) < rate
chrom[mask] = 1- chrom[mask]
return chrom
Kết quả
- Configuration của bài toán:
#Algorithm configuration
chrom_size =10
pop_size =5
generations =21
elitism =2
crossover_rate = 0.9
mutation_rate = 0.1
#fitness_type =
#selection_type =
- Các thử nghiệm cần kiểm tra:
EXPERIMENTS = [
{
"title": "Tournament + onemax",
"selection": "tournament",
"fitness type": "onemax"
},
{
"title": "Proportional + onemax",
"selection": "proportional",
"fitness type": "onemax"
},
{
"title": "Tournament + trap",
"selection": "tournament",
"fitness type": "trap"
},
{
"title": "Proportional + trap",
"selection": "proportional",
"fitness type": "trap"
}
]
- Mô tả trên matplotlib:
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.flatten()
for ax, result in zip(axes, results):
history = result["history"]
gens = range(len(history))
ax.plot(gens, history, marker="o", linewidth=2, label="Best fitness")
max_possible = chrom_size
ax.axhline(
y=max_possible,
color="r",
linestyle="--",
alpha=0.6,
label="Fitness tối đa",
)
ax.set_title(result["title"], fontsize=12, fontweight="bold")
ax.set_xlabel("Thế hệ")
ax.set_ylabel("Fitness")
ax.set_xticks(list(gens))
ax.grid(alpha=0.4)
ax.legend(fontsize=8, loc="lower right")
plt.tight_layout()
plt.show()
for result in results:
reported = result["final_fitness"]
best = result["best_individual"]
max_possible = chrom_size
print(
f"{result['title']}: best fitness = {reported} / {max_possible} | individual = {best}")
Kết quả nhận được là
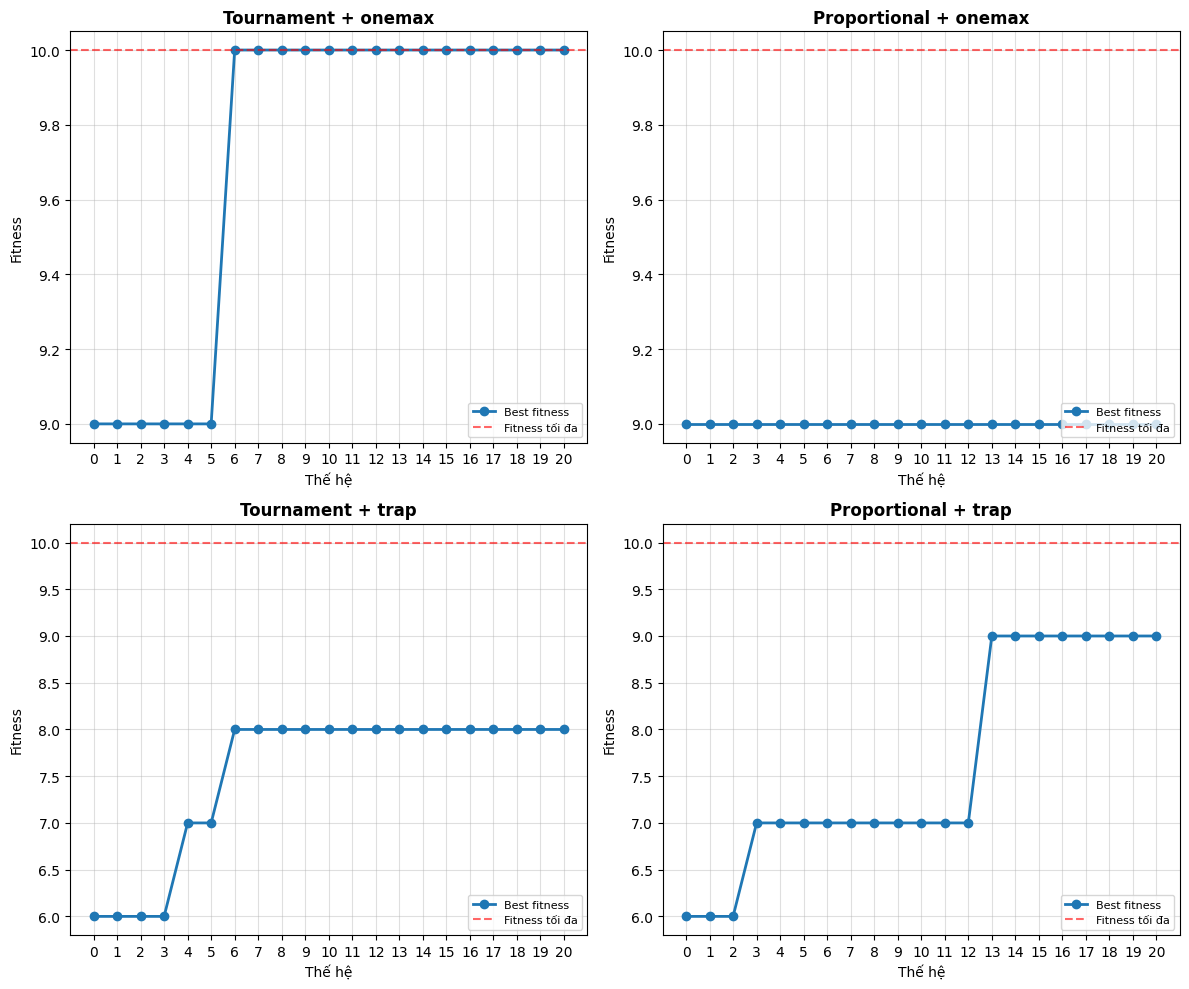
Kết quả 4 thí nghiệm tiến hành
Tournament + onemax: best fitness = 10 / 10 | individual = [1 1 1 1 1 1 1 1 1 1]
Proportional + onemax: best fitness = 9 / 10 | individual = [1 0 1 1 1 1 1 1 1 1]
Tournament + trap: best fitness = 8 / 10 | individual = [0 0 0 0 0 0 0 0 0 1]
Proportional + trap: best fitness = 9 / 10 | individual = [0 0 0 0 0 0 0 0 0 0]
Nhận xét:
- Onemax tốt hơn hàm trap fitness vì hàm trap fitness bị mắc kẹt ở tối ưu cục bộ
- Tournament perform tốt hơn proportional vì tournament vẫn chọn ra cá thể mạnh nhất ở các vòng random, trong khi proportional vẫn có xác suất chọn ra các cá thể yếu dù dựa trên weights.
Bài 1': Áp dụng thư viện pyGAD trong bài toán onemax vs trap fitness
- Định nghĩa lại hàm fitness
def onemax_fitness_pygad(ga_instance, solution, solution_idx):
return np.sum(solution)
def trap_fitness_pygad(ga_instance, solution, solution_idx):
n = len(solution)
score = np.sum(solution)
return n if n == score else (n - 1 - score)
- Định nghĩa hàm ga
def run_ga(fitness_func, parent_selection):
ga = pygad.GA(
#Configuration
num_generations=generations,
num_parents_mating=2,
sol_per_pop=pop_size,
num_genes=chrom_size,
gene_type=int,
gene_space=[0, 1],
fitness_func=fitness_func,
# Mutation
mutation_percent_genes=mutation_rate * 100,
mutation_type="random",
# Crossover
crossover_type="uniform",
crossover_probability=crossover_rate,
# Selection
parent_selection_type=parent_selection,
# Elitism
keep_elitism=elitism,
)
ga.run()
sol, fit, idx = ga.best_solution()
history = ga.best_solutions_fitness
return sol, fit, history, ga
- Chạy trên các thử nghiệm:
# EXPERIMENTS CONFIGURATION
EXPERIMENTS = [
{
"title": "Tournament + OneMax",
"fitness type": onemax_fitness_pygad,
"selection": "tournament"
},
{
"title": "RWS + OneMax",
"fitness type": onemax_fitness_pygad,
"selection": "rws"
},
{
"title": "Tournament + Trap",
"fitness type": trap_fitness_pygad,
"selection": "tournament"
},
{
"title": "RWS + Trap",
"fitness type": trap_fitness_pygad,
"selection": "rws"
}
]
- Kết quả
results = []
for experiment in EXPERIMENTS:
print(f"\n>>> Running: {experiment['title']}")
sol, fit, history, ga_instance = run_ga(
experiment['fitness type'],
experiment['selection']
)
results.append({
"title": experiment['title'],
"solution": sol,
"fitness": fit,
"history": history,
"ga": ga_instance
})
print(f" Best solution: {sol}")
print(f" Best fitness: {fit} / {chrom_size}")
print(f" Convergence: Gen 0: {history[0]:.1f} → Gen {generations-1}: {history[-1]:.1f}")
>>> Running: Tournament + OneMax
Best solution: [1 1 1 1 1 1 1 1 1 1]
Best fitness: 10 / 10
Convergence: Gen 0: 5.0 → Gen 20: 10.0
>>> Running: RWS + OneMax
Best solution: [1 1 1 1 1 1 1 1 1 1]
Best fitness: 10 / 10
Convergence: Gen 0: 6.0 → Gen 20: 10.0
>>> Running: Tournament + Trap
Best solution: [0 0 0 0 0 0 0 0 0 0]
Best fitness: 9 / 10
Convergence: Gen 0: 7.0 → Gen 20: 9.0
>>> Running: RWS + Trap
Best solution: [0 0 0 0 0 0 0 0 0 0]
Best fitness: 9 / 10
Convergence: Gen 0: 5.0 → Gen 20: 9.0
5. Visualisation
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
fig.suptitle('PyGAD - Genetic Algorithm Performance', fontsize=16, fontweight='bold')
for idx, result in enumerate(results):
row = idx // 2
col = idx % 2
ax = axes[row, col]
history = result["history"]
gens = range(len(history))
# Plot fitness history
ax.plot(gens, history, marker="o", linewidth=2, markersize=4,
label="Best fitness", color='blue')
# Optimal line
ax.axhline(y=chrom_size, color="r", linestyle="--", alpha=0.6,
label=f"Optimal ({chrom_size})")
ax.set_title(result["title"], fontsize=12, fontweight="bold")
ax.set_xlabel("Generation", fontsize=10)
ax.set_ylabel("Fitness", fontsize=10)
ax.grid(alpha=0.4)
ax.legend(fontsize=9, loc="lower right")
ax.set_ylim(0, chrom_size + 1)
# Annotate final fitness
final_fit = history[-1]
ax.text(len(history)-1, final_fit, f'{final_fit:.1f}',
ha='left', va='bottom', fontsize=9, fontweight='bold',
bbox=dict(boxstyle='round', facecolor='yellow', alpha=0.5))
plt.tight_layout()
plt.show()
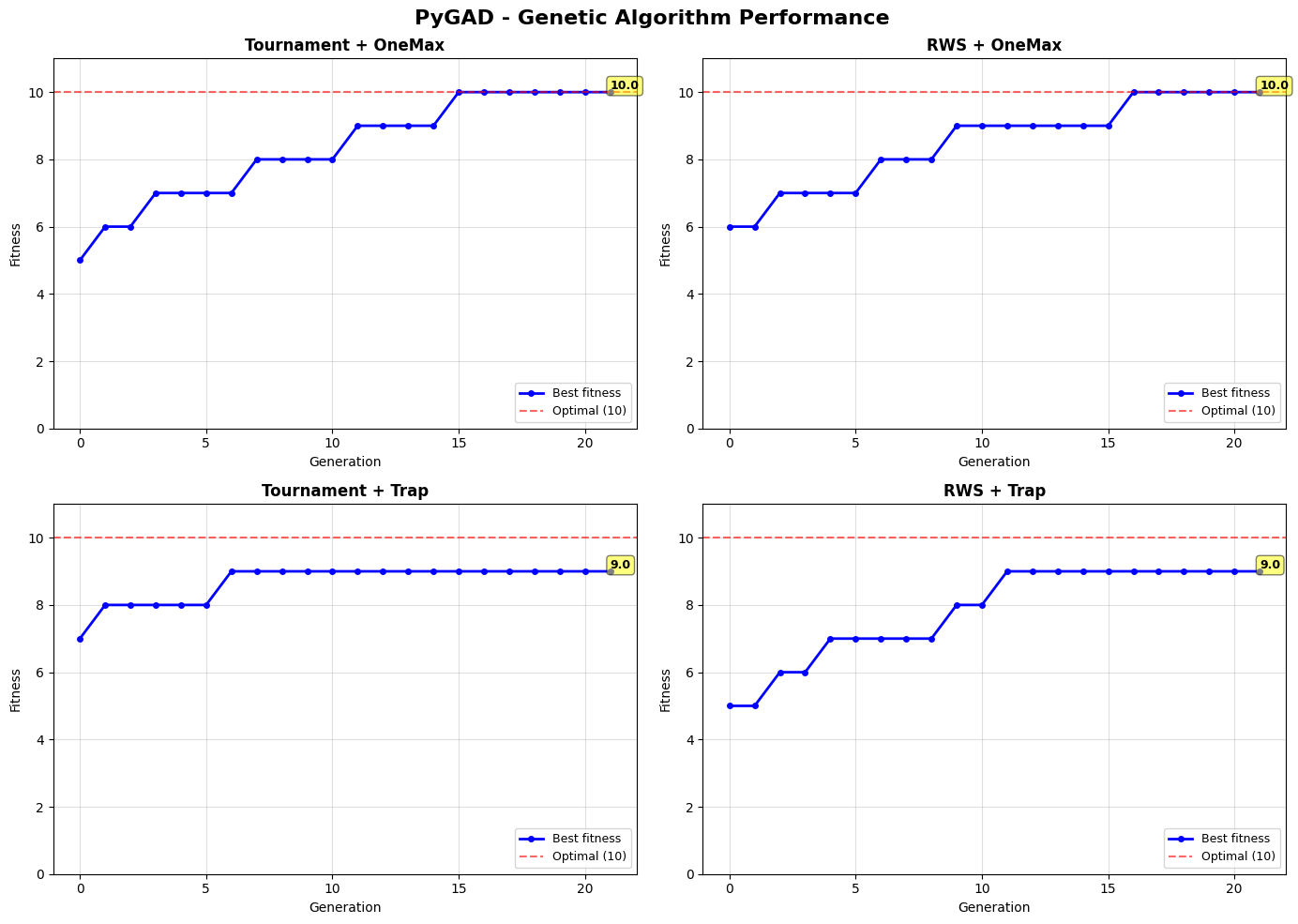
Trực quan hoá kết quả
Bài 2: Linear regression on genetic algorithm
Nội dung:
Sử dụng GA để tìm trọng số tối ưu trong hồi quy tuyến tính trên bộ dữ liệu Diabetes đã chuẩn hoá.
-> Mỗi chromosome là một vector thực θ = [w; b]. Hàm fitness dựa trên Mean Squared Error (MSE), MSE giảm thì fitness tăng.
Sau khi hoàn thành chương trình, ta so sánh hai cơ chế chọn lọc Tournament Selection và Proportional Selection, quan sát đường hội tụ, chất lượng dự đoán và ảnh hưởng của tham số đột biến σ.
Xử lý dữ liệu
Đầu tiên cần tạo bộ dữ liệu, ở đây dùng dataset diabetes có sẵn trên scikitlearn, từ đó tiến hành chia tập train(80%)-test(20%). Sau đó, tiến hành scale x_train và x_test.
data = load_diabetes()
X_full = data.data
y_full = data.target
X_train_raw, X_test_raw, y_train, y_test = train_test_split(
X_full,
y_full,
test_size=0.2,
random_state=RANDOM_STATE,
)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train_raw)
X_test = scaler.transform(X_test_raw)
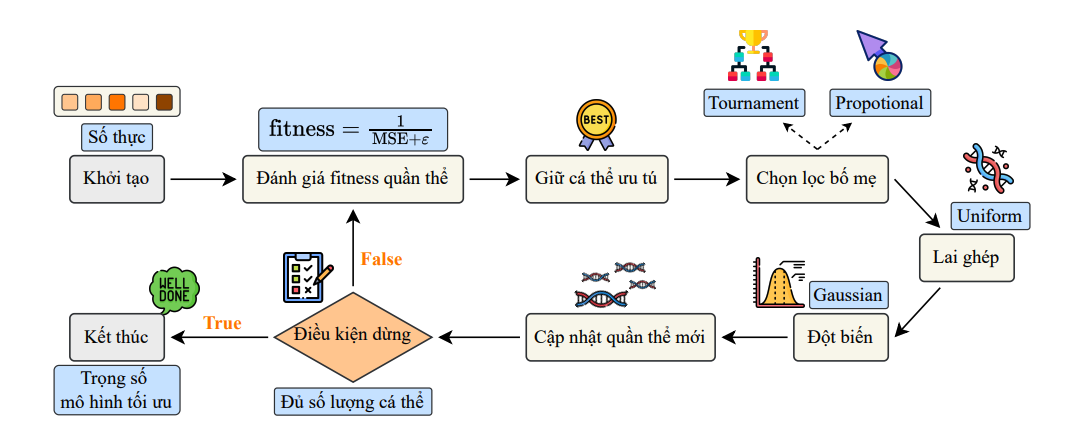
Pipeline bài toán
Ở đây bài toán sẽ có 1 số thay đổi như
- Khởi tạo quần thể:
Tạo 1 quần thể gồm các dãy số thực
def init_population(pop_size, chrom_size):
return random_lst = np.random.randn(pop_size, chrom_size)
- Tính hàm fitness:
Dựa trên giá trị MSE của linear regression, công thức fitness:
$$ \text{fitness} = \frac{1}{\varepsilon + \text{Loss}} $$
với $ \text{Loss} = \text{MSE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2 $ và $\varepsilon$ là giá trị rất nhỏ ($10^{-8}$)
def predict_linear(theta, X):
w = theta[:-1]
b= theta[-1]
y_hat = X @ w+b
return y_hat
def mse_loss(theta, X, y):
y_hat = predict_linear(theta,X)
loss = float(np.mean((y-y_hat)**2))
return loss
def fitness_fn(losses):
return 1/(losses +1e-8)
- Công thức mutation: theo phân phối chuẩn Guassian:
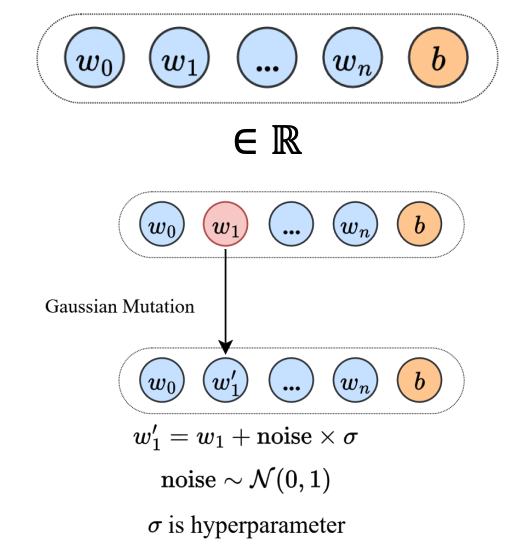
Đột biến theo phân phối chuẩn Guassion
def gaussian_mutation(theta, mutation_rate, sigma):
mask = np.random.rand(len(theta)) <= mutation_rate
noise = np.random.randn(len(theta))*sigma
mutated = theta.copy()
mutated[mask] += noise[mask]
return mutated
Ngoài ra do X ở dạng matrix (array 2 chiều) trên có 1 số thay đổi trong lựa chọn bố mẹ:
def tournament_select(population, losses, tournament_size=2):
n= len(population)
idx = np.random.choice(n,min(tournament_size,n), replace = True)
fitness = fitness_fn(losses[idx])
best_local = idx[np.argmax(fitness)]
return population[best_local].copy()
def proportional_select(population, losses):
weight = fitness_fn(losses)
probs = weight/ np.sum(weight)
pick = np.random.choice(population.shape[0],p=probs )
return population[pick].copy()
def uniform_crossover(parent1, parent2, rate):
child1 = parent1.copy()
child2 = parent2.copy()
mask = np.random.rand(parent1.shape[0]) <= rate
child1[mask], child2[mask] = parent2[mask], parent1[mask]
return child1, child2
Kết quả:
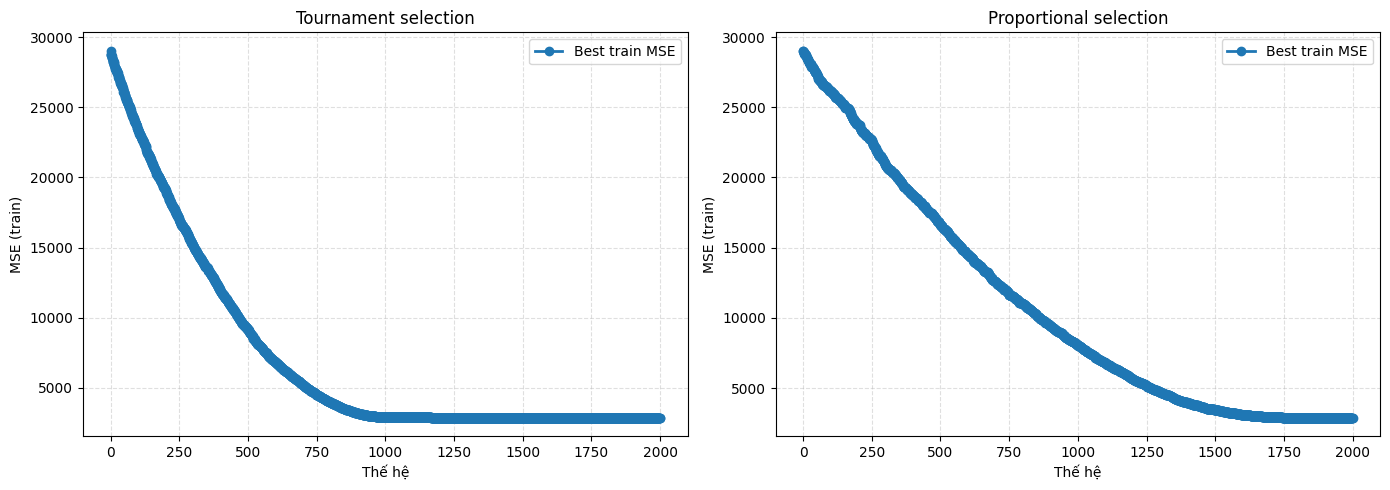
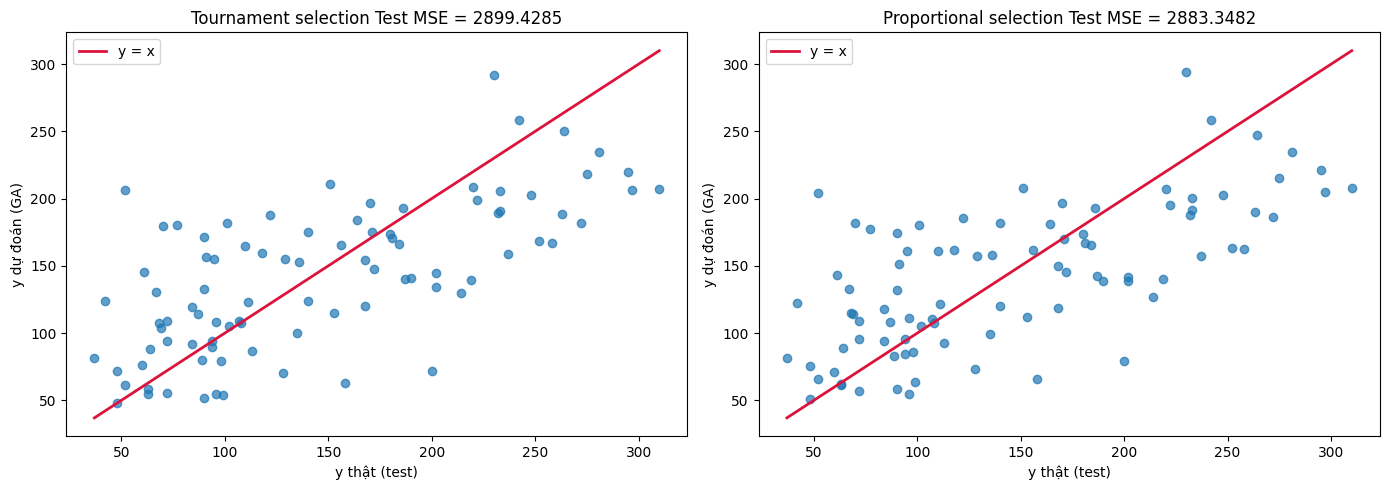
Nhận xét: Tournament có tốc độ hội tụ lớn hơn proportional. Tuy nhiên kết quả sau cùng (MSE) thì tương đương nhau
Ứng dụng pyGAD trong bài toán Linear Regression
Sau khi chia train/test tiến hành gộp 1 mảng 1 vào tập train + định nghĩa hàm fitness:
X_train_with_bias = np.c_[X_train, np.ones(X_train.shape[0])]
X_test_with_bias = np.c_[X_test, np.ones(X_test.shape[0])]
def fitness_fn(ga_instance, solution, solution_idx):
y_pred = X_train_with_bias @ solution
mse = np.mean((y_pred - y_train) ** 2)
eps = 1e-8
fitness = (1/(mse+eps))
return fitness
Cấu trúc pyGAD trong trường hợp có mutation Guassian được định nghĩa như sau
def run_ga(parent_selection):
ga = pygad.GA(
num_generations=generations,
num_parents_mating=2,
sol_per_pop=pop_size,
num_genes=chrom_size,
gene_type=float,
fitness_func=fitness_fn,
init_range_low=-5.0,
init_range_high=5.0,
# Mutation
mutation_percent_genes=mutation_rate * 100,
mutation_type="random",
mutation_by_replacement = False,
random_mutation_min_val=-3 * mutation_sigma, # -3σ
random_mutation_max_val=3 * mutation_sigma,
# Crossover
crossover_type="uniform",
crossover_probability=crossover_rate,
# Selection
parent_selection_type=parent_selection,
# Elitism
keep_elitism=elitism,
)
# Run GA
ga.run()
# Get best solution
sol, fit, idx = ga.best_solution()
print(f"\n✓ GA completed!")
print(f" Best fitness: {fit:.6f}")
print(f" Best MSE: {1/fit:.4f}")
history = ga.best_solutions_fitness
return sol, fit, history, ga
Kết quả
PARENT_SELECTIONS = ["tournament", "rws"]
results = []
for selection in PARENT_SELECTIONS:
set_random_seed(RANDOM_STATE)
sol, fit, history, ga_instance = run_ga(selection)
# Evaluate on all sets
y_train_pred = X_train_with_bias @ sol
y_test_pred = X_test_with_bias @ sol
train_mse = mean_squared_error(y_train, y_train_pred)
test_mse = mean_squared_error(y_test, y_test_pred)
train_r2 = r2_score(y_train, y_train_pred)
test_r2 = r2_score(y_test, y_test_pred)
results.append({
"selection": selection,
"solution": sol,
"fitness": fit,
"history": history,
"train_mse": train_mse,
"test_mse": test_mse,
"train_r2": train_r2,
"test_r2": test_r2,
"ga": ga_instance
})
print(f'\n huấn luyện {selection}')
print(f"\n Train MSE: {train_mse:.4f}, R²: {train_r2:.4f}")
print(f" Test MSE: {test_mse:.4f}, R²: {test_r2:.4f}")
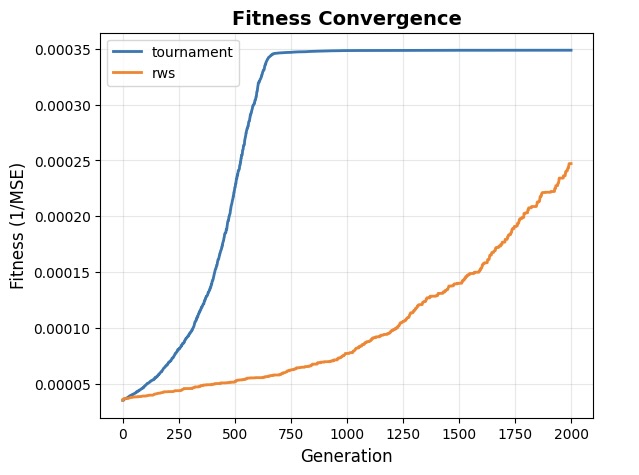
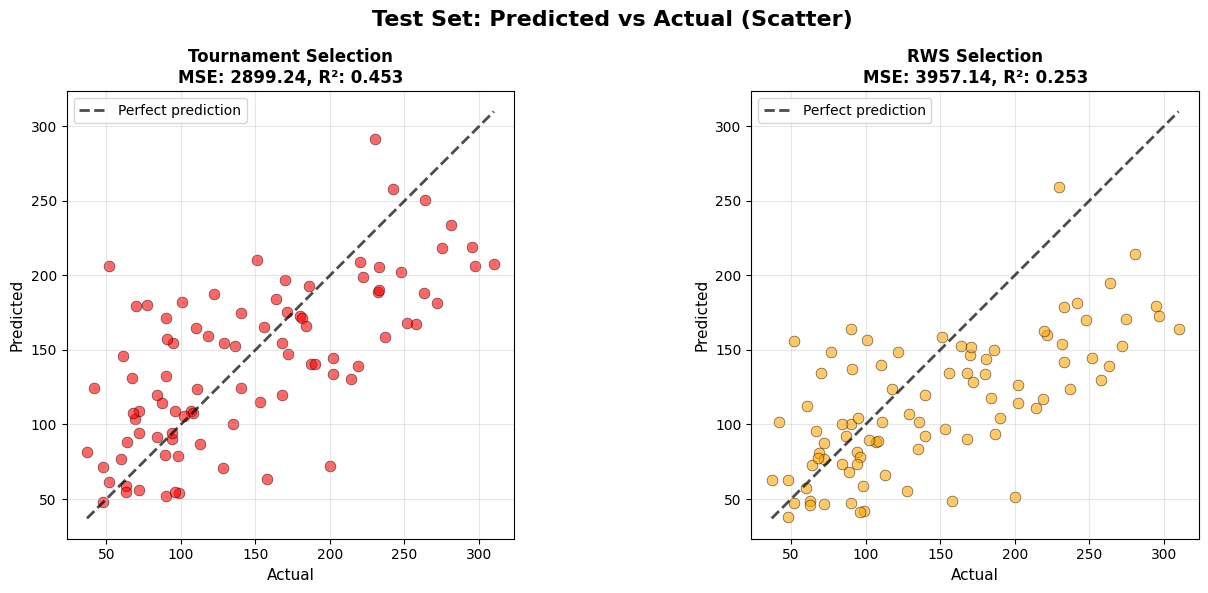
Minh hoạ đồ thị linear regression của GA theo tournament selection và RWS selection (proportional)
Nhận xét: Tournament có tốc độ hội tụ và độ chính xác cao hơn RWS
Chưa có bình luận nào. Hãy là người đầu tiên!