I. Giới thiệu
Dự báo giá nhà là một ứng dụng thiết thực của học máy trong lĩnh vực tài chính và bất động sản. Khả năng dự đoán chính xác giá trị bất động sản rất quan trọng, hỗ trợ nhà đầu tư ra quyết định sáng suốt, giúp tổ chức tài chính đánh giá rủi ro và cơ quan quản lý hoạch định chính sách đô thị.
Bài toán này đặt ra thách thức lớn do tính phức tạp và đa dạng của dữ liệu, bao gồm các yếu tố về vị trí, thị trường và biến động kinh tế vĩ mô.
Mô hình hồi quy tuyến tính truyền thống thường hạn chế khi áp dụng cho dữ liệu thực tế, nơi các mối quan hệ thường phi tuyến và có sự tương tác phức tạp giữa các đặc trưng. Hơn nữa, dữ liệu bất động sản hay gặp phải các vấn đề như giá trị thiếu, ngoại lai, phân phối lệch và đa cộng tuyến. Những yếu tố này làm cho các mô hình đơn giản dễ bị quá khớp (overfitting) hoặc cho kết quả không ổn định.
Do đó, việc nghiên cứu tập trung vào việc áp dụng các kỹ thuật tiên tiến để khắc phục những hạn chế này. Điều này bao gồm:
- Kỹ thuật tiền xử lý dữ liệu tinh vi: Xử lý thông minh các giá trị thiếu và kiểm soát ảnh hưởng của các giá trị ngoại lai.
- Tạo đặc trưng phi tuyến: Xây dựng các đặc trưng mới nhằm nắm bắt các mối quan hệ phức tạp trong dữ liệu mà không gây ra hiện tượng "nổ chiều" (curse of dimensionality).
- Lựa chọn và đánh giá mô hình: Áp dụng các thuật toán mạnh mẽ hơn để đạt được độ chính xác và khả năng tổng quát hóa tốt hơn.
- Giải thích mô hình: Đảm bảo khả năng minh bạch trong kết quả dự đoán.
Mục tiêu cuối cùng là tạo ra một hệ thống dự báo hiệu quả và đáng tin cậy dựa trên việc tích hợp các phương pháp xử lý dữ liệu và mô hình hóa nâng cao.
II. Tổng quan nghiên cứu
1. Các mô hình hồi quy cơ bản
Hồi quy tuyến tính (Linear Regression) là nền tảng của các phương pháp học có giám sát cho bài toán dự báo giá trị liên tục. Mô hình này giả định rằng tồn tại một mối quan hệ tuyến tính giữa các biến đầu vào và biến mục tiêu, được biểu diễn dưới dạng:
$$ y = w_0 + w_1x_1 + w_2x_2 + ... + w_px_p + \epsilon $$
trong đó $w_j$ là các hệ số hồi quy, $x_j$ là các đặc trưng, $y$ là biến mục tiêu, $\epsilon$ là sai số ngẫu nhiên. Quá trình huấn luyện mô hình nhằm tối thiểu hóa tổng bình phương sai số giữa giá trị dự đoán và giá trị thực tế thông qua các thuật toán tối ưu như Gradient Descent.
Tuy nhiên, trong thực tế, mối quan hệ giữa các đặc trưng và giá nhà thường không tuân theo dạng tuyến tính đơn giản. Nhiều hiện tượng có tính phi tuyến hoặc tồn tại các tương tác phức tạp giữa các biến, khiến mô hình tuyến tính không thể nắm bắt được đầy đủ cấu trúc dữ liệu. Điều này dẫn đến nhu cầu mở rộng sang các mô hình hồi quy phi tuyến, đặc biệt là hồi quy đa thức (Polynomial Regression), cho phép mô hình học được các mối quan hệ cong và các tương tác bậc cao giữa các đặc trưng.
Hồi quy đa thức mở rộng không gian đặc trưng bằng cách thêm vào các số hạng bậc ao của các biến đầu vào cũng như các tương tác giữa chúng. Ví dụ, với hai biến đầu vào $x_1$ và $x_2$ và bậc đa thức $d = 2$, các đặc trưng mới được tạo ra bao gồm $x_1$, $x_2$, $x_1^2$, $x_2^2$, $x_1x_2$. Điều này cho phép mô hình học được các đường cong phức tạp và các mối quan hệ tương tác, nâng cao đáng kể khả năng biểu diễn của mô hình.
2. Các kỹ thuật Regularization
Khi tăng độ phức tạp của mô hình thông qua việc thêm các đặc trưng đa thức, nguy cơ quá khớp (overfitting) cũng tăng theo, đặc biệt khi số lượng đặc trưng lớn so với số lượng mẫu huấn luyện. Regularization là một kỹ thuật quan trọng để giải quyết vấn đề này bằng cách thêm thành phần vào hàm mất mát, nhằm kiểm soát độ lớn của các hệ số và duy trì tính ổn định của mô hình.
Ridge Regression (L2 Regularization)
Ridge Regression thêm vào hàm mất mát một thành phần dựa trên tổng bình phương của các hệ số:
$$ J(w) = \sum_{i=1}^{m}{(y - \hat{y})^2} + \lambda\sum_{j=1}^{n}{w_j^2} $$
trong đó $\lambda$ là hệ số regularization kiểm soát mức độ phạt. Khi $\lambda$ tăng, các hệ số bị co nhỏ về gần 0 nhưng không bao giờ bằng 0 hoàn toàn, giúp giảm overfitting trong khi vẫn giữ lại tất cả các đặc trưng.
Lasso Regression (L1 Regularization)
Lasso Regression sử dụng thành phần phạt dựa trên tổng giá trị tuyệt đối của các hệ số:
$$ J(w) = \sum_{i=1}^{m}{(y - \hat{y})^2} + \lambda\sum_{j=1}^{n}{|w_j|} $$
Một đặc tính quan trọng của Lasso là khả năng đưa một số hệ số về đúng bằng $0$, từ đó thực hiện chọn lọc đặc trưng tự động và tạo ra các mô hình thưa (sparse models). Điều này đặc biệt hữu ích khi làm việc với dữ liệu có nhiều đặc trưng nhưng chỉ một phần nhỏ thực sự quan trọng.
Elastic Net ($L_1$ + $L_2$)
Elastic Net là sự kết hợp giữa Ridge và Lasso, sử dụng cả hai thành phần phạt $L_1$ và $L_2$:
$$ J(w) = \sum_{i=1}^{m}{(y - \hat{y})^2} + \lambda_1\sum_{j=1}^{n}{|w_j|} + \lambda_2\sum_{j=1}^{n}{w_j^2} $$
Elastic Net kế thừa khả năng chọn lọc đặc trưng từ Lasso và tính ổn định trong xử lý đa cộng tuyến từ Ridge, đặc biệt hiệu quả khi các đặc trưng có tương quan cao với nhau.
Các mô hình Robust Regression
Các mô hình hồi quy truyền thống thường nhạy cảm với giá trị ngoại lai, có thể ảnh hưởng lớn đến kết quả dự báo. Các mô hình robust regression được thiết kế để giảm thiểu ảnh hưởng này.
HuberRegressor sử dụng hàm mất mát Huber, kết hợp giữa bình phương sai số cho các điểm gần và giá trị tuyệt đối cho các điểm xa, giúp mô hình ổn định hơn trước ngoại lai.
QuantileRegressor tối thiểu hóa MAE hoặc Pinball loss, cho phép dự báo các phân vị khác nhau của phân phối thay vì chỉ giá trị trung bình.
RANSACRegressor sử dụng phương pháp lấy mẫu ngẫu nhiên để xác định các điểm inliers và loại bỏ ảnh hưởng của outliers trong quá trình huấn luyện.
III. Phuơng pháp cải tiến đề xuất
1. Chuẩn bị và xử lý dữ liệu.
Nhóm sử dụng bộ dữ liệu House Prices - Advanced Regression Techniques. Bộ dữ liệu gồm 1460 dữ liệu và khoảng 81 biến đặc trưng mô tả thông tin kiến trúc, vị trí, vật liệu và các thuộc tính tiện nghi (ví dụ: diện tích tầng trệt, diện tích hầm, năm xây, chất lượng ngoại thất, số phòng tắm, loại mái, gara, v.v.). Mục tiêu dự đoán là SalePrice — giá bán bằng đơn vị tiền tệ.
Nhóm tiến hành EDA (Exploratory Data Analyst) trên bộ dữ liệu này.
Loại bỏ các cột không mang thông tin dự đoán hữu ích hoặc có tần suất thiếu rất cao
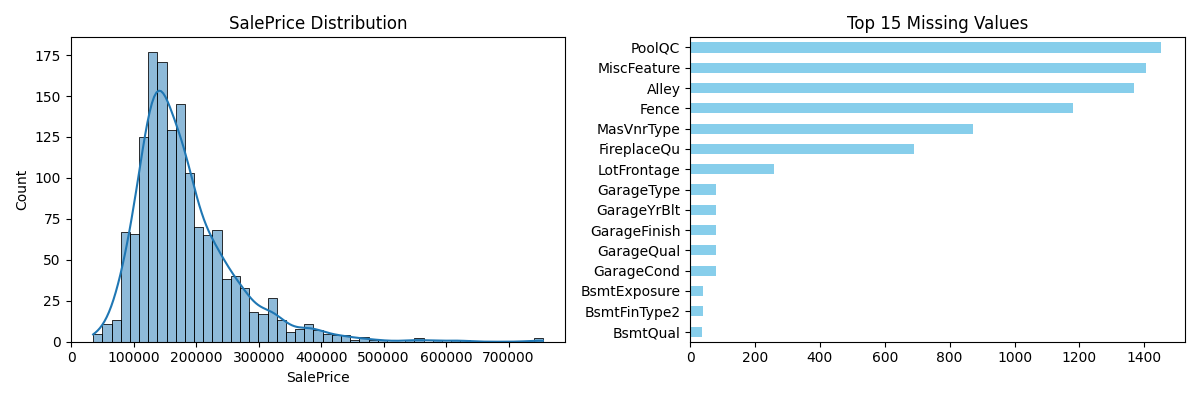 Hình 1. Phân Phối biến mục tiêu SalePrice và ranking các feature missing
Hình 1. Phân Phối biến mục tiêu SalePrice và ranking các feature missing
Bộ dữ liệu đang có những đặc trưng có missing value rất lớn. Chính vì vậy, nhóm loại bỏ các cột không mang thông tin dự đoán hữu ích hoặc có tần suất thiếu rất cao. Cột định danh duy nhất (Id) sẽ bị loại bỏ vì không chứa thông tin suy đoán. Các thuộc tính có nhiều giá trị thiếu hệ thống ($> 50\%$) như Alley, PoolQC, Fence và MiscFeature cũng sẽ bị loại bỏ khỏi phân tích chính do tỷ lệ thiếu quá lớn khiến việc suy diễn ý nghĩa trở nên rủi ro hoặc yêu cầu giả thiết bổ sung không mong muốn. Việc loại bỏ này nhằm tập trung vào các biến có thông tin thực tế và tránh xử lý dữ liệu hiếm khiến mô hình bị lệch.
Xử lý các đặc trưng có độ lệch tuyệt đối lớn
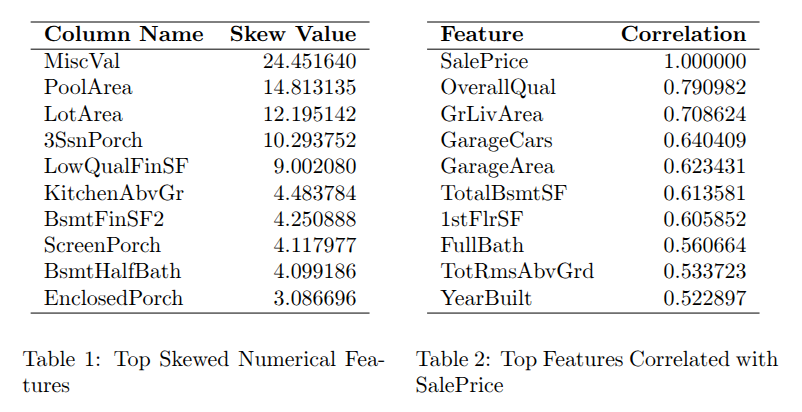
Dựa vào bảng 1, nhóm nhận thấy rằng độ lệch tuyệt đối của phân phối mục tiêu đang có giá trị rất lớn trên một số đặc trưng. Chính vì vậy, nhóm đề xuất sử dụng phép biến đổi $\text{Yeo-Johnson}$ và $\text{log1p}$ lên các đặc trưng có $|\text{skew}| > 1$ để ổn định phương sai và giảm độ lệch (skewness) của dữ liệu, giúp mô hình Machine Learning hoạt động hiệu quả hơn.
$$ f(x, \lambda) = \begin{cases} \frac{(x + 1)^{\lambda} - 1}{\lambda} & \text{nếu } x \geq 0, \lambda \neq 0 \\ \log(x + 1) & \text{nếu } x \geq 0, \lambda = 0 \\ \frac{(1 - x)^{2 - \lambda} - 1}{\lambda - 2} & \text{nếu } x < 0, \lambda \neq 2 \\ -\log(1 - x) & \text{nếu } x < 0, \lambda = 2 \end{cases} $$
Xử lý giá trị outlier và giá trị thiếu.
Mặc dù nhóm đã loại bỏ đi các đặc trưng có missing-value lớn hơn $50\%$ nhưng vẫn tồn tại các đăc trưng missing-value trong bộ dữ liệu. Nhóm đề xuất sử dụng KNNImputer để xử lý các missing-value nhằm duy trì mối quan hệ và cấu trúc cục bộ của dữ liệu, giúp bảo tồn cấu trúc dữ liệu.
Đối với các giá trị ngoại lại, nhóm đề xuất hai kỹ thuật Winsorization và Interquartile Range.
-
Đối với Winsorization, do các đặc trưng đang có xu hướng lệch phải, 2% các giá trị thấp nhất trong mỗi cột sẽ được thay thế bằng giá trị ở phân vị thứ 2%, giúp nâng các điểm dữ liệu quá thấp lên mức hợp lý hơn để tránh kéo lệch trung bình xuống quá mức. Ngược lại, 5% các giá trị cao nhất sẽ được thay thế bằng giá trị ở phân vị thứ 95%, từ đó hạ các điểm dữ liệu quá cao xuống mức biên an toàn.
-
Đối với Interquartile Range, các giá trị nằm ngoài phạm vi $Q_1 \pm 1.5 \times \text{IQR}$ sẽ được cắt và thay thế bằng giá trị của Rào chắn gần nhất.
Scaling và Encoding
Nhóm sử dụng lần lượt cả ba phương scaling bao gồm MinMaxScaler, StandardScaler và RobustScaler để chuẩn hoá và đưa dữ liệu về cùng một phạm vi giá trị.
Nhóm áp dụng Mã hóa Thứ tự ($\text{OrdinalEncoder}$) cho các biến phân loại có thứ tự. Các biến phân loại còn lại được xử lý bằng $\text{OneHotEncoder}$ để bảo tồn thông tin bậc thang trong các đặc trưng có cấu trúc thứ bậc, đồng thời giảm số lượng đặc trưng đầu ra so với mã hóa $\text{OneHot}$ toàn bộ.
Feature Engineering
Nhóm đề xuất thêm ba đặc trưng mới $\text{Age}$ (năm bán trừ năm xây dựng), $\text{TotalSF}$ (tổng diện tích trên mặt đất và tầng hầm), và $\text{TotalBath}$ (tổng số phòng tắm).
-
Age = YrSold − YearBuilt: Thông thường, năm xây dựng căn nhà chỉ mang thông tin bổ sung để suy ra được thời gian tồn tại của căn nhà. Nhóm tạo một đặc trưng Age chuyển từ năm xây sang tuổi nhà biến một biến mang tính mốc thời gian thành một biến liên hệ trực tiếp với giá trị tài sản, cho phép mô hình học mối quan hệ “nhà càng cũ thì giá càng thấp” một cách rõ ràng hơn.
-
TotalSF = GrLivArea + TotalBsmtSF: là đặc trưng tổng diện tích sử dụng phản ánh trực tiếp giá trị tài sản, khắc phục giới hạn của việc nhìn từng biến rời rạc. Trong thực tế định giá nhà, giá trị không chỉ phụ thuộc vào diện tích nổi mà cả diện tích sử dụng tổng thể. Gộp hai biến thành TotalSF giúp mô hình nhận ra rằng một căn có 120 m² + 80 m² tầng hầm có giá trị tương tự căn chỉ có 200 m² nền mà không có tầng hầm — điều mà mô hình rất khó học nếu hai biến để rời.
-
TotalBath = FullBath + 0.5 x HalfBath + BsmtFullBath + 0.5 x BsmtHalfBath: giúp mô hình hiểu giá trị tiện ích phòng tắm dưới dạng một biến duy nhất có trọng số được hiệu chỉnh hợp lý. Trong định giá bất động sản, mỗi phòng tắm đầy đủ (full bath) đóng góp nhiều giá trị hơn phòng tắm nửa (half bath). Việc tổng hợp quy đổi về số phòng tắm tương đương đầy đủ giúp mô hình học một quan hệ gần tuyến tính thay vì 4 cột rời rạc với độ quan trọng khác nhau.
2. Mô hình dự đoán
Nhóm sử dụng QuantileRegressor (với $\text{quantile}=0.5$) để huẩn luyện trên dữ liệu huấn luyện đã qua xử lý. Siêu tham số của mô hình được giữ nguyên là $\alpha=0.001$ và $\text{solver=highs}$.
Mặc dù việc biến đổi $\text{log1p}$ được áp dụng để giảm độ lệch của $\text{SalePrice}$, phân phối mục tiêu sau biến đổi có thể vẫn không phải là phân phối chuẩn hoàn hảo. QuantileRegressor ít nhạy cảm hơn nhiều đối với các ngoại lai trong biến mục tiêu ($\text{SalePrice}$). Bằng cách giảm thiểu sai số tuyệt đối thay vì sai số bình phương, mô hình cung cấp một ước lượng mạnh mẽ hơn, ít bị kéo về phía các giá trị giá nhà cực cao hoặc cực thấp.
IV. Kết quả
Nhóm thực hiện huấn luyến theo chiến lược tiến triển (progressive ablation). Mục tiêu là phân tách lợi ích thuần của từng thành phần (outlier handling, scaling, ordinal encoding, feature engineering) và xác định các tương tác có ý nghĩa giữa chúng, bao gồm năm cấp độ:
-
Baseline (B): Áp dụng KNN imputer cho cả thuộc tính số và phân loại. Mỗi cấu hình thử nghiệm một Scaler khác nhau (MinMaxScaler, StandardScaler, RobustScaler). Không áp dụng xử lý ngoại lai, skew transform, mã hóa thứ tự, hoặc kỹ thuật đặc trưng FE.
-
Stage 1: Thử nghiệm các biến thể xử lý ngoại lai (Winsorization và IQR Clipping).
-
Stage 2: Thêm Skew Transform (Yeo-Johnson và log1p) vào các cấu hình của Stage 1.
-
Stage 3: Thêm Ordinal Encoding cho các biến phân loại có thứ tự.
-
Stage 4: Bổ sung ba đặc trưng mới được kỹ thuật hóa (Age, TotalSF, TotalBath).
Mỗi cấu hình được đánh giá một lần trên tập kiểm thử (no cross-validation, no hyperparameter tuning) để cô lập ảnh hưởng của tiền xử lý; mô hình được cố định dưới dạng QuantileRegressor (quantile = 0.5, $\alpha$ = 0.001, solver = 'highs') để đảm bảo tính ổn định và tránh nhiễu do điều chỉnh siêu tham số.
1. Baseline

Tất cả các pipeline đều cho kết quả tốt với $R^2$ khoảng 93%, chỉ có một chút sự khác biệt nằm ở RMSE và RAE, nơi mà các scaler ảnh hưởng đến độ chính xác dự đoán.
Nhóm sử dụng pipeline KNN Imputer + RobustScaler làm pipeline chính (Baseline) cho các pipeline phía sau vì nó vượt trội ở RMSE và RAE (thấp nhất), đồng thời duy trì $R^2$ cao.
2. Stage 1: Xử lý ngoại lai
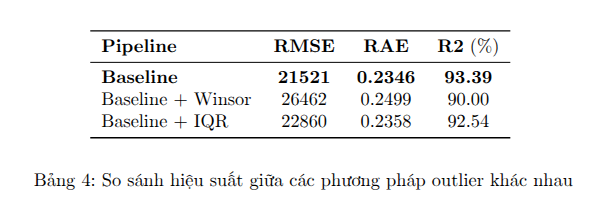
Việc áp dụng xử lý outlier lại cho kết quả tệ hơn: Winsor làm giảm hiệu suất rõ rệt, trong khi IQR chỉ giảm nhẹ. Điều này gợi ý rằng dữ liệu có thể không có nhiều outlier nghiêm trọng. Baseline sẽ không sử dụng bất kỳ phương pháp xử lý ngoại lai nào cho các pipeline sau.
3. Stage 2: Skew Transform
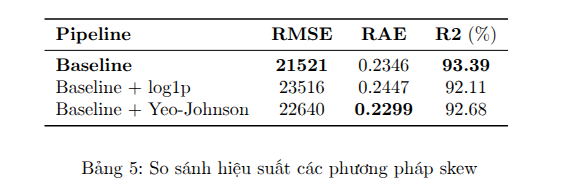
Cả hai pipeline đều cho kết quả khá tốt với $R^2$ trên 92%. Tuy nhiên, sự khác biệt giữa hai phương pháp là rõ rệt, Yeo-Johnson vượt trội hơn ở tất cả các chỉ số (RMSE và RAE thấp hơn, $R^2$ cao hơn). So với Baseline gốc ban đầu thì độ chính xác có giảm một chút (RMSE cao hơn, $R^2$ thấp hơn). Chính vì vậy, nhóm sẽ không sử dụng bất kỳ phương pháp xử lý phân phối lệch nào cho các pipeline phía sau.
4. Stage 3: Ordinal Encoding cho các biến phân loại có thứ tự.
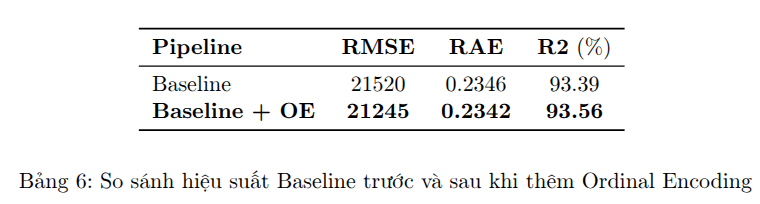
Việc thêm Ordinal Encoding chỉ mang lại cải thiện nhẹ nhưng nhất quán, cho thấy OE giúp xử lý tốt hơn các biến phân loại có thứ tự, làm cho dữ liệu phù hợp hơn với mô hình mà không gây overfitting. Ở stage cuối cùng Ordinal Encoding sẽ là pipeline mặc định.
5. Stage 4: Bổ sung ba đặc trưng mới
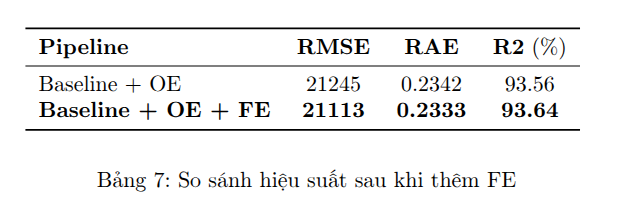
Việc thêm Feature Engineering tiếp tục cải thiện nhẹ nhưng nhất quán, cho thấy FE giúp mô hình khai thác sâu hơn các mối quan hệ ẩn trong dữ liệu, tăng khả năng dự đoán mà không gây overfitting.
6. Cải thiện độ chính xác với Optuna
Mô hình $\text{QuantileRegressor}$ ban đầu được cố định với siêu tham số mặc định ($\text{alpha}=0.001$) để cô lập tác động của pipeline preprocessing. Tuy nhiên, để xác định hiệu suất tiềm năng tối đa của các cấu hình pipeline tốt nhất, bước tối ưu hóa siêu tham số (Hyperparameter Tuning) là bắt buộc.
Nhóm sử dụng thư viện $\text{Optuna}$ để quản lý quá trình tối ưu hóa, tìm kiếm các siêu tham số tối ưu. Hiệu suất của mỗi bộ siêu tham số được đánh giá bằng Xác thực Chéo $5$ lần trên tập huấn luyện. Phương pháp này đảm bảo rằng các siêu tham số được chọn là mạnh mẽ (robust) và không bị khớp quá mức (overfit) với một tập con huấn luyện cụ thể.
Quá trình tối ưu hóa với $20$ lần thử nghiệm đã xác định $\alpha = 0.00248$, giúp gia tăng độ chính xác:
-
$\text{R}^2$ từ $93.64\%$ (với $\alpha$ cố định) lên $94.03\%$
-
RAE giảm từ $0.2333$ xuống $0.2236$
-
RMSE giảm từ $21113$ xuống $20458$
7. Giải thích mô hình (XAI)
Mô hình được giải thích bằng các phương pháp SHAP (SHapley Additive exPlanations) và Permutation Importance để xác định các đặc trưng quan trọng nhất trong việc dự đoán biến mục tiêu (đã được biến đổi logarit).
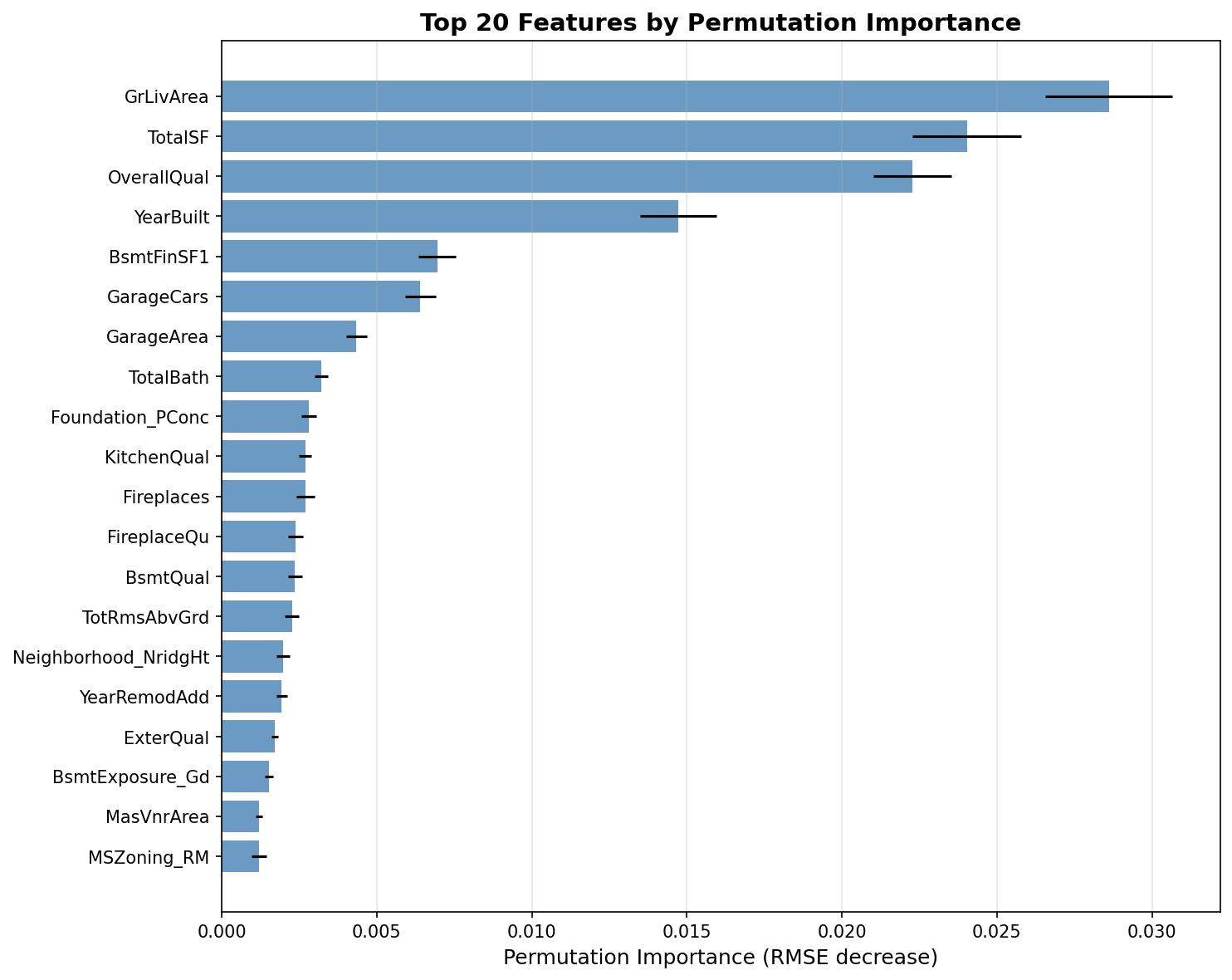
Hình 2. Ranking các đặc trưng quan trọng nhất được xác định bởi phương pháp PI.
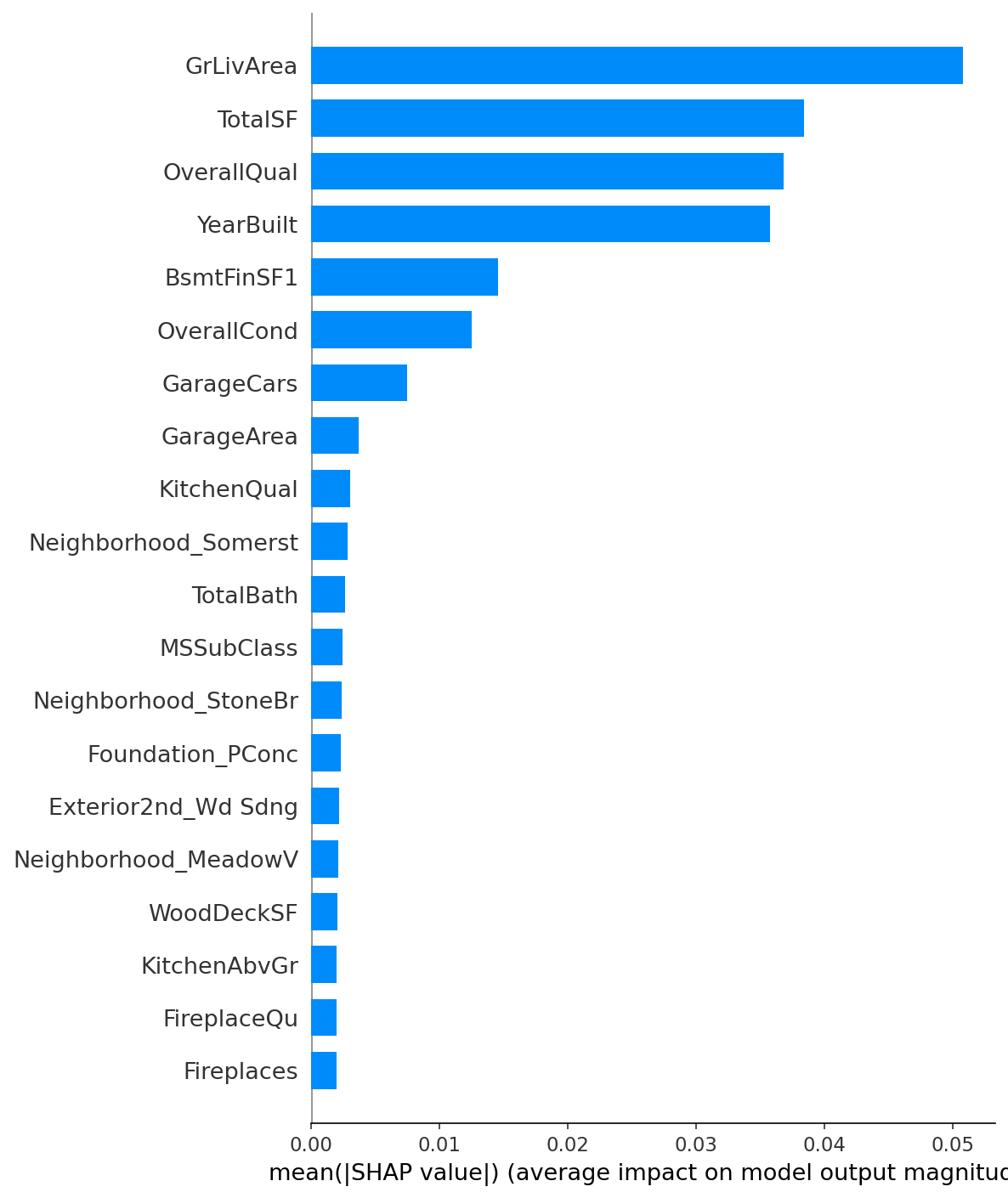
Hình 3. Ranking các đặc trưng quan trọng nhất được xác định bởi SHAP.
Dựa vào hình 2 và hình 3, ta thấy rằng các đặc trưng GrLivArea, TotalSF, OverallQual, và YearBuilt là quan trọng nhất và ổn định ở top đầu theo cả hai phương pháp. Điều này cho thấy diện tích sinh hoạt trên mặt đất, tổng diện tích (TotalSF sinh bởi FE), chất lượng tổng thể, và năm xây dựng là những yếu tố then chốt trong dự đoán giá nhà. Nếu thực hiện các phương pháp tiền xử dữ lý dữ liệu mới trên các đặc trưng này có thể ảnh hưởng mạnh tới độ chính xác của mô hình.
8. Thực nghiệm với nhiều tổ hợp khác nhau
Để tìm ra cấu hình pipeline tối ưu nhất, một chiến lược thử nghiệm toàn diện dựa trên nguyên tắc tìm kiếm lưới (grid search) đã được áp dụng, bao gồm việc khám phá mọi sự kết hợp có thể có giữa các bước tiền xử lý dữ liệu và các mô hình học máy. Cụ thể, trong giai đoạn tiền xử lý, nhóm đã thử nghiệm các phương pháp xử lý dữ liệu thiếu như Simple, Iterative và KNN Imputer; các chiến lược xử lý ngoại lai bao gồm Winsorization, IQR, và bỏ qua (none); các phép biến đổi độ xiên như log1p, Yeo-Johnson, và bỏ qua (none); cùng với các thuật toán chuẩn hóa dữ liệu (MinMax, Standard, và Robust Scaler). Hơn nữa, ảnh hưởng của việc sử dụng tính năng Ordinal Encoding cho các biến phân loại có thứ tự cũng được đánh giá. Sau đó, mỗi cấu hình tiền xử lý đã được kết hợp với một loạt các mô hình hồi quy đa dạng, bao gồm Hồi quy Tuyến tính (Linear Regression), Ridge, Lasso, ElasticNet, Huber, RANSAC, và Quantile Regression.
Bằng cách thử nghiệm mọi pipeline được tạo ra từ việc tổ hợp các tùy chọn này, nhóm đảm bảo rằng không bỏ sót bất kỳ cấu hình tiềm năng nào, từ đó xác định được pipeline có hiệu suất dự đoán tốt nhất dựa trên tiêu chí đánh giá đã thiết lập.
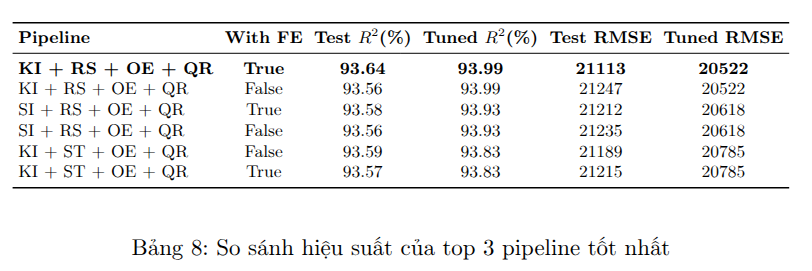
Chú thích:
* KI: KNN Imputer
* SI: Simple Imptuer
* RS: Robust Scaler
* ST: Standard Scaler
* OE: Ordinal Encoding
* QR: Quantile Regressor
Dựa trên Bảng 8, có thể rút ra các nhận xét quan trọng về hiệu suất và sự đóng góp của từng thành phần trong pipeline:
-
Tác động của Feature Engineering (FE): Việc sử dụng Feature Engineering có tác động tích cực đến hiệu suất tổng thể của các pipeline sử dụng Robust Scaler (RS):
-
KNN Imputer (KI) tỏ ra vượt trội hơn khi góp mặt 2/3 pipeline có độ chính xác cao nhất.
-
Mô hình Quantile Regressor là mô hình tốt nhất khi góp mặt cả 3/3 pipeline có độ chính xác cao nhất.
Nhóm cũng thực hiện so sánh độ chính xác các pipeline top đầu trước và sau khi tối ưu tham số với Optuna.
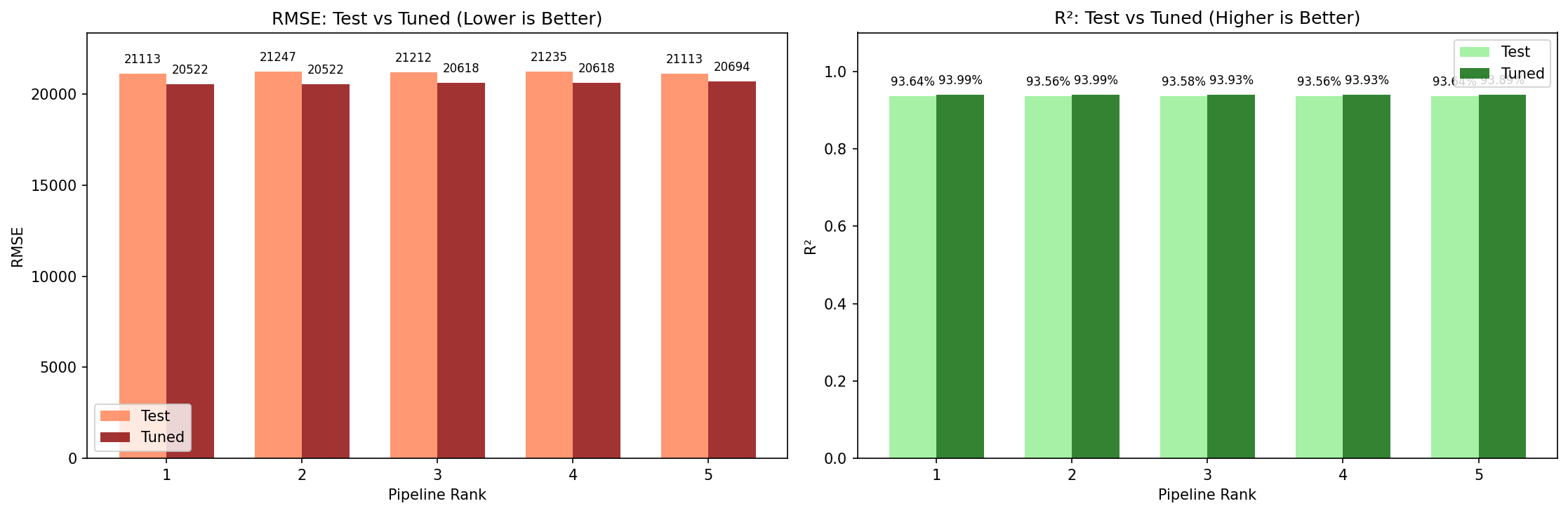
Hình 4. Biểu đồ thể hiện kết quả trước và sau khi tối ưu ở top 5 pipeline.
Từ hình 4, ta thấy rằng việc tinh chỉnh siêu tham số là bước không thể thiếu trong pipeline và đã mang lại sự cải thiện hiệu suất rõ rệt (tăng $R^2$ và giảm RMSE) cho tất cả các mô hình hàng đầu.
V. Kết luận
Nhóm đã thành công trong việc xây dựng một pipeline học máy hiệu quả và mạnh mẽ để dự đoán giá nhà, vượt qua các thách thức ban đầu về tính phi tuyến, ngoại lai và phân phối lệch của dữ liệu bất động sản. Mục tiêu tạo ra một hệ thống dự báo đáng tin cậy đã được hiện thực hóa thông qua việc kết hợp các kỹ thuật tiền xử lý dữ liệu tinh vi và mô hình hồi quy ổn định.
Tóm tắt các đóng góp chính và kết quả:
-
Xây dựng Pipeline Tối ưu: Pipeline cuối cùng đạt hiệu suất tốt nhất được xác định là sự kết hợp giữa KNN Imputer (để duy trì cấu trúc cục bộ của dữ liệu bị thiếu), Robust Scaler (để giảm thiểu ảnh hưởng của các điểm dữ liệu lớn), Ordinal Encoding cho các biến có thứ tự và Feature Engineering (tạo các đặc trưng TotalSF, Age, TotalBath).
-
Khẳng định Hiệu quả của Kỹ thuật Đặc trưng (FE): Các thử nghiệm tiến triển đã chứng minh Feature Engineering là một trong những thành phần quan trọng nhất, mang lại sự cải thiện hiệu suất nhất quán, cho phép mô hình khai thác sâu hơn giá trị tiềm ẩn của bất động sản thông qua các biến tổng hợp như TotalSF.
-
Lựa chọn Mô hình Mạnh mẽ: Việc sử dụng Quantile Regressor tại phân vị $\text{quantile}=0.5$ đã cung cấp một ước lượng mạnh mẽ cho giá nhà, ít bị ảnh hưởng bởi các ngoại lai trong biến mục tiêu so với các mô hình bình phương sai số truyền thống.
-
Tối ưu hóa Hiệu suất: Quá trình tinh chỉnh siêu tham số bằng Optuna là bước quyết định, nâng cao độ chính xác tổng thể của mô hình. Cụ thể, pipeline tốt nhất sau khi tối ưu siêu tham số đạt được hiệu suất dự đoán cao nhất: $R^2$ là $94.03\%$ và RMSE là $20458$.
-
Phân tích Khả năng Giải thích (XAI): Thông qua các phương pháp SHAP và Permutation Importance, nghiên cứu đã xác nhận các yếu tố then chốt chi phối giá nhà là GrLivArea (Diện tích sinh hoạt trên mặt đất), TotalSF (Tổng diện tích sử dụng), OverallQual (Chất lượng tổng thể vật liệu và hoàn thiện), và YearBuilt (Năm xây dựng).
Các bạn có thể tải mã nguồn tại đây nhé: github
VI. Tài liệu tham khảo
- AI Việt Nam, "Module 5 Week 4: House Price Prediction – Advanced Regression Techniques course material", 2025.
Chưa có bình luận nào. Hãy là người đầu tiên!