1. Giới thiệu
1.1. Bối cảnh
Hồi quy tuyến tính (Linear Regression) đóng vai trò nền tảng trong phân tích dữ liệu và dự đoán giá trị liên tục. Tuy nhiên, giả định tuyến tính đơn giản thường không phản ánh đầy đủ bản chất phi tuyến và đa chiều của dữ liệu thực tế, dẫn đến hạn chế về hiệu quả mô hình.
Để khắc phục, các phương pháp mở rộng như hồi quy đa thức (Polynomial Regression) cho phép mô hình hóa mối quan hệ phức tạp hơn, trong khi các kỹ thuật điều chuẩn (Regularization) như Ridge (L2) và Lasso (L1) giúp kiểm soát hiện tượng quá khớp (overfitting). Tuy nhiên, dữ liệu thường tồn tại vấn đề thiếu giá trị, ngoại lai, phân phối lệch, hoặc có cấu trúc đặc thù cần xử lý trước khi mô hình hóa. Đồng thời, việc lựa chọn đặc trưng và bậc đa thức tối ưu là yếu tố then chốt để tránh “nổ chiều” và đảm bảo tính hiệu quả.
Với định hướng này, nghiên cứu không chỉ dừng lại ở việc minh họa các mô hình hồi quy cơ bản, mà còn hướng tới xây dựng một quy trình tiền xử lý, biểu diễn đặc trưng và mô hình hóa tốt hơn, có khả năng áp dụng thực tiễn và mở rộng cho nhiều dạng dữ liệu khác nhau.
1.2. Đề tài liên quan
Dựa trên Project 5.1. House Price Prediction được thực hiện bởi TA&STA, đề tài có mục tiêu ước lượng chính xác giá bán (SalePrice) bằng cách áp dụng các kỹ thuật hồi quy nâng cao, bao gồm Polynomial Regression, Ridge Regression và Lasso Regression, nhằm mô hình hóa các quan hệ phi tuyến và giảm thiểu hiện tượng overfitting.
Theo kết quả huấn luyện trước và sau khi áp dụng PolynomialFeatures, độ chính xác lần lượt là 90% và 89% trên tập kiểm thử. Lý giải cho việc này, khi dữ liệu không có dấu hiệu phi tuyến rõ ràng hoặc số đặc trưng đầu vào đã lớn, việc thêm các đa thức sẽ làm tăng số lượng biến rất nhanh, khiến mô hình trở nên phức tạp, tốn tài nguyên tính toán và dễ dẫn đến overfitting.

Hình 1. Kết quả huấn luyện khi không sử dụng PolynomialFeatures do TA&STA thực hiện

Hình 2. Kết quả huấn luyện khi sử dụng PolynomialFeatures do TA&STA thực hiện
Tuy nhiên, đề tài tồn tại vài vấn đề cần cân nhắc:
- Chưa thực hiện chuẩn hóa phân phối đối với giá trị ngoại lai hay biến đổi log cho các biến có độ lệch lớn.
- Áp dụng cross-validation để đánh giá mô hình khách quan hơn thay vì chỉ dựa vào một lần chia tập dữ liệu huấn luyện và kiểm thử.
- Chưa áp dụng Elastic Net hay các mô hình robust trước ngoại lai như HuberRegressor, QuantileRegressor
1.3. Những cải tiến đề xuất
-
Tiền xử lý và đảm bảo chất lượng dữ liệu: Xử lý thiếu và ngoại lai theo nguyên tắc/mô hình phù hợp: KNNImputer hoặc IterativeImputer; chuẩn hóa phân phối bằng winsorization/IQR; cân nhắc biến đổi log/Box–Cox/Yeo–Johnson cho các biến (đặc biệt là mục tiêu) có độ lệch lớn.
-
Biểu diễn đặc trưng (Feature Engineering) có kiểm soát: Đánh giá có hệ thống giữa PolynomialFeatures đầy đủ và interaction–only; lựa chọn bậc đa thức tối ưu bằng cross–validation nhằm hạn chế “nổ chiều”.
-
Mô hình hoá và quy chuẩn hóa (Regularization) nâng cao:
-
Bổ sung Elastic Net để dung hòa chọn biến (L1) và ổn định hoá hệ số (L2); dò tìm α theo thang log và tối ưu l1_ratio bằng lưới hoặc tìm kiếm ngẫu nhiên.
-
Xem xét các mô hình hồi quy robust trước ngoại lai: HuberRegressor, QuantileRegressor (MAE/Pinball loss), RANSACRegressor cùng mô hình XGBoost nhằm khai thác sức mạnh boosting phi tuyến; so sánh đánh giá để cải tiến với Ridge/Lasso/ElasticNet trên cùng tập dữ liệu.
-
2. Phương pháp thực hiện
2.1. Quy trình thực hiện
- Khởi tạo và chuẩn bị dữ liệu
-
Khám phá dữ liệu (Exploratory Data Analysis – EDA)
- Thống kê mô tả, xác định kích thước và đặc điểm cơ bản của dữ liệu.
- Phân phối biến mục tiêu, đánh giá xu hướng và độ lệch.
- Xây dựng ma trận tương quan nhận diện các đặc trưng có quan hệ mạnh với biến mục tiêu và phân tích đặc trưng có tương quan cao.
-
Tiền xử lý dữ liệu
- Xử lý giá trị thiếu: Loại bỏ các cột có tỷ lệ thiếu > 50%. Với biến số, áp dụng IterativeImputer để dự đoán giá trị thiếu thay vì SimpleImputer.
- Xử lý giá trị ngoại lai: Giới hạn các giá trị cực đoan ở percentile 1% và 99%.
- Chuẩn hóa phân phối qua Yeo-Johnson cho các biến có độ lệch lớn.
- Mã hóa dữ liệu phân loại qua One-hot Encoding và chuẩn hóa dữ liệu số qua Min-Max Scaling để đưa các đặc trưng về cùng thang đo [0,1].
- Chia thành tập huấn luyện (75%) và tập kiểm tra (25%).
-
Xây dựng mô hình hồi quy cơ bản
- Mô hình sử dụng: Linear Regression, Ridge Regression, Lasso Regression, ElasticNet, HuberRegressor, QuantileRegressor, RANSACRegressor, và XGBoost Regressor.
- Áp dụng KFold cross-validation (k=5) để huấn luyện kết hợp GridSearchCV nhằm tìm siêu tham số tối ưu và tính trung bình RMSE và R² trên toàn bộ các fold để chọn ra mô hình tốt nhất.
- Huấn luyện lại mô hình tốt nhất trên toàn bộ tập huấn luyện và dự đoán và đánh giá trên tập kiểm tra qua việc tính RMSE và R² để đánh giá khả năng tổng quát hóa của mô hình.
-
Xây dựng mô hình hồi quy với đặc trưng đa thức
- Thực hiện biểu diễn đặc trưng có kiểm soát qua việc tạo đặc trưng phi tuyến. Áp dụng PolynomialFeatures với hai phương án: Tạo cả lũy thừa và tương tác; Chỉ tạo tương tác giữa các biến, không tạo lũy thừa (Interaction-only).
- Lựa chọn bậc đa thức tối ưu: Sử dụng cross-validation để đánh giá hiệu suất với bậc đa thức 2,3. So sánh validation RMSE giữa PolynomialFeatures đầy đủ và interaction-only. Chọn cấu hình có validation RMSE thấp nhất, ưu tiên độ phức tạp thấp hơn nếu chênh lệch không đáng kể.
- Nếu bậc đa thức tốt nhất sau khi biểu diễn đặc trưng lớn hơn 1, ta thực hiện xây dựng mô hình hồi quy với đặc trưng đa thức. Quy trình và kỹ thuật thực hiện tương tự việc xây dựng mô hình hồi quy tuyến tính cơ bản tại bước 4.
2.2. Công cụ và kỹ thuật sử dụng
- Ngôn ngữ: Python (Pandas, NumPy, Scikit-learn, Matplotlib, Seaborn).
- Xử lý dữ liệu: IterativeImputer, Winsorization, Yeo-Johnson, One-hot Encoding, Min-Max Scaling.
- Học máy: Linear & Regularized Regression (Ridge, Lasso, ElasticNet), Robust Regression (Huber, RANSAC, Quantile), Polynomial Regression, Gradient Boosting (XGBoost).
- Tối ưu siêu tham số: GridSearchCV.
2.3. Mô tả dữ liệu
Mục tiêu: Xây dựng mô hình dự đoán giá nhà dựa trên tập dữ liệu chứa nhiều đặc trưng mô tả thông tin về ngôi nhà, khu đất và điều kiện bán (diện tích, vị trí, kiểu nhà, năm xây dựng, tình trạng bán). Bộ dữ liệu bao gồm 1460 mẫu dữ liệu với 81 cột (bao gồm 80 đặc trưng và 1 cột biến mục tiêu cần dự đoán là SalePrice).
Biến mục tiêu SalePrice được trực quan hóa thông qua biểu đồ phân phối nhằm quan sát mức độ phân tán của giá nhà. Biểu đồ cho thấy phần lớn các căn nhà có giá nằm trong khoảng 100,000 – 200,000 và dữ liệu giá nhà phân phối lệch phải, có skewness dương, và cần xử lý trước khi đưa vào mô hình dự đoán.
sns.histplot(df['SalePrice'], kde=True)
plt.axvline(df['SalePrice'].mean(), color='red', linestyle='dashed', linewidth=1, label='Mean')
plt.axvline(df['SalePrice'].median(), color='green', linestyle='dashed', linewidth=1, label='Median')
plt.title('Distribution of SalePrice', fontsize=14)
plt.xlabel('SalePrice', fontsize=12)
plt.ylabel('Frequency', fontsize=12)
plt.legend()
plt.show()
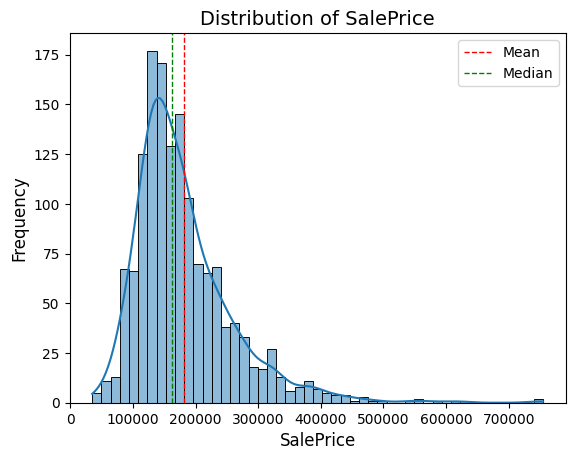
Hình 3. Biểu đồ phân bố giá nhà
Thống kê dữ liệu bị khuyết ở các đặc trưng được thể hiện thông qua biểu đồ bên dưới. Những đặc trưng với hơn 50% dữ liệu bị thiếu nên được loại bỏ để tránh làm giảm tính chính xác của mô hình: PoolQC, MiscFeature, Alley, Fence, MasVnrType, FireplaceQua.
# sns.set()
missing = df.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.barh(edgecolor='black')
plt.title('Missing Value Count by Feature', fontsize=14)
plt.xlabel('Number of Missing Values', fontsize=12)
plt.ylabel('Feature', fontsize=12)
plt.grid(axis="x", linestyle="--", alpha=0.7)
plt.show()
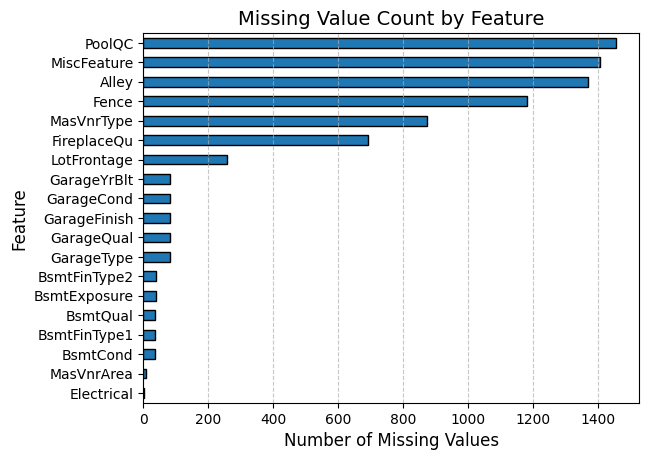
Hình 4. Biểu đồ thống kê dữ liệu bị thiếu của các đặc trưng
Biểu đồ ma trận tương quan dưới đây thể hiện mức độ tương quan giữa các biến số trong tập dữ liệu. Các giá trị tương quan được mã hóa bằng thang màu.
numerical_cols = df.drop('SalePrice', axis=1).dtypes[df.dtypes != 'object'].index.tolist()
selected_numerical_feature_cols = [x for x in numerical_cols + ['SalePrice'] if x not in missing[missing > 600].index.tolist()]
plt.figure(figsize=(10,8))
sns.heatmap(df[selected_numerical_feature_cols].corr(), annot=False, cmap='coolwarm')
plt.title('Correlation Heatmap of Numerical Features', fontsize=14)
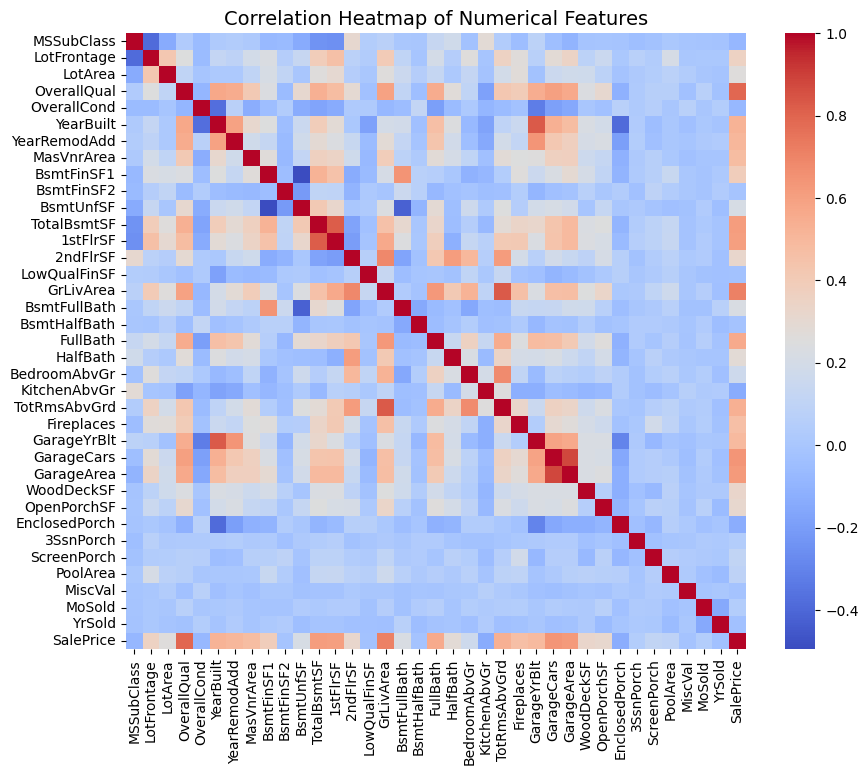
Hình 5. Biểu đồ ma trận tương quan giữa các biến số
Sau khi xác định các đặc trưng có tương quan cao với biến mục tiêu SalePrice, ta tiến hành biểu diễn qua biểu đồ hộp nhằm quan sát phạm vi giá trị, xu hướng phân phối và các giá trị ngoại lệ mỗi thuộc tính.
# Chọn 8 đặc trưng numeric quan trọng nhất dựa trên tương quan với SalePrice
important_cols = [
"OverallQual", "GrLivArea", "GarageCars", "GarageArea",
"TotalBsmtSF", "1stFlrSF", "FullBath", "YearBuilt"
]
fig, axes = plt.subplots(2, 4, figsize=(18, 8))
axes = axes.flatten()
for i, col in enumerate(important_cols):
sns.boxplot(data=house_df, y=col, ax=axes[i], color="skyblue")
axes[i].set_title(col, fontsize=12, fontweight="bold")
axes[i].tick_params(labelsize=9)
for i in range(len(important_cols), len(axes)):
axes[i].set_visible(False)
plt.suptitle("Boxplots of Top 8 Numerical Features", fontsize=16, fontweight="bold", y=1.03)
plt.tight_layout()
plt.show()

Hình 6. Biểu đồ hộp biểu diễn giá trị 8 đặc trưng có tương quan cao với giá nhà
3. Kết quả cải tiến
3.1. Tiền xử lý dữ liệu
Các hương pháp cải tiến được triển khai nhằm nâng cao độ chính xác và khả năng tổng quát của mô hình thông qua việc điều chỉnh các bước trong quy trình tiền xử lý dữ liệu. Các thay đổi tập trung vào việc xử lý dữ liệu thiếu, kiểm soát giá trị ngoại lai, chuẩn hoá phân phối và đảm bảo tính nhất quán giữa tập huấn luyện và kiểm tra.
Ban đầu, TA&STA điền giá trị thiếu bằng trung bình qua phương pháp SimpleImputer. Vì chỉ dựa vào thông tin đơn biến, không khai thác được mối tương quan giữa các đặc trưng.
Nhóm nghiên cứu thay thế bằng IterativeImputer, một kỹ thuật dự đoán giá trị thiếu dựa trên mô hình hồi quy đa biến. Phương pháp này lần lượt coi từng cột có giá trị thiếu như một biến mục tiêu và dự đoán nó từ các cột còn lại. Quá trình được lặp đi lặp lại cho đến khi hội tụ, nhờ đó duy trì được cấu trúc và mối quan hệ tự nhiên giữa các biến trong dữ liệu.
Tuy nhiên, IterativeImputer yêu cầu thời gian tính toán lớn hơn, đặc biệt khi dữ liệu có nhiều đặc trưng hoặc tỷ lệ giá trị thiếu cao. Do đó, cần chọn số vòng lặp hợp lý và theo dõi sự thay đổi của phân phối dữ liệu sau khi điền để đảm bảo ổn định.
from sklearn.model_selection import train_test_split
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
# create training and validation sets
train_df, test_df = train_test_split(
house_df,
test_size=0.25,
random_state=42
)
# Separate target variable (SalePrice) from features for both train and test sets
y_train = train_df["SalePrice"].values
y_test = test_df["SalePrice"].values
train_df = train_df.drop(["SalePrice"], axis=1)
test_df = test_df.drop(["SalePrice"], axis=1)
# Separate numeric and categorical columns from the training dataset
num_cols = [col for col in train_df.columns if train_df[col].dtype in ["float64","int64"]]
cat_cols = [col for col in train_df.columns if train_df[col].dtype not in ["float64","int64"]]
# fill none for categorical columns
train_df[cat_cols] = train_df[cat_cols].fillna("none")
test_df[cat_cols] = test_df[cat_cols].fillna("none")
from sklearn.preprocessing import OneHotEncoder
# One-hot encode categorical columns
encoder = OneHotEncoder(handle_unknown="ignore", sparse_output=False)
encoder.fit(train_df[cat_cols])
encoded_cols = list(encoder.get_feature_names_out(cat_cols))
train_df[encoded_cols] = encoder.transform(train_df[cat_cols])
test_df[encoded_cols] = encoder.transform(test_df[cat_cols])
# Create independent copies of train and test datasets for advanced preprocessing
train_adv, test_adv = train_df.copy(), test_df.copy()
# Impute missing numeric values using IterativeImputer
imputer_adv = IterativeImputer(random_state=42)
train_adv[num_cols] = imputer_adv.fit_transform(train_adv[num_cols])
test_adv[num_cols] = imputer_adv.transform(test_adv[num_cols])
Cách thức thực hiện ban đầu chưa có bước xử lý ngoại lai, khiến các giá trị ngoại lai dễ làm lệch trung bình và ảnh hưởng đến việc ước lượng tham số trong các mô hình tuyến tính.
Winsorization là một phương pháp xử lý giá trị ngoại lai bằng cách thay thế các giá trị ngoại lai bằng các giá trị ở ngưỡng nhất định, thay vì loại bỏ chúng hoàn toàn. Việc xác định ngưỡng thông qua phân vị hay IQR.
Cách thức hoạt động:
- Các giá trị nhỏ hơn phân vị thấp (5th percentile), thay thế bằng giá trị tại phân vị đó.
- Các giá trị lớn hơn phân vị cao (95th percentile), thay thế bằng giá trị tại phân vị đó.
- Các giá trị nằm trong khoảng giữa, giữ nguyên.
Phương pháp này giúp giữ lại cỡ mẫu và giảm ảnh hưởng của giá trị ngoại lai. Tuy nhiên, cần kiểm tra lại phân phối dữ liệu bằng boxplot hoặc histogram sau khi áp dụng để đảm bảo quá trình cắt ngưỡng không làm mất tính đa dạng tự nhiên của tập dữ liệu.
Các giá trị ngoại lai trong tập dữ liệu được giới hạn bằng Winsorization ở mức 1%–99%.
from scipy.stats.mstats import winsorize
# Apply winsorization to cap extreme outliers at the 1st and 99th percentiles
for col in num_cols:
train_adv[col] = winsorize(train_adv[col], limits=[0.01, 0.01])
TA&STA không áp dụng các phương pháp biến đổi cho các biến có độ lệch lớn. Một số biến như SalePrice, GrLivArea hay TotalBsmtSF có phân phối lệch phải, khiến mô hình tuyến tính khó học được mối quan hệ tuyến tính giữa biến đầu vào và đầu ra.
Khi dữ liệu lệch mạnh, đặc biệt ở biến mục tiêu hoặc các đặc trưng chính, Yeo–Johnson là một công cụ linh hoạt để làm giảm skewness, ổn định phương sai và đưa phân phối tiến gần phân phối chuẩn hơn — ngay cả khi có giá trị âm, điều mà log/Box–Cox không xử lý được. Điều này giúp mô hình tuyến tính hội tụ ổn định hơn và ước lượng sai số ít biến động hơn, đặc biệt khi dữ liệu ban đầu lệch mạnh.
from sklearn.preprocessing import StandardScaler, PowerTransformer
# Apply Yeo-Johnson power transformation to normalize feature distributions
pt = PowerTransformer(method="yeo-johnson")
train_adv[num_cols] = pt.fit_transform(train_adv[num_cols])
test_adv[num_cols] = pt.transform(test_adv[num_cols])
3.2. Biểu diễn đặc trưng có giám sát
Trong bài toán huấn luyện mô hình sử dụng đặc trưng đa thức (PolynomialFeatures) tùy ý tại bước 5 do TA&STA thực hiện (degree=2, interaction_only=True) đã gây ra quá khớp (overfitting). Dựa trên kết quả thực nghiệm, train $R^2$ = 0.98 nhưng Test $R^2$ chỉ còn 0.56 (Chi tiết tại mục 1.2). Điều này gây ra nổ chiều (Dimensional Explosion) và làm giảm hiệu suất của cả Ridge/Lasso so với khi không dùng đa thức.
Polynomial Features là kỹ thuật feature engineering tạo ra các đặc trưng phi tuyến từ các đặc trưng tuyến tính ban đầu. Mục đích là giúp các mô hình tuyến tính (Linear Regression, Logistic Regression) có thể học được các mối quan hệ phi tuyến phức tạp trong dữ liệu.
Giả sử biến đầu vào là x, mô hình hồi quy đa thức được mô tả như sau:
$$y = w_0 + w_1x + w_2x^2 + \cdots + w_nx^n + \epsilon$$
Trong đó ϵ là sai số ngẫu nhiên (noise). Khi bậc n tăng lên, mô hình có khả năng mô tả dữ liệu tốt hơn, nhưng đồng thời cũng có nguy cơ học quá kỹ dữ liệu huấn luyện (overfitting), khiến mô hình hoạt động kém trên dữ liệu mới. Vì vậy, việc lựa chọn bậc đa thức phù hợp là rất quan trọng để đạt được sự cân bằng giữa độ chính xác và khả năng tổng quát hóa.
Cách thức hoạt động:
-
Full polynomial (interaction_only=False): Tạo ra tất cả các kết hợp có thể từ các biến gốc, bao gồm cả việc nhân một biến với chính nó (lũy thừa) và nhân giữa các biến khác nhau (tương tác). Chính vì thế, không nên áp dụng nếu số lượng đặc trưng lớn so với dữ liệu hay quan hệ phi tuyến không rõ ràng.
-
Interaction only (interaction_only=True): Tạo ra các tích giữa các biến khác nhau, hoàn toàn loại bỏ việc nhân biến với chính nó. Cân nhắc việc áp dụng nếu quan tâm chính là tương tác giữa các biến.
Tập dữ liệu có 35 đặc trưng số sau khi tiền xử lý. Việc áp dụng degree=2 và interaction_only=True đã gây ra nổ chiều và quá khớp. Giả sử tăng bậc hay dùng full polynomial, số đặc trưng sẽ tăng vọt, làm tình trạng quá khớp trầm trọng hơn. Thay vì chọn bậc đa thức và tham số regularization ngẫu nhiên, ta dùng GridSearchCV để:
- Tìm kiếm có hệ thống trên một lưới tham số.
- Đánh giá bằng cross-validation để cân bằng giữa bias và variance.
- Chọn mô hình tối ưu dựa trên hiệu suất trung bình trên nhiều tập con dữ liệu.
# === 1. Định nghĩa lưới tham số ===
param_grid_ridge_lasso = {
'poly__degree': [1, 2, 3], # Dò bậc 1–2
'poly__interaction_only': [True, False],
}
param_grid_linear = {
'poly__degree': [1, 2, 3],
'poly__interaction_only': [True, False]
}
# === 2. Các model cần dò ===
models_to_tune = {
"Linear Regression": (LinearRegression(), param_grid_linear),
"Ridge": (Ridge(), param_grid_ridge_lasso),
"Lasso": (Lasso(), param_grid_ridge_lasso)
}
# === 3. Chạy GridSearchCV ===
results_data = []
print("\n--- BẮT ĐẦU DÒ BẬC & TỐI ƯU ---")
for name, (model, param_grid) in models_to_tune.items():
print(f"\nĐang tìm kiếm cho mô hình: {name}...")
# Tạo pipeline chỉ gồm PolynomialFeatures + Model
pipeline = Pipeline([
('poly', PolynomialFeatures(include_bias=False)),
('model', model)
])
grid_search = GridSearchCV(
pipeline,
param_grid=param_grid,
cv=5,
scoring='r2',
n_jobs=1,
verbose=1
)
grid_search.fit(X_train_adv, y_train)
# Lấy mô hình tốt nhất
best_model = grid_search.best_estimator_
# Dự đoán
y_train_pred = best_model.predict(X_train_adv)
y_test_pred = best_model.predict(X_test_adv)
# Metrics
train_rmse = np.sqrt(mean_squared_error(y_train, y_train_pred))
test_rmse = np.sqrt(mean_squared_error(y_test, y_test_pred))
train_r2 = r2_score(y_train, y_train_pred)
test_r2 = r2_score(y_test, y_test_pred)
print("=" * 60)
print(f"🔹 Mô hình: {name}")
print(f" - Cấu hình tốt nhất: {grid_search.best_params_}")
print(f" - R2 (CV) tốt nhất: {grid_search.best_score_:.4f}")
print(f" - Train RMSE: {train_rmse:.4f}")
print(f" - Test RMSE: {test_rmse:.4f}")
print(f" - Train R2: {train_r2:.4f}")
print(f" - Test R2: {test_r2:.4f}")
print("=" * 60)
Trong quá trình dò tìm tham số, GridSearchCV tối ưu các siêu tham số của bước PolynomialFeatures (degree và interaction_only). Với mỗi mô hình (Linear, Ridge, Lasso), ta tạo một Pipeline gồm PolynomialFeatures và mô hình. GridSearchCV chia dữ liệu train thành 5 folds, huấn luyện và đánh giá R² cho từng tổ hợp tham số. Sau khi thử hết, nó chọn ra cấu hình tốt nhất và huấn luyện lại trên toàn bộ tập train để tạo best_estimator_. Mô hình này sau đó được dùng để dự đoán và tính toán RMSE, R² trên tập huấn luyện và kiểm tra.
| STT | Model | Cấu hình tốt nhất | CV R² | Train RMSE | Train R² | Test RMSE | Test R² |
|---|---|---|---|---|---|---|---|
| 1 | Ridge | degree=1, interaction_only=True | 0.8166 | 22,589.82 | 0.9160 | 29,785.63 | 0.8734 |
| 2 | Lasso | degree=1, interaction_only=True | 0.8032 | 21,709.56 | 0.9224 | 30,442.75 | 0.8677 |
| 3 | Linear Regression | degree=2, interaction_only=False | 0.7952 | 0.00 | 1.0000 | 30,289.53 | 0.8690 |
Bảng 1. Kết quả biểu diễn đặc trưng có giám sát
Dựa trên thực nghiệm sau khi cải tiến tiền xử lý dữ liệu, ta không nên áp dụng hồi quy tuyến tính với đặc trưng đa thức vì:
- Linear Regression với bậc đa thức băng 2 bị quá khớp (Train R² = 1.0, nhưng CV R² thấp).
- Ridge và Lasso với đặc trưng tuyến tính cho kết quả tổng quát hóa tốt hơn (CV R² cao hơn). Trong đó, Ridge đạt Test R² cao nhất (0.8732) và CV R² cao nhất (0.8166).
3.3. Huấn luyện mô hình
Những mô hình dựa trên nền tảng hồi quy tuyến tính (Linear Regression-based models) được mở rộng và cải tiến trên nền Linear Regression để khắc phục những hạn chế của mô hình cơ bản.
Nhắc lại mô hình hồi quy tuyến tính cơ bản với mục tiêu tối thiểu hóa tổng bình phương sai số (MSE) giữa dự đoán và thực tế. Nhược điểm của mô hình này là dễ bị ảnh hưởng bởi dữ liệu ngoại lai (outlier) và dễ overfit nếu có nhiều đặc trưng hoặc các đặc trưng có quan hệ đa cộng tuyến (multicollinearity).
$$ min_{𝛃}\sum_{i=1}^n (y_i - \hat{y}_i)^2 $$
Dưới đây là các hướng mô hình mở rộng từ nền tảng Linear Regression
Linear Regression
│
├── Regularized models: Nhóm mô hình chống overfitting và xử lý đa cộng tuyến
│ ├── Ridge (L2)
│ ├── Lasso (L1)
│ └── ElasticNet (L1 + L2)
│
├── Robust models: Nhóm mô hình chống dữ liệu ngoại lai outlier
│ ├── Huber
│ ├── RANSAC
│ ├── Quantile
│ └── Theil–Sen
│
└── Extended models: Nhóm mô hình sử dụng các đặc trưng đa thức giúp mô hình học các quan hệ phi tuyến tính
├── Polynomial Regression
├── Stepwise Regression
└── Bayesian Ridge
Đặc biệt, hai nhóm Robust models và Extended models hoàn toàn có thể áp dụng thêm khoản phạt (penalty terms) L1 hoặc L2 hoặc kết hợp cả hai để giảm overfitting và ảnh hưởng của đa cộng tuyến. Trong Scikit-learn, HuberRegressor được hỗ trợ L2 và QuantileRegressor được hỗ trợ L1.
3.3.1. Lasso Regression
Lasso Regression (Least Absolute Shrinkage and Selection Operator) là một biến thể của Linear Regression có bổ sung thêm ràng buộc L1 regularization để giảm overfitting và chọn lọc đặc trưng tự động. Biểu diễn hàm mất mát như sau:
$$ J(\beta)=\sum_{i=1}^{n}(y_i-\hat{y_i})^2+\lambda \sum_{j=1}^{p}|\beta_{j}| $$
trong đó:
* $(y_i-\hat{y_i})^2$ là hàm tính lỗi dự đoán bình phương của Linear Regression
* $\lambda \sum|\beta_{j}|$ là thành phần phạt L1 (L1 regularization term)
* $\lambda$ là siêu tham số điều chỉnh độ mạnh của ràng buộc. $\lambda$ càng lớn thì mô hình càng phạt nặng khi có trọng số $\beta_{j}$ lớn khiến cho $\beta_{j}$ bị ép về 0.
Lasso thêm điều kiện phạt để kiểm soát độ phức tạp của mô hình bằng cách ép các trọng số $\beta_{j}$ không cần thiết phải nhỏ lại hoặc bằng 0, làm mô hình đơn giản hơn, ít nhạy với nhiễu. Những đặc trưng tương ứng với $\beta_{j} = 0$ bị loại khỏi mô hình và các đặc trưng còn lại ($\beta_{j} \neq 0$) là những đặc trưng quan trọng nhất cho dự đoán.
3.3.2. Ridge Regression
Ridge Regression (còn gọi là L2 Regularized Linear Regression) là một mở rộng của Linear Regression có bổ sung thêm ràng buộc L2 regularization được thiết kế để (i) giảm overfitting, (ii) xử lý trường hợp đa cộng tuyến của các đặc trưng có tương quan cao và (iii) ổn định trọng số của mô hình. Biểu diễn hàm mất mát như sau:
$$ J(\beta)=\sum_{i=1}^{n}(y_i-\hat{y_i})^2+\lambda \sum_{j=1}^{p}\beta_{j}^2 $$
trong đó:
* $(y_i-\hat{y_i})^2$ là hàm tính lỗi dự đoán bình phương của Linear Regression
* $\lambda \sum \beta_{j}^2$ là thành phần phạt L2 (L2 regularization term)
* $\lambda$ là siêu tham số điều chỉnh độ mạnh của ràng buộc.
Với mô hình hồi quy tuyến tính thông thường, hàm mục tiêu là $(y_i-\hat{y_i})^2$. Thành phần $\lambda \sum_{j}\beta_{j}^2$ phạt trọng số lớn buộc mô hình phải giữ các hệ số nhỏ.
3.3.3. ElasticNet Regression
ElasticNet Regression là một mô hình hồi quy tuyến tính có regularization kép (cả L1 và L2). Do đó nó có thể tận dụng ưu điểm của cả 2 thành phần phạt. ElasticNet có thể giúp mô hình tránh overfitting, giữ khả năng chọn đặc trưng của Lasso và ổn định hơn trong trường hợp các đặc trưng có tương quan cao như Ridge. Biểu diễn hàm mất mát như sau:
$$ J(\beta)=\frac{1}{2n} \sum_{i=1}^{n}(y_i-\hat{y_i})^2+\lambda [ \alpha \sum_{j=1}^{p}|\beta_{j}| + \frac{1-\alpha}{2}\sum_{j=1}^{p}\beta_{j}^2 ] $$
Trong đó:
- $\lambda$ là hệ số điều khiển độ phạt tổng thể
- $\alpha$ là hệ số điều chỉnh tỉ lệ giữa L1 và L2
3.3.4. Huber Regression
Huber Regression là một mô hình mở rộng từ Linear Regression truyền thống, được thiết kế đặc biệt để chống lại ảnh hưởng của dữ liệu ngoại lai mà vẫn giữ được tính hiệu quả cao. Hàm mất mát Huber Loss kết hợp ưu điểm của MSE và MAE. Biểu diễn hàm mất mát như sau:
$$ L_{\delta}(r) = \begin{cases} \frac{1}{2}r^2, & \text{nếu } |r| \leq \delta \\[6pt] \delta (|r|-\frac{1}{2}\delta), & \text{nếu } |r| > \delta \\[6pt] \end{cases} $$
Trong đó:
- $r=y_i-\hat{y_i}$ là sai số dự đoán
- $delta$ là ngưỡng để xác định khi nào chuyển đổi từ MSE sang MAE
Khi sai số dự đoán nhỏ, mô hình hoạt động như MSE để giữ độ mượt. Khi sai số lớn, mô hình sử dụng trị tuyệt đối sai số để giảm tác động của dữ liệu ngoại lai.
3.3.5. Quantile Regression
Quantile Regression là một kỹ thuật mạnh mẽ để mô hình hóa phân vị (quantile) của biến mục tiêu thay vì chỉ trung bình (mean).
Mô hình hồi quy tuyến tính cơ bản có mục tiêu là tìm đường hồi quy sao cho MSE nhỏ nhất. Do đó, mô hình dễ bị ảnh hưởng mạnh bởi outlier và chỉ mô tả xu hướng trung tâm.
Trong khi đó, Quantile Regression có mục tiêu là tìm đường hồi quy sao cho quantile q của phân phối điều kiện $y|\mathbf{X}$ được mô tả chính xác. Điều này giúp mô hình hiểu toàn bộ phân phối của y, chứ không chỉ trung bình. Biểu diễn hàm mất mát như sau:
$$ L_q(r) = \begin{cases} qr, & \text{nếu } r \leq 0 \\[6pt] (q-1)r, & \text{nếu } r > 0 \\[6pt] \end{cases} $$
trong đó $r=y-\hat{y}$
Với quantile 0.5 (trung vị), hàm mất mát giống MAE (đối xứng). Với quantile khác, mất mát lệch, khiến mô hình dự đoán lệch lên/xuống tương ứng với phân vị.
3.3.6. RANSAC Regression
RANSAC là viết tắt của RANdom SAmple Consensus — một thuật toán lặp ngẫu nhiên được thiết kế để tìm mô hình tốt nhất trong dữ liệu nhiễu, bằng cách tập trung vào inliers (dữ liệu hợp lý) và bỏ qua giá trị ngoại lai.
Giả sử tập dữ liệu $D$ gồm các điểm (x, y), nhưng một số điểm bị lỗi hoặc nhiễu rất mạnh. RANSAC hoạt động như sau:
-
Lặp nhiều lần
- Ngẫu nhiên chọn một mẫu nhỏ các điểm từ $D$.
- Huấn luyện mô hình chỉ trên các điểm đó.
- Tính sai số giữa mô hình và toàn bộ dữ liệu.
- Xác định inliers — những điểm có sai số nhỏ hơn ngưỡng.
-
Chọn mô hình có nhiều inliers nhất.
- Huấn luyện lại mô hình cuối cùng chỉ trên tập inliers này.
Tóm lại, RANSAC từ chối học từ dữ liệu nhiễu, chỉ tập trung vào phần dữ liệu mà nó cho là đáng tin cậy.
# Ridge, Lasso, ElasticNet
alphas = np.logspace(-3, 2, 6) # [0.001, 0.01, 0.1, 1, 10, 100]
ridge_grid = {
"model": [Ridge()],
"model__alpha": alphas
}
lasso_grid = {
"model": [Lasso()],
"model__alpha": alphas
}
enet_grid = {
"model": [ElasticNet()],
"model__alpha": alphas,
"model__l1_ratio": [0.2, 0.5, 0.8, 1.0]
}
Đầu tiên chúng ta định nghĩa hệ số theo thang log cho ba model để ổn định hóa hệ số và giảm overfitting bằng GridSearchCV trên tham số α theo thang log từ 0.001 đến 100. Với ElasticNet, thêm tham số l1_ratio được dò để cân bằng giữa L1 và L2, giúp vừa chọn biến vừa ổn định hóa hệ số. Quá trình này đảm bảo mô hình đạt hiệu quả dự đoán cao và khả năng khái quát tốt trên dữ liệu.
# Huber, Quantile,RANSAC,XGBoost
huber_grid = {
"model": [HuberRegressor()],
"model__alpha": [0.0001, 0.001, 0.01, 0.1],
"model__epsilon": [1.1, 1.35, 1.5, 2.0]
}
quantile_grid = {
"model": [QuantileRegressor(solver="highs")],
"model__alpha": [0.001, 0.01, 0.1],
"model__quantile": [0.25, 0.5, 0.75]
}
ransac_grid = {
"model": [RANSACRegressor(random_state=42)],
"model__min_samples": [0.5, 0.7, 0.9, None],
"model__residual_threshold": [1.0, 2.0, 5.0, None]
}
xgb_grid = {
"model": [XGBRegressor(
objective="reg:squarederror",
random_state=42,
n_jobs=-1,
tree_method="hist"
)],
"model__n_estimators": [100, 300, 500],
"model__max_depth": [3, 5, 7],
"model__learning_rate": [0.01, 0.05, 0.1],
"model__subsample": [0.8, 1.0],
"model__colsample_bytree": [0.8, 1.0]
}
Áp dụng thêm các robust regression – các mô hình này được thiết kế để giảm ảnh hưởng của ngoại lai (outliers) và các điểm dữ liệu bất thường trong quá trình huấn luyện, giúp mô hình dự đoán ổn định hơn trên dữ liệu thực tế. Bên cạnh đó, XGBoost cũng được bổ sung như một mô hình boosting mạnh mẽ, có khả năng xử lý dữ liệu phi tuyến và cải thiện hiệu năng dự đoán.
# Tạo pipeline chung và metrics
cv = KFold(n_splits=5, shuffle=True, random_state=42)
# Tạo scoring mreics
scoring = {
"RMSE": make_scorer(root_mean_squared_error, greater_is_better=False),
"R2": make_scorer(r2_score)
}
model_grids = [
("Ridge", ridge_grid),
("Lasso", lasso_grid),
("ElasticNet", enet_grid),
("Huber", huber_grid),
("QuantileRegressor", quantile_grid),
("RANSAC", ransac_grid),
("XGBoost", xgb_grid)
]
results = []
base_pipe = Pipeline([("model", Ridge())])
for name, grid in model_grids:
# Tạo GridSearchCV với KFold
search = GridSearchCV(
base_pipe, grid, scoring=scoring, cv=cv,
n_jobs=-1, refit="R2"
)
search.fit(X_train_adv, y_train)
# Lấy model tốt nhất
best_model = search.best_estimator_
# Dự đoán trên tập train và test
y_train_pred = best_model.predict(X_train_adv)
y_test_pred = best_model.predict(X_test_adv)
# Metrics
train_rmse = root_mean_squared_error(y_train, y_train_pred)
train_r2 = r2_score(y_train, y_train_pred)
test_rmse = root_mean_squared_error(y_test, y_test_pred)
test_r2 = r2_score(y_test, y_test_pred)
# Lưu lại kết quả
results.append({
"Model": name,
"BestParams": search.best_params_,
"CV R2 (GridSearch)": search.best_score_,
"Train RMSE": train_rmse,
"Train R2": train_r2,
"Test RMSE": test_rmse,
"Test R2": test_r2
})
searched_results = pd.DataFrame(results).sort_values("Test R2", ascending=False)
searched_results
Sau khi định nghĩa các lưới tham số cho từng mô hình, bổ sung robust regression và XGBoost, quá trình GridSearchCV với K-Fold được thực hiện trên từng mô hình để tìm ra cấu hình tối ưu nhất dựa trên chỉ số R². Mỗi mô hình tốt nhất sau khi tối ưu được sử dụng để dự đoán trên cả tập huấn luyện và tập kiểm tra, từ đó tính các chỉ số RMSE và R² nhằm đánh giá hiệu quả dự đoán và khả năng khái quát hóa.
4. Kết luận
| STT | Model | Best Params | CV R² | Train RMSE | Train R² | Test RMSE | Test R² |
|---|---|---|---|---|---|---|---|
| 1 | XGBoost | lr=0.05, depth=3, n=500, subsample=0.8, colsample=0.8 | 0.8645 | 9,012.71 | 0.9866 | 23,878.80 | 0.9186 |
| 2 | Lasso | α = 100.0 | 0.8401 | 23,985.56 | 0.9052 | 28,594.99 | 0.8833 |
| 3 | ElasticNet | α = 100.0, l1_ratio = 0.5 | 0.8401 | 23,985.56 | 0.9052 | 28,594.99 | 0.8833 |
| 4 | QuantileRegressor | α = 0.01, quantile = 0.5 | 0.8492 | 27,760.68 | 0.8731 | 29,586.60 | 0.8750 |
| 5 | Ridge | α = 10.0 | 0.8376 | 24,740.93 | 0.8992 | 29,651.29 | 0.8745 |
| 6 | Huber | α = 0.0001, ε = 1.35 | 0.8489 | 27,244.26 | 0.8777 | 29,774.11 | 0.8735 |
| 7 | RANSAC | min_samples = 0.5 | 0.6901 | 52,711.81 | 0.5424 | 58,786.79 | 0.5067 |
Bảng 2. Kết quả huấn luyện sau tối ưu hóa Regularization
Từ kết quả huấn luyện, ta rút ra kết luận như sau:
-
XGBoost là mô hình tốt nhất với R² đạt 91.86% trên tập kiểm tra (+1.86% so với baseline ban đầu) và RMSE giảm đáng kể, đạt độ chính xác cao và khái quát tốt. Tuy nhiên, cân nhắc điều chỉnh thêm tham số regularization (lambda, alpha) để giảm tình trạng quá khớp để đảm bảo mô hình bền vững khi triển khai thực tế.
-
Các mô hình hồi quy tuyến tính và robust regression nhìn chung có train–test gap nhỏ hơn baseline, thể hiện khả năng tổng quát hóa ổn định hơn, dù hiệu suất dự đoán kém hơn XGBoost.
-
Lasso và ElasticNet với α = 100 (regularization mạnh) cải thiện R² trên tập kiểm tra lên 88.33% so với 87.34% ở giai đoạn biểu diễn đặc trưng có giám sát.
Chưa có bình luận nào. Hãy là người đầu tiên!