Trong các mô hình machine learning — như là dự đoán giá nhà, dự báo thời tiết hay tính toán xu hướng chứng khoán — đều cần tính tự động hóa cũng như những các điều chỉnh các thiết lập bên trong mô hình (được biết đến là tham số (parameters), mục đích là để cải thiện độ chính xác.
Một trong những công cụ toán học có thể hỗ trợ quá trình biến hóa tối ưu ưu liên tục này chính là Đạo hàm (Derivative).
Đạo hàm là gì?
Nói đơn giản, đạo hàm được sử dụng để đo độ dốc của một hàm số tại một điểm cụ thể — tức là độ dốc hoặc tốc độ thay đổi của hàm số.
Có thể hiểu nó giống như khi bạn đang đi bộ trên một con dốc: đạo hàm cho bạn biết độ dốc của con đường ngay dưới chân bạn.
Tóm tắt :
Đạo hàm cho biết mức độ nhạy cảm của đầu ra (output) của hàm đối với thay đổi nhỏ ở đầu vào (input) — và hướng thay đổi đó là đi lên hay đi xuống.
Đạo hàm đóng vai trò gì trong Machine Learning
Trong machine learning, đạo hàm được dùng để tối thiểu hóa Hàm mất mát (Loss Function) — thước đo cho biết mô hình dự đoán sai lệch bao nhiêu.
Với mục tiêu là điều chỉnh các tham số sao cho giá trị loss nhỏ nhất có thể.
1. Đo lường độ nhạy và hướng thay đổi
Đạo hàm hoạt động như một “cảm biến”, cho biết đầu ra của mô hình thay đổi thế nào khi ta thay đổi các tham số của nó.
| Điều đạo hàm cho biết | Ví dụ minh họa : bịt mắt trên đồi |
|---|---|
| Độ nhạy (Sensitivity) | Độ dốc của mặt đất — giá trị lớn nghĩa là loss thay đổi nhiều. |
| Hướng đi (Direction) | Hướng đi xuống dốc — nơi loss giảm nhanh nhất. |
2. Tính Gradient cho nhiều tham số
Một mô hình thường có nhiều tham số cần điều chỉnh cùng lúc. Để xử lý điều này, ta dùng gradient — một vector mở rộng khái niệm đạo hàm sang nhiều chiều.
Gradient liệt kê đạo hàm cho mọi tham số và cho mô hình biết:
- Mỗi tham số nên di chuyển theo hướng nào
- Nó nên di chuyển bao nhiêu
Nhiệm vụ của nó là hướng dẫn mô hình điều chỉnh tất cả các tham số cùng nhau để giảm thiểu tổn thất (loss) tổng thể.
3. Thuật toán Gradient Descent
Vai trò quan trọng nhất của đạo hàm là trong Gradient Descent — thuật toán cốt lõi giúp mô hình học.
Nguyên tắc vàng khi sử dụng:
Để giảm loss (điểm cực tiểu hoặc có thể hiểu là đáy của đạo hàm), hãy luôn di chuyển ngược hướng của gradient.
| Giá trị Gradient | Ý nghĩa (Hình dạng địa hình) | Hành động của mô hình |
|---|---|---|
| Dương (lên dốc) | Loss tăng khi tham số tăng | Giảm giá trị tham số |
| Âm (xuống dốc) | Loss giảm khi tham số tăng | Tăng giá trị tham số |
Khi quá trình này lặp đi lặp lại — mô hình “bước” dần xuống vùng thấp nhất của đồ thị loss, cho đến khi đạt điểm thấp nhất (tối ưu nhất).
Tối ưu hóa cùng đạo hàm
Khái niệm :
Trong Machine Learning, tối ưu hóa là việc tìm ra nghiệm tốt nhất — tức là chi phí (loss) thấp nhất hoặc phần thưởng cao nhất.
Điều này giống như khi bạn bịt mắt và phải tìm đáy của một cái chén — bạn không nhìn thấy gì, nhưng có một “hướng dẫn viên” giúp bạn. Người đó chính là đạo hàm.
Đạo hàm – Chiếc la bàn của sự thay đổi
Đạo hàm giống như một chiếc la bàn thông minh. Nó cho bạn biết hai điều:
1. Hướng di chuyển: dốc đi lên (dương) hay đi xuống (âm)?
2. Độ dốc: bạn đang ở sườn núi thoai thoải hay vách đá đứng?
Ví dụ:
Cho một hàm phổ biến là : f(x) = x²
Thì nó sẽ tạo thành một parabol hình chữ U, có điểm thấp nhất tại x = 0.
Đạo hàm: sẽ là f'(x) = 2x
| Vị trí hiện tại (x) | f′(x) | Ý nghĩa & Hành động |
|---|---|---|
| x = 5 | +10 | Dốc lên cao → đi sang trái, bước lớn |
| x = 1 | +2 | Dốc nhẹ → đi sang trái, bước nhỏ |
| x = 0 | 0 | Bằng phẳng → đã đến đáy, dừng lại |
| x = -3 | -6 | Xuống dốc → đi sang phải, bước lớn |
Ý tưởng chính: Đạo hàm luôn chỉ bạn về hướng cực tiểu, và cho biết nên đi nhanh hay chậm.
Gradient Descent: Hành trình tìm vị trí cực tiểu
Giờ đây khi đã biết đạo hàm cho chúng ta biết phương hướng như thế nào, chúng ta có thể dùng nó để lặp đi lặp lại nhằm đạt đến điểm cực tiểu
Công thức sử dụng:
$$x_{\text{new}} = x_{\text{old}} - η \times f'(x)$$
Trong đó η (eta) là tốc độ học (learning rate) — quyết định độ lớn của mỗi bước.
Ví dụ: Ta có x₀ = 70, η = 0.1
Mỗi bước, x tiến gần về 0 hơn, và khi đạo hàm nhỏ dần, bước đi cũng nhỏ dần — giúp mô hình chậm lại tự nhiên khi tới điểm cực tiểu.
Tốc độ học – chọn bước đi “vừa đủ”
| Learning Rate (η) | Ví dụ | Kết quả |
|---|---|---|
| Quá nhỏ (0.001) | 🐜 Bước kiến — đi 1 cm mỗi lần | Rất chậm, tốn thời gian |
| Vừa đủ (0.1) | 🚶 Bước đều đặn, tự tin | Tiến nhanh, ổn định |
| Quá lớn (1.1) | 🤸 Nhảy quá xa | Vượt qua cực tiểu, dao động mãi |
=>Bài học: tốc độ học cần phải “vừa phải” — không nên quá nhanh để bỏ lỡ, không nên quá chậm để lãng phí thời gian.
Như thế nào là một Hàm Mất Mát (Loss function) “tốt”?
Để Gradient Descent hoạt động tốt, Hàm Mất Mát cần phải “trơn tru”.
| Loại | Ví dụ | Đặc điểm |
|---|---|---|
| ✅ Tốt | f(x) = x² | Mịn như chiếc bát → đạo hàm tồn tại khắp nơi |
| ⚠️ Khó | f(x) = giá trị tuyệt đối của x | Không trơn tại x = 0 — độ dốc (slope) đột ngột đổi hướng → đạo hàm không xác định tại đúng điểm đó. |
| ❌ Xấu | Step function | Mất tính liên tục, đạo hàm không tồn tại |
Nếu Hàm Mất Mát chạy mượt mà, “la bàn đạo hàm” sẽ dẫn bạn chính xác đến đáy.
Vấn đề với các góc nhọn (MAE vs. MSE)
Bây giờ chúng ta hãy xem tại sao một số hàm mất mát (loss functions) lại khó tối ưu hơn những hàm khác.
Lấy Sai số Tuyệt đối Trung bình (Mean Absolute Error - MAE) làm ví dụ, nó có hình dạng giống chữ 'V' — sắc và nhọn ở đáy.
f(x) = |x|
Nếu:
- x > 0 → f′(x) = 1
- x < 0 → f′(x) = −1
- x = 0 → không xác định
➡ Dốc luôn không đổi → bước nhảy không giảm → khó dừng đúng tại điểm thấp nhất.
Như vậy nghĩa là vị trí x dù có đang ở xa (x = 100) hay ở gần (x = 0.1), độ dốc (slope) vẫn luôn giữ nguyên độ dốc ($\pm 1$).
Có thể hiểu là bước chân của bạn không bao giờ chậm lại — dù khoảng cách ngay tại điểm nhọn có gần đi chăng nữa và cứ tiếp tục thực hiện các bước đi đều đặn, và điều này khiến cho khó khăn khi tiếp cận đến điểm cực tiểu.
Và ngược lại:
Sai số Bình phương Trung bình (Mean Squared Error - MSE) có thể tạo ra một cái chén trơn tru.
Khi tiến gần đến điểm cực tiểu , đạo hàm sẽ ngày càng nhỏ đi, cho phép các bước chân của bạn tự động thu nhỏ lại — điều này đảm bảo sự hội tụ ổn định và chính xác.
Tổng kết ý chính
- Tối ưu hóa : Tìm điểm thấp nhất trên một "cảnh quan" (landscape).
- Đạo hàm: Chiếc la bàn cho bạn biết nên di chuyển theo hướng nào.
- Gradient Descent : Chiến lược tuân theo la bàn đó, từng bước một.
- Tốc độ học : Nút điều chỉnh tốc độ di chuyển của bạn.
- Hàm mất mát (Loss Function) :Địa hình quyết định hành trình của bạn sẽ trơn tru hay gồ ghề.
Khi tất cả các yếu tố này hoạt động hài hòa, thì ta sẽ có được trái tim của mọi thuật toán machine learning — một hệ thống học hỏi bằng cách đi xuống dốc về phía giải pháp tối ưu.
Tối ưu hóa trong thực tế
Tối ưu hóa 1 chiều (1 Dimention - 1D)
Trong tối ưu hóa dựa trên Gradient (như Gradient Descent), chúng ta sẽ bắt đầu tại một điểm khởi tạo $x$. Và sử dụng đạo hàm (hoặc gradient) của hàm số, để chỉ ra hướng lên dốc nhất. Bằng cách di chuyển theo hướng ngược lại của đạo hàm, chúng ta lặp đi lặp lại việc cập nhật $x$ để tìm ra giá trị cực tiểu (điểm thấp nhất) của hàm số.
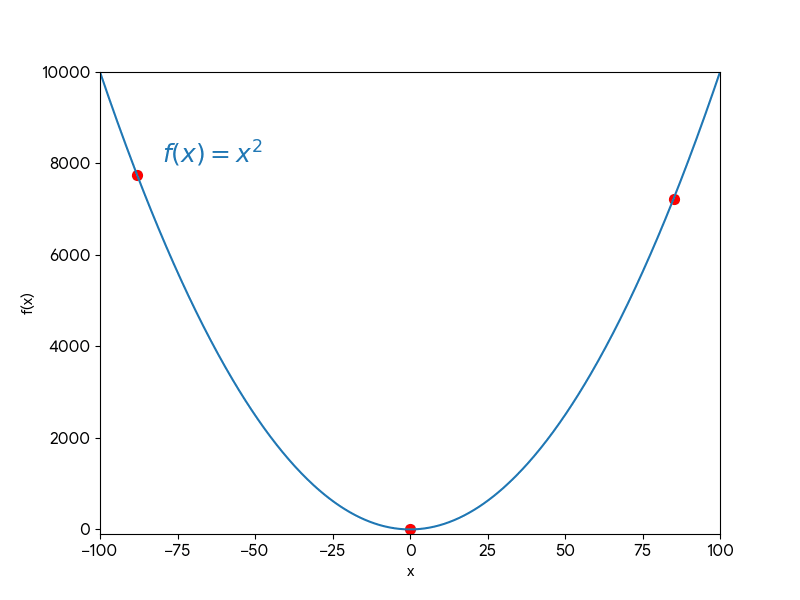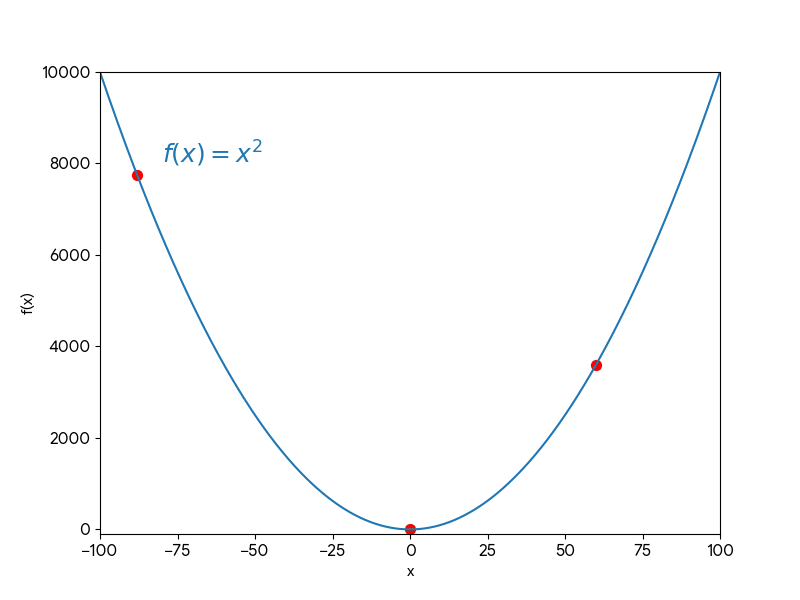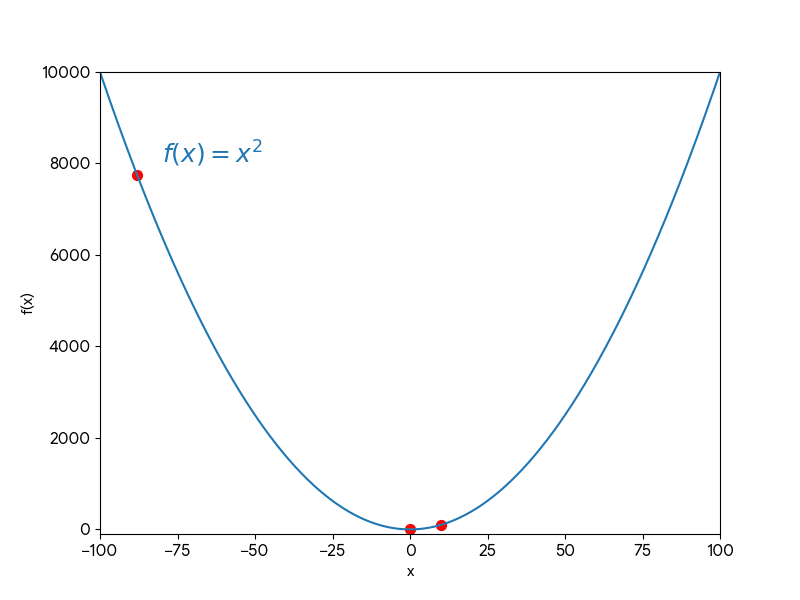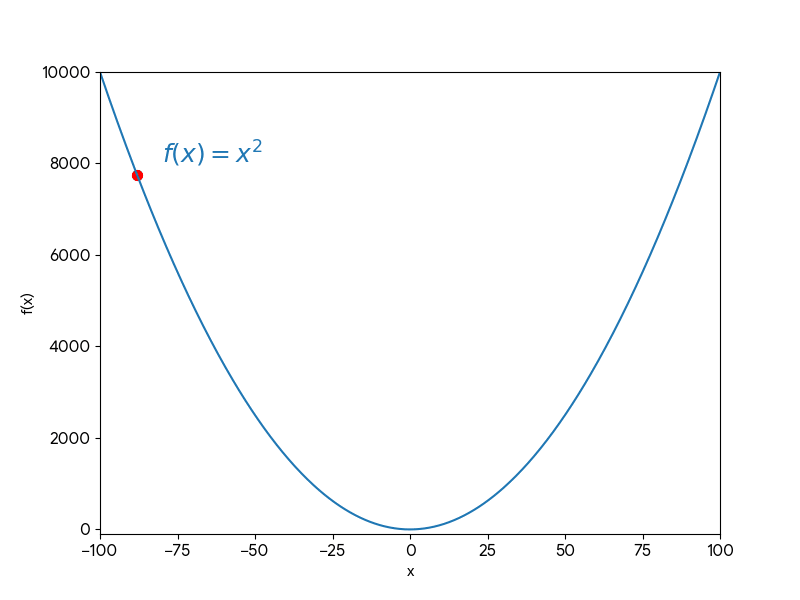
Ví dụ:
Mục tiêu của Giảm đạo hàm (Gradient Descent) là tìm giá trị của $x$ để tối thiểu hóa $f(x)$, đó là $x=0$ đối với hàm $f(x)=x^2$.
1. Thiết lập
- Hàm số ($f(x)=x^2$): Hàm mà chúng ta muốn tối thiểu hóa.
- Điểm Khởi tạo ($x_0=70$): Chúng ta bắt đầu ở rất xa điểm cực tiểu.
- Tốc độ Học (Learning Rate) ($\eta=0.1$): Đại lượng kiểm soát kích thước của mỗi bước.
2. Công thức áp dụng
Sử dụng công thức cho Gradient Descent là:
$$x_{\text{new}} = x_{\text{old}} - η \times f'(x)$$
Đầu tiên, chúng ta có đạo hàm của $f(x)=x^2$ và $f'(x)=2x$
3. Bước đầu tiên (Bước Lớn)
- Bắt đầu: $x_0=70$.
- Đạo hàm: $f'(70)=2(70)=140$. (Độ dốc dương lớn)
- $x$ mới ($x_1$):
$$x\_1=70−0.1⋅(140)=70−14=56$$
Như vậy Bước đầu tiên dài 14 đơn vị.
4. Hành trình tiếp diễn (Các Bước Thu Nhỏ)
Khi quá trình này lặp lại, $x$ tiến gần hơn đến $0$.
-
Bước Tiếp theo (cho $x \approx 5.6$):
- Đạo hàm: $f'(5.6)=2(5.6)=11.2$.
- Kích thước Bước: $\eta \cdot f'(x)=0.1 \cdot 11.2=1.12$.
- Kích thước bước đã nhỏ hơn nhiều.
-
Gần Điểm Cực Tiểu ($x \approx 0.7$):
- Đạo hàm: $f'(0.7)=2(0.7)=1.4$.
- Kích thước Bước: $\eta \cdot f'(x)=0.1 \cdot 1.4=0.14$.
- Kích thước bước đã thu nhỏ đáng kể.
Tại sao đây là các bước đi "Tuyệt vời"
Các bước này được cho là "Tuyệt vời" vì kích thước bước chân tỷ lệ thuận với đạo hàm $f'(x)$.
$$\text{Kích thước Bước} = \eta \cdot |f'(x)|$$
Khi $x$ ở xa điểm cực tiểu (như $x=70$), độ dốc $f'(x)$ lớn, dẫn đến một bước nhảy lớn để nhanh chóng tiếp cận điểm cực tiểu.
* Khi $x$ ở gần điểm cực tiểu (như $x=0$), độ dốc $f'(x)$ gần như bằng $0$ ($f'(0)=0$), và tạo nên một bước nhỏ giúp quá trình giảm tốc độ một cách tự nhiên và ngăn ngừa việc nhảy vượt qua* điểm cực tiểu.
Tối ưu hóa trong 2 chiều (2 Dimentions - 2D)
Cho đến nay, chúng ta đã thấy cách tối ưu hóa hoạt động trong một chiều, với một hàm đơn giản như $f(x) = x^2$. Tuy nhiên, thực tế các bài toán machine leraning hiếm khi chỉ có một tham số. Chúng thường liên quan đến hàng nghìn hoặc thậm chí hàng tỷ tham số.
Bây giờ, chúng ta hãy mở rộng ý tưởng tương tự đó sang đa chiều (multiple dimensions)
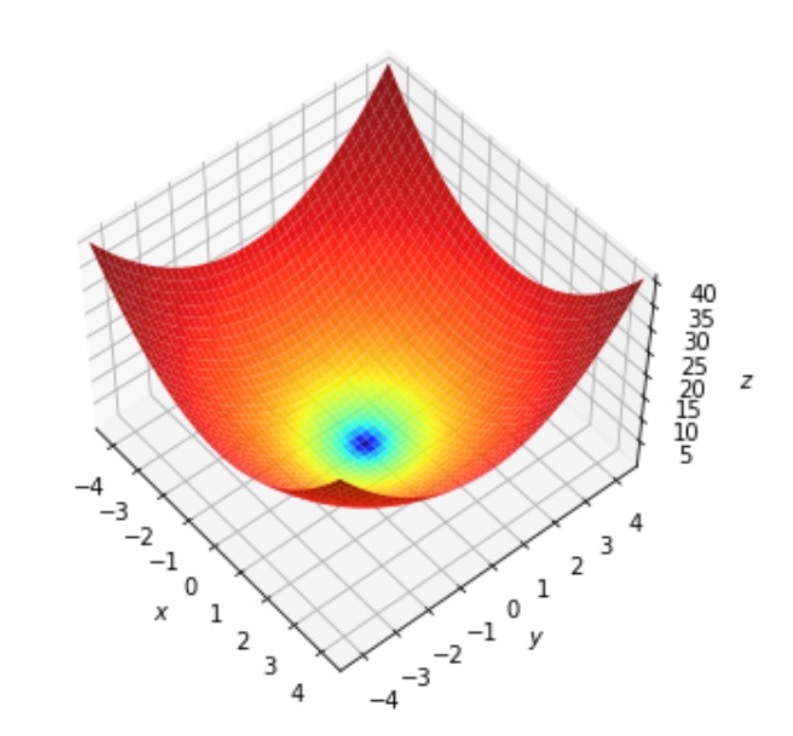
1. Hàm số và Hình học của nó
Hãy lấy một ví dụ đơn giản trong không gian hai chiều:
$$f(x, y) = x^2 + y^2$$
📐 Hình học:
Hàm này tạo thành một bề mặt có hình dạng cái chén trong không gian 3D, được gọi là mặt paraboloid.
-
Không gian đầu vào là mặt phẳng 2D (trục $x$ và $y$).
-
Đầu ra $f(x, y)$ là chiều cao của bề mặt so với mặt phẳng đó.
Và mục tiêu sẽ là :
👉 Tìm điểm thấp nhất trên bề mặt này — đáy của cái chén — tại (x,y)=(0,0). Đó là điểm cực tiểu của chúng ta.
2. Gradient: Đạo hàm trong Đa chiều
Trong một chiều, đạo hàm cho chúng ta biết hàm số dốc lên hay dốc xuống bao nhiêu khi chúng ta di chuyển dọc theo $x$.
Trong nhiều chiều, chúng ta sẽ sử dụng gradient, viết là $\nabla f$ ("nabla f").
Gradient là một vectơ — nó chứa độ dốc cho từng hướng di chuyển.
| Đạo hàm Riêng phần | Ý nghĩa |
|---|---|
| $\frac{∂f}{∂x} = 2x$ | Độ dốc là bao nhiêu nếu chúng ta chỉ di chuyển theo hướng $x$ |
| $\frac{∂f}{∂y} = 2y$ | Độ dốc là bao nhiêu nếu chúng ta chỉ di chuyển theo hướng $y$ |
Mỗi một đạo hàm từng chiều cho chúng ta biết việc thay đổi một biến số đó (trong khi giữ các biến khác không đổi) ảnh hưởng đến giá trị của hàm như thế nào.
=> Kết hợp lại, chúng tạo thành vectơ gradient:
$$\nabla f(x, y) = [2x, 2y]$$
Gradient luôn chỉ theo hướng lên dốc — hướng tăng dốc nhất. Để tối thiểu hóa hàm số, chúng ta di chuyển theo hướng ngược lại.
3. Quy tắc Cập nhật: Di chuyển đúng Hướng
Giống như trong giảm đạo hàm 1D, chúng ta cũng thiết lặp sự lặp đi lặp lại việc cập nhật các biến — nhưng bây giờ sẽ áp dụng cho cả $x$ và $y$:
$$x_{\text{mới}} = x_{\text{cũ}} - \eta \frac{∂f}{∂x}$$
$$y_{\text{mới}} = y_{\text{cũ}} - \eta \frac{∂f}{∂y}$$
Trong đó:
- $\eta$ (eta) = tốc độ học (learning rate)
- $\frac{∂f}{∂x}$, $\frac{∂f}{∂y}$ = các đạo hàm riêng phần
Ví dụ: ta có (x0,y0)=(6,9) và η=0.1
$$x_{\text{mới}} = 6 - 0.1 \times (2 \times 6) = 6 - 1.2 = 4.8$$
$$y_{\text{mới}} = 9 - 0.1 \times (2 \times 9) = 9 - 1.8 = 7.2$$
=> Vị trí mới: $(4.8, 7.2)$ — một bước trơn tru tiến gần hơn đến $(0, 0)$, điểm cực tiểu.
Mở Rộng sang machine learning
Ý tưởng chính xác này là mở rộng một cách liền mạch từ 2 tham số lên tới 2 triệu, hoặc thậm chí 2 tỷ tham số.
Trong machine learning:
-
Các tham số chính là các trọng số (weights) và độ lệch (biases) của mô hình.
-
Hàm tổn thất (Loss function) là hàm $f(x, y, \ldots)$ của bạn — nó đo lường mức độ sai lệch giữa dự đoán của mô hình so với giá trị thực.
-
Gradient chứa đạo hàm riêng phần của hàm tổn thất theo từng tham số.
Trong quá trình huấn luyện (training):
-
Tính toán gradient cho mọi tham số.
-
Di chuyển từng tham số theo hướng ngược lại của gradient của nó.
-
Lặp lại cho đến khi hàm tổn thất không thể nhỏ hơn nhiều nữa.
Đó là cách các mạng nơ-ron hiện đại — với hàng tỷ tham số — học từ dữ liệu. Mỗi trọng số đều nhận được một "cú đẩy" nhỏ bé, và được hướng dẫn bởi độ dốc cục bộ của nó trong "cảnh quan tổn thất".
Chú ý:
Giảm đạo hàm (Gradient Descent) không phụ thuộc vào số chiều.
Dù cho có 2 tham số hay 2 tỷ tham số, nguyên tắc vẫn là hoàn toàn giống nhau
Điều chỉnh mỗi tham số theo chiều giúp giảm thiểu tổn thất.
Quy tắc đơn giản và thanh lịch này cung cấp năng lượng cho hầu hết mọi mô hình trong AI hiện đại — từ hồi quy tuyến tính (linear regression) cho đến các mô hình AI phổ biến như mô hình GPT.
Quy tắc Chuỗi trong Neural Network
Trong machine learning, đặc biệt là trong Mạng nơ-ron (Neural Networks), mục tiêu là tối thiểu hóa Hàm Mất Mát (Loss Function) — đây là thước đo độ sai sót trong dự đoán của mô hình. Để tối thiểu hóa hàm này, chúng ta điều chỉnh các tham số (trọng số và độ lệch) của mô hình.
Nhưng để biết cần điều chỉnh bao nhiêu và theo hướng nào, thì sẽ cần sử dụng gradient — tức là độ nhạy của hàm tổn thất đối với từng tham số.
Và đó chính xác là những gì Quy tắc Chuỗi (Chain Rule) sẽ giúp chúng ta tính toán.
Tại sao cần Quy tắc Chuỗi (Chain Rule)?
Mỗi tầng (layer) của mạng nơ-ron có thể được xem là một hàm số, và bản thân mô hình là sự kết hợp của nhiều hàm số. Có thể hiểu
$$\text{Tổn thất} = L(\text{Đầu ra}) = L(\text{Tầng}_n(\ldots(\text{Tầng}_1(\text{Đầu vào}))\ldots))$$
Vì vậy, nếu muốn biết một thay đổi nhỏ trong trọng số ($w_1$) của một tầng sớm hơn ảnh hưởng đến Mất Mát cuối cùng như thế nào, chúng ta phải "xâu chuỗi" lại các ảnh hưởng:
- Trọng số đó ảnh hưởng đến đầu ra của tầng nó ra sao,
- Đầu ra của tầng đó ảnh hưởng đến tầng tiếp theo như thế nào,
- ...và đầu ra cuối cùng ảnh hưởng đến Mất Mát ra sao.
"Xâu chuỗi" các phụ thuộc này chính xác là những gì Quy tắc Chuỗi tính toán.
Công thức Quy tắc Chuỗi:
Nếu ta có một hàm số hợp thành:
$$y = g(f(x))$$
Thì đạo hàm của nó là:
$$\frac{dy}{dx} = \frac{dg}{df} \times \frac{df}{dx}$$
Điều đó có nghĩa là:
(Đạo hàm của hàm ngoài theo hàm trong) $\times$ (Đạo hàm của hàm trong theo $x$)
Ví dụ:
Hãy trình bày lại ví dụ của bạn theo từng bước:
-
Hàm trong: $f(x) = 2x - 1$
-
Hàm ngoài: $g(f) = (f - 3)^2$
-
Hàm hợp thành: $g(f(x)) = ((2x - 1) - 3)^2 = (2x - 4)^2$
Bây giờ áp dụng Quy tắc Chuỗi:
1 . $f'(x) = 2$
2 . $g'(f) = 2(f - 3)$
3 . Kết hợp chúng lại:
$$\frac{d}{dx} g(f(x)) = g'(f) \times f'(x) = [2(f - 3)] \times 2$$
4 . Thay thế $f=2x−1$
$$=4((2x - 1) - 3) = 8x - 16$$
=>Kết quả: $\frac{d}{dx} g(f(x)) = 8x - 16$
Kết nối với Lan truyền Ngược (Backpropagation)
Trong Lan truyền Ngược (Backpropagation):
- Gradient của mỗi tầng được tính toán bằng cách sử dụng Quy tắc Chuỗi.
- Chúng ta bắt đầu từ Hàm Mất Mát (tầng ngoài cùng) và lan truyền gradient ngược về các tầng sớm hơn.
Ví dụ:
$$\frac{\partial \text{Tổn thất}}{\partial W_1} = \frac{\partial \text{Tổn thất}}{\partial \text{Tầng}_n} \times \frac{\partial \text{Tầng}_n}{\partial \ldots} \times \ldots \times \frac{\partial \text{Tầng}_1}{\partial W_1}$$
Điều này cho phép mô hình biết chính xác mỗi trọng số đã đóng góp bao nhiêu vào lỗi sai, để nó có thể cập nhật chúng một cách chính xác trong quá trình huấn luyện.
=> Có thể hiểu là :
Lan Truyền Ngược (Backpropagation) =
“tính mức độ mỗi trọng số gây ra lỗi bằng Quy tắc Chuỗi, rồi cập nhật lại tất cả trọng số để giảm lỗi.”
Chưa có bình luận nào. Hãy là người đầu tiên!