I. Tổng quan về thuật toán hồi quy tuyến tính (Linear Regression)
1️. Giới thiệu
Hồi quy tuyến tính (Linear Regression) là một trong những thuật toán học máy có giám sát (Supervised Learning) cơ bản và quan trọng nhất.
Mục tiêu:
Tìm ra mối quan hệ tuyến tính (một đường thẳng hoặc siêu phẳng) phù hợp nhất với dữ liệu, nhằm dự đoán giá trị đầu ra liên tục (label) dựa trên một hoặc nhiều biến đầu vào (feature).
2️. Ví dụ: Dự đoán giá nhà
Giả sử bạn là một nhà môi giới bất động sản. Dưới đây là dữ liệu về diện tích và giá của một số căn nhà đã bán:
| Diện tích (m²) | Giá (cây vàng) |
|---|---|
| 350 | 4.6 |
| 460 | 5.9 |
| 550 | 6.7 |
| 670 | 9.1 |
| 600 | ??? |
Một khách hàng khác có căn nhà 600 m², hỏi bạn giá hợp lý để bán là bao nhiêu? Đây chính là lúc chúng ta dùng Linear Regression.
Để dễ hình dung ta mô tả dữ liệu bằng các điểm trên trục tọa độ.
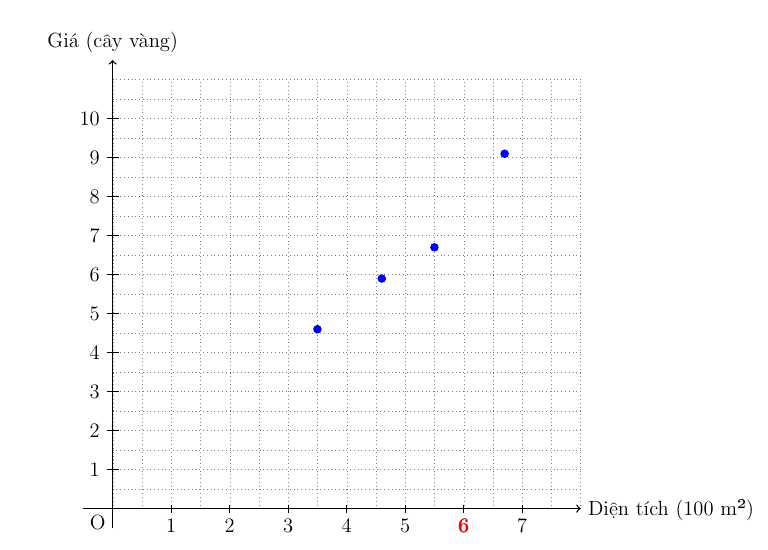
Hình 1.1. Biểu diễn các điểm dữ liệu trên trục tọa độ
Về cơ bản, Linear Regression là tìm ra một đường thẳng phù hợp nhất đi qua các điểm dữ liệu mà chúng ta có.
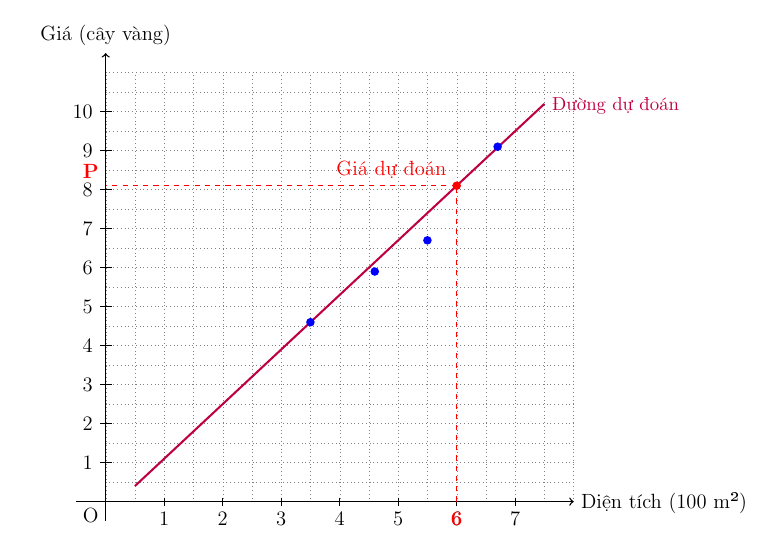
Hình 1.2. Đường thẳng phù hợp nhất với tập dữ liệu
3️. Biểu diễn dữ liệu
- Mỗi điểm dữ liệu là một cặp (diện tích, giá).
- Mục tiêu là tìm đường thẳng phù hợp nhất đi qua các điểm dữ liệu đó.
Đường thẳng này có công thức quen thuộc mà bạn đã học ở cấp 2: $y = a x + b$
Trong bài toán này:
$$price = w \times area + b$$
Giải thích các biến:
| Ký hiệu | Ý nghĩa |
|---|---|
area |
Biến đầu vào (feature) |
price |
Biến đầu ra (label) |
w |
Hệ số góc (slope) |
b |
Hệ số chặn (intercept) |
Mục tiêu:
Tìm cặp (w, b) sao cho đường thẳng phù hợp nhất với dữ liệu.
4️. Làm sao để tìm đường thẳng “tốt nhất”?
Làm sao máy tính biết được đường thẳng nào là "tốt nhất"? Nó dựa vào một khái niệm gọi là "Hàm mất mát" (Loss Function).
i. Máy tính vẽ đại một đường thẳng (tức là chọn ngẫu nhiên w và b).
ii. Với mỗi căn nhà trong dữ liệu, nó so sánh giá thật và giá dự đoán (giá trên đường thẳng).
iii. Khoảng chênh lệch (trên hình) giữa giá thật và giá dự đoán chính là "lỗi" (error).
iv. "Hàm mất mát" sẽ tính toán tổng lỗi của tất cả các điểm dữ liệu. Lỗi càng nhỏ, đường thẳng càng tốt.
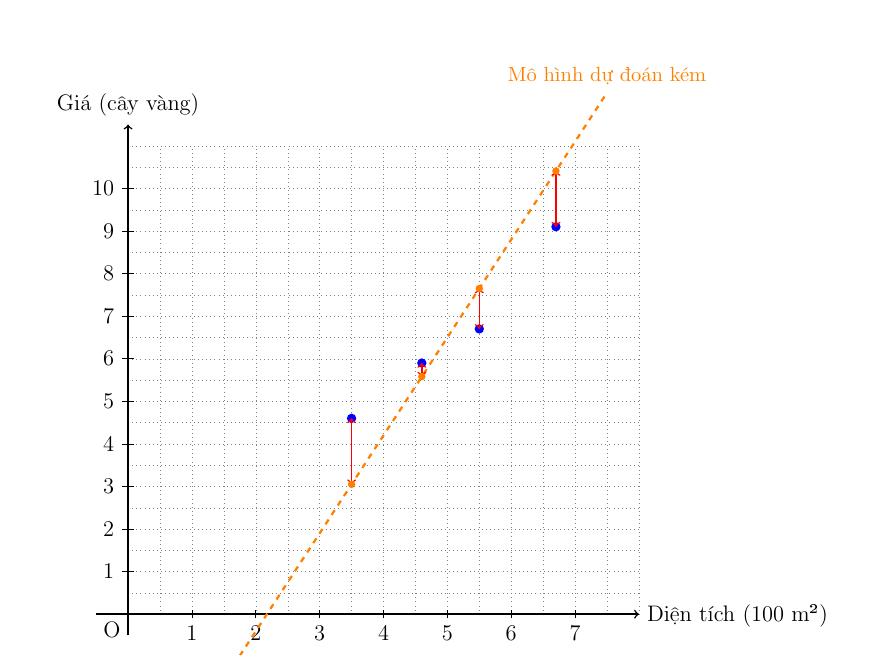
Hình 1.3. Mô hình dự đoán kém
Hàm mất mát phổ biến:
$$L = (\text{Giá dự đoán} - \text{Giá thật})^2$$
Chúng ta bình phương lên để lỗi luôn là số dương và "phạt" nặng hơn những dự đoán sai lệch nhiều.
Vậy bài toán bây giờ trở thành: Tìm w và b sao cho hàm mất mát (tổng lỗi) là nhỏ nhất có thể. Đây chính là bài toán Tối ưu hóa (Optimization).
5️. Bài toán tối ưu hóa và Gradient Descent
Ý tưởng:
Ta thấy hàm mất mát này là hàm số bậc hai có dạng Parabol quen thuộc.
Để tìm giá trị nhỏ nhất của hàm mất mát, chúng ta dùng một kỹ thuật gọi là Gradient Descent
Hãy tưởng tượng hàm mất mát của chúng ta giống như một thung lũng hay một cái bát. Bạn đang đứng ở một sườn dốc và muốn đi xuống điểm thấp nhất (đáy bát). Bạn sẽ làm gì?
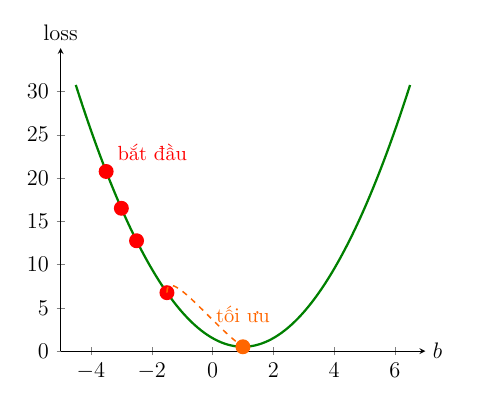
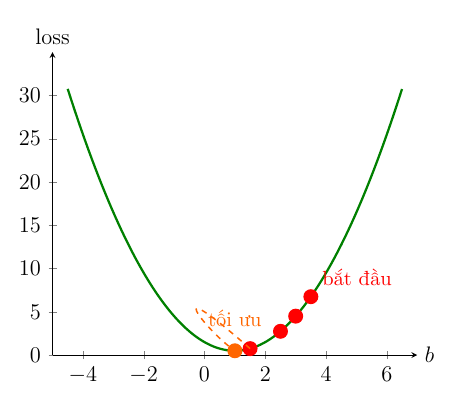
Hình 1.4. Minh họa đường đi của các điểm về vị trí tối ưu
Bước 1: Nhìn xem dốc nghiêng về hướng nào: Chỗ bạn đứng đang dốc lên hay dốc xuống?
Bước 2: Bước một bước nhỏ về phía ngược lại của dốc: Nếu dốc đang đi lên, bạn sẽ lùi lại. Nếu đang đi xuống, bạn sẽ tiến tới.
Bước 3: Lặp lại: Cứ lặp lại việc kiểm tra độ dốc và bước đi, chẳng mấy chốc bạn sẽ tới được đáy thung lũng.
Trong toán học, "độ dốc" chính là đạo hàm (derivative).
· Đạo hàm > 0 (dốc lên): Chúng ta cần giảm giá trị của w và b.
· Đạo hàm < 0 (dốc xuống): Chúng ta cần tăng giá trị của w và b.
. Đạo hàm = 0: Chúc mừng! Chúng ta đã ở đáy, tức là tìm thấy điểm có lỗi nhỏ nhất.
Gradient Descent hoạt động như sau:
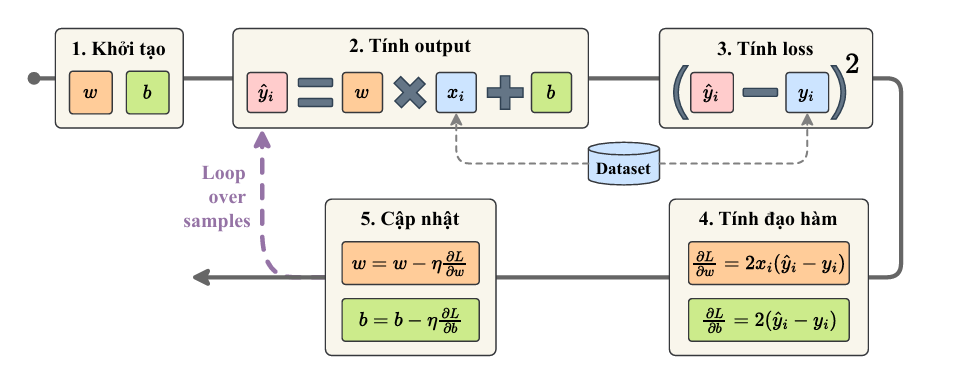
Hình 1.5. Quá trình tính toán của thuật toán Linear Regression
Bước 1: Khởi tạo: Chọn ngẫu nhiên $w$ và $b$, với $w$ là trọng số (weight )của đặc trưng đầu vào và $b$ là bias (độ chệch)
Bước 2: Tính dự đoán: $\hat{y}$ = $w x + b$.
Bước 3: Tính loss: So sánh $\hat{y}$ với $y$.
Bước 4: Tính đạo hàm: $\frac{\partial L}{\partial w}$, $\frac{\partial L}{\partial b}$ lần lượt là đạo hàm của hàm loss theo biến $w$ và $b$
Bước 5: Cập nhật tham số: Cập nhật lại w và b bằng cách đi một bước nhỏ ngược chiều đạo hàm.
$$w_{\text{mới}} = w_{\text{cũ}} - \eta \times \frac{\partial L}{\partial w}$$
$$ b_{\text{mới}} = b_{\text{cũ}} - \eta \times \frac{\partial L}{\partial b}$$
Trong công thức trên, $\eta$ (eta) là tốc độ học (learning rate). Nó quyết định "bước chân" của chúng ta dài hay ngắn.
Nếu $\eta$ quá lớn, chúng ta có thể "bước qua" luôn cả đáy bát và không bao giờ tìm được điểm thấp nhất.
Nếu $\eta$ quá nhỏ, chúng ta sẽ đi rất chậm và tốn nhiều thời gian.
Bước 6: Lặp lại: Quay về bước 2 và tiếp tục cho đến khi lỗi không còn giảm được nữa ta thu được cặp $(w, b)$ tối ưu nhất để có hàm dự đoán giá ban đầu.
$$ price = w\times{area} + b $$
6️. Ví dụ Tính Toán Cụ Thể
- Vòng lặp 1
Bây giờ, chúng ta sẽ tính toán lỗi và cập nhật $(w, b)$ lần đầu tiên.
Khởi tạo:
$w$ = 0, $b$ = 0, $\eta$ = 0.01
i/ Tính giá trị dự đoán $\hat{y}$ và tính đạo hàm cho từng điểm dữ liệu:
| $x_i$ | $y_i$ | $\hat{y_i}$ | Sai số ($\hat{y_i}-y_i$) | $\frac{\partial L}{\partial w}$ = $2x_i(\hat{y_i} - y_i)$ | $\frac{\partial L}{\partial b}$ = $2(\hat{y_i} - y_i)$ |
|---|---|---|---|---|---|
| 3.5 | 4.6 | 0.000 | -4.600 | -32.20 | -9.20 |
| 4.6 | 5.9 | 0.000 | -5.900 | -54.28 | -11.80 |
| 5.5 | 6.7 | 0.000 | -6.700 | -73.70 | -13.40 |
| 6.7 | 9.1 | 0.000 | -9.100 | -121.94 | -18.20 |
ii/ Tính đạo hàm trung bình:
$$\frac{\partial L}{\partial w} = -70.53, \quad \frac{\partial L}{\partial b} = -13.15$$
Cập nhật:
$$w = 0.7053, \quad b = 0.1315$$
- Vòng lặp 2:
Giá trị ban đầu: $w$ = 0.7053, $b = 0.1315$
| $x_i$ | $y_i$ | $\hat{y_i}$ | Sai số ($\hat{y_i}-y_i$) | $\frac{\partial L}{\partial w}$ = $2x_i(\hat{y_i} - y_i)$ | $\frac{\partial L}{\partial b}$ = $2(\hat{y_i} - y_i)$ |
|---|---|---|---|---|---|
| 3.5 | 4.6 | 2.600 | -2.000 | -14.000 | -4.000 |
| 4.6 | 5.9 | 3.376 | -2.524 | -23.221 | -5.048 |
| 5.5 | 6.7 | 4.011 | -2.689 | -29.579 | -5.378 |
| 6.7 | 9.1 | 4.857 | -4.243 | -56.858 | -8.486 |
$$\frac{\partial L}{\partial w} = -30.9145, \quad \frac{\partial L}{\partial b} = -5.728 $$
Cập nhật:
$$w = 1.0144, \quad b = 0.1888$$
7️. Quá trình hội tụ
Quá trình trên sẽ được lặp đi lặp lại nhiều lần. Ở mỗi bước, giá trị của $w$ và $b$ sẽ được điều chỉnh một chút để giảm thiểu tổng lỗi. Sau hàng trăm hoặc hàng nghìn vòng lặp, các giá trị này sẽ dần hội tụ đến điểm tối ưu, tức là khi lỗi không còn giảm được nữa.
8️. Dự đoán cho căn nhà mới 600 m²
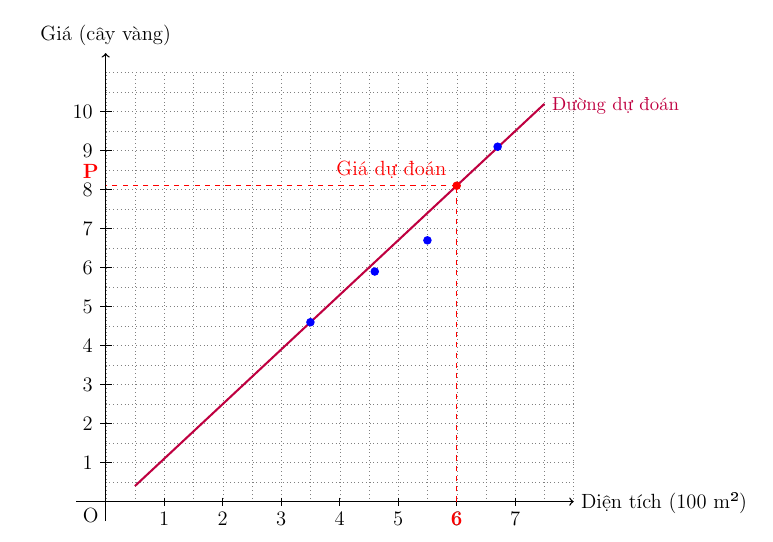
Hình 1.6. Kết quả dự đoán giá nhà của mô hình dựa trên diện tích của căn nhà
Khi đã có cặp ($w$, $b$) tối ưu, ta có thể sử dụng mô hình để dự đoán cho dữ liệu mới.
Diện tích: 600 m² => $x = 6.0$
Giá dự đoán: $price = w\times{x} + b = 1.3 \times 6.0 + 0.2 = 8.0$
Kết luận: Vậy, giá hợp lý cho căn nhà rộng 600 m² là khoảng 8.0 cây vàng, kết quả này phù hợp với giá trị dự đoán trên biểu đồ trong tài liệu.
Tóm tắt Quy trình Linear Regression
| Bước | Mô tả |
|---|---|
| 1 | Thu thập dữ liệu |
| 2 | Biểu diễn dữ liệu |
| 3 | Xây dựng mô hình ( $y = wx + b$ ) |
| 4 | Xác định hàm mất mát |
| 5 | Áp dụng Gradient Descent để tối ưu |
| 6 | Lặp lại cho đến khi hội tụ |
| 7 | Dự đoán giá trị mới |
II. Hàm Mất Mát trong Hồi Quy Tuyến Tính: Tại sao $ y - \hat{y}$ lại quan trọng?
Giới thiệu: Mục tiêu cơ bản của Hồi quy Tuyến tính
Trong Hồi quy Tuyến tính, mục tiêu cốt lõi của chúng ta là tìm ra các tham số (parameters) $w$ (trọng số) và $b$ (hệ số chặn) tốt nhất để mô hình có thể dự đoán chính xác nhất.
Phương trình tuyến tính cơ bản được sử dụng để tính giá trị dự đoán ($\hat{y}$) dựa trên đặc trưng đầu vào ($x$) là:
$$ \hat{y} = wx + b $$
Để đánh giá mức độ "tốt" của các tham số này, chúng ta cần tính toán sai số (error) hay mất mát (loss) giữa giá trị dự đoán ($\hat{y}$) và giá trị thực tế ($y$).
Quá trình huấn luyện mô hình sau đó sử dụng Gradient Descent để cực tiểu hóa hàm mất mát này. Quy trình này thường đi theo 5 bước chính cho mỗi mẫu dữ liệu:
Bước 1: Chọn một mẫu dữ liệu $(x, y)$.
Bước 2: Tính giá trị dự đoán $\hat{y}$.
Bước 3: Tính mất mát $L$.
Bước 4: Tính đạo hàm ($\frac{\partial L}{\partial w}$, $\frac{\partial L}{\partial b}$) cho từng tham số.
Bước 5: Cập nhật các tham số ($w$ và $b$) bằng tốc độ học $\eta$ (learning rate).
1. MSE: Sai số Bình phương Trung bình (Mean Squared Error)
Hàm mất mát truyền thống nhất trong Hồi quy Tuyến tính là Sai số Bình phương (Squared Loss) hay MSE.
- Công thức và Đặc điểm
Đối với một mẫu dữ liệu, Squared Loss được định nghĩa là:
$L(\hat{y}, y) = (\hat{y} - y)^2$
-
Tính toán Đạo hàm: Đạo hàm của MSE đối với các tham số rất rõ ràng và dễ tính. Ví dụ:
$\frac{\partial L}{\partial w} = 2x(\hat{y} - y)$
$\frac{\partial L}{\partial b} = 2(\hat{y} - y)$ -
Tóm tắt cách làm

Vấn đề: Khi sai số $(\hat{y} - y)$ lớn, hàm $ f(x) = x^2 $ khiến giá trị mất mát tăng lên rất nhanh. Điều này có nghĩa là MSE rất nhạy cảm với các giá trị ngoại lai (outliers). Nếu có một điểm dữ liệu nhiễu (noise) hoặc ngoại lai, hàm $ g(x) = x^2 $ sẽ có "ảnh hưởng tiêu cực lớn hơn" so với $ f(x)=|x| $ (MAE).
2. MAE: Sai số Tuyệt đối Trung bình (Mean Absolute Error)
Để khắc phục vấn đề nhạy cảm với ngoại lai của MSE, chúng ta có thể sử dụng MAE.
-
Công thức và Ưu điểm
Đối với một mẫu dữ liệu, MAE được định nghĩa là:
$L(\hat{y}, y) = |\hat{y} - y|$ -
Tóm tắt cách làm

Ưu điểm: Khi so sánh $f(x) = |x|$ và $g(x) = x^2$, nếu $x$ (sai số) lớn, MAE sẽ có độ lớn nhỏ hơn nhiều so với MSE. Do đó, MAE ít bị ảnh hưởng bởi các giá trị ngoại lai.
- Vấn đề của MAE
Mặc dù MAE rất tốt trong việc xử lý ngoại lai, nó gặp khó khăn với quá trình tối ưu hóa. Các thuật toán tối ưu hóa dựa trên đạo hàm (như Gradient Descent) yêu cầu hàm mất mát phải liên tục (Continuous) và khả vi (Differentiable).
Hàm giá trị tuyệt đối $f(x) = |x|$ có đạo hàm tồn tại, trừ trường hợp $x = \theta$. Điểm không khả vi tại $\theta$ có thể gây ra vấn đề cho thuật toán tối ưu, đặc biệt khi mô hình đã gần đến điểm tối ưu.
3. Huber Loss: Sự kết hợp hoàn hảo
Huber Loss được thiết kế để kết hợp các ưu điểm của MSE (khả vi và trơn tru gần điểm tối ưu) và MAE (chống chịu ngoại lai).
Yêu cầu về Hàm Mất mát: Để Gradient Descent hoạt động hiệu quả, hàm mất mát phải thỏa mãn các điều kiện về tính liên tục và tính khả vi.
Huber Loss sử dụng một ngưỡng $\delta$ để chuyển đổi giữa hai dạng hàm:
-
Khi Sai số Nhỏ (Near optimal): Nếu sai số $|\hat{y} - y|$ nhỏ hơn hoặc bằng ngưỡng $\delta$, Huber Loss sẽ sử dụng dạng bình phương (giống MSE) để đảm bảo tính khả vi và trơn tru:
$L(\hat{y}, y) = \frac{1}{2}(\hat{y} - y)^2 \quad \text{cho } |\hat{y} - y| \le \delta$ -
Khi Sai số Lớn (Outliers): Nếu sai số $|\hat{y} - y|$ lớn hơn $\delta$, Huber Loss sẽ chuyển sang dạng tuyến tính (giống MAE) để giảm thiểu ảnh hưởng của ngoại lai:
$L(\hat{y}, y) = \delta |\hat{y} - y| - \frac{1}{2}\delta^2 \quad \text{ngược lại}$
Huber Loss được xây dựng một cách cẩn thận để đảm bảo rằng hàm số vẫn liên tục và khả vi tại điểm chuyển đổi x = $\delta$.
Tóm tắt cách làm

4. Mở rộng Mô hình và Chính quy hóa (Regularization)
Các khái niệm trên có thể được áp dụng không chỉ cho Hồi quy Tuyến tính đơn biến ($y = wx + b$), mà còn cho Hồi quy Tuyến tính Đa biến (General Formula).
Ví dụ, khi dự đoán Doanh số (Sale) dựa trên chi tiêu quảng cáo qua TV, Radio và Newspaper, mô hình sẽ có nhiều trọng số hơn:
$\hat{y} = w_1 \cdot TV + w_2 \cdot Radio + w_3 \cdot Newspaper + b$
Chính quy hóa (Regularization)
Trong các mô hình phức tạp hơn, một vấn đề có thể phát sinh liên quan đến các trọng số $w$. Chính quy hóa là một kỹ thuật giải quyết vấn đề này bằng cách thêm một thuật ngữ phạt (penalty term) vào hàm mất mát.
Hàm mất mát với Chính quy hóa sẽ trông như sau (ví dụ: sử dụng L2/Ridge Regularization): $L(w_1, w_2, b) = (\hat{y} - y)^2 + \lambda(w_1^2 + w_2^2)$
-
Mục đích: Thuật ngữ phạt $\lambda(w_1^2 + w_2^2)$ giúp kiểm soát độ lớn của các trọng số.
-
Ảnh hưởng đến Đạo hàm: Khi tính đạo hàm, thuật ngữ phạt này cũng được tính toán và ảnh hưởng đến cách cập nhật trọng số. Ví dụ:
$\frac{\partial L}{\partial w_1} = 2x(\hat{y} - y) + 2\lambda w_1$
Tóm lại, Chính quy hóa được sử dụng để giải quyết các vấn đề liên quan đến trọng số, thường giúp mô hình tổng quát hóa tốt hơn trên dữ liệu mới.
i. Linear regression Đa biến

Đây là các bước tính toán trong thuật toán Linear Regression dành cho nhiều đặc trưng dữ liệu
ii. Regularization cho đa biến

Đây là các bước tính toán trong kỹ thuật Regularization dành cho nhiều đặc trưng dữ liệu
III. Các Chiến Lược "Nạp" Dữ Liệu
Khi thực hiện Gradient Descent, có nhiều cách để chúng ta "nạp" dữ liệu vào mô hình.
Chúng ta sẽ sử dụng tiếp dữ liệu dự đoán giá nhà
| Diện tích (x 100m²) | Giá (chục lượng vàng) |
|---|---|
| 3.5 | 4.6 |
| 4.6 | 5.9 |
| 5.5 | 6.7 |
| 6.7 | 9.1 |
1. Stochastic Gradient Descent (SGD) - "Học từng thứ một"
Đây là phương pháp mà mô hình cập nhật các tham số (weights và bias) sau mỗi một mẫu dữ liệu. Quá trình này còn được gọi là Stochastic Gradient Descent (SGD).
Quy trình chung
Quy trình huấn luyện cho một mẫu được tóm tắt trong 5 bước, lặp đi lặp lại cho từng mẫu trong bộ dữ liệu:
Bước 1: Chọn 1 mẫu $(x, y)$ từ dữ liệu huấn luyện.
Bước 2: Tính toán đầu ra (output) $\hat{y}$ (dự đoán).
Bước 3: Tính toán mất mát (loss) $L$ (sai số).
Bước 4: Tính toán đạo hàm (derivative) cho từng tham số.
Bước 5: Cập nhật tham số $w$ và $b$.
Chi tiết tính toán
Các công thức toán học cho 5 bước trên (sử dụng Squared Loss) là:
- Bước 1: Khởi tạo giá trị $w$ và $b$
-
Bước 2: Tính Output: $\hat{y} = wx + b$
-
Bước 3: Tính Loss: $L = (\hat{y} - y)^2$
-
Bước 4: Tính Đạo hàm:
-
$\frac{\partial L}{\partial w} = 2x(\hat{y} - y)$
-
$\frac{\partial L}{\partial b} = 2(\hat{y} - y)$
-
Bước 5: Cập nhật tham số: (với $\eta$ là tốc độ học (learning rate))
-
$w = w - \eta \frac{\partial L}{\partial w}$
-
$b = b - \eta \frac{\partial L}{\partial b}$
Ví dụ tính toán (với 1 mẫu)
Chúng ta sẽ lấy mẫu thứ 4 từ bộ dữ liệu (Area, Price) cho trước làm ví dụ, với $x = 6.7$, $y = 9.1$.
Bước 1: Khởi tạo:
-
$w = -0.34$
-
$b = 0.04$
-
Learning rate $\eta = 0.01$
Bước 2: Tính Output (Forward Propagation):
- $\hat{y} = w \cdot x + b = (-0.34 \times 6.7) + 0.04 = -2.278 + 0.04 = -2.238$
Bước 3: Tính Loss:
- $L = (\hat{y} - y)^2 = (-2.238 - 9.1)^2 = (-11.338)^2 \approx 128.55$
Bước 4: Tính Đạo hàm (Backpropagation):
-
$\frac{\partial L}{\partial b} = 2(\hat{y} - y) = 2(-2.238 - 9.1) = -22.676$
-
$\frac{\partial L}{\partial w} = 2x(\hat{y} - y) = 2 \times 6.7 \times (-2.238 - 9.1) \approx -151.929$
Bước 5: Cập nhật tham số:
-
$w_{new} = w - \eta \frac{\partial L}{\partial w} = -0.34 - (0.01 \times -151.929) \approx 1.179$
-
$b_{new} = b - \eta \frac{\partial L}{\partial b} = 0.04 - (0.01 \times -22.676) \approx 0.266$
Sau một lần cập nhật này, loss đã giảm đáng kể từ $128.55$ xuống còn $0.868$. Đồ thị loss của phương pháp này thường biến động mạnh (như hình zigzag) vì mỗi mẫu có thể kéo mô hình về một hướng khác nhau.
Ưu điểm:
- Tốc độ nhanh: Mô hình sẽ cập nhật rất nhanh vì mỗi bước chỉ thực hiện tính toán cho một mẫu.
- Tiết kiệm bộ nhớ: Không cần lưu trữ nhiều mẫu hoặc toàn bộ tập dữ liệu để thực hiện một lần cập nhật.
- Thoát khỏi cực tiểu cục bộ: Các cập nhật ngẫu nhiên có thể giúp thuật toán thoát khỏi các điểm cực tiểu cục bộ kém, có khả năng tìm ra giải pháp tổng thể tốt hơn.
Nhược điểm:
- Quá trình học không ổn định: Đường đi xuống đáy dốc sẽ "loạng choạng" và nhiễu. Lí do cho kết quả này là vì mô hình muốn tối thiểu hóa chênh lệch giữa giá trị dự đoán và giá trị thực tế, hay nói cách khác là mong muốn kết quả của hàm loss đạt giá trị nhỏ nhất
- Cần tinh chỉnh: Tốc độ học (learning rate) cần được điều chỉnh cẩn thận để tránh tình trạng dao động quá lớn hoặc hội tụ quá chậm.
2. Batch Gradient Descent - "Học tất cả cùng lúc"
Đây là phương pháp mà mô hình tính toán sai số và đạo hàm trên toàn bộ $N$ mẫu trong bộ dữ liệu huấn luyện. Việc cập nhật tham số chỉ xảy ra một lần sau khi đã xử lý tất cả dữ liệu.
Quy trình chung
Bước 1: Chọn tất cả $N$ mẫu $(x^{(i)}, y^{(i)})$ từ dữ liệu huấn luyện.
Bước 2: Tính Output $\hat{y}^{(i)}$ cho tất cả $N$ mẫu.
Bước 3: Tính Loss $L$ (là giá trị trung bình của loss trên toàn bộ $N$ mẫu).
Bước 4: Tính Đạo hàm cho $N$ mẫu và lấy trung bình.
Bước 5: Cập nhật tham số $w$ và $b$ (1 lần).
Chi tiết tính toán
Thay vì thành phấn đạo hàm của $w$ và $b$ được tính theo từng mẫu như Stochastic Gradient Descent (SGD), chúng sẽ được tính theo trung bình tất cả các mẫu của dữ liệu. Công thức sẽ được áp dụng cho Mini-Batch, nhưng $N$ (tổng số mẫu) được thay bằng $m$ (số lượng mẫu trong 1 mini batch).
-
Bước 1: Khởi tạo vector trọng số $w$ và $b$
-
Bước 2: Tính Output: $\hat{y}^{(i)} = wx^{(i)} + b$ (cho mỗi $i$ từ $0$ đến $N-1$)
-
Bước 3: Tính Loss: $L = \frac{1}{N} \sum_{i} (\hat{y}^{(i)} - y^{(i)})^2$ (Tổng loss của $N$ mẫu chia cho $N$).
-
Bước 4: Tính Đạo hàm (trung bình):
-
$\frac{\partial L}{\partial w}_{avg} = \frac{1}{N} \sum_{i} \frac{\partial L^{(i)}}{\partial w} = \frac{1}{N} \sum_{i} 2x^{(i)}(\hat{y}^{(i)} - y^{(i)})$
-
$\frac{\partial L}{\partial b}_{avg} = \frac{1}{N} \sum_{i} \frac{\partial L^{(i)}}{\partial b} = \frac{1}{N} \sum_{i} 2(\hat{y}^{(i)} - y^{(i)})$
-
Bước 5: Cập nhật tham số:
-
$w = w - \eta \cdot (\frac{\partial L}{\partial w}_{avg})$
-
$b = b - \eta \cdot (\frac{\partial L}{\partial b}_{avg})$
Ví dụ tính toán (với $N=4$)
Slide minh họa với toàn bộ bộ dữ liệu $N=4$:
-
$x = [6.7, 4.6, 3.5, 5.5]$
-
$y = [9.1, 5.9, 4.6, 6.7]$
Bước 1: Khởi tạo: $w = -0.34$, $b = 0.04$, $\eta = 0.01$. Vì dữ liệu chỉ có 1 đặc trưng nên $w$ chỉ có 1 giá trị
Bước 2: Tính Output (Vectorized):
- $\hat{y}$ (vector) = $[-2.238, -1.524, -1.15, -1.83]$
Bước 3: Tính Loss:
-
$L^{(i)}$ (vector) = $[128.55, 55.11, 33.06, 72.76]$
-
$L_{avg} = \frac{128.55 + 55.11 + 33.06 + 72.76}{4} = \frac{289.48}{4} = 72.37$
Bước 4: Tính Đạo hàm (trung bình):
-
$\frac{\partial L}{\partial w}$ (vector) = $[-151.929, -68.3008, -40.25, -93.83]$
-
$\frac{\partial L}{\partial b}$ (vector) = $[-22.676, -14.848, -11.5, -17.06]$
-
$\frac{\partial L}{\partial w}_{avg} = \frac{sum(\dots)}{4} = -88.5775$
-
$\frac{\partial L}{\partial b}_{avg} = \frac{sum(\dots)}{4} = -16.521$
Bước 5: Cập nhật tham số:
-
$w_{new} = -0.34 - (0.01 \times -88.5775) = 0.54$
-
$b_{new} = 0.04 - (0.01 \times -16.521) = 0.205$
Ưu điểm:
- Độ chính xác cao: Do sử dụng toàn bộ dữ liệu, gradient ước tính sẽ chính xác và ổn định hơn. Đo đó đường đi xuống đáy dốc rất mượt mà và ổn định vế phía điểm tối ưu.
- Đảm bảo hội tụ: Batch Gradient Descent có khả năng hội tụ về điểm cực tiểu toàn cục (global minimum) đối với các hàm chi phí lồi (convex)
Nhược điểm:
- Chi phí tính toán cao: Rất chậm và tốn bộ nhớ nếu bộ dữ liệu của bạn có hàng triệu điểm.
- Tiêu tốn bộ nhớ lớn: Yêu cầu một lượng lớn bộ nhớ để lưu trữ toàn bộ dữ liệu huấn luyện trong quá trình tính toán.
- Tốc độ chậm: Với dữ liệu lớn, thời gian cho mỗi lần cập nhật tham số rất lâu, dẫn đến tốc độ huấn luyện chậm.
3. Mini-batch Gradient Descent - "Sự cân bằng hoàn hảo"
Đây là phương pháp thỏa hiệp giữa One-Sample và Batch. Mô hình tính toán sai số và đạo hàm trên một nhóm nhỏ $m$ mẫu (một "mini-batch") trước khi cập nhật tham số. Kích thước $m$ thường là $1 < m < N$ (với $N$ là tổng số mẫu).
Quy trình chung
Bước 1: Chọn $m$ mẫu $(x^{(i)}, y^{(i)})$ từ dữ liệu huấn luyện (thường được xáo trộn (shuffled) mỗi epoch).
Bước 2: Tính Output $\hat{y}^{(i)}$ cho tất cả $m$ mẫu.
Bước 3: Tính Loss $L$ (là giá trị trung bình của loss trên $m$ mẫu).
Bước 4: Tính Đạo hàm cho $m$ mẫu và lấy trung bình.
Bước 5: Cập nhật tham số $w$ và $b$ (chỉ 1 lần).
Chi tiết tính toán
-
Bước 1: Khởi tạo vector trọng số $w$ và $b$
-
Bước 2: Tính Output: $\hat{y}^{(i)} = wx^{(i)} + b$ (cho mỗi $i$ từ $0$ đến $m-1$)
-
Bước 3: Tính Loss: $L = \frac{1}{m} \sum_{i} (\hat{y}^{(i)} - y^{(i)})^2$ (Tổng loss của $m$ mẫu chia cho $m$).
-
Bước 4: Tính Đạo hàm (trung bình): Tính đạo hàm $\frac{\partial L^{(i)}}{\partial w}$ và $\frac{\partial L^{(i)}}{\partial b}$
cho từng mẫu $i$, sau đó lấy trung bình:
$$ \frac{\partial L}{\partial w}_{avg} = \frac{1}{m} \sum_{i} \frac{\partial L^{(i)}}{\partial w} = \frac{1}{m} \sum_{i} 2x^{(i)}(\hat{y}^{(i)} - y^{(i)}) $$
$$ \frac{\partial L}{\partial b}_{avg} = \frac{1}{m} \sum_{i} \frac{\partial L^{(i)}}{\partial b} = \frac{1}{m} \sum_{i} 2(\hat{y}^{(i)} - y^{(i)}) $$
-
Bước 5: Cập nhật tham số:
-
$w = w - \eta \cdot (\frac{\partial L}{\partial w}_{avg})$
-
$b = b - \eta \cdot (\frac{\partial L}{\partial b}_{avg})$
Ví dụ tính toán (với $m=2$)
Slide minh họa với $m=2$, sử dụng 2 mẫu đầu tiên:
-
Mẫu 1: $x^{(1)} = 6.7$, $y^{(1)} = 9.1$
-
Mẫu 2: $x^{(2)} = 4.6$, $y^{(2)} = 5.9$
Bước 1: Khởi tạo: $w = -0.34$, $b = 0.04$, $\eta = 0.01$.
Bước 2: Tính Output (Vectorized):
-
$\hat{y}^{(1)} = (-0.34 \times 6.7) + 0.04 = -2.238$
-
$\hat{y}^{(2)} = (-0.34 \times 4.6) + 0.04 = -1.524$
Bước 3: Tính Loss:
-
$L^{(1)} = (-2.238 - 9.1)^2 = 128.55$
-
$L^{(2)} = (-1.524 - 5.9)^2 = 55.11$
-
$L_{avg} = \frac{128.55 + 55.11}{2} = 91.83$
Bước 4: Tính Đạo hàm (trung bình):
-
$\frac{\partial L^{(1)}}{\partial w} = -151.929$; $\frac{\partial L^{(2)}}{\partial w} = 2 \times 4.6 \times (-1.524 - 5.9) = -68.3008$
-
$\frac{\partial L^{(1)}}{\partial b} = -22.676$; $\frac{\partial L^{(2)}}{\partial b} = 2 \times (-1.524 - 5.9) = -14.848$
-
$\frac{\partial L}{\partial w}_{avg} = \frac{-151.929 + (-68.3008)}{2} = -110.115$
-
$\frac{\partial L}{\partial b}_{avg} = \frac{-22.676 + (-14.848)}{2} = -18.762$
Bước 3: Cập nhật tham số:
-
$w_{new} = -0.34 - (0.01 \times -110.115) = 0.761$
-
$b_{new} = 0.04 - (0.01 \times -18.762) = 0.227$
Ưu điểm:
- Hiệu quả tính toán: Vừa nhanh hơn Batch Gradient Descent, nhất là khi xử lí trên 1 tập dữ liệu cực lớn. Thuật toán tận dụng được khả năng xử lý song song của các thiết bị hiện đại như GPU.
- Sự ổn định cao: Các lần cập nhật tham số ít nhiễu loạn hơn so với Stochastic Gradient Descent, dẫn đến đường hội tụ mượt mà và ổn định hơn.
- Thoát khỏi cực tiểu cục bộ: Việc sử dụng các mini-batch ngẫu nhiên mang lại một mức độ nhiễu nhất định, giúp thuật toán có khả năng thoát ra khỏi các cực tiểu cục bộ không tối ưu.
- Hiệu quả bộ nhớ: Giảm yêu cầu bộ nhớ đáng kể so với Batch Gradient Descent, cho phép xử lý các tập dữ liệu khổng lồ mà không gây tràn bộ nhớ.
Nhược điểm: Cần điều chỉnh siêu tham số: Cần phải chọn kích thước mini-batch và tốc độ học (learning rate) phù hợp, vì chúng ảnh hưởng trực tiếp đến hiệu suất của thuật toán. Việc chọn kích thước quá nhỏ có thể gây nhiễu, còn quá lớn lại làm chậm quá trình học.
4. Một ví dụ so sánh 3 phương pháp Gradient Descent được nêu ở trên
Một ví dụ đã được thực nghiệm trên bộ dataset Advertising sử dụng thuật toán Gradient Descent theo 3 phiên bản đã được giới thiệu ở các mục trên. Các bạn có thể xem qua source code tại đây: Link Source Code
Giá trị hàm loss qua từng vòng lặp được trực quan hóa như 3 biểu đồ dưới đây:
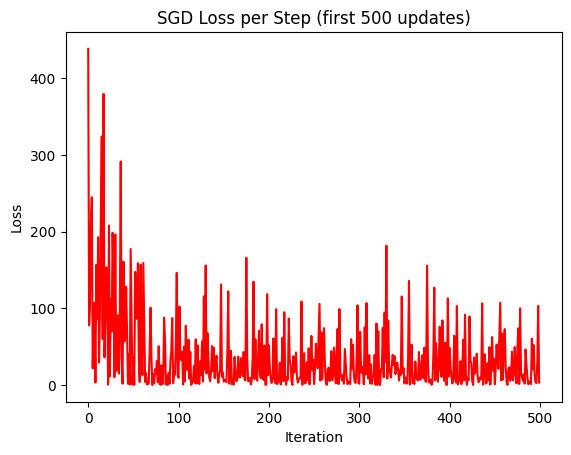
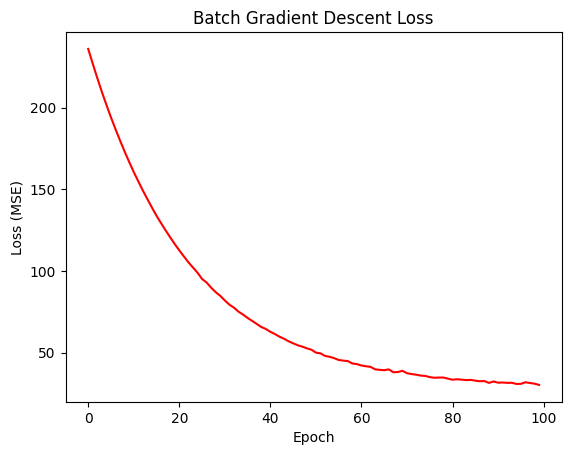
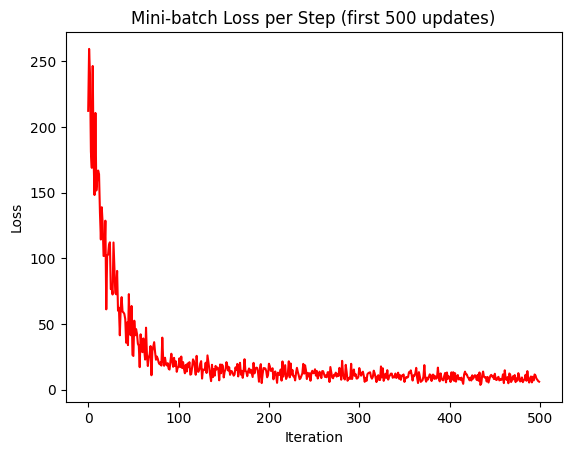
Đồ thị hàm loss khi qua từng vòng lặp, lần lượt là các phương pháp Gradient Descent: Stochastic, Batch và Mini-Batch
Từ 3 biểu đồ được trực quan hóa, ta có thể thấy rằng SGD Loss có sự biến động cao (như các hình zigzag), Batch Loss có sự ổn định và mượt mà nhất. Mini-batch có sự mượt mà hơn SGD Loss nhưng vẫn có biến động nhỏ.
IV. Vectorized Linear Regression
Cho dữ liệu
| Diện tích (x 100m²) | Giá (chục lượng vàng) |
|---|---|
| 3.5 | 4.6 |
| 4.6 | 5.9 |
| 5.5 | 6.7 |
| 6.7 | 9.1 |
Hạn chế của thuật toán hồi quy tuyến tính đơn giản
Khi chuyển sang các bài toán đa đặc trưng (Multivariate Dataset), ví dụ như dự đoán Lương (Salary) dựa trên Kinh nghiệm ($x_1$) và Học vấn ($x_2$), phương trình mô hình trở thành:
$$ \hat{y} = w_1x_1 + w_2x_2 + \cdots + b $$
Vấn đề lớn nhất là: Việc triển khai phải được cập nhật thủ công khi số lượng đặc trưng đầu vào thay đổi. Điều này gây bất tiện và thiếu linh hoạt khi lập trình. Vectorization được giới thiệu để giải quyết vấn đề này
1. Vector hóa cho 1 Mẫu (1-Sample Vectorization)

Hình 4.1. Sự khác nhau trong các bước tính toán của thuật toán Linear Regression truyền thống và thuật toán đã được vector hóa
Để chuyển từ phương trình vô hướng (scalar) sang dạng vector, chúng ta tái định nghĩa các biến.
Bước 1: Định nghĩa vector đầu vào và tham số
Chúng ta gộp tất cả các tham số ($w$ và $b$) vào một vector tham số $\theta$ và gộp đặc trưng đầu vào $x$ cùng với hệ số chặn 1 vào vector $x$: - Vector tham số: $$ \theta = \begin{pmatrix}b \\w\end{pmatrix} $$ - Vector đầu vào (với hệ số chặn): $$ x = \begin{pmatrix}1 \\x\end{pmatrix} $$
Bước 2: Tính toán đầu ra (Prediction)
Việc dự đoán $\hat{y}=wx+b$ được thay thế bằng phép tích vô hướng (Dot Product) của $\theta^T$ và $x$: $$ \hat{y} = \theta^T x \quad \text{hoặc} \quad \hat{y} = x^T \theta $$ Với loss function: $$L(\hat{y}, y) = (\hat{y} - y)^2$$
Bước 3: Tính toán Gradient Vector
Thay vì tính đạo hàm riêng lẻ cho $w$ và $b$, chúng ta tính vector gradient $\nabla_{\theta} L$ (hoặc $*L_{\theta}^{T}*$) cho tất cả các tham số cùng lúc: $$ \nabla_{\theta} L =\begin{pmatrix}\frac{\partial L}{\partial b} \\ \frac{\partial L}{\partial w}\end{pmatrix} $$ Dạng vector hóa của Gradient là: $$\nabla_{\theta} L = 2x(\hat{y} - y)$$
Bước 4: Cập nhật tham số vector
Vector tham số $\theta$ được cập nhật trong một phép toán duy nhất: $$ \theta = \theta - \eta \nabla_{\theta} L $$ Ví dụ minh họa Vector hóa cho 1 Mẫu (1-Sample Vectorization) Giả sử chúng ta có một mẫu dữ liệu $(x, y)$ và các tham số $\theta$ đã được khởi tạo.
Dữ liệu mẫu:
- Đầu vào $x$ (ví dụ: Kinh nghiệm): $x=6.7$
- Đầu ra thực tế $y$ (ví dụ: Lương): $y=9.1$
- Tốc độ học $η$: $η=0.01$
Bước 1: Khởi tạo tham số $\boldsymbol{\theta}$: $$ \theta =\begin{pmatrix}b \\w\end{pmatrix}=\begin{pmatrix}0.049 \\-0.34\end{pmatrix} $$ Vector đầu vào $x$: $$x =\begin{pmatrix}1 \\x\end{pmatrix}=\begin{pmatrix}1 \\6.7\end{pmatrix}$$
Bước 2: Tính toán (Forward Pass) - Tính toán Đầu ra dự đoán ($\hat{y}$). Sử dụng công thức vector hóa $\hat{y} = \theta^T x$ $$\hat{y} = \theta^T x = \begin{pmatrix}0.049 & -0.34\end{pmatrix}\begin{pmatrix}1 \\6.7\end{pmatrix}$$ $$\hat{y}=0.049×1+(−0.34)×6.7=0.049−2.278=−2.238$$ - Tính toán Loss. Sử dụng Squared Loss $L = (\hat{y} - y)^2$ $$ L = (\hat{y} - y)^2 = (-2.238 - 9.1)^2 = (-11.338)^2 \approx 128.5 $$
Bước 3 và 4: Tính toán Gradient (Backward) và Cập nhật
- Tính toán Gradient Vector ($\nabla_{\boldsymbol{\theta}} L$): Sử dụng công thức vector hóa $\nabla_{\theta} L = 2x(\hat{y} - y)$
- Giá trị sai số: $\hat{y} - y =−2.238−9.1=−11.338$
- Gradient vector: $$ \nabla_{\theta} L = 2 \begin{pmatrix}1 \\ 6.7 \end{pmatrix} (-11.338) = 2 \begin{pmatrix} -11.338 \\ -75.9646 \end{pmatrix} = \begin{pmatrix} -22.676 \\ -151.9292 \end{pmatrix} $$
- Cập nhật Tham số $\boldsymbol{\theta}$. Sử dụng công thức: $\theta = \theta - \eta \nabla_{\theta} L$
$$ \theta_{\text{mới}} = \begin{pmatrix}0.049 \\-0.34\end{pmatrix}- 0.01\begin{pmatrix}-22.676 \\-151.9292\end{pmatrix}$$
$$\theta_{\text{mới}} =\begin{pmatrix}0.049 + 0.22676 \\-0.34 + 1.519292\end{pmatrix}=\begin{pmatrix}0.27576 \\1.179292\end{pmatrix} $$
2. Vector hóa cho N Mẫu (N-Samples Vectorization)

Hình 4.2. Pipeline của Mini-batch Gradient Descent Vector hóa
Khi áp dụng Vectorization cho toàn bộ N mẫu dữ liệu (hoặc một Mini-batch m mẫu), chúng ta tận dụng khả năng tính toán ma trận để tối ưu hóa hiệu suất (thường được thực hiện bằng các thư viện như NumPy)
2.1. Pipeline của Gradient Descent Vector hóa (N-Samples)
Quy trình huấn luyện qua các bước được Vector hóa hoàn toàn:
| Bước | Mô tả | Công thức Vector hóa (Sử dụng N mẫu) |
|---|---|---|
| 1. Lấy mẫu | Lấy tất cả N mẫu từ dữ liệu huấn luyện. | Chọn $X$ (Ma trận đầu vào) và $y$ (Vector nhãn). |
| 2. Prediction | Tính vector dự đoán $\hat{y}$ cho tất cả N mẫu. | $\hat{y} = X\theta$ |
| 3. Loss | Tính Hàm lỗi Bình phương Trung bình (Average Squared Loss). | $L(\hat{y}, y) = \frac{1}{N} (\hat{y} - y)^{T} (\hat{y} - y)$ |
| 4. Gradient | Tính vector sai số $k$ và sau đó là Gradient $\nabla_{\theta} L$. | Sai số: $k = 2(\hat{y} - y)$ Gradient: $\nabla_{\theta} L = X^{T} k$ |
| 5. Update | Cập nhật vector tham số $\theta$. | $\theta = \theta - \eta \frac{1}{N} \nabla_{\theta} L$ |
2.2. Ý nghĩa của các Phép toán Ma trận
- Prediction $\hat{\mathbf{y}} = \mathbf{X} \boldsymbol{\theta}$: Đây là phép nhân ma trận giữa ma trận đầu vào X (kích thước $N×(D+1)$, với $D$ là số đặc trưng) và vector tham số $\theta$ (kích thước $(D+1)×1$). Kết quả là vector $\hat{y} (N×1)$ chứa tất cả các giá trị dự đoán cho mọi mẫu.
- Loss $L = \frac{1}{N} (\hat{\mathbf{y}} - \mathbf{y})^T (\hat{\mathbf{y}} - \mathbf{y})$: Phép nhân ma trận này tương đương với việc tính tổng bình phương của tất cả các sai số, sau đó chia cho $*N*$ để lấy giá trị trung bình.
- Gradient $\nabla_{\boldsymbol{\theta}} L = \mathbf{X}^T \mathbf{k}$: Phép nhân này hiệu quả hơn nhiều so với việc tính tổng của gradient trên từng mẫu. Nó tính toán đạo hàm đồng thời cho tất cả các tham số, sử dụng ma trận chuyển vị $X^{T}$.
Ví dụ minh họa Vector hóa cho N Mẫu (N-Samples Vectorization)
Sử dụng dữ liệu có hai đặc trưng: Kinh nghiệm ($x_1$) và Học vấn ($x_2$), và đầu ra là Lương (Salary)
Bước 1: Khởi tạo tham số và siêu tham số:
- $N=4$ (số lượng mẫu)- Tốc độ học $\eta=0.001$
- Tham số ban đầu (Epoch 1): $b=10,w_1=3,w_2=2$
$$ \theta =\begin{pmatrix}b \\w_1 \\w_2\end{pmatrix}=\begin{pmatrix}10 \\3 \\2\end{pmatrix} $$
Bước 2: Ma trận đầu vào $X$ và vector nhãn $y$: (Ma trận $X$ bao gồm cột 1 cho hệ số chặn) $$ X =\begin{pmatrix}1 & 3 & 12 \\1 & 4 & 13 \\1 & 5 & 14 \\1 & 6 & 15\end{pmatrix},\quad y =\begin{pmatrix}60 \\55 \\66 \\93\end{pmatrix} $$
- Prediction: Sau một lần tính toán (Epoch 1):
$$ \hat{y} = X\theta $$
$$ \hat{y} = \begin{pmatrix}1 & 3 & 12 \\1 & 4 & 13 \\1 & 5 & 14 \\1 & 6 & 15\end{pmatrix} \begin{pmatrix}10 \\3 \\2\end{pmatrix} = \begin{pmatrix}43 \\48 \\53 \\58\end{pmatrix} $$
Bước 3: Tính hàm Loss $$ L(\hat{y}, y) = \frac{1}{N} (\hat{y} - y)^{T} (\hat{y} - y) $$ $$ \hat{y} - y =\begin{pmatrix}43 \\48 \\53 \\58\end{pmatrix}-\begin{pmatrix}60 \\55 \\66 \\93\end{pmatrix}=\begin{pmatrix}-17 \\-7 \\-13 \\-35\end{pmatrix} $$ $$ (\hat{y} - y)^{T} (\hat{y} - y)= (-17)^2 + (-7)^2 + (-13)^2 + (-35)^2= 1732\\L = \frac{1}{4} \times 1732 = 433 $$
Bước 4: Tính Gradient: $ \nabla_{\theta} L = X^T k $, trong đó k = 2($\hat{y}$ - y)
$$ k = 2 \begin{bmatrix}-17 \\-7 \\-13 \\-35\end{bmatrix}=\begin{bmatrix}-34 \\-14 \\-26 \\-70\end{bmatrix} $$
$$ X^Tk =\begin{bmatrix}1 & 3 & 12 \\1 & 4 & 13 \\1 & 5 & 14 \\1 & 6 & 15\end{bmatrix}\begin{bmatrix}-34 \\-14 \\-26 \\-70\end{bmatrix} $$
-
Thành phần 1 (Đạo hàm theo $b$): $1⋅(−34)+1⋅(−14)+1⋅(−26)+1⋅(−70)=−34−14−26−70=−144$
-
Thành phần 2 (Đạo hàm theo $w_1$): $3⋅(−34)+4⋅(−14)+5⋅(−26)+6⋅(−70) = −708$
-
Thành phần 3 (Đạo hàm theo $w_2$): $12⋅(−34)+13⋅(−14)+14⋅(−26)+15⋅(−70) = −2004$
$$\nabla_{\theta} L = X^T k=\begin{bmatrix}-144 \\-708 \\-2004\end{bmatrix}$$
Bước 5: Cập nhật trọng số
$$\theta =\begin{bmatrix}10 \\3 \\2\end{bmatrix}- 0.001 \times\begin{bmatrix}-144 \\-708 \\-2004\end{bmatrix}=\begin{bmatrix}10.036 \\3.177 \\2.501\end{bmatrix}$$
Sau Epoch 1, các tham số đã được cập nhật thành $b=10.036$, $w_1=3.177$, $w_2=2.501$
Vectorization cho phép thực hiện toàn bộ quá trình này (bao gồm cả cập nhật $b,w1,w2$...) chỉ trong một vài phép toán ma trận.
3. Kết luận
Vectorization là một công cụ bắt buộc phải có khi làm việc với Học máy quy mô lớn. Nó không chỉ giúp code trở nên gọn gàng, linh hoạt và dễ mở rộng khi số lượng đặc trưng thay đổi, mà còn tận dụng hiệu quả khả năng xử lý song song của các hệ thống máy tính, đặc biệt là khi sử dụng các thư viện tối ưu hóa Đại số Tuyến tính. Bằng cách chuyển đổi các công thức Hồi quy Tuyến tính sang dạng Vector/Ma trận, chúng ta đã biến một thuật toán đơn giản thành một công cụ mạnh mẽ, sẵn sàng đối phó với dữ liệu phức tạp nhất!
V. Mở rộng: Linear Regression vs Logistic Regression
1. Tổng quan vể Logistic Regression
1.1. Tình huống thực tế
Giờ hãy tưởng tượng một bài toán khác:
Bạn sắp có 1 bài kiểm tra kết thúc học phần của Module 5, bạn dự định học 4 tiếng một ngày, vậy với thời gian biểu như vậy thì liệu rằng bạn sẽ đậu hay trượt bài kiểm tra đó?
| Giờ học | Kết quả (Pass=1 / Fail=0) |
|---|---|
| 0.5 | 0 |
| 1.0 | 0 |
| 1.5 | 0 |
| 2.0 | 0 |
| 2.5 | 1 |
| 3.0 | 1 |
| 3.5 | 1 |
| 4.0 | 1 |
Ở đây, đầu ra chỉ có 0 hoặc 1, chứ không phải số thực như hồi quy tuyến tính.
Nên ta không thể vẽ một đường thẳng và nói “giờ học 2.7 → kết quả 1.3” được!
=> Cần một mô hình cho phân loại – và đó chính là Logistic Regression.
1.2. Công thức thần kỳ – Hàm Sigmoid
$$\sigma(z) = \frac{1}{1 + e^{-z}}$$
Nếu vẽ đồ thị, sigmoid trông giống như một chữ S mềm mại, chuyển từ 0 sang 1.
Khi $z$ nhỏ (âm), $\sigma(z)$ gần 0 → dự đoán “Fail”
Khi $z$ lớn (dương), $\sigma(z)$ gần 1 → dự đoán “Pass”
Máy sẽ học sao cho tại khoảng 2.5 giờ học là ranh giới chia hai lớp – đúng như trực giác của ta!
1.3. Hàm mất mát (Loss function)
Khác với MSE, Logistic Regression dùng Binary Cross Entropy:
$$\displaystyle L = - \left[ y \log(\hat{y}) + (1 - y) \log(1 - \hat{y}) \right]$$
Nếu dự đoán gần với nhãn thật (0 hoặc 1), loss nhỏ → tốt.
Nếu sai lệch nhiều → loss lớn.
Và vẫn dùng công thức quen thuộc:
$$\theta = \theta - \eta \nabla_{\theta} L$$
trong đó:
$$\nabla_{\theta} L = x (\hat{y} - y)$$
🧠 Giải thích:
$\nabla_{\theta} L$: Gradient của hàm mất mát theo tham số $\theta$
$x$: Đặc trưng (feature) đầu vào
$\hat{y}$: Giá trị dự đoán
$y$: Giá trị thực tế
1.4. Khi sigmoid chưa đủ – Hàm Tanh (Tiếp tuyến Hyperbolic) xuất hiện
Ngoài sigmoid, người ta còn dùng hàm Tanh (hyperbolic tangent):
$$\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$$
Tanh cho đầu ra trong khoảng (-1, 1) thay vì (0, 1).
Vì trung tâm ở 0, gradient lớn hơn → học nhanh hơn một chút.
Cả hai hàm sigmoid và tanh đều giúp mô hình hiểu được “xác suất” của mỗi lớp, chứ không chỉ là kết quả cứng nhắc 0–1.
2. Tổng hợp nhanh: Linear vs Logistic Regression
| Đặc điểm | Linear Regression | Logistic Regression |
|---|---|---|
| Loại bài toán | Dự đoán giá trị liên tục | Phân loại nhị phân |
| Hàm kích hoạt | Không có | Sigmoid (hoặc Tanh) |
| Loss function | MSE | Binary Cross Entropy |
| Output | Số thực bất kỳ | Xác suất (0 → 1) |
| Ứng dụng | Dự đoán giá nhà, điểm thi | Dự đoán đậu/rớt, email spam, bệnh có/không |
Kết bài:
Phía sau đường thẳng tưởng chừng đơn giản là một chuỗi quá trình tinh vi: biểu diễn dữ liệu bằng vector, tính toán hàm mất mát, tối ưu bằng Gradient Descent, và kiểm soát độ khớp bằng Regularization. Linear Regression không chỉ là một mô hình dự đoán — nó là nền tảng của toàn bộ tư duy học máy.
Khi hiểu rõ cách Linear Regression học từ dữ liệu, bạn sẽ thấy những mô hình phức tạp hơn như Logistic Regression, Neural Network hay Deep Learning cũng dựa trên cùng nguyên tắc: xây dựng hàm mất mát, tìm cực tiểu, và tổng quát hóa tốt nhất cho dữ liệu mới.
Vì thế, nắm vững Linear Regression không chỉ giúp bạn “vẽ một đường thẳng đẹp” mà còn giúp bạn hiểu cách máy học nhìn thế giới — bằng toán học, logic và dữ liệu.
Reference:
Các hình ảnh được lấy từ tài liệu khóa học AIO Module 05 Tuần 01 và 02
và từ các hình tự vẽ
Chưa có bình luận nào. Hãy là người đầu tiên!