1. Cơ sở lý thuyết
1.1. Phương trình Đường thẳng (Mô hình)
Mô hình Simple Linear Regression (SLR) được biểu diễn bằng phương trình:
$$
\hat{y} = wx +b
$$
Trong đó:
- $\hat{y}$: Giá trị dự đoán (ví dụ: lương dự đoán).
- x: Biến đầu vào/độc lập (ví dụ: số năm kinh nghiệm).
- w: Trọng số/Hệ số góc (Weight), điều chỉnh độ nghiêng của đường thẳng.
- b: Sai số/Hệ số chặn (Bias), điều chỉnh vị trí giao điểm trên trục tung.
1.2. Hàm Mất mát (Loss Function)
- Hàm mất mát phổ biến được sử dụng là Tổng Sai số Bình phương (Sum of Squared Errors - SSE), hoặc có thể coi là một biến thể của MSE:
$$ L(w,b)=∑^N_{i=1}(\hat{y_i}−y_i)^2=∑^N_{i=1}(wx_i+b−y_i)^2 $$ - Mục tiêu là tìm w∗ và b∗ sao cho L(w,b) là nhỏ nhất.
- Các hàm mất mát:
| Tiêu chí | Mean Square Error (MSE) | Mean Absolute Error (MAE) |
|---|---|---|
| Công thức | $L(w,b)=∑^N_{i=1}(\hat{y_i}−y_i)^2$ | $L(w,b)=∑^N_{i=1} |
| Nhạy với outlier | Rất cao | Thấp |
| Gradient (độ dốc) | Mạnh với lỗi lớn | Không đổi |
| Độ trơn | Trơn toàn phần | Không trơn tại 0 |
| Tốc độ học | Nhanh hơn | Chậm hơn |
| Dễ diễn giải | Khó hơn (đơn vị bình phương) | Dễ hơn (đơn vị gốc) |
| Khi nên dùng | Khi dữ liệu ít nhiễu, muốn mô hình chính xác | Khi dữ liệu có outlier hoặc nhiễu lớn |
1.3 Cập nhật Tham số bằng Gradient Descent
GD là một quá trình lặp để tối ưu hóa L(w,b) bằng cách tính đạo hàm riêng (gradient) theo từng tham số.
1.3.1. Tính đạo hàm riêng theo hàm loss
- Gradient theo w:
- MSE:
$$ \frac{∂w}{∂L}=∑^N_{i=1}2x_i(\hat{y_i}−y_i) $$ - MAE:
$$ \frac{∂w}{∂L}=∑^N_{i=1}2x_i\frac{\hat{y_i}−y_i}{|\hat{y_i}−y_i|} $$
- MSE:
- Gradient theo b:
- MSE:
$$ \frac{∂b}{∂L}=∑^N_{i=1}2(\hat{y_i}−y_i) $$ - MAE:
$$ \frac{∂w}{∂L}=∑^N_{i=1}2\frac{\hat{y_i}−y_i}{|\hat{y_i}−y_i|} $$
- MSE:
1.3.2. Cập nhật Tham số
Các tham số được cập nhật theo công thức:
$$
w_{new}=w_{old}−η⋅\frac{∂w}{∂L}
$$
$$
b_{new}=b_{old}−η⋅\frac{∂b}{∂L} $$
Trong đó:
- η (eta): Tốc độ học (Learning Rate), là một siêu tham số (hyperparameter) quyết định độ lớn của bước nhảy trong không gian tham số.
2. Vấn đề của MSE và MAE
2.1. Mean Squared Error (MSE)
Định nghĩa:
$$L = (\hat{y} - y)^2$$
Ưu điểm:
- Liên tục và khả vi, dễ áp dụng Gradient Descent để tối ưu.
- Nhạy trong việc phát hiện sai số vì sai số lớn được khuếch đại bởi bình phương.
Vấn đề:
- Nhạy cảm với outliers: Khi dữ liệu có các điểm ngoại lai (giá trị sai số lớn), phần bình phương làm cho lỗi của các điểm đó chi phối quá trình học.
- Mô hình bị "lệch" để giảm lỗi của outliers thay vì tối ưu cho phần lớn dữ liệu trung tâm.
Ví dụ: nếu phần lớn sai số trong khoảng 1-2, nhưng có một điểm sai số = 10, giá trị lỗi là $10^2 = 100$, gấp 50-100 lần lỗi trung bình.
Khi sai số lớn, gradient cũng lớn tương ứng. Mô hình tăng tốc độ cập nhật tham số mạnh chỉ để giảm lỗi của một vài điểm cực đoan. Kết quả:
- Hướng cập nhật của gradient bị lệch khỏi xu hướng trung bình của dữ liệu.
- Mô hình học "thiên vị" theo outliers, thay vì tối ưu cho đa số điểm dữ liệu.Việc này khiến mô hình kém tổng quát hóa và có khả năng overfitting cục bộ.
2.2. Mean Absolute Error (MAE)
Định nghĩa:
$$L = |\hat{y} - y|$$
Ưu điểm:
- Ít bị ảnh hưởng bởi outliers vì độ tăng tuyến tính.
- Phù hợp cho dữ liệu có nhiều nhiễu hoặc phân phối lệch.
Vấn đề:
- Không khả vi tại 0: Hàm trị tuyệt đối có điểm gãy tại 0, khiến đạo hàm không xác định, khó áp dụng Gradient Descent chuẩn.
- Hội tụ chậm: Độ dốc của MAE là hằng số, tốc độ học không phản ánh đúng độ lớn sai số, mô hình học chậm hơn, đặc biệt khi gần điểm hội tụ.
2.3. Giải pháp
Cả MSE và MAE đều có hạn chế riêng. Cần một hàm mất mát kết hợp ưu điểm của cả hai – vừa khả vi, vừa ít nhạy với outliers.Điều này dẫn đến sự ra đời của Huber Loss.
3. Huber Loss
3.1 Giới thiệu
Huber Loss là một hàm mất mát được đề xuất nhằm khắc phục những hạn chế của MSE và MAE, bằng cách kết hợp ưu điểm của cả hai. Hàm này hoạt động như MSE đối với các lỗi nhỏ (giúp gradient mượt và hội tụ nhanh), và như MAE đối với các lỗi lớn (giảm ảnh hưởng của outliers).
Định nghĩa:
$$L(\hat{y}, y) =
\begin{cases}
\frac{1}{2}(\hat{y} - y)^2, & \text{nếu } |\hat{y} - y| \le \delta \\
\delta|\hat{y} - y| - \frac{1}{2}\delta^2, & \text{nếu } |\hat{y} - y| > \delta
\end{cases}
$$
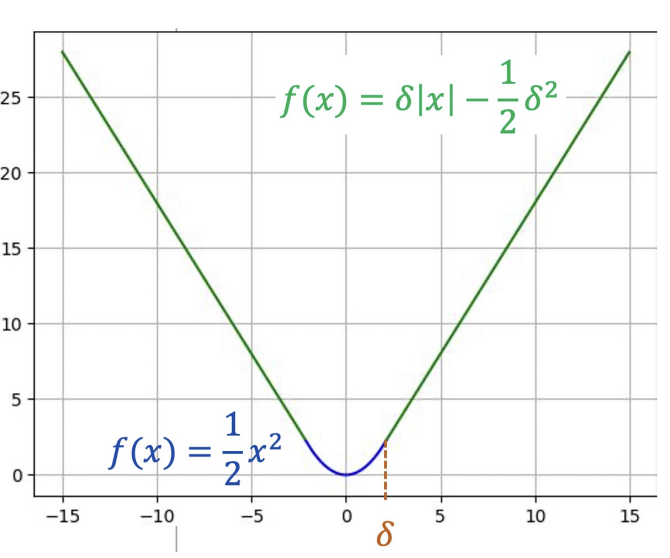
Hình 1. Đồ thị hàm Huber Loss (From AIO 2025)
Trong đó:
- $δ$: ngưỡng giới hạn.
- $\hat{y}$: giá trị dự đoán.
- $y$: giá trị thực tế.
3.2. Ý tưởng hoạt động
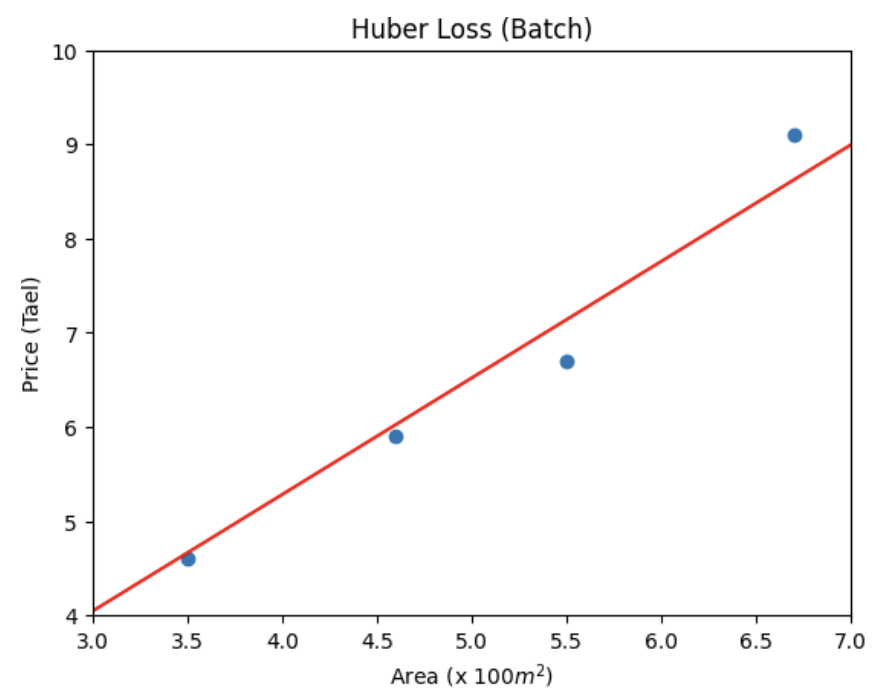
Hình 2. Kết quả sau khi áp dụng Huber Loss
- Khi sai số nhỏ hơn $δ$, Huber Loss hoạt động như MSE giúp gradient trơn tru và tối ưu nhanh.
- Khi sai số lớn hơn $δ$, hoạt động như MAE giảm tác động của các điểm ngoại lai.
- Nhờ vậy, mô hình học ổn định hơn, vừa nhanh hội tụ như MSE, vừa chống nhiễu như MAE.
3.3. Lý do cần dùng Huber Loss
| Tiêu chí | MSE | MAE | Huber Loss |
|---|---|---|---|
| Ảnh hưởng của outliers | Rất cao | Thấp | Trung bình (được kiểm soát bởi δ) |
| Khả vi | Có | Không tại 0 | Có (trơn toàn miền) |
| Gradient | Lớn khi lỗi lớn | Hằng số | Điều chỉnh linh hoạt |
| Tốc độ hội tụ | Nhanh | Chậm | Ổn định và mượt mà |
Lý do chính nên dùng Huber Loss:
- Giảm ảnh hưởng của outliers: Khi dữ liệu có nhiễu, Huber Loss tránh cho mô hình bị kéo lệch bởi các giá trị cực đoan.
- Giữ gradient mượt: Không bị điểm gãy như MAE, dễ áp dụng Gradient Descent.
- Tối ưu ổn định hơn: Tránh dao động mạnh khi học, đặc biệt ở giai đoạn đầu huấn luyện.
- Ứng dụng thực tế: Được sử dụng phổ biến trong hồi quy tuyến tính, regression robust, và các mô hình deep learning như Faster R-CNN, SSD (dưới tên gọi Smooth L1 Loss).
3.4. Kết luận
Huber Loss là một sự dung hòa thông minh giữa MSE và MAE:
- Giữ được tính khả vi, dễ tối ưu.
- Giảm nhạy cảm với ngoại lai, tăng độ ổn định và khả năng tổng quát.
- Là lựa chọn hiệu quả khi dữ liệu có một lượng nhỏ nhiễu hoặc outliers, nhưng vẫn cần tốc độ hội tụ nhanh và gradient mượt mà.
4. Normalization & Regularization
4.1. Normalization (Chuẩn hoá dữ liệu)
Trong các bài toán hồi quy tuyến tính, mỗi đặc trưng (feature) đầu vào có thể mang đơn vị đo lường và phạm vi giá trị khác nhau.
Ví dụ:
diện tích nhàcó thể dao động từ 30–300 $m^2$số phòng ngủchỉ nằm trong khoảng 1–5
Nếu ta không xử lý sự khác biệt này, feature có giá trị lớn hơn (ví dụ: diện tích) sẽ chi phối quá trình học, khiến mô hình:
- Tối ưu sai hướng (do gradient bị mất cân bằng).
- Hội tụ chậm hoặc dao động mạnh.
- Cần learning rate rất nhỏ mới ổn định.
Mục tiêu:
Giúp các đặc trưng
đầu vào có cùng thang đo, đảm bảo mỗi feature đóng góp công bằng vào quá trình huấn luyện.
Công thức chuẩn hóa Min-Max Normalization:
$$x' = \frac{x - x_{min}}{x_{max} - x_{min}}$$
Ngoài ra còn một số công thức Normalization khác như:
Z-score Normalization:
$$x' = \frac{x - \mu}{\sigma}$$
Với:
- $\mu$ là trung bình,
- $\sigma$ là độ lệch chuẩn.
Lợi ích:
- Gradient descent hội tụ nhanh hơn và ổn định hơn.
- Giúp learning rate hoạt động nhất quán trên các chiều dữ liệu.
- Tránh tình trạng mô hình thiên vị feature có phạm vi giá trị lớn.
Ví dụ:
Khi dự đoán giá nhà từ 2 đặc trưng diện tích ($m^2$) và số phòng ngủ, nếu không chuẩn hóa, trọng số của diện tích sẽ rất lớn để bù cho sự chênh lệch thang đo, gây bất ổn trong quá trình tối ưu.
4.2. Regularization (Điều chuẩn)
Khi mô hình có quá nhiều tham số hoặc dữ liệu huấn luyện chưa nhiều, nó có thể học thuộc lòng (overfitting) thay vì học xu hướng tổng quát.
Điều này khiến mô hình:
- Dự đoán rất chính xác trên tập huấn luyện.
- Nhưng sai lệch nghiêm trọng trên tập kiểm tra hoặc dữ liệu thực tế.
Regularization ra đời để kiểm soát độ phức tạp của mô hình, bằng cách thêm một điều khoản phạt (penalty term) vào hàm mất mát gốc, nhằm:
- Giới hạn độ lớn của trọng số (weights) trong mô hình.
- Buộc mô hình phải học đơn giản hơn (đường hồi quy ít dao động hơn).
- Ngăn trọng số tăng quá cao chỉ để "vừa khít" một vài điểm dữ liệu nhiễu.
Ví dụ:
- Nếu không có regularization, mô hình có thể tạo ra đường hồi quy "uốn cong" mạnh chỉ để đi qua tất cả các điểm dữ liệu — dẫn đến overfitting.
- Regularization thêm "lực kéo" để làm phẳng đường hồi quy, giúp mô hình tổng quát hơn.
Công thức tổng quát:
$$L_{reg} = L_{original} + \lambda R(w)$$
Trong đó:
- $L_{original}$: hàm mất mát ban đầu (MSE, Huber, ...)
- $R(w)$: hàm phạt dựa trên trọng số
- $\lambda$: hệ số điều chỉnh mức độ phạt
Các loại phổ biến:
| Loại | Hàm phạt | Tác dụng | Đặc điểm |
|---|---|---|---|
| L2 (Ridge) | $R(w) = \sum w_i^2$ | Giảm độ lớn của trọng số | Mô hình mượt, không loại bỏ đặc trưng |
| L1 (Lasso) | $R(w) = \sum |w_i|$ | Một số trọng số bị ép về 0 | Giúp chọn lọc đặc trưng |
| Elastic Net | Kết hợp L1 + L2 | Cân bằng giữa độ ổn định và chọn lọc | Linh hoạt, dùng nhiều trong thực tế |
Lợi ích:
- Giảm overfitting, cải thiện khả năng tổng quát hóa.
- Giữ trọng số nhỏ, mô hình đơn giản và ổn định hơn.
- L1 giúp tự động loại bỏ feature không quan trọng.
5. Vectorization cho Linear Regression
Ở các phần trước ta đã bàn về hàm mất mát (MSE/MAE/Huber), chuẩn hoá và điều chuẩn. Phần này tập trung vào cách hiện thực hoá tối ưu hoá bằng đại số tuyến tính để chạy nhanh và gọn với NumPy.
5.1. Từ 1 mẫu (scalar) -> vector
Gom bias vào cùng với trọng số bằng cách thêm 1 vào đặc trưng:
$$x = \begin{bmatrix} 1 \\ x_1 \\ \vdots \\ x_d \end{bmatrix}, \quad \theta = \begin{bmatrix} b \\ w_1 \\ \vdots \\ w_d \end{bmatrix}, \quad \hat{y} = \theta^T x.$$
Với MSE đơn mẫu $L = (\hat{y} - y)^2$, gradient:
$$\nabla_\theta L = 2(\hat{y} - y)x$$
Luật cập nhật SGD:
$$\theta \leftarrow \theta - \eta \nabla_\theta L$$
Việc "hấp thụ bias" làm cho mọi tham số được cập nhật bằng một công thức duy nhất – rất hợp với vectorization.
5.2. m-sample (mini-batch)
Gom $m$ mẫu vào ma trận-vector:
$$X = \begin{bmatrix} (x^{(0)})^T \\ \vdots \\ (x^{(m-1)})^T \end{bmatrix} \in \mathbb{R}^{m \times (d+1)}, \quad y = \begin{bmatrix} y^{(0)} \\ \vdots \\ y^{(m-1)} \end{bmatrix} \in \mathbb{R}^{m}.$$
Dự đoán hàng loạt:
Mất mát trung bình mini-batch: $L = \frac{1}{m}(\hat{y} - y)^T (\hat{y} - y)$
Gradient gọn:
$$\nabla_\theta L = \frac{1}{m} X^T k = \frac{2}{m} X^T (\hat{y} - y)$$
Cập nhật:
$$\theta \leftarrow \theta - \eta \nabla_\theta L$$
Một số tài liệu xếp mẫu theo cột (samples-as-columns). Khi đó $\hat{y} = \theta^T X$ và $\nabla_\theta L = \frac{1}{m} X k^T$. Hai cách tương đương, chỉ khác chiều.
5.3. N-sample (full-batch)
Khi dùng toàn bộ dữ liệu ($m=N$):
$$\hat{y} = X\theta$$
$$\nabla_\theta L = \frac{2}{N} X^T (X\theta - y)$$
$$\theta \leftarrow \theta - \eta \frac{2}{N} X^T (X\theta - y)$$
- Ưu điểm: gradient ổn định.
- Nhược: mỗi bước đắt khi NNN lớn.
- Thực hành: mini-batch (32-512) cần bằng tốc độ và độ ổn định.
5.4. Kết hợp với Regularization
Nếu điều chuẩn Ridge (L2) với hệ số $\lambda$ (không phạt bias):
$$\nabla_\theta L_{Ridge} = \frac{2}{m} X^T (\hat{y} - y) + 2\lambda \tilde{\theta}, \quad \tilde{\theta} = \begin{bmatrix} 0 \\ w_1 \\ \vdots \\ w_d \end{bmatrix}$$
Lasso (L1): $\nabla_\theta L_{Lasso} = \frac{2}{m} X^T (\hat{y} - y) + \lambda \text{sign}(\tilde{\theta})$ (dưới đạo hàm tại 0).
Huber (tham số $\delta$) - đạo hàm theo dự đoán:
$$\frac{\partial L}{\partial \hat{y}} = \begin{cases} \hat{y} - y, & |\hat{y} - y| \le \delta \\ \delta \cdot \text{sign}(\hat{y} - y), & |\hat{y} - y| \> \delta \end{cases} \Rightarrow \nabla\_\theta L = \frac{1}{m} X^T g, \quad g\_i = \frac{\partial L}{\partial \hat{y}^{(i)}} $$
6. Cài đặt NumPy
6.1. API huấn luyện tối thiểu (MSE)
import numpy as np
def predict(X, theta):
# X: (m, d+1) đã có cột 1
# theta: (d+1, 1)
return X @ theta # (m, 1)
def mse_grad(X, y, theta):
y_hat = predict(X, theta)
# (2.0 / X.shape[0]) * (X.T @ (y_hat - y)) # (d+1, 1)
return (2.0 / X.shape[0]) * (X.T @ (y_hat - y))
def fit_mse(X, y, lr=1e-2, epochs=200, batch_size=None, theta0=None, seed=0):
m, d1 = X.shape
theta = np.zeros((d1, 1)) if theta0 is None else theta0.copy()
if batch_size is None: batch_size = m # full-batch
rng = np.random.default_rng(seed)
for _ in range(epochs):
perm = rng.permutation(m)
for s in range(0, m, batch_size):
j = perm[s:s+batch_size]
theta -= lr * mse_grad(X[j], y[j], theta)
return theta
6.2. Thay Huber Loss (mượt, chống nhiễu)
def huber_grad(X, y, theta, delta=1.0):
y_hat = predict(X, theta)
r = y_hat - y
g = np.where(np.abs(r) <= delta, r, delta * np.sign(r)) # ∂L/∂ŷ
return (1.0 / X.shape[0]) * (X.T @ g)
6.3. Thêm Ridge (L2) dễ dàng
def ridge_grad(X, y, theta, lam=1e-3):
grad = mse_grad(X, y, theta)
reg = theta.copy()
reg[0] = 0.0 # không phạt bias
return grad + 2.0 * lam * reg
Chỉ cần thay hàm *_grad tương ứng trong vòng lặp là xong.
7. Ví dụ mini: House Price & Advertising
- House price (1 biến)
- $X = [\text{1, area}] \in \mathbb{R}^{N \times 2}, \quad \theta = [b, w]^T$
fit_mse(X, y, lr=0.01, epochs=300, batch_size=32)
- Advertising (3 biến)
- $X = [\text{1, TV, Radio, Newspaper}] \in \mathbb{R}^{N \times 4}$
- Hữu ích khi so sánh: MSE vs Huber (outliers báo chí) và Ridge (khi TV/Radio đồng tuyến tính tương đối).
Kỳ vọng:
- Huber thường cho đường học ổn định hơn khi có vài điểm lệch lớn.
- Ridge giảm phương sai và hệ số phình to, đặc biệt khi feature scale đã chuẩn hoá.
8. Best practices & Lỗi thường gặp
- Chuẩn hoá trước khi học (Z-score/Min-Max).
- Thêm cột 1 cho bias, bảo đảm
X.shape = (m, d+1). - Kiểm tra chiều: Lỗi phổ biến nhất là nhầm "samples-as-rows" và "samples-as-columns".
- Learning rate: Bắt đầu
1e-2hoặc1e-3, theo dõi loss; nếu loss tăng vọt $\rightarrow$ giảm $\eta$. - Tách train/val + early stopping (đặc biệt khi dùng L2/L1).
- Đánh giá: không chỉ MSE/MAE mà còn R2/$\text{R2R}^2$, residual plots để phát hiện mô hình thiếu tuyến tính hay outliers hệ thống.
- Regularization:
- Ridge khi nghi ngờ đa cộng tuyến (features liên quan chặt chẽ).
- Lasso khi muốn chọn đặc trưng (đẩy nhiều hệ số về 0).
- Elastic Net khi cần cân bằng hai mục tiêu trên.
TL;DR (ghi nhớ nhanh)
- Gom bias vào vector: $x = [1, ...]^T, \theta = [b, w_1, ...]^T$
- Mini/Full-batch: $\hat{y} = X\theta, \nabla_\theta L = \frac{2}{m} X^T (\hat{y} - y)$
- Huber: thay $(\hat{y} - y)$ bằng $g = \text{clip}(\hat{y} - y, [-\delta, \delta])$
- Ridge/Lasso: cộng thêm hạng phạt vào gradient; không phạt bias.
- Vectorization giúp code ngắn, nhanh, ít lỗi, mở rộng dễ dàng cho các biến thể loss/regularization.
9. Tổng kết
Để xây dựng một mô hình hồi quy hiệu quả, cần kết hợp hài hòa giữa việc chọn hàm mất mát phù hợp, chuẩn hóa dữ liệu đầu vào, và áp dụng regularization để đạt được sự cân bằng giữa độ chính xác và tính ổn định.
- Loss Function: MSE, MAE và Huber Loss đều có mục tiêu chung là đo lường sai số giữa dự đoán và thực tế, nhưng khác nhau ở cách xử lý outliers.
- MSE học nhanh nhưng nhạy với nhiễu.
- MAE ổn định nhưng khó tối ưu.
- Huber Loss là lựa chọn cân bằng, kết hợp ưu điểm của cả hai.
- Normalization: Giúp các đặc trưng có cùng thang đo, tránh việc một đặc trưng chi phối quá trình học, đồng thời tăng tốc độ và độ ổn định của mô hình.
- Regularization: Giúp kiểm soát độ phức tạp của mô hình, hạn chế overfitting và cải thiện khả năng tổng quát hóa trên dữ liệu mới.
Để dễ hiểu, hãy xem xây dựng mô hình hồi quy như bộ lắp ghép gồm bốn mảnh. Mỗi mảnh có vai trò rõ ràng, dùng đúng thì mô hình học nhanh, ổn định và tổng quát tốt.
Mảnh 1 — Hàm mất mát: đo sai ở đâu, sửa ở đó
- MSE: phù hợp khi dữ liệu sạch. Ưu điểm là đạo hàm trơn $\rightarrow$ tối ưu nhanh. Nhược điểm: cực kỳ nhạy với outliers.
- MAE: bền với outliers. Tuy nhiên không trơn tại 0 $\rightarrow$ tốc độ tối ưu có thể chậm.
- Huber: kết hợp hai bên.
- Lỗi nhỏ $\rightarrow$ hành xử như MSE (học nhanh).
- Lỗi lớn $\rightarrow$ hành xử như MAE (chống nhiễu).
- $\rightarrow$ Lựa chọn an toàn khi dữ liệu có một ít điểm lệch.
Ghi nhớ: Có nhiễu $\rightarrow$ ưu tiên Huber; dữ liệu sạch $\rightarrow$ MSE.
Mảnh 2 — Chuẩn hoá (Normalization): đưa mọi thuốc đo về cùng "đơn vị"
- Đặc trưng khác thang đo ($m^2$, phòng ngủ, ...) làm gradient lệch và học chậm.
- Dùng Z-score/Min-Max để đưa về cùng thang đo.
- Kết quả: bước cập nhật cân bằng, hội tụ nhanh và mượt hơn.
Ghi nhớ: Hầu như luôn chuẩn hoá trước khi huấn luyện.
Mảnh 3 — Điều chuẩn (Regularization): tránh "học thuộc lòng"
- Ridge (L2): kìm hệ số phình to (đa cộng tuyến), giúp đường hồi quy mượt.
- Lasso (L1): đẩy nhiều hệ số về 0 $\rightarrow$ chọn đặc trưng tự nhiên.
- Elastic Net: cân bằng L1 + L2 khi vừa muốn ổn định, vừa muốn lọc đặc trưng.
Ghi nhớ: Điều chuẩn để giảm overfitting; không phạt bias.
Mảnh 4 — Vectorization: học thông minh, không học vất vả
- Viết dự đoán theo ma trận: $\hat{y} = X\theta$ (thêm cột 1 để hấp thụ bias).
- Gradient tổng quát: $\nabla_\theta L = \frac{1}{m} X^T g$, trong đó $g = \frac{\partial L}{\partial \hat{y}}$ (MSE: $g = 2(\hat{y} - y)$; Huber: $g = \text{clip}(\hat{y} - y, \pm \delta)$).
- Dùng mini-batch 32-512 để cân bằng tốc độ và ổn định; full-batch khi dữ liệu nhỏ.
Ghi nhớ: Vector hóa giúp code ngắn, chạy nhanh, khó sai chiều.
Quy trình 5 bước (checklist thực hành)
- Chuẩn hoá tất cả đặc trưng (Z-score).
- Chọn loss: Huber (có outliers) / MSE (dữ liệu sạch).
- Thêm regularization: Ridge/Lasso/Elastic Net (không phạt bias).
- Huấn luyện có vectorization + mini-batch; bắt đầu LR $10^{-2}$ hoặc $10^{-3}$.
- Theo dõi loss và residuals; tinh chỉnh $\eta$, $\lambda$, $\delta$; dùng early stopping khi cần.$$
10. Tài liệu tham khảo
- Quang-Vinh Dinh, Advanced Linear Regression Loss Functions, AIO 2025
- Quang-Vinh Dinh, Vectorization for Linear Regression, AIO 2025
Chưa có bình luận nào. Hãy là người đầu tiên!