Đề tài: Ứng dụng Hồi quy Phi tuyến và Regularization trong Dự đoán Cường độ Nén Bê tông
Chương 1 – Giới thiệu đề tài
1.1. Bối cảnh của dự án
Trong thực tế, mối quan hệ giữa các thành phần vật liệu trong bê tông và cường độ chịu nén của nó thường rất phức tạp và phi tuyến. Ví dụ, lượng xi măng, nước, phụ gia siêu dẻo, hay tuổi của bê tông không ảnh hưởng độc lập mà có thể tương tác với nhau theo những cách không dễ mô hình hóa bằng hồi quy tuyến tính đơn giản. Chẳng hạn, một hỗn hợp bê tông có lượng xi măng cao nhưng thiếu phụ gia hoặc nước không phù hợp có thể không đạt được cường độ như mong muốn. Những mối quan hệ phi tuyến và tương tác giữa các đặc trưng này đòi hỏi các mô hình hồi quy linh hoạt hơn để mô phỏng chính xác.
Do đó, việc áp dụng các mô hình hồi quy phi tuyến như Polynomial Regression, kết hợp với các kỹ thuật điều chuẩn như Ridge (L2) và Lasso (L1), là cần thiết để cải thiện độ chính xác và khả năng tổng quát hóa của mô hình trong việc dự đoán cường độ chịu nén của bê tông.
1.2. Vấn đề nghiên cứu
Làm thế nào để xây dựng một mô hình hồi quy có khả năng dự đoán chính xác cường độ chịu nén của bê tông, đồng thời tránh hiện tượng overfitting khi dữ liệu có nhiều đặc trưng vật liệu và mối quan hệ phi tuyến giữa chúng?
1.3. Mục tiêu và câu hỏi cải tiến
Mục tiêu của dự án là xây dựng một mô hình hồi quy có khả năng dự đoán chính xác cường độ chịu nén của bê tông dựa trên các thành phần vật liệu và thời gian đông kết. Mô hình cần đảm bảo tính tổng quát hóa tốt, tránh hiện tượng overfitting, đồng thời có thể giải thích được các mối quan hệ phi tuyến giữa các đặc trưng đầu vào.
Để đạt được mục tiêu này, dự án đặt ra các câu hỏi cải tiến sau:
- Làm thế nào để lựa chọn và biến đổi đặc trưng đầu vào nhằm phản ánh tốt hơn các mối quan hệ phi tuyến?
- Mô hình hồi quy phi tuyến nào (ví dụ: Polynomial Regression, Ridge, Lasso) phù hợp nhất với bài toán này?
- Việc điều chuẩn mô hình bằng các kỹ thuật như Ridge (L2) và Lasso (L1) có giúp cải thiện độ chính xác và giảm overfitting không?
- Có thể sử dụng các kỹ thuật trực quan hóa hoặc phân tích hệ số để hiểu rõ hơn về ảnh hưởng của từng thành phần vật liệu đến cường độ bê tông?
1.4. Phương pháp áp dụng
- Áp dụng các mô hình: Linear Regression, Polynomial Regression, Ridge và Lasso.
- Thực hiện tiền xử lý dữ liệu, tạo đặc trưng đa thức, chuẩn hóa và đánh giá mô hình bằng các chỉ số MSE, R².
Trong bài blog này, người đọc sẽ được giới thiệu các khái niệm và lý thuyết nền tảng về hồi quy tuyến tính và hồi quy phi tuyến, cùng với phân tích ưu và nhược điểm của từng mô hình. Trong nhiều trường hợp thực tế, hồi quy phi tuyến tỏ ra hiệu quả hơn nhờ khả năng mô hình hóa các mối quan hệ phức tạp giữa các biến. Tuy nhiên, khi áp dụng mô hình phi tuyến, nguy cơ overfitting cũng tăng cao, khiến mô hình dễ bị sai lệch khi gặp dữ liệu mới. Để khắc phục điều này, các kỹ thuật điều chuẩn như L1 (Lasso) và L2 (Ridge) sẽ được áp dụng nhằm kiểm soát độ lớn của các trọng số và tăng tính ổn định cho mô hình.
Các định nghĩa và khái niệm cơ bản sẽ được trình bày chi tiết trong Chương 2. Từ Chương 3, bài viết sẽ đi sâu vào phần thực hành, bao gồm cách triển khai dự án, phân tích dữ liệu, và quy trình xây dựng mô hình dự báo. Bên cạnh việc cải thiện mô hình, tiền xử lý dữ liệu cũng là một bước quan trọng không thể bỏ qua để đảm bảo chất lượng đầu vào cho mô hình học máy.
Cuối cùng, Chương 4 sẽ tổng hợp lại các kết quả thực nghiệm sau khi áp dụng các kỹ thuật mở rộng từ chương trước, giúp đánh giá hiệu quả của từng phương pháp và rút ra bài học kinh nghiệm cho các dự án tương tự trong tương lai.
Chương 2 – Cơ sở lý thuyết
2.1. Khái niệm và định nghĩa cơ bản
2.1.1. Hồi quy tuyến tính (Linear Regression)
- Định nghĩa: Là phương pháp hồi quy trong đó mối quan hệ giữa biến đầu vào và đầu ra được mô hình hóa bằng một hàm tuyến tính. Dạng tổng quát của mô hình là:
$$ y = w_0 + w_1x_1 + w_2x_2 + \dots + w_nx_n + \varepsilon $$
-
Trong đó:
- $y$: Giá trị đầu ra (biến phụ thuộc)
- $w_0$: Hệ số chặn (intercept) – giá trị $y$ khi tất cả $x_i = 0$
- $w_i$: Hệ số hồi quy (weight) ứng với biến đầu vào $x_i$
- $x_i$: Biến đầu vào (biến độc lập)
- $\varepsilon$: Sai số ngẫu nhiên (error term), biểu diễn phần nhiễu hoặc yếu tố không quan sát được
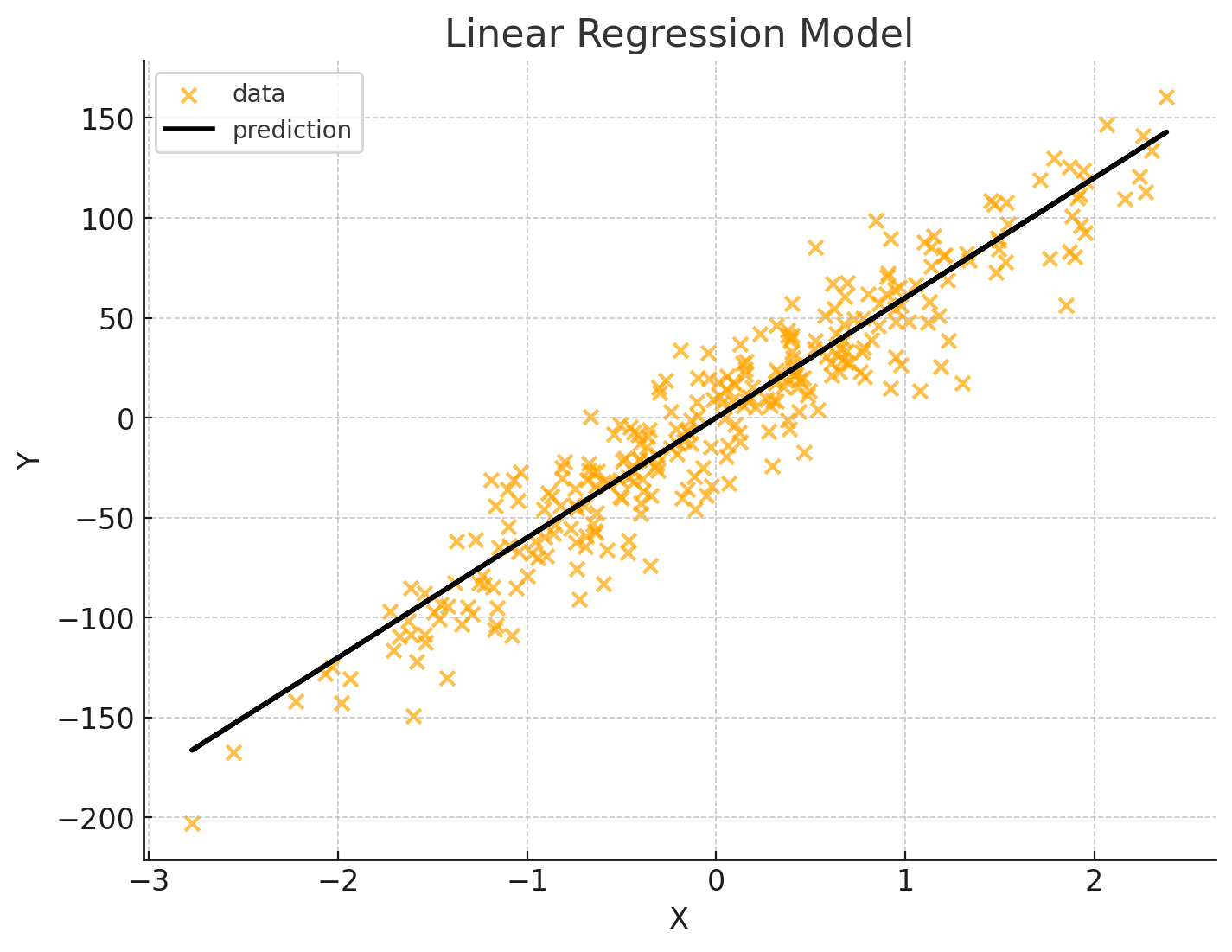
Hình 1: Hình ảnh minh họa về Linear Regression
-
Ưu điểm:
- Dễ hiểu, dễ triển khai.
- Tính toán nhanh, hiệu quả với dữ liệu lớn.
- Dễ giải thích kết quả (ý nghĩa của từng hệ số hồi quy).
-
Nhược điểm:
- Không phù hợp khi mối quan hệ giữa biến đầu vào và đầu ra là phi tuyến.
- Nhạy cảm với ngoại lệ (outliers).
- Giả định mạnh về phân phối dữ liệu (ví dụ: phân phối chuẩn của sai số).
2.2.2. Hồi quy phi tuyến (Polynomial Regression)
-
Định nghĩa:
Là phương pháp hồi quy trong đó mối quan hệ giữa biến đầu vào và đầu ra được mô hình hóa bằng một hàm phi tuyến, ví dụ như hàm bậc hai, hàm mũ, logarit, sigmoid,....
$$ y = w_0 + w_1x + w_2x^2 + \dots + w_nx^n + \varepsilon $$
- Trong đó:
- $y$: Giá trị dự đoán (biến phụ thuộc)
- $w_0$: Hệ số chặn (intercept)
- $w_1, w_2, \dots, w_n$: Các hệ số hồi quy (weights)
- $x, x^2, \dots, x^n$: Các bậc của biến đầu vào (polynomial terms)
- $\varepsilon$: Sai số ngẫu nhiên (error term)

Hình 2: Hình ảnh minh họa về Polynomial Regression
-
Ưu điểm:
- Mô hình hóa được các mối quan hệ phức tạp, phi tuyến.
- Linh hoạt hơn trong việc mô tả dữ liệu thực tế.
-
Nhược điểm:
- Khó triển khai và giải thích hơn.
- Dễ bị overfitting nếu không kiểm soát tốt.
- Tốn thời gian tính toán và yêu cầu kỹ thuật cao hơn.
2.2.3. Regularization:
-
Định nghĩa: Regularization là kỹ thuật quan trọng trong học máy, đặc biệt trong hồi quy, giúp giảm overfitting bằng cách thêm một điều khoản phạt vào hàm mất mát. Hai phương pháp phổ biến nhất là L1 (Lasso) và L2 (Ridge). Dưới đây là phần giải thích chi tiết:
2.2.3.1. Lasso Regression (L1) - (Least Absolute Shrinkage and Selection Operator)
L1 thêm tổng giá trị tuyệt đối của các hệ số vào hàm mất mát:
$$ Loss_{L1} = MSE + \lambda \sum_{j=1}^{n} |w_j| $$
với:
$$ MSE = \frac{1}{m} \sum_{i=1}^{m} (y_i - \hat{y_i})^2 $$
- Trong đó:
- $y_i$: Giá trị thực tế (ground truth)
- $\hat{y_i}$: Giá trị dự đoán của mô hình
- $w_j$: Trọng số (weight) tương ứng với đặc trưng $x_j$
- $\lambda$: Hệ số điều chỉnh mức độ regularization
- $m$: Số lượng mẫu dữ liệu
- $n$: Số đặc trưng (features)
=> Thành phần phạt $λ∑_{j=1}^n∣w_i∣$ giúp mô hình vừa giới hạn độ lớn của các trọng số, vừa tự động lựa chọn những đặc trưng quan trọng nhất. Khi λ lớn, nhiều trọng số sẽ bị triệt tiêu về 0 (feature selection), làm cho mô hình đơn giản và dễ hiểu hơn
-
Ưu điểm:
- Giúp giảm số lượng đặc trưng không cần thiết → mô hình đơn giản hơn.
- Tốt khi có nhiều đặc trưng nhưng chỉ một số ít là quan trọng.
2.2.3.2. Ridge regression (L2)
L2 thêm tổng bình phương các hệ số vào hàm mất mát:
$$ Loss_{L2}=MSE+λ∑_{i=1}^n w_i^2 $$
với:
$$
MSE = \frac{1}{m} \sum_{i=1}^{m} (y_i - \hat{y_i})^2
$$
- Trong đó:
- $y_i$: Giá trị thực tế (ground truth)
- $\hat{y_i}$: Giá trị dự đoán của mô hình
- $w_j$: Trọng số (weight) tương ứng với đặc trưng $x_j$
- $\lambda$: Hệ số điều chỉnh mức độ regularization
- $m$: Số lượng mẫu dữ liệu
- $n$: Số đặc trưng (features)
Nhờ vào cơ chế điều chỉnh độ lớn của các hệ số, Ridge giúp mô hình trở nên ổn định hơn, giảm độ nhạy với nhiễu trong dữ liệu và tránh việc học quá mức những biến động nhỏ trong tập huấn luyện.
Tuy nhiên, khác với Lasso, Ridge không loại bỏ hoàn toàn bất kỳ đặc trưng nào, các hệ số chỉ bị thu nhỏ chứ không bị đẩy về 0.
Vì vậy, Ridge thường được sử dụng trong các trường hợp mà ta muốn giữ lại toàn bộ đặc trưng, nhưng vẫn cần kiểm soát ảnh hưởng của những đặc trưng ít quan trọng để tránh làm phức tạp mô hình.
-
Ưu điểm:
- Tốt khi tất cả đặc trưng đều có ảnh hưởng nhỏ.
- Ổn định hơn khi có nhiều đặc trưng tương quan.
2.3. Nhược điểm và khoảng trống chưa được khắc phục của L1 và L2 Regularization
-
L1 Regularization (Lasso)
-
Không ổn định với đặc trưng tương quan cao
Khi các đặc trưng đầu vào có mối tương quan mạnh với nhau, Lasso có xu hướng chọn một đặc trưng và bỏ qua các đặc trưng còn lại, dẫn đến mô hình không ổn định và thiếu tính tổng quát.
-
Chọn lọc đặc trưng quá mức
Với giá trị λ lớn, Lasso có thể đẩy quá nhiều hệ số về 0, làm mất đi thông tin quan trọng và dẫn đến underfitting.
-
Không tối ưu cho bài toán có nhiều đặc trưng nhỏ nhưng quan trọng
Trong các bài toán mà nhiều đặc trưng có ảnh hưởng nhỏ nhưng cộng lại tạo ra ảnh hưởng lớn, Lasso có thể bỏ qua những đặc trưng này vì nó ưu tiên sự đơn giản.
-
-
L2 Regularization (Ridge)
-
Không thực hiện chọn lọc đặc trưng
Ridge giữ lại tất cả đặc trưng, kể cả những đặc trưng không quan trọng, dẫn đến mô hình phức tạp và khó giải thích.
-
Không hiệu quả khi số lượng đặc trưng lớn hơn số lượng mẫu
Trong trường hợp dữ liệu có chiều cao (high-dimensional), Ridge không thể loại bỏ đặc trưng dư thừa, gây khó khăn trong việc giảm nhiễu.
-
Không xử lý tốt dữ liệu thưa (sparse data)
Với dữ liệu mà phần lớn giá trị là 0 (như dữ liệu văn bản), Ridge không thể tận dụng tính thưa để đơn giản hóa mô hình như Lasso.
-
-
Khoảng trống chung chưa được khắc phục
-
Thiếu sự linh hoạt trong việc cân bằng giữa chọn lọc và giữ lại đặc trưng
Không có phương pháp nào trong L1 hoặc L2 có thể vừa chọn lọc đặc trưng hiệu quả vừa giữ lại thông tin từ các đặc trưng tương quan.
-
Không tự động điều chỉnh theo cấu trúc dữ liệu
Cả hai phương pháp đều yêu cầu người dùng chọn giá trị λ phù hợp, nhưng không có cơ chế nội tại để tự điều chỉnh theo đặc điểm của dữ liệu.
-
Không xử lý tốt dữ liệu phi tuyến
L1 và L2 đều hoạt động tốt trong mô hình tuyến tính, nhưng không đủ mạnh để xử lý mối quan hệ phi tuyến giữa các biến.
-
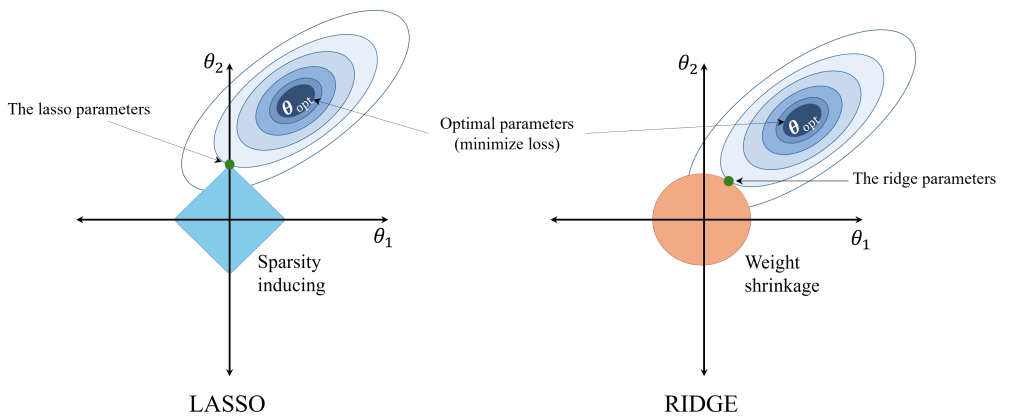
Hình 3: So sánh ý nghĩa hình học của Lasso Regression (L1) và Ridge Regression (L2) (AI Viet Nam)
2.4. Cải tiến với ElasticNet Regression (L1 + L2)
Định nghĩa:
ElasticNet kết hợp phạt L1 (Lasso) và L2 (Ridge) vào hàm mất mát:
$${Loss_{ElasticNet} = \underbrace{\frac{1}{m} \sum_{i=1}^{m} (y_i - \hat{y}_i)^2}_{MSE} + \underbrace{\alpha \cdot \rho \cdot \sum_{j=1}^{n} |w_j|}_{L1} + \underbrace{\alpha \cdot (1 - \rho) \cdot \sum_{j=1}^{n} w_j^2}_{L2}}$$
Trong đó:
- $m$: Số mẫu dữ liệu
- $n$: Số đặc trưng
- $y_i$: Giá trị thực tế (sức mạnh bê tông)
- $\hat{y}_i$: Giá trị dự đoán
- $w_j$: Hệ số hồi quy của đặc trưng $j$
- $\alpha \geq 0$: Tổng mức độ điều chuẩn (càng lớn → phạt càng mạnh)
- $\rho \in [0,1]$ (l1_ratio): Tỷ lệ L1
- $\rho = 1 \rightarrow$ Lasso
- $\rho = 0 \rightarrow$ Ridge
- $0 < \rho < 1 \rightarrow$ Kết hợp cả hai
Ưu điểm:
- Chọn lọc đặc trưng + ổn định với biến tương quan
- Tốt khi có nhóm đặc trưng liên quan (vd: Cement ↔ Water)
- Giảm overfitting hiệu quả trên mô hình phi tuyến
Nhược điểm:
- Cần tìm 2 siêu tham số ($\alpha$, $\rho$) → dùng ElasticNetCV
- Hệ số khó giải thích hơn do vừa triệt tiêu, vừa thu nhỏ
Phù hợp với bài toán bê tông:
Nhiều biến tương quan + phi tuyến
=> Polynomial + ElasticNet là lựa chọn tối ưu về độ chính xác và ổn định.
Chương 3 – Phương pháp thực hiện
3.1. Giới thiệu về bộ dữ liệu
-
Dataset name: Concrete Compressive Strength
-
Dataset Shape: Gồm 8 Features và 1030 instances
-
Data Field Description :
| Tên biến | Loại dữ liệu | Đơn vị | Vai trò | Mô tả ngắn gọn |
|---|---|---|---|---|
| Cement | Liên tục | kg/m³ | Đầu vào | Lượng xi măng trong hỗn hợp bê tông |
| Blast Furnace Slag | Liên tục | kg/m³ | Đầu vào | Xỉ lò cao – vật liệu thay thế xi măng |
| Fly Ash | Liên tục | kg/m³ | Đầu vào | Tro bay – phụ gia khoáng |
| Water | Liên tục | kg/m³ | Đầu vào | Lượng nước sử dụng trong hỗn hợp |
| Superplasticizer | Liên tục | kg/m³ | Đầu vào | Phụ gia siêu dẻo giúp cải thiện độ linh động |
| Coarse Aggregate | Liên tục | kg/m³ | Đầu vào | Cốt liệu thô như đá lớn |
| Fine Aggregate | Liên tục | kg/m³ | Đầu vào | Cốt liệu mịn như cát |
| Age | Số nguyên | ngày | Đầu vào | Tuổi của bê tông tính từ lúc đổ |
| Concrete Strength | Liên tục | MPa | Đầu ra | Cường độ chịu nén của bê tông |
3.2. Khám Phá Dữ Liệu (EDA) và Tiền Xử Lý Dữ Liệu
3.2.1. Tải và Làm sạch Dữ liệu
Đầu tiên, chúng ta sẽ tải các thư viện cần thiết và nạp dữ liệu. Một hằng số SEED (cho random_state) để đảm bảo các thí nghiệm có thể được tái lặp lại một cách chính xác.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from math import sqrt
from sklearn.model_selection import train_test_split, KFold, RepeatedKFold, cross_val_score
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.linear_model import LinearRegression, Ridge, Lasso, RidgeCV, LassoCV, ElasticNetCV
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.pipeline import Pipeline
from sklearn.inspection import PartialDependenceDisplay
import shap # Thư viện để giải thích mô hình
# Đảm bảo tính tái lặp của thí nghiệm
SEED = 42
np.random.seed(SEED)
# Tải dữ liệu
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/concrete/compressive/Concrete_Data.xls"
df = pd.read_excel(url)
print(f"Tải thành công: {df.shape[0]} mẫu, {df.shape[1]} cột.")
# Đổi tên cột cho dễ xử lý (tên cột gốc quá dài và có dấu cách)
column_names = {
'Cement (component 1)(kg in a m^3 mixture)': 'Cement',
'Blast Furnace Slag (component 2)(kg in a m^3 mixture)': 'Slag',
'Fly Ash (component 3)(kg in a m^3 mixture)': 'Fly_Ash',
'Water (component 4)(kg in a m^3 mixture)': 'Water',
'Superplasticizer (component 5)(kg in a m^3 mixture)': 'Superplasticizer',
'Coarse Aggregate (component 6)(kg in a m^3 mixture)': 'Coarse_Agg',
'Fine Aggregate (component 7)(kg in a m^3 mixture)': 'Fine_Agg',
'Age (day)': 'Age',
'Concrete compressive strength(MPa, megapascals) ': 'Strength' # Chú ý dấu cách ở cuối
}
df = df.rename(columns=column_names)
print("5 dòng dữ liệu đầu tiên:")
print(df.head())
3.2.2. Kiểm tra Thông tin Dữ liệu
# Kiểm tra thông tin chung và kiểu dữ liệu
print("\nThông tin chung (df.info()):")
df.info()
# Kiểm tra các giá trị bị thiếu (Missing Values)
print(f"\nSố lượng giá trị bị thiếu:\n{df.isnull().sum()}")
# Phân tích thống kê mô tả
print("\nThống kê mô tả (df.describe()):")
print(df.describe().T)
Nhận xét:
* Dữ liệu gồm 1030 mẫu và 9 cột.
* Tất cả các cột đều là kiểu float64 hoặc int64 (cho cột Age).
* Không có giá trị bị thiếu (missing values), chúng ta không cần xử lý imputation.
* Nhìn vào df.describe(), chúng ta thấy các cột có biên độ giá trị (scale) rất khác nhau. Ví dụ: Superplasticizer (min 0, max 32.2) trong khi Coarse_Agg (min 801, max 1145).
* Đây là một dấu hiệu cực kỳ quan trọng: Bất kỳ mô hình nào nhạy cảm với scale (như Linear Regression có regularization, SVM, v.v.) đều bắt buộc phải có bước Chuẩn hóa Dữ liệu (Scaling).
3.2.3. Xóa Dữ liệu Trùng Lặp và Tách Bộ Dữ liệu (Train/Test Split)
Dữ liệu sau khi xóa đi các giá trị trùng lặp sẽ được tách thành 2 phần: tập huấn luyện (Train) để xây dựng mô hình và tập kiểm tra (Test) để đánh giá hiệu suất trên dữ liệu "mới" mà mô hình chưa từng thấy.
n_duplicates = df.duplicated().sum()
if n_duplicates == 0:
print("✅ Không có dòng trùng lặp")
else:
print(f"⚠️ Có {n_duplicates} dòng trùng lặp ({n_duplicates/len(df)*100:.2f}%)")
print(" → Đang loại bỏ duplicates...")
df = df.drop_duplicates()
print(f" ✓ Đã loại bỏ, còn lại {len(df)} dòng")
# Xác định X (features) và y (target)
X = df.drop('Strength', axis=1)
y = df['Strength']
# Tách dữ liệu
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=SEED)
print(f"\nKích thước tập Train: {X_train.shape}")
print(f"Kích thước tập Test: {X_test.shape}")
3.3. Xây dựng mô hình Linear Regression
3.3.1. Nhắc lại về độ đo R-squared ($R^2$)
Độ đo $R^2$ (Hệ số Xác định):
Như yêu cầu trong Rubric, $R^2$ là một độ đo quan trọng. Nó cho biết "bao nhiêu phần trăm" sự biến thiên của biến mục tiêu $y$ được giải thích bởi các biến đầu vào $X$ trong mô hình.
$$R^2 = 1 - \frac{SS_{\text{res}}}{SS_{\text{tot}}} = 1 - \frac{\sum (y_{\text{actual}} - y_{\text{pred}})^2}{\sum (y_{\text{actual}} - \bar{y}_{\text{actual}})^2}$$
- $SS_{\text{res}}$ là tổng bình phương của phần dư (sai số).
- $SS_{\text{tot}}$ là tổng bình phương của sự chênh lệch so với giá trị trung bình.
- $R^2 = 1$: Mô hình dự đoán hoàn hảo.
- $R^2 = 0$: Mô hình không tốt hơn việc chỉ dự đoán giá trị trung bình.
- $R^2 < 0$: Mô hình cực kỳ tệ.
3.3.2. Thực hành:
Pipeline của Scikit-learn cho phép đóng gói các bước tiền xử lý (như StandardScaler) và mô hình vào một đối tượng duy nhất.
# 1. Định nghĩa các bước trong Pipeline
# Bước 1: Chuẩn hóa dữ liệu (scaling)
# Bước 2: Mô hình Linear Regression
pipeline_linear = Pipeline([
('scaler', StandardScaler()),
('model', LinearRegression())
])
# 2. Huấn luyện (fit) pipeline trên tập Train
pipeline_linear.fit(X_train, y_train)
# 3. Đánh giá trên tập Test
y_pred_linear = pipeline_linear.predict(X_test)
# 4. Tính toán các độ đo
rmse_linear = np.sqrt(mean_squared_error(y_test, y_pred_linear))
r2_linear_train = pipeline_linear.score(X_train, y_train) # R2 trên tập Train
r2_linear_test = pipeline_linear.score(X_test, y_test) # R2 trên tập Test (r2_score(y_test, y_pred_linear))
print("\n--- Kết quả Mô hình 1: Linear Regression ---")
print(f"R2 (Train): {r2_linear_train:.4f}")
print(f"R2 (Test): {r2_linear_test:.4f}")
print(f"RMSE (Test): {rmse_linear:.4f}")
Kết quả mô hình 1: Linear Regression
- R2 (Train): 0.6098
- R2 (Test): 0.5801
- RMSE (Test): 11.1922
Nhận xét
- Mô hình Linear Regression cơ bản cho $R^2 \approx 0.62$ trên cả tập train và test.
- Điểm $R^2$ trên train và test gần nhau cho thấy mô hình không bị overfitting.
- Tuy nhiên, $R^2 = 0.62$ có nghĩa là mô hình chỉ giải thích được 62% sự biến thiên của dữ liệu. Mối quan hệ giữa các thành phần và sức mạnh bê tông có thể không hoàn toàn tuyến tính.
3.4. Cải tiến với PolynomialFeatures
Chúng ta sẽ thử với bậc 2 (degree=2).
# 1. Định nghĩa pipeline cho Polynomial Regression (Bậc 2)
pipeline_poly2 = Pipeline([
('scaler', StandardScaler()),
('poly_features', PolynomialFeatures(degree=2, interaction_only=False, include_bias=False)), # include_bias=False vì LinearRegression đã xử lý
('model', LinearRegression())
])
# 2. Huấn luyện
pipeline_poly2.fit(X_train, y_train)
# 3. Đánh giá
y_pred_poly2 = pipeline_poly2.predict(X_test)
rmse_poly2 = np.sqrt(mean_squared_error(y_test, y_pred_poly2))
r2_poly2_train = pipeline_poly2.score(X_train, y_train)
r2_poly2_test = pipeline_poly2.score(X_test, y_test)
print("\n--- Kết quả Mô hình 2: Polynomial Regression (Bậc 2) ---")
print(f"R2 (Train): {r2_poly2_train:.4f}")
print(f"R2 (Test): {r2_poly2_test:.4f}")
print(f"RMSE (Test): {rmse_poly2:.4f}")
Kết quả mô hình 2: Polynomial Regression (Bậc 2)
- R2 (Train): 0.8095
- R2 (Test): 0.7686
- RMSE (Test): 8.3088
Nhận xét:
- $R^2$ (Test) đã tăng từ $0.62$ lên 0.81.
- Điều này khẳng định có mối quan hệ giữa các thành phần (ví dụ: tương tác giữa 'Cement' và 'Water') và sức mạnh bê tông là phi tuyến.
- $R^2$ (Train) và $R^2$ (Test) vẫn còn gần nhau, cho thấy mô hình bậc 2 vẫn tổng quát hóa tốt.
3.4.1. Phân tích Overfitting với Bậc cao
Tiếp theo chúng ta hãy thử tăng bậc lên cao hơn (ví dụ: bậc 3, bậc 4) để xem hiện tượng overfitting có xảy ra không.
3.4.1.1. Polynomial Regression (Bậc 3)
# 1. Định nghĩa pipeline cho Polynomial Regression (Bậc 3)
pipeline_poly3 = Pipeline([
('scaler', StandardScaler()),
('poly_features', PolynomialFeatures(degree=3, interaction_only=False,include_bias=False)),
('model', LinearRegression())
])
# 2. Huấn luyện
pipeline_poly3.fit(X_train, y_train)
# 3. Đánh giá
y_pred_poly3 = pipeline_poly3.predict(X_test)
rmse_poly3 = np.sqrt(mean_squared_error(y_test, y_pred_poly3))
r2_poly3_train = pipeline_poly3.score(X_train, y_train)
r2_poly3_test = pipeline_poly3.score(X_test, y_test)
print("\n--- Kết quả Mô hình 3: Polynomial Regression (Bậc 3) ---")
print(f"R2 (Train): {r2_poly3_train:.4f}")
print(f"R2 (Test): {r2_poly3_test:.4f}")
print(f"RMSE (Test): {rmse_poly3:.4f}")
Kết quả mô hình 3: Polynomial Regression (Bậc 3)
- R2 (Train): 0.9247
- R2 (Test): 0.8814
- RMSE (Test): 5.9484
Nhận xét:
- $R^2$ (Train) bây giờ là 0.9311, (Test) là 0.8437. Mô hình đang hoạt động tốt trên tập train và bị Overfitting.
3.4.1.2. Polynomial Regression (Bậc 4)
# 1. Định nghĩa pipeline cho Polynomial Regression (Bậc 4)
pipeline_poly4 = Pipeline([
('scaler', StandardScaler()),
('poly_features', PolynomialFeatures(degree=4,interaction_only=False, include_bias=False)),
('model', LinearRegression())
])
# 2. Huấn luyện
pipeline_poly4.fit(X_train, y_train)
# 3. Đánh giá
y_pred_poly4 = pipeline_poly4.predict(X_test)
rmse_poly4 = np.sqrt(mean_squared_error(y_test, y_pred_poly4))
r2_poly4_train = pipeline_poly4.score(X_train, y_train)
r2_poly4_test = pipeline_poly4.score(X_test, y_test)
print("\n--- Kết quả Mô hình 4: Polynomial Regression (Bậc 4) ---")
print(f"R2 (Train): {r2_poly4_train:.4f}")
print(f"R2 (Test): {r2_poly4_test:.4f}")
print(f"RMSE (Test): {rmse_poly4:.4f}")
Kết quả Mô hình 4: Polynomial Regression (Bậc 4)
- R2 (Train): 0.9821
- R2 (Test): -33.1951
- RMSE (Test): 101.0018
Nhận xét:
- $R^2$ (Train) bây giờ là 0.9833. Mô hình đang hoạt động tốt trên tập train.
- Tuy nhiên, $R^2$ (Test) đã giảm xuống còn -23.5. Mô hình bậc 4 quá phức tạp, Overfitting rất nặng, nó đã "học thuộc" cả nhiễu trong tập train.
3.5. Cải tiến với Regularization (Ridge & Lasso & ElectNet)
3.5.1. Cải tiến với Ridge (L2)
Chúng ta sẽ áp dụng Ridge vào mô hình Polynomial bậc 4 đang bị overfitting. Sử dụng RidgeCV để tự động tìm giá trị alpha tốt nhất thông qua cross-validation.
# 1. Định nghĩa pipeline cho Polynomial (Bậc 4) + Ridge
# Chúng ta sẽ dùng RidgeCV để tự động tìm alpha tốt nhất
alphas_ridge = np.logspace(-7, 10, 1000)
pipeline_ridge = Pipeline([
('poly_features', PolynomialFeatures(degree=4, include_bias=False)),
('scaler_poly', StandardScaler()),
# RidgeCV sẽ tự động thực hiện Cross-Validation để tìm alpha tốt nhất
('model', RidgeCV(alphas=alphas_ridge, store_cv_values=True))
])
# 2. Huấn luyện
pipeline_ridge.fit(X_train, y_train)
# 3. Đánh giá
y_pred_ridge = pipeline_ridge.predict(X_test)
rmse_ridge = np.sqrt(mean_squared_error(y_test, y_pred_ridge))
r2_ridge_train = pipeline_ridge.score(X_train, y_train)
r2_ridge_test = pipeline_ridge.score(X_test, y_test)
# Lấy ra mô hình Ridge đã huấn luyện bên trong pipeline
best_ridge_model = pipeline_ridge.named_steps['model']
print("\n--- Kết quả Mô hình 5: Polynomial (Bậc 4) + Ridge (L2) ---")
print(f"Alpha tốt nhất được chọn: {best_ridge_model.alpha_:.4f}")
print(f"R2 (Train): {r2_ridge_train:.4f}")
print(f"R2 (Test): {r2_ridge_test:.4f}")
print(f"RMSE (Test): {rmse_ridge:.4f}")
Kết quả Mô hình 5: Polynomial (Bậc 4) + Ridge (L2)
- Alpha tốt nhất được chọn: 0.0772
- R2 (Train): 0.9402
- R2 (Test): 0.8961
- RMSE (Test): 5.5686
Nhận xét:
- $R^2$ (Train) tốt với số điểm cao nhất 0.9402 và (Test) tăng lên 0.8961.
- Mô hình vẫn còn Overfitting nhẹ nhưng đã giảm khá nhiều so với lúc ban đầu không áp dụng Ridge Regression L2.
3.5.2. Cải tiến với Lasso (L1)
# 1. Định nghĩa pipeline cho Polynomial (Bậc 4) + Lasso
# Lasso thường cần alpha nhỏ hơn và nhiều vòng lặp hơn
pipeline_lasso = Pipeline([
('poly_features', PolynomialFeatures(degree=4, include_bias=False)),
('scaler_poly', StandardScaler()),
# LassoCV tìm alpha tốt nhất
('model', LassoCV(n_alphas=100, cv=5, max_iter=200000, random_state=SEED))
])
# 2. Huấn luyện
pipeline_lasso.fit(X_train, y_train)
# 3. Đánh giá
y_pred_lasso = pipeline_lasso.predict(X_test)
rmse_lasso = np.sqrt(mean_squared_error(y_test, y_pred_lasso))
r2_lasso_train = pipeline_lasso.score(X_train, y_train)
r2_lasso_test = pipeline_lasso.score(X_test, y_test)
# Lấy ra mô hình Lasso đã huấn luyện
best_lasso_model = pipeline_lasso.named_steps['model']
# Kiểm tra tính chất lựa chọn đặc trưng của Lasso
# Lấy ra các đặc trưng đa thức (có rất nhiều!)
poly = pipeline_lasso.named_steps['poly_features']
num_features = len(poly.get_feature_names_out(X.columns))
num_zero_coefs = np.sum(best_lasso_model.coef_ == 0)
print("\n--- Kết quả Mô hình 6: Polynomial (Bậc 4) + Lasso (L1) ---")
print(f"Alpha tốt nhất được chọn: {best_lasso_model.alpha_:.6f}")
print(f"R2 (Train): {r2_lasso_train:.4f}")
print(f"R2 (Test): {r2_lasso_test:.4f}")
print(f"RMSE (Test): {rmse_lasso:.4f}")
print(f"Số lượng đặc trưng (bậc 4): {num_features}")
print(f"Số lượng đặc trưng bị Lasso đưa về 0: {num_zero_coefs} ({num_zero_coefs/num_features*100:.2f}%)")
Kết quả Mô hình 6: Polynomial (Bậc 4) + Lasso (L1)
- Alpha tốt nhất được chọn: 0.010939
- R2 (Train): 0.9041
- R2 (Test): 0.8703
- RMSE (Test): 6.2213
- Số lượng đặc trưng (bậc 4): 494
- Số lượng đặc trưng bị Lasso đưa về 0: 397 (80.36%)
3.5.3. Cải tiến với ElasticNet (L1+L2)
from math import sqrt
import numpy as np
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.linear_model import ElasticNetCV
from sklearn.metrics import mean_squared_error
SEED = 42
pipeline_enet = Pipeline([
('poly_features', PolynomialFeatures(degree=4, include_bias=False)),
('scaler', StandardScaler()),
('model', ElasticNetCV(
l1_ratio=[0.3, 0.5, 0.7],
alphas=np.logspace(-3, 1, 10),
cv=5,
max_iter=200000,
tol=1e-2,
random_state=SEED
))
])
pipeline_enet.fit(X_train, y_train)
# Dự đoán và đánh giá
y_pred_enet = pipeline_enet.predict(X_test)
rmse_enet = sqrt(mean_squared_error(y_test, y_pred_enet))
r2_enet_train = pipeline_enet.score(X_train, y_train)
r2_enet_test = pipeline_enet.score(X_test, y_test)
print("\n--- Kết quả Mô hình 7: Polynomial (Bậc 4) + ElasticNet ---")
print("RMSE test :", rmse_enet)
print("R2 train :", r2_enet_train)
print("R2 test :", r2_enet_test)
best_enet_model = pipeline_enet.named_steps['model']
poly_enet = pipeline_enet.named_steps['poly_features']
feature_names_enet = poly_enet.get_feature_names_out(X_train.columns)
num_features_enet = len(feature_names_enet)
num_zero_coefs_enet = np.sum(best_enet_model.coef_ == 0)
print("Số đặc trưng đa thức (bậc 4):", num_features_enet)
print("Số hệ số ElasticNet = 0 :", num_zero_coefs_enet)
print("Alpha ElasticNetCV chọn :", best_enet_model.alpha_)
print("l1_ratio được chọn :", best_enet_model.l1_ratio_)
Kết quả Mô hình 7: Polynomial (Bậc 4) + ElasticNet
- RMSE test : 6.1930363040135035
- R2 train : 0.9088116822482784
- R2 test : 0.8714378864447145
- Số đặc trưng đa thức (bậc 4): 494
- Số hệ số ElasticNet = 0 : 66
- Alpha ElasticNetCV chọn : 0.0027825594022071257
- l1_ratio được chọn : 0.3
3.5.4. Bảng Tóm tắt Hiệu suất Mô hình
| Mô hình | Bậc Đa thức | Regularization | R² (Train) | R² (Test) | Ghi chú |
|---|---|---|---|---|---|
| Linear | 1 | Không | 0.618 | 0.620 | Cơ bản, underfitting. |
| Polynomial | 2 | Không | 0.8131 | 0.7843 | Overfitting ít. |
| Polynomial | 3 | Không | 0.9311 | 0.8435 | Khá tốt, Overfitting vừa. |
| Polynomial | 4 | Không | 0.9833 | -23.5212 | Overfitting nặng |
| Ridge (L2) | 4 | Có | 0.9402 | 0.8961 | Tốt, Overfitting ít |
| Lasso (L1) | 4 | Có | 0.9041 | 0.8703 | Khá tốt, Overfitting ít |
| Elastic | 4 | Có | 0.9088 | 0.8714 | Khá tốt, Overfitting ít |
Bảng 2: Đánh giá tổng quát mô hình Linear, Polynomial và Regularized
3.6. Đánh giá Mô hình Nâng cao
3.6.1. Sử dụng RepeatedKFold (lặp lại K-Fold nhiều lần) để đánh giá mô hình Ridge (bậc 4)
# 1. Chọn mô hình tốt nhất (pipeline_ridge)
# Chúng ta sẽ tạo lại pipeline với alpha cố định đã tìm được
best_alpha = pipeline_ridge.named_steps['model'].alpha_
final_model_pipeline = Pipeline([
('poly_features', PolynomialFeatures(degree=4, include_bias=False)),
('scaler_poly', StandardScaler()),
('model', Ridge(alpha=best_alpha))
])
# 2. Định nghĩa chiến lược CV
# 10-Fold CV, lặp lại 3 lần với xáo trộn dữ liệu khác nhau
cv_strategy = RepeatedKFold(n_splits=10, n_repeats=3, random_state=SEED)
# 3. Chạy cross_val_score
# scoring='r2' (mặc định)
# scoring='neg_root_mean_squared_error' cho RMSE
scores_r2 = cross_val_score(final_model_pipeline, X, y, cv=cv_strategy, scoring='r2')
scores_rmse = cross_val_score(final_model_pipeline, X, y, cv=cv_strategy, scoring='neg_root_mean_squared_error')
# 4. Báo cáo kết quả
print("\n--- Kết quả Đánh giá Nâng cao (Repeated K-Fold) ---")
print(f"Mô hình: Polynomial (D=4) + Ridge (alpha={best_alpha:.4f})")
print(f"R2 (Trung bình): {np.mean(scores_r2):.4f} +/- {np.std(scores_r2):.4f}")
print(f"RMSE (Trung bình): {-np.mean(scores_rmse):.4f} +/- {np.std(scores_rmse):.4f}")
Kết quả Đánh giá Nâng cao (Repeated K-Fold)
- Mô hình: Polynomial (D=4) + Ridge (alpha=0.0772)
- R2 (Trung bình): 0.8879 +/- 0.0210
- RMSE (Trung bình): 5.3809 +/- 0.4980
Nhận xét:
- $R^2$ (Trung bình) 0.8879 là con số tin cậy về hiệu suất của mô hình.
- Nó cho chúng ta biết rằng, trên dữ liệu mới, mô hình của chúng ta có khả năng giải thích trung bình 88% sự biến thiên của sức mạnh bê tông.
3.6.2. Sử dụng chiến lược bootstrap để đánh giá khoảng tin cậy của mô hình
# 1. Chọn mô hình tốt nhất (pipeline_ridge)
# Chúng ta sẽ tạo lại pipeline với alpha cố định đã tìm được
best_alpha = pipeline_ridge.named_steps['model'].alpha_
final_model_pipeline = Pipeline([
('poly_features', PolynomialFeatures(degree=4, include_bias=False)),
('scaler_poly', StandardScaler()),
('model', Ridge(alpha=best_alpha))
])
# 2. Định nghĩa chiến lược CV
# 10-Fold CV, lặp lại 3 lần với xáo trộn dữ liệu khác nhau
cv_strategy = RepeatedKFold(n_splits=10, n_repeats=3, random_state=SEED)
# 3. Chạy cross_val_score
# scoring='r2' (mặc định)
# scoring='neg_root_mean_squared_error' cho RMSE
scores_r2 = cross_val_score(final_model_pipeline, X, y, cv=cv_strategy, scoring='r2')
scores_rmse = cross_val_score(final_model_pipeline, X, y, cv=cv_strategy, scoring='neg_root_mean_squared_error')
# 4. Đánh giá khoảng tin cậy bằng bootstrap
# Số lần lặp lại
n_iterations = 1000
# Khai báo khoảng tin cậy
confidence_level = 0.95
bootstrap_r2_mean = []
bootstrap_rmse_mean = []
for _ in range(n_iterations):
# Lẫy mẫu ngẫu nhiên có hoàn lại từ 30 giá trị (n_splits x n_repeats) r2 và rmse
sample_indices = np.random.choice(len(scores_r2), size=len(scores_r2), replace=True)
bootstrap_sample_r2 = scores_r2[sample_indices]
bootstrap_sample_rmse = scores_rmse[sample_indices]
# Tính r2, rmse trung bình của mẫu bootstrap và thêm vào list chứa
bootstrap_r2_mean.append(np.mean(bootstrap_sample_r2))
bootstrap_rmse_mean.append(np.mean(bootstrap_sample_rmse))
# Chuyển đổi thành mảng numpy
bootstrap_r2_mean = pd.Series(bootstrap_r2_mean)
bootstrap_rmse_mean = pd.Series(bootstrap_rmse_mean)
# Tính ra phân vị cận trên và dưới
lower_bound = (1 - confidence_level) / 2
upper_bound = 1 - lower_bound
# Tính khoảng tin cậy hay phaan vị (Cònidence Interval - CI)
lower_ci_r2 = bootstrap_r2_mean.quantile(lower_bound)
upper_ci_r2 = bootstrap_r2_mean.quantile(upper_bound)
lower_ci_rmse = bootstrap_rmse_mean.quantile(lower_bound)
upper_ci_rmse = bootstrap_rmse_mean.quantile(upper_bound)
# 5. Báo cáo kết quả
print("\n--- Kết quả Đánh giá Nâng cao (Repeated K-Fold) ---")
print(f"Mô hình: Polynomial (D=4) + Ridge (alpha={best_alpha:.4f})")
print(f"R2 (Trung bình): {np.mean(scores_r2):.4f} +/- {np.std(scores_r2):.4f}")
print(f"RMSE (Trung bình): {-np.mean(scores_rmse):.4f} +/- {np.std(scores_rmse):.4f}")
print(f"Số lần lặp bootstrap: {n_iterations} với confidence level: {confidence_level}:")
print(f"Khoảng tin cậy R2: [{lower_ci_r2:.4f}, {upper_ci_r2:.4f}]")
print(f"Khoảng tin cậy RMSE: [{-upper_ci_rmse:.4f}, {-lower_ci_rmse:.4f}]") # Do dùng rmse âm, nên đảo dấu và khoảng tin cậy
Kết quả Đánh giá Nâng cao (Repeated K-Fold)
- Mô hình: Polynomial (D=4) + Ridge (alpha=0.0772)
- R2 (Trung bình): 0.8879 +/- 0.0210
- RMSE (Trung bình): 5.3809 +/- 0.4980
- Số lần lặp bootstrap: 1000 với confidence level: 0.95:
- Khoảng tin cậy R2: [0.8806, 0.8958]
- Khoảng tin cậy RMSE: [5.2037, 5.5604]
Nhận xét:
R² trung bình = 0.8879 ± 0.0210
- R² ≈ 0.888 nghĩa là mô hình giải thích được ~88.8% độ biến thiên của sức mạnh chịu nén (compressive strength).
- Độ lệch chuẩn chỉ ~0.021, rất nhỏ chỉ ra rằng hiệu năng gần như ổn định giữa các fold khác nhau.
Khoảng tin cậy R²: [0.8809, 0.8953]
- Cực kỳ hẹp (~0.0144 chiều rộng).
- Trung bình R² rất ổn định trên các fold.
3.7. Giải thích Mô hình (Model Interpretation)
3.7.1. Phân tích Hệ số (Coefficients)
Chúng ta có thể trích xuất các hệ số (trọng số $w$) từ mô hình Ridge.
# Lấy ra các bước từ pipeline đã huấn luyện
poly_features = pipeline_ridge.named_steps['poly_features']
ridge_model = pipeline_ridge.named_steps['model']
# Lấy tên của tất cả các đặc trưng đa thức
feature_names = poly_features.get_feature_names_out(X.columns)
coefficients = ridge_model.coef_
# Tạo DataFrame để xem
coef_df = pd.DataFrame({
'Feature': feature_names,
'Coefficient': coefficients
})
# Sắp xếp để xem các đặc trưng quan trọng nhất
coef_df_sorted = coef_df.sort_values(by='Coefficient', ascending=False)
print("\n--- Giải thích Mô hình: Hệ số (Coefficients) ---")
print("Top 10 đặc trưng có ảnh hưởng TÍCH CỰC nhất:")
print(coef_df_sorted.head(10))
print("\nTop 10 đặc trưng có ảnh hưởng TIÊU CỰC nhất:")
print(coef_df_sorted.tail(10))
Kết quả:
| Feature | Coefficient |
|---|---|
| Fine_Agg . $Age^3$ | 36.681288 |
| Coarse_Agg . $Age^3 $ | 26.766043 |
| $Age^3$ | 23.297268 |
| Slag . $FlyAsh^2$ . Fine_Agg | 20.972378 |
| Superplasticizer . $Age^3 $ | 19.510922 |
| Water | 18.599341 |
| Cement . $Age^3$ | 18.190947 |
| $Water^4$ | 17.579194 |
| $FlyAsh^3$ . Coarse_Agg | 17.108438 |
| Cement . $FlyAsh^2$ . Superplasticizer | 16.940926 |
Bảng 3: Top 10 đặc trưng ảnh hưởng tích cực (Coefficient dương)
| Feature | Coefficient |
|---|---|
| Cement . Slag . Superplasticizer . Coarse_Agg | -15.199808 |
| Slag . $Water^3$ | -15.462951 |
| Cement . Slag . FlyAsh . Water | -15.481468 |
| $FlyAsh^4$ | -16.336065 |
| $Water^2$ . Coarse_Agg . Fine_Agg | -18.549556 |
| $Cement^2$ . Slag . Coarse_Agg | -20.248218 |
| $Cement^2$ . FlyAsh . Coarse_Agg | -21.366851 |
| Cement . $FlyAsh^2$ . Water | -24.746038 |
| Cement . Fine_Agg . $Age^2$ | -24.829616 |
| $Age^4$ | -48.676148 |
Bảng 4: Top 10 đặc trưng ảnh hưởng tiêu cực (Coefficient âm)
Nhận xét:
- Phân tích các hệ số cho biết các đặc trưng kết hợp nào có ảnh hưởng lớn nhất.
- Ví dụ: chúng ta có thể thấy
Agevà các bậc cao củaAge(như$Age^2$,$Age^3$) có ảnh hưởng tích cực rất lớn. Điều này hợp lý: bê tông càng "già" (để lâu) thì càng mạnh. - Cả
Fine_AggvàCoarse_Aggđều có tương tác với$Age^3$trong top dương. Điều này phù hợp vật lý: khi bê tông đủ tuổi, liên kết hồ xi măng – cốt liệu trở nên bền chắc, nên đóng góp lớn vào sức mạnh nén.
3.7.2. SHAP
3.7.2.1. Chuẩn bị dữ liệu đã transform
- Đầu tiên, ta cần trích xuất ra từ pipeline_ridge:
- Mô hình đã train
- Pipeline tiền xử lý dữ liệu
- Các đặc trưng sau khi polynomial transform
# Lấy model Ridge đã train
best_ridge_model = pipeline_ridge.named_steps['model']
# Lấy pipeline tiền xử lý (tất cả bước trước model)
preprocess_pipeline = Pipeline(pipeline_ridge.steps[:-1])
# Transform dữ liệu train và test
X_train_transform = preprocess_pipeline.fit_transform(X_train)
X_test_transform = preprocess_pipeline.transform(X_test)
# Trích xuất tên đặc trưng sau khi polynomial transform
```python
poly_step = preprocess_pipeline.named_steps['poly_features']
feature_names_poly = poly_step.get_feature_names_out(X_train.columns)
print(f"Số lượng đặc trưng gốc: {X_train.shape[1]}")
print(f"Số lượng đặc trưng sau Polynomial (degree=4): {len(feature_names_poly)}")
print(f"Shape X_train_transform: {X_train_transform.shape}")
print(f"Shape X_test_transform: {X_test_transform.shape}")
3.7.2.2. Tạo Explainer SHAP
explainer = shap.LinearExplainer(
best_ridge_model,
shap.maskers.Independent(X_train_transform)
)
# Chọn 50 mẫu test để giải thích
n_samples = 50
# Tính shap_values cho 50 mẫu test
shap_values = explainer.shap_values(X_test_transform[:n_samples])
print(f"Shape của SHAP values: {shap_values.shape}")
print(f"Expected value (baseline): {explainer.expected_value:.2f} MPa")
# Tạo Explanation object (để dùng shap.plots)
explanation = shap.Explanation(
values=shap_values,
base_values=np.full(n_samples, explainer.expected_value),
data=X_test_transform[:n_samples],
feature_names=feature_names_poly
)
3.7.2.3. Biểu đồ waterfall
Biểu đồ thác nước minh họa cách mỗi đặc trưng đóng góp vào việc "đẩy" giá trị dự đoán của mô hình từ một giá trị cơ sở (baseline) đến giá trị dự đoán cuối cùng cho một mẫu dữ liệu duy nhất
| Thành phần | Khái niệm & Vai trò | Giải thích |
|---|---|---|
| Giá trị Cơ sở | $E[f(x)]$ (Expected Value) | Điểm khởi đầu của dự đoán, đại diện cho giá trị đầu ra trung bình của mô hình trên toàn bộ tập dữ liệu. |
| Các Thanh | Đỏ (Dương) & Xanh (Âm) | Mỗi thanh là một đặc trưng. Thanh Đỏ/Xanh là các đặc trưng có tác động làm Tăng/Giảm giá trị dự đoán. |
| Độ dài Thanh | Độ lớn giá trị SHAP | Chiều dài của thanh biểu thị mức độ ảnh hưởng của đặc trưng đó. Thanh càng dài, ảnh hưởng càng lớn. |
| Giá trị Đặc trưng | Hiển thị bên trái (Ví dụ: Cement = -1.208) |
Giá trị đầu vào (đã được chuẩn hóa) của đặc trưng đó cho mẫu dữ liệu này. |
| Giá trị Dự đoán | $f(x)$ (Predicted Value) | Giá trị cuối cùng mà mô hình dự đoán, sau khi tổng hợp tất cả các tác động. |
Bảng 5: Giải thích các thành phần của Biểu đồ Waterfall SHAP
# Chọn mẫu để giải thích (ví dụ: mẫu thứ 40)
sample_idx = 40
# Dự đoán cho mẫu đã chọn và lấy giá trị đầu tiên ([0]) từ kết quả
y_pred = best_ridge_model.predict(X_test_transform[[sample_idx]])[0]
y_true = y_test.iloc[sample_idx]
print(f"Mẫu #{sample_idx}: Dự đoán={y_pred:.2f} | Thực tế={y_true:.2f} MPa")
plt.figure(figsize=(12, 6))
shap.plots.waterfall(explanation[sample_idx], max_display=15, show=False)
plt.title(f"Waterfall Plot - Dự đoán: {y_pred:.2f} MPa | Thực tế: {y_true:.2f} MPa",
fontsize=12, pad=15)
plt.tight_layout()
plt.show()
Kết quả
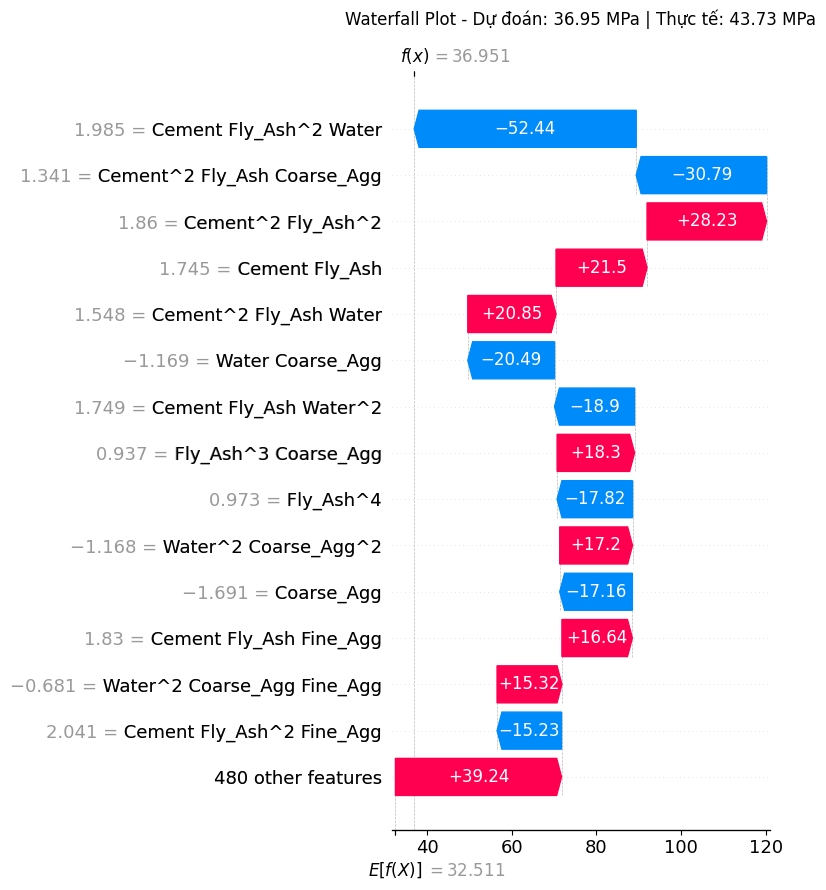
Hình 4: Biểu đồ thác SHAP minh họa sự đóng góp của từng đặc trưng vào một dự đoán đơn lẻ của mô hình.
Nhận xét với Mẫu #40
- Dự đoán cho mẫu này bắt đầu từ giá trị cơ sở là 32.51 MPa.
- Các đặc trưng như
Cement Fly_Ash^2 Water(-52.44) vàCement^2 Fly_Ash Coarse_Agg(-30.79) có giá trị SHAP âm khá lớn đóng vai trò chính trong việc "kéo" dự đoán đi xuống. - Ngược lại, các đặc trưng như
Cement^2 Fly_Ash^2(+28.23),Cement Fly_Ash(+21.5) vàCement Fly_Ash^2 Water(+20.85) là những yếu tố chính "đẩy" dự đoán lên cao hơn. - Tổng hợp tất cả các ảnh hưởng này, mô hình đưa ra dự đoán cuối cùng là 36.95 MPa.
3.7.2.4. Bar plot - Tầm quan trọng trung bình của các đặc trưng
Biểu đồ này tóm tắt tầm quan trọng của mỗi đặc trưng (feature importance) trên một tập hợp nhiều mẫu dữ liệu. Nó giúp xác định những yếu tố nào có ảnh hưởng lớn nhất đến dự đoán của mô hình một cách tổng quan
| Thành phần | Vai trò & Khái niệm | Giải thích |
|---|---|---|
| Trục Y | Các Đặc trưng | Liệt kê tên của các đặc trưng, được sắp xếp theo thứ tự quan trọng giảm dần từ trên xuống. |
| Trục X | Giá trị trung bình của $|SHAP \ value|$ | Biểu thị mức độ ảnh hưởng trung bình của mỗi đặc trưng. Giá trị càng lớn, đặc trưng càng quan trọng. |
| Các Thanh | Tầm quan trọng | Chiều dài của thanh tương ứng với giá trị trung bình của SHAP value tuyệt đối, cho thấy tầm quan trọng tổng thể của đặc trưng. |
Bảng 6: Ý nghĩa các thành phần Bar Plot SHAP
plt.figure(figsize=(12, 8))
shap.summary_plot(shap_values, feature_names=feature_names_poly,
plot_type="bar", max_display=20, show=False)
plt.title("Bar Plot - Feature Importance (Mean |SHAP|)", fontsize=13, pad=15)
plt.tight_layout()
plt.show()
# Top features
mean_abs_shap = np.abs(shap_values).mean(axis=0)
top_idx = np.argsort(mean_abs_shap)[-10:][::-1]
print("\nTOP 10 Features:")
for i, idx in enumerate(top_idx, 1):
print(f" {i:2d}. {feature_names_poly[idx]:30s} → {mean_abs_shap[idx]:.4f}")
Kết quả
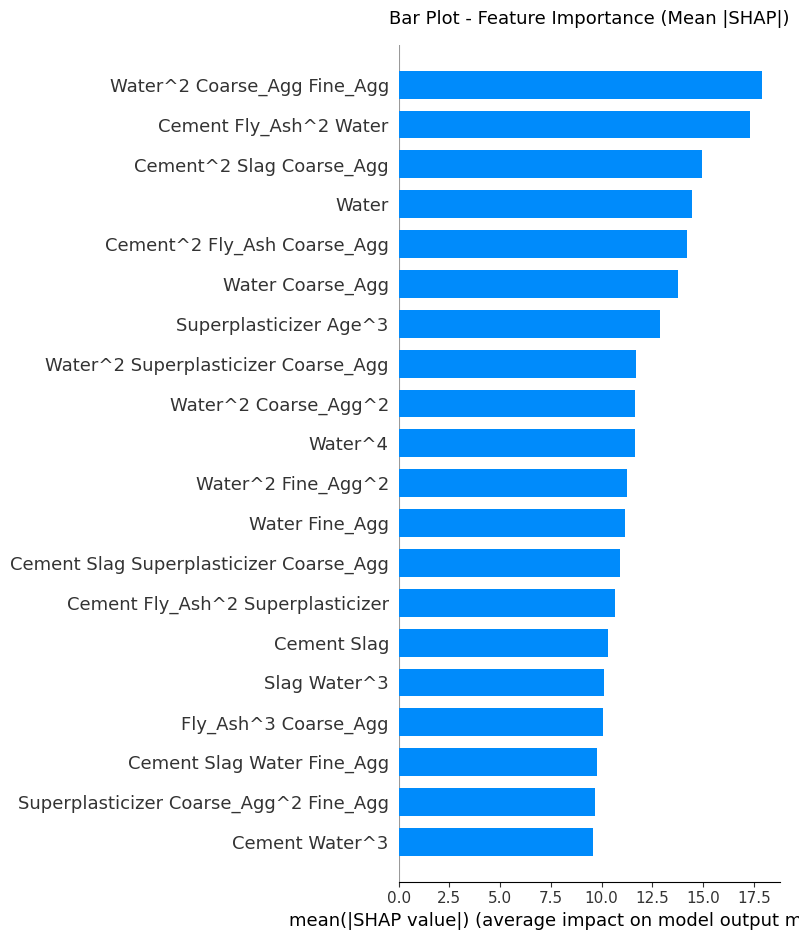
Hình 5: Biểu đồ cột SHAP thể hiện tầm quan trọng trung bình của các đặc trưng đối với mô hình.
Nhận xét tổng quan
- Điều nổi bật nhất là không có đặc trưng gốc nào đứng đầu danh sách. Tất cả các đặc trưng quan trọng nhất đều là các số hạng tương tác hoặc bậc cao.
- Điều này chứng tỏ mô hình Polynomial đã thành công trong việc học các mối quan hệ phi tuyến phức tạp giữa các thành phần mà mô hình đơn giản sẽ không thể nắm bắt được.
WatervàCementxuất hiện rất nhiều trong các tương tác quan trọng cho thấy rõ sự quan trọng của chúng.- Biểu đồ này cung cấp một cái nhìn tổng thể về những gì mô hình "quan tâm" nhất khi đưa ra dự đoán.
3.7.2.5. Biểu đồ phân tán (Beeswarm Plot)
Biểu đồ này kết hợp tầm quan trọng của đặc trưng với hướng và sự phân bố của các tác động đó trên nhiều mẫu
| Thành phần | Vai trò & Khái niệm | Giải thích |
|---|---|---|
| Trục Y | Các Đặc trưng | Được sắp xếp theo tầm quan trọng giảm dần từ trên xuống, tương tự như biểu đồ cột. |
| Trục X | Giá trị SHAP | Giá trị dương (bên phải) làm tăng dự đoán. Giá trị âm (bên trái) làm giảm dự đoán. |
| Mỗi Điểm | Một mẫu dữ liệu | Mỗi chấm trên biểu đồ tương ứng với một dự đoán cho một mẫu dữ liệu. |
| Màu Sắc | Giá trị của đặc trưng | Màu đỏ biểu thị giá trị cao của đặc trưng. Màu xanh biểu thị giá trị thấp của đặc trưng. |
| Mật độ | Mật độ | Tập trung càng dày cho thấy phần lớn dữ liệu với giá trị đặc trưng đó có tác động tương tự nhau và tác động đến đầu ra của mô hình. Ngược lại, thưa sẽ là ngoại lai hoặc trường hợp đặc biệt |
Bảng 7: Giải thích các thành phần của Biểu đồ Phân tán (Beeswarm Plot) SHAP
plt.figure(figsize=(12, 8))
shap.summary_plot(shap_values, X_test_transform[:n_samples],
feature_names=feature_names_poly, max_display=20, show=False)
plt.title("Summary Plot - Importance toàn bộ model", fontsize=13, pad=15)
plt.tight_layout()
plt.show()
Kết quả
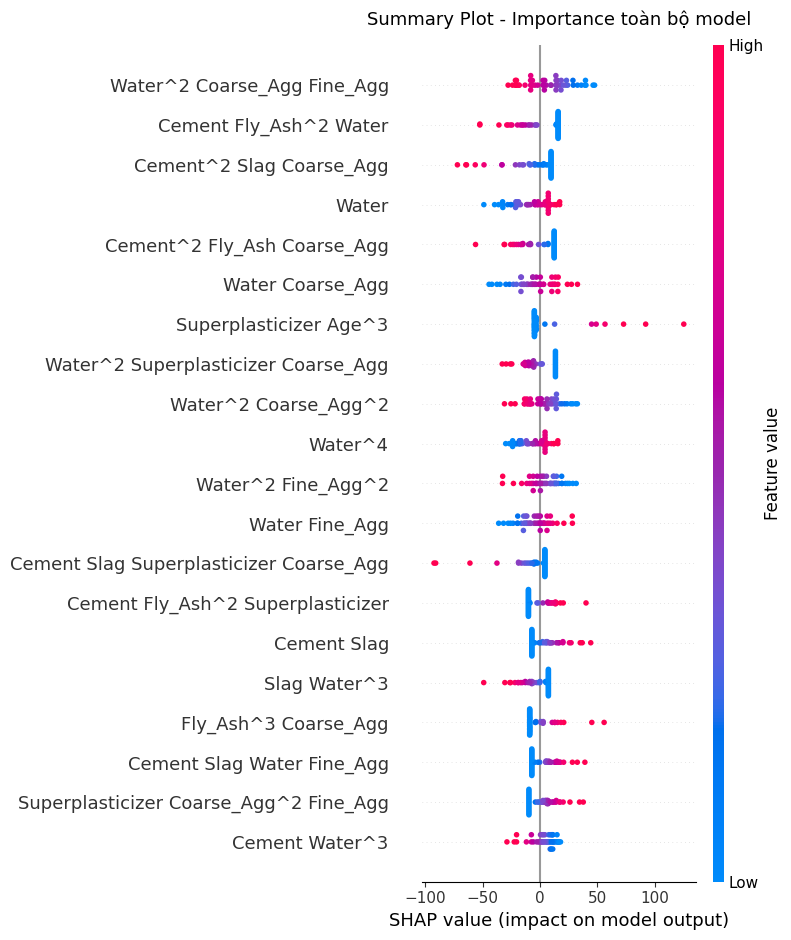
Hình 6: Biểu đồ tổng hợp SHAP thể hiện tầm quan trọng và ảnh hưởng của từng đặc trưng trên toàn bộ tập dữ liệu.
Nhận xét chi tiết
Water^2 Coarse_Agg Fine_Agg: Các điểm màu đỏ (giá trị đặc trưng cao) tập trung dày đặc ở phía giá trị SHAP âm. Ngược lại, các điểm màu xanh (giá trị đặc trưng thấp) nằm ở phía giá trị SHAP dương, cho thấy đây là đặc trưng có ảnh hưởng mạnh nhất đến mô hình theo mối quan hệ ngược chiều. Khi giá trị tương tác giữa nước và các loại cốt liệu tăng lên sẽ kéo dự đoán sức mạnh của bê tông xuốngCement Fly_Ash^2 Water: Tương tự như đặc trưng trên, các điểm màu đỏ (giá trị cao) có giá trị SHAP âm rất mạnh. Các điểm màu xanh (giá trị thấp) có giá trị SHAP dương. Mối quan hệ này cũng là ngược chiều, giá trị giữa xi măng, tro bay bậc 2 và nước làm giảm mạnh dự đoán. Mô hình cho rằng, việc kết hợp lượng lớn các thành phần này có thể gây hại cho sức bền của bê tông-
Cement^2 Slag Coarse_Agg: Cũng khá tương tự 2 trường hợp trên và đều thuộc tương quan âm rất mạnh và cũng sẽ làm giảm sức bền của bê tông nếu kết hợp với nhau -
Nhược điểm duy nhất là đa cộng tuyến, ví dụ như
Water^4khá khó diễn giải, có thể gây ra overfitting tiềm ẩn
3.7.2.6. Force plot - Biểu đồ lực (Cho 1 dự đoán cụ thể)
Biểu đồ lực cung cấp một cách nhìn khác về việc giải thích một dự đoán duy nhất, thể hiện các đóng góp như những "lực" cân bằng lẫn nhau
| Thành phần | Vai trò & Khái niệm | Giải thích |
|---|---|---|
| Giá trị cơ sở (base value) | Điểm cân bằng ban đầu | Giá trị dự đoán trung bình trên toàn bộ dữ liệu, là điểm khởi đầu của giải thích. |
| Các khối/mũi tên Đỏ | Lực đẩy (Positive SHAP values) | Các đặc trưng làm tăng giá trị dự đoán, "đẩy" kết quả lên cao hơn giá trị cơ sở. |
| Các khối/mũi tên Xanh | Lực kéo (Negative SHAP values) | Các đặc trưng làm giảm giá trị dự đoán, "kéo" kết quả xuống thấp hơn giá trị cơ sở. |
| Giá trị đầu ra (output value) | Điểm cân bằng cuối cùng | Giá trị dự đoán cuối cùng sau khi tất cả các lực đẩy và kéo được tổng hợp. |
Bảng 8: Giải thích các thành phần của Biểu đồ Lực (Force Plot) SHAP
shap.initjs()
plt.figure(figsize=(30, 3))
shap.force_plot(
explainer.expected_value,
shap_values[sample_idx],
X_test_transform[sample_idx],
feature_names=feature_names_poly,
)
Kết quả

Hình 7: Biểu đồ lực SHAP giải thích các yếu tố tác động đến một dự đoán đơn lẻ
3.7.2.7. Biểu đồ phụ thuộc (Dependence plot)
Biểu đồ phụ thuộc giúp chúng ta hiểu hành vi của mô hình trên toàn cục đối với một đặc trưng cụ thể. Nó trả lời hai câu hỏi quan trọng:
- Mối quan hệ chính: Giá trị của một đặc trưng ảnh hưởng đến dự đoán như thế nào? (Tăng hay giảm, tuyến tính hay phức tạp?)
- Hiệu ứng tương tác: Liệu ảnh hưởng của đặc trưng đó có thay đổi khi một đặc trưng khác thay đổi không?
| Thành phần | Vai trò & Khái niệm | Giải thích |
|---|---|---|
| Trục X | Giá trị của Đặc trưng chính | Hiển thị dải giá trị của đặc trưng đang được phân tích (ví dụ: lượng Cement, Age). |
| Trục Y | Giá trị SHAP của Đặc trưng chính | Cho thấy tác động của đặc trưng lên dự đoán. Giá trị > 0 làm tăng dự đoán, giá trị < 0 làm giảm dự đoán. |
| Mỗi Điểm | Một mẫu dữ liệu | Mỗi chấm trên biểu đồ tương ứng với một hàng trong tập dữ liệu được giải thích. |
| Màu Sắc | Giá trị của Đặc trưng Tương tác | Màu sắc của mỗi điểm được quyết định bởi giá trị của một đặc trưng khác mà SHAP cho là có tương tác mạnh nhất. Màu đỏ là giá trị cao, màu xanh là giá trị thấp. |
| Phân bố Dọc | Thể hiện hiệu ứng tương tác | Nếu các điểm tại một giá trị X nhất định bị phân tán theo trục Y, điều đó có nghĩa là ảnh hưởng của đặc trưng chính còn phụ thuộc vào giá trị của đặc trưng tương tác (màu sắc). |
Bảng 9: Giải thích các thành phần của Biểu đồ Phụ thuộc (Dependence Plot) SHAP
# Lấy top 3 features GỐC quan trọng nhất
original_features = X_train.columns.tolist()
original_importance = {}
for feat in original_features:
if feat in feature_names_poly:
idx = list(feature_names_poly).index(feat)
original_importance[feat] = np.abs(shap_values[:, idx]).mean()
top_3_orig = sorted(original_importance.items(), key=lambda x: x[1], reverse=True)[:3]
print("\n🎯 Phân tích TOP 3 features gốc:\n")
for rank, (feat_name, importance) in enumerate(top_3_orig, 1):
print(f"{'─' * 70}")
print(f"#{rank}. {feat_name} (Mean |SHAP|: {importance:.4f})")
print(f"{'─' * 70}")
feat_idx = list(feature_names_poly).index(feat_name)
# Tính correlation
feat_vals = X_test_transform[:n_samples, feat_idx]
shap_vals = shap_values[:, feat_idx]
corr = np.corrcoef(feat_vals, shap_vals)[0, 1]
# Dependence plot
fig, ax = plt.subplots(figsize=(10, 6))
shap.dependence_plot(
feat_idx,
shap_values,
X_test_transform[:n_samples],
feature_names=feature_names_poly,
interaction_index="auto",
ax=ax,
show=False
)
plt.title(f"Dependence Plot: {feat_name} (correlation={corr:.3f})",
fontsize=12, pad=15)
plt.tight_layout()
plt.show()
Kết quả
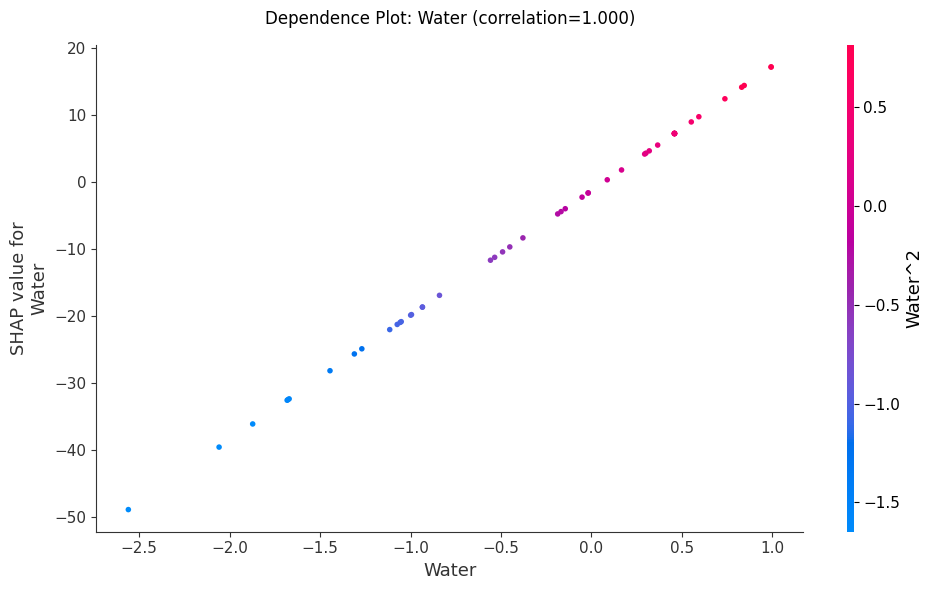
Hình 8: Biểu đồ phụ thuộc SHAP thể hiện ảnh hưởng của đặc trưng Water lên dự đoán của mô hình.
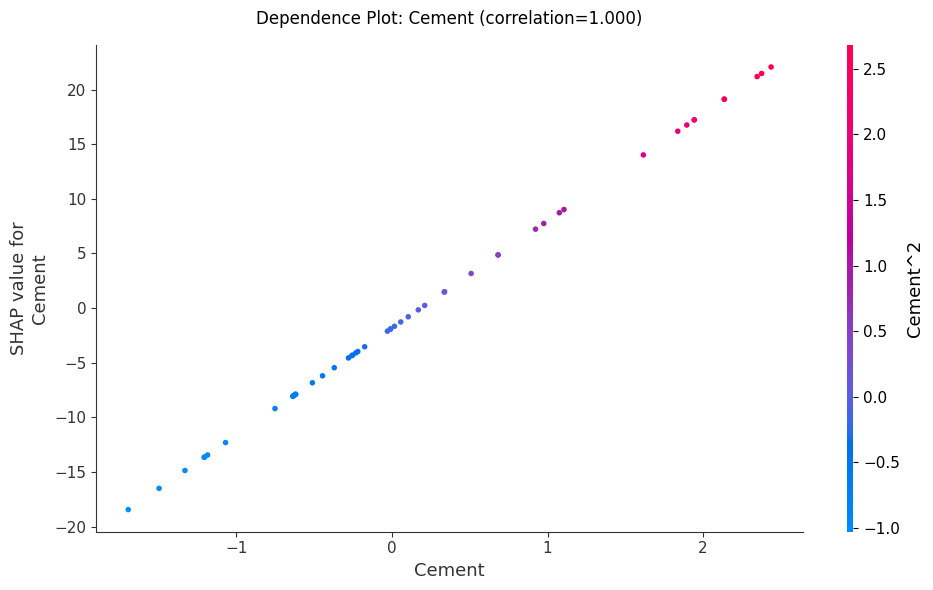
Hình 9: Biểu đồ phụ thuộc SHAP thể hiện ảnh hưởng của đặc trưng Cement lên dự đoán của mô hình.
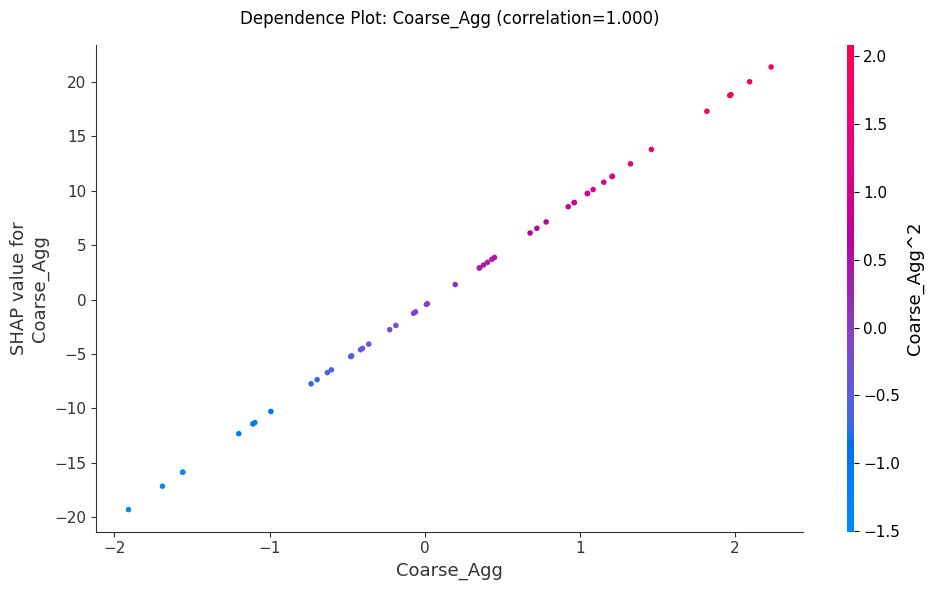
Hình 10: Biểu đồ phụ thuộc SHAP thể hiện ảnh hưởng của đặc trưng Coarse_Agg lên dự đoán của mô hình
Nhận xét từ các Biểu đồ
- Water (Nước), Cement (Xi măng) và Coarse_Agg () có mối quan hệ tích cực rõ ràng, khi các giá tỉ này càng nhiều sẽ giúp tăng giá tị dự đoán SHAP như càng nhiều nước, bê tông sẽ làm tăng dự đoán sức mạnh của bê tông
Chương 4 – Demo ứng dụng với Streamlit
4.1. Giới thiệu
Sau khi hoàn thành phân tích và xây dựng mô hình, chúng ta triển khai một ứng dụng web tương tác bằng Streamlit để người dùng có thể dễ dàng sử dụng mô hình mà không cần kiến thức lập trình.
4.2. Chuẩn bị & Clone mã nguồn
4.2.1. Clone từ GitHub
git clone https://github.com/VinhIT2019/projectPolyNomial_05.git
cd projectPolyNomial_05
Trong thư mục projectPolyNomial_05 có các file:
app.py: Code chính của ứng dụngrequirements.txt: Danh sách thư viện cần cài
4.2.2. Tạo và kích hoạt môi trường ảo
Trên Windows (PowerShell):
python -m venv venv
.\venv\Scripts\Activate
Trên Linux / macOS:
python3 -m venv venv
source venv/bin/activate
4.2.3. Cài đặt thư viện
pip install --upgrade pip
pip install -r requirements.txt
4.2.4. Chạy ứng dụng
streamlit run app.py
Ứng dụng sẽ mở tại: http://localhost:8501
4.3. Hướng dẫn sử dụng
4.3.1. Tải dữ liệu
- Ở sidebar (cột trái), bấm "Tải dataset"
- Chọn file CSV hoặc Excel (.xlsx)
- Ứng dụng hiển thị kích thước của bộ dữ liệu sau khi xóa đi các dòng trùng lặp và preview 5 dòng đầu tiên
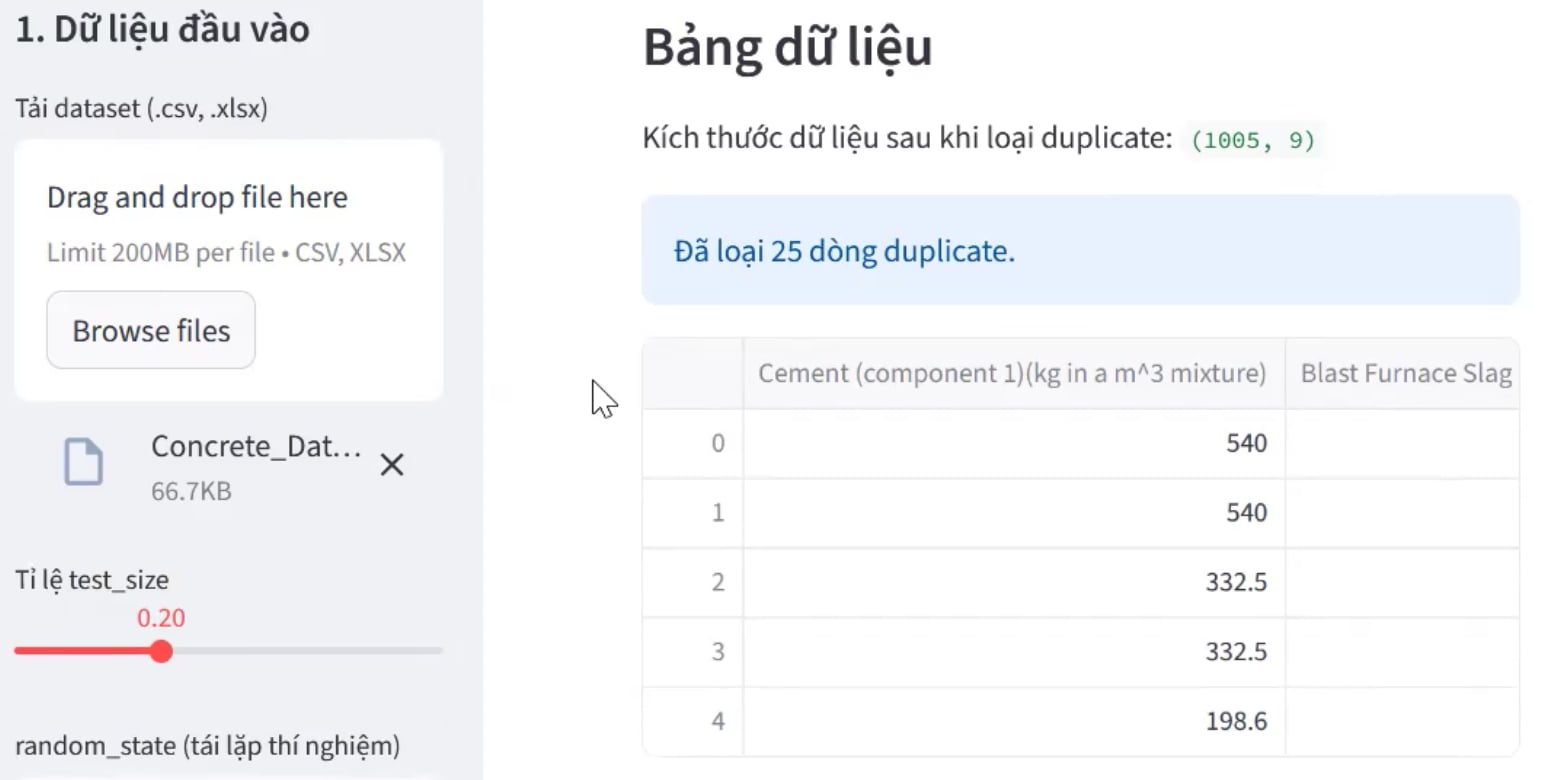
Hình 11: Giao diện upload và làm sạch dữ liệu
4.3.2. Chọn target & features
- Target: Mặc định là cột cuối cùng (có thể thay đổi trong dropdown)
- Features: Mặc định là tất cả các cột còn lại (có thể bỏ chọn)
Ví dụ:
- Target:
Strength - Features:
Cement,Water,Age,Superplasticizer, v.v.

Hình 12: Giao diện chọn biến mục tiêu và các đặc trưng đầu vào cho mô hình
4.3.3. Chọn mô hình & tùy chỉnh tham số
Trong phần "Chọn mô hình" có 5 lựa chọn:
- LinearRegression (no polynomial) - Hồi quy tuyến tính cơ bản
- Poly3 + LinearRegression - Đa thức bậc 3
- Poly4 + RidgeCV - Đa thức bậc 4 + Ridge (khuyến nghị)
- Poly4 + LassoCV - Đa thức bậc 4 + Lasso
- Poly4 + ElasticNetCV - Đa thức bậc 4 + ElasticNet
Tùy chỉnh tham số:
test_size: Tỉ lệ tách tập test (mặc định: 0.2)random_state: Seed để tái lập kết quả (mặc định: 42)- Tham số riêng cho từng model:
1. Ridge/Lasso:min_alpha,max_alpha,n_alphas,max_iter
2. ElasticNet: thêml1_ratio
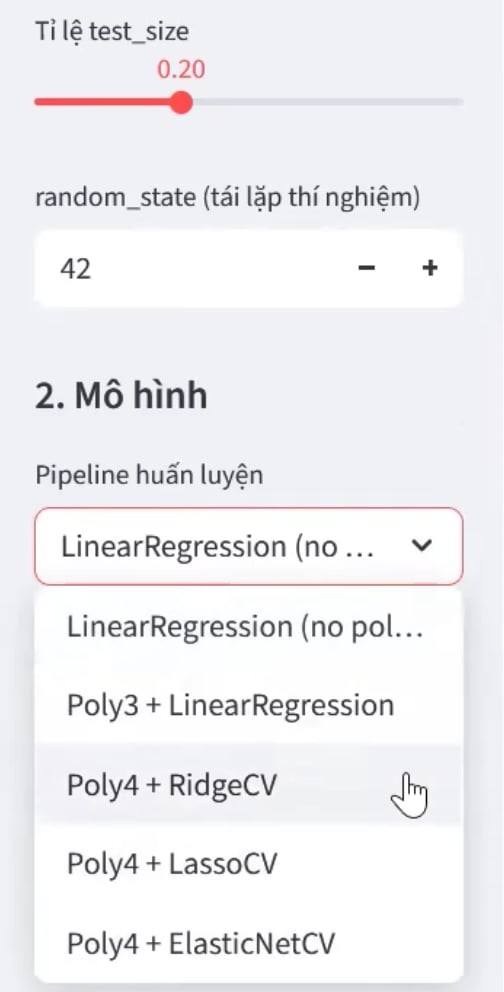 |
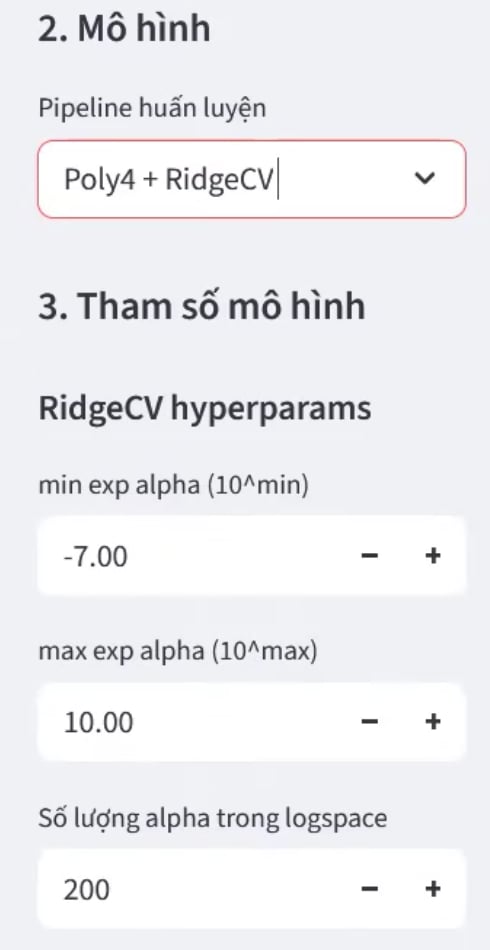 |
Hình 13 và 14: Giao diện thiết lập tham số huấn luyện và lựa chọn mô hình
4.3.4. Train & Đánh giá
Nhấn nút "Train / Evaluate model". Ứng dụng sẽ:
-
Chia dữ liệu train/test theo
test_size -
Huấn luyện mô hình và hiển thị:
- R² (train/test)
- RMSE (test)
- Cross-Validation (RepeatedKFold 10-fold × 3 repeats):
- R² (Mean ± Std)
- RMSE (Mean ± Std)
- Vẽ biểu đồ scatter: y_true vs y_pred
- Hiển thị bảng hệ số:
- Top 10 hệ số tích cực (ảnh hưởng dương)
- Top 10 hệ số tiêu cực (ảnh hưởng âm)

|
||

|

|

|
Hình 15, 16, 17, 18: Giao diện kết quả sau khi huấn luyện mô hình Poly4 + RidgeCV với đầy đủ chỉ số đánh giá, biểu đồ so sánh dự đoán và phân tích mức độ quan trọng của các đặc trưng
Chương 5 – Tổng kết
Đề tài đã hoàn thành mục tiêu nghiên cứu và xây dựng mô hình dự đoán cường độ chịu nén của bê tông dựa trên dữ liệu thực nghiệm. Quá trình thực hiện cho thấy, việc kết hợp giữa hiểu biết chuyên môn và các phương pháp học máy mang lại hiệu quả rõ rệt trong việc mô hình hóa và phân tích các mối quan hệ phức tạp giữa các thành phần vật liệu.
5.1. Những đóng góp chính
- Về mặt kỹ thuật:
- Chứng minh mối quan hệ phi tuyến giữa thành phần vật liệu và cường độ bê tông
- So sánh hiệu quả của 5 mô hình khác nhau
- Đạt R² = 0.896 và RMSE = 5.57 MPa với mô hình Poly4 + Ridge
- Về mặt giải thích:
- Phân tích hệ số để hiểu ảnh hưởng của từng thành phần
- Sử dụng SHAP để giải thích quyết định mô hình
- Về mặt ứng dụng:
- Xây dựng ứng dụng Streamlit cho người dùng không chuyên
- Cung cấp công cụ hỗ trợ thiết kế hỗn hợp bê tông
5.2. Bài học kinh nghiệm
- EDA là bước quan trọng không thể bỏ qua
- Regularization giúp kiểm soát overfitting hiệu quả
- Cross-validation cung cấp ước lượng tin cậy về hiệu suất
- Giải thích mô hình quan trọng không kém dự đoán
5.3. Kết luận
Kết quả không chỉ chứng minh tính khả thi của mô hình mà còn mở ra hướng tiếp cận mới trong việc ứng dụng trí tuệ nhân tạo vào lĩnh vực xây dựng. Bên cạnh giá trị kỹ thuật, đề tài cũng là trải nghiệm giúp người thực hiện nhận ra rằng, trong mọi công nghệ — sự hiểu biết và tư duy khoa học của con người vẫn là nền tảng quan trọng nhất.
Công nghệ có thể hỗ trợ, nhưng chính con người mới là yếu tố tạo nên giá trị cho tri thức.
Chương 6 - Tài liệu tham khảo
- Slide Project Sales Prediction (Nguyễn Quốc Thái, Hồ Quang Hiển, Đinh Quang Vinh):
-
Hồi qui Ridge và Lasso – DeepAI Book (Phạm Đình Khánh):
https://phamdinhkhanh.github.io/deepai-book/ch_ml/index_RidgedRegression.html -
Xác thực chéo (Cross-validation): Đánh giá hiệu năng của mô hình – scikit-learn User Guide:
https://scikit-learn.org/stable/modules/cross_validation.html -
Concrete Compressive Strength Dataset – UCI Machine Learning Repository:
https://archive.ics.uci.edu/ml/datasets/Concrete+Compressive+Strength
Chưa có bình luận nào. Hãy là người đầu tiên!