I. Vượt Ra Ngoài Mệnh Lệnh: Vì Sao AI Cần Đến Học Tăng Cường (Reinforcement Learning)”
1. Khi AI cần nhiều hơn là “làm theo chỉ dẫn”
Bạn đã bao giờ tự hỏi làm thế nào một chiếc xe tự lái có thể điều hướng qua một giao lộ đông đúc, một chương trình máy tính có thể đánh bại nhà vô địch thế giới trong trò chơi cờ vây phức tạp, hay một robot có thể tự học cách mở cửa chưa?
Trong nhiều năm, AI chủ yếu hoạt động dựa trên các tập dữ liệu rõ ràng (ví dụ: nếu thấy A, làm B) hoặc dữ liệu được gán nhãn (ví dụ: Đây là mèo, đây là chó). Nhưng để AI thực sự phát triển — để nó có thể ra quyết định trong môi trường phức tạp, thay đổi liên tục, nơi không có sẵn câu trả lời đúng — thì những phương pháp này là không đủ.
Chúng ta cần một phương pháp cho phép AI tự khám phá và thích nghi... một phương pháp mà không cần con người phải lập trình từng hành động cụ thể. Chính nhu cầu này đã dẫn đến sự ra đời và bùng nổ của Học tăng cường.
2. Reinforcement Learning: AI học bằng thử–sai như sinh vật sống
Học tăng cường (Reinforcement Learning - RL) là một nhánh của Học máy, mô phỏng cách sinh vật học tự nhiên học hỏi. Thay vì được cung cấp các cặp đầu vào/đầu ra chính xác, một tác nhân AI (Agent) được đặt trong một môi trường và phải học cách thực hiện một chuỗi hành động để đạt được một mục tiêu cụ thể.
Quá trình này dựa trên cơ chế thử-sai và phản hồi thông qua một hệ thống "phần thưởng" và "hình phạt":
-
Phần thưởng: Một hành động tốt sẽ mang lại điểm tích cực.
-
Hình phạt: Một hành động sai sẽ mang lại điểm tiêu cực (hoặc không có phần thưởng).
Mục tiêu cốt lõi của tác nhân AI là học được một chiến lược, hay còn gọi là chính sách (Policy), để tối đa hóa tổng phần thưởng nhận được về lâu dài.
3. RL – Bước chuyển giúp AI trở nên tự chủ và thích nghi
Không chỉ là một thuật toán khác. Nó là bước chuyển mình mang tính nền tảng, thúc đẩy các hệ thống AI tự chủ và thích nghi thực sự ngày nay, cho phép chúng học hỏi, đưa ra quyết định tối ưu và thực hiện hành động một cách độc lập mà không cần sự can thiệp liên tục từ con người. RL chính là chìa khóa để AI bước "Ngoài Lệnh Chỉ Dẫn".
II. The Core Components — Bốn Trụ Cột Tạo Thành Vòng Lặp Reinforcement Learning
Để hiểu cách AI học thông qua Reinforcement Learning, chúng ta cần nắm vững cấu trúc của RL Loop — vòng lặp học tập liên tục nơi Agent tương tác với Môi trường, nhận phản hồi và cải thiện chính sách của mình theo thời gian.
Dưới đây là những thành phần cốt lõi tạo nên mọi hệ thống RL, từ robot nhặt đồ vật cho đến AI chơi game hay mô hình giao dịch chứng khoán.
A. Agent (Tác tử)
Agent là thực thể học hỏi và ra quyết định trong hệ thống RL (e.g., a robot, a program, or a neural network).
Tác nhân là thực thể học hỏi và ra quyết định trong hệ thống RL.
-
Nó có thể là một robot đang cố gắng hoàn thành nhiệm vụ, một thuật toán chơi game, hay một mạng thần kinh (Neural Network) đang học cách điều khiển.
-
Nhiệm vụ chính của Agent là quan sát môi trường, sau đó chọn hành động tối ưu để tối đa hóa phần thưởng tích lũy về sau.
B. Environment (Môi trường)
Môi trường là toàn bộ thế giới mà Agent tương tác cùng (ví dụ: bàn cờ, thế giới mô phỏng, hay thị trường chứng khoán). Nó nhận hành động từ Agent và trả về trạng thái mới cùng với phần thưởng.
- Đây có thể là một bàn cờ tĩnh, một thế giới mô phỏng phức tạp (ví dụ: thế giới ảo trong game), hoặc một hệ thống thực (ví dụ: thị trường chứng khoán, một dây chuyền sản xuất).
C. State (S) and Action (A)
-
State (S): Tình trạng hiện tại của Agent (những gì nó “quan sát” được). Ví dụ: vị trí các quân cờ trên bàn cờ, hoặc các chỉ số tốc độ và góc quay của robot.
-
Action (A): Hành động mà Agent lựa chọn để thực hiện. Ví dụ: di chuyển quân Mã, hoặc tăng lực đẩy động cơ.
D. Reward (R)
Reward là tín hiệu phản hồi ngay lập tức (dương hoặc âm) mà Agent nhận được sau khi thực hiện một hành động.
- Trọng tâm: Agent học cách tối đa hóa tổng phần thưởng dài hạn (còn gọi là Return), chứ không chỉ phần thưởng tức thời. Ví dụ: trong cờ vua, việc hy sinh một quân cờ nhỏ để đổi lấy lợi thế vị trí có thể mang lại phần thưởng tức thời thấp (mất điểm) nhưng sẽ dẫn đến phần thưởng lớn hơn về sau (chiến thắng ván cờ).
E. Policy ($\pi$)
Policy ($\pi$) là chiến lược của Agent—hay còn gọi là "bộ não" của nó.
-
Policy ánh xạ từ State ($\mathbf{S}$) → Action ($\mathbf{A}$). Nó trả lời câu hỏi: "Khi đang ở trạng thái này, tôi nên làm gì?"
-
Mục tiêu của quá trình huấn luyện RL là tìm ra Policy tối ưu ($\pi^*$) để Agent luôn chọn được hành động mang lại phần thưởng tích lũy cao nhất.
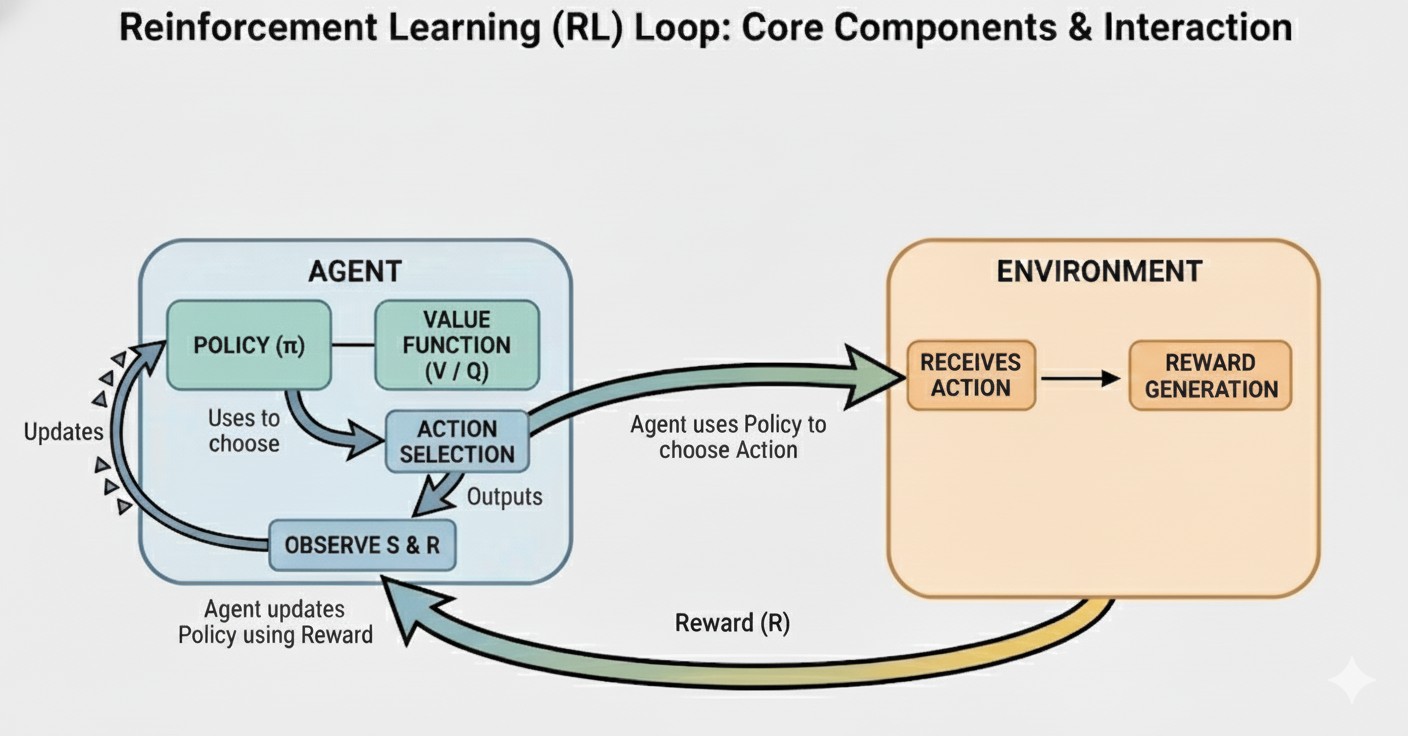
Figure 1. Reinforcement Learning Loop
III. Thách thức Trọng Tâm: Khám Phá (Exploration) vs. Khai Thác (Exploitation)
Trong lĩnh vực Học tăng cường (RL), việc Agent học được Policy tối ưu ($\pi^*$) phụ thuộc vào khả năng giải quyết một vấn đề đánh đổi cơ bản và quan trọng nhất: Khám phá những điều chưa biết, hay Khai thác những điều đã biết là tốt.
Đây là vấn đề đánh đổi quan trọng nhất và khó khăn nhất trong RL, quyết định liệu Agent có tìm thấy giải pháp tối ưu hay không.
A. Exploration (Khám phá)
Khám phá là hành động thử các hành động mới, chưa chắc chắn, và có thể chưa từng được thực hiện trước đây, nhằm mục đích thu thập thêm thông tin về Môi trường.
-
Định nghĩa: Thử các hành động mới, chưa chắc chắn để tìm ra phần thưởng tốt hơn.
-
Ví dụ: Bạn đang lái xe trong một thành phố xa lạ và quyết định thử tuyến đường mới mà GPS chưa gợi ý, hy vọng tìm thấy một con đường ngắn hơn hoặc ít tắc nghẽn hơn.
-
Mục đích: Để đảm bảo Agent không bị mắc kẹt ở một tối ưu cục bộ (local optimum)—một giải pháp tốt, nhưng không phải tốt nhất có thể.
B. Exploitation (Khai thác)
Khai thác là hành động sử dụng hành động tốt nhất đã biết cho đến thời điểm hiện tại để tối đa hóa phần thưởng tức thời.
-
Định nghĩa: Sử dụng hành động tốt nhất đã biết để tối đa hóa phần thưởng hiện tại.
-
Ví dụ: Bạn đã biết tuyến đường đi làm cũ vốn hiệu quả và đáng tin cậy, vì vậy bạn đi lại tuyến đường đó để đảm bảo đến nơi đúng giờ.
-
Mục đích: Để kiếm được phần thưởng cao nhất dựa trên kiến thức hiện có của Agent.
C. Cân bằng đánh đổi (Trade-off Balance)
Việc cân bằng giữa Khám phá và Khai thác là chìa khóa để học được chính sách tối ưu ($\pi^*$) trong dài hạn.
-
Mối nguy Khai thác quá mức: Agent sẽ chỉ lặp lại các hành động mà nó đã biết là tốt, bỏ lỡ cơ hội tìm ra các hành động hoặc chiến lược tốt hơn rất nhiều chưa được khám phá.
-
Mối nguy Khám phá quá mức: Agent sẽ hành động ngẫu nhiên, không tận dụng được những gì nó đã học, dẫn đến hiệu suất thấp và lãng phí thời gian.
Các thuật toán RL như $\epsilon$-greedy là những kỹ thuật được thiết kế để giải quyết vấn đề này. Các thuật toán này cho phép Agent:
-
Khám phá nhiều hơn lúc ban đầu (khi Agent chưa biết gì).
-
Dần dần chuyển sang Khai thác nhiều hơn khi Agent đã tích lũy đủ kiến thức và tin tưởng hơn vào những hành động mà nó đã tìm thấy.
Việc thiết lập và điều chỉnh tham số cân bằng này (như giá trị $\epsilon$) chính là một trong những thách thức cốt lõi khi thiết kế và huấn luyện một hệ thống RL hiệu quả.
IV. Key Algorithms: How the Agent Learns (The Mechanics)
Có hai phương pháp tiếp cận chính để giải quyết bài toán Reinforcement Learning: Value-Based Methods (học hàm giá trị) và Policy-Based Methods (học chính sách trực tiếp).
A. Value-Based Methods:
(Learning the Value Function)
Trong phương pháp này, Agent không học trực tiếp chiến lược hành động. Thay vào đó, nó học cách ước lượng giá trị kỳ vọng của mỗi trạng thái và hành động—tức là định giá tương lai. Khi Agent nắm được hàm giá trị chính xác, việc ra quyết định trở nên đơn giản: chọn hành động dẫn đến trạng thái có giá trị cao nhất (Greedy Policy).
Chúng ta sẽ khảo sát hai thuật toán nền tảng: Q-Learning (phương pháp bảng cổ điển) và Deep Q-Network (DQN) (phương pháp xấp xỉ hàm hiện đại).
1. Mathematical Foundation: The Bellman Equation
Trước khi đi vào chi tiết thuật toán, chúng ta cần hiểu khái niệm Q-Value và nền tảng toán học của nó.
Định nghĩa: Ký hiệu Qπ(s, a) là tổng phần thưởng chiết khấu kỳ vọng (expected discounted return) khi Agent ở trạng thái s, thực hiện hành động a, và sau đó tuân theo chính sách π.
Công thức tổng phần thưởng (Cumulative Return):
$$ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} $$
Trong đó:
-
R (Reward): Phần thưởng tức thời nhận được tại mỗi bước.
-
γ (Discount Factor): Hệ số chiết khấu, với 0 ≤ γ ≤ 1.
-
Khi γ = 0: Agent chỉ quan tâm đến phần thưởng tức thời (myopic behavior).
-
Khi γ → 1: Agent ưu tiên lợi ích dài hạn (far-sighted behavior).
Phương trình Bellman tối ưu (Optimal Bellman Equation):
Đây là phương trình đệ quy cơ bản thiết lập mối quan hệ giữa giá trị hiện tại và giá trị tương lai:
$$ Q^*(s, a) = \mathbb{E} [ r + \gamma \max_{a'} Q^*(s', a') ] $$
- Ý nghĩa: Giá trị tối ưu của cặp trạng thái-hành động (s, a) bằng phần thưởng tức thời r cộng với giá trị tối ưu được chiết khấu của trạng thái kế tiếp s'. Phương trình này cho phép Agent "dự đoán tương lai" bằng cách lan truyền thông tin giá trị ngược về quá khứ.
2. Q-Learning: Thuật toán cổ điển (Tabular Method)
Q-Learning giải quyết bài toán bằng cách lập một bảng tra cứu (Q-Table). Ban đầu bảng này chứa các số ngẫu nhiên. Qua thời gian, nó được cập nhật để tiệm cận với phương trình Bellman.
Bản chất: Tạo ra một "Bảng cửu chương" khổng lồ gọi là Q-Table.
-
Hàng là Trạng thái (State).
-
Cột là Hành động (Action).
-
Ô giao nhau chứa giá trị Q (Chất lượng — Quality).
Quy tắc cập nhật:
Đây là công thức quan trọng nhất cần nhớ trong Q-Learning. Tại mỗi bước thời gian t, sau khi thực hiện hành động at tại st, nhận thưởng rt và sang trạng thái mới st+1, ta cập nhật ô Q(st, at) như sau:
$$ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \cdot \left[ \underbrace{r_t + \gamma \max_{a} Q(s_{t+1}, a)}_{\text{TD Target}} - Q(s_t, a_t) \right] $$
Phân tích toán học chi tiết:
-
TD Target (r + γ max Q...): Đây là thực tế vừa xảy ra (Reward) cộng với dự đoán tốt nhất về tương lai. Nó đóng vai trò là "Giáo viên", chỉ ra giá trị thực sự nên là bao nhiêu.
-
TD Error (Temporal Difference Error): Sự chênh lệch giữa "Thực tế" (Target) và "Dự đoán cũ" của Agent.
-
Nếu TD Error > 0: Agent đã đánh giá thấp hành động này → Cần tăng Q.
-
Nếu TD Error < 0: Agent đã quá lạc quan → Cần giảm Q.
- α (Learning Rate): Tốc độ học (0 < α ≤ 1). Quyết định xem Agent tin vào kiến thức mới bao nhiêu phần trăm so với kiến thức cũ.
Hiểu nôm na: "Kinh nghiệm hôm nay sửa sai cho dự đoán hôm qua".
Điểm yếu: Chỉ hoạt động tốt trong môi trường nhỏ (như mê cung bé). Với bài toán lớn (như Cờ Vây), số lượng trạng thái nhiều hơn số nguyên tử trong vũ trụ — ta không thể lập nổi bảng này (tràn bộ nhớ). Đây gọi là Curse of Dimensionality.
3. Deep Q-Network (DQN): Kỷ nguyên Deep Learning
Vấn đề của Q-Learning: Hãy tưởng tượng bài toán xử lý ảnh (như game Atari). Một khung hình 84×84 pixels, mỗi pixel 256 màu → Số lượng trạng thái là 25684×84. Không một máy tính nào trên thế giới chứa nổi cái bảng Q-Table này.
Giải pháp DQN: Thay vì dùng bảng, ta dùng một hàm xấp xỉ (Function Approximator). Cụ thể là một Mạng nơ-ron (Neural Network) với tham số trọng số là θ.
$$ Q(s, a; \theta) \approx Q^*(s, a) $$
Mạng nơ-ron nhận đầu vào là s (ảnh pixel) và xuất ra giá trị Q cho tất cả các hành động a.
Sự đột phá: DeepMind (Google) nghĩ ra một ý tưởng táo bạo: Vứt bỏ bảng Q-Table!
Thay vào đó, họ dùng Mạng nơ-ron sâu (Deep Neural Network).
-
Đầu vào: Hình ảnh màn hình game (các pixel).
-
Đầu ra: Giá trị Q cho từng nút bấm (lên, xuống, trái, phải...).
-
Lúc này, AI không "tra cứu bảng" nữa mà nhìn và cảm nhận để đưa ra dự đoán—giống trực giác con người.
Hàm mất mát (Loss Function):
Để huấn luyện mạng nơ-ron, ta cần cực tiểu hóa sai số giữa "Dự đoán" và "Mục tiêu". Trong DQN, hàm Loss (Mean Squared Error) được định nghĩa là:
$$ L(\theta) = \mathbb{E}*{(s,a,r,s') \sim D} \left[ \left( \underbrace{r + \gamma \max*{a'} Q(s', a'; \theta^-)}*{\text{Target } y_i} - \underbrace{Q(s, a; \theta)}*{\text{Prediction}} \right)^2 \right] $$
Tại đây xuất hiện 2 kỹ thuật toán học cực kỳ quan trọng giúp DQN hoạt động được (nếu không có 2 cái này, thuật toán sẽ phân kỳ và thất bại):
Hai chìa khóa thành công (The Mathematical Stability Tricks):
Kỹ thuật 1: Experience Replay (Bộ nhớ đệm trải nghiệm D)
-
Vấn đề: Trong Deep Learning, giả định cơ bản là dữ liệu phải i.i.d (độc lập và có cùng phân phối). Nhưng trong game, trạng thái st+1 phụ thuộc chặt chẽ vào st. Dữ liệu có tính tương quan cao (Correlated) khiến Gradient Descent bị dao động mạnh, không hội tụ.
-
Giải pháp: Lưu các bước đi (s, a, r, s') vào một bộ nhớ D. Khi huấn luyện, ta lấy mẫu ngẫu nhiên (Random Batch) từ D. Điều này phá vỡ sự tương quan thời gian, giúp mạng học ổn định.
-
Ẩn dụ: Khi con người ngủ, não bộ tua lại các ký ức trong ngày để học. DQN cũng vậy: nó lưu trải nghiệm vào "bộ nhớ đệm", rồi bốc ngẫu nhiên các ký ức cũ ra để học lại. Điều này giúp AI học ổn định hơn, không bị cuốn theo những phản ứng nhất thời của chuỗi hành động vừa xong.
Kỹ thuật 2: Target Network (θ−)
-
Vấn đề: Hãy nhìn vào công thức Loss ở trên. Cả "Prediction" Q(s,a;θ) và "Target" r + γ max Q(s',a';θ) đều dùng chung một mạng nơ-ron (θ). Điều này giống như con chó đuổi theo cái đuôi của mình. Khi ta cập nhật θ để Prediction tiến tới Target, thì vô tình Target cũng bị dịch chuyển theo. Mục tiêu di động liên tục khiến mạng không bao giờ hội tụ.
-
Giải pháp: Tạo ra hai mạng riêng biệt:
-
Main Network (θ): Dùng để chọn hành động và được cập nhật liên tục sau mỗi bước (như Gradient Descent bình thường).
-
Target Network (θ−): Dùng để tính toán giá trị mục tiêu (Target yi). Tham số θ− được giữ nguyên (đóng băng) trong một khoảng thời gian (ví dụ: 1000 bước), sau đó mới copy từ Main Network sang (θ− ← θ).
-
Kết quả toán học: Mục tiêu yi trở thành hằng số trong ngắn hạn, biến bài toán RL quay trở về bài toán Supervised Learning ổn định (Target cố định → Prediction đuổi theo Target).
Thành tựu: Đây chính là thuật toán phá đảo các game Atari và mở ra kỷ nguyên Deep Reinforcement Learning.
Tóm lại:
Value-Based Methods là hành trình đi tìm lời giải cho phương trình Bellman Q(s, a).
-
Nếu không gian nhỏ → Giải chính xác bằng bảng Q-Table.
-
Nếu không gian lớn → Giải xấp xỉ bằng cách cực tiểu hóa hàm Loss L(θ) trong DQN, với sự trợ giúp của toán học xác suất (Experience Replay) và kỹ thuật ổn định mục tiêu (Target Network).
B. Policy-Based Methods: "Bậc thầy phản xạ"
(Học Trực Tiếp Chiến Lược - Policy Optimization)
Nếu Value-Based Methods (DQN) là những nhà toán học tính toán chi li từng điểm số, thì Policy-Based Methods chính là những "nghệ sĩ" học cách hành động bằng trực giác và phản xạ. Đây là phương pháp đứng sau sự thành công của những robot nhảy parkour (Boston Dynamics) hay ChatGPT (thông qua RLHF).
Tư duy cốt lõi:
Trong phương pháp này, chúng ta bỏ qua việc tìm hàm giá trị trung gian Q(s,a). Thay vào đó, ta tối ưu hóa trực tiếp một hàm tham số hóa πθ(a|s) – gọi là Policy Network (Mạng chiến lược).
- Đầu vào: Trạng thái s.
- Đầu ra: Một phân phối xác suất trên các hành động π(a|s) (Ví dụ: 70% sang trái, 30% sang phải).
Mục tiêu tối thượng là tìm bộ tham số θ (trọng số mạng nơ-ron) để tối đa hóa Hàm mục tiêu J(θ) (Tổng phần thưởng kỳ vọng):
$$ J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta} [R(\tau)] $$
(Kỳ vọng phần thưởng R trên quỹ đạo τ được sinh ra bởi chính sách πθ).
Ví dụ: Khi bạn tập đi xe đạp, cơ bắp tự điều chỉnh để giữ thăng bằng (Policy) chứ không tính toán vật lý góc nghiêng (Value).
1. Nền tảng toán học: The Policy Gradient Theorem
(Định lý Gradient Chiến lược - Trái tim của phương pháp)
Vấn đề lớn nhất: Làm sao chúng ta lấy đạo hàm (gradient) của một thứ mang tính ngẫu nhiên như "lấy mẫu hành động"? Chúng ta không thể lan truyền ngược (backprop) qua một hành động ngẫu nhiên được.
Các nhà toán học đã sử dụng "Log-Probability Trick" để chứng minh định lý tuyệt đẹp sau:
$$ \nabla_\theta J(\theta) \approx \mathbb{E}_t \left[ \underbrace{\nabla_\theta \log \pi_\theta(a_t | s_t)}_{\text{Hướng điều chỉnh}} \cdot \underbrace{A_t}_{\text{Độ lớn điều chỉnh}} \right] $$
Giải phẫu công thức:
- ∇θ log πθ(at | st): Vector chỉ hướng để tăng xác suất lặp lại hành động at trong trạng thái st.
- At (Advantage - Lợi thế): Cho biết hành động at tốt hay xấu.
- Nếu At > 0 (Kết quả tốt): Gradient sẽ đẩy tham số θ để hành động này diễn ra thường xuyên hơn.
- Nếu At < 0 (Kết quả tệ): Gradient sẽ đảo chiều, làm giảm xác suất hành động này.
⇒ Bản chất: Đây là sự mô hình hóa toán học của quá trình Thử và Sai.
2. REINFORCE: Thuật toán sơ khai (Monte Carlo Policy Gradient)
REINFORCE là ứng dụng trực tiếp nhất của định lý trên.
Quy trình:
- Cho Agent chơi hết một ván (Episode) để thu được chuỗi: s₀, a₀, r₁, ... sT.
- Tính tổng phần thưởng tích lũy từ thời điểm t đến cuối ván (Gt). Ta dùng Gt thay cho At trong công thức trên.
- Cập nhật mạng nơ-ron một lần duy nhất khi ván game kết thúc.
Ưu điểm: Có thể học các chiến lược ngẫu nhiên (ví dụ: trong oẳn tù tì, chiến lược tốt nhất là ra ngẫu nhiên để đối thủ không bắt bài). DQN không làm được điều này.
Vấn đề chết người (High Variance):
Vì nó chờ hết ván mới học, kết quả phụ thuộc rất nhiều vào may mắn.
- Ví dụ: Agent chơi 100 nước đi cực hay, nhưng nước đi thứ 101 xui xẻo làm thua cả ván. REINFORCE sẽ "trừng phạt" cả 100 nước đi hay trước đó vì kết quả cuối cùng là âm. Điều này khiến việc học cực kỳ rung lắc (noisy) và chậm hội tụ.
3. Proximal Policy Optimization (PPO): Tiêu chuẩn vàng hiện đại
(Thuật toán ổn định nhất - Được dùng bởi OpenAI)
Vị thế: Đây là thuật toán đứng sau thành công của OpenAI (dùng để huấn luyện ChatGPT qua RLHF). Nó cân bằng giữa sự đơn giản và hiệu quả.
Để khắc phục sự rung lắc của REINFORCE, PPO giới thiệu một ý tưởng: "Trust Region" (Vùng tin cậy).
Triết lý: "Hãy cải thiện, nhưng đừng thay đổi quá nhanh. Nếu bước đi quá dài, bạn sẽ rơi xuống vực."
A. Tỷ lệ xác suất (The Probability Ratio)
PPO so sánh chính sách mới (πθ) và chính sách cũ (πθ_old) thông qua tỷ số:
$$ r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)} $$
- Nếu rt > 1: Hành động này có xác suất cao hơn trong chính sách mới.
- Nếu rt < 1: Hành động này ít khả năng xảy ra hơn.
B. Hàm mục tiêu "Cắt ngọn" (The Clipped Surrogate Objective)
Đây là công thức làm nên tên tuổi của PPO. Thay vì để Gradient chạy tự do, PPO kìm hãm nó lại:
$$ L^{CLIP}(\theta) = \mathbb{E}_t \left[ \min \left( r_t(\theta) A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) A_t \right) \right] $$
Giải thích cơ chế toán học (Cực kỳ thông minh):
Giả sử ε = 0.2 (cho phép thay đổi tối đa 20%).
- Khi hành động là tốt (At > 0): Ta muốn tăng xác suất (rt tăng).
- Nhưng nếu rt tăng quá 1.2 (1+ε), hàm clip sẽ chặn lại tại 1.2.
- Ý nghĩa: Đừng tham lam tăng xác suất quá đà, vì lỡ đánh giá sai thì sao? Chỉ tăng đến giới hạn an toàn thôi.
- Khi hành động là xấu (At < 0): Ta muốn giảm xác suất (rt giảm).
- Nhưng nếu rt giảm xuống dưới 0.8 (1-ε), hàm clip chặn lại.
- Ý nghĩa: Đừng hủy hoại hoàn toàn một chiến lược chỉ vì một lần thất bại.
⇒ Kết quả: Quá trình học trở nên trơn tru (smooth). Agent cải thiện từ từ nhưng chắc chắn (monotonically improving), tránh được hiện tượng "Model Collapse" (Mô hình sụp đổ - học xong còn ngu hơn lúc chưa học) thường thấy ở các thuật toán RL khác.
Tại sao nó cuốn hút: PPO cực kỳ ổn định, dễ tinh chỉnh (tune), và hoạt động tốt trên hầu hết các bài toán—từ chơi game, điều khiển robot, cho đến căn chỉnh ngôn ngữ AI.
Tổng kết sự khác biệt về toán học (Mental Model):
| Đặc điểm | Value-Based (DQN) | Policy-Based (PPO) |
|---|---|---|
| Cái được học | Hàm Q(s,a) (Giá trị kỳ vọng) | Hàm π(a |
| Toán học cốt lõi | Phương trình Bellman (Quy hoạch động) | Gradient Ascent (Leo đồi) |
| Không gian hành động | Rời rạc (Discrete) - VD: Nút bấm game | Liên tục (Continuous) - VD: Góc quay robot |
| Độ ổn định | Khá ổn định nhờ Target Network | Ổn định nhờ Clipping (PPO) |
| Triết lý | "Tính kỹ rồi hẵng làm" | "Luyện phản xạ cho chuẩn" |
Tóm lại:
-
DQN (Value-based): Như nhà phân tích tài chính—nhìn vào bảng số liệu (State) để tính toán lợi nhuận kỳ vọng (Q-value) rồi mới quyết định đầu tư.
-
PPO (Policy-based): Như vận động viên thể thao—luyện tập phản xạ cơ bắp (Policy) để phản ứng tức thì với tình huống mà không cần tính toán quá nhiều.
V. RL in the Real World: Applications & Impact
(Từ Phòng Thí Nghiệm Ra Đời Thực)
Sức mạnh thực sự của RL nằm ở khả năng giải quyết các bài toán ra quyết định tuần tự (Sequential Decision Making) trong những môi trường mà con người không thể lập trình cứng (hard-code) từng dòng lệnh if-then-else.
A. Game & Benchmarks: "Thao trường luyện tập của AI"
Tại sao các nhà khoa học lại ám ảnh với Game? Vì Game là mô phỏng hoàn hảo của đời thực: có luật chơi, có mục tiêu, và có tính đối kháng, nhưng lại an toàn để thử sai.
- AlphaGo (DeepMind) - Cú sốc lịch sử:
-
Bản chất: Cờ vây có số lượng trạng thái là 10¹⁷⁰ (nhiều hơn số nguyên tử trong vũ trụ). Máy tính không thể "tính hết các nước" như cờ vua.
-
Cơ chế RL: AlphaGo kết hợp Value Network (định giá thế cờ: Đen thắng hay Trắng thắng?) và Policy Network (gợi ý nước đi: Nên đặt quân vào đâu?).
-
Tác động: Nước đi thứ 37 trong ván đấu với Lee Sedol được coi là "nước đi của thần thánh". Đó là một hành động Exploration (Khám phá) mà con người không bao giờ nghĩ tới. RL đã chứng minh nó có thể sáng tạo ra chiến thuật mới, vượt qua trí tuệ ngàn năm của nhân loại.
- Atari & Dota 2:
- OpenAI Five đã đánh bại đội vô địch thế giới Dota 2. Điều kinh khủng là nó phải điều khiển 5 con tướng, phối hợp nhóm, và xử lý thông tin trong thời gian thực (Real-time) với không gian quan sát bị che khuất (Fog of War). Đây là bước đệm để AI bước vào thế giới thực đa chiều.
B. Robotics & Hệ thống tự động: "Bộ não cho cơ thể sắt"
Lập trình cho robot đi bộ là cực khó (Nghịch lý Moravec: Việc dễ với người lại khó với máy). Bạn không thể viết công thức vật lý cho mọi cú vấp ngã.
- Sim-to-Real Transfer (Từ Giả lập ra Thực tế):
-
Vấn đề: Robot rất đắt. Nếu cho nó học bằng RL (thử-sai) ngoài đời, nó sẽ ngã gãy cổ sau 5 phút.
-
Giải pháp: Tạo ra một môi trường giả lập vật lý (như The Matrix). Robot sẽ luyện tập ngã hàng triệu lần trong đó (dùng thuật toán PPO). Sau khi học xong "Policy" đi lại hoàn hảo, bộ não đó được nạp (upload) vào robot thật.
- Manipulation (Cầm nắm):
- Các cánh tay robot trong kho hàng Amazon hay dây chuyền lắp ráp dùng RL để học cách cầm những vật thể lạ (hình dạng bất kỳ) mà không làm vỡ chúng, tự động điều chỉnh lực dựa trên cảm giác xúc giác (xử lý không gian hành động liên tục).
C. GenAI Alignment (RLHF): "Dạy AI làm người tử tế"
Đây là ứng dụng quan trọng nhất và nóng nhất hiện nay. ChatGPT hay Claude sẽ chỉ là những cỗ máy nói nhảm nếu thiếu RL.
- Vấn đề của LLM (Large Language Models):
- Mô hình ngôn ngữ gốc (Base Model) chỉ biết dự đoán từ tiếp theo. Nếu bạn hỏi "Cách chế tạo bom?", nó sẽ vui vẻ hướng dẫn bạn vì nó học được điều đó trên internet. Nó thông minh nhưng thiếu "đạo đức" và "mục đích".
- Giải pháp RLHF (Reinforcement Learning from Human Feedback):
-
Bước 1 (Supervised): Con người viết mẫu câu trả lời tốt để AI bắt chước.
-
Bước 2 (Reward Modeling): Con người chấm điểm các câu trả lời của AI (Ví dụ: Câu A an toàn hơn Câu B → Điểm cao hơn). Ta huấn luyện một mô hình RL học được "gu" chấm điểm này.
-
Bước 3 (PPO - Proximal Policy Optimization): Dùng thuật toán PPO để tinh chỉnh mô hình ngôn ngữ. Mục tiêu: Sinh ra câu chữ sao cho tối đa hóa điểm số từ mô hình thưởng.
-
Kết quả: AI học được cách từ chối câu hỏi xấu, trả lời hữu ích và an toàn. RL chính là "lương tâm" được cấy vào AI.
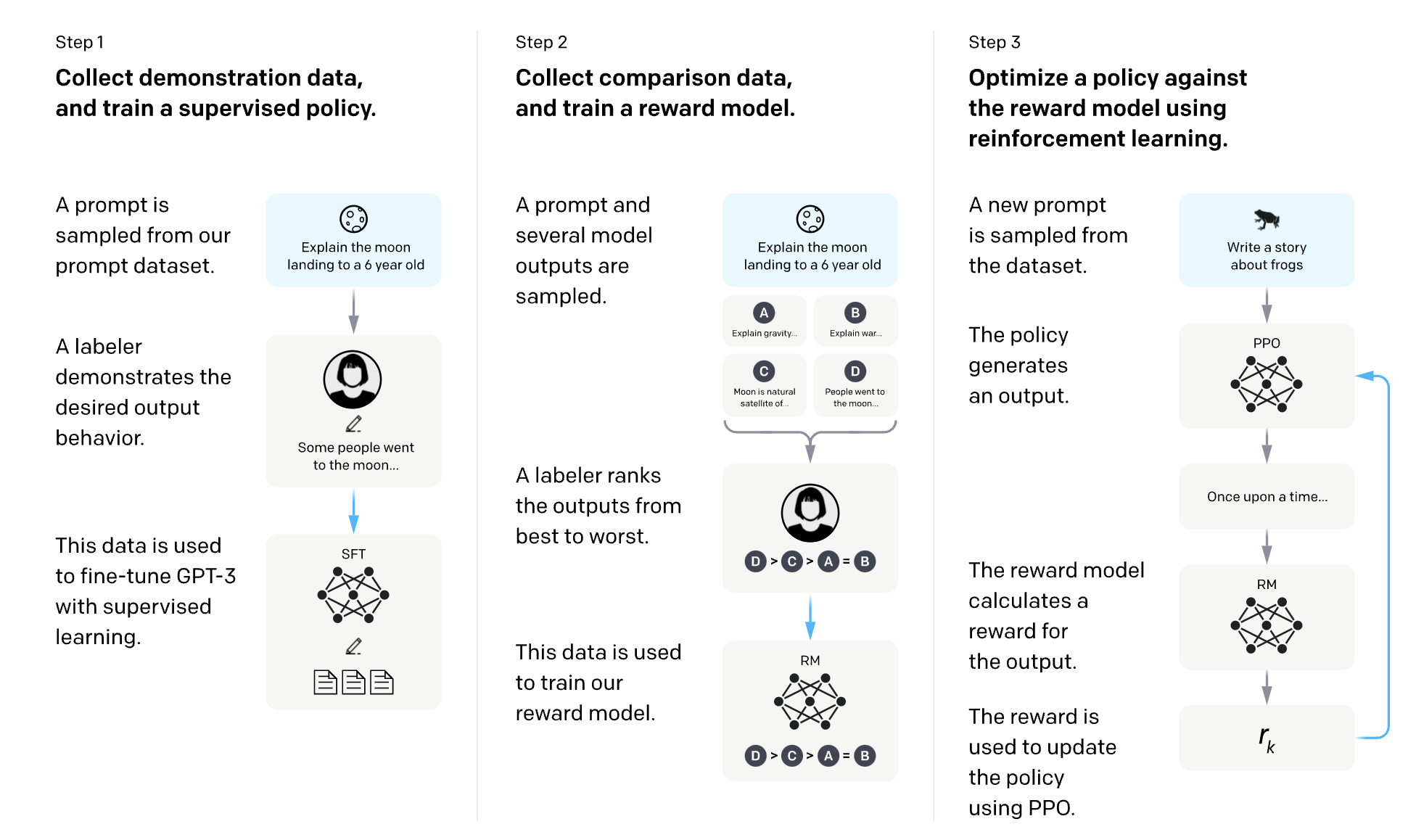
Figure 2
Overview of the Reinforcement Learning from Human Feedback (RLHF) process.[1]
D. Tài chính & Tối ưu hóa: "Những quyết định triệu đô"
Trong thế giới tài chính và công nghiệp, sai một ly đi một dặm.
- Algorithmic Trading (Giao dịch thuật toán):
- Thị trường chứng khoán là môi trường nhiễu động (Stochastic Environment). RL Agent học cách quản lý danh mục đầu tư, tự động quyết định Mua/Bán/Giữ (Action) dựa trên biến động giá (State) để tối đa hóa lợi nhuận (Reward), đồng thời quản lý rủi ro (tránh mức lỗ quá giới hạn).
- Quản lý năng lượng (DeepMind & Google):
-
Google đã giao quyền kiểm soát hệ thống làm mát trung tâm dữ liệu khổng lồ cho một AI dùng RL.
-
AI tự động điều chỉnh hàng nghìn van khí, quạt gió. Kết quả: Giảm 40% năng lượng tiêu thụ. Nó tìm ra những cách phối hợp luồng khí động lực học phức tạp mà kỹ sư con người không thể tính toán nổi.
References
[1] OpenAI. (2022). Illustration of the RLHF training process [Diagram]. https://openai.com/blog/instruction-following
Chưa có bình luận nào. Hãy là người đầu tiên!