1.Giới Thiệu: Bài Toán Dự Đoán Chuỗi Thời Gian
Dự đoán giá cổ phiếu luôn là một trong những thách thức hấp dẫn nhất trong lĩnh vực phân tích chuỗi thời gian. Với sự biến động phức tạp, phi tuyến tính của thị trường, việc xây dựng một mô hình đơn giản nhưng hiệu quả là mục tiêu của nhiều nhà nghiên cứu.
Bài viết này khám phá cách chúng ta sử dụng các mô hình tuyến tính tiên tiến như DLinear và NLinear, kết hợp với kỹ thuật Ensemble (Kết hợp mô hình) để dự đoán giá cổ phiếu FPT.
2. Chuẩn Bị Dữ Liệu
Dữ liệu huấn luyện (FPT_train.csv) chứa thông tin giá đóng cửa của cổ phiếu FPT từ 2020-08-03 đến 2025-03-10.
Kỹ Thuật Log-Transform
- Để ổn định phương sai (variance) của chuỗi thời gian, ta áp dụng phép biến đổi logarit tự nhiên lên cột giá đóng cửa (close):$$\text{close\_log} = \ln(\text{close})$$
Việc này giúp mô hình làm việc hiệu quả hơn với chuỗi thời gian có xu hướng tăng theo cấp số nhân (exponential growth).
Cấu Hình Mô Hình
Chúng ta định nghĩa các tham số quan trọng cho bài toán dự đoán:
- INPUT_LEN (Số ngày input): $14$ ngày gần nhất dùng để dự đoán.
- OUTPUT_LEN (Số ngày output): $3$ ngày tiếp theo được dự đoán trong mỗi bước.
- TOTAL_PREDICT_DAYS (Tổng số ngày dự đoán): $100$ ngày.
INPUT_LEN = 14
OUTPUT_LEN = 3
TOTAL_PREDICT_DAYS = 100
3. Các Mô Hình Tuyến Tính Hiện Đại
Thay vì chỉ sử dụng mô hình tuyến tính cơ bản, nhóm áp dụng hai cải tiến mạnh mẽ: DLinear (Decomposition Linear) và NLinear (Normalized Linear).
3.1. DLinear: Phân Tách Xu Hướng và Tính Mùa Vụ
DLinear hoạt động dựa trên nguyên lý phân tách chuỗi thời gian thành hai thành phần chính: Xu hướng (Trend) và Tính mùa vụ (Seasonal).
$$\text{input} = \text{Trend} + \text{Seasonal}$$
- Xu hướng (Trend): Được trích xuất bằng cách sử dụng Hàm trung bình trượt (Moving Average).
- Tính mùa vụ (Seasonal): Là phần còn lại sau khi trừ đi xu hướng.
Sau đó, hai mô hình tuyến tính độc lập sẽ được huấn luyện để dự đoán tương lai của từng thành phần.
$$\text{output} = \text{Linear}_{\text{Trend}}(\text{Trend}) + \text{Linear}_{\text{Seasonal}}(\text{Seasonal})$$
Mô hình này giúp giảm bớt sự phức tạp của chuỗi thời gian, cho phép các mô hình tuyến tính đơn giản nắm bắt được các đặc trưng phức tạp.
class DLinear(nn.Module):
"""Decomposition Linear for univariate time series - handles trend and seasonality"""
def __init__(self, seq_len, pred_len=7, moving_avg=5):
super(DLinear, self).__init__()
self.seq_len = seq_len
self.pred_len = pred_len
self.moving_avg = min(moving_avg, seq_len - 1)
# Linear layers for trend and seasonal components
self.linear_trend = nn.Linear(self.seq_len, self.pred_len)
self.linear_seasonal = nn.Linear(self.seq_len, self.pred_len)
# Create moving average kernel for trend extraction
self.register_buffer('avg_kernel', torch.ones(1, 1, self.moving_avg) / self.moving_avg)
def decompose(self, x):
"""Decompose series into trend and seasonal components"""
batch_size, seq_len = x.shape
x_reshaped = x.unsqueeze(1)
# Apply moving average for trend
padding = self.moving_avg // 2
x_padded = torch.nn.functional.pad(x_reshaped, (padding, padding), mode='replicate')
trend = torch.nn.functional.conv1d(x_padded, self.avg_kernel, padding=0)
trend = trend.squeeze(1)
# Ensure trend has same length as input
if trend.shape[1] != seq_len:
trend = torch.nn.functional.interpolate(
trend.unsqueeze(1), size=seq_len, mode='linear', align_corners=False
).squeeze(1)
seasonal = x - trend
return trend, seasonal
def forward(self, x):
trend, seasonal = self.decompose(x)
trend_pred = self.linear_trend(trend)
seasonal_pred = self.linear_seasonal(seasonal)
return trend_pred + seasonal_pred
3.2. NLinear: Xử lý Distribution Shift
NLinear giải quyết vấn đề Distribution Shift – sự thay đổi trong phân phối dữ liệu chuỗi thời gian theo thời gian. Ý tưởng cốt lõi là chuẩn hóa chuỗi thời gian bằng cách trừ đi giá trị cuối cùng của chuỗi input, sau đó thêm lại giá trị này vào kết quả dự đoán.$$\text{x}_{\text{normalized}} = x - x_{last}$$$$\text{pred}_{\text{normalized}} = \text{Linear}(\text{x}_{\text{normalized}})$$$$\text{pred} = \text{pred}_{\text{normalized}} + x_{last}$$Kỹ thuật đơn giản này giúp mô hình tập trung dự đoán sự thay đổi (deviation) từ giá trị gần nhất thay vì dự đoán giá trị tuyệt đối, từ đó cải thiện độ chính xác đáng kể.
class NLinear(nn.Module):
"""Normalized Linear for univariate time series - handles distribution shift"""
def __init__(self, seq_len, pred_len=7):
super(NLinear, self).__init__()
self.seq_len = seq_len
self.pred_len = pred_len
self.linear = nn.Linear(self.seq_len, self.pred_len)
def forward(self, x):
# Normalize by subtracting last value
last_value = x[:, -1].unsqueeze(-1)
x_normalized = x - last_value
pred_normalized = self.linear(x_normalized)
pred = pred_normalized + last_value
return pred
4. Kỹ Thuật Ensemble: Kết Hợp Sức Mạnh
Để tận dụng ưu điểm của cả DLinear và NLinear, chúng ta sử dụng kỹ thuật Ensemble (kết hợp mô hình). Trong notebook, mô hình Stacking Meta Model đã được chọn.
Stacking Meta Model
Trong Stacking, đầu ra (predictions) của các mô hình cơ sở (Base Models - ở đây là NLinear và DLinear) sẽ được sử dụng làm đầu vào cho một mô hình meta (Meta Model - ở đây là một lớp tuyến tính đơn giản) để đưa ra dự đoán cuối cùng.
-
Đầu ra Base Models:
$y_N = \text{NLinear}(x)$
$y_D = \text{DLinear}(x)$ -
Mô hình Meta: Kết hợp các đầu ra này.
$\text{input}_{\text{meta}} = \text{Concatenate}(y_N, y_D)$
$y_{\text{final}} = \text{MetaLinear}(\text{input}_{\text{meta}})$
class StackingMetaModel(nn.Module):
def __init__(self, base_a, base_b, pred_len):
super().__init__()
self.A = base_a
self.B = base_b
# Meta model is a simple linear layer
self.meta = nn.Linear(pred_len * 2, pred_len)
def forward(self, x):
out_a = self.A(x) # (B, pred_len)
out_b = self.B(x) # (B, pred_len)
concat = torch.cat([out_a, out_b], dim=1) # (B, 2*pred_len)
return self.meta(concat)
5. Huấn Luyện và Dự Đoán Lặp
Mô hình Ensemble được huấn luyện bằng hàm mất mát MSE (Mean Squared Error), với mục tiêu giảm thiểu sự khác biệt bình phương giữa giá trị logarit dự đoán và giá trị logarit thực tế.$$\text{Loss} = \text{MSE}(\text{predictions\_log}, \text{targets\_log})$$
Quá trình dự đoán 100 ngày tiếp theo được thực hiện theo phương pháp iterative (lặp):
1. Sử dụng $14$ ngày cuối của dữ liệu huấn luyện làm input ban đầu.
2. Mô hình dự đoán $3$ ngày tiếp theo (OUTPUT_LEN).
3. Cập nhật input cho bước tiếp theo bằng cách loại bỏ $3$ ngày đầu của chuỗi input cũ và thêm $3$ ngày dự đoán mới vào cuối chuỗi.
4. Lặp lại quá trình này cho đến khi đạt được $100$ ngày dự đoán.
Cuối cùng, tất cả các dự đoán (vẫn ở dạng logarit) được chuyển đổi ngược lại về giá đóng cửa (VND) bằng hàm mũ:
$$\text{close} = e^{\text{close\_log}}$$
6. Kết Quả
Kết quả dự đoán (hình dưới) cho thấy mô hình Ensemble đã nắm bắt được xu hướng tăng mạnh mẽ của cổ phiếu FPT trong $100$ ngày tiếp theo.
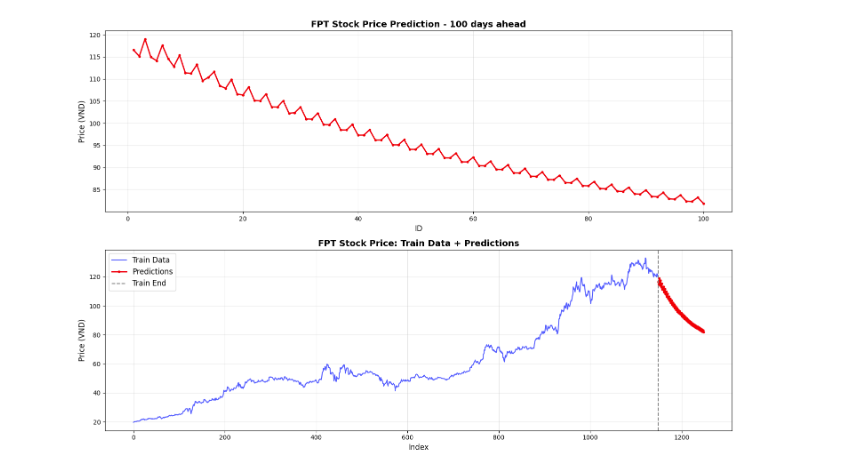
Hình 1: Kết quả dự đoán của mô hình Stacking Meta Model kết hợp NLinear và DLinear trên bộ dữ liệu cổ phiếu của FPT
7. So sánh với các mô hình khác
Dưới đây là bảng so sánh chi tiết hiệu suất của các mô hình dự đoán giá cổ phiếu FPT, được đánh giá qua các chỉ số RMSE, MAE, và R² trên các độ dài input (seq_len) khác nhau.
| Input Length | Mô Hình | RMSE | MAE | R² |
|---|---|---|---|---|
| 7d | Linear | 0.0908 | 0.0700 | -1.1759 |
| 7d | DLinear | 0.0348 | 0.0264 | 0.6800 |
| 7d | NLinear | 0.0292 | 0.0218 | 0.7759 |
| 7d | Stacking Meta Model | 0.0327 | 0.0242 | 0.7174 |
| --- | --- | --- | --- | --- |
| 30d | Linear | 0.0511 | 0.0409 | 0.3073 |
| 30d | DLinear | 0.0501 | 0.0392 | 0.3354 |
| 30d | NLinear | 0.0307 | 0.0226 | 0.7503 |
| 30d | Stacking Meta Model | 0.0335 | 0.0253 | 0.7027 |
| --- | --- | --- | --- | --- |
| 120d | Linear | 0.0589 | 0.0494 | 0.0876 |
| 120d | DLinear | 0.0561 | 0.0472 | 0.1740 |
| 120d | NLinear | 0.0295 | 0.0215 | 0.7715 |
| 120d | Stacking Meta Model | 0.0425 | 0.0332 | 0.5263 |
| --- | --- | --- | --- | --- |
| 480d | Linear | 0.4074 | 0.3773 | -69.6459 |
| 480d | DLinear | 0.3016 | 0.2935 | -37.7060 |
| 480d | NLinear | 0.0365 | 0.0286 | 0.4336 |
| 480d | Stacking Meta Model | 0.1353 | 0.1127 | -6.7930 |
Mô hình NLinear thể hiện hiệu suất vượt trội và ổn định nhất trên toàn bộ các độ dài input.
- Hiệu suất tối ưu: NLinear đạt chỉ số RMSE thấp nhất và R² cao nhất ở mọi độ dài input (7d, 30d, 120d và 480d). Đặc biệt, với input 7 ngày, NLinear đạt $RMSE = 0.0292$ và $R² = 0.7759$, cho thấy nó có thể giải thích gần 80% phương sai của dữ liệu.
- Minh chứng cho Chuẩn hóa: Kết quả này chứng minh rằng chiến lược chuẩn hóa bằng cách trừ đi giá trị cuối cùng của NLinear là yếu tố quan trọng nhất. Phương pháp này giúp mô hình tập trung vào việc dự đoán sự thay đổi tương đối so với giá trị gần nhất, thay vì cố gắng nắm bắt giá trị tuyệt đối, từ đó xử lý hiệu quả vấn đề Distribution Shift của chuỗi thời gian tài chính.
Mô hình Linear Model cơ bản cho thấy hiệu suất kém nhất, đặc biệt với input dài (480d), nơi chỉ số $R²$ là một giá trị âm rất lớn ($-69.6459$). $\text{R²}$ âm chỉ ra rằng mô hình tệ hơn đáng kể so với việc chỉ sử dụng giá trị trung bình để dự đoán, xác nhận rằng mô hình tuyến tính đơn giản không phù hợp cho dự đoán chuỗi thời gian không ổn định.
Hiệu quả của Kỹ thuật Cải tiến (DLinear và Stacking)
Cả DLinear và Stacking Meta Model đều cải thiện hiệu suất rõ rệt so với Linear Model cơ bản. Stacking Meta Model thường có $\text{RMSE}$ tốt hơn DLinear (ví dụ: $0.0327$ so với $0.0348$ ở input 7d).
Hạn chế của Ensemble: Tuy nhiên, mô hình Stacking không thể vượt qua NLinear. Điều này gợi ý rằng mô hình NLinear đơn lẻ đã nắm bắt được phần lớn thông tin cần thiết. Việc kết hợp thêm DLinear (với cơ chế phân tách Trend/Seasonal) có thể không mang lại giá trị gia tăng đáng kể, hoặc thậm chí gây nhiễu cho mô hình Meta trong lần huấn luyện này.
Kết Luận
Việc sử dụng các mô hình tuyến tính tiên tiến như DLinear và NLinear, kết hợp với chiến lược Stacking Ensemble, chứng minh rằng sự đơn giản vẫn có thể mang lại hiệu quả cao trong dự đoán chuỗi thời gian, đặc biệt khi xử lý các vấn đề cơ bản như xu hướng, tính mùa vụ và distribution shift.
Chưa có bình luận nào. Hãy là người đầu tiên!