I. Giới thiệu: Từ Ma trận Số đến Thị giác Máy tính
Trong kỷ nguyên của Trí tuệ Nhân tạo (AI), Thị giác máy tính (Computer Vision) đang hiện diện khắp nơi—từ tính năng FaceID trên điện thoại, hệ thống xe tự lái phân tích làn đường, cho đến các phần mềm chẩn đoán y tế phức tạp. Tuy nhiên, đằng sau những ứng dụng hào nhoáng đó là một câu hỏi nền tảng mà bất kỳ kỹ sư AI nào cũng phải đối mặt: Làm thế nào một cỗ máy vô tri có thể "hiểu" được những gì nó "nhìn" thấy?
Đối với con người, việc nhận diện một chiếc áo hay một con số viết tay là bản năng tự nhiên. Nhưng với máy tính, một bức ảnh rực rỡ thực chất chỉ là một ma trận khổng lồ của các con số vô hồn. Khoảng cách giữa những giá trị pixel rời rạc và việc định danh chính xác đối tượng (Classification) chính là "hố sâu ngăn cách" mà các mô hình học máy cần phải lấp đầy.
Trong bài viết này, chúng ta sẽ không đi đường tắt bằng việc gọi các hàm thư viện có sẵn một cách máy móc. Thay vào đó, chúng ta sẽ cùng nhau giải phẫu vấn đề từ gốc rễ toán học và kiến trúc hệ thống:
-
Giải mã dữ liệu ảnh: Hiểu cách máy tính "nhìn" thế giới qua các tensor và ma trận.
-
Xây dựng nền móng: Bắt đầu từ mô hình Hồi quy Softmax (Softmax Regression) đơn giản nhất.
-
Nâng cấp kiến trúc: Chuyển sang Mạng nơ-ron đa lớp (Multi-Layer Perceptron - MLP) để giải quyết các vấn đề phi tuyến tính.
-
Tối ưu hóa chuyên sâu: Phân tích các kỹ thuật cốt lõi như Normalization, Initialization và Optimizer để biến một mô hình lý thuyết thành một hệ thống hoạt động hiệu quả.
II. Từ Image Data đến MLP cơ bản
1. Image Data
1.1. Khi nhìn vào một bức ảnh, máy tính “thấy” gì?
Khi con người nhìn vào một chiếc áo, một chiếc giày hay một con số viết tay, chúng ta dễ dàng nhận ra ngay nhờ thị giác nhưng máy tính thì không.
Máy tính chỉ nhìn thấy các con số.
Trong các mô hình học máy, đặc biệt là khi xử lý ảnh, một bức ảnh thực chất là một ma trận giá trị số - nơi mỗi ô trong ma trận tương ứng với một pixel.
1.2. Grayscale images - ảnh đen trắng là ma trận số
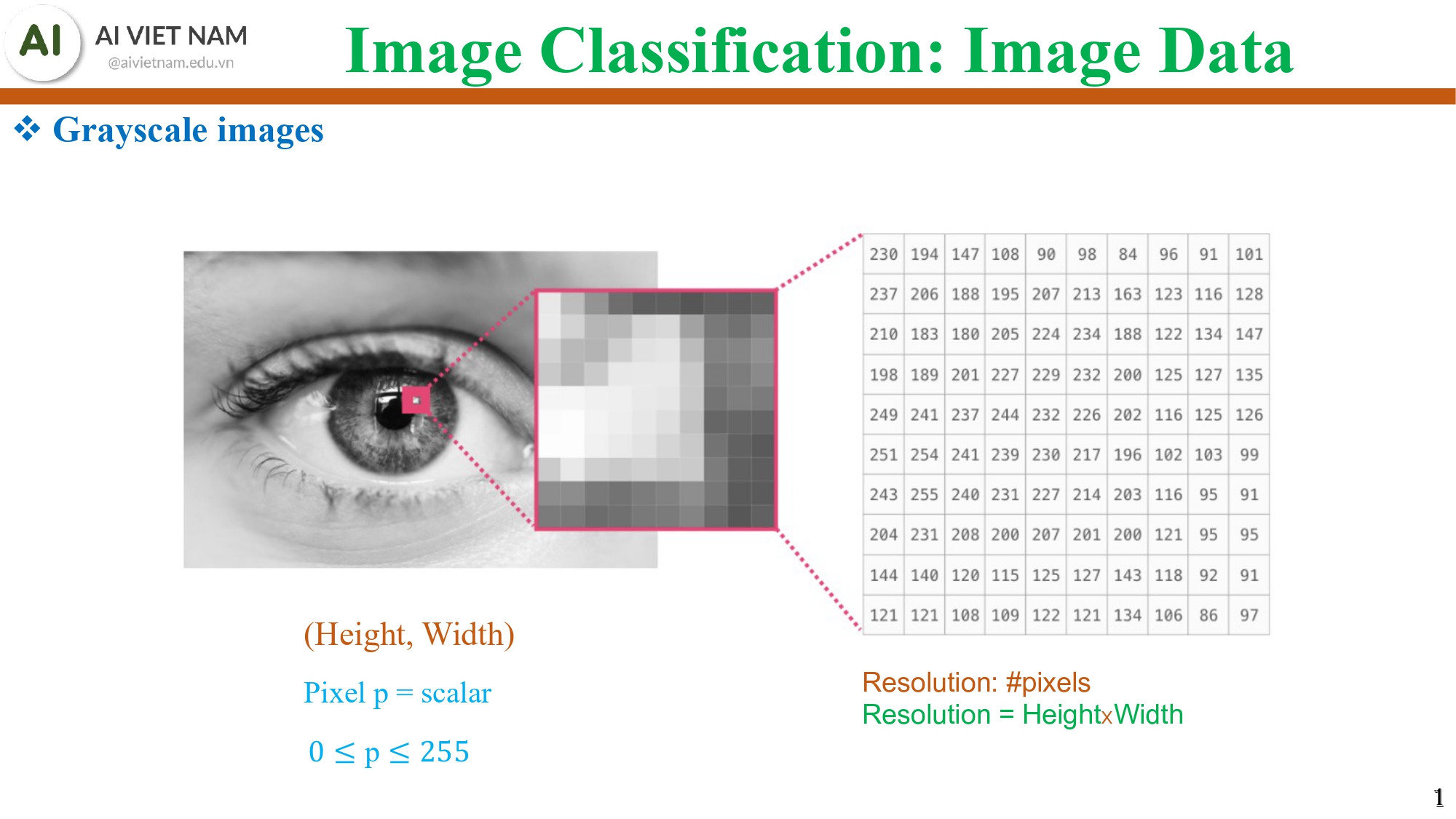
Hình 1: Ma trận số của hình ảnh trắng đen
Một ảnh grayscale có cấu trúc:
- Kích thước: (Height, Width)
- Mỗi pixel là một số từ 0 đến 255
- 0 → đen
- 255 → trắng
- các số ở giữa → mức xám
Ví dụ: ảnh 28×28 của MNIST hoặc Fashion-MNIST.
Khi nhìn vào bảng pixel trong slide, chúng ta có thể thấy các số như: 238, 147, 196, 89,…
→ Đây chính là “hình ảnh” dưới con mắt của máy tính.
Từ đó chúng ta có thể rút ra nhận xét đơn giản để dễ hình dung về ý nghĩa:
→ Một bức ảnh = một ma trận số thuận tiện để đưa vào mô hình toán học.
1.3. Color images - ảnh màu là 3 ma trận chồng lên nhau
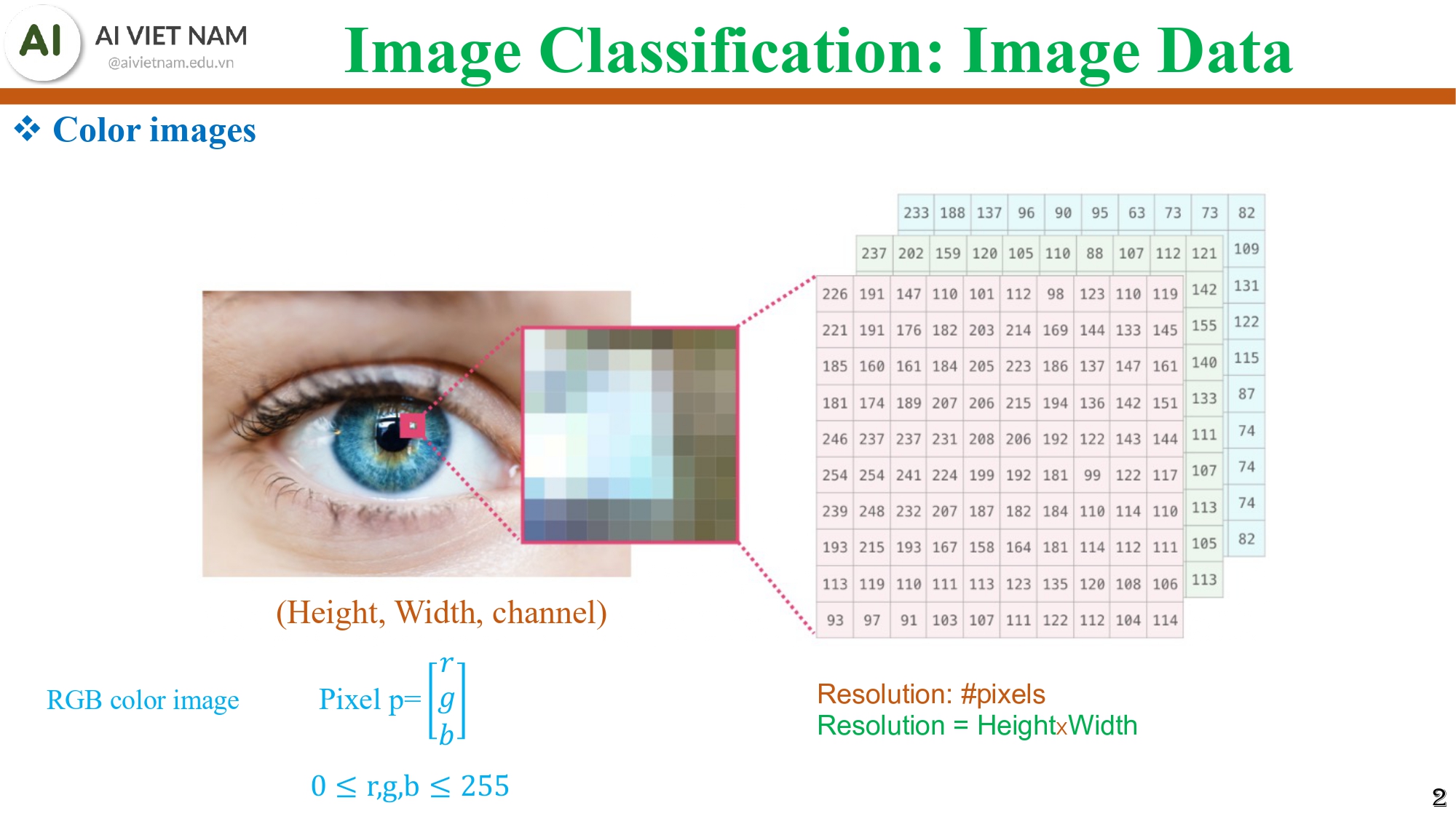
Hình 2: Ma trận số của hình ảnh màu, với 3 kênh màu là red(đỏ), xanh lá(green), và xanh dương(blue)
Tiếp theo, chúng ta cùng xem việc ảnh màu (RGB) được biểu diễn dưới dạng như nào: (Height,Width,Channel)
Mỗi pixel:
$$p = \begin{bmatrix} r \\ g \\ b \end{bmatrix},\; 0 \le r, g, b \le 255$$
Nói cách khác:
- Ảnh grayscale → 1 lớp ma trận
- Ảnh màu → 3 lớp ma trận: đỏ, xanh lá, xanh dương
→ Khi làm việc với ảnh màu, mô hình phải xử lý gấp 3 lần lượng thông tin.
1.4. Dùng Python để đọc và hiển thị ảnh
Giờ chúng ta sẽ cùng làm quen với các thao tác cơ bản trong python nhé:
- Tải ảnh về máy: urllib.request.urlretrieve(url, name)
- Mở ảnh: Image.open(name)
- Hiển thị ảnh: plt.imshow(img)
Điểm quan trọng ở đây là: Python cho phép chúng ta thao tác với ảnh như với dữ liệu số, không cần công cụ đặc biệt. Điều này giúp "người mới bắt đầu" cảm thấy việc xử lý ảnh không hề “đáng sợ”.
1.5. MNIST & Fashion-MNIST - Hai bộ dữ liệu kinh điển
Giờ chúng ta cùng đến với hai bộ dữ liệu hình ảnh thường dùng để học mô hình phân loại:
MNIST - chữ số viết tay
- 70,000 ảnh 28×28 grayscale
- 10 lớp (0-9)
- Mỗi ảnh là nét viết tay của một con số

Hình 3: Minh họa vài sample của bộ dữ liệu MNIST, với mỗi sample là hình ảnh của chữ số viết tay
Fashion-MNIST - ảnh quần áo
- 28×28 grayscale
- 60,000 ảnh train + 10,000 ảnh test
- Các lớp bao gồm: T-shirt, Trouser, Dress, Coat, Sandal, Bag, Ankle Boot…

Hình 4: Minh họa vài sample của bộ dữ liệu Fashion-MNIST, với mỗi sample là hình ảnh các món đồ thời trang
Các điểm giống nhau của 2 mô hình:
- Kích thước nhỏ (28×28) → phù hợp để dạy mô hình MLP
- Ảnh grayscale → dễ xử lý
- Thường được dùng làm dataset mẫu để hiểu cách mô hình đọc ảnh.
1.6. Vì sao phải “flatten” ảnh?
Flatten = bước chuyển đổi bắt buộc để ảnh có thể đi vào mô hình MLP hoặc Softmax Regression.
Ảnh 28×28 = ma trận 2D → MLP không hiểu được dạng này.
MLP yêu cầu vector 1 chiều. Do đó chúng ta phải flatten ảnh theo thứ tự hàng hoặc cột thành một vector 784 phần tử.
Ví dụ:
| Pixel 1 | Pixel 2 | … | Pixel 784 |
Sau khi flatten:
- Chúng ta có thể đưa vào mô hình Linear, Softmax, MLP
- Các phép nhân ma trận mới trở nên hợp lệ
1.7. Dataset trong PyTorch
Giờ chúng ta chuyển sang cách tổ chức dữ liệu trong PyTorch :
1 ảnh = (image_tensor, label)
- image_tensor là tensor 1×28×28
- label là số từ 0 đến 9
Tập dữ liệu được chia thành batch
Ví dụ: batch size = 1024
→ Mỗi batch chứa 1024 ảnh
Khi huấn luyện:
- Mô hình đọc từng batch
- Tính loss
- Cập nhật trọng số
Việc chia batch giúp:
- Huấn luyện nhanh hơn
- Dùng GPU hiệu quả hơn
- Giảm dao động trong quá trình học
torch.Size([1024, 1, 28, 28])
Điều này nghĩa là:
- 1024 ảnh
- Mỗi ảnh 1 kênh (grayscale)
- Kích thước 28×28
2. Softmax Regression cho ảnh
2.1. Softmax Regression - Ý tưởng trực quan

Hình 5: Hình ảnh mô tả quá trình tính toán của Softmax Regression và các công thức tính toán cần thiết
Giả sử chúng ta có 1 mô hình được minh họa như sau:
- Ban đầu có một ảnh flatten thành vector 784 giá trị
- Mỗi ảnh được đưa qua một phép biến đổi tuyến tính (linear): $$z_j = x w_j + b_j$$
- Sau đó, toàn bộ 10 giá trị $z_0,\, z_1,\, \dots,\, z_9$ được đưa vào hàm Softmax để chuyển thành phân phối xác suất.
Hàm Softmax đảm bảo rằng:
- Mọi giá trị đầu ra đều trong khoảng [0,1]
- Tổng 10 giá trị = 1
- Giá trị lớn nhất → lớp mà mô hình dự đoán
Nói nôm na: Softmax giống như “ra quyết định”, rằng ảnh này giống với lớp nào nhất trong 10 lớp.
2.2. Công thức đầy đủ của mô hình
a. Tính điểm (logits)
Mỗi lớp $j$ có trọng số $w_j$ và bias $b_j$:
$$z_j = x w_j + b_j$$
Toàn bộ các $z_j$ tạo thành vector $\mathbf{z}$.
b. Tính xác suất bằng Softmax
Công thức Softmax: $$y_j = \dfrac{e^{z_j}}{\sum_k e^{z_k}}$$
Đây là xác suất ảnh thuộc lớp $j$.
c. One-hot encoding cho nhãn
- Nếu nhãn thật là 0: $y = [1\;0]$
- Nếu nhãn thật là 1: $y = [0\;1]$
Với Fashion-MNIST (10 lớp), chúng ta có vector 10 phần tử.
2.3. Loss function và đạo hàm
Loss của một mẫu:
$$L = - \sum_j y_j \log(\hat{y}_j)$$
Và gradient:
$$\frac{\partial L}{\partial z_j} = \hat{y}_j - y_j$$
$$\frac{\partial L}{\partial w_j} = x(\hat{y}_j - y_j)$$
$$\frac{\partial L}{\partial b_j} = \hat{y}_j - y_j$$
Trong đó:
- $\hat{y}_j$: Giá trị dự đoán của mô hình
- $y_j$: Giá trị thực tế của mẫu
- $\frac{\partial L}{\partial z_j}$: Đạo hàm của hàm loss với biến $z_j$
- $\frac{\partial L}{\partial w_j}$: Đạo hàm của hàm loss với biến $w_j$
- $\frac{\partial L}{\partial b_j}$: Đạo hàm của hàm loss với biến $b_j$
Điều quan trọng ở đây:
- Toàn bộ tính toán đều rất đơn giản: nhân ma trận + hàm mũ + log
- Softmax Regression học rất nhanh, nhưng khả năng biểu diễn yếu (vì chỉ là tuyến tính).
2.4. “Flatten đặt ở đâu?” - Câu hỏi quan trọng

Hình 6: Hình ảnh minh họa vị trí đặt tầng Flatten trong 1 mạng MLP
Ảnh (28×28) → Flatten (784) → Linear → Softmax
Flatten luôn nằm ngay sau bước chuẩn hóa và trước lớp fully connected.
Điều này quan trọng vì:
- Nếu không flatten, mô hình không thể thực hiện phép nhân $𝑥𝑤$
- Đây là yêu cầu cấu trúc đối với MLP và Softmax Regression
2.5. Case study 1 - Không có normalization + learning rate = 0.01
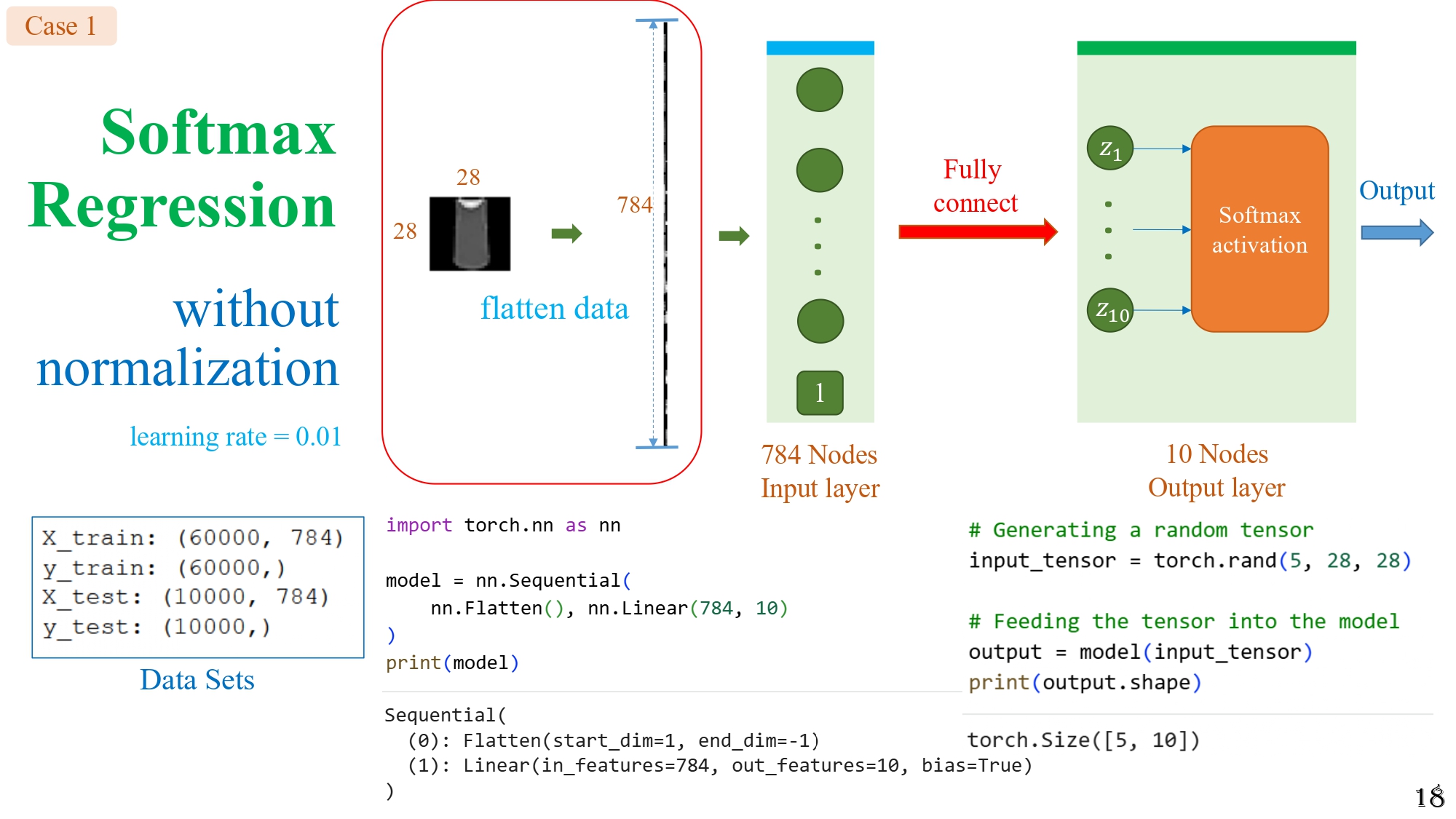
Hình 7: Trường hợp - Không sử dụng normalization và chỉnh tốc độ học learning rate = 0.01
Kết quả biểu đồ cho thấy:
- Độ chính xác train/test dao động mạnh
- Loss giảm nhưng rất nhiễu
- Test accuracy không ổn định → thấp
- Đường train/test văng qua văng lại
Vậy câu hỏi đặt ra là tại sao lại xuất hiện tình huống như vậy?
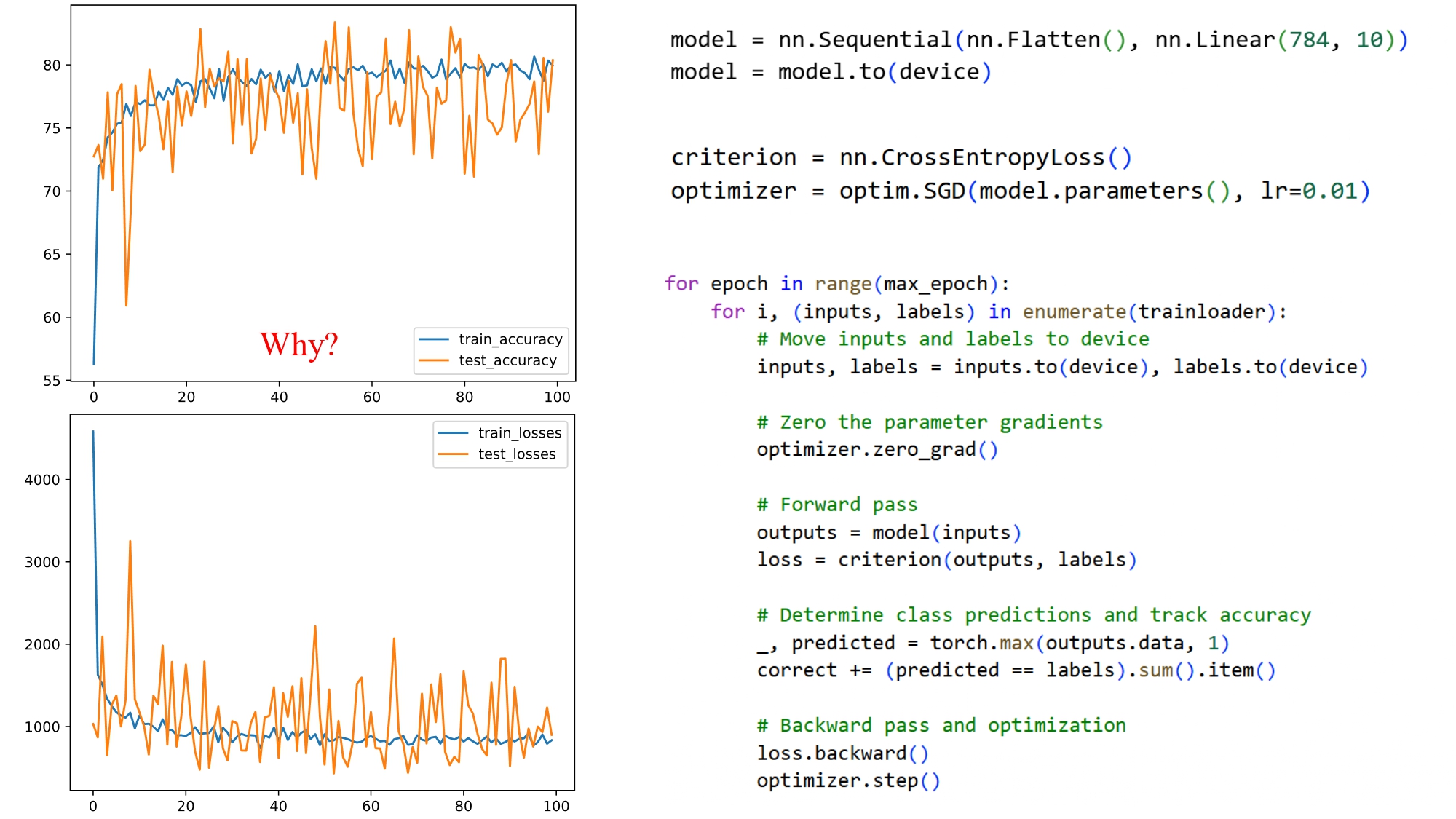
Hình 8: Kết quả - Không sử dụng normalization và chỉnh tốc độ học learning rate = 0.01
Nguyên nhân là vì:
- Pixel có giá trị từ 0 → 255
- Khi nhân với trọng số trong quá trình tính gradient, các giá trị này tạo ra những bước nhảy gradient quá lớn
- Learning rate 0.01 khiến mô hình “nhảy quá xa” → Gây dao động và học thiếu ổn định
Kết luận: Không chuẩn hóa pixel = học kém hiệu quả.
2.6. Case study 2 - Không normalization nhưng learning rate rất nhỏ (0.00001)
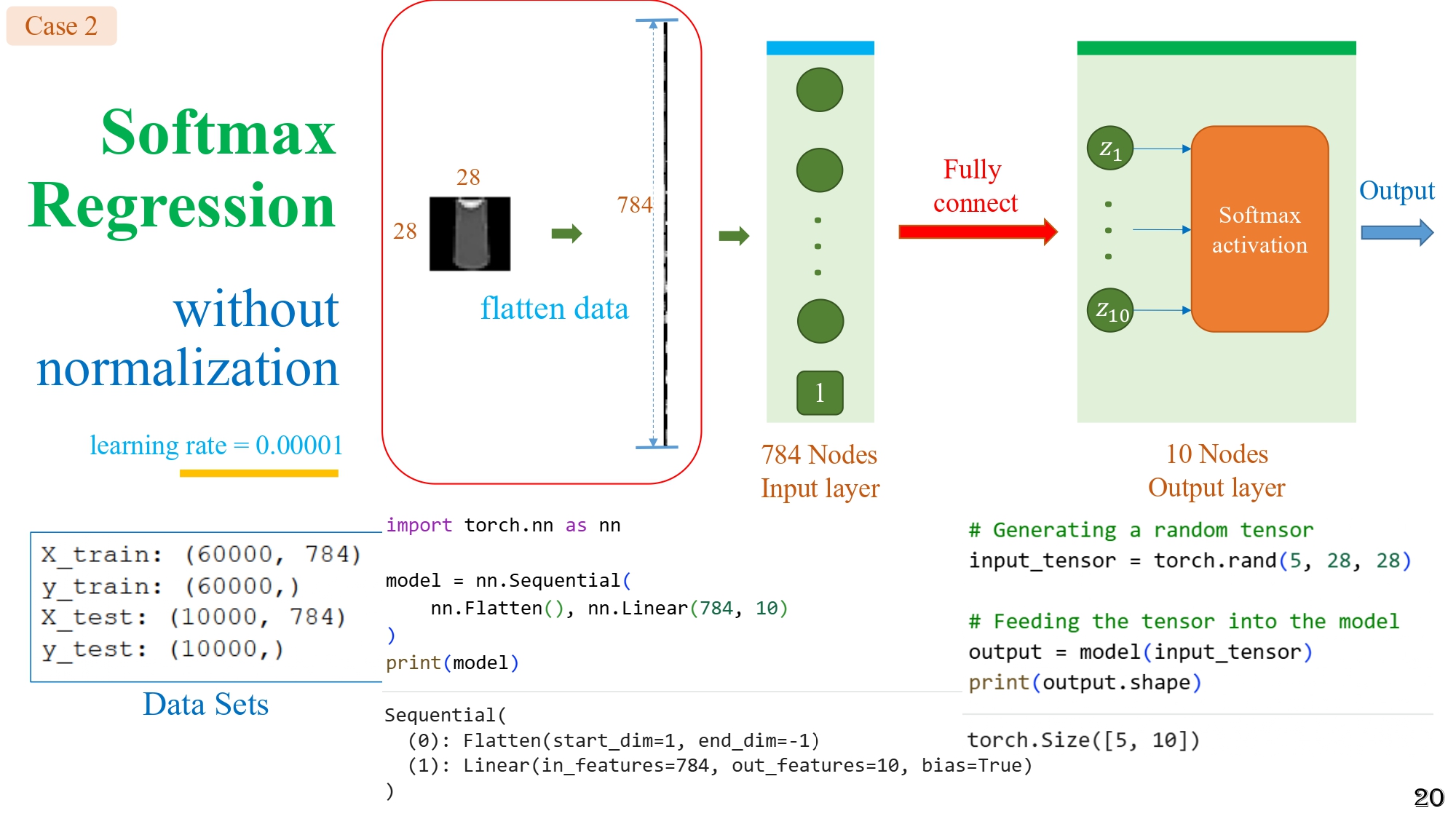
Hình 9: Trường hợp - Không sử dụng normalization và chỉnh tốc độ học learning rate = 0.00001
Khi giảm learning rate:
- Các đường loss và accuracy ổn định, mượt hơn
- Mô hình học dần dần mà không dao động
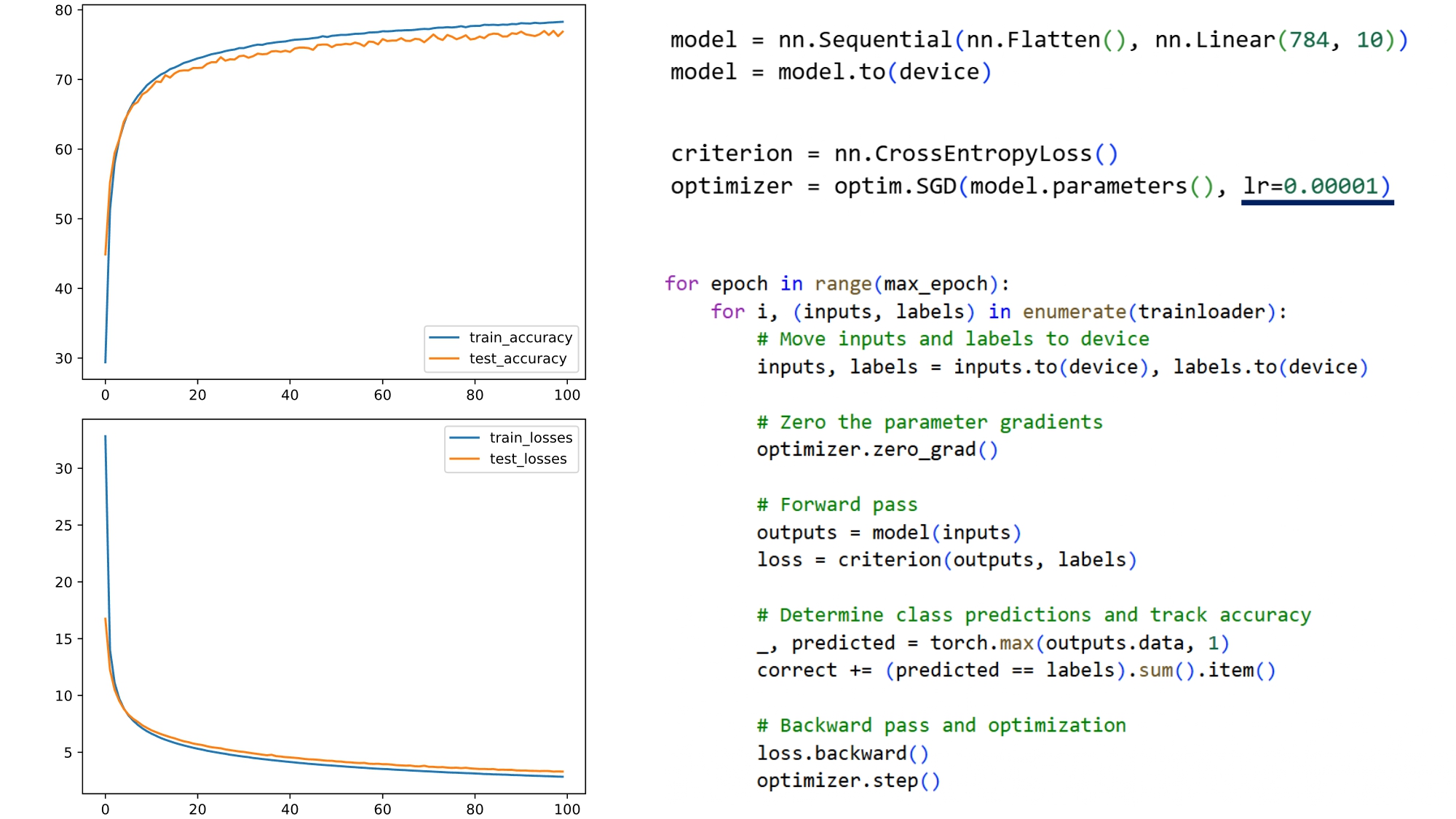
Hình 10: Kết quả - Không sử dụng normalization và chỉnh tốc độ học learning rate = 0.00001
Nhưng:
- Accuracy vẫn thấp
- Tốc độ học chậm
- Softmax Regression vẫn quá yếu với dữ liệu ảnh
Qua đó, chúng ta có thể thấy:
- Learning rate không thể giải quyết triệt để vấn đề.
- Normalization mới là chìa khóa.
2.7. Tầm quan trọng của Normalization
Chúng ta cùng xem 3 cách normalization phổ biến:
a. Chia 255 → đưa về [0,1]
$$x = \frac{\text{pixel}}{255}$$
Đây là cách đơn giản nhất, giúp hạn chế việc pixel quá lớn
b. Chuẩn hoá về [-1, 1]
$$x = \frac{\text{pixel}}{127.5} -1$$
Điều này giúp dữ liệu:
- Có mean gần 0
- Gradient học ổn định hơn
c. Z-score normalization
$$x = \frac{x - \mu}{\sigma}$$
Trong đó:
- $\mu$: giá trị trung bình của tất cả các pixel
- $\sigma$: độ lệch chuẩn của tất cả các pixel
Đây là cách hiệu quả nhất:
- mean = 0
- std = 1
→ Cách này giúp tối ưu hóa hiệu quả hơn, đặc biệt trong deep learning.
- Softmax Regression + Normalization
Giờ chúng ta sẽ cùng xem qua 3 Case tương ứng với 3 cách chuẩn hóa ở phần trên:
Case 3 - Normalization về [0,1]
Ảnh chia 255
→ Mô hình học ổn định hơn rõ rệt
→ Accuracy cải thiện
Case 4 - Normalization về [-1,1]
$$x = \frac{x}{127.5} - 1$$
→ Tốt hơn Case 3
Case 5 - Z-score normalization
$$ = \frac{x - \mu}{\sigma}$$
→ Hiệu quả nhất trong 3 phương pháp
→ Slide cho thấy biểu đồ đẹp hơn, loss giảm mượt và accuracy cao hơn
3. Multi-layer Perceptron (MLP)
MLP là mô hình nền tảng của deep learning. Chúng ta có thể coi nó là phiên bản “nâng cấp” của Softmax Regression.
3.1. Vì sao cần mô hình mạnh hơn Softmax Regression?
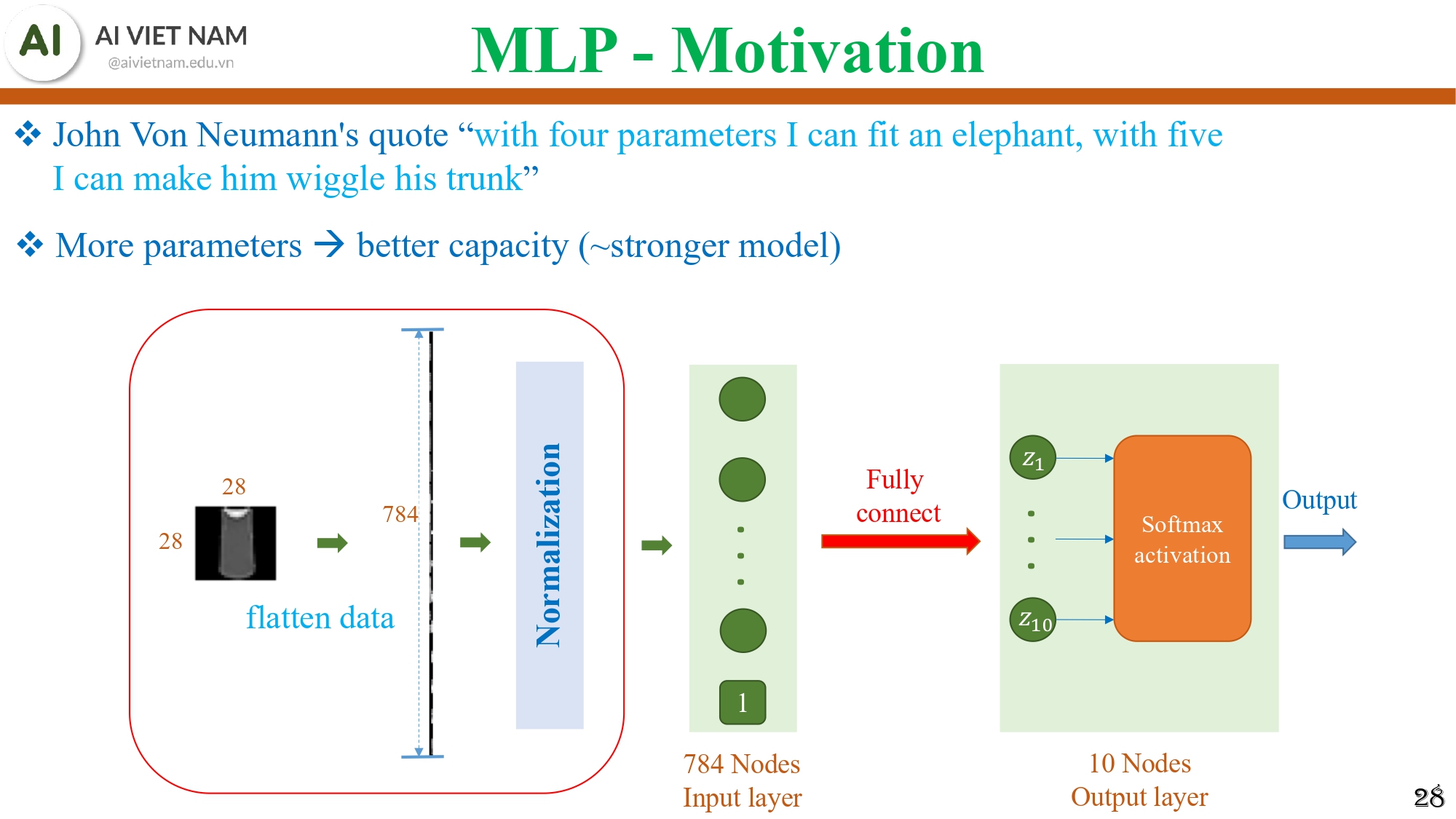
Hình 11: Mô hình Softmax Regression
Softmax Regression là mô hình tuyến tính: $z=xW+b$
Nhưng thực tế dữ liệu ảnh:
- rất phức tạp
- có nhiều ranh giới phi tuyến
- quần áo, giày, áo khoác không thể tách nhau chỉ bằng đường thẳng
Chúng ta cùng nhắc lại một câu nói mang tính minh hoạ khá là thú vị:
“Với bốn tham số tôi có thể fit một con voi, với năm tham số tôi có thể làm nó vẫy vòi.” - John Von Neumann
Ý câu này: Mô hình nhiều tham số → có khả năng biểu diễn rất mạnh.
Vì vậy, Softmax Regression (chỉ có 784×10 tham số) là quá yếu.
Do đó, chúng ta cần mô hình:
- có nhiều lớp
- có nhiều tham số
- học được mối quan hệ phi tuyến
Đó chính là MLP.
3.2. Multi-Layer Perceptron là gì?
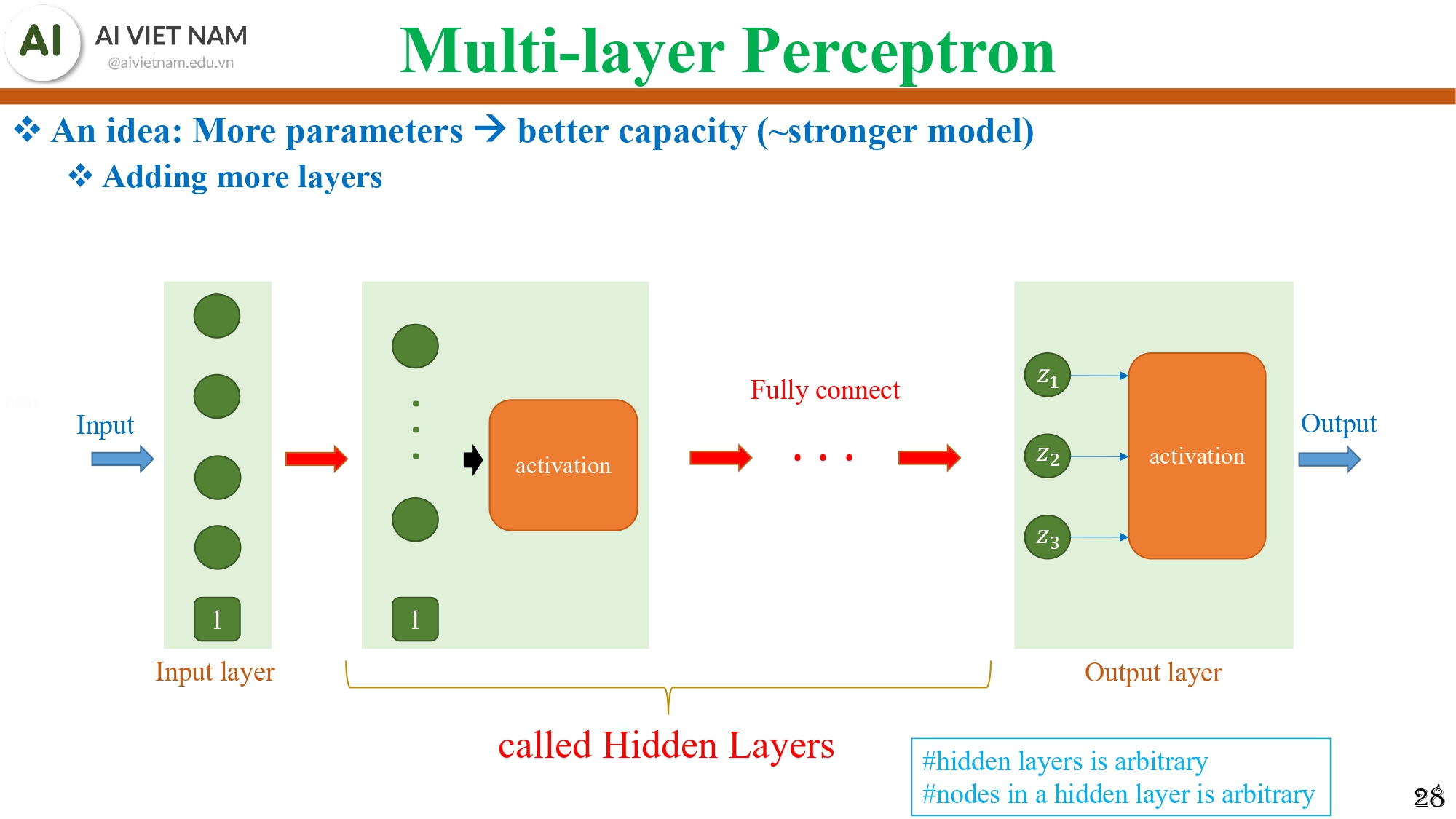
Hình 12: Minh họa 1 mô hình MLP cơ bản
MLP gồm:
- Input layer
- Một hoặc nhiều Hidden layers
- Output layer
Nếu Softmax Regression chỉ có: Input → Linear → Softmax
Thì MLP có dạng: Input → Linear → Activation → Linear → Activation → ... → Linear → Softmax
Điểm quan trọng cần lưu ý với MLP:
- Số lượng hidden layers tùy ý
- Số lượng neuron trong mỗi hidden layer tùy ý
- Kết nối trong MLP là fully connected
→ Đây chính là lý do MLP có “sức mạnh”: càng nhiều lớp và neuron → mô hình càng giàu khả năng biểu diễn.
3.3. ReLU - Trái tim của MLP hiện đại
Một neural network mạnh không chỉ vì nhiều lớp, mà vì có activation function.
$\text{ReLU}(x) = 0 \quad \text{khi } x < 0$
$\text{ReLU}(x) = x \quad \text{khi } x \ge 0$
Vì sao dùng ReLU?
- Tính toán cực nhanh
- Không bị bão hòa như sigmoid/tanh
- Giúp gradient truyền dễ hơn trong mô hình sâu
→ ReLU là activation function phổ biến nhất hiện nay.
3.4. Cấu trúc của một MLP hoàn chỉnh
MLP có thể xem như bản nâng cấp của Softmax Regression.

Hình 13: Minh họa quá trình mở rộng MLP từ ví dụ nhỏ đến mô hình hoàn chỉnh cho Fashion-MNIST
Với một hidden layer, cấu trúc cơ bản là:
Input (flatten 784) → Linear → ReLU → Hidden Layer → Linear → Softmax → Output (10 lớp)
Khi mở rộng lên hai hidden layers, chúng ta chỉ cần thêm một vòng Linear → ReLU nữa. Mỗi hidden layer giúp mô hình học các đặc trưng trừu tượng dần: layer đầu có thể nhận ra các đường biên, layer sau học các phần phức tạp hơn, và cuối cùng output kết hợp mọi thứ để dự đoán.
Trong bài toán Fashion-MNIST, đề xuất về kiến trúc chuẩn:
Normalize ảnh → Flatten 784 → Hidden layer 256 nodes (ReLU) → Output 10 lớp (Softmax)
Mô hình này mạnh hơn hẳn Softmax Regression vì có khả năng học quan hệ phi tuyến.
3.5. Ví dụ chi tiết tính toán Forward Pass
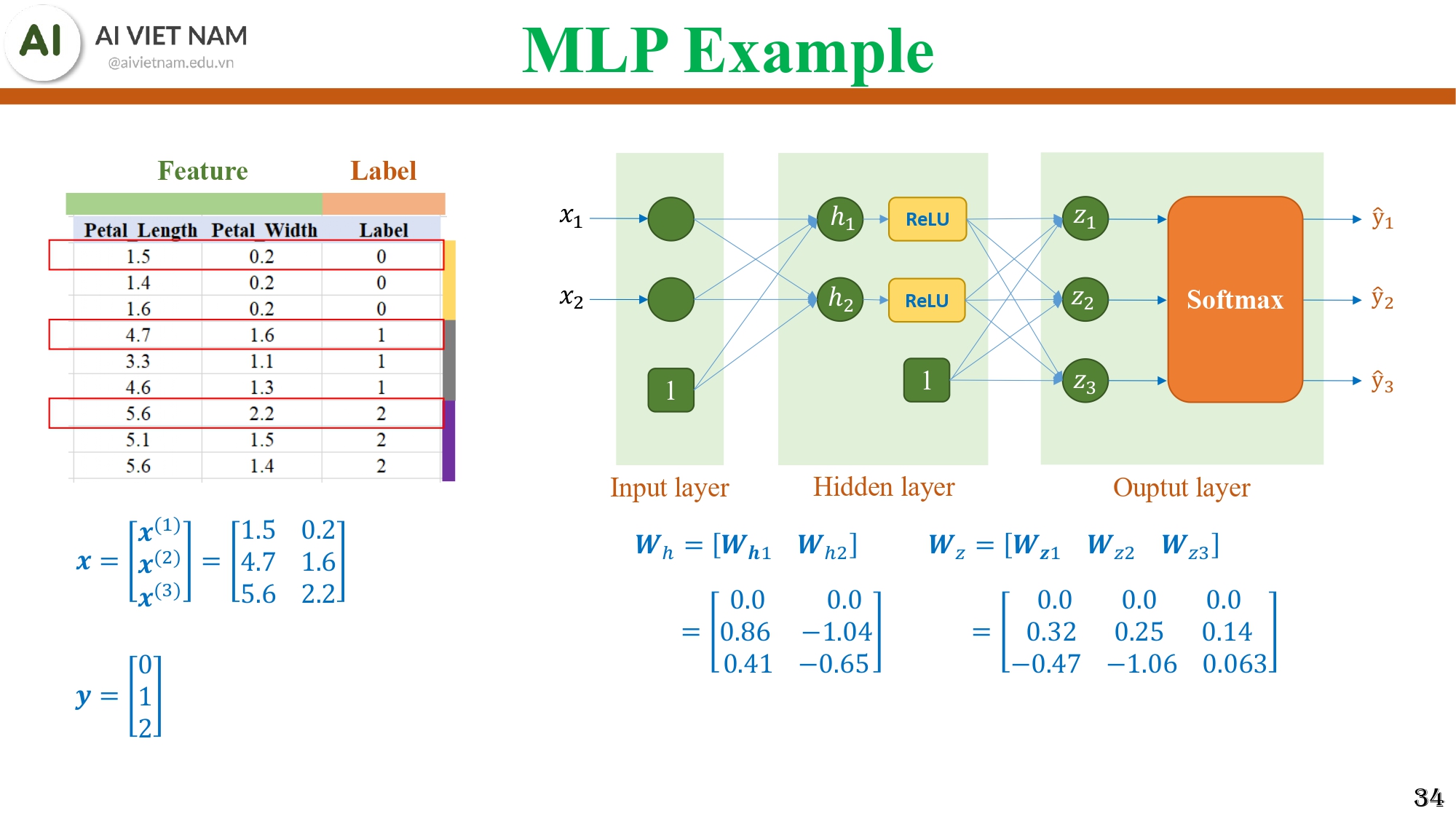
Hình 14: Ví dụ MLP nhỏ với 3 mẫu dữ liệu, một hidden layer (ReLU) và một output layer dùng Softmax
Ví dụ gồm:
- 3 mẫu dữ liệu $(x)$
- Một hidden layer
- Một output layer
- Activation dùng ReLU
- Output dùng Softmax
Bước 1 - Tính $h = xWₕ$
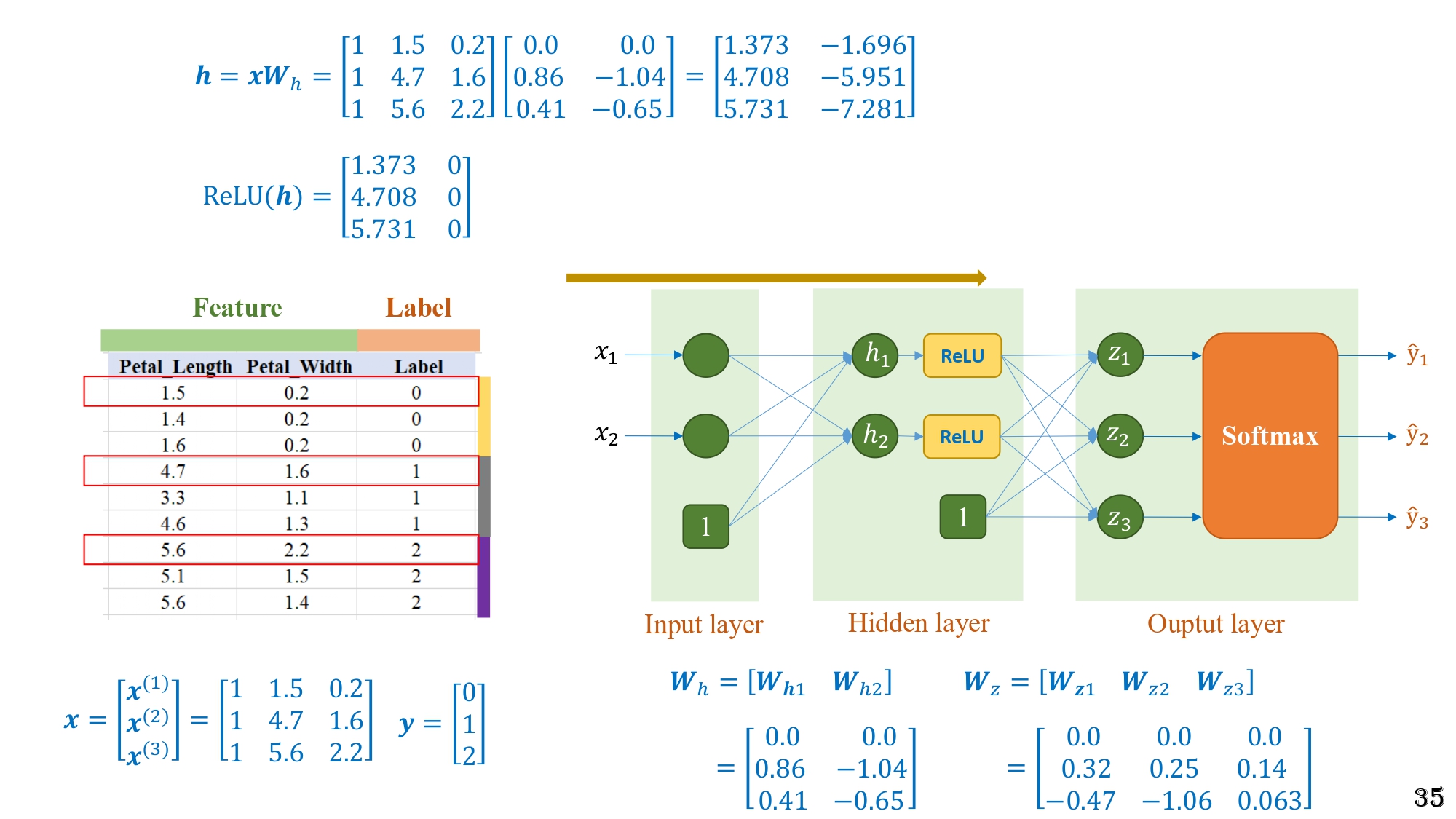
Hình 15: Minh họa chi tiết các bước tính toán forward của MLP
Bước 2 - Áp dụng ReLU
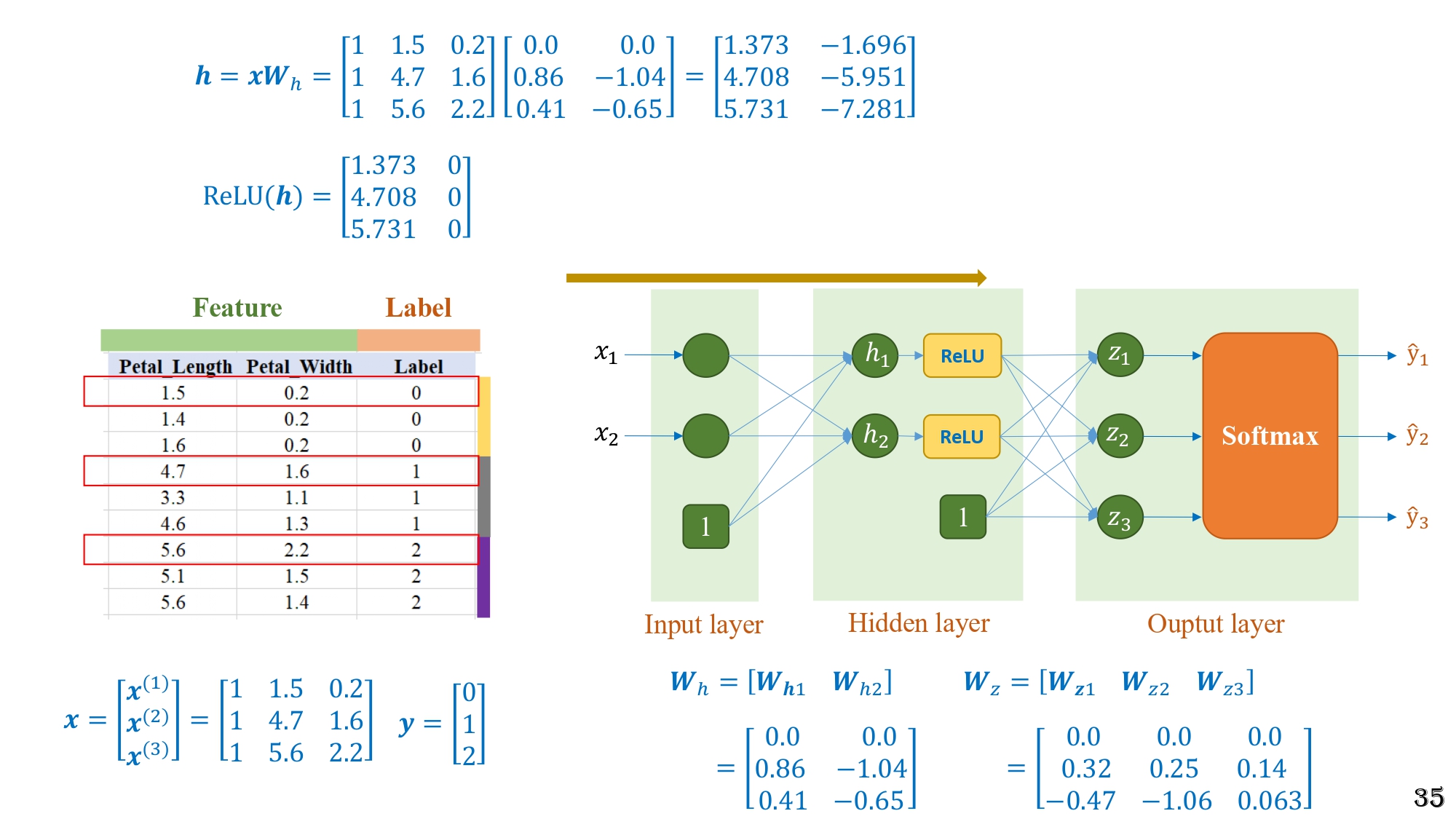
Hình 16: Kết quả bước 2 trong forward pass, áp dụng ReLU lên ma trận trước khi truyền sang tầng output
Bước 3 - Tính $z = hWₓ$
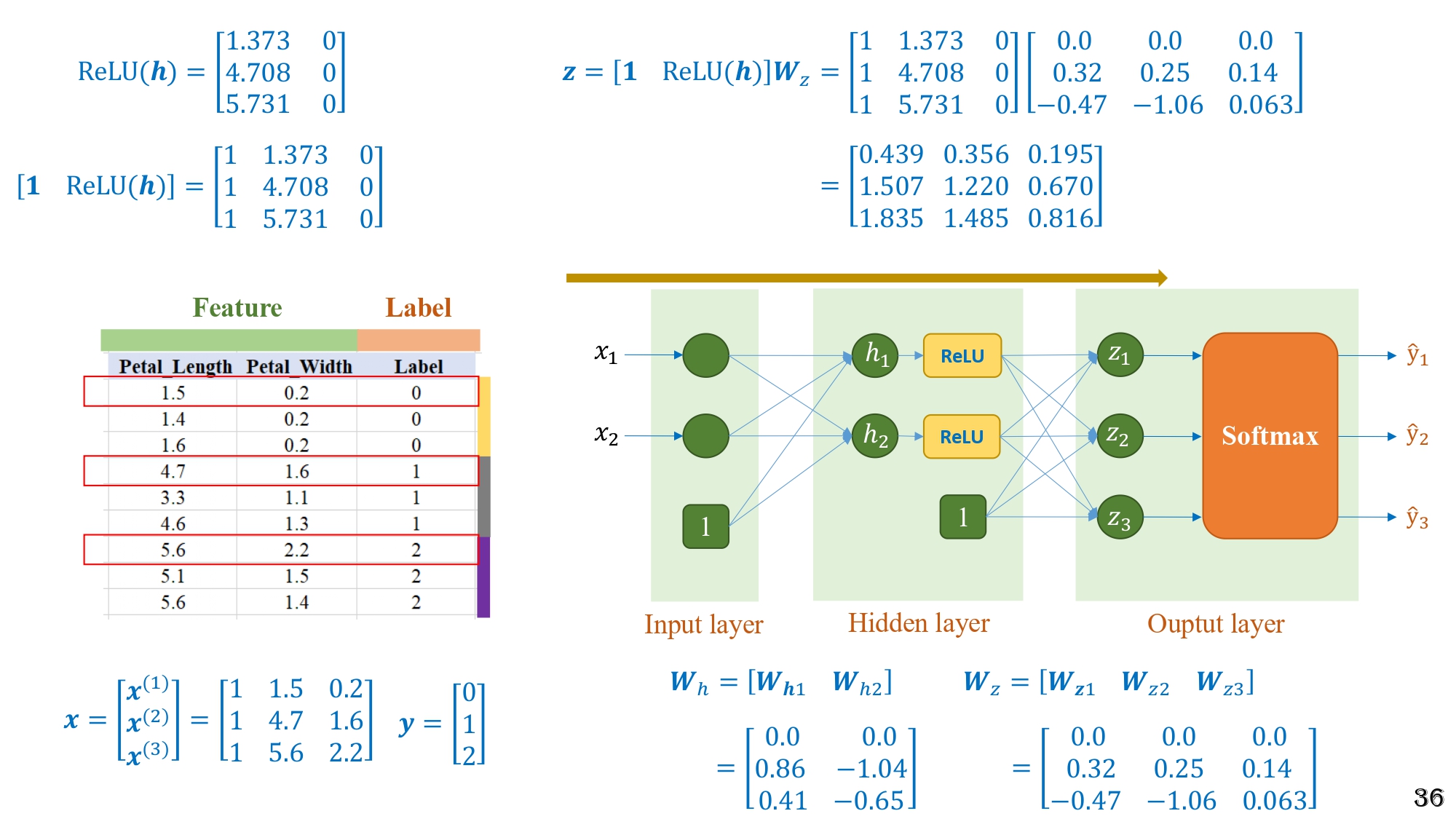
Hình 17: Sau khi qua ReLU, dữ liệu được nhân tiếp với trọng số tầng output để tạo ra các giá trị $z$ chuẩn bị cho bước Softmax
Bước 4 - Tính Softmax
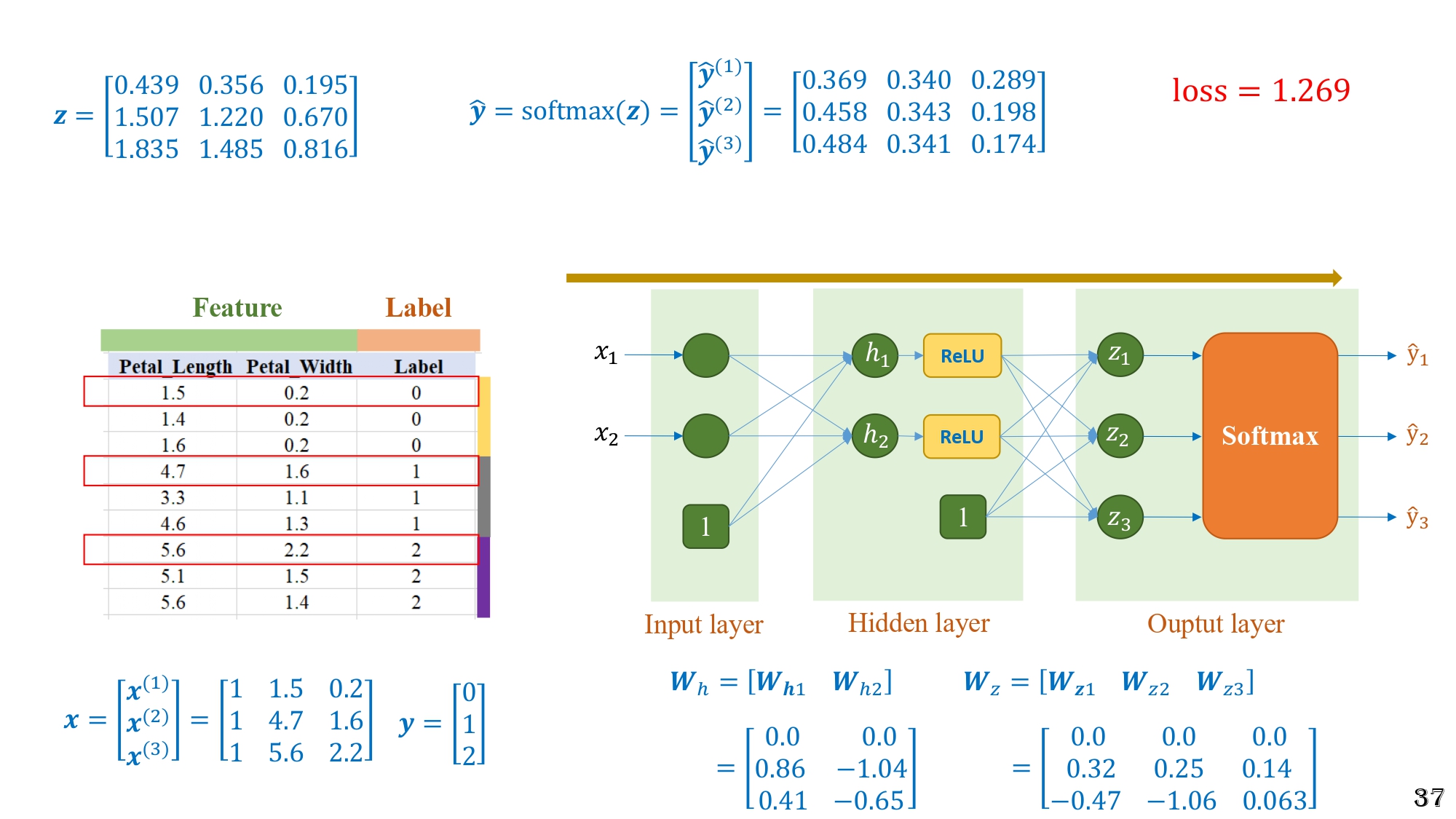
Hình 18: Bước 4 của forward pass – áp dụng Softmax lên vector $z$ để tạo ra dự đoán $\hat{y}$ và tính loss
Bước 5 - Tính Loss
Loss = 1.269
-> Toàn bộ mạng MLP (dù có thêm ReLU, hidden layer) vẫn chỉ là nhân ma trận + ReLU + Softmax, không có gì “ma thuật”.
3.6. Cài đặt MLP theo từng bước
Bước 1 - Data Preparation
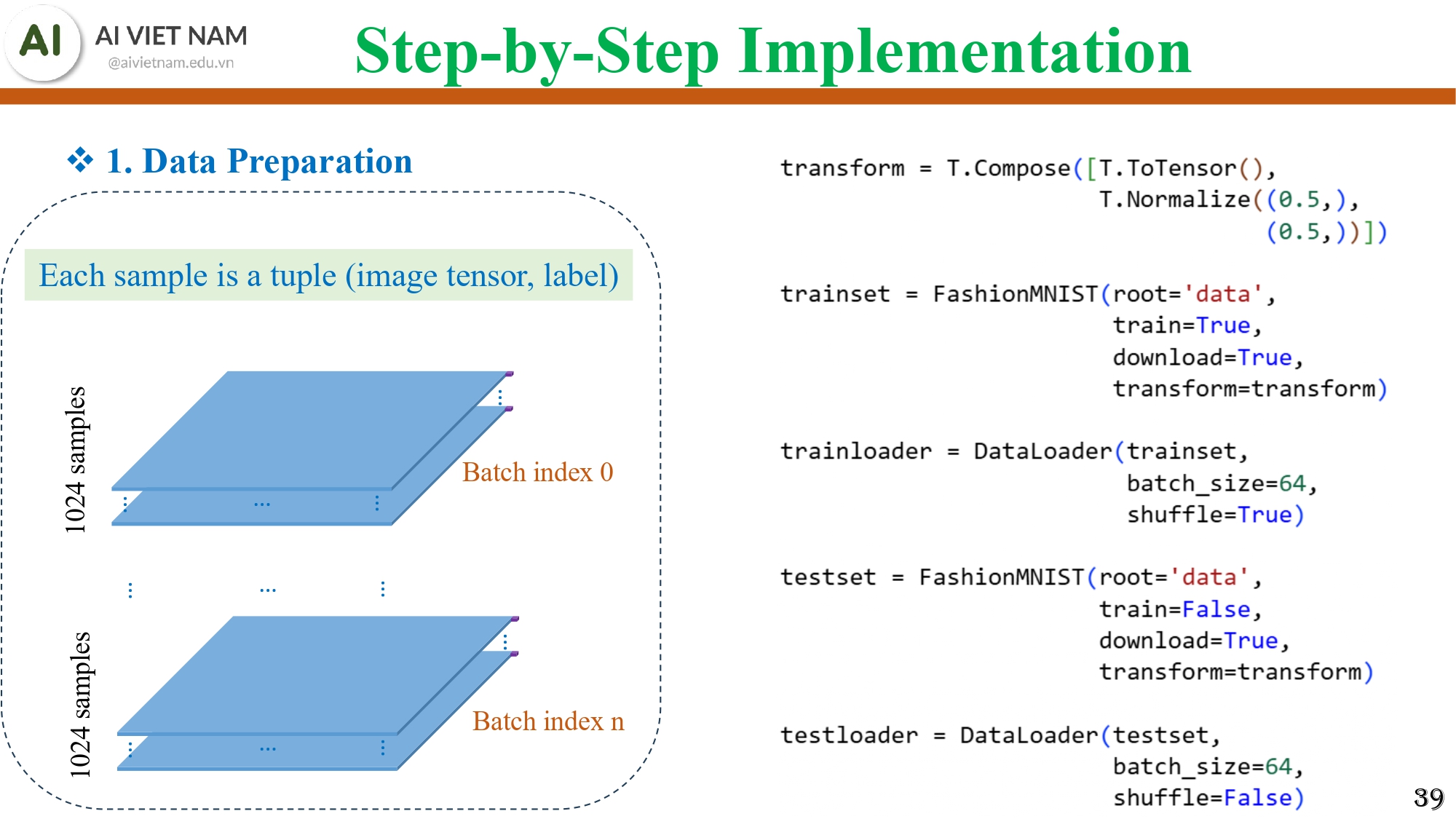
Hình 19: Minh hoạ cho việc chuẩn bị dữ liệu với mỗi mẫu dữ liệu là một cặp (image tensor, label); dữ liệu Fashion-MNIST được transform (ToTensor + Normalize) và đưa vào DataLoader để tạo các batch cho train và test
- Dùng DataLoader
- Batch size tùy chọn (ví dụ: 1024)
- Mỗi batch = (image_tensor, label)
- Shuffle để mô hình học tốt hơn
Bước 2 - Model, Loss, Optimizer
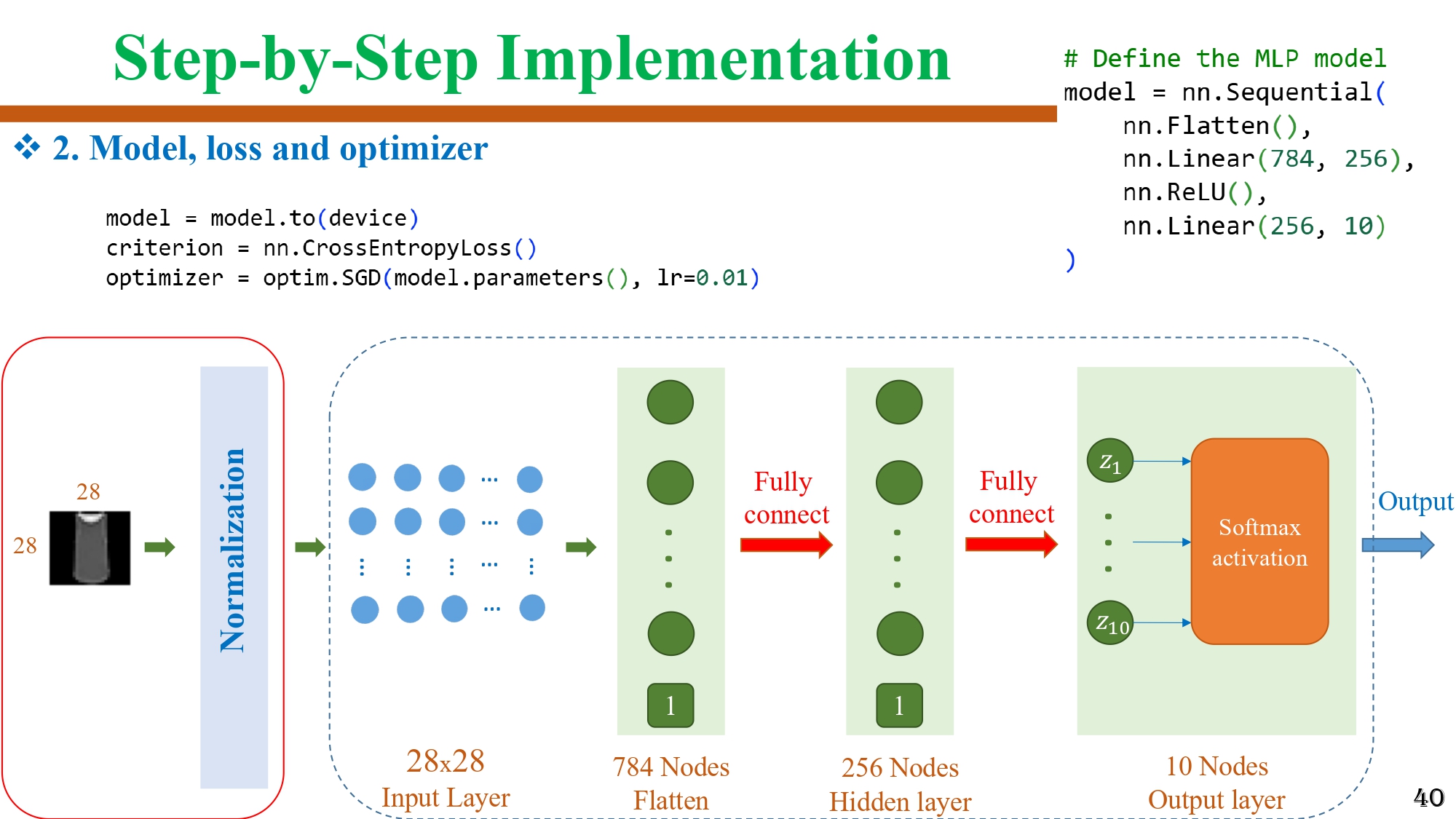
Hình 20: Khai báo mô hình MLP cùng hàm loss và optimizer cho quá trình huấn luyện
MLP:
Flatten → Linear(784→256) → ReLU → Linear(256→10)
Loss: CrossEntropyLoss
Optimizer: SGD
Đây là công thức chuẩn cho bài toán phân loại nhiều lớp.
Bước 3 - Training
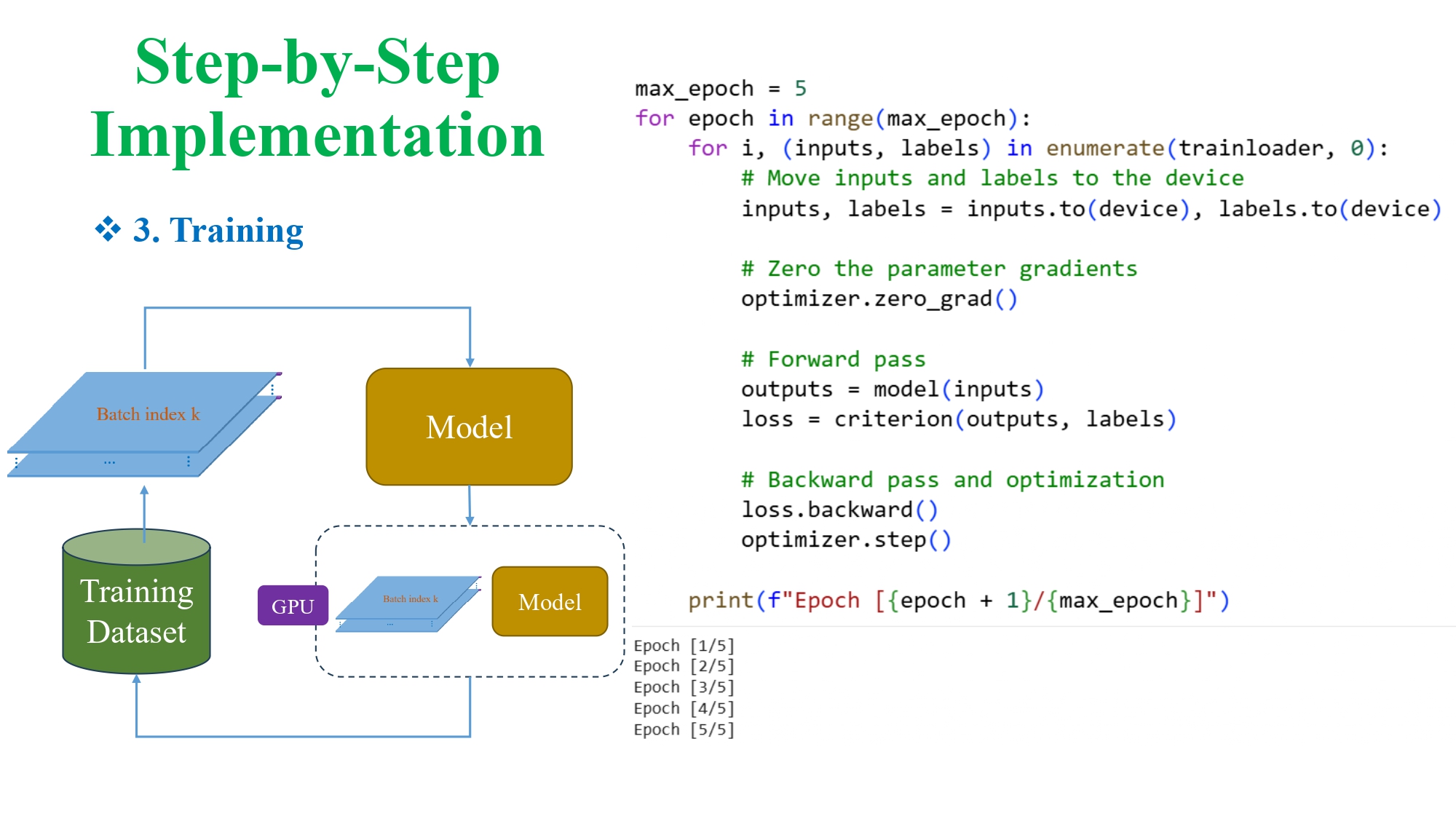
Hình 21: Mô tả vòng lặp huấn luyện: mô hình đọc từng batch, tính loss, lan truyền ngược và cập nhật trọng số
Quy trình:
- đưa batch vào GPU (model.to(device))
- forward pass
- tính loss
- backward()
- optimizer.step()
Bước 4 - Inference
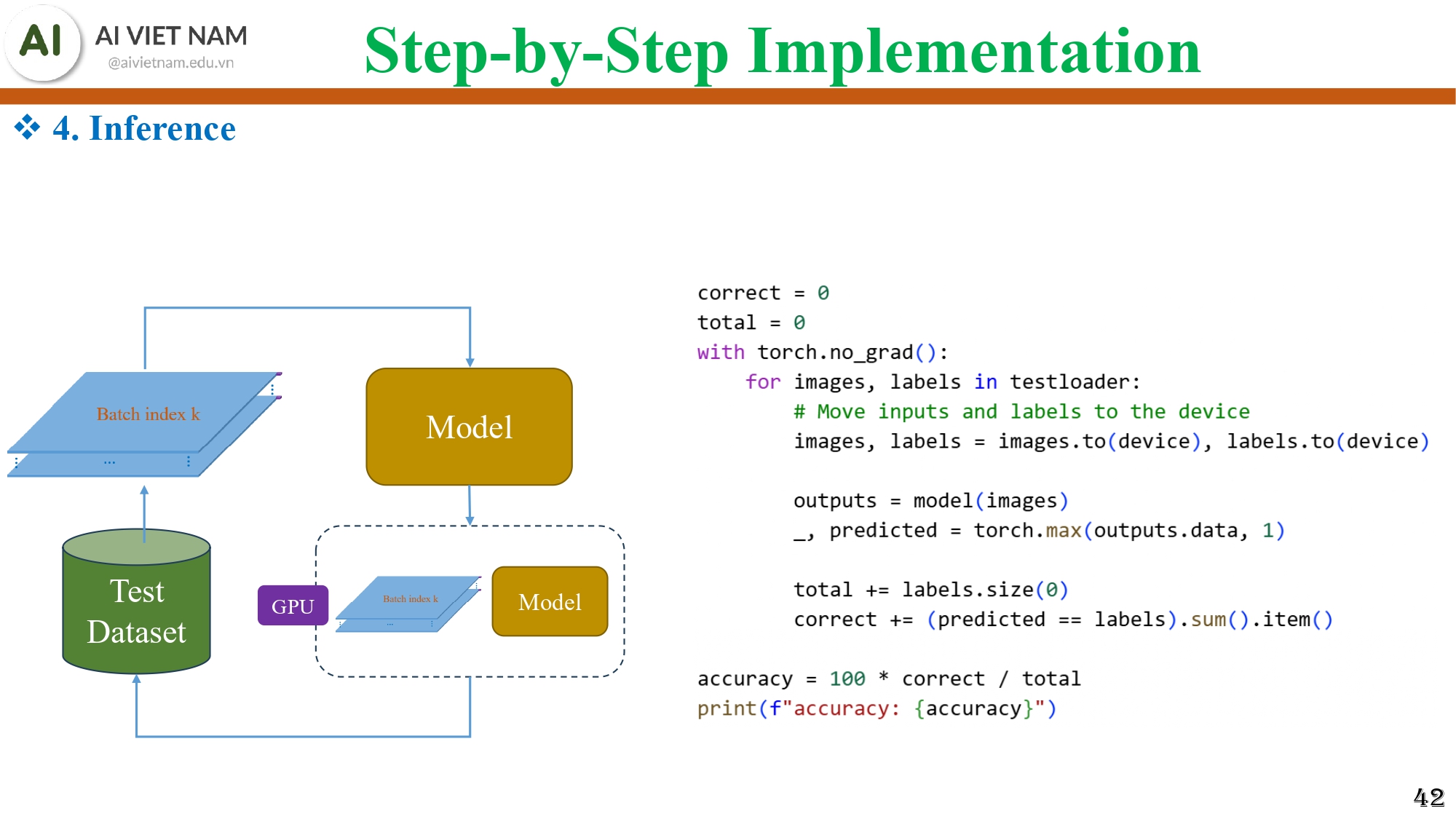
Hình 22: Mô hình được chạy trên dữ liệu test để xem dự đoán đúng bao nhiêu và tính ra độ chính xác
- Tắt tính gradient
- Chạy model trên tập test
- Tính test accuracy
Lưu ý: Khi tính Train/Test Accuracy
- Tính đúng loss và accuracy cho train
- Tính đúng loss và accuracy cho test
- Tắt BatchNorm/Dropout (nếu có) khi inference
- Dùng
torch.no_grad()để tăng tốc
3.7. Softmax vs MLP - So sánh hiệu suất
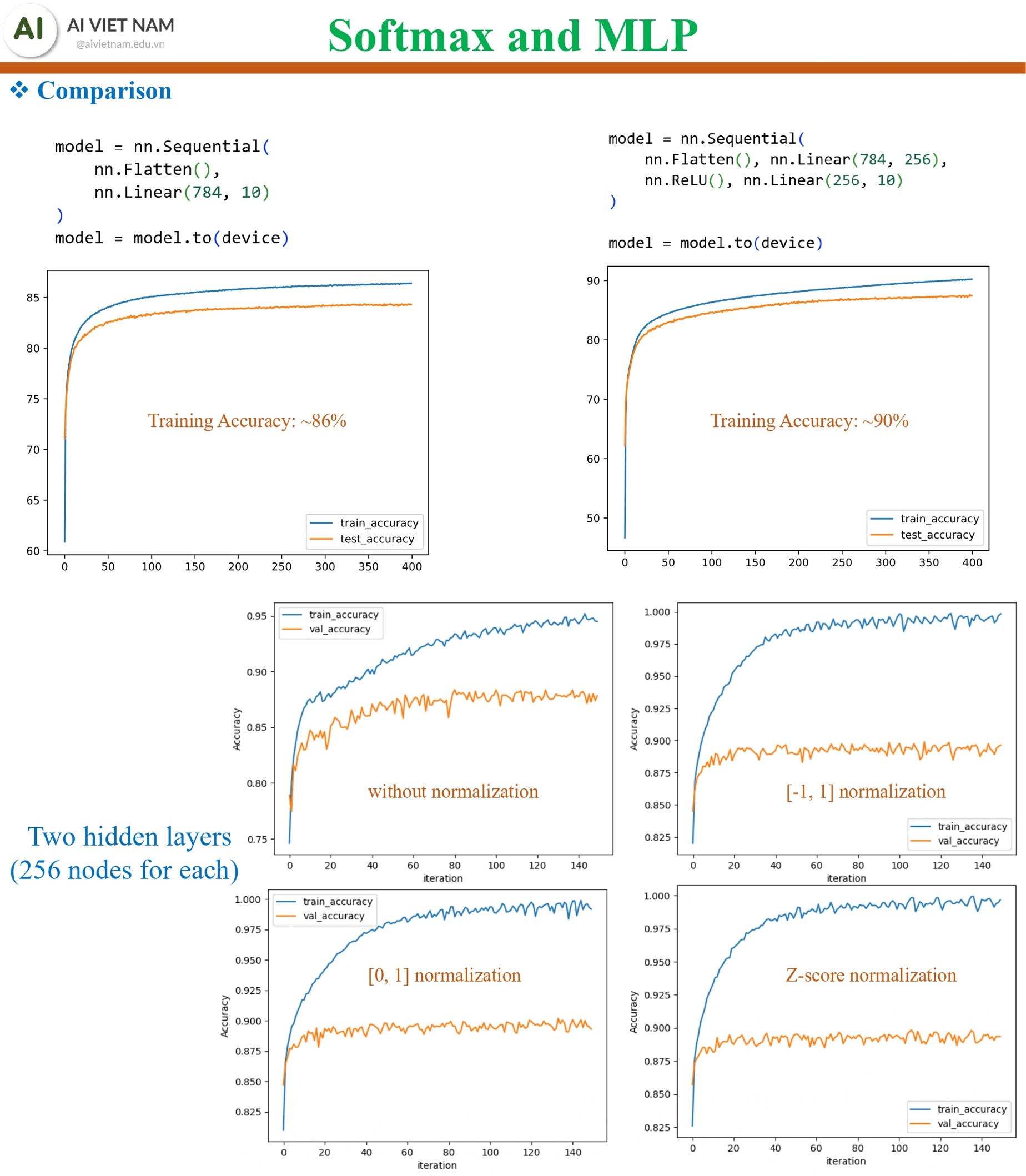
Hình 23: Hiệu suất MLP vượt trội so với Softmax, và normalization giúp mô hình ổn định hơn và đạt accuracy cao hơn
| Mô hình | Độ chính xác |
|---|---|
| Softmax Regression | ~86% |
| MLP (2 hidden layers × 256 nodes) | ~90% |
Như vậy:
- Softmax Regression: nhanh nhưng yếu
- MLP: mạnh hơn vì có nhiều lớp + ReLU
4. Training Pipeline
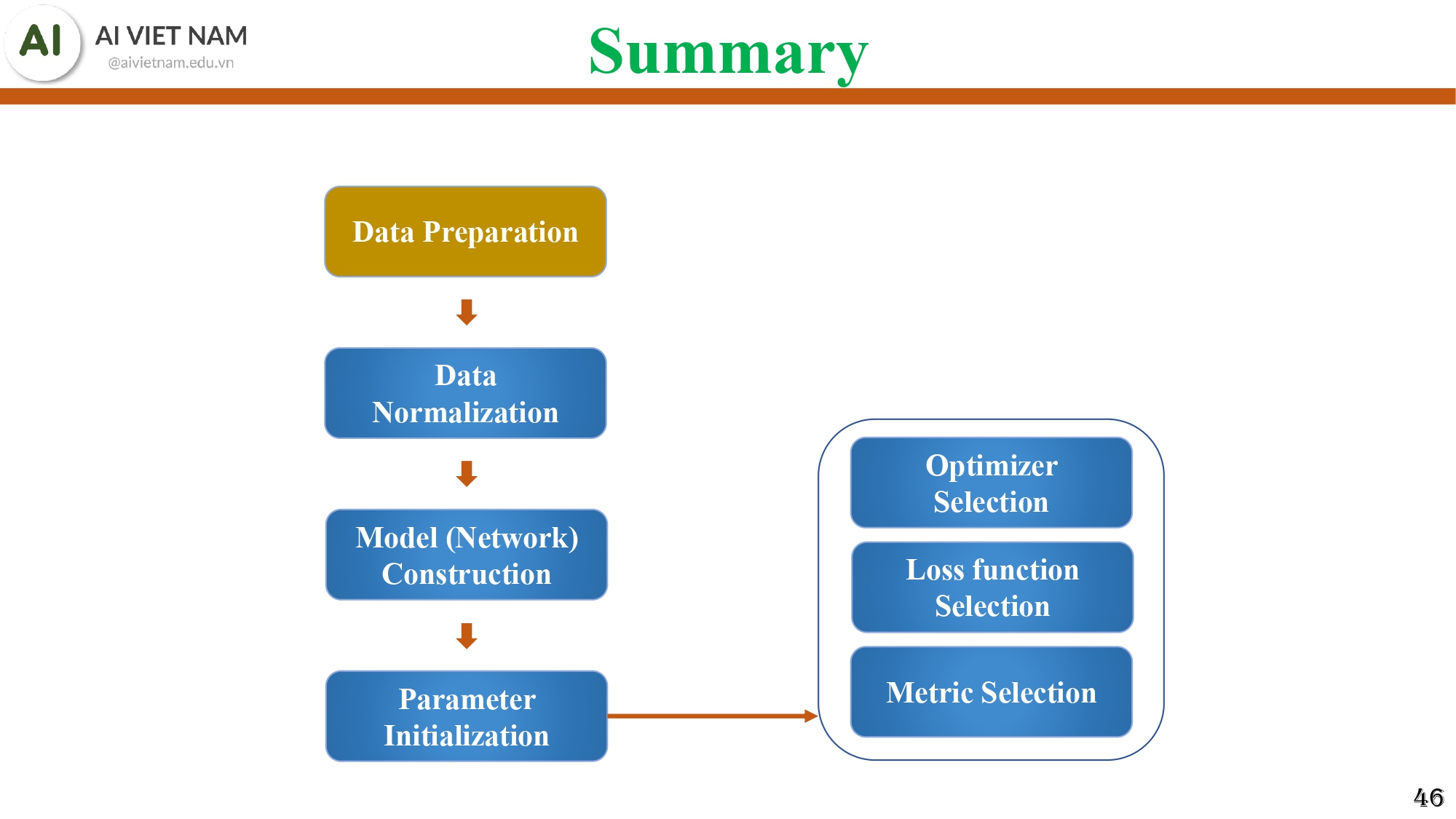
Hình 24: Sơ đồ tổng kết các bước chính khi huấn luyện MLP
Chúng ta sẽ tóm tắt lại bằng một sơ đồ gồm 7 phần quan trọng:
- Data Preparation
- Data Normalization
- Model Construction
- Parameter Initialization
- Optimizer Selection
- Loss Function Selection
4.1. Chuẩn bị dữ liệu - Data Preparation
Mọi mô hình đều bắt đầu bằng dữ liệu.
Dữ liệu được chia thành hai phần:
- Training Data - dùng để dạy mô hình học từ ví dụ.
- Testing Data - dùng để kiểm tra mô hình sau khi học xong.
Training và Testing không được trộn lẫn. Testing giúp đảm bảo mô hình không “học vẹt” mà thực sự hiểu dữ liệu mới.
4.2. Chuẩn hóa ảnh - Data Normalization
Đây là bước quan trọng bậc nhất trước khi đưa ảnh vào mạng nơ-ron.
Các pixel 0–255 được đưa về dạng “đẹp” hơn:
- [0,1]: chia 255
- [-1,1]: chia 127.5 rồi trừ 1
- Z-score: trừ mean, chia độ lệch chuẩn
Trong PyTorch, chỉ cần một dòng:
Normalize(mean, std)
Normalization giúp MLP học nhanh hơn, ổn định hơn và chính xác hơn.
4.3. Xây dựng mô hình - Model Construction
Đây là lúc chúng ta quyết định kiến trúc của mạng:
- Softmax Regression
- Hay một MLP:
Flatten → Linear → ReLU → Linear → Softmax
4.4. Khởi tạo tham số - Parameter Initialization
Mỗi lớp trong mạng có nhiều tham số (weights & biases).
Trước khi học, chúng cần được khởi tạo - thường là các giá trị ngẫu nhiên nhỏ.
Trong PyTorch, việc này diễn ra tự động khi chúng ta tạo các lớp Linear.
Việc khởi tạo tốt giúp mô hình học hiệu quả hơn.
4.5. Chọn thuật toán tối ưu - Optimizer Selection
Optimizer giống như “động cơ” giúp mô hình tự điều chỉnh trọng số.
Ví dụ: SGD (Stochastic Gradient Descent)
Sau mỗi vòng lặp huấn luyện, optimizer cập nhật trọng số theo chiều làm giảm loss.
4.6. Chọn hàm mất mát - Loss Function Selection
Loss cho biết mô hình sai thế nào.
Với phân loại nhiều lớp, slide sử dụng: CrossEntropyLoss
Loss càng thấp → mô hình càng học tốt.
Tất cả bước backward và cập nhật trọng số đều dựa vào giá trị này.
4.7. Chọn chỉ số đánh giá - Metrics Selection
Trong bài toán phân loại ảnh, chỉ số quan trọng nhất là: Accuracy - tỷ lệ dự đoán đúng
Loss dùng để học, còn Accuracy dùng để đánh giá chất lượng mô hình.
III. Chuyên sâu về MLP: Activation Functions, Initialization, và Tối ưu hóa
1. To-do List for Training
Sơ đồ các bước huấn luyện:
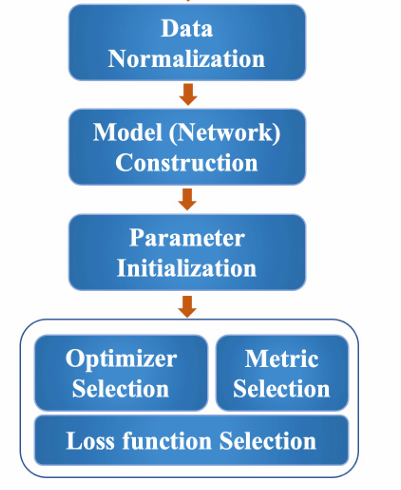
Hình 25: Sơ đồ "Checklist" các bước thiết lập quan trọng trong quy trình huấn luyện mô hình Deep Learning.
- Chuẩn bị Dữ liệu (Data Preparation): Phân chia dữ liệu thành tập huấn luyện (Training Data) và tập kiểm tra (Testing Data), và thực hiện Chuẩn hóa Dữ liệu.
- Xây dựng Mô hình (Model/Network Construction): Thiết kế kiến trúc mạng (số lớp, số node, hàm kích hoạt).
- Khởi tạo Tham số (Parameter Initialization): Đặt giá trị ban đầu cho trọng số ($W$) và độ lệch ($b$).
- Lựa chọn Trình tối ưu hóa (Optimizer Selection): Xác định cơ chế cập nhật tham số (ví dụ: Adam, SGD).
- Lựa chọn Hàm Mất mát (Loss function Selection): Định nghĩa hàm đo lường lỗi (ví dụ: Cross-Entropy Loss).
- Lựa chọn Tiêu chí đánh giá (Metric Selection): Đánh giá hiệu suất mô hình (ví dụ: Accuracy).
Các bước này là nền tảng để đảm bảo mô hình hội tụ và đạt được hiệu suất tốt.
1.1. Chuẩn hóa Dữ liệu (Data Normalization)
huẩn hóa dữ liệu là một bước tiền xử lý bắt buộc để đưa các đặc trưng (features) về cùng một phạm vi giá trị. Điều này giúp ổn định quá trình học và tăng tốc độ hội tụ của thuật toán Gradient Descent.
a. Các phương pháp chuẩn hóa phổ biến
Cho dữ liệu đầu vào $X$ (ví dụ: giá trị pixel ảnh trong phạm vi $[0, 255]$), ba phương pháp chuẩn hóa thường được sử dụng là:
a. Phạm vi $[0, 1]$:
$$
Image = \frac{Image}{255}
$$
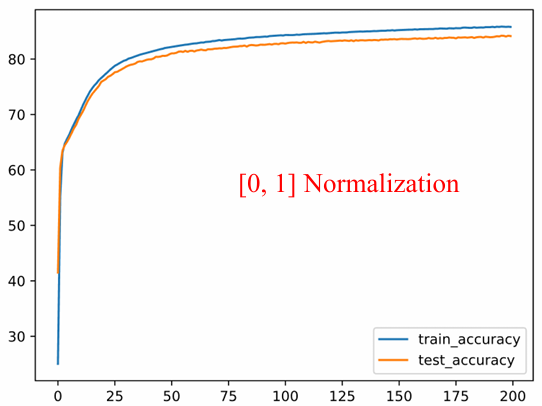
Hình 26: Kết quả huấn luyện mô hình khi áp dụng phương pháp chuẩn hóa về khoảng $[0, 1]$.
b. Phạm vi $[-1, 1]$:
$$
Image = \frac{Image}{127.5} - 1
$$
c. Chuẩn hóa Z-score (Standardization): Căn giữa dữ liệu về 0 và chia cho độ lệch chuẩn $\sigma$.
$$
Image = \frac{Image - \mu}{\sigma}
$$
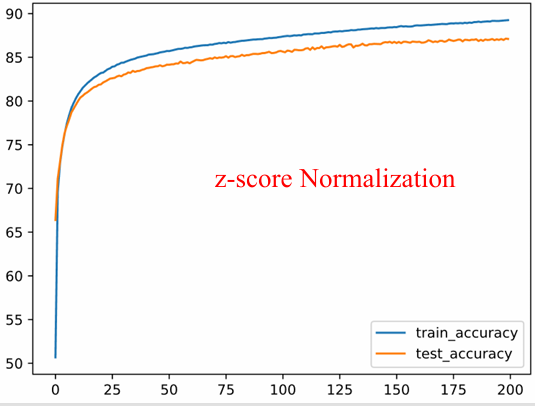
Hình 28: Kết quả huấn luyện với phương pháp chuẩn hóa Z-score (Standardization) dựa trên tham số trung bình ($\mu$) và độ lệch chuẩn ($\sigma$).
b. So sánh Hiệu suất
Các nghiên cứu thực nghiệm cho thấy, đối với một mô hình MLP cơ bản:
- Chuẩn hóa $[-1, 1]$ và Z-score thường cho kết quả Accuracy và tốc độ hội tụ tốt hơn so với chuẩn hóa $[0, 1]$.
- Chuẩn hóa $[-1, 1]$ giúp các hàm kích hoạt đối xứng như $\tanh$ hoặc các hàm kích hoạt hiện đại (như GELU, Swish) hoạt động hiệu quả hơn, vì dữ liệu đầu vào được căn giữa xung quanh 0.
1.2. Xây dựng Mô hình (Model/Network Construction)
Thiết kế kiến trúc MLP là quá trình xác định ba siêu tham số (hyperparameters) chính: số lớp ẩn, số node trong mỗi lớp, và hàm kích hoạt.
Cấu trúc tổng quát:
Input Layer $\rightarrow$ Hidden Layers (Linear + Activation) $\rightarrow$ Output Layer
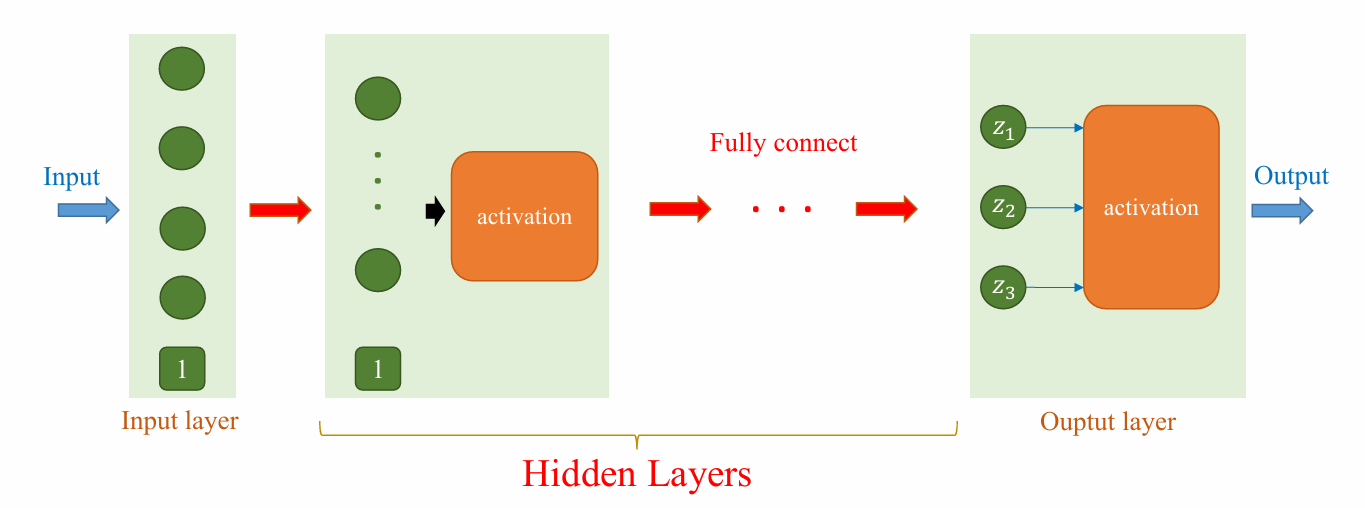
Hình 29: Mô hình hóa kiến trúc tổng quát của mạng nơ-ron đa lớp với các lớp ẩn và hàm kích hoạt.
a. Số lượng Node trong Lớp Ẩn?
Số lượng node trong một lớp ẩn quyết định khả năng học các biểu diễn phức tạp của mô hình (Model Capacity).
Cấu hình thử nghiệm:
* Normalization: $[-1, 1]$
* Loss: Cross-entropy
* Optimizer: SGD (lr=0.01)
Dưới đây là các cấu trúc mô hình (PyTorch) tương ứng với các thử nghiệm:
Model 1: 64 nodes
model = nn.Sequential(
nn.Flatten(),
nn.Linear(784, 64),
nn.ReLU(),
nn.Linear(64, 10)
)
Model 2: 256 nodes
model = nn.Sequential(
nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10)
)
Model 3: 1024 nodes
model = nn.Sequential(
nn.Flatten(),
nn.Linear(784, 1024),
nn.ReLU(),
nn.Linear(1024, 10)
)
Kết quả thực nghiệm:
| Số Node | Train Accuracy | Test Accuracy | Nhận xét |
|---|---|---|---|
| 64 nodes | 89% | 86% | Mức cơ sở. |
| 256 nodes | 90% | 87% | Cải thiện tốt so với 64 nodes. |
| 1024 nodes | 90% | 87% | Không cải thiện nhiều so với 256 nodes, chi phí tính toán cao hơn. |
- Kết luận: Tăng số lượng node từ 64 lên 256 giúp cải thiện hiệu suất, nhưng tăng tiếp lên 1024 không mang lại lợi ích lớn. Mô hình 256 node là điểm cân bằng tốt cho bài toán này.
b. Số lượng hidden layers?
Trong học sâu, việc tăng độ sâu (số lớp ẩn) thường hiệu quả hơn việc tăng độ rộng (số node) của mạng.
- Thực nghiệm:
- 1 Lớp Ẩn: Train-Acc: 90%, Test-Acc: 87%.
- 2 Lớp Ẩn: Train-Acc: 91%, Test-Acc: 88%.
- 3/4 Lớp Ẩn: Train-Acc: 92%, Test-Acc: 88%.
- Kết luận: Việc tăng độ sâu từ 1 lên 2 lớp ẩn mang lại cải thiện rõ rệt.
- Lưu ý quan trọng: Đối với các kiến trúc rất sâu sử dụng hàm
SigmoidhoặcTanhmà không cóNormalizationphù hợp, có thể dẫn đến hiện tượng Vanishing Gradient, khiến mô hình không thể hội tụ.
1.3. Các Hàm Kích hoạt (Activation Functions)
Hàm kích hoạt là yếu tố quyết định khả năng học các mối quan hệ phi tuyến tính của mạng.
$z = Wx + b$ (Tuyến tính)
$h = f(z)$ (Phi tuyến)
a. Hàm Sigmoid và Tanh
- Sigmoid:
$$ sigmoid(x)=\frac{1}{1+e^{-x}} \quad (\in [0, 1]) $$ - Tanh:
$$ tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \quad (\in [-1, 1]) $$ - Vấn đề: Cả hai đều gặp vấn đề Vanishing Gradient khi giá trị $|x|$ lớn (đạo hàm tiến về 0).
b. Hàm ReLU và các Biến thể (The ReLU Family)
-
ReLU (Rectified Linear Unit):
$$ ReLU(x)=\begin{cases}0&if~x\le0\\ x&if~x>0\end{cases} $$- Ưu điểm: Tính toán nhanh, khắc phục Vanishing Gradient cho $x>0$.
- Nhược điểm: Dying ReLU (nơ-ron chết nếu đầu vào luôn âm).
-
Leaky ReLU:
$$ LeakyReLU(x)=\begin{cases}0.01x&if~x\le0\\ x&if~x>0\end{cases} $$- Khắc phục Dying ReLU bằng cách cho phép một độ dốc nhỏ ở miền âm.
-
PReLU (Parametric ReLU): Tương tự Leaky ReLU nhưng hệ số $\alpha$ được học trong quá trình huấn luyện.
c. Các Hàm Hiện đại (Swish và GELU)
-
Swish (SiLU):
$$ swish(x)=\frac{x}{1+e^{-x}}=x \cdot \sigma(x) $$- Đặc điểm: Tự cổng, không đơn điệu, mượt mà hơn ReLU.
-
GELU (Gaussian Error Linear Unit):
$$ GELU(x) \approx x \cdot sigmoid(1.702x) $$- Đặc điểm: Tiêu chuẩn cho kiến trúc Transformer (BERT, GPT), vượt trội hơn ReLU trong NLP và Vision.
1.4. Tác Động Của Khởi Tạo Tham Số Đến Sự Hội Tụ Của Mạng Nơ-ron Đa Lớp
a. Chiến lược Khởi tạo Đồng nhất (Zero Initialization)
Giả thuyết đặt ra là khởi tạo tất cả các trọng số $W = 0$ và độ lệch $b = 0$. Hiệu quả của phương pháp này phụ thuộc hoàn toàn vào kiến trúc mô hình.
Đối với Hồi quy Tuyến tính (Linear Regression):
Trong các mô hình tuyến tính đơn giản ($\hat{y} = Wx + b$), hàm mất mát là hàm lồi (convex).
* Cơ sở toán học: Đạo hàm của hàm mất mát $L$ theo trọng số $w$ được tính bởi:
$$\frac{\partial L}{\partial w} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial w} \propto (\hat{y} - y) \cdot x$$
* Nhận định: Do $x$ và $y$ biến thiên theo từng mẫu dữ liệu, gradient $\nabla_w L$ sẽ khác 0 ngay cả khi $w=0$. Do đó, mô hình vẫn có khả năng cập nhật tham số và hội tụ về điểm tối ưu toàn cục.
Đối với Mạng Nơ-ron Đa lớp (MLP):
Khi áp dụng cho MLP, khởi tạo đồng nhất dẫn đến vấn đề nghiêm trọng gọi là "Sự phá vỡ tính đối xứng" (Failure of Symmetry Breaking).
* Hiện tượng: Xét một lớp ẩn có $k$ nơ-ron. Nếu $W$ được khởi tạo như nhau, mọi nơ-ron trong lớp ẩn đó sẽ nhận cùng một tín hiệu đầu vào, áp dụng cùng một hàm kích hoạt, và tạo ra cùng một giá trị đầu ra.
* Hệ quả: Trong quá trình lan truyền ngược (Backpropagation), gradient tại mọi nơ-ron là đồng nhất:
$$\frac{\partial L}{\partial w_{i}} = \frac{\partial L}{\partial w_{j}}, \quad \forall i, j$$
Điều này khiến các nơ-ron cập nhật theo cùng một hướng và độ lớn, làm cho lớp ẩn đó thực chất chỉ hoạt động như một nơ-ron duy nhất, bất kể kích thước thực tế của mạng.
Kết luận 1: Tuyệt đối không sử dụng Zero Initialization cho các trọng số ($W$) trong mạng nơ-ron để đảm bảo tính đa dạng của các đặc trưng học được.
b. Chiến lược Khởi tạo Ngẫu nhiên (Random Initialization) và Vấn đề Độ sâu
Để phá vỡ tính đối xứng, phương pháp phổ biến là khởi tạo $W$ theo phân phối chuẩn Gaussian $N(0, \sigma^2)$. Tuy nhiên, độ lớn của phương sai $\sigma^2$ trở thành yếu tố then chốt khi độ sâu của mạng tăng lên.
Thực nghiệm về Độ sâu (Depth Analysis):
Dựa trên kết quả thực nghiệm huấn luyện mạng MLP sử dụng hàm kích hoạt Sigmoid và SGD:
* Mạng nông (2 lớp ẩn): Hàm mất mát (Loss) giảm dần theo thời gian, mô hình hội tụ tốt.
* Mạng sâu (7 lớp ẩn): Hàm mất mát không thay đổi (loss stagnation) ngay từ các epoch đầu tiên.
Cơ chế thất bại: Triệt tiêu Gradient (Vanishing Gradient)
Trong mạng sâu, việc không kiểm soát phương sai của trọng số dẫn đến hai trạng thái cực đoan của tín hiệu đầu ra:
1. Exploding: Tín hiệu tăng theo cấp số nhân, gây tràn số.
2. Vanishing: Tín hiệu giảm về 0. Đối với các hàm kích hoạt bão hòa (như Sigmoid/Tanh), khi đầu vào quá lớn hoặc quá nhỏ, đạo hàm cục bộ tiến về 0. Theo quy tắc chuỗi (chain rule), tích của các đạo hàm này sẽ triệt tiêu gradient truyền về các lớp đầu, khiến trọng số không được cập nhật.
c. He Initialization
Để khắc phục hiện tượng triệt tiêu hoặc bùng nổ gradient, Kaiming He đề xuất phương pháp khởi tạo nhằm bảo toàn phương sai của tín hiệu khi đi qua các lớp, đặc biệt tối ưu cho các hàm kích hoạt thuộc họ Rectified Linear Unit (ReLU, GELU).
Công thức Toán học:
Trọng số được khởi tạo ngẫu nhiên theo phân phối chuẩn với phương sai phụ thuộc vào số lượng kết nối đầu vào ($n_{in}$) của lớp đó:
$$W \sim \mathcal{N}\left(0, \sqrt{\frac{2}{n_{in}}}\right)$$
Ưu điểm:
* Ổn định phương sai: Đảm bảo phương sai của đầu ra xấp xỉ phương sai của đầu vào ($Var(y) \approx Var(x)$), giúp dòng chảy tín hiệu ổn định qua mạng sâu.
* Tương thích ReLU/GELU: Hệ số $\sqrt{2}$ được đưa vào để bù đắp cho việc hàm ReLU triệt tiêu một nửa miền giá trị (miền âm) của phân phối.
d. Kết luận và Kiến nghị Thực nghiệm:
Dựa trên cơ sở lý thuyết và các bằng chứng thực nghiệm từ tài liệu, quy trình thiết lập tham số khởi tạo cho các mạng MLP hiện đại cần tuân thủ các nguyên tắc sau:
- Loại bỏ Zero Init: Không khởi tạo trọng số bằng 0 để tránh suy biến mô hình.
- Chuẩn hóa dữ liệu: Luôn áp dụng chuẩn hóa đầu vào về khoảng $[-1, 1]$ hoặc Z-score để hỗ trợ quá trình hội tụ.
- Cấu hình tiêu chuẩn (Gold Standard):
- Hàm kích hoạt: Sử dụng ReLU hoặc GELU (cho Transformer/NLP) kết hợp với Batch Normalization.
- Khởi tạo: Sử dụng He Initialization (Kaiming Normal).
- Tối ưu hóa: Sử dụng thuật toán Adam để tận dụng khả năng thích ứng của learning rate.
1.5. Optimizer Selection
Bên cạnh việc khởi tạo tham số, việc lựa chọn Thuật toán tối ưu (Optimizer) đóng vai trò quyết định tốc độ hội tụ và khả năng thoát khỏi các điểm tối ưu cục bộ (local minima) hoặc điểm yên ngựa (saddle points) của mô hình.
Dựa trên phả hệ phát triển của các thuật toán (Slide 62), chúng ta có thể phân loại và phân tích sự tiến hóa của chúng để đi đến lựa chọn tối ưu nhất.
a. Gradient Descent và Các Biến thể Cơ bản (SGD)
Thuật toán cơ bản nhất là Stochastic Gradient Descent (SGD). Quy tắc cập nhật tham số $\theta$ tại bước $t$ dựa trên đạo hàm của hàm mất mát $L$:
$$\theta_{t+1} = \theta_t - \eta \cdot \nabla_\theta L(\theta_t)$$
(Trong đó $\eta$ là tốc độ học - learning rate)
- Hạn chế: SGD thuần túy gặp khó khăn tại các bề mặt lỗi có độ cong (curvature) khác nhau theo các hướng khác nhau. Nó dễ bị dao động (oscillate) quanh điểm tối ưu hoặc kẹt tại các điểm yên ngựa.
b. Sự Cải tiến: Momentum và Nesterov
Để khắc phục sự dao động của SGD, khái niệm Động lượng (Momentum) được đưa vào.
* Cơ chế: Thuật toán "ghi nhớ" hướng cập nhật của các bước trước đó (tương tự như một quả cầu lăn xuống dốc có quán tính).
* Hiệu quả: Giúp tăng tốc độ hội tụ theo hướng có độ dốc nhất quán và giảm dao động theo các hướng nhiễu.
c. Adaptive Methods
Vấn đề lớn nhất của SGD và Momentum là Learning Rate ($\eta$) cố định cho mọi tham số. Trong mạng nơ-ron sâu, một số tham số cần cập nhật nhanh, số khác cần cập nhật chậm.
Các thuật toán thích ứng giải quyết vấn đề này bằng cách tự động điều chỉnh $\eta$ cho từng tham số:
1. AdaGrad: Giảm learning rate đối với các tham số thường xuyên được cập nhật (phù hợp dữ liệu thưa). Nhược điểm là learning rate giảm quá nhanh về 0.
2. RMSprop: Khắc phục AdaGrad bằng cách sử dụng trung bình trượt (moving average) của bình phương gradient, giúp learning rate không bị triệt tiêu quá sớm.
d. Adam (Adaptive Moment Estimation)
Adam là sự kết hợp tinh tế giữa hai ý tưởng lớn:
1. Momentum: Sử dụng trung bình của gradient (First moment - $m_t$).
2. RMSprop: Sử dụng trung bình của bình phương gradient (Second moment - $v_t$).
Quy tắc cập nhật (đơn giản hóa):
$$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \cdot \hat{m}_t$$
- Ưu điểm vượt trội:
- Kết hợp được khả năng vượt qua điểm tối ưu cục bộ của Momentum.
- Tự động điều chỉnh learning rate cho từng trọng số như RMSprop.
- Hoạt động ổn định với các siêu tham số mặc định (thường là $\eta = 0.001$, $\beta_1 = 0.9$, $\beta_2 = 0.999$).
2. Tổng kết Quy trình Xây dựng MLP.
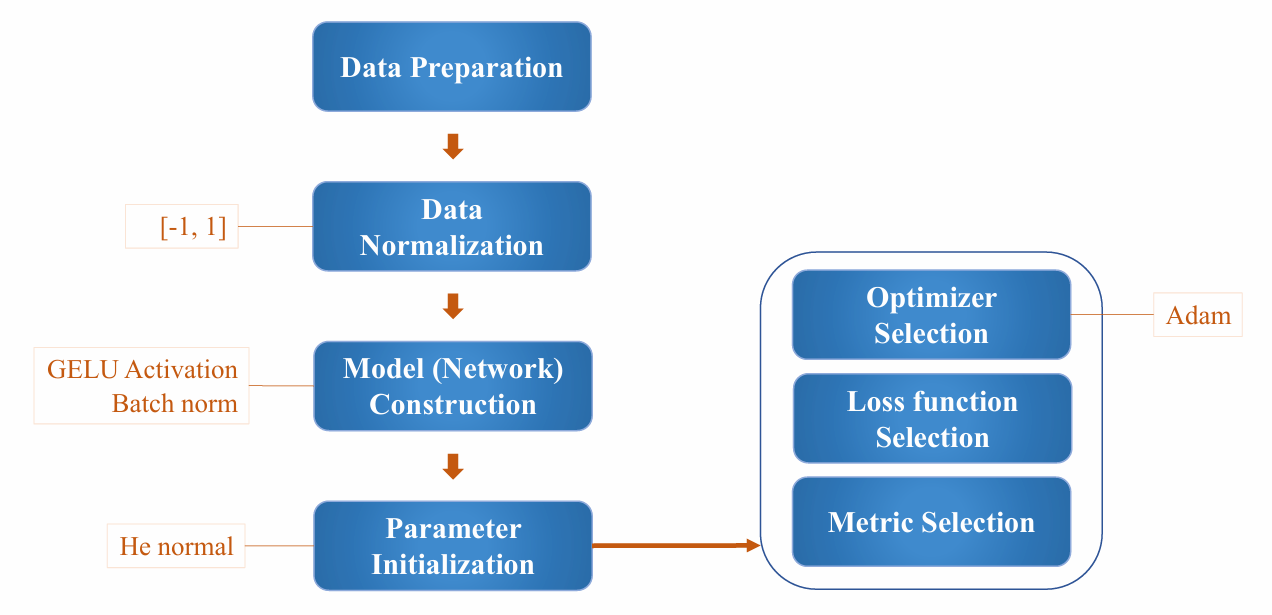
Hình 30: Các thiết lập cấu hình đề xuất (Best Practices) để xây dựng một quy trình huấn luyện Deep Learning hiệu quả.
2.1. Về Xử lý Dữ liệu (Data Pipeline)
- Chiến lược: Chuẩn hóa dữ liệu về khoảng $[-1, 1]$ (thay vì $[0, 1]$).
- Lý do: Việc đưa dữ liệu về dạng "Zero-centered" (căn giữa 0) phối hợp tốt hơn với các thuật toán tối ưu hóa, giúp Gradient không bị lệch về một hướng (zigzagging), từ đó mô hình hội tụ nhanh và ổn định hơn.
2.2. Về Kiến trúc Mạng (Model Architecture)
- Chiến lược: Sử dụng hàm kích hoạt GELU kết hợp lớp Batch Normalization.
- Lý do:
- GELU (Gaussian Error Linear Unit): Là hàm kích hoạt hiện đại (tiêu chuẩn trong BERT, GPT), khắc phục điểm yếu "gãy khúc" tại 0 của ReLU, giúp lan truyền gradient mượt mà hơn.
- Batch Norm: Giúp ổn định phân phối đầu vào qua các lớp ẩn, cho phép huấn luyện mạng sâu hơn mà không bị "bão hòa" (saturation) hay biến mất gradient.
2.3. Về Khởi tạo Tham số (Initialization)
- Chiến lược: Sử dụng He Normal (Kaiming Initialization).
- Lý do: Đây là phương pháp khởi tạo tối ưu dành cho các họ hàm kích hoạt ReLU/GELU. Nó đảm bảo phương sai của tín hiệu đầu ra không bị suy giảm qua nhiều lớp, tránh hiện tượng mô hình không học được gì ngay từ những epoch đầu tiên.
2.4. Về Tối ưu hóa (Optimization)
- Chiến lược: Lựa chọn Adam.
- Lý do: Adam (Adaptive Moment Estimation) tự động điều chỉnh learning rate cho từng tham số, thường hội tụ nhanh hơn và ít nhạy cảm với việc chọn Learning Rate ban đầu so với SGD truyền thống.
IV. Kết luận
Chúng ta đã cùng nhau đi qua một hành trình dài, từ việc mổ xẻ cấu trúc của một pixel đơn lẻ đến việc thiết kế và tối ưu hóa hoàn chỉnh một mạng nơ-ron đa lớp (MLP). Những kiến thức này không chỉ gói gọn trong bài toán phân loại số viết tay (MNIST) hay quần áo (Fashion-MNIST), mà chính là những viên gạch nền tảng cho toàn bộ lĩnh vực Deep Learning hiện đại.
Để khép lại bài viết, dưới đây là 3 nguyên tắc vàng được đúc kết từ quá trình xây dựng mô hình mà bạn cần ghi nhớ:
1. Dữ liệu là khởi nguồn, nhưng "Chuẩn hóa" mới là chìa khóa
Một mô hình dù có kiến trúc tinh vi đến đâu cũng sẽ thất bại nếu dữ liệu đầu vào hỗn loạn. Việc chuẩn hóa pixel (Normalization) về khoảng $[-1, 1]$ hoặc sử dụng Z-score không chỉ là quy ước sách giáo khoa, mà là yếu tố sống còn giúp cân bằng dòng chảy gradient, đảm bảo mô hình hội tụ nhanh và ổn định.
2. Sức mạnh nằm ở sự Phi tuyến (Non-linearity)
Chúng ta đã thấy Softmax Regression thất bại như thế nào trước các dữ liệu phức tạp. Sức mạnh thực sự của Deep Learning đến từ việc xếp chồng các lớp ẩn (Hidden Layers) kết hợp với các hàm kích hoạt phi tuyến như ReLU hay GELU. Chính sự phi tuyến này cho phép mô hình "bẻ cong" không gian dữ liệu để phân tách các đặc trưng mà các mô hình tuyến tính không thể làm được.
3. Sự tinh tế trong Tối ưu hóa (Optimization)
Sự khác biệt giữa một mô hình "chạy được" và một mô hình SOTA (State-of-the-art) thường nằm ở các tiểu tiết kỹ thuật:Khởi tạo tham số: Sử dụng He Initialization thay vì ngẫu nhiên hay khởi tạo bằng 0.Thuật toán tối ưu: Lựa chọn Adam để tận dụng khả năng thích ứng (adaptive learning rate).Kiến trúc: Kết hợp Batch Normalization để huấn luyện mạng sâu hơn.
V. References
[1] Các hình ảnh và code được tham khảo từ slide và bài tập của tài liệu AIO2025, Module 06
Chưa có bình luận nào. Hãy là người đầu tiên!