I. Giới thiệu
Trong khuôn khổ của Học máy có giám sát (Supervised Learning), các thuật toán hồi quy đóng vai trò là nền tảng lý thuyết cốt lõi cho việc mô hình hóa mối quan hệ giữa các biến đầu vào và biến mục tiêu. Mặc dù Hồi quy Tuyến tính (Linear Regression) cung cấp một cách tiếp cận trực quan và hiệu quả cho các bài toán dự đoán giá trị liên tục, việc áp dụng trực tiếp mô hình này vào các không gian biến thiên rời rạc - đặc trưng của bài toán phân loại - lại bộc lộ những khiếm khuyết nghiêm trọng về mặt toán học và ngữ nghĩa.
Bài viết này trình bày một khảo sát hệ thống về quá trình chuyển đổi tất yếu từ các mô hình tuyến tính sang các mô hình xác suất, cụ thể là Hồi quy Logistic và Hồi quy Softmax (Multinomial Logistic Regression). Chúng ta sẽ đi sâu phân tích cơ sở toán học của việc xây dựng hàm giả thuyết phi tuyến, lý giải sự ưu việt của hàm mất mát Cross-Entropy so với Mean Squared Error trong tối ưu hóa lồi. Đồng thời, bài viết sẽ minh họa việc hiện thực hóa các cấu trúc lý thuyết này thông qua PyTorch—một framework tính toán tensor (tensor computation) hiện đại với cơ chế vi phân tự động (automatic differentiation), nhằm thu hẹp khoảng cách giữa công thức toán học trừu tượng và lập trình ứng dụng.
II. From Linear Regression To Logistic Regression
Hồi quy Tuyến tính (Linear Regression) là một thuật toán nền tảng trong học máy có giám sát, nổi bật nhờ tính đơn giản và khả năng diễn giải. Tuy nhiên, mô hình này bộc lộ những hạn chế cố hữu khi áp dụng cho các bài toán phân loại (classification). Hồi quy Logistic (Logistic Regression) được phát triển như một sự mở rộng để giải quyết những thách thức này, cung cấp một phương pháp luận mạnh mẽ để mô hình hóa xác suất của các kết quả rời rạc.
1. Mô hình Hồi quy Tuyến tính và Phạm vi Ứng dụng
Linear Regression được thiết kế để giải quyết các bài toán hồi quy, với mục tiêu dự đoán một biến phụ thuộc (biến mục tiêu) có giá trị liên tục. Các ứng dụng điển hình bao gồm dự đoán giá trị tài sản (ví dụ: giá nhà dựa trên diện tích) hoặc các chỉ số đo lường liên tục khác.
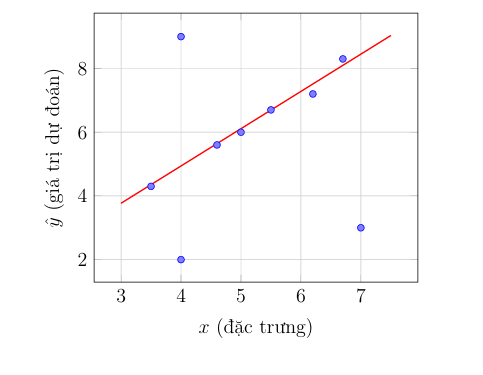
Về mặt toán học, mô hình này giả định một mối quan hệ tuyến tính giữa biến độc lập $x$ và biến dự đoán $\hat{y}$. Phương trình giả thuyết (hypothesis function) có dạng: $\hat{y} = wx + b$. Quá trình huấn luyện mô hình bao gồm việc tìm ra một đường thẳng "khớp" nhất (line of best fit) với dữ liệu quan sát, sau đó sử dụng đường thẳng này để ngoại suy hoặc nội suy cho các điểm dữ liệu mới.
2. Hạn chế của Hồi quy Tuyến tính đối với Bài toán Phân loại
Vấn đề phát sinh khi áp dụng trực tiếp Linear Regression cho các bài toán phân loại. Trong kịch bản này, biến mục tiêu $y$ không còn liên tục mà mang tính rời rạc, thường là nhị phân (ví dụ: "Loại 0" và "Loại 1"). Ví dụ, phân loại mẫu hoa dựa trên đặc trưng (như độ dài cánh hoa) thành $y=0$ hoặc $y=1$. Khi trực quan hóa, dữ liệu này biểu hiện dưới dạng các cụm điểm tập trung tại các giá trị $y=0$ và $y=1$, thay vì tuân theo một xu hướng tuyến tính.
Việc áp dụng một mô hình tuyến tính cho dữ liệu phân loại dẫn đến hai bất cập nghiêm trọng:
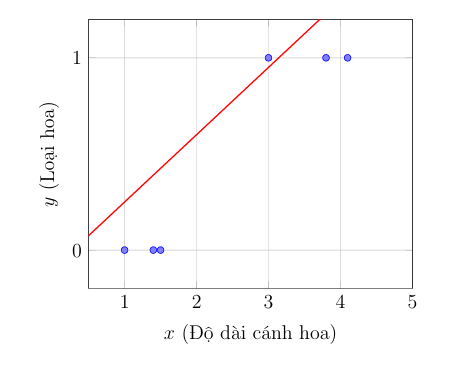
- Miền giá trị không phù hợp: Hàm giả thuyết $\hat{y} = wx + b$ có miền giá trị đầu ra là $(-\infty, +\infty)$. Miền giá trị này không tương thích về mặt ngữ nghĩa với các nhãn mục tiêu (ví dụ: 0 và 1). Các giá trị dự đoán như $\hat{y} = 1.7$ hoặc $\hat{y} = -0.3$ trở nên vô nghĩa và không thể diễn giải được trong bối cảnh phân loại.
- Thiếu diễn giải xác suất: Mô hình tuyến tính không cung cấp một đầu ra có thể được diễn giải trực tiếp dưới dạng xác suất (tức là một giá trị trong khoảng $[0, 1]$). Đây là một yêu cầu cơ bản trong nhiều bài toán phân loại.
Do đó, một đường thẳng tuyến tính được xem là một công cụ mô hình hóa không phù hợp cho loại dữ liệu này.
3. Hồi quy Logistic và Hàm Sigmoid
Để giải quyết những hạn chế trên, cần một hàm phi tuyến có khả năng ánh xạ đầu ra tuyến tính $z = wx + b$ (với $z \in (-\infty, +\infty)$) vào một miền giá trị có ý nghĩa, cụ thể là khoảng $(0, 1)$ để biểu thị xác suất.
Hàm Sigmoid, hay còn gọi là hàm Logistic, đáp ứng yêu cầu này. Hàm Sigmoid được định nghĩa bởi công thức:
$$
\sigma(z) = \frac{1}{1 + e^{-z}}
$$
Hàm này có các đặc tính tiệm cận quan trọng:
- Khi $z \rightarrow +\infty$, $\sigma(z) \rightarrow 1$.
- Khi $z \rightarrow -\infty$, $\sigma(z) \rightarrow 0$.
- Khi $z = 0$, $\sigma(z) = 0.5$.
Những đặc tính này cho phép hàm Sigmoid chuyển đổi bất kỳ giá trị thực nào thành một giá trị trong khoảng $(0, 1)$, cho phép diễn giải đầu ra của mô hình dưới dạng xác suất.
Mô hình Hồi quy Logistic được xây dựng bằng cách kết hợp hàm tuyến tính và hàm Sigmoid. Quá trình dự đoán bao gồm hai giai đoạn:
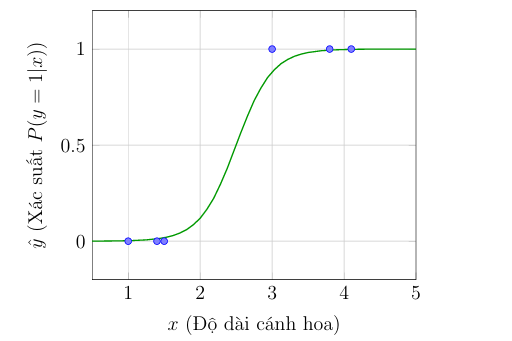
- Tính toán tổ hợp tuyến tính (Logit): Tương tự như Hồi quy Tuyến tính, mô hình tính toán một giá trị $z$ (được gọi là log-odds) từ các đặc trưng đầu vào: $z = wx + b$.
- Ánh xạ qua Sigmoid: Giá trị $z$ sau đó được đưa qua hàm Sigmoid để thu được xác suất $\hat{y}$ (tức là $P(y=1|x)$): $\hat{y} = \sigma(z)$.
Kết quả là một mô hình có đầu ra, ví dụ $\hat{y} = 0.9$, có thể được diễn giải một cách rõ ràng là "xác suất 90% mẫu thuộc về Loại 1." Đường cong dự đoán hình chữ S (sigmoid) mà mô hình này tạo ra thể hiện sự phù hợp (fit) với dữ liệu phân loại nhị phân tốt hơn đáng kể so với một đường thẳng. Sự chuyển đổi này đánh dấu sự ra đời của Hồi quy Logistic như một thuật toán phân loại nền tảng.
4. Xây dựng Hàm Mất mát (Loss Function)
4.1. Thử nghiệm với Sai số Bình phương (MSE)
Cách tiếp cận đầu tiên và trực quan nhất là sử dụng lại hàm mất mát từ Linear Regression:
$$
L = (\hat{y} - y)^2
$$
Ý tưởng: Hàm này đo lường "khoảng cách" bình phương giữa dự đoán $\hat{y}$ và giá trị thật $y$.
Tuy nhiên, khi áp dụng hàm MSE cho mô hình Hồi quy Logistic (có hàm Sigmoid), một vấn đề lớn xuất hiện:
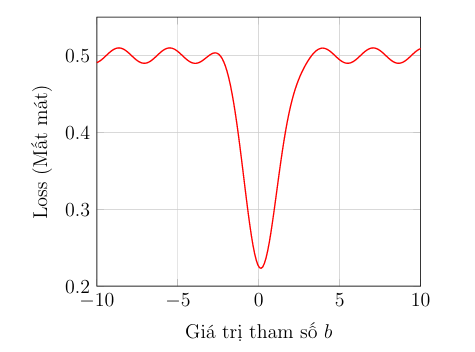
- Vấn đề: Hàm mất mát tổng thể trở nên không lồi (non-convex).
- Hậu quả: Một hàm "không lồi" có nhiều "cực tiểu cục bộ" (local minima). Khi sử dụng thuật toán Gradient Descent, nó có thể bị "kẹt" trong một điểm cực tiểu cục bộ mà không tìm được điểm "cực tiểu toàn cục" (global minimum), dẫn đến một mô hình không tối ưu.
Do đó, chúng ta cần một hàm mất mát khác.
4.2. Tư duy lại cho bài toán Xác suất
Mục tiêu của chúng ta là xây dựng một hàm mất mát mới cho đầu ra là xác suất $\hat{y}$ (từ 0 đến 1). Chúng ta chia bài toán thành hai trường hợp.
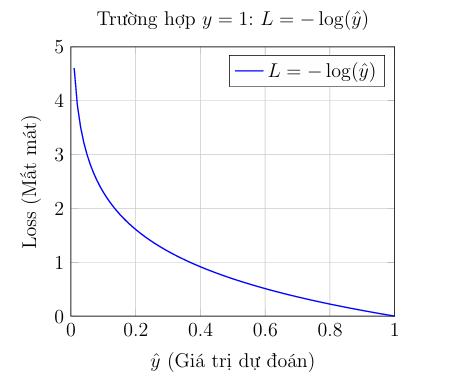
Trường hợp 1: Nhãn thực tế là $y = 1$ (Loại 1)
- Mục tiêu: Chúng ta muốn hàm mất mát bằng 0 khi dự đoán $\hat{y}=1$ (dự đoán đúng).
- Hình phạt: Chúng ta muốn hàm mất mát tiến đến vô cùng ($\infty$) khi dự đoán $\hat{y}=0$ (dự đoán cực sai).
- Hàm được chọn: $L = -\log(\hat{y})$.
- Kiểm tra: Nếu $\hat{y} \rightarrow 1$, thì $L = -\log(1) \rightarrow 0$ (Rất tốt, không phạt).
- Kiểm tra: Nếu $\hat{y} \rightarrow 0$, thì $L = -\log(0) \rightarrow \infty$ (Phạt rất nặng).
Trường hợp 2: Nhãn thực tế là $y = 0$ (Loại 0)
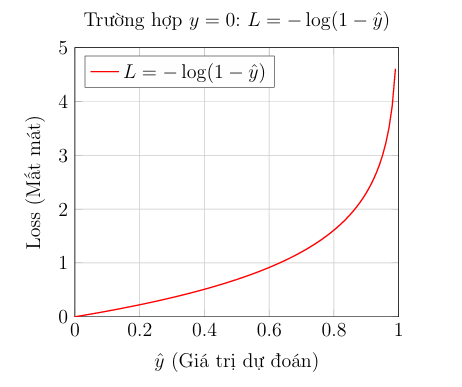
- Mục tiêu: Chúng ta muốn hàm mất mát bằng 0 khi dự đoán $\hat{y}=0$ (dự đoán đúng).
- Hình phạt: Chúng ta muốn hàm mất mát tiến đến vô cùng ($\infty$) khi dự đoán $\hat{y}=1$ (dự đoán cực sai).
- Hàm được chọn: $L = -\log(1 - \hat{y})$.
- Kiểm tra: Nếu $\hat{y} \rightarrow 0$, thì $L = -\log(1-0) \rightarrow 0$ (Rất tốt, không phạt).
- Kiểm tra: Nếu $\hat{y} \rightarrow 1$, thì $L = -\log(1-1) \rightarrow \infty$ (Phạt rất nặng).
4.3. Binary Cross-Entropy (BCE)
Bây giờ chúng ta có hai hàm mất mát riêng biệt, phụ thuộc vào câu lệnh "nếu" (if $y=1 \dots$ if $y=0 \dots$). Điều này rất bất tiện cho việc tính toán đạo hàm.
Chúng ta sử dụng một "mẹo" toán học để kết hợp cả hai trường hợp thành một phương trình duy nhất bằng cách sử dụng chính nhãn $y$:
$$
L(y, \hat{y}) = -y \cdot \log(\hat{y}) - (1 - y) \cdot \log(1 - \hat{y})
$$
Hàm này được gọi là Binary Cross-Entropy (BCE).
Hãy kiểm tra xem nó hoạt động như thế nào:
- Khi $y = 1$: Phương trình trở thành:
$L = -1 \cdot \log(\hat{y}) - (1 - 1) \cdot \log(1-\hat{y})$
$L = -\log(\hat{y}) - 0$
$\Rightarrow$ $L = -\log(\hat{y})$. (Giống hệt Trường hợp 1). - Khi $y = 0$: Phương trình trở thành:
$L = -0 \cdot \log(\hat{y}) - (1 - 0) \cdot \log(1-\hat{y})$
$L = 0 - 1 \cdot \log(1 - \hat{y})$
$\Rightarrow$ $L = -\log(1 - \hat{y})$. (Giống hệt Trường hợp 2).
Quá trình xây dựng hàm loss này thành công vì Binary Cross-Entropy có một đặc tính toán học cực kỳ quan trọng:
Khi kết hợp với hàm Sigmoid, hàm mất mát BCE đảm bảo là một hàm lồi (convex).
Không giống như MSE, một hàm lồi chỉ có một điểm cực tiểu toàn cục duy nhất (giống như đáy của một cái bát). Điều này đảm bảo rằng thuật toán Gradient Descent, dù bắt đầu ở đâu, cũng sẽ tìm được bộ tham số $w$ và $b$ tốt nhất cho mô hình.
III. Softmax Regression
Softmax Regression là một mô hình cơ bản nhưng vô cùng mạnh mẽ, thường được sử dụng trong lĩnh vực Học máy (Machine Learning) để giải quyết các vấn đề phân loại khi có nhiều hơn hai lớp đầu ra.
Bài viết này sẽ đi sâu vào định nghĩa, cơ chế hoạt động, và các thành phần cốt lõi của Softmax Regression, còn được biết đến là hồi quy logistic đa thức (multinomial logistic regression)
1. Softmax Regression là gì? (Softmax Regression Overview)
Trong khi mô hình Hồi quy Logistic (Logistic Regression) được thiết kế để xử lý các bài toán phân loại nhị phân (Binary Classification)—tức là phân loại dữ liệu vào hai lớp riêng biệt (ví dụ: {0, 1})—thì Softmax Regression được tạo ra để xử lý các bài toán phân loại đa lớp (Multi-class Classification). Mô hình này cho phép chúng ta phân loại dữ liệu thành C lớp, nơi C≥2 (ví dụ: {0, 1, 2, 3})
Softmax Regression giải quyết vấn đề mà việc sử dụng nhiều hàm Sigmoid (phương pháp "một chống lại phần còn lại" - one vs rest) có thể gặp phải trong phân loại đa lớp
2. Thành phần cốt lõi: Hàm Softmax
Hàm Softmax đóng vai trò chuyển đổi các giá trị đầu vào (thường là kết quả tuyến tính z từ mô hình) thành một phân phối xác suất
2.1. Công thức và Tính chất
Công thức cơ bản của Hàm Softmax cho xác suất của lớp $i$ là
$$P_i = f(z_i) = \frac{e^{z_i}}{\sum_{j} e^{z_j}}$$
Hàm này có hai tính chất cực kỳ quan trọng:
1. Mỗi giá trị đầu ra nằm trong khoảng từ 0 đến 1 $(0≤f(z_i)≤1)$
2. Tổng của tất cả các xác suất đầu ra bằng 1 $(\sum_{i} f(z_i) = 1)$
Điều này đảm bảo rằng đầu ra của mô hình có thể được diễn giải trực tiếp dưới dạng xác suất mà mẫu đầu vào thuộc về từng lớp
2.2. Softmax Ổn định (Stable Softmax)
Trong tính toán thực tế, khi giá trị $z_i$ trở nên quá lớn, $e^{z_i}$ cũng sẽ rất lớn, dẫn đến hiện tượng Overflow (tràn số) khi tính toán trên máy tính. Để tăng tính ổn định, phiên bản Softmax Ổn định được sử dụng
Softmax ổn định sử dụng kỹ thuật trừ đi một hằng số $c$ (thường là giá trị lớn nhất $m$ trong vector $z$) từ tất cả các $z_i$:
$$P_i = f(z_i) = \frac{e^{\,z_i - c}}{\sum_{j} e^{\,z_j - c}}$$ Việc này giúp giữ cho giá trị của $e^{z_i - c}$ nằm trong phạm vi tính toán an toàn
3. Hàm Mất Mát và Mã hóa
Để huấn luyện mô hình Softmax Regression, chúng ta cần một hàm mất mát để đo lường mức độ sai khác giữa xác suất dự đoán $\hat{y}$ và nhãn thực tế $(y)$.
3.1. Mã hóa One-hot
Softmax Regression yêu cầu nhãn thực tế $y$ phải được biểu diễn dưới dạng Mã hóa One-hot (One-hot Encoding). Nếu có $C$ lớp, nhãn $y$ sẽ được chuyển thành vector $y$ có kích thước $C$, trong đó chỉ có một phần tử bằng 1 (lớp đúng), và các phần tử còn lại bằng 0
Ví dụ, với 3 lớp ({0, 1, 2}):
- $y = 0 \rightarrow y = [1\ 0\ 0]$
- $y = 1 \rightarrow y = [0\ 1\ 0]$
3.2. Hàm mất mát Cross-Entropy
Softmax Regression sử dụng Hàm mất mát Cross-Entropy (Cross-Entropy Loss), ký hiệu là $H(y, \hat{y})$. Công thức của hàm mất mát này cho Softmax Regression là:
$$L(\theta) = - \sum_{i} y_i \log(\hat{y}_i)$$ Hoặc viết dưới dạng ma trận:
$$L(\theta) = -\, y^{T} \log(\hat{y})$$
Mục tiêu của việc tối ưu hóa là giảm thiểu hàm mất mát này. Khi xác suất dự đoán $(\hat{y_i})$ cho lớp đúng tiệm cận 1, giá trị mất mát sẽ nhỏ
4. Tối ưu hóa bằng Gradient Descent
Mô hình Softmax Regression được huấn luyện bằng cách điều chỉnh các tham số $(θ)$ thông qua Thuật toán Gradient Descent. Quá trình này bao gồm các bước chính sau (khi áp dụng Stochastic Gradient Descent—SGD, sử dụng một mẫu):
1. Chọn một mẫu $(x,y)$ từ dữ liệu huấn luyện.
2. Tính output $\hat{y}$ (sử dụng hàm Softmax).
3. Tính Loss (Cross-Entropy)
4. Tính đạo hàm (Gradient) $\nabla_{\theta} L$
5. Cập nhật tham số $\theta = \theta - \eta \, \nabla_{\theta} L$, trong đó $η$ là tốc độ học (learning rate).
Đạo hàm của hàm mất mát theo $z_i$ (đầu vào của hàm Softmax) có công thức đơn giản là: $$\frac{\partial L}{\partial z_i} = \hat{y}_i - y_i$$
Sử dụng đạo hàm này, đạo hàm của hàm mất mát theo ma trận tham số $θ$ được tính bằng công thức:
$$\nabla_{\theta} L = x (\hat{y} - y)^T$$
5. Ranh giới Quyết định (Decision Boundary)
Một đặc điểm quan trọng của Softmax Regression là tính chất của ranh giới quyết định. Ranh giới quyết định giữa lớp $i$ và lớp $j$ được xác định tại điểm mà xác suất dự đoán cho hai lớp này bằng nhau $(P_i = P_j)$.
Điều kiện $P_i = P_j$ dẫn đến $e^{z_i} = e^{z_j}$, do đó $\quad z_i = z_j$
Vì $z_i = \theta_i^T x$ và $z_j = \theta_j^T x$, ranh giới quyết định được định nghĩa là tập hợp các điểm $x$ thỏa mãn phương trình tuyến tính sau:
$$(\theta_i - \theta_j)^T x = 0$$
Điều này có nghĩa là Softmax Regression tạo ra các ranh giới quyết định tuyến tính (linear decision boundaries) giữa các lớp.
Softmax Regression là bước phát triển hợp lý từ Logistic Regression, cung cấp một khuôn khổ vững chắc cho các nhiệm vụ phân loại đa lớp. Bằng cách kết hợp phép toán tuyến tính, hàm Softmax để chuẩn hóa xác suất, và hàm mất mát Cross-Entropy cùng Gradient Descent để tối ưu hóa, mô hình này là một nền tảng quan trọng trong Học máy, đặc biệt là trong các lớp đầu tiên của mạng nơ-ron sâu.
IV. PyTorch Framework
PyTorch là một Deep Learning Framework mã nguồn mở mạnh mẽ , được xây dựng dựa trên cấu trúc dữ liệu cốt lõi là Tensor—một dạng mảng đa chiều tương tự NumPy nhưng có khả năng vận hành hiệu quả trên GPU để tăng tốc tính toán. Sức mạnh đặc trưng của PyTorch nằm ở cơ chế Autograd (tự động tính đạo hàm) , cho phép hệ thống tự động theo dõi và tính toán gradient cho các biến số trong đồ thị tính toán, từ đó hỗ trợ đắc lực cho việc huấn luyện các mô hình học máy đa dạng từ hồi quy tuyến tính, logistic đến các mạng nơ-ron phân loại hình ảnh phức tạp thông qua các thuật toán tối ưu hóa như SGD.
1. Kiến trúc cơ bản của PyTorch
1.1. Tensor
Trong PyTorch, Tensor là cấu trúc dữ liệu nền tảng, đại diện cho sự tổng quát hóa toán học của số vô hướng (scalar), vectơ và ma trận thành các mảng nhiều chiều ($n$-dimensional arrays) để lưu trữ thông tin phức tạp như dữ liệu hình ảnh hay tham số mô hình. Mặc dù có giao diện tương đồng với mảng NumPy, Tensor vượt trội nhờ khả năng thực thi tính toán song song trên GPU và tích hợp sâu với cơ chế Autograd (tự động tính đạo hàm), cho phép thực hiện thuật toán lan truyền ngược (Backpropagation) để tối ưu hóa và huấn luyện các mạng nơ-ron sâu.
a. Cách tạo tensor trong PyTorch
import torch
data = [1, 2, 3]
data = torch.tensor(data)
print(data)
# OUTPUT
tensor([1, 2, 3])
b. Cơ chế broadcasting trong PyTorch Tensor
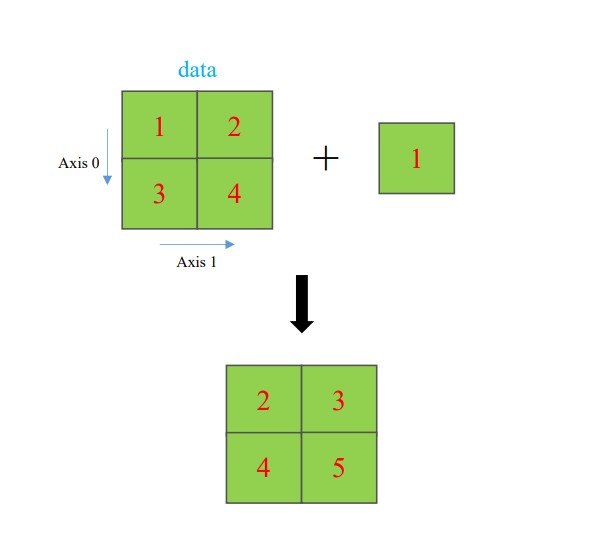
Hình ảnh minh họa cơ chế broadcasting trong ma trận
# broadcasting
import numpy as np
# create 2 tensors
tensor1 = torch.tensor([[1, 2],
[3, 4]])
tensor2 = torch.tensor([1])
print(f'Tensor1:\n {tensor1}')
print(f'Tensor2:\n {tensor2}')
# Addition between two tensors
tensor3 = tensor1 + tensor2
print(f'Tensor3:\n {tensor3}')
# OUTPUT
Tensor1:
tensor([[1, 2],
[3, 4]])
Tensor2:
tensor([1])
Tensor3:
tensor([[2, 3],
[4, 5]])
c. Các hàm quan trọng
- Squared Difference
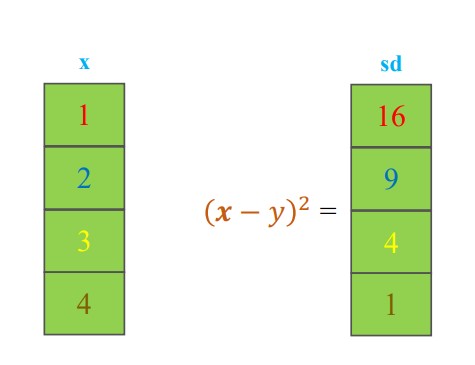
Hình ảnh minh họa phép tính Squared Difference trong ma trận
# Compute squared difference
import torch
# Create two tensors
x = torch.tensor([1.0, 2.0, 3.0, 4.0])
y = 5
# Compute squared difference
squared_diff = (x - y) ** 2
print(f'x:\n {x}')
print(f'y = {y}')
print(f'squared_diff:\n {squared_diff}')
# OUTPUT
x:
tensor([1., 2., 3., 4.])
y = 5
squared_diff:
tensor([16., 9., 4., 1.])
- Mean Squared Error
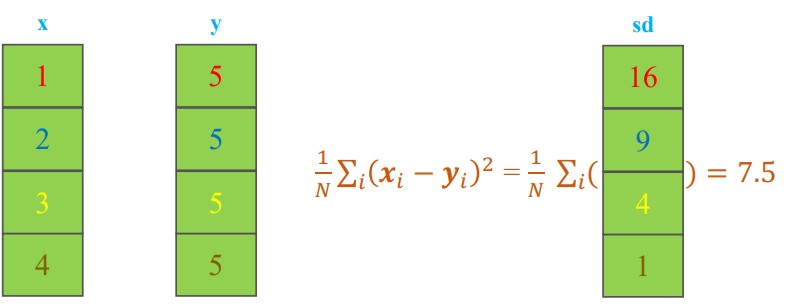
Hình ảnh minh họa phép tính Squared Difference trong ma trận
# Compute squared difference
import torch
# Create two tensors
x = torch.tensor([1.0, 2.0, 3.0, 4.0])
y = torch.tensor([5.0, 5.0, 5.0, 5.0])
# Compute squared difference
loss_fn = torch.nn.MSELoss()
mse = loss_fn(x,y)
print(f'x:\n {x}')
print(f'y = {y}')
print(f'mse:\n {mse}')
# OUTPUT
x:
tensor([1., 2., 3., 4.])
y = tensor([5., 5., 5., 5.])
mse:
7.5
- Tensor Concatenation
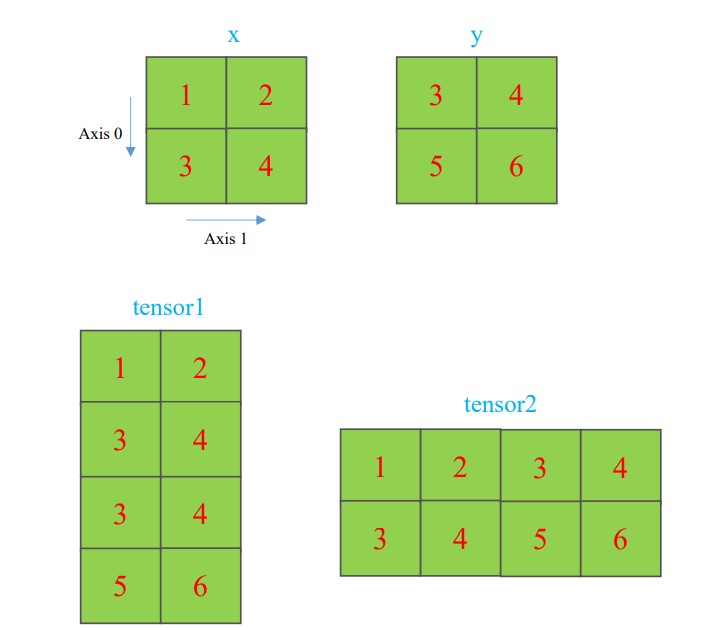
Hình ảnh minh họa phép ghép nối các ma trận
# Concatenate tensors
import torch
# Create two tensors
x = torch.tensor([[1, 2],
[3, 4]])
y = torch.tensor([[3, 4],
[5, 6]])
# Concat tensors along the first dim
tensor1 = torch.cat((x, y), dim=0)
print(f'Tensor1:\n {tensor1}')
# Concat tensors along the second dim
tensor2 = torch.cat((x, y), dim=1)
print(f'Tensor2:\n {tensor2}')
# OUTPUT
Tensor1:
tensor([[1, 2],
[3, 4],
[3, 4],
[5, 6]])
Tensor2:
tensor([[1, 2, 3, 4],
[3, 4, 5, 6]])
- Tìm chỉ số của giá trị lớn nhất (hoặc nhỏ nhất) trong PyTorch Tensor

Hình ảnh minh họa phép tìm chỉ số của giá trị lớn nhất trong ma trận tương ứng với theo cột và theo hàng
# argmax
import torch
# Creates a 3x2 tensor
data = torch.randint(low=0, high=9, size=(3, 2))
print(f'data:\n {data}')
# Compute argmax across the rows (dimension 0)
argmax_dim0 = torch.argmax(data, dim=0)
print(f'argmax1:\n {argmax_dim0}')
# Compute argmax across the columns (dimension 1)
argmax_dim1 = torch.argmax(data, dim=1)
print(f'argmax1:\n {argmax_dim1}')
# OUTPUT
data:
tensor([[1, 4],
[1, 2],
[3, 8]])
argmax1:
tensor([2, 2])
argmax1:
tensor([1, 1, 1])
1.2. Tính toán Gradient
a. Computational Graph (Đồ thị tính toán)
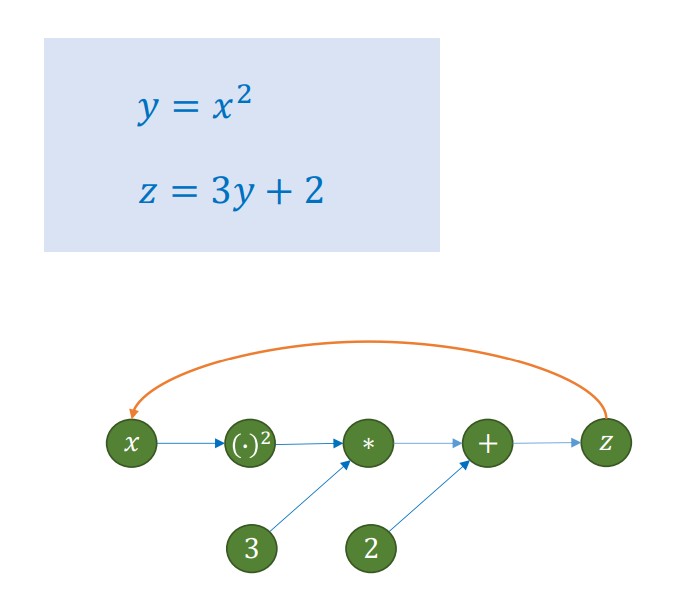
Computational Graph biểu diễn quá trình tính toán của một chuỗi các phép toán và cách đạo hàm (gradient) được truyền ngược về biến đầu vào
- Biểu diễn Toán học:
Biểu đồ minh họa hàm hợp $z = 3(x^2) + 2$, được phân rã thành chuỗi phép tính tuần tự: đầu tiên bình phương đầu vào ($y=x^2$), sau đó thực hiện biến đổi tuyến tính ($z=3y+2$).
- Cấu trúc Đồ thị Tính toán:
PyTorch mô hình hóa hàm số trên thành các nút (chứa dữ liệu hoặc toán tử) và hai luồng xử lý:
* Chiều xuôi (Forward - Mũi tên xanh): Dữ liệu chảy từ $x \rightarrow z$ để tính ra kết quả cuối cùng.
* Chiều ngược (Backward - Mũi tên cam): Hệ thống tự động đi ngược từ $z \rightarrow x$ thông qua Quy tắc chuỗi (Chain Rule) để tính đạo hàm ($\frac{dz}{dx} = 6x$), phục vụ cho việc tối ưu hóa mô hình.
b. Đoạn code thực hiện tính toán Gradient
# autograd
import torch
# Create a tensor to compute gradients
x = torch.tensor(2.0, requires_grad=True)
# operation
y = x ** 2
z = 3*y + 2
print(f'z: {z}')
# Backpropagate to compute gradients
z.backward()
# Print the gradient. dz/dx at x=2.0
print(f"Gradient of z w.r.t. x: {x.grad}")
# OUTPUT:
z: 14.0
Gradient of z w.r.t. x: 12.0
1.3. nn.Sequential()
a. Vai trò
nn.Sequential là một container (thùng chứa) cho phép đóng gói các lớp mạng nơ-ron theo một trình tự nhất định. Dữ liệu đầu vào sẽ tự động đi qua lần lượt các lớp được khai báo bên trong nó để tạo ra đầu ra .
b. Code minh họa
- Input: 3 đặc trưng | Output: 1 giá trị
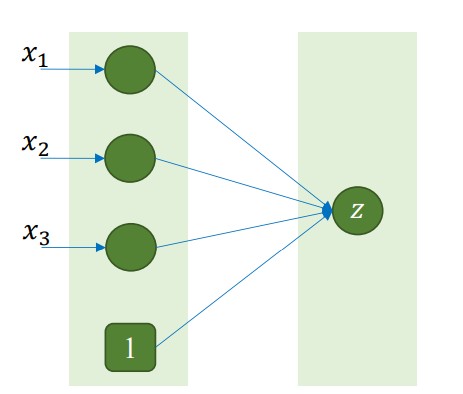
import torch.nn as nn
from torchsummary import summary
model = nn.Sequential(
nn.Linear(in_features=3, out_features=1)
)
summary(model, input_size=(3,))
# OUTPUT:
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 1] 4
================================================================
- Input: 4 đặc trưng | Output: 3 giá trị
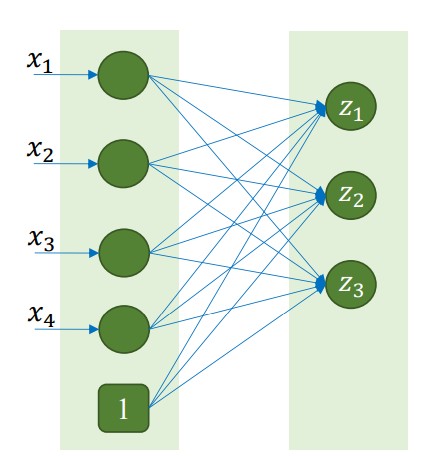
import torch.nn as nn
from torchsummary import summary
model = nn.Sequential(
nn.Linear(in_features=4, out_features=3)
)
summary(model, input_size=(4,))
# OUTPUT
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 3] 15
================================================================
2. Xây dựng mô hình
2.1. Linear Regression
a. Bài toán dự đoán giá 1 căn nhà dựa trên 1 đặc trưng đầu vào là diện tích của căn nhà đó
Cho dữ liệu sau:
| area | price |
|---|---|
| 6.7 | 9.1 |
| 4.6 | 5.9 |
| 3.5 | 4.6 |
| 5.5 | 6.7 |
Mô hình cho bài toán:
$$
price = w * area + b
$$
$$ \hat{y} = wx + b$$
Bài toán này yêu cầu dùng 1 đặc trưng đầu vào là area để dự đoán price. Vì vậy số lượng đặc trưng đầu vào và số lượng đặc trưng đầu ra đều là 1.
Hình ảnh minh họa cho mô hình bài toán này
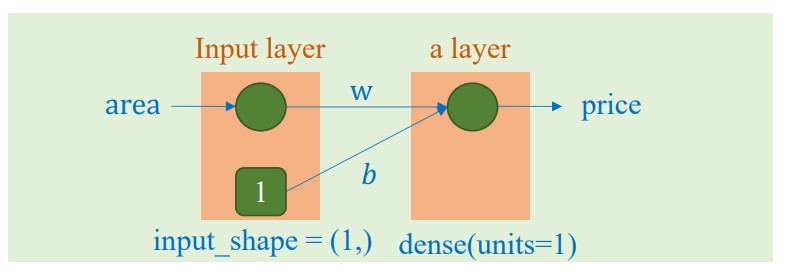
Đoạn code minh họa cách khởi tạo mô hình
import torch.nn as nn
from torchsummary import summary
model = nn.Sequential(
nn.Linear(in_features=1, out_features=1)
)
summary(model, input_size=(1,))
# OUTPUT
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 1] 2
================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
Từ kết quả của hàm summary(), ta có thể thấy số lượng tham số cần huấn luyện là 2, cụ thể là $w$ và $b$ như được minh họa trong hình ảnh.
b. Bài toán sử dụng dữ liệu quảng cáo để dự đoán doanh số bán hàng
Cho dữ liệu sau:
| TV | Radio | Newspaper | Sales |
|---|---|---|---|
| 230.1 | 37.8 | 69.2 | 22.1 |
| 44.5 | 39.3 | 45.1 | 10.4 |
| 17.2 | 45.9 | 69.3 | 12 |
| 151.5 | 41.3 | 58.5 | 16.5 |
Mô hình cho bài toán
$$\text{Sale} = w_1 * TV + w_2 * Radio + w_3 * Newspaper + b$$
Bài toán này yêu cầu dùng 3 đặc trưng đầu vào là dữ liệu quảng cáo từ TV, Radio và Newspaper để dự đoán Sales. Vì vậy số lượng đặc trưng đầu vào là 3 và số lượng đặc trưng đầu ra là 1.
Hình ảnh minh họa cho mô hình bài toán này
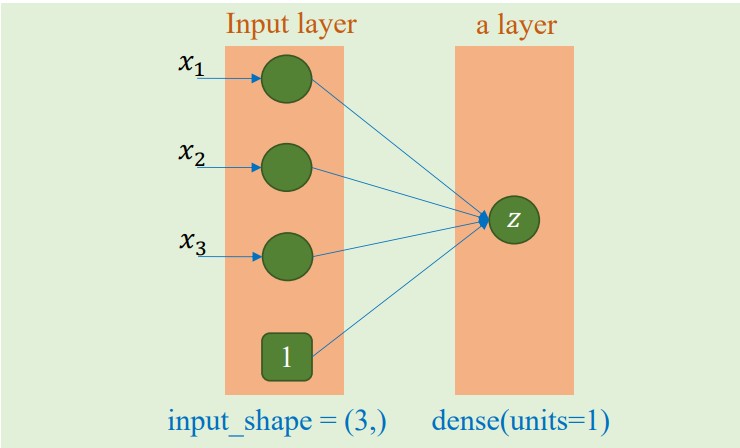
Đoạn code minh họa cách khởi tạo mô hình
import torch.nn as nn
from torchsummary import summary
model = nn.Sequential(
nn.Linear(in_features=3, out_features=1)
)
summary(model, input_size=(3,))
# OUTPUT
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 1] 4
================================================================
Total params: 4
Trainable params: 4
Non-trainable params: 0
Từ kết quả của hàm summary(), ta có thể thấy số lượng tham số cần huấn luyện là 4, cụ thể là $w_1$, $w_2$, $w_3$ và $b$ như được minh họa trong hình ảnh.
2.2. Logistic Regression
a. Bài toán phân loại hoa dựa trên độ dài cánh hoa
Cho dữ liệu sau:
| Petal_Length | Category |
|---|---|
| 1.4 | 0 |
| 1 | 0 |
| 1.5 | 0 |
| 3 | 1 |
| 3.8 | 1 |
| 4.1 | 1 |
Mô hình cho bài toán
$$ z = \theta^\top x $$
$$
\hat{y} = \frac{1}{1 + e^{-x}}
$$
Bài toán này yêu cầu dùng 1 đặc trưng đầu vào là độ dài cánh hoa để dự đoán loại hoa. Vì vậy số lượng đặc trưng đầu vào là 1 và số lượng đặc trưng đầu ra là 1.
Hình ảnh minh họa cho mô hình bài toán này
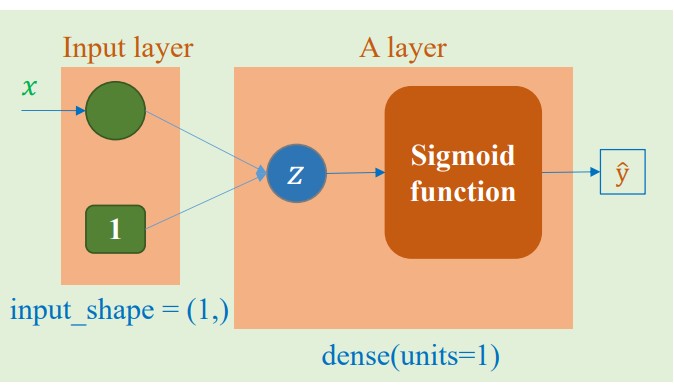
Đoạn code minh họa cách khởi tạo mô hình
import torch.nn as nn
from torchsummary import summary
model = nn.Sequential(
nn.Linear(in_features=1, out_features=1)
# don't include a sigmoid layer
)
summary(model, input_size=(1,))
# OUTPUT
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 1] 2
================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
Từ kết quả của hàm summary(), ta có thể thấy số lượng tham số cần huấn luyện là 2, tương ứng với 2 mũi tên chỉ đến $z$ như trong hình ảnh minh họa.
b. Bài toán phân loại hoa dựa trên độ dài và độ rộng cánh hoa
Cho dữ liệu sau:
| Petal_Length | Petal_Width | Category |
|---|---|---|
| 1.4 | 0.2 | 0 |
| 1 | 0.2 | 0 |
| 1.5 | 0.2 | 0 |
| 3 | 1.6 | 1 |
| 3.8 | 1.1 | 1 |
| 4.1 | 1.3 | 1 |
Mô hình cho bài toán
$$ z = \theta^\top x $$
$$
\hat{y} = \frac{1}{1 + e^{-x}}
$$
Bài toán này yêu cầu dùng 1 đặc trưng đầu vào là độ dài cánh hoa để dự đoán loại hoa. Vì vậy số lượng đặc trưng đầu vào là 1 và số lượng đặc trưng đầu ra là 1.
Hình ảnh minh họa cho mô hình bài toán này
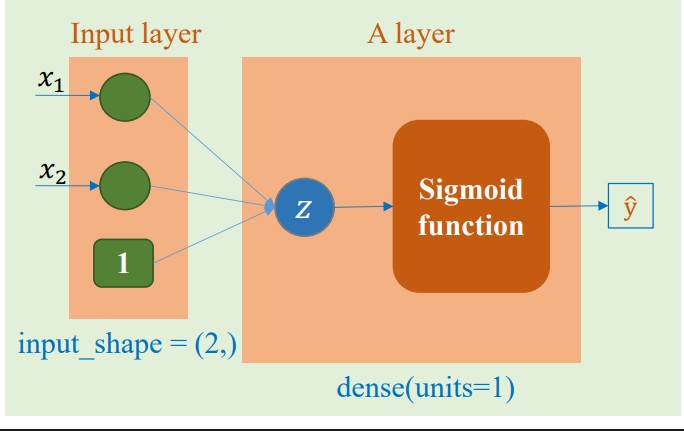
Đoạn code minh họa cách khởi tạo mô hình
import torch.nn as nn
from torchsummary import summary
model = nn.Sequential(
nn.Linear(in_features=2, out_features=1)
# don't include a sigmoid layer
)
summary(model, input_size=(2,))
# OUTPUT
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 1] 3
================================================================
Total params: 3
Trainable params: 3
Non-trainable params: 0
Từ kết quả của hàm summary(), ta có thể thấy số lượng tham số cần huấn luyện là 3, tương ứng với 3 mũi tên chỉ đến $z$ như trong hình ảnh minh họa.
2.3. Softmax Regression
a. Bài toán phân loại hoa vào 2 lớp dựa trên độ dài cánh hoa
Cho dữ liệu sau:
| Petal_Length | Category |
|---|---|
| 1.4 | 1 |
| 1 | 1 |
| 1.5 | 1 |
| 3 | 2 |
| 3.8 | 2 |
| 4.1 | 2 |
Mô hình cho bài toán:
$$ z_1 = xw_1 + b_1 $$
$$ z_2 = xw_2 + b_2 $$
$$ \hat{y_1} = \frac{e^{z_1}}{\sum_{i=1}^{2} e^{z_j}} $$
$$ \hat{y_2} = \frac{e^{z_2}}{\sum_{i=1}^{2} e^{z_j}} $$
Bài toán này yêu cầu dùng 1 đặc trưng đầu vào là độ dài cánh hoa để dự đoán loại hoa, với output là xác suất mà 1 hoa thuộc vào loại nào. Vì vậy số lượng đặc trưng đầu vào là 1 và số lượng đặc trưng đầu ra là 2, tương ứng với 2 loại hoa.
Hình ảnh minh họa cho mô hình bài toán này
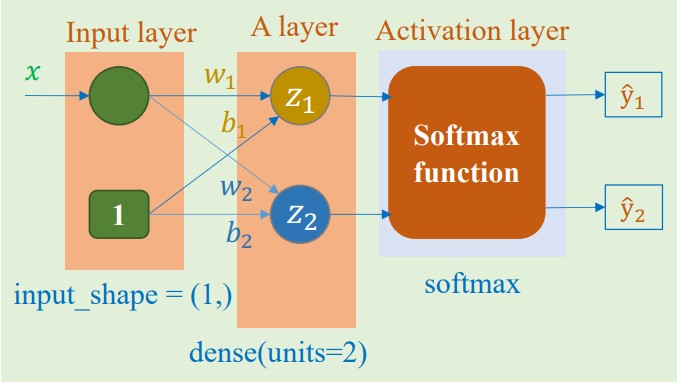
Đoạn code minh họa cách khởi tạo mô hình
import torch.nn as nn
from torchsummary import summary
model = nn.Sequential(
nn.Linear(in_features=1, out_features=2)
# don't include a sigmoid layer
)
summary(model, input_size=(1,))
# OUTPUT
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 2] 4
================================================================
Total params: 4
Trainable params: 4
Non-trainable params: 0
Từ kết quả của hàm summary(), ta có thể thấy số lượng tham số cần huấn luyện là 4, cụ thể là $w_1$, $b_1$, $w_2$ và $b_2$ như trong hình ảnh minh họa.
b. Bài toán phân loại hoa vào 3 lớp dựa trên độ dài cánh hoa
Cho dữ liệu sau:
| Petal_Length | Category |
|---|---|
| 1.4 | 1 |
| 1.3 | 1 |
| 1.5 | 1 |
| 4.5 | 2 |
| 4.1 | 2 |
| 4.6 | 2 |
| 5.2 | 3 |
| 5.6 | 3 |
| 5.9 | 3 |
Mô hình cho bài toán:
$$ z_1 = xw_1 + b_1 $$
$$ z_2 = xw_2 + b_2 $$
$$ z_3 = xw_3 + b_3 $$
$$ \hat{y_1} = \frac{e^{z_1}}{\sum_{i=1}^{3} e^{z_j}} $$
$$ \hat{y_2} = \frac{e^{z_2}}{\sum_{i=1}^{3} e^{z_j}} $$
$$ \hat{y_3} = \frac{e^{z_3}}{\sum_{i=1}^{3} e^{z_j}} $$
Bài toán này yêu cầu dùng 1 đặc trưng đầu vào là độ dài cánh hoa để dự đoán loại hoa, với output là xác suất mà 1 hoa thuộc vào loại nào. Vì vậy số lượng đặc trưng đầu vào là 1 và số lượng đặc trưng đầu ra là 3, tương ứng với 3 loại hoa.
Hình ảnh minh họa cho mô hình bài toán này
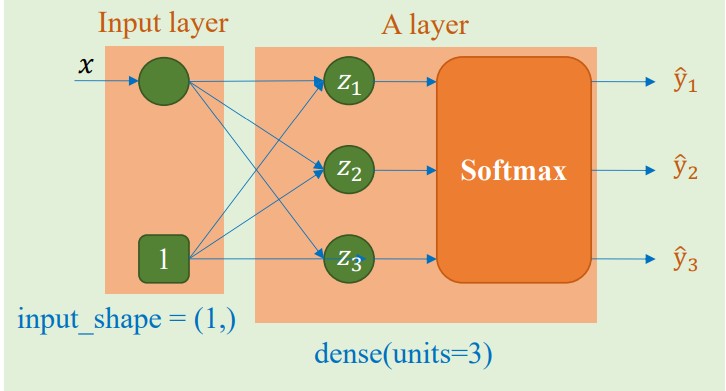
Đoạn code minh họa cách khởi tạo mô hình
import torch.nn as nn
from torchsummary import summary
model = nn.Sequential(
nn.Linear(in_features=1, out_features=3)
# don't include a sigmoid layer
)
summary(model, input_size=(1,))
# OUTPUT
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 3] 6
================================================================
Total params: 6
Trainable params: 6
Non-trainable params: 0
Từ kết quả của hàm summary(), ta có thể thấy số lượng tham số cần huấn luyện là 6, cụ thể là $w_1$, $b_1$, $w_2$, $b_2$, $w_3$ và $b_3$ tương ứng với 6 mũi tên trong hình ảnh minh họa.
3. Quy trình huấn luyện và suy luận (Training and Inference)
Quá trình tối ưu hóa tham số trong các mô hình hồi quy được thực hiện thông qua một quy trình lặp (iterative process) bao gồm bốn giai đoạn cốt lõi:
i. Lan truyền xuôi (Forward Propagation): Thực hiện tính toán giá trị dự đoán $\hat{y}$ thông qua việc ánh xạ dữ liệu đầu vào $x$ qua hàm giả thuyết (hypothesis function) của mô hình.
ii. Đánh giá Hàm mục tiêu (Loss Function Evaluation): Lượng hóa sai số giữa giá trị dự đoán $\hat{y}$ và nhãn thực tế $y$. Việc lựa chọn hàm mất mát phụ thuộc vào đặc thù của bài toán tối ưu:
- Sử dụng Mean Squared Error (MSE) cho Hồi quy Tuyến tính.
- Sử dụng Binary Cross-Entropy cho Hồi quy Logistic.
- Sử dụng Categorical Cross-Entropy cho Hồi quy Softmax.
iii. Lan truyền ngược (Backward Propagation): Tính toán vector gradient (đạo hàm riêng) của hàm mất mát đối với từng tham số trong mô hình, sử dụng quy tắc chuỗi (chain rule).
iv. Cập nhật Tham số (Parameter Update): Điều chỉnh các trọng số và hệ số chệch (weights and biases) dựa trên giá trị gradient đã tính toán và tốc độ học (learning rate), thường thông qua thuật toán Gradient Descent hoặc các biến thể của nó nhằm cực tiểu hóa hàm mất mát.
3.1. Logistic Regression
a. Nhắc lại các bước huấn luyện trong bài toán Logistic Regression
| Bước | Công thức cần thiết |
|---|---|
| Forward Propagation | $z = \theta\top x$ $\hat{y} = \sigma(z) = \frac{1}{1 + e^{-z}}$ |
| Loss Function Evaluation | $L(\theta) = -y\top log\hat{y} - (1-y)\top log(1-\hat{y})$ |
| Backward Propagation | $ \frac{\partial{L}}{\partial{\theta}} = x\top (\hat{y} - y) $ |
| Parameter Update | $\theta = \theta - \eta \frac{\partial{L}}{\partial{\theta}}$ |
b. Đoạn code sử dụng PyTorch để thực hiện các bước trên
Cài đặt thư viện và bộ dữ liệu
Trong ví dụ này ta sẽ dùng data sau:
| Petal_Length | Petal_Width | Category |
|---|---|---|
| 1.4 | 0.2 | 0 |
| 1.5 | 0.2 | 0 |
| 3 | 1.6 | 1 |
| 4.1 | 1.3 | 1 |
Bộ data này được lưu trong file iris_1D_2c.csv
import numpy as np
import torch
import torch.nn as nn
### Data preparation
data = np.genfromtxt('iris_2D_demo.csv', delimiter=',', skip_header=1)
X = torch.from_numpy(data[:,0:2]).float()
y = torch.from_numpy(data[:,2:]).float()
print('X\n', X)
print('y\n', y)
# OUTPUT
X
tensor([[1.4000, 0.2000],
[1.5000, 0.2000],
[3.0000, 1.1000],
[4.1000, 1.3000]])
y
tensor([[0.],
[0.],
[1.],
[1.]])
Huấn luyện mô hình
# Create fully connected layer
linear = nn.Linear(2, 1)
# Define loss function and optimization technique
loss_fn = torch.nn.BCELoss()
optimizer = torch.optim.SGD(linear.parameters(),
lr=0.1) # Stochastic gradient descent
epochs = 2000
# training
losses = []
for epoch in range(epochs):
# Forward Propagation: compute y_hat
y_hat = torch.sigmoid(linear(X))
# Loss Function Evaluation
loss = loss_fn(y_hat, y)
losses.append(loss.item())
# Backward Propagation
optimizer.zero_grad()
loss.backward()
# Parameter Update
optimizer.step()
Kết quả
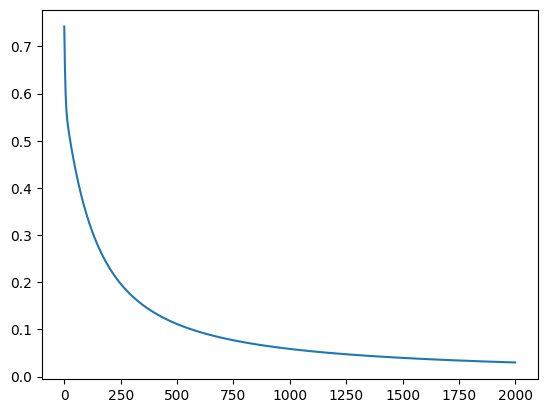
3.2. Softmax Regression
a. Nhắc lại các bước huấn luyện trong bài toán Logistic Regression
| Bước | Công thức cần thiết |
|---|---|
| Forward Propagation | $z = \theta\top x$ $\hat{y} = \sigma(z) = \frac{e^{z}}{\sum_{i=1}^{k} e^{z_i}}$ |
| Loss Function Evaluation | $L(\theta) = -\sum_{i=1}^{k} y_ilog\hat{y_i}$ |
| Backward Propagation | $ \frac{\partial{L}}{\partial{\theta}} = x (\hat{y_i} - y_i) $ |
| Parameter Update | $\theta = \theta - \eta \frac{\partial{L}}{\partial{\theta}}$ |
b. Đoạn code sử dụng PyTorch để thực hiện các bước trên
Cài đặt thư viện và bộ dữ liệu
Trong ví dụ này ta sẽ dùng data sau:
| Petal_Length | Category |
|---|---|
| 1.4 | 0 |
| 1.3 | 0 |
| 1.5 | 0 |
| 4.5 | 1 |
| 4.1 | 1 |
| 4.6 | 1 |
Bộ data này được lưu trong file iris_1D_2c.csv
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
# Load data
iris = np.genfromtxt('/content/iris_1D_2c.csv', dtype=None, delimiter=',', skip_header=1)
X = torch.tensor(iris[:, 0:1], dtype=torch.float32)
y = torch.tensor(iris[:, 1], dtype=torch.int64)
Huấn luyện mô hình
class SoftmaxRegression(nn.Module):
def __init__(self, input_dim, output_dim):
super(SoftmaxRegression, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
# set value (for illustration)
self.linear.weight.data = torch.Tensor([[0.2], [-0.1]])
self.linear.bias.data = torch.Tensor([0.1, 0.05])
def forward(self, x):
return self.linear(x)
input_dim = X.shape[1]
output_dim = len(torch.unique(y))
model = SoftmaxRegression(input_dim, output_dim)
# Loss and optimizer
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
# Training loop
max_epoch = 5
for epoch in range(max_epoch):
for i in range(X.shape[0]):
xi = X[i].unsqueeze(0)
yi = y[i].unsqueeze(0)
print(f'xi: {xi}')
print(f'yi: {yi}')
# Zero the gradients
optimizer.zero_grad()
# Forward Propagation: compute y_hat
outputs = model(xi)
print(f'outputs: {outputs.data}')
# Loss Function Evaluation
loss = criterion(outputs, yi)
print(f'loss: {loss}')
# Backward Propagation
loss.backward()
# Parameter Update
optimizer.step()
break
V. Kết luận
Tổng kết lại, sự phát triển từ Hồi quy Tuyến tính đến Hồi quy Logistic và Softmax không đơn thuần là sự thay đổi về công thức, mà đại diện cho một bước chuyển đổi tư duy quan trọng: từ việc xấp xỉ hình học các giá trị thực sang việc ước lượng phân phối xác suất có điều kiện. Việc xác lập hàm Sigmoid và Softmax, kết hợp với hàm mục tiêu Cross-Entropy, đã giải quyết triệt để bài toán tối ưu hóa trong không gian phân loại, đảm bảo tính lồi của hàm mất mát và sự hội tụ hiệu quả của thuật toán Gradient Descent.
Bên cạnh đó, việc làm chủ PyTorch thông qua các khái niệm cốt lõi như Tensor và Computational Graph (Đồ thị tính toán) cung cấp một nền tảng kỹ thuật vững chắc để triển khai các mô hình này. Sự kết hợp giữa tính chặt chẽ của toán học thống kê và khả năng tính toán mạnh mẽ của các framework hiện đại chính là tiền đề thiết yếu để tiếp cận các kiến trúc phức tạp hơn trong Deep Learning, như Mạng Nơ-ron Tích chập (CNN) hay các mô hình Transformer trong những nghiên cứu tiếp theo.
VI. Reference
[1] Các hình ảnh và code được tham khảo từ slide và bài tập của tài liệu AIO2025, Module 06
Chưa có bình luận nào. Hãy là người đầu tiên!