Giới thiệu

Chào mừng các bạn đến với blog kỹ thuật của team chúng tôi!

Trong thế giới Trí tuệ Nhân tạo và Học máy, việc xây dựng một mô hình có độ chính xác cao mới chỉ là bước khởi đầu. Để thực sự tạo ra giá trị, chúng ta cần hiểu rõ tại sao mô hình đưa ra quyết định đó và làm thế nào để vận hành nó một cách bền vững trong môi trường thực tế.

Bài viết này là một hành trình khám phá toàn diện, được thiết kế để dẫn dắt bạn đi qua ba trụ cột cốt lõi của Khoa học Dữ liệu ứng dụng: từ việc xây dựng mô hình nền tảng, giải mã cơ chế hoạt động, cho đến việc triển khai và vận hành chuyên nghiệp.

Bố cục hành trình

Chúng tôi đã cấu trúc nội dung blog theo một lộ trình học tập có chủ đích, giúp bạn đọc dễ dàng kết nối các khái niệm từ cơ bản đến nâng cao:

1. Phần 1 (Mục I - VI): Xây dựng Nền tảng – Linear Regression
   Chúng tôi bắt đầu với "viên gạch đầu tiên" của mọi mô hình học máy: Hồi quy tuyến tính. Phần này không chỉ dừng lại ở các khái niệm làm quen (Warm-up) và lý thuyết về các hàm mất mát như MSE và MAE, mà còn đi sâu vào kỹ thuật tối ưu hóa hiệu suất tính toán thông qua Numpy và Vectorization – chìa khóa để xử lý dữ liệu lớn.

2. Phần 2 (Mục VII - VIII): Giải mã Hộp đen – Explainable AI (XAI)
   Một khi mô hình đã được xây dựng, làm thế nào chúng ta có thể tin tưởng vào quyết định của nó? Phần này sẽ giới thiệu về XAI (AI có thể giải thích), tập trung vào hai giải thuật hàng đầu là LIME và ANCHOR. Đây là những công cụ mạnh mẽ giúp chúng ta "nhìn thấu" bên trong các mô hình phức tạp, tăng cường tính minh bạch và độ tin cậy.

3. Phần 3 (Mục IX - X): Vận hành Chuyên nghiệp – MLOps
   Từ mô hình nghiên cứu đến một sản phẩm AI phục vụ hàng triệu người dùng là một thách thức khổng lồ về kỹ thuật. Phần cuối cùng này đi vào các khái niệm MLOps thiết yếu, bao gồm Quản lý phiên bản dữ liệu (Data Version Control) để đảm bảo tính tái lập, và cách phục vụ dữ liệu hiệu suất cao (Serving Data) bằng công cụ Feast.

Đội ngũ thực hiện

Dự án này là thành quả nỗ lực chung của tất cả các thành viên trong team. Dưới đây là sự phân công chi tiết cho từng nội dung mà các bạn sẽ đọc:

I. W1 - Linear Regression (Warm-up) (bạn Tuấn)
II. W1 - A Bridge to Linear Regression (bạn Tuấn)
III. W1 - Linear Regression (MSE and MAE) (bạn Thịnh)
IV. W2 - Linear Regression (Numpy) (bạn Thịnh)
V. W2 - Vectorization for Linear Regression (bạn Quang - Nhóm trưởng)
VI. W2 - Loss Functions for Linear Regression (bạn Quang)
VII. W1 - (XAI) Giải thuật LIME (bạn Trà)
VIII. W2 - (XAI) Giải thuật ANCHOR (bạn Trà)
IX. W1 - (MLOps) Data Version Control (bạn Tâm)
X. W2 - (MLOps) Serving Data Using Feast (bạn Tâm)

Chúng tôi hy vọng rằng hành trình kiến thức này sẽ mang lại cho các bạn những góc nhìn sâu sắc và hữu ích. Mời các bạn bắt đầu khám phá nội dung chi tiết ngay sau đây!

I. Linear Regression

---

1) Linear Regression là gì?

Linear Regression (Hồi quy tuyến tính) là một trong những thuật toán học máy (Machine Learning) cơ bản và được sử dụng rộng rãi nhất. Nó thuộc nhóm Học có giám sát (Supervised Learning) và được dùng cho các bài toán Hồi quy (Regression), tức là dự đoán một biến mục tiêu liên tục dựa trên một hoặc nhiều biến đầu vào.

Mục tiêu chính của Linear Regression là tìm ra một mối quan hệ tuyến tính giữa biến đầu vào (biến độc lập) $x$ và biến đầu ra (biến phụ thuộc) $y$ bằng cách vẽ một đường thẳng (hoặc một mặt phẳng/siêu phẳng trong không gian nhiều chiều) phù hợp nhất với dữ liệu.

Ví dụ ứng dụng thực tế:
- Dự đoán giá nhà theo diện tích, vị trí, số phòng ngủ…
- Dự đoán doanh thu theo ngân sách quảng cáo.
- Dự đoán tiền lương của nhân viên dựa trên số năm kinh nghiệm của họ.

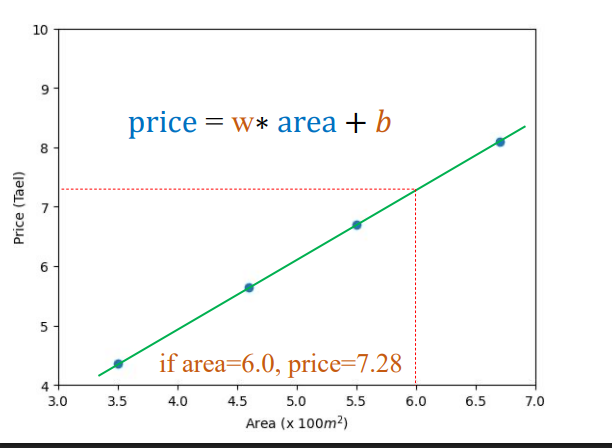
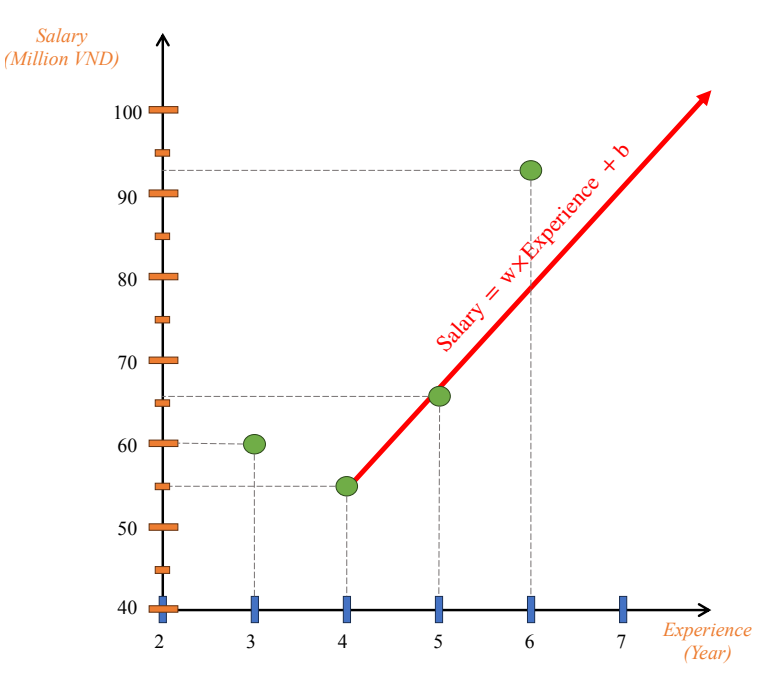
Hình 1: ví dụ về dự đoán giá nhà (hình bên trái) và dự đoán mức lương (hình bên phải) [1].

---

2) Simple Linear Regression (1 biến)

$$ \hat{y} \approx w x + b $$

• (x): giá trị các biến đầu vào
• (w): trọng số (mức ảnh hưởng của từng biến)
• (b): bias (độ lệch)
• (y): giá trị thực tế
• $\hat{y}$: giá trị mô hình dự đoán

Ta có thể thấy với mỗi cặp ($w$, $b$) khác nhau sẽ cho ra một dự đoán khác nhau. Vì thế mục tiêu là tìm ra bộ hệ số tối ưu ($w$, $b$) sao cho $\hat{y}$ gần với giá trị thực tế $y$ nhất.
Bộ hệ số tối ưu ($w$, $b$) tức là khoảng cách từ các điểm dữ liệu đến đường thẳng phải là ngắn nhất. Trong đó, ta sẽ tạm gọi chênh lệch theo trục tung là error và tổng bình phương sai số là loss (tạm dịch: hàm mất mát).

Với x là dữ liệu đầu vào nên sẽ không thay đổi được, ta chỉ có thể thay đổi 2 giá trị w và b để khiến loss giảm đi, sau đây là 2 hình ảnh trực quan cho các đường thẳng với các giá trị w và b khác nhau (được thay đổi theo một hướng tích cực) và giá trị loss tương ứng với đường thẳng đó:

---

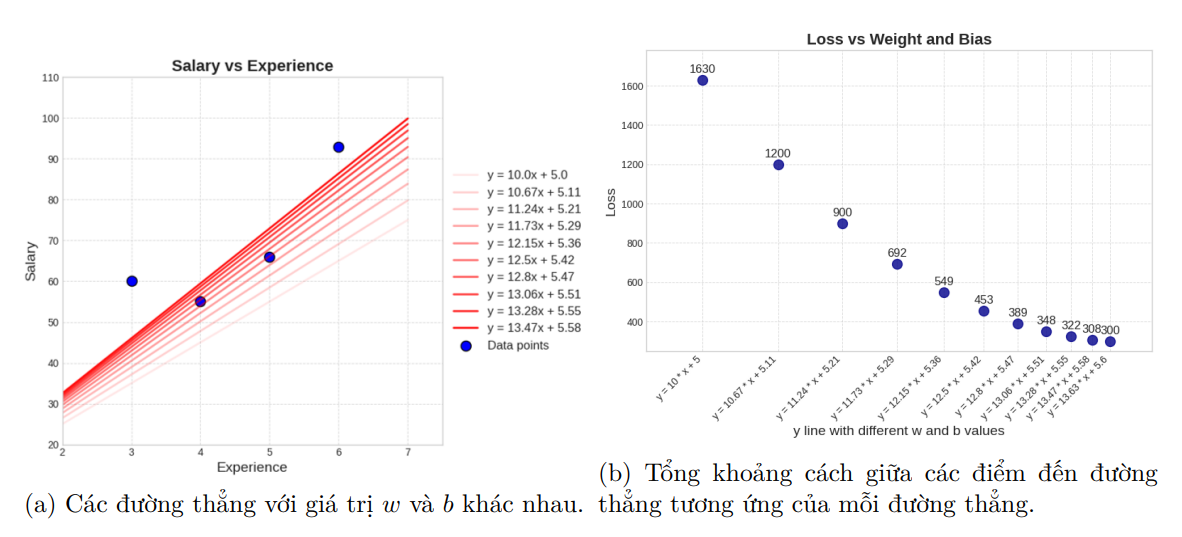
4) Cách tối ưu hóa các tham số (Optimization)

Mục tiêu của việc tối ưu các tham số $w$ và $b$ trong Hồi quy Tuyến tính Đơn giản (Simple Linear Regression) là để tìm ra một đường thẳng tối ưu nhất, tức là đường thẳng có khả năng dự đoán chính xác nhất, làm cho hàm mất mát (loss function) đạt giá trị nhỏ nhất. Quá trình này được thực hiện bằng cách sử dụng công cụ tối ưu hóa dựa trên đạo hàm, hay còn gọi là Gradient Descent.

4.1. Nền tảng: Mục tiêu và Hàm Mất Mát (Loss Function)

Đường thẳng dự đoán trong Hồi quy Tuyến tính có phương trình là $\hat{y} = f(x) = wx + b$.

• Tham số cần tối ưu:
  • $w$: Hệ số góc / Trọng số (weight).
  • $b$: Tung độ gốc / Độ chệch (bias).
• Hàm Mất Mát (Loss Function): Để đánh giá mức độ phù hợp của đường thẳng, ta sử dụng hàm mất mát $L$, thường là hàm Sai số Bình phương (Squared Error), đo lường sự chênh lệch giữa giá trị dự đoán ($\hat{y}_i$) và giá trị thực tế ($y_i$).
  • Mất mát tại một mẫu dữ liệu $i$: $L_i = (\hat{y}_i - y_i)^2$.
• Mục tiêu: Thay đổi $w$ và $b$ để làm giảm giá trị loss, cho đến khi $w$ và $b$ tạo ra đường thẳng tối ưu nhất và loss đạt giá trị nhỏ nhất.

4.2. Ý tưởng Tối ưu hóa: Gradient Descent (Sử dụng Đạo hàm)

Đạo hàm (Derivative) là công cụ toán học được sử dụng để tối ưu hóa.

1. Tính chất của Đạo hàm: Đạo hàm tại một điểm cho biết thông tin về độ dốc của hàm số tại điểm đó.
   • Nếu giá trị đạo hàm dương ($\frac{dJ}{d\theta} > 0$), hàm số đang tăng tại điểm đó.
   • Nếu giá trị đạo hàm âm ($\frac{dJ}{d\theta} < 0$), hàm số đang giảm tại điểm đó.
2. Nguyên tắc di chuyển: Trong bài toán tối ưu, hàm mất mát (loss) thường có dạng parabol (khi xét riêng $w$ hoặc $b$) và có một điểm cực tiểu. Để tiến đến điểm cực tiểu này (nơi loss nhỏ nhất), ta cần di chuyển ngược hướng với đạo hàm (hoặc gradient).
   • Ví dụ, nếu đạo hàm dương (hàm đang tăng), ta cần đi sang trái (giảm giá trị tham số).

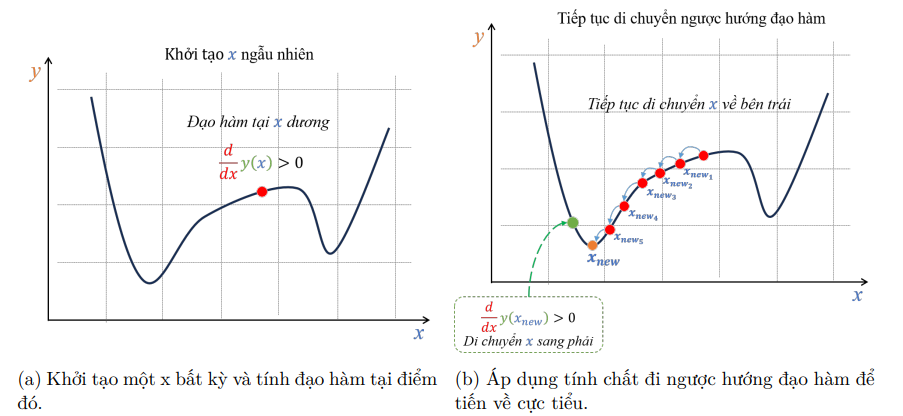
3. Công thức Cập nhật (General Update Rule): Việc cập nhật tham số ($\theta$) được thực hiện theo công thức chung:
   $$\theta_{\text{new}} = \theta_{\text{old}} - \eta \frac{\partial J(\theta_{\text{old}})}{\partial \theta}$$
   Trong đó, $\eta$ (eta) là hệ số học (learning rate), quyết định độ lớn của bước di chuyển.

4.3. Quy trình Tổng quát để Tối ưu $w$ và $b$

Toàn bộ quá trình tối ưu (Gradient Descent) để tìm $w$ và $b$ tối ưu bao gồm các bước lặp lại sau:

Bước 1: Khởi tạo

Khởi tạo ngẫu nhiên giá trị ban đầu cho hai tham số $w$ và $b$.
* Ví dụ minh họa: Giả sử khởi tạo $w = 10, b = 5$ và hệ số học $\eta = 0.01$.

Bước 2: Lặp qua từng Mẫu dữ liệu (Loop over samples)

Với mỗi mẫu dữ liệu thứ $i$ có đầu vào $x_i$ (kinh nghiệm) và đầu ra thực tế $y_i$ (tiền lương), ta thực hiện các bước sau:

2.a. Tính Output ($\hat{y}_i$)

Sử dụng phương trình đường thẳng hiện tại để dự đoán giá trị đầu ra:
$$\hat{y}_i = f(x_i) = w x_i + b$$
* Ví dụ (Mẫu 0: $x_0=3, y_0=60$): $\hat{y}_0 = 10 \times 3 + 5 = 35$.

2.b. Tính Loss ($L_i$)

Tính sự chênh lệch giữa giá trị dự đoán và giá trị thực tế bằng hàm Squared Error:
$$L(\hat{y}_i, y_i) = (\hat{y}_i - y_i)^2$$
* Ví dụ: $L_0 = (35 - 60)^2 = 625$.

2.c. Tính Đạo hàm Riêng (Gradient)

Tính đạo hàm riêng của hàm mất mát $L$ theo từng tham số $w$ và $b$ để xác định hướng đi và độ dốc cần thiết để giảm loss.
* Đạo hàm theo $b$ ($\frac{\partial L}{\partial b}$):
$$\frac{\partial L}{\partial b} = 2(\hat{y}_i - y_i)$$
* Ví dụ: $\frac{\partial L}{\partial b} = 2 \times (35 - 60) = -50$.
* Đạo hàm theo $w$ ($\frac{\partial L}{\partial w}$):
$$\frac{\partial L}{\partial w} = 2x_i(\hat{y}_i - y_i)$$
* Ví dụ: $\frac{\partial L}{\partial w} = 2 \times 3 \times (35 - 60) = -150$.

2.d. Cập nhật Tham số (Update Parameters)

Áp dụng công thức cập nhật tham số bằng cách di chuyển ngược hướng gradient, nhân với hệ số học $\eta$:

• Cập nhật $w$:
  $$w_{\text{new}} = w - \eta \frac{\partial L}{\partial w}$$
  • Ví dụ: $w_{\text{new}} = 10 - 0.01 \times (-150) = 11.5$.
• Cập nhật $b$:
  $$b_{\text{new}} = b - \eta \frac{\partial L}{\partial b}$$
  • Ví dụ: $b_{\text{new}} = 5 - 0.01 \times (-50) = 5.5$.

Bước 3: Lặp lại

Lặp lại Bước 2 cho đến khi xử lý hết tất cả các mẫu dữ liệu trong bộ dữ liệu. Sau khi hoàn thành một lượt duyệt qua tất cả các mẫu, ta thu được các giá trị $w$ và $b$ đã được điều chỉnh. Quá trình này sẽ được lặp lại nhiều lần (epochs) cho đến khi mô hình đạt được sự tối ưu.

Việc cập nhật lặp đi lặp lại đảm bảo rằng các tham số $w$ và $b$ dần dần được điều chỉnh để giảm thiểu tổng mất mát trên toàn bộ dữ liệu, giúp đường thẳng dự đoán (mô hình) trở nên phù hợp hơn.

---

5) Code ví dụ (sklearn)

✅ Chuẩn bị dữ liệu giả lập: dự đoán giá nhà

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split, KFold, cross_val_score
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
import matplotlib.pyplot as plt
rng = np.random.RandomState(42)

n = 1200
size_m2     = rng.normal(70, 20, n).clip(20, 200)
bedrooms    = rng.randint(1, 6, n)
age_years   = np.abs(rng.normal(15, 10, n)).clip(0, 80)
is_center   = rng.binomial(1, 0.35, n)
distance_km = rng.exponential(3, n).clip(0.2, 25)

price = (
    0.9 * size_m2
  + 15  * bedrooms
  - 0.5 * age_years
  + 40  * is_center
  - 1.8 * distance_km
  + rng.normal(0, 15, n)
)

df = pd.DataFrame({
    "size_m2": size_m2,
    "bedrooms": bedrooms,
    "age_years": age_years,
    "is_center": is_center,
    "distance_km": distance_km,
    "price_k": price
})

df.head()

---

Reference

---

II. A Bridge to Linear Regression

1) Mục tiêu và Dữ liệu cơ bản

Mục tiêu chính của các slide này là giới thiệu các khái niệm Tối ưu hóa (Optimization) và Giải quyết vấn đề (Problem Solving) để tiến tới Hồi quy Tuyến tính (Towards Linear Regression).

1.1 Khái niệm Feature và Label

Trong học máy, chúng ta làm việc với dữ liệu có hai thành phần chính:
* Feature (Đặc trưng): Là các yếu tố đầu vào được sử dụng để dự đoán.
* Label (Nhãn): Là giá trị đầu ra mà chúng ta muốn dự đoán.

1.2 Ví dụ về Dữ liệu

• Dữ liệu giá nhà (House price data): Feature là diện tích (area), Label là giá (price).
  • Ví dụ: Nếu $\text{area} = 6.0$, $\text{price} = ?$.
  • Mô hình dự đoán đơn giản có thể là: $\text{price} = w \times \text{area} + b$.
• Dữ liệu Quảng cáo (Advertising data): Các Feature có thể là chi phí quảng cáo trên TV, Radio, và Báo chí (Newspaper).
  • Ví dụ: Nếu $\text{TV}=55.0$, $\text{Radio}=34.0$, và $\text{Newspaper}=62.0$, $\text{price}=?$.

1.3 Bài toán dự đoán

Mục tiêu là tìm ra các tham số $w$ và $b$ phù hợp nhất. Ví dụ, chúng ta có thể có nhiều mô hình khác nhau: $\text{price} = w_1 \times \text{area} + b_1$, $\text{price} = w_2 \times \text{area} + b_2$, v.v..

---

2) Đạo hàm (Derivative)

Đạo hàm là công cụ toán học nền tảng được sử dụng trong tối ưu hóa.

2.1 Định nghĩa và Ý nghĩa

• Đạo hàm đại diện cho độ dốc (slope) của hàm số.
• Công thức định nghĩa đạo hàm của hàm liên tục $f(x)$ là:
  $$\frac{d}{dx} f(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$$.
• Ý nghĩa: Để đạo hàm thể hiện chính xác độ dốc tại điểm $x$, khoảng cách $\Delta x$ cần tiến về 0, để đường tiếp tuyến tiến về hàm $f(x)$ trong vùng lân cận tại $x$.
• Các ký hiệu phổ biến cho đạo hàm bao gồm $dy/dx$, $y'$, và $f'(x)$.

2.2 Ví dụ về Đạo hàm

• Đạo hàm của hàm bình phương: $f(x) = x^2$.
  • Áp dụng công thức giới hạn: $\frac{d}{dx} f(x) = \lim_{\Delta x \to 0} \frac{(x + \Delta x)^2 - x^2}{\Delta x} = \lim_{\Delta x \to 0} \frac{2x\Delta x + (\Delta x)^2}{\Delta x} = 2x$.
• Đạo hàm của $f(x) = kx$: $f'(x) = k$.
• Đạo hàm của $f(x) = 1/x$: $f'(x) = -1/x^2$.
• Đạo hàm của $f(x) = \sqrt{x}$: $f'(x) = 1 / (2\sqrt{x})$.

---

3) Tối ưu hóa và Gradient Descent

Trong học máy, tối ưu hóa (Optimization) được sử dụng để tìm các tham số ($w, b$) của mô hình sao cho hàm chi phí (Loss function) đạt giá trị nhỏ nhất (minimum).

3.1 Mục tiêu Tối ưu hóa

Cho một hàm $f(x)$, mục tiêu là tìm giá trị $x_{optimal}$ sao cho $f(x_{optimal})$ là nhỏ nhất. Tương tự, với hàm 2 chiều $f(x, y)$, tìm cặp $(x_{optimal}, y_{optimal})$ sao cho $f(x_{optimal}, y_{optimal})$ nhỏ nhất.

3.2 Phương pháp Gradient Descent (Sự Giảm Gradient)

Gradient Descent là kỹ thuật tối ưu hóa dựa trên đạo hàm. Nó hoạt động theo nguyên tắc sau:
1. Khởi tạo giá trị ban đầu cho tham số (ví dụ $x$).
2. Tính đạo hàm (gradient) tại điểm hiện tại.
3. Di chuyển tham số theo hướng ngược lại với đạo hàm (Move opposite of $dx$).

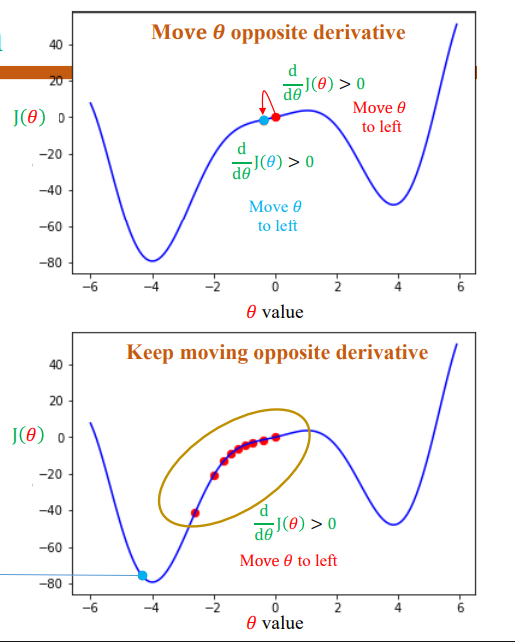
3.3 Ý nghĩa của việc di chuyển ngược hướng đạo hàm

• Đạo hàm cho biết độ dốc. Nếu đạo hàm $\frac{d}{d\theta} J(\theta)$ là dương ($> 0$), hàm số đang tăng, vì vậy ta cần di chuyển $\theta$ sang trái để giảm giá trị $J(\theta)$.
• Nếu đạo hàm $\frac{d}{d\theta} J(\theta)$ là âm ($< 0$), hàm số đang giảm, ta cần di chuyển $\theta$ sang phải (ngược hướng) để tiếp tục giảm cho đến khi đạt cực tiểu.

3.4 Công thức cập nhật

Việc cập nhật tham số (ví dụ $x$) trong Gradient Descent được thực hiện bằng công thức:
$$x_{new} = x_{old} - \eta f'(x_{old})$$.
Trong đó:
* $\eta$ (eta) là tốc độ học tập (Learning Rate).
* $f'(x_{old})$ là đạo hàm tại $x_{old}$.

3.5 Ví dụ Tối ưu hóa 1D ($f(x) = x^2$)

Giả sử ta muốn tìm cực tiểu của $f(x) = x^2$ trong khoảng $-100 \le x \le 100$.
* Đạo hàm: $f'(x) = 2x$.
* Khởi tạo: $x_0 = 70.0$, $\eta = 0.1$.
* Lần 1: $f'(x_0) = 140.0$.
* $x_1 = x_0 - \eta f'(x_0) = 70.0 - 0.1 \times 140.0 = 56.0$.
* Lần 2: $f'(x_1) = 112.0$.
* $x_2 = 56.0 - 0.1 \times 112.0 = 44.8$.
Quá trình này lặp lại, giá trị $x$ sẽ dần tiến về 0 (điểm cực tiểu).

3.6 Tối ưu hóa Hàm 2D ($f(x, y) = x^2 + y^2$)

Khi có nhiều tham số (ví dụ $x$ và $y$), chúng ta sử dụng đạo hàm riêng (partial derivatives):
* Cập nhật $x$: $x = x - \eta \frac{\partial f(x, y)}{\partial x}$.
* Cập nhật $y$: $y = y - \eta \frac{\partial f(x, y)}{\partial y}$.

Sau mỗi lần cập nhật, giá trị của hàm mục tiêu sẽ không lớn hơn giá trị trước đó, tức là $f(x_{new}, y_{new}) \le f(x_{old}, y_{old})$.

---

4) Đạo hàm Hàm hợp và Quy tắc Chuỗi (Chain Rule)

Quy tắc Chuỗi được sử dụng khi tính đạo hàm của một hàm được xây dựng từ các hàm khác (hàm hợp).

4.1 Công thức Quy tắc Chuỗi

Cho hàm hợp $g(f(x))$. Đạo hàm của nó theo $x$ là:
$$\frac{d}{dx} g(f(x)) = \frac{d}{df} g(f) \times \frac{d}{dx} f(x)$$.

4.2 Ví dụ áp dụng

Cho $f(x) = 2x - 1$ và $g(f) = (f - 3)^2$:
* Tính đạo hàm của hàm bên trong ($f(x)$): $f'(x) = 2$.
* Tính đạo hàm của hàm bên ngoài ($g(f)$) theo $f$: $g'(f) = 2(f - 3)$.
* Áp dụng Quy tắc Chuỗi:
$$\frac{dg}{dx} = g'(f) \times f'(x) = 2(f - 3) \times 2$$.
* Thay $f$ bằng $2x - 1$:
$$\frac{dg}{dx} = 4((2x - 1) - 3) = 4(2x - 4) = 8x - 16$$.

---

5) Giải quyết vấn đề hướng tới Hồi quy Tuyến tính

Phần này áp dụng tối ưu hóa dựa trên gradient để tìm các tham số của một đường thẳng sao cho nó khớp với một hoặc nhiều điểm dữ liệu.

Hàm chi phí (Loss Function): Trong các ví dụ này, hàm chi phí được sử dụng là lỗi bình phương (Squared Error) giữa giá trị dự đoán $f$ và giá trị mục tiêu $y$: $g(f) = (f - y)^2$.

5.1 Vấn đề 1: Đường thẳng qua gốc tọa độ ($f(a) = ax$)

• Tham số cần tối ưu: $a$.
• Mục tiêu: Di chuyển đường màu xanh (initial line) để nó đi qua điểm mục tiêu màu xanh (target line).
• Công thức cập nhật: $a_{new} = a_{old} - \eta g'(a_{old})$.
• Đạo hàm riêng theo $a$: $\frac{\partial g}{\partial a} = 2x(f - y)$. (Sử dụng Quy tắc Chuỗi).

5.2 Vấn đề 3: Đường thẳng đầy đủ ($f(a, b) = ax + b$)

Đây là mô hình Hồi quy Tuyến tính đơn giản, tìm cả hệ số góc $a$ và độ lệch $b$.
* Tham số cần tối ưu: $(a, b)$.
* Nguyên tắc: Khởi tạo $(a, b)$, tính đạo hàm riêng tại $(a, b)$, và di chuyển $(a, b)$ ngược hướng với đạo hàm $(\frac{\partial g}{\partial a}, \frac{\partial g}{\partial b})$.

5.3 Công thức Đạo hàm Riêng cho $f(a, b) = ax + b$

Với hàm chi phí $g(f) = (f - y)^2$, đạo hàm riêng theo $a$ và $b$ là:
* $\frac{\partial g}{\partial a} = \frac{\partial g}{\partial f} \times \frac{\partial f}{\partial a} = 2(f - y) \times x = 2x(f - y)$.
* $\frac{\partial g}{\partial b} = \frac{\partial g}{\partial f} \times \frac{\partial f}{\partial b} = 2(f - y) \times 1 = 2(f - y)$.

5.4 Xử lý nhiều mẫu dữ liệu

Khi có nhiều điểm dữ liệu (ví dụ $(x_1, y_1)$ và $(x_2, y_2)$), có hai cách tiếp cận chính để cập nhật các tham số $(a, b)$:

• Cách tiếp cận 1 (Mẫu đơn lẻ/Stochastic): Lần lượt chọn từng mẫu dữ liệu. Tính toán đạo hàm riêng tại mẫu đó và cập nhật $(a, b)$ ngay lập tức. Sau đó chuyển sang mẫu tiếp theo.

• Cách tiếp cận 2 (Trung bình Gradient/Batch): Chọn một nhóm mẫu dữ liệu (ví dụ 2 mẫu). Tính toán đạo hàm riêng cho từng mẫu, sau đó tính trung bình các đạo hàm này. Chỉ thực hiện một lần cập nhật $(a, b)$ dựa trên giá trị trung bình đó.

  • Ví dụ tính trung bình gradient theo $a$ (cho 2 mẫu): $\frac{1}{2} (\frac{d g_1}{d a} + \frac{d g_2}{d a})$.

Reference

[1] Tất cả ảnh trong bài viết được lấy từ tài liệu AIO module05 week 01, 02

III. Hồi quy tuyến tính – Từ khái niệm đến tối ưu hoá

---

1. Khái niệm & Ý tưởng cốt lõi

Linear Regression là mô hình dự đoán tuyến tính đơn giản nhất — ước lượng quan hệ giữa biến đầu vào và biến đầu ra theo công thức:

$$ \hat{y} = wx + b $$

với (w) là trọng số, (b) là độ chệch (bias).
Mục tiêu của mô hình là tìm cặp ((w, b)) sao cho khoảng cách giữa giá trị dự đoán và giá trị thực tế nhỏ nhất.

---

2. Mục tiêu huấn luyện & Hàm mất mát

Sai số tại mỗi điểm dữ liệu:
$$ error_i = \hat{y}_i - y_i $$

Hàm mất mát (Mean Squared Error – MSE):

$$ L(w,b) = \frac{1}{N}\sum_{i=1}^{N}(\hat{y}_i - y_i)^2 $$

Tối ưu hóa nghĩa là giảm (L(w,b)) bằng cách điều chỉnh (w,b).

---

3. Gradient Descent – Trực giác tối ưu

Gradient Descent cho phép mô hình tự học bằng cách di chuyển ngược hướng gradient:

$$ \begin{aligned} w &\leftarrow w - \eta \frac{\partial L}{\partial w} \\ b &\leftarrow b - \eta \frac{\partial L}{\partial b} \end{aligned} $$

trong đó:
- $\eta$: learning rate – tốc độ học.
- $\frac{\partial L}{\partial w}$,\, $\frac{\partial L}{\partial b}$: độ dốc (slope) cho biết hướng cần giảm loss.

🔍 Hình dung như việc “trượt xuống đáy thung lũng” của bề mặt hàm mất mát.

---

4. Các chế độ huấn luyện

4.1. Stochastic Gradient Descent (One-sample)

• Cập nhật sau mỗi mẫu dữ liệu.
• Nhanh, phản ứng tức thời với dữ liệu mới, nhưng có độ dao động cao (noisy).
• Phù hợp với bài toán online learning hoặc streaming data.

4.2. Mini-Batch Gradient Descent

• Cập nhật theo nhóm nhỏ gồm (m) mẫu.
• Giảm nhiễu, tăng ổn định khi hội tụ.
• Là phương pháp phổ biến nhất trong thực tế.

$$ \frac{\partial L}{\partial w} = \frac{2}{m}\sum_{i=1}^{m}x_i(\hat{y}_i - y_i) $$

4.3. Batch Gradient Descent

• Sử dụng toàn bộ tập dữ liệu để tính gradient.
• Độ chính xác cao, nhưng tốn tài nguyên và chậm khi dữ liệu lớn.

Phương pháp	Tốc độ	Ổn định	Ứng dụng
One-sample (SGD)	⚡ Nhanh	⚠️ Thấp	Online learning
Mini-batch	⚖️ Trung bình	✅ Cao	Thực tế
Batch	🐢 Chậm	💎 Rất cao	Phân tích nhỏ, mô hình đơn giản

---

5. MSE & MAE – Hai cách đo sai số phổ biến

Mean Squared Error (MSE)

$$ L = \frac{1}{N}\sum_{i=1}^{N}(\hat{y}_i - y_i)^2 $$

• Ưu điểm: mượt, dễ đạo hàm.
• Nhược điểm: nhạy với outlier.

Mean Absolute Error (MAE)

$$ L = \frac{1}{N}\sum_{i=1}^{N}|\hat{y}_i - y_i| $$

• Ưu điểm: chống nhiễu tốt.
• Nhược điểm: không khả vi tại 0.

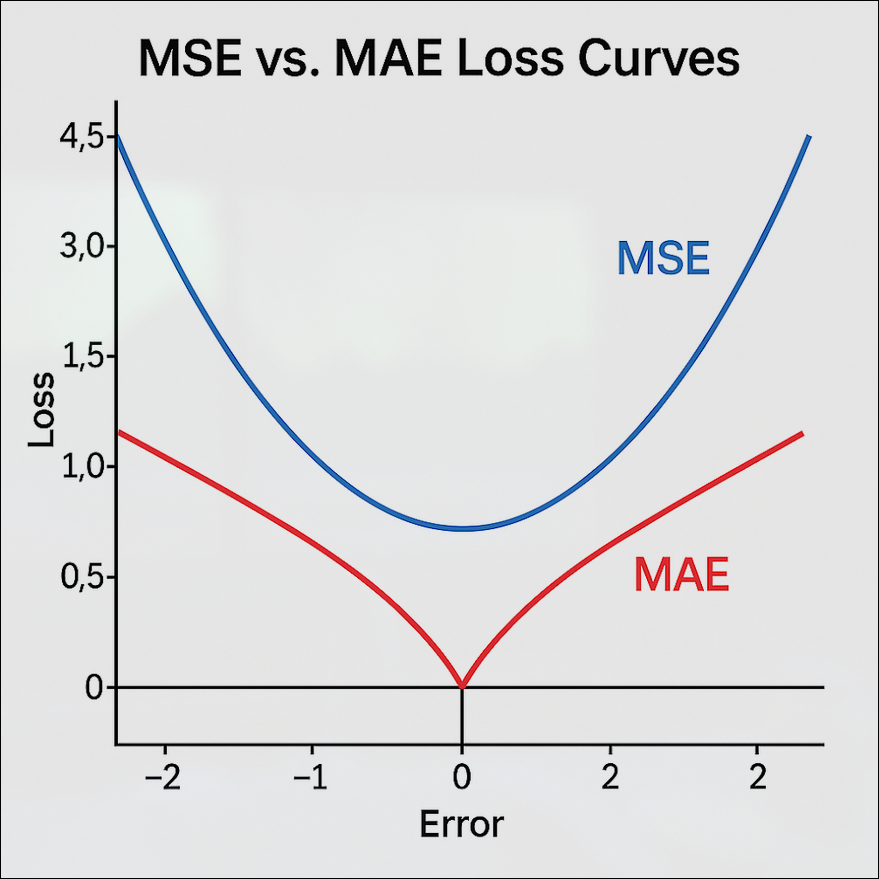
Hình 1. So sánh đường cong hàm mất mát MSE (Mean Squared Error) và MAE (Mean Absolute Error) theo sai số (Error).
Đường cong MSE (màu xanh) có dạng parabol mượt, tăng nhanh khi sai số lớn – thể hiện tính nhạy cảm với outlier.
Ngược lại, MAE (màu đỏ) có dạng hàm tuyến tính gấp khúc, tăng đều hai phía – giúp mô hình ổn định hơn với nhiễu nhưng khó tối ưu hóa do không khả vi tại điểm 0.**

---

6. Hồi quy tuyến tính đa biến

Mở rộng cho nhiều đặc trưng:

$$ \hat{y} = w_1x_1 + w_2x_2 + \ldots + w_nx_n + b $$

Dạng vector hóa:

$$ \hat{y} = \mathbf{w}^T\mathbf{x} + b $$

Gradient cho toàn bộ vector trọng số:

$$ \nabla_\mathbf{w}L = \frac{2}{N}\sum_{i=1}^{N}(\hat{y}_i - y_i)\mathbf{x}_i $$

---

7. Ý nghĩa hình học & liên hệ mô hình khác

• Trong không gian 2D: mô hình là đường thẳng.
• Trong không gian n-chiều: là siêu phẳng (hyperplane).
• Các mô hình phức tạp hơn như Logistic Regression hay Neural Network chỉ là mở rộng của Linear Regression, thêm hàm kích hoạt (activation) và tầng sâu hơn.

Hình 2. Minh hoạ mô hình hồi quy tuyến tính đa biến dưới dạng mặt phẳng (plane) trong không gian ba chiều. Các điểm đỏ biểu diễn dữ liệu thực tế, còn mặt phẳng màu xanh là mặt phẳng hồi quy (regression plane).
— biểu diễn quan hệ tuyến tính giữa các biến đầu vào $x_1, x_2$ và đầu ra $y$. Khoảng cách vuông góc từ các điểm dữ liệu đến mặt phẳng chính là sai số dự đoán (residuals), phản ánh độ lệch giữa giá trị thực tế và giá trị mô hình dự đoán.

Hình 3. Minh hoạ khái niệm siêu phẳng (hyperplane) trong không gian khác nhau.
Ở không gian $\mathbb{R}^2$, siêu phẳng là đường thẳng phân tách dữ liệu (hình trái).
Còn trong không gian $\mathbb{R}^3$, siêu phẳng trở thành mặt phẳng (hình phải).
Khái niệm này tổng quát hoá cho mọi mô hình tuyến tính — mỗi siêu phẳng biểu diễn một quan hệ tuyến tính giữa các đặc trưng dữ liệu và đầu ra dự đoán.

---

8. Kết luận ngắn

Linear Regression là cầu nối giữa toán học cơ bản và học sâu:
Từ công thức (wx+b), ta học được tư duy tối ưu hóa dựa trên sai số — nền tảng của mọi mô hình học máy.

Reference

[1] Tất cả ảnh được chính tác giả vẽ.

V. Vectorization for Linear Regression

1. Động cơ (Motivation): Vì sao cần Vectorization

Trong học máy, Linear Regression (Hồi quy tuyến tính) là một trong những mô hình cơ bản nhất.
Mục tiêu của nó là tìm ra một đường thẳng (hoặc siêu phẳng) phù hợp nhất để mô tả mối quan hệ giữa đặc trưng (feature) và nhãn (label) của dữ liệu.

Ví dụ, khi ta muốn dự đoán giá nhà, ta có thể mô hình hóa:

$$ \hat{y} = w \cdot \text{area} + b $$

hoặc với nhiều đặc trưng hơn:

$$ \hat{y} = w_1 x_1 + w_2 x_2 + w_3 x_3 + b $$

trong đó:

• $x_i$: các đặc trưng (ví dụ: diện tích, số phòng, vị trí,...).
• $w_i$: các trọng số (weights).
• $b$: hệ số chệch (bias).

---

Hạn chế của cách tính thủ công (Scalar Implementation)

Nếu triển khai huấn luyện Linear Regression theo cách tính từng mẫu, ta phải:

1. Duyệt qua từng mẫu $(x_i, y_i)$ trong tập huấn luyện.
2. Tính đầu ra dự đoán:
   $$ \hat{y}_i = w x_i + b $$
3. Tính hàm mất mát (loss):
   $$ L_i = (\hat{y}_i - y_i)^2 $$
4. Tính đạo hàm từng phần:
   $$ \frac{\partial L_i}{\partial w} = 2x_i(\hat{y}_i - y_i), \quad \frac{\partial L_i}{\partial b} = 2(\hat{y}_i - y_i) $$
5. Cập nhật tham số bằng Gradient Descent:
   $$ w \leftarrow w - \eta \frac{\partial L_i}{\partial w}, \quad b \leftarrow b - \eta \frac{\partial L_i}{\partial b} $$
   với $\eta$ là learning rate.

---

Vấn đề của cách làm này

• Chậm: phải lặp qua từng mẫu, không tận dụng được khả năng song song của phần cứng.
• Dễ sai sót: khi có nhiều đặc trưng hoặc nhiều mẫu, số vòng lặp và phép tính tăng nhanh.
• Khó mở rộng: khó chạy trên GPU hoặc dữ liệu lớn, dạng tính này không hiệu quả.

---

Tư duy Vectorization

Vectorization giải quyết các nhược điểm trên bằng cách:

Thay vì tính từng mẫu một, hãy biểu diễn toàn bộ dữ liệu bằng vector và ma trận, để máy tính xử lý tất cả cùng lúc.

Điều này mang lại ba lợi ích chính:

• Tốc độ: tận dụng tối đa khả năng tính toán song song (CPU/GPU).
• Ngắn gọn: code súc tích, dễ đọc, dễ debug.
• Khái quát: công thức tổng quát áp dụng cho cả 1, m hay N mẫu chỉ bằng cách thay đổi kích thước ma trận.

---

Minh họa trực quan

So sánh giữa tính thủ công (loop-based) và vector hóa (matrix-based)

Loop-based	Vectorized
Tính từng mẫu một	Xử lý toàn bộ tập dữ liệu cùng lúc
Nhiều vòng lặp, dễ sai	Gọn nhẹ, chính xác
Khó tận dụng GPU	Tối ưu phần cứng hiện đại

2. Từ dạng công thức và hướng (Scalar Form) đến dạng vector

Khi số đặc trưng tăng, viết từng phương trình riêng lẻ trở nên cồng kềnh. Ta chuyển toàn bộ về dạng vector để tính toán gọn và nhất quán.

---

Công thức dạng hướng

Công thức Linear Regression cho một mẫu có (n) đặc trưng:
$$ \hat{y} = w_1 x_1 + w_2 x_2 + \dots + w_n x_n + b $$

---

Biểu diễn bằng vector

Gom các hệ số và đặc trưng thành vector cột:
$$ \mathbf{w} = \left[ \begin{array}{c} w_1 \\ w_2 \\ \vdots \\ w_n \end{array} \right], \quad \mathbf{x} = \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] $$

Viết gọn:
$$ \hat{y} = \mathbf{w}^{\top}\mathbf{x} + b $$

---

Gộp bias vào vector tham số

Thêm phần tử (1) vào đầu vector đặc trưng để gộp (b) chung tham số:
$$ \boldsymbol{\theta} = \left[ \begin{array}{c} b \\ w_1 \\ w_2 \\ \vdots \\ w_n \end{array} \right], \quad \mathbf{x'} = \left[ \begin{array}{c} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] $$

Lúc này:
$$ \hat{y} = \boldsymbol{\theta}^{\top}\mathbf{x'} $$

---

Loss và gradient (1 mẫu) trong dạng vector

Hàm mất mát:
$$ L = (\hat{y} - y)^2 $$

Gradient theo $\boldsymbol{\theta}$:
$$ \nabla_{\boldsymbol{\theta}} L = 2\,\mathbf{x'}\,(\hat{y} - y) $$

Cập nhật tham số (Gradient Descent):
$$ \boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \eta\,\nabla_{\boldsymbol{\theta}} L $$

---

Minh họa trực quan

Hình minh họa từ scalar form tới Vector form [1]

3. Biểu diễn ma trận cho nhiều mẫu (Matrix Form)

Khi huấn luyện trên nhiều mẫu cùng lúc, thay vì xử lý từng cặp $(x, y)$, ta gom toàn bộ dữ liệu vào ma trận đặc trưng (X) và vector nhãn $\mathbf{y}$.
Đây chính là bước chuyển từ vector hóa 1 mẫu sang ma trận hóa toàn bộ dữ liệu.

---

Ma trận đặc trưng và vector nhãn

Với (m) mẫu huấn luyện, mỗi mẫu có (n) đặc trưng (đã thêm phần tử 1 cho bias):

$$ X = \left[ \begin{array}{ccccc} 1 & x_{11} & x_{12} & \dots & x_{1n} \\ 1 & x_{21} & x_{22} & \dots & x_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{m1} & x_{m2} & \dots & x_{mn} \end{array} \right], \quad \mathbf{y} = \left[ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_m \end{array} \right] $$

---

Dự đoán đầu ra

Toàn bộ dự đoán đầu ra được tính bằng một phép nhân ma trận duy nhất:

$$ \hat{\mathbf{y}} = X \boldsymbol{\theta} $$

Mỗi hàng của (X) tương ứng với một mẫu $\mathbf{x'}^{(i)}$,
và phép nhân này cho ra toàn bộ các giá trị dự đoán $\hat{y}^{(i)}$ cùng lúc.

---

Hàm mất mát trung bình

Hàm mất mát trung bình trên (m) mẫu:

$$ L = \frac{1}{m} (\hat{\mathbf{y}} - \mathbf{y})^\top (\hat{\mathbf{y}} - \mathbf{y}) $$

---

Gradient và cập nhật tham số

Gradient theo vector tham số:

$$ \nabla_{\boldsymbol{\theta}} L = \frac{2}{m} X^\top (\hat{\mathbf{y}} - \mathbf{y}) $$

Cập nhật bằng Gradient Descent:

$$ \boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \eta \nabla_{\boldsymbol{\theta}} L $$

---

Ví dụ minh họa

Ví dụ minh họa biểu diễn ma trận cho nhiều mẫu [1]

---

4. Từ 1-sample đến m-sample và N-sample (Tổng quát hóa quá trình Vectorization)

Phần này minh họa quá trình chuyển từ việc xử lý 1 mẫu sang nhiều mẫu (mini-batch) và cuối cùng là toàn bộ tập dữ liệu (N-sample) – chính là quá trình vector hóa dần dần.

---

4.1. Trường hợp 1-sample (Sample đơn lẻ)

Với một mẫu $(\mathbf{x}, y)$:

1. Dự đoán đầu ra:
   $$ \hat{y} = \boldsymbol{\theta}^\top \mathbf{x} $$

2. Hàm mất mát:
   $$ L = (\hat{y} - y)^2 $$

3. Gradient:
   $$ \nabla_{\boldsymbol{\theta}} L = 2\,\mathbf{x}(\hat{y} - y) $$

4. Cập nhật tham số:
   $$ \boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \eta\,\nabla_{\boldsymbol{\theta}} L $$
   Ví dụ từng bước
   
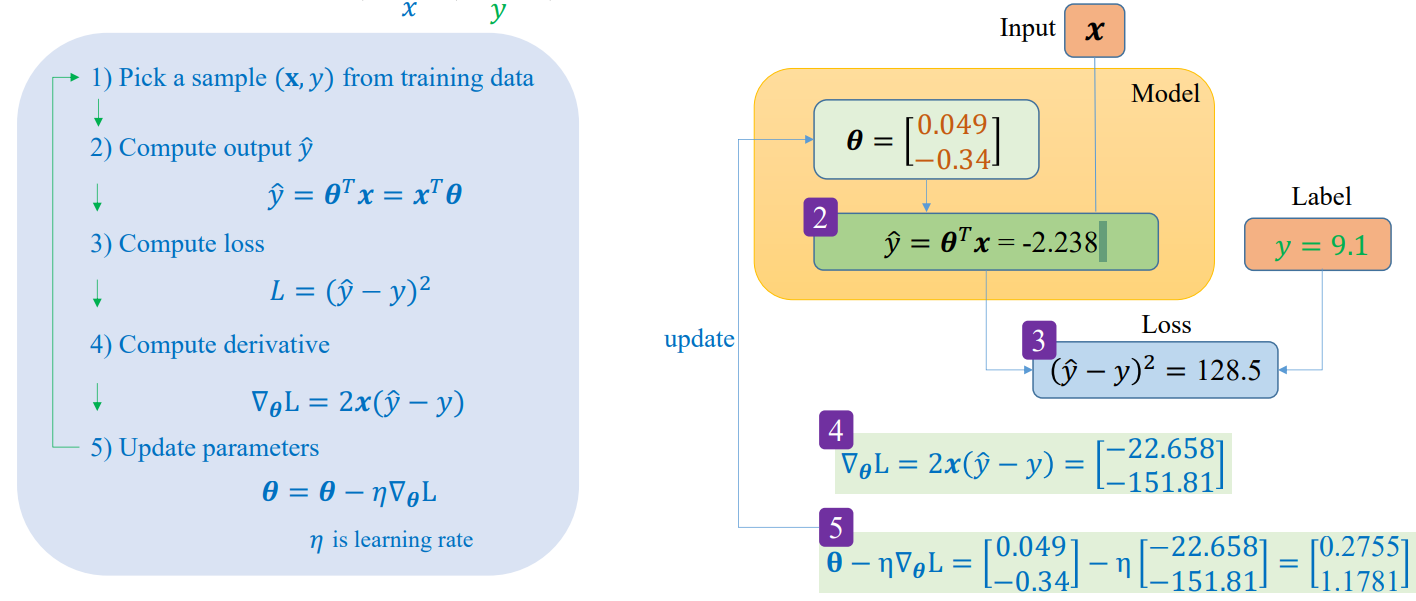
   Ví dụ minh họa các bước training với 1 sample bằng số liệu cụ thể[1]

---

4.2. Trường hợp m-sample (Mini-batch)

Thay vì cập nhật sau mỗi mẫu, ta gom m mẫu lại thành một batch nhỏ:

1. Tập đặc trưng và nhãn:

$$ X_m = \left[ \begin{array}{ccccc} 1 & x_{11} & x_{12} & \dots & x_{1n} \\ 1 & x_{21} & x_{22} & \dots & x_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{m1} & x_{m2} & \dots & x_{mn} \end{array} \right], \quad \mathbf{y}_m = \left[ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_m \end{array} \right] $$

2. Dự đoán đầu ra:
   $$ \hat{\mathbf{y}}_m = X_m \boldsymbol{\theta} $$

3. Hàm mất mát trung bình:
   $$ L = \frac{1}{m} (\hat{\mathbf{y}}_m - \mathbf{y}_m)^\top (\hat{\mathbf{y}}_m - \mathbf{y}_m) $$

4. Gradient và cập nhật:
   $$ \nabla_{\boldsymbol{\theta}} L = \frac{2}{m} X_m^\top (\hat{\mathbf{y}}_m - \mathbf{y}_m) $$
   $$ \boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \eta\,\nabla_{\boldsymbol{\theta}} L $$

Ví dụ minh họa

Ví dụ minh họa các bước training với m sample bằng số liệu cụ thể[1]

---

4.3. Trường hợp N-sample (Toàn bộ tập dữ liệu)

Khi m = N, tức là dùng toàn bộ dữ liệu huấn luyện để tính toán mỗi lần cập nhật.

1. Dự đoán toàn bộ:
   $$ \hat{\mathbf{y}} = X \boldsymbol{\theta} $$

2. Hàm mất mát toàn phần:
   $$ L = \frac{1}{N} (\hat{\mathbf{y}} - \mathbf{y})^\top (\hat{\mathbf{y}} - \mathbf{y}) $$

3. Gradient toàn phần:
   $$ \nabla_{\boldsymbol{\theta}} L = \frac{2}{N} X^\top (\hat{\mathbf{y}} - \mathbf{y}) $$

4. Cập nhật tham số:
   $$ \boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \eta\,\nabla_{\boldsymbol{\theta}} L $$

Ví dụ về data

Ví dụ minh họa data N sample[1]

---

4.4. So sánh nhanh ba trường hợp

Cấp độ	Ký hiệu	Kích thước xử lý	Ưu điểm	Nhược điểm
1-sample	SGD	1 mẫu/lần	Cập nhật nhanh, online	Dao động mạnh, nhiễu
m-sample	Mini-batch GD	m mẫu/lần	Cân bằng giữa tốc độ & độ ổn định	Cần chọn m hợp lý
N-sample	Batch GD	Toàn bộ dữ liệu	Gradient chính xác, mượt	Chậm, tốn bộ nhớ

---

5. Triển khai Vectorization bằng NumPy (Implementation)

Sau khi hiểu bản chất toán học của vectorization, ta có thể hiện thực hóa toàn bộ quy trình bằng thư viện NumPy.
Điểm quan trọng là: mọi phép tính đều nên viết dưới dạng phép nhân ma trận thay vì vòng lặp for.

---

5.1. Cấu trúc dữ liệu đầu vào

• X: ma trận đặc trưng kích thước $(m, n+1)$, mỗi hàng là một mẫu (đã thêm cột 1 cho bias).
• y: vector cột nhãn $(m, 1)$.
• $\theta$: vector tham số $(n+1, 1)$.

Ví dụ (dữ liệu quảng cáo):

$$ X = \left[ \begin{array}{cccc} 1 & 55 & 34 & 62 \\ 1 & 20 & 45 & 25 \\ 1 & 15 & 10 & 12 \end{array} \right], \quad \mathbf{y} = \left[ \begin{array}{c} 22.1 \\ 9.5 \\ 7.2 \end{array} \right] $$

---

5.2. Các bước tính toán vector hóa

1. Dự đoán đầu ra

$$ \hat{\mathbf{y}} = X \boldsymbol{\theta} $$

2. Tính sai số (error)

$$ \mathbf{e} = \hat{\mathbf{y}} - \mathbf{y} $$

3. Tính hàm mất mát

$$ L = \frac{1}{m}\mathbf{e}^\top \mathbf{e} $$

4. Tính gradient

$$ \nabla_{\boldsymbol{\theta}} L = \frac{2}{m}X^\top \mathbf{e} $$

5. Cập nhật tham số

$$ \boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \eta\,\nabla_{\boldsymbol{\theta}} L $$

---

5.3. Mã ví dụ với NumPy

import numpy as np

# 1. Khởi tạo dữ liệu
X = np.array([
    [1, 55, 34, 62],
    [1, 20, 45, 25],
    [1, 15, 10, 12]
])
y = np.array([[22.1], [9.5], [7.2]])

# 2. Khởi tạo tham số
theta = np.zeros((X.shape[1], 1))
eta = 0.01
m = len(y)

# 3. Huấn luyện bằng vectorization
for epoch in range(1000):
    y_hat = X @ theta
    error = y_hat - y
    grad = (2 / m) * X.T @ error
    theta -= eta * grad

print("Theta sau huấn luyện:\n", theta)

---

5.4. Lợi ích khi dùng Vectorization

Ưu điểm	Giải thích
Nhanh hơn rất nhiều	NumPy tận dụng BLAS & SIMD, thực thi song song trên CPU/GPU.
Code ngắn và rõ ràng	Không cần vòng for, chỉ vài dòng biểu thức ma trận.
Ổn định và mở rộng tốt	Dễ áp dụng cho batch, mini-batch, hoặc toàn bộ dataset.

---

6. Tài liệu tham khảo chương V

[1] Ảnh lấy từ slide AIO 2025 Module 05 Tuần 01 và 02.

VI. Loss Functions for Linear Regression

---

1. Giới thiệu (Introduction)

Trong Linear Regression (Hồi quy tuyến tính), mục tiêu của mô hình là giảm thiểu sai lệch giữa giá trị dự đoán $\hat{y}$ và giá trị thực $y$.
Để đo lường sai lệch này, ta sử dụng Loss Function (Hàm mất mát) — một hàm định lượng mức độ "tệ" của dự đoán so với dữ liệu thực.

Một Loss Function tốt cần thỏa mãn:

• Liên tục (Continuous) trong toàn miền giá trị.
• Khả vi (Differentiable) hoặc ít nhất là khả vi từng phần (Piecewise Differentiable) để tối ưu bằng Gradient Descent.

Các dạng phổ biến trong Linear Regression bao gồm:

1. Mean Squared Error (MSE) – nhạy với outlier.
2. Mean Absolute Error (MAE) – bền vững hơn với nhiễu.
3. Huber Loss – kết hợp ưu điểm của MSE và MAE.
4. Normalization & Regularization – giúp mô hình ổn định và tránh overfitting.

---

2. Mean Squared Error (MSE)

2.1. Công thức

Hàm mất mát bình phương trung bình được định nghĩa như sau:

$$ L_{MSE}(\hat{y}, y) = \frac{1}{N} \sum_{i=1}^{N} (\hat{y}_i - y_i)^2 $$

Với một mẫu duy nhất:
$$ L = (\hat{y} - y)^2 $$

2.2. Đạo hàm (Gradient)

Đạo hàm của $L$ theo tham số $w$ và $b$:

$$ \frac{\partial L}{\partial w} = 2x(\hat{y} - y), \quad \frac{\partial L}{\partial b} = 2(\hat{y} - y) $$

Cập nhật tham số bằng Gradient Descent:

$$ w \leftarrow w - \eta \frac{\partial L}{\partial w}, \quad b \leftarrow b - \eta \frac{\partial L}{\partial b} $$

2.3. Trực quan

• MSE phạt sai số lớn mạnh hơn vì bình phương sai số.
• Nhạy với outlier, do sai số lớn làm tăng bình phương nhanh chóng.

---

3. Mean Absolute Error (MAE)

3.1. Công thức

Hàm mất mát tuyệt đối trung bình được định nghĩa như sau:

$$ L_{MAE}(\hat{y}, y) = \frac{1}{N} \sum_{i=1}^{N} |\hat{y}_i - y_i| $$

Với một mẫu duy nhất:
$$ L = |\hat{y} - y| $$

3.2. Đạo hàm

MAE không khả vi tại điểm (\hat{y} = y), nhưng có thể xét đạo hàm riêng biệt:

$$ \frac{\partial L}{\partial w} = x \cdot \text{sign}(\hat{y} - y), \quad \frac{\partial L}{\partial b} = \text{sign}(\hat{y} - y) $$

Trong đó:
$$ \text{sign}(z) = \begin{cases} +1, & z > 0 \\ -1, & z < 0 \end{cases} $$

3.3. Đặc điểm

• MAE ít bị ảnh hưởng bởi outlier, do không bình phương sai số.
• Tuy nhiên, gradient không ổn định khi sai số nhỏ (vì đạo hàm rời rạc tại 0).

Hình minh họa so sánh MSE và MAE theo giá trị lỗi

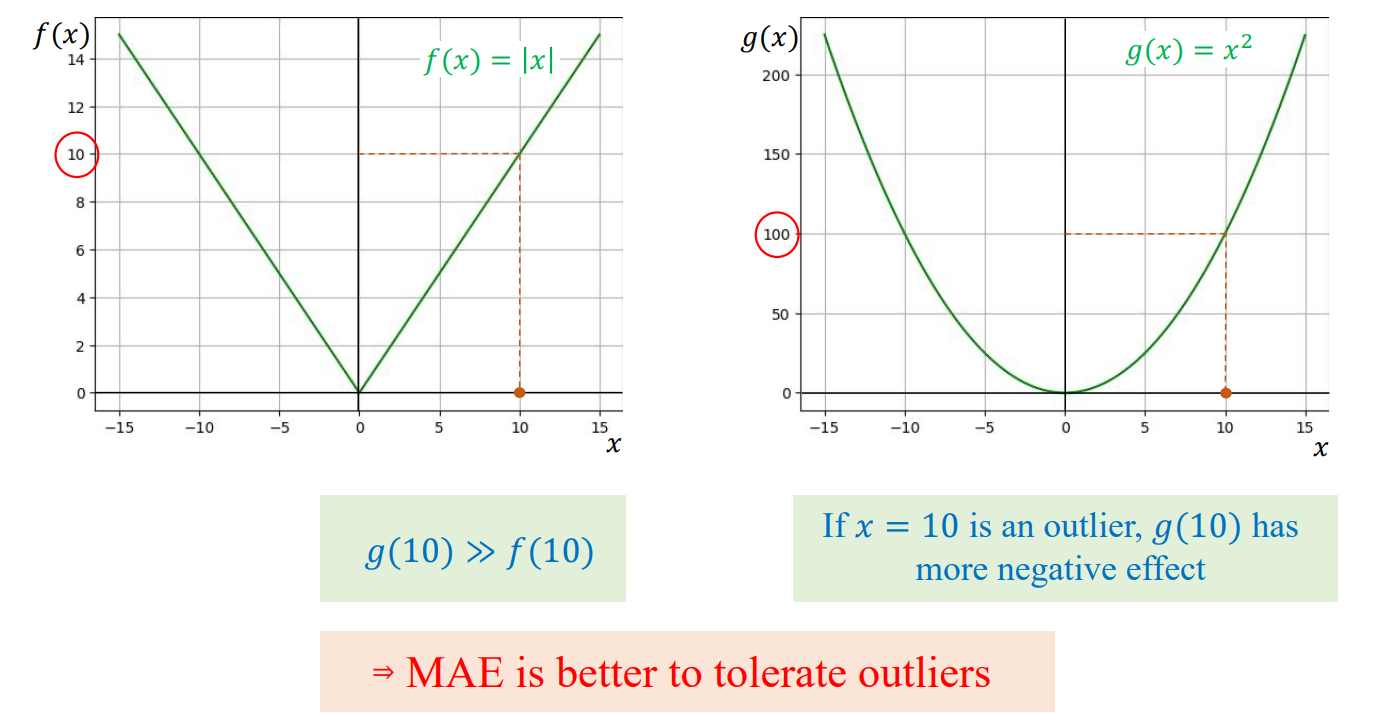
4. Huber Loss

4.1. Mục tiêu

Huber Loss được thiết kế để kết hợp ưu điểm của MSE và MAE:

• Giống MSE khi sai số nhỏ (liên tục, khả vi, học ổn định).
• Giống MAE khi sai số lớn (ít bị ảnh hưởng bởi outlier).

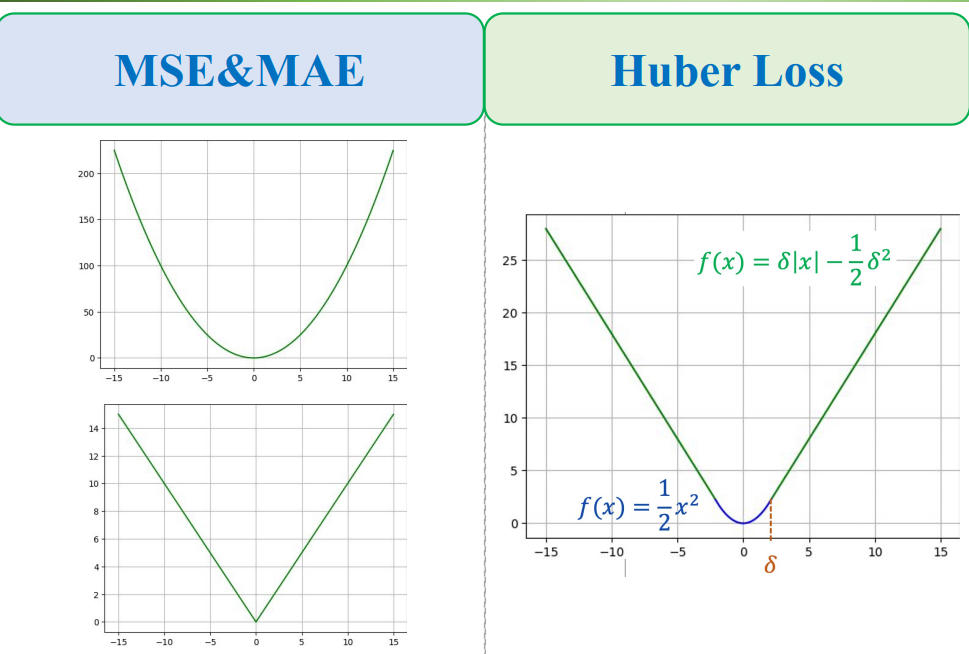
4.2. Định nghĩa

$$ L_{Huber}(\hat{y}, y) = \begin{cases} \frac{1}{2}(\hat{y} - y)^2, & \text{nếu } |\hat{y} - y| \le \delta \\ \delta(|\hat{y} - y| - \frac{1}{2}\delta), & \text{nếu } |\hat{y} - y| > \delta \end{cases} $$

Với $\delta$ là ngưỡng chuyển giữa hai vùng.

4.3. Đạo hàm

$$ \frac{\partial L}{\partial w} = \begin{cases} x(\hat{y} - y), & |\hat{y} - y| \le \delta \\ \delta x \cdot \text{sign}(\hat{y} - y), & |\hat{y} - y| > \delta \end{cases} $$

4.4. So sánh với MSE và MAE

Thuộc tính	MSE	MAE	Huber
Nhạy với outlier	Cao	Thấp	Trung bình
Gradient ổn định	Có	Không	Có
Liên tục & khả vi	Có	Không	Có

---

5. Data Normalization & Regularization

5.1. Data Normalization

Trong thực tế, các đặc trưng (feature) thường có đơn vị và thang đo khác nhau.

Nếu không chuẩn hóa, gradient sẽ cập nhật không đồng đều, khiến quá trình hội tụ chậm hoặc không ổn định.

Công thức Min-Max Normalization:

$$ x' = \frac{x - x_{min}}{x_{max} - x_{min}} $$

Khi dữ liệu được chuẩn hóa, ta có thể dùng learning rate ổn định hơn và mô hình hội tụ nhanh hơn.

---

5.2. Regularization

Regularization giúp tránh hiện tượng overfitting bằng cách thêm thành phần phạt vào hàm mất mát:

a) L2 Regularization (Ridge Regression)

$$ L = (\hat{y} - y)^2 + \lambda \sum_i w_i^2 $$

Gradient:
$$ \frac{\partial L}{\partial w_i} = 2x_i(\hat{y} - y) + 2\lambda w_i $$

b) L1 Regularization (Lasso Regression)

$$ L = (\hat{y} - y)^2 + \lambda \sum_i |w_i| $$

Giúp một số trọng số $w_i$ trở về 0 → chọn lọc đặc trưng (feature selection).

---

6. Tổng kết (Summary)

Loss Function	Ưu điểm	Nhược điểm	Ứng dụng phù hợp
MSE	Gradient mượt, dễ tối ưu	Nhạy cảm với outlier	Khi dữ liệu sạch, ít nhiễu
MAE	Bền vững với nhiễu	Gradient không ổn định	Khi có outlier mạnh
Huber	Cân bằng giữa MSE và MAE	Cần chọn tham số $\delta$	Khi cần mô hình ổn định và chịu nhiễu

Gợi ý thực hành:
- Bắt đầu với MSE khi huấn luyện cơ bản.
- Dùng Huber Loss cho bài toán thực tế có nhiễu nhẹ.
- Kết hợp Regularization nếu dữ liệu có nhiều đặc trưng liên quan.

---

7. Tài liệu tham khảo chương VI.

[1] Ảnh lấy từ slide AIO 2025 Module 05 Tuần 01 và 02.

---

VII. (XAI) Giải thuật LIME

---

1) XAI

1.1 Thách thức "Hộp Đen" trong AI Hiện Đại

Sự phát triển vượt bậc của Trí tuệ nhân tạo (AI) trong những năm gần đây đã đưa các ứng dụng công nghệ len lỏi vào mọi khía cạnh của đời sống, từ các trợ lý ảo phổ biến như ChatGPT cho đến những hệ thống phức tạp như xe tự hành. Sự bùng nổ này mang lại nhiều tiện ích, nhưng đồng thời đặt ra một thách thức lớn về tính minh bạch và khả năng giải thích đối với các mô hình học sâu (deep learning). Các mô hình này thường được gọi là "hộp đen" (black box).

Khái niệm "hộp đen" mô tả tình trạng người dùng chỉ có thể cung cấp dữ liệu đầu vào và nhận kết quả đầu ra, nhưng không thể nhìn thấu quy trình bên trong hay các thuật toán phức tạp đang diễn ra để hiểu rõ lý do mô hình đưa ra kết luận.

Trong những lĩnh vực quan trọng như y tế, tài chính hay đặc biệt là pháp luật, sự mù mờ này có thể dẫn đến những rủi ro nghiêm trọng về đạo đức và xã hội. Một minh chứng rõ ràng là việc ứng dụng AI trong hệ thống đánh giá rủi ro tái phạm tội phạm (ví dụ: COMPAS) đã cho thấy sự thiên vị đáng lo ngại: hệ thống có xu hướng gán nhãn rủi ro cao hơn cho người da màu so với người da trắng, ngay cả khi lịch sử phạm tội của người da trắng nguy hiểm hơn. Vấn đề căn bản này, bắt nguồn từ sự phức tạp và thiếu khả năng giải thích của mô hình, đã tạo ra động lực cấp thiết để phát triển mạnh mẽ lĩnh vực eXplainable AI (XAI).

Mục tiêu chung của XAI là tạo ra các lời giải thích dễ hiểu đối với con người, trả lời cho câu hỏi lý do (why) và cách thức (how) một mô hình học máy đưa ra dự đoán cụ thể. Báo viết này tập trung phân tích hai trong số những phương pháp XAI hậu kiểm (Post-hoc) quan trọng nhất: LIME và ANCHOR.

1.2 Phân biệt Interpretability và Explainability

Trong XAI, hai khái niệm thường được sử dụng đan xen là khả năng diễn giải (Interpretability) và khả năng giải thích (Explainability), mặc dù chúng mang sắc thái khác nhau.

• Khả năng Diễn giải (Interpretability): Khái niệm này đề cập đến khả năng hiểu trực tiếp quá trình hoạt động bên trong của một mô hình hoặc thuật toán. Các mô hình có tính diễn giải cao thường có cấu trúc đơn giản, trực quan, dễ hình dung, ví dụ điển hình là Hồi quy Tuyến tính (Linear Regression) hoặc Cây Quyết định (Decision Tree). Trong một mô hình dự đoán giá nhà dạng $y=w_{1}x_{1}+w_{2}x_{2}+b$, các hệ số hồi quy $w_{1}$, $w_{2}$ thể hiện trực tiếp mức độ ảnh hưởng của các biến đầu vào $x_{1}$ và $x_{2}$ lên giá nhà $y$. Mô hình này đơn giản và không cần công cụ giải thích bổ sung.
• Khả năng Giải thích (Explainability): Khái niệm này tập trung vào việc làm rõ lý do và bằng chứng cho quyết định của các mô hình phức tạp (black box), theo cách mà đa số người dùng có thể hiểu được, mà không nhất thiết phải làm rõ toàn bộ cơ chế nội bộ. Ví dụ, đối với một mạng nơ-ron sâu nhận diện khuôn mặt, người dùng không thể giải thích ý nghĩa của hàng triệu trọng số, mà cần các phương pháp XAI để chỉ ra phần nào của khuôn mặt ảnh hưởng đến kết quả dự đoán.

Sự khác biệt này gắn liền với mối quan hệ đánh đổi giữa Hiệu suất (Performance) và Khả năng Diễn giải (Interpretability). Các mô hình đơn giản thường dễ hiểu nhưng có hiệu suất thấp hơn trong các bài toán phức tạp. Ngược lại, các mô hình phức tạp (như Mạng nơ-ron sâu hay các phương pháp Ensemble như XGBoost) đạt hiệu suất cao hơn nhờ khả năng học các mối quan hệ phi tuyến tính, nhưng đồng thời lại mất đi tính khả diễn giải.

1.3 Phân loại và Vị trí của LIME/ANCHOR

Các thuật toán giải thích trong XAI được phân loại dựa trên hai tiêu chí chính :

1. Thời điểm giải thích:
   • Giải thích Nội tại (Intrinsic): Mô hình tự giải thích (ví dụ: Hồi quy Tuyến tính).
   • Giải thích Hậu kiểm định (Post-hoc): Áp dụng sau khi mô hình đã được huấn luyện, có tính tổng quát cao (model-agnostic).
2. Phạm vi áp dụng:
   • Global: Cung cấp cái nhìn tổng quan về toàn bộ hoạt động của mô hình.
   • Local: Tập trung giải thích một dự đoán riêng lẻ, cụ thể.

LIME và ANCHOR, hai phương pháp được nghiên cứu trong báo cáo này, đều thuộc loại Post-hoc, Model-agnostic và Local. Điều này có nghĩa là chúng có thể áp dụng cho hầu hết mọi mô hình "hộp đen" và tập trung vào việc cung cấp lời giải thích cho từng quyết định riêng lẻ.

---

2) LIME (Local Interpretable Model-Agnostic Explanations)

LIME là một thuật toán giải thích cục bộ được giới thiệu vào năm 2016. Thuật toán này đã trở thành một trong những kỹ thuật XAI độc lập với mô hình (model-agnostic) được áp dụng rộng rãi nhất.

2.1 Ý tưởng Cốt lõi và Cơ sở Toán học

Nguyên lý Xấp xỉ Tuyến tính Cục bộ

Ý tưởng cốt lõi của LIME là thay vì cố gắng phân tích toàn bộ cấu trúc phức tạp của mô hình gốc ($f$), thuật toán chỉ tập trung vào việc diễn giải quyết định của mô hình tại một điểm dữ liệu cụ thể ($x$). Giả thuyết nền tảng là: ngay cả khi ranh giới quyết định của mô hình tổng thể là phi tuyến tính và phức tạp, nếu ta thu hẹp phạm vi quan sát vào một vùng lân cận rất nhỏ quanh điểm $x$, ranh giới quyết định đó vẫn có thể được xấp xỉ một cách trung thực bằng một mô hình đơn giản và dễ hiểu (interpretable model, ký hiệu là $g$).

Công thức Tối ưu hóa

LIME giải quyết bài toán tìm kiếm mô hình giải thích $g$ thuộc tập hợp các mô hình dễ diễn giải ($G$) bằng cách cân bằng giữa độ trung thực cục bộ (local fidelity) và tính đơn giản (interpretability). Công thức tối ưu hóa có dạng:

$\xi(x) = \operatorname{argmin}{g \in G} L(f, g, \pi{x}) + \Omega(g)$

Trong đó:

• $L(f, g, \pi_{x})$ là độ đo độ thiếu trung thực (unfaithfulness) của $g$ khi xấp xỉ hành vi của $f$ trong vùng lân cận được định nghĩa bởi hàm khoảng cách $\pi_{x}$.
• $\Omega(g)$ là độ phức tạp của mô hình giải thích $g$. Để đảm bảo tính diễn giải, $g$ thường được chọn là một mô hình tuyến tính thưa (sparse linear model), do đó $\Omega(g)$ sẽ đại diện cho số lượng đặc trưng được sử dụng.

Bằng cách tối thiểu hóa hàm này, LIME tìm được mô hình đơn giản nhất ( $\Omega(g)$ thấp) nhưng vẫn trung thực nhất ($\min L$) trong phạm vi cục bộ của $x$.

2.2 Cơ chế Thuật toán LIME chi tiết

Quá trình hoạt động của LIME, được thực hiện sau khi mô hình hộp đen ($f$) đã được huấn luyện, bao gồm sáu bước chính:

1. Tạo mẫu dữ liệu lân cận (Perturbation): Thuật toán sinh ra nhiều điểm dữ liệu giả ($z$) xung quanh điểm dữ liệu gốc $x$ bằng cách thêm nhiễu, hoán vị, hoặc loại bỏ các thành phần đặc trưng. Để lời giải thích dễ hiểu, dữ liệu gốc được chuyển sang một biểu diễn "diễn giải được" (interpretable representation), ví dụ: vector nhị phân đại diện cho sự hiện diện/vắng mặt của superpixel (đối với ảnh) hoặc từ (đối với văn bản).
2. Dự đoán bằng mô hình gốc (Black-box Prediction): Các mẫu dữ liệu giả $z$ được đưa vào mô hình phức tạp $f$ để thu thập nhãn dự đoán (hoặc xác suất dự đoán) của mô hình gốc.
3. Tính khoảng cách và trọng số (Local Weighting): Khoảng cách ($d_{i}$) giữa mỗi mẫu giả $z_{i}$ và mẫu gốc $x$ được tính toán (ví dụ: sử dụng Cosine Similarity). Khoảng cách này sau đó được chuyển thành trọng số ($w_{i}$) thông qua một hàm kernel (thường là Kernel Gaussian, $w_{i}=exp(-\frac{d_{i}^{2}}{2\sigma^{2}})$). Các mẫu càng gần $x$ sẽ có trọng số $w_{i}$ càng cao. Tham số $\sigma$ (kernel width) là siêu tham số kiểm soát độ rộng của vùng cục bộ được xét, ảnh hưởng trực tiếp đến độ trung thực của xấp xỉ.
4. Chọn các đặc trưng quan trọng (Feature Selection): Thuật toán lựa chọn một tập hợp nhỏ ($m$) các đặc trưng có ảnh hưởng lớn nhất. Việc giảm số lượng đặc trưng (giảm $\Omega(g)$) là cần thiết để đảm bảo tính diễn giải của mô hình $g$.
5. Huấn luyện mô hình đơn giản (Surrogate Model Fitting): Một mô hình tuyến tính đơn giản ($g$, ví dụ: hồi quy tuyến tính) được huấn luyện trên tập hợp các mẫu giả $z$, sử dụng nhãn dự đoán của $f$ làm mục tiêu và áp dụng trọng số $w_{i}$ đã tính. Mô hình $g$ này được tối ưu để xấp xỉ hành vi của $f$ chỉ trong vùng lân cận của $x$.
6. Giải thích kết quả (Interpretation): Phân tích các hệ số hồi quy ($\beta_{i}$) của mô hình đơn giản $g$. Các hệ số này biểu thị mức độ ảnh hưởng của từng đặc trưng đã chọn đến dự đoán của mô hình phức tạp $f$ tại điểm $x$.

2.3 Ứng dụng LIME qua các Dạng Dữ liệu

LIME có tính độc lập với mô hình và có thể áp dụng cho nhiều loại dữ liệu khác nhau.

Dữ liệu Bảng (Tabular Data)

Trong trường hợp dữ liệu bảng (ví dụ: bộ dữ liệu Iris), để tạo mẫu nhiễu loạn hiệu quả, các đặc trưng liên tục thường được chuyển đổi thành các khoảng rời rạc (discretize). Sau khi huấn luyện mô hình, LIME (Local Interpretable Model-agnostic Explanations) sẽ tạo ra các mẫu giả lân cận để giải thích dự đoán của mô hình.
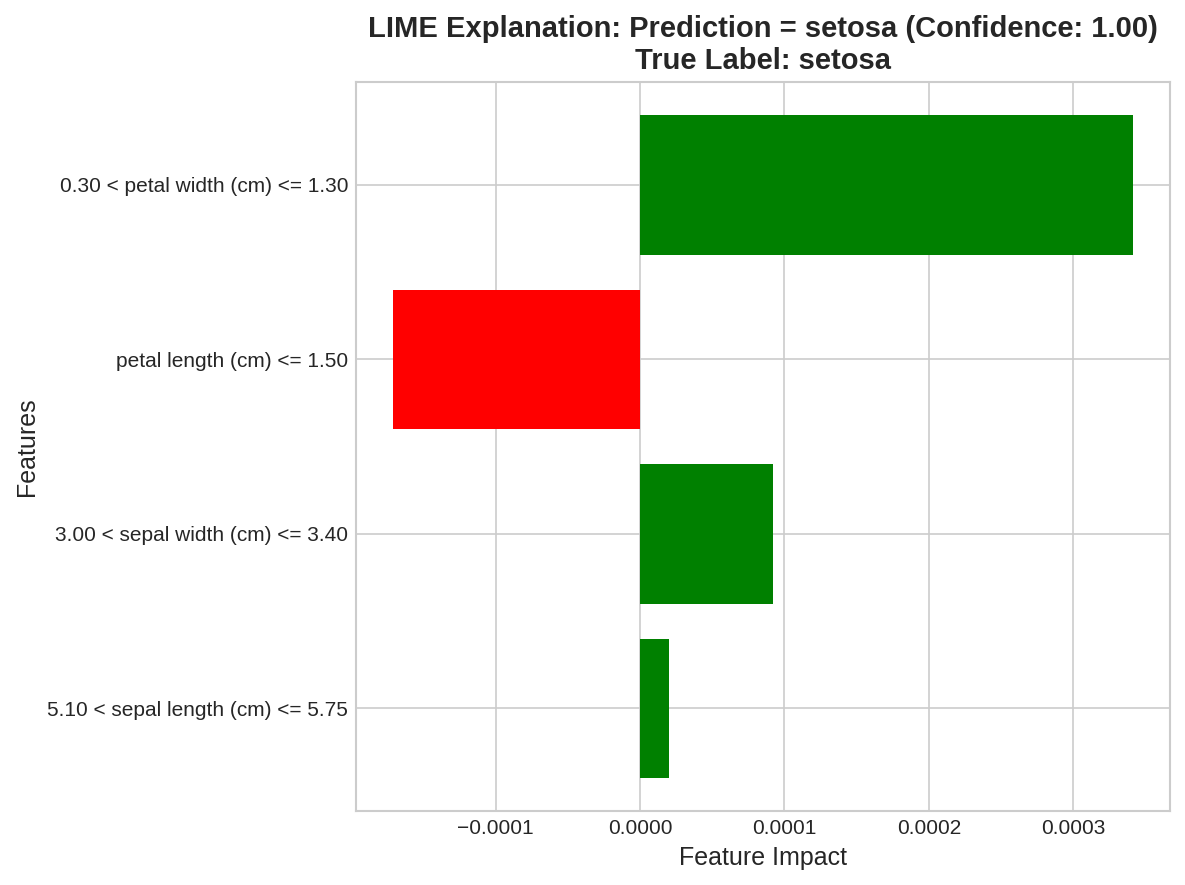
Ví dụ, đối với một mẫu cụ thể, mô hình đã đưa ra Dự đoán = setosa với độ Tin cậy: 1.00 và Nhãn thực: setosa. Biểu đồ LIME cho thấy các điều kiện sau đây là các yếu tố chính đóng góp vào dự đoán này:
• Đóng góp tích cực (thúc đẩy dự đoán setosa - thanh màu xanh lá):
◦ $0.30 < \text{petal width (cm)} \le 1.30$ có tác động mạnh mẽ nhất.
◦ $3.00 < \text{sepal width (cm)} \le 3.40$ có tác động tích cực.
◦ $5.10 < \text{sepal length (cm)} \le 5.75$ có tác động tích cực nhỏ nhất.
• Đóng góp tiêu cực (ngược lại với dự đoán setosa - thanh màu đỏ):
◦ $\text{petal length (cm)} \le 1.50$ là yếu tố có tác động tiêu cực mạnh nhất.
Điều này có nghĩa là, với mẫu này, việc chiều rộng cánh hoa (petal width) nằm trong khoảng từ 0.30 cm đến 1.30 cm là yếu tố quan trọng nhất khiến mô hình dự đoán nó là lớp setosa, trong khi việc chiều dài cánh hoa (petal length) nhỏ hơn hoặc bằng 1.50 cm lại là yếu tố chống lại dự đoán này.

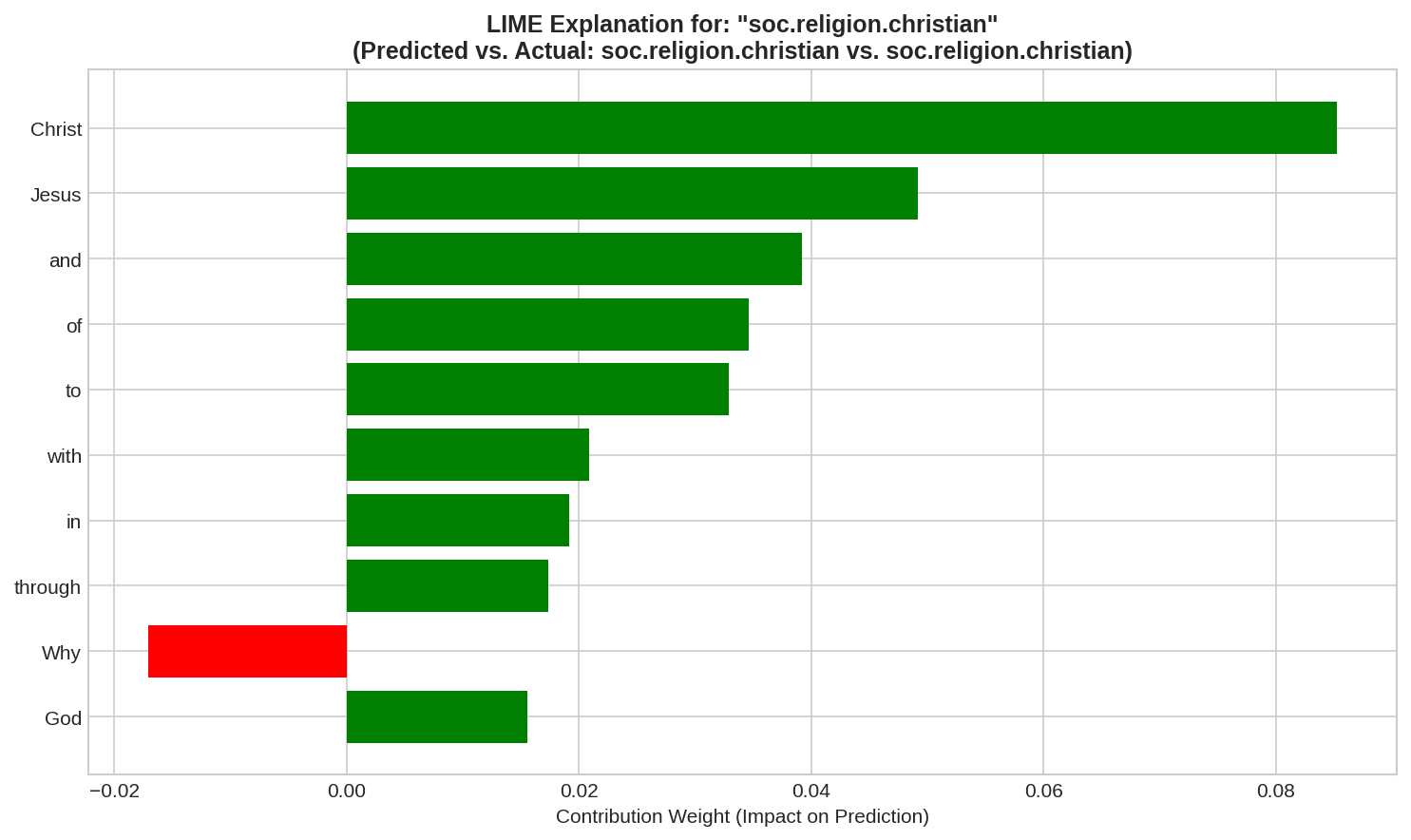
Dữ liệu Văn bản (Text Data)

Với dữ liệu văn bản (ví dụ: phân loại nội dung tôn giáo), LIME tạo mẫu lân cận bằng cách ngẫu nhiên loại bỏ hoặc che (masking) các từ trong câu gốc. Khi phân tích một câu được mô hình dự đoán là có nội dung liên quan đến tôn giáo, LIME có thể làm nổi bật các từ như 'Christ' (+0.0853), 'Jesus' (+0.0492) và 'God' (+0.0156). Điều này chỉ ra rằng mô hình dựa chủ yếu vào sự xuất hiện của các từ mang tính tôn giáo này để đưa ra kết luận,các từ mang tính trung lập, đặt câu hỏi như 'Why' (-0.0171) nhưng không đủ sức mạnh để thay đổi kết quả cuối cùng.

Dữ liệu Hình ảnh (Image Data)

Đối với hình ảnh, LIME chia ảnh thành các vùng nhỏ đồng nhất gọi là superpixel (segment). Mỗi superpixel được xem là một đơn vị đặc trưng. Quá trình nhiễu loạn là việc giữ lại hoặc loại bỏ các superpixel này. Khi LIME được áp dụng để giải thích quyết định của mô hình (ví dụ: ResNet50) về ảnh con mèo này, phân tích hệ số hồi quy cho thấy các superpixel tập trung ở vùng mặt mèo (mũi, miệng) và một phần tai có hệ số cao nhất, chứng tỏ đây là thành phần ảnh hưởng mạnh mẽ nhất đến quyết định phân loại. Các vùng quan trọng được đánh dấu bằng đường viền vàng và hiển thị rõ ở ảnh "Chỉ vùng quan trọng" (như mũi, miệngcủa mèo) đã xác định hiệu quả các vùng mà mô hình sử dụng để nhận diện con mèo.

2.4 Hạn chế và Thách thức Nội tại của LIME

Mặc dù LIME là phương pháp tiên phong trong XAI cục bộ, nó vẫn tồn tại những hạn chế đáng kể, đặc biệt liên quan đến độ tin cậy và tính ổn định.

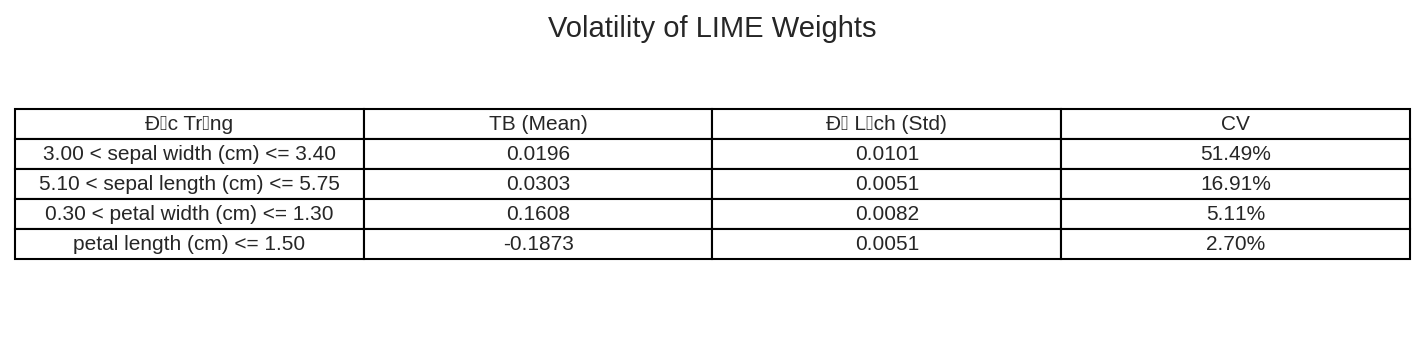
• Tính Không Ổn định (Instability/Inconsistency): Đây là nhược điểm cốt lõi của LIME. LIME phụ thuộc vào việc lấy mẫu ngẫu nhiên (Monte Carlo sampling) trong vùng lân cận. Do đó, việc chạy lại thuật toán nhiều lần với cùng một điểm dữ liệu có thể tạo ra các tập mẫu và mô hình tuyến tính cục bộ khác nhau, dẫn đến các lời giải thích không nhất quán. Tính không ổn định này làm giảm độ tin cậy của giải thích và có thể bị khai thác để thao túng kết quả (ví dụ: XAIFOOLER). Việc thiếu sự đảm bảo về tính ổn định làm cho LIME không phù hợp trong các môi trường pháp lý hoặc các ứng dụng yêu cầu tính tuân thủ cao.
• Giới hạn Cục bộ và Độ Trung thực: Lời giải thích của LIME chỉ phản ánh hành vi của mô hình trong phạm vi lân cận hẹp. Giả định tuyến tính cục bộ có thể thất bại khi ranh giới quyết định thực sự là phi tuyến tính hoặc khi vùng lân cận được mở rộng quá mức, dẫn đến các dự đoán sai lệch.
• Phụ thuộc vào Siêu tham số: Kết quả của LIME nhạy cảm với các tham số như số lượng mẫu giả, cách đo lường độ tương đồng ($\sigma$ của hàm kernel), và phương pháp chuyển đổi biểu diễn dữ liệu. Việc điều chỉnh không cẩn thận các tham số này có thể dẫn đến lời giải thích không chính xác.
• Hiệu năng Tính toán: Quá trình tạo mẫu nhiễu loạn và gọi mô hình hộp đen nhiều lần có thể tốn kém về mặt tính toán, đặc biệt đối với các mô hình phức tạp hoặc dữ liệu lớn (ví dụ: hình ảnh độ phân giải cao), hạn chế ứng dụng trong các tình huống đòi hỏi tốc độ cao.

---

3) Kết

LIME giúp ta hiểu mô hình dự đoán như thế nào, nhưng kết quả đôi khi thiếu ổn định và khó diễn giải thành quy tắc rõ ràng. Để khắc phục điều đó, phương pháp ANCHOR ra đời – hướng tới việc tạo ra các quy tắc giải thích cụ thể và đáng tin cậy hơn.

Blog kế tiếp sẽ giới thiệu về ANCHOR – bước phát triển tiếp theo sau LIME trong Explainable AI.

Tài liệu Tham khảo

1. Duong, T. B., Nguyen, P. T., & Dinh, Q. V. (2024). XAI Introduction: LIME and ANCHOR. AI VIETNAM AIO Course 2024 Reading Material.
2. Ribeiro, M. T., Singh, S., & Guestrin, C. (2016). "Why Should I Trust You?": Explaining the Predictions of Any Classifier (LIME). arXiv:1602.04938.
3. Ribeiro, M. T., Singh, S., & Guestrin, C. (2018). Anchors: High-Precision Model-Agnostic Explanations. Proceedings of the AAAI Conference on Artificial Intelligence, 32.
4. Molnar, C. (2022). Interpretable Machine Learning: A Guide for Making Black Box Models Explainable.
5. Zhong, C., et al. (2023). XAIFOOLER: Manipulating LIME Explanations with Word Replacement. EMNLP 2023.
6. Shagunsodhani, S. (2016). Original paper "LIME: 'Why Should I Trust You?'".
7. LIME Original Paper (2016). The mathematical formulation for LIME's optimization.
8. Ribeiro, M. T., et al. (2016). Nothing Else Matters: Model-Agnostic Explanations By Identifying Prediction Invariance.
9. Aysel, H. I., Cai, X., & Prugel-Bennett, A. (n.d.). The difference between LIME and Anchors approaches. ResearchGate.
10. TUDublin (2023). Comparative research on credit card fraud detection using XAI methods

---

VIII. (XAI) Giải thuật ANCHOR

Trong blog trước, ta đã tìm hiểu về LIME, phương pháp giải thích dự đoán theo hướng cục bộ.

Bài viết này tiếp nối với ANCHOR– cách tiếp cận mới nhằm đưa ra quy tắc “neo” giúp mô hình có thể được giải thích rõ ràng và ổn định hơn. Cùng xem ANCHOR hoạt động thế nào và vì sao nó được xem là bước tiến sau LIME.

1) ANCHOR (High-Precision Model-Agnostic Explanations)

Để khắc phục những hạn chế cố hữu của LIME, đặc biệt là tính không ổn định và giới hạn của xấp xỉ tuyến tính cục bộ, thuật toán ANCHOR (High-Precision Model-Agnostic Explanations) đã được chính nhóm tác giả của LIME đề xuất vào năm 2018. ANCHOR chuyển trọng tâm từ xấp xỉ hành vi mô hình sang việc tìm kiếm các điều kiện đảm bảo độ tin cậy cao.

1.1 Động lực, Mục tiêu và Khái niệm Vùng Neo

Động lực và Vấn đề của LIME

Sự cần thiết của ANCHOR xuất phát từ các trường hợp mà LIME thất bại trong việc xấp xỉ chính xác hành vi phi tuyến tính của mô hình, đặc biệt khi mở rộng vùng cục bộ. Ví dụ, trong bài toán phân tích cảm xúc, LIME gán trọng số cho từ "not" một cách mơ hồ. ANCHOR giải quyết vấn đề này bằng cách tìm ra các luật tương tác rõ ràng (ví dụ: nếu câu chứa {not} AND {bad}, dự đoán là Positive).[1]

Khái niệm Anchor (Vùng Neo)

ANCHOR hoạt động bằng cách xác định một tập hợp các quy tắc (rules) hoặc điều kiện (predicates) dưới dạng luật IF-THEN. Anchor $A$ đại diện cho các điều kiện đủ (sufficient conditions) để mô hình đưa ra cùng một dự đoán. Quy tắc này phải đảm bảo rằng khi một mẫu dữ liệu thỏa mãn các điều kiện trong $A$, mô hình sẽ duy trì dự đoán ban đầu với xác suất cao.

1.2 Thang đo Precision và Coverage

ANCHOR được xây dựng dựa trên hai chỉ số định lượng có ràng buộc thống kê, giúp người dùng hiểu rõ về tính tin cậy và phạm vi áp dụng của lời giải thích.

Độ Chính xác (Precision - $\text{prec}(A)$)

Độ chính xác của Anchor $A$ đo lường tỷ lệ các mẫu nhiễu loạn ($z$) thỏa mãn các điều kiện trong $A$ mà mô hình hộp đen ($f$) vẫn dự đoán cùng nhãn với mẫu gốc ($x$).

$\text{prec}(A)=\mathbb{E}{\mathcal{D}(z|A)}[\mathbb{I}{f(x)=f(z)}] \quad$

Trong thực tế, do không thể biết chính xác phân phối dữ liệu, ANCHOR tìm kiếm các anchor thỏa mãn một ràng buộc thống kê cao về độ chính xác ước lượng:

$P(\text{prec}(A)\ge\tau)\ge1-\delta \quad$

Trong đó, $\tau$ là ngưỡng độ chính xác tối thiểu (ví dụ: 90%), và $1-\delta$ là mức ý nghĩa (mức độ tin cậy thống kê). Ràng buộc này đảm bảo rằng anchor được tìm thấy gần như chắc chắn là đáng tin cậy.

Độ Bao phủ (Coverage - $\text{cov}(A)$)

Độ bao phủ của Anchor $A$ đo lường tính tổng quát của luật giải thích, tức là xác suất một mẫu ngẫu nhiên từ không gian nhiễu loạn thỏa mãn điều kiện của $A$.

$\text{cov}(A)=\mathbb{E}_{\mathcal{D}(z)}[A(z)] \quad$

Anchor có độ bao phủ cao có nghĩa là luật giải thích có thể áp dụng được cho nhiều mẫu dữ liệu khác nhau, cung cấp một cái nhìn khái quát hơn về hành vi cục bộ của mô hình.

Bài toán tối ưu hóa của ANCHOR là tìm kiếm Anchor $A$ có độ bao phủ lớn nhất ($\max \text{cov}(A)$) nhưng vẫn phải thỏa mãn ràng buộc thống kê nghiêm ngặt về độ chính xác ($\text{prec}(A)\ge\tau$).

1.3 Thuật toán Tìm kiếm Anchor Tối ưu

Quá trình tìm kiếm Anchor tối ưu được mô hình hóa thành bài toán Multi-Armed Bandit (MAB), một kỹ thuật thường dùng trong học tăng cường (Reinforcement Learning) để thăm dò hiệu quả không gian tìm kiếm.

Quy trình Beam Search và KL-LUCB

1. Sinh Luật Ứng viên (Bottom-up): Thuật toán bắt đầu bằng cách sinh ra các predicate đơn lẻ từ các đặc trưng của mẫu gốc. Sau đó, các predicate này được kết hợp dần dần (bottom-up construction) để tạo ra các anchor ứng viên phức tạp hơn. Phương pháp này ưu tiên tìm kiếm các anchor ngắn gọn, vì chúng có khả năng có độ bao phủ cao hơn.
2. Tạo mẫu Lân cận có Điều kiện: Khác với LIME (lấy mẫu ngẫu nhiên), ANCHOR tạo mẫu nhiễu loạn ($z$) bằng cách cố định các đặc trưng đã có trong Anchor $A$ và chỉ thay đổi các đặc trưng không thuộc $A$. Điều này đảm bảo rằng các mẫu giả sinh ra luôn thỏa mãn điều kiện của anchor đang xét.
3. Tối ưu hóa Bằng KL-LUCB: Thuật toán KL-LUCB (Kullback–Leibler Lower Upper Confidence Bound) được sử dụng để ước lượng độ chính xác của các anchor ứng viên một cách hiệu quả.
   • Thuật toán này liên tục lấy mẫu và tính toán khoảng tin cậy cho độ chính xác của từng anchor.
   • Nếu giới hạn dưới (lower bound) của độ chính xác của một anchor vượt qua ngưỡng $\tau$, anchor đó được chấp nhận.
   • Nếu giới hạn trên (upper bound) của độ chính xác không thể đạt được ngưỡng $\tau$, anchor đó bị loại bỏ.
   • Quá trình tìm kiếm sử dụng Beam Search để khám phá không gian giải pháp, tập trung vào các ứng viên tốt nhất ở mỗi bước mở rộng.

Việc sử dụng KL-LUCB giúp ANCHOR tối ưu hóa số lần gọi mô hình hộp đen cần thiết để đạt được ràng buộc thống kê $1-\delta$, giải quyết trực tiếp chi phí tính toán cao vốn là một nhược điểm chung của các phương pháp dựa trên nhiễu loạn.

1.4 Ứng dụng ANCHOR qua các Dạng Dữ liệu

Dữ liệu Bảng (Tabular Data)

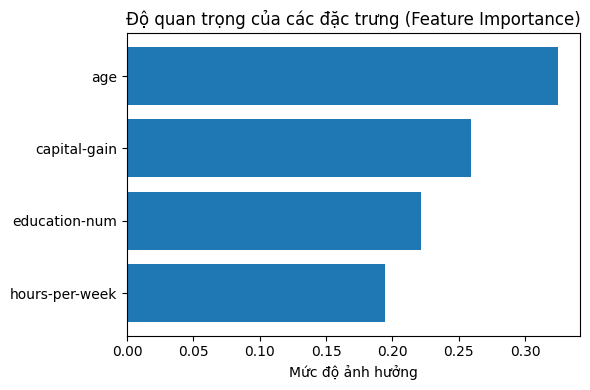
Biểu đồ đầu tiên cho thấy mức độ ảnh hưởng của từng đặc trưng đến quyết định của mô hình Random Forest. Dễ thấy rằng tuổi (age) là yếu tố quan trọng nhất, tiếp theo là lãi vốn (capital-gain), số năm học (education-num) và số giờ làm việc mỗi tuần (hours-per-week). Điều này phản ánh khá đúng thực tế: người lớn tuổi thường có nhiều kinh nghiệm, có khả năng đạt mức thu nhập cao hơn; những người có lãi vốn thường thuộc nhóm có đầu tư hoặc tài sản; và trình độ học vấn cao cũng góp phần lớn vào cơ hội có thu nhập trên 50K. Mặc dù số giờ làm việc mỗi tuần cũng có tác động, nhưng yếu tố này yếu hơn so với học vấn và tuổi tác, cho thấy rằng “chất lượng” (kinh nghiệm, học vấn, tài sản) có ảnh hưởng lớn hơn “số lượng” (thời gian làm việc).

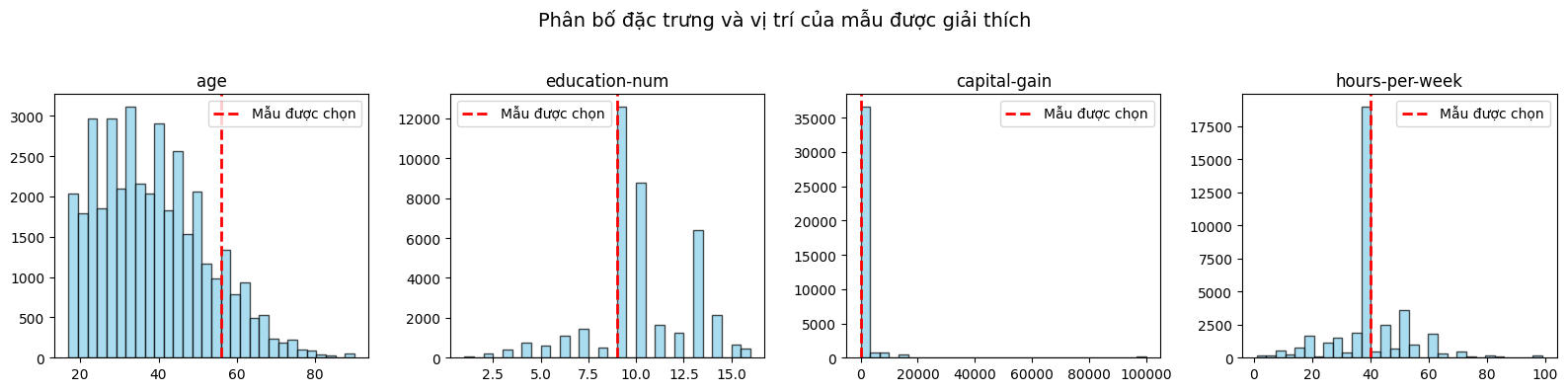
Biểu đồ thứ hai minh họa vị trí của mẫu được giải thích trong phân bố của toàn bộ tập dữ liệu. Đường đỏ biểu thị giá trị của mẫu — một người khoảng 60 tuổi, có 10 năm học (tương đương trình độ đại học), không có lãi vốn, và làm việc 40 giờ/tuần. So với phần lớn dữ liệu, người này lớn tuổi hơn và có trình độ cao hơn trung bình, dù không có thu nhập đầu tư. Anchor rule được sinh ra bởi mô hình cho thấy rằng chỉ cần hai điều kiện “tuổi > 50” và “số năm học ≥ 9” đã đủ để mô hình gần như chắc chắn dự đoán thu nhập > 50K, với độ tin cậy rất cao. Điều này giúp ta hiểu rằng mô hình “neo” quyết định của nó vào những yếu tố mang tính nền tảng (tuổi và học vấn) hơn là yếu tố ngẫu nhiên như lãi vốn hay số giờ làm việc.

Dữ liệu Văn bản (Text Data)

Phương pháp ANCHOR giúp giải thích rõ ràng cách mô hình phân loại văn bản đưa ra quyết định. Trong thí nghiệm với bộ dữ liệu 20 Newsgroups (alt.atheism và soc.religion.christian), mô hình Random Forest đạt độ chính xác 0.93. Anchor phát hiện các từ khóa đặc trưng như "god", "church", "jesus" cho lớp Christian và "atheist", "belief" cho lớp Atheism. Kết quả cho thấy Precision = 0.97 và Coverage = 0.12, nghĩa là khi xuất hiện các từ như "god" và "christian", mô hình dự đoán đúng tới 97%, dù quy tắc chỉ bao phủ khoảng 12% dữ liệu. Điều này chứng minh Anchor cung cấp giải thích cục bộ có độ tin cậy cao, giúp xác định khi nào mô hình thực sự chắc chắn về dự đoán của mình và làm rõ những đặc trưng ngôn ngữ then chốt quyết định phân loại.

Dữ liệu Hình ảnh (Image Data)

Anchor cho dự đoán lớp "tiger cat" bằng ResNet50

ResNet50 cho lớp "tiger cat" bằng với Anchor, Các siêu điểm ảnh được khoanh viền vàng biểu thị Anchor—tập hợp các pixel quan trọng nhất (chủ yếu là khuôn mặt và phần thân) mà mô hình dựa vào để đưa ra dự đoán. Với Precision (Độ chính xác) là 1.000, Anchor này cho thấy sự hiện diện của các đặc trưng được đánh dấu là điều kiện cần và đủ tuyệt đối để mô hình luôn phân loại là "tiger cat". Coverage (Độ phủ) 0.504 chỉ ra rằng tập hợp các đặc trưng quan trọng này chiếm 50.4% diện tích hình ảnh, chứng tỏ mô hình không cần nhìn toàn bộ bức ảnh, mà chỉ cần tập trung vào hơn một nửa các chi tiết nổi bật của con mèo để đưa ra quyết định với độ tin cậy tuyệt đối.

1.5 Hạn chế và Thách thức của ANCHOR

Mặc dù ANCHOR cung cấp lời giải thích có độ tin cậy cao hơn LIME, thuật toán này vẫn phải đối mặt với một số thách thức kỹ thuật và thực tiễn.

• Độ phức tạp Cài đặt: ANCHOR yêu cầu nhiều tham số điều chỉnh hơn so với LIME.[1] Hơn nữa, việc thiết kế hàm lấy mẫu (sampling function) cho các mẫu nhiễu loạn phải được tùy chỉnh và phù hợp với từng loại dữ liệu (ví dụ: cách tạo mẫu nhiễu loạn cho hình ảnh, văn bản), làm tăng độ phức tạp trong quá trình triển khai.
• Đánh đổi Coverage và Specificity: Thường xuyên xảy ra sự đánh đổi giữa độ chính xác và độ bao phủ.Các anchor có độ chính xác rất cao ($\tau$) thường rất cụ thể, dẫn đến độ bao phủ thấp (ví dụ: 2% trong ví dụ dữ liệu bảng). Để tăng độ bao phủ, cần phải áp dụng các kỹ thuật như phân rã (discretization) hoặc gom nhóm (aggregation) các điều kiện. Tuy nhiên, nếu thực hiện không đúng cách, các kỹ thuật này có thể làm mất đi tính trung thực của lời giải thích.
• Chi phí Tính toán Cao và Tính không ổn định: Mặc dù thuật toán MAB/KL-LUCB được thiết kế để giảm thiểu số lần gọi mô hình, ANCHOR vẫn yêu cầu nhiều lần gọi mô hình hộp đen để đạt được ràng buộc thống kê nghiêm ngặt. Điều này làm cho thời gian chạy có thể chậm và không ổn định, tùy thuộc vào tốc độ của mô hình gốc.
• Thiếu Tường minh trong Định nghĩa Coverage: Khái niệm độ bao phủ (coverage) không phải lúc nào cũng có định nghĩa phổ quát cho mọi loại dữ liệu. Ví dụ, cách so sánh các superpixel giữa các bức ảnh khác nhau để tính coverage vẫn chưa hoàn toàn rõ ràng, dẫn đến sự không nhất quán hoặc khó hiểu trong giải thích phạm vi áp dụng của luật.

2) So sánh LIME và ANCHOR:

LIME và ANCHOR, mặc dù được phát triển bởi cùng một nhóm nghiên cứu và đều thuộc nhóm phương pháp XAI hậu kiểm cục bộ, lại đại diện cho hai triết lý giải thích khác nhau. LIME tập trung vào xấp xỉ tuyến tính, trong khi ANCHOR tập trung vào đảm bảo phi tuyến thông qua luật quyết định.

2.1 Khác biệt Cấu trúc Lời Giải thích

LIME cung cấp lời giải thích dưới dạng trọng số tương đối của các đặc trưng, cho biết đặc trưng nào quan trọng hơn trong vùng cục bộ. Mô hình thay thế là tuyến tính, khiến cho việc giải thích các tương tác phi tuyến tính phức tạp (ví dụ: tác động kép của từ not với các từ khác) trở nên mơ hồ.

Ngược lại, ANCHOR cung cấp lời giải thích dưới dạng quy tắc tuyệt đối (IF-THEN). Các quy tắc này đại diện cho các điều kiện đủ, có tính ngữ nghĩa rõ ràng, giúp người dùng hiểu chính xác tập hợp điều kiện nào dẫn đến quyết định, vượt qua giới hạn tuyến tính của LIME.

2.2 Độ Ổn định và Tính Đảm bảo Fidelity

Sự khác biệt lớn nhất nằm ở độ tin cậy của lời giải thích.

LIME, do phụ thuộc vào quá trình lấy mẫu ngẫu nhiên và xấp xỉ tuyến tính, có tính không ổn định cao. Việc chạy lại thuật toán có thể tạo ra các kết quả khác nhau, làm giảm độ tin cậy của giải thích trong các môi trường quan trọng.

ANCHOR được thiết kế để mang lại đảm bảo thống kê cao. Việc tìm kiếm được điều khiển bởi ràng buộc $P(\text{prec}(A)\ge\tau)\ge1-\delta$ đảm bảo rằng độ chính xác của Anchor gần như chắc chắn đạt ngưỡng yêu cầu. Điều này làm cho ANCHOR ổn định và đáng tin cậy hơn nhiều so với LIME trong các ứng dụng sản xuất.

2.3 Tính Khái quát hóa Cục bộ (Local Generalization)

Cả hai phương pháp đều cung cấp giải thích cục bộ, nhưng ANCHOR định lượng khả năng khái quát hóa này bằng chỉ số Coverage. Coverage cho biết phạm vi không gian dữ liệu rộng hơn mà quy tắc Anchor có thể áp dụng được, mang lại tính tái sử dụng cho lời giải thích trên các mẫu mới trong vùng neo.

LIME thiếu một cơ chế định lượng rõ ràng để xác định phạm vi mà tại đó xấp xỉ tuyến tính vẫn còn trung thực. Khả năng khái quát hóa của LIME bị giới hạn trong vùng lân cận rất hẹp của điểm $x$.

2.4 Khác biệt về Cơ chế Tối ưu hóa và Chi phí

LIME sử dụng phương pháp dựa trên tối ưu hóa xấp xỉ hàm (fitting a surrogate model). ANCHOR sử dụng phương pháp dựa trên thăm dò hiệu quả (MAB/KL-LUCB) để đảm bảo ràng buộc thống kê. Sự chuyển đổi này cho thấy sự thay đổi cơ chế cốt lõi từ việc tìm kiếm mô hình thay thế tốt nhất sang tìm kiếm điều kiện đảm bảo độ tin cậy cao nhất.

Mặc dù phức tạp hơn, ANCHOR cố gắng tối ưu hóa số lần gọi mô hình hộp đen bằng KL-LUCB. Tuy nhiên, do yêu cầu về ràng buộc thống kê nghiêm ngặt, chi phí tính toán tổng thể của ANCHOR thường cao hơn và phức tạp hơn để triển khai so với LIME.

Bảng So sánh Chuyên sâu LIME và ANCHOR

Tiêu chí	LIME (Local Interpretable Model-Agnostic Explanations)	ANCHOR (High-Precision Model-Agnostic Explanations)
Triết lý Giải thích	Xấp xỉ tuyến tính cục bộ (Local Approximation)	Điều kiện đủ phi tuyến, Bất biến dự đoán (Sufficient Conditions)
Cấu trúc Đầu ra	Trọng số Đặc trưng (Relative Contribution)	Luật IF-THEN rõ ràng, có thể tái sử dụng
Tính Đảm bảo Fidelity	Thấp (Dễ bị lỗi khi ranh giới quyết định phức tạp)	Cao (High Precision Guarantee: $P(\text{prec}(A)\ge\tau)\ge1-\delta$) [1]
Độ Ổn định (Stability)	Thấp (Dễ thay đổi do lấy mẫu ngẫu nhiên)	Cao (Luật được thiết kế để ổn định trên vùng dữ liệu) [8]
Khả năng Khái quát	Rất hẹp, chỉ áp dụng cho một điểm $x$	Khái quát hóa cục bộ được định lượng bằng Coverage
Cơ chế Tối ưu hóa	Huấn luyện mô hình thay thế có trọng số	Thuật toán KL-LUCB (Multi-Armed Bandit) và Beam Search [1, 9]
Chi phí Tính toán	Trung bình, phụ thuộc vào số lượng mẫu $N$	Thường Cao hơn, do quá trình tìm kiếm tối ưu và ràng buộc thống kê [1]

3) Kết luận

3.1 Tóm tắt Những Đóng góp Khoa học Chính

Sự phát triển của LIME và ANCHOR đại diện cho bước tiến lớn trong lĩnh vực XAI cục bộ, cho phép các nhà nghiên cứu và người dùng "mở" các hộp đen phức tạp.

LIME (2016) đã thiết lập nền tảng cho các phương pháp XAI hậu kiểm bằng cách chứng minh tính khả thi của việc sử dụng các mô hình thay thế đơn giản để xấp xỉ hành vi cục bộ của mô hình gốc.[2] Mặc dù LIME mang lại tính linh hoạt (model-agnostic) và trực quan, tính không ổn định vốn có do dựa vào lấy mẫu ngẫu nhiên và xấp xỉ tuyến tính đã đặt ra những giới hạn nghiêm trọng về độ tin cậy.

ANCHOR (2018) là sự cải tiến khoa học trực tiếp, chuyển trọng tâm từ "xấp xỉ" sang "đảm bảo". Bằng cách giới thiệu khái niệm Anchor (luật IF-THEN) với ràng buộc thống kê cao về độ chính xác (Precision Guarantee), ANCHOR đã nâng cao đáng kể mức độ tin cậy và khả năng tái sử dụng của lời giải thích cục bộ, giải quyết hiệu quả những vấn đề mà LIME còn tồn đọng. Sự chuyển đổi này cho thấy yêu cầu ngày càng cao của cộng đồng AI đối với các giải thích không chỉ đơn giản mà còn phải có tính đảm bảo thống kê nghiêm ngặt.

3.2 Ứng dụng Thực tiễn

Việc lựa chọn giữa LIME và ANCHOR nên dựa trên mục tiêu ứng dụng và mức độ quan trọng của hệ thống:

• LIME được khuyến nghị sử dụng trong giai đoạn phát triển và gỡ lỗi (debugging). LIME cung cấp phản hồi trực quan, nhanh chóng về tầm quan trọng tương đối của các đặc trưng, giúp nhà phát triển xác định các mô hình có thể dựa vào các đặc trưng không mong muốn hoặc bị thiên vị.
• ANCHOR là lựa chọn vượt trội cho các ứng dụng sản xuất quan trọng (high-stakes), như y tế, tài chính, hoặc các hệ thống yêu cầu tuân thủ quy định pháp lý. Khả năng cung cấp các luật giải thích có độ tin cậy cao, định lượng được phạm vi áp dụng (Coverage), khiến ANCHOR trở thành công cụ lý tưởng khi cần bằng chứng giải thích không thể phủ nhận. Khả năng tìm kiếm các điều kiện đủ (sufficient conditions) cho phép ANCHOR phát hiện các quy tắc hiếm nhưng cực kỳ đáng tin cậy (độ chính xác 97%, độ bao phủ thấp), rất quan trọng trong việc kiểm tra tính tuân thủ hoặc phát hiện bất thường.

Kịch bản Ứng dụng	LIME	ANCHOR
Giai đoạn Debug/Phát triển	Nên dùng. Cung cấp phản hồi trực quan, nhanh chóng về các đặc trưng chính ảnh hưởng đến dự đoán.	Có thể dùng. Cần thiết khi nghi ngờ mô hình dựa vào các tương tác phi tuyến.
Ứng dụng Sản xuất (High-Stakes)	Không nên dùng. Thiếu độ tin cậy và đảm bảo thống kê cần thiết cho các hệ thống yêu cầu tuân thủ.	Nên dùng. Lý tưởng khi yêu cầu tính minh bạch và độ tin cậy cao, cung cấp bằng chứng giải thích có thể tái sử dụng (Coverage).
Cấu trúc Giải thích Yêu cầu	Khi chỉ cần biết đặc trưng nào quan trọng hơn đặc trưng nào (Trọng số tương đối).	Khi cần biết tập hợp đặc trưng nào là điều kiện đủ để quyết định xảy ra.

3.3 Triển vọng Tương lai của XAI

Sự thành công của LIME và ANCHOR đã định hình lĩnh vực XAI cục bộ dựa trên nhiễu loạn. Các nghiên cứu tiếp theo sẽ tập trung giải quyết các thách thức còn tồn tại, bao gồm chi phí tính toán cao và sự đánh đổi giữa Coverage/Precision. Việc tích hợp các lợi thế của ANCHOR (độ tin cậy) với các phương pháp hiệu quả hơn (ví dụ: cải tiến thuật toán MAB) và mở rộng khả năng giải thích sang các mô hình phức tạp hơn (như mô hình ngôn ngữ lớn và mô hình sinh) sẽ là trọng tâm chính của XAI trong tương lai. Mục tiêu cuối cùng là tạo ra các lời giải thích không chỉ đơn giản và trung thực, mà còn phải ổn định và có thể áp dụng rộng rãi với sự đảm bảo thống kê tuyệt đối.

Tài liệu Tham khảo

1. Duong, T. B., Nguyen, P. T., & Dinh, Q. V. (2024). XAI Introduction: LIME and ANCHOR. AI VIETNAM AIO Course 2024 Reading Material.
2. Ribeiro, M. T., Singh, S., & Guestrin, C. (2016). "Why Should I Trust You?": Explaining the Predictions of Any Classifier (LIME). arXiv:1602.04938.
3. Ribeiro, M. T., Singh, S., & Guestrin, C. (2018). Anchors: High-Precision Model-Agnostic Explanations. Proceedings of the AAAI Conference on Artificial Intelligence, 32.
4. Molnar, C. (2022). Interpretable Machine Learning: A Guide for Making Black Box Models Explainable.
5. Zhong, C., et al. (2023). XAIFOOLER: Manipulating LIME Explanations with Word Replacement. EMNLP 2023.
6. Shagunsodhani, S. (2016). Original paper "LIME: 'Why Should I Trust You?'".
7. LIME Original Paper (2016). The mathematical formulation for LIME's optimization.
8. Ribeiro, M. T., et al. (2016). Nothing Else Matters: Model-Agnostic Explanations By Identifying Prediction Invariance.
9. Aysel, H. I., Cai, X., & Prugel-Bennett, A. (n.d.). The difference between LIME and Anchors approaches. ResearchGate.
10. TUDublin (2023). Comparative research on credit card fraud detection using XAI methods

IX. (MLOps) Data Version Control

1) Góc nhìn lý thuyết

1.1) Tóm tắt về AI, MLOps

1.1.1) AI trong Software

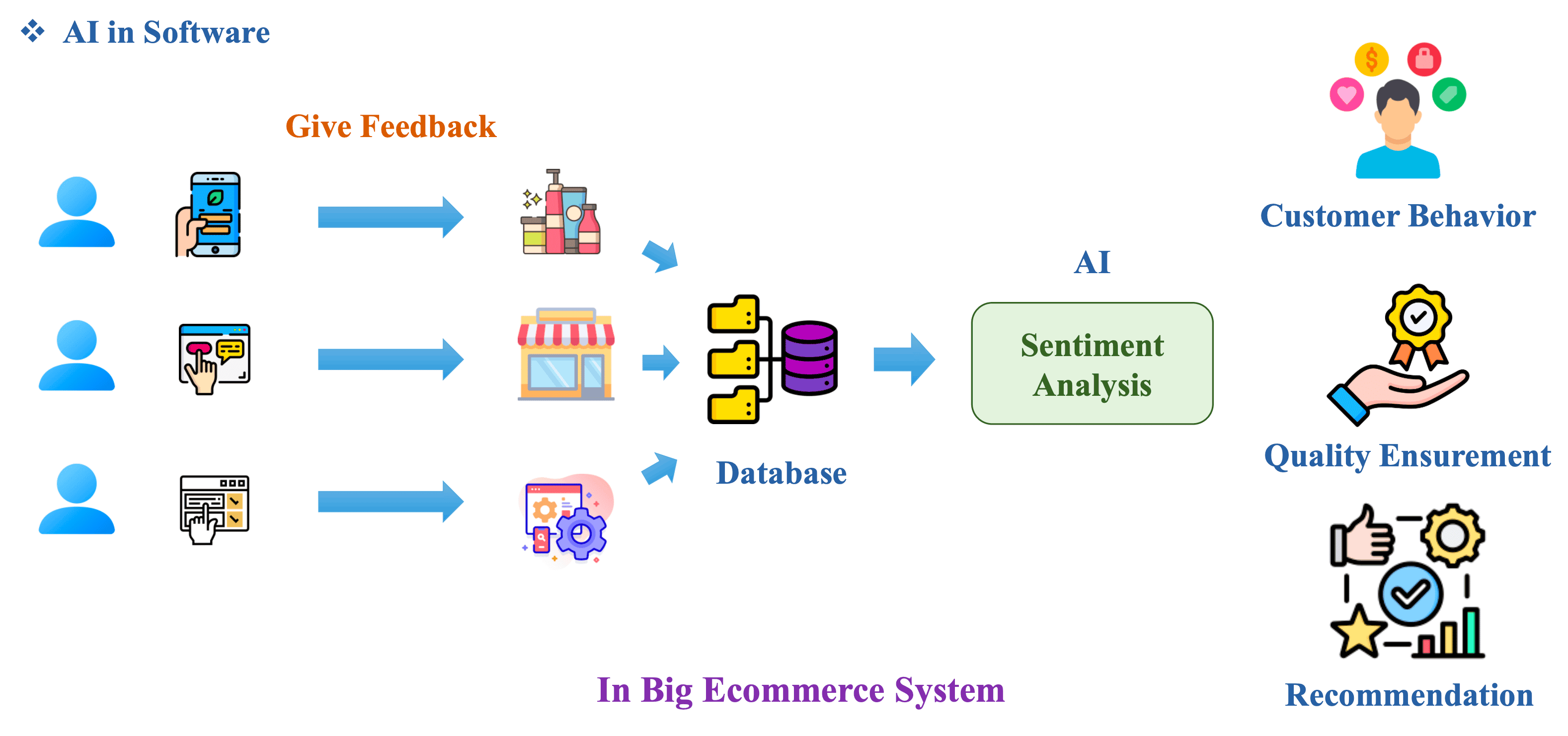
Hình 1: AI in Big Ecommerce System [1]

AI chỉ là một function để giải các bài toán cụ thể trong 1 hệ thống lớn. Ví dụ, trong hệ thống thương mại điện tử, AI có thể dùng để phân loại cảm xúc của khách hàng, giúp doanh nghiệp:

• Phân tích hành vi khách hàng.
• Đảm bảo chất lượng sản phẩm.
• Gợi ý sản phẩm theo sở thích khách hàng.

1.2) ML Life Cycle

Hình 2: Machine Learning Life Cycle [1]

Một Machine Learning Life Cycle gồm các bước theo thứ tự sau:

• Vòng ngoài (Chu trình cấp cao - Màu xanh):

• Business Require (Yêu cầu kinh doanh): Xác định mục tiêu, giá trị mà doanh nghiệp muốn có từ ML.

• Problem Define (Định nghĩa vấn đề): Chuyển đổi yêu cầu kinh doanh thành bài toán ML cụ thể.

• Deploy Model (Triển khai mô hình): Đưa mô hình đã xây dựng vào sử dụng thực tế.

• Monitoring & Analyse Insights (Giám sát và phân tích): Theo dõi hiệu suất mô hình, phát hiện các sự cố, khai thác kết quả để liên tục cải tiến.

• Khi phát hiện model không đáp ứng yêu cầu hoặc thị trường, vòng này bắt đầu lại từ “Business Require”, đảm bảo sản phẩm ML luôn phục vụ tối ưu các mục tiêu của doanh nghiệp.

• Vòng trong (Chu trình kỹ thuật - Màu nâu):

• Data Collection (Thu thập dữ liệu): Tập hợp dữ liệu cần thiết cho dự án.

• Data Processing (Xử lý dữ liệu): Làm sạch, chuẩn hoá dữ liệu.

• Feature Engineering (Xây dựng đặc trưng): Tạo các biến số tối ưu phục vụ huấn luyện model.

• Model Training (Huấn luyện mô hình): Đào tạo mô hình ML với dữ liệu đã xử lý.

• Model Evaluate (Đánh giá mô hình): Kiểm định chất lượng, độ chính xác; nếu chưa đạt thì cần lặp lại các bước trên cho đến khi tốt hơn.

2) Data versioning

Khi team AI cùng làm các experiment về các model AI, họ thường gặp các vấn đề sau:

• Quá nhiều file data version
• Data file và code không quản lý cùng nhau
  -> Teamwork và tốc độ, hiệu suất công việc bị giảm đáng kể
  -> Data versioning ra đời để giải quyết các hạn chế trên
  
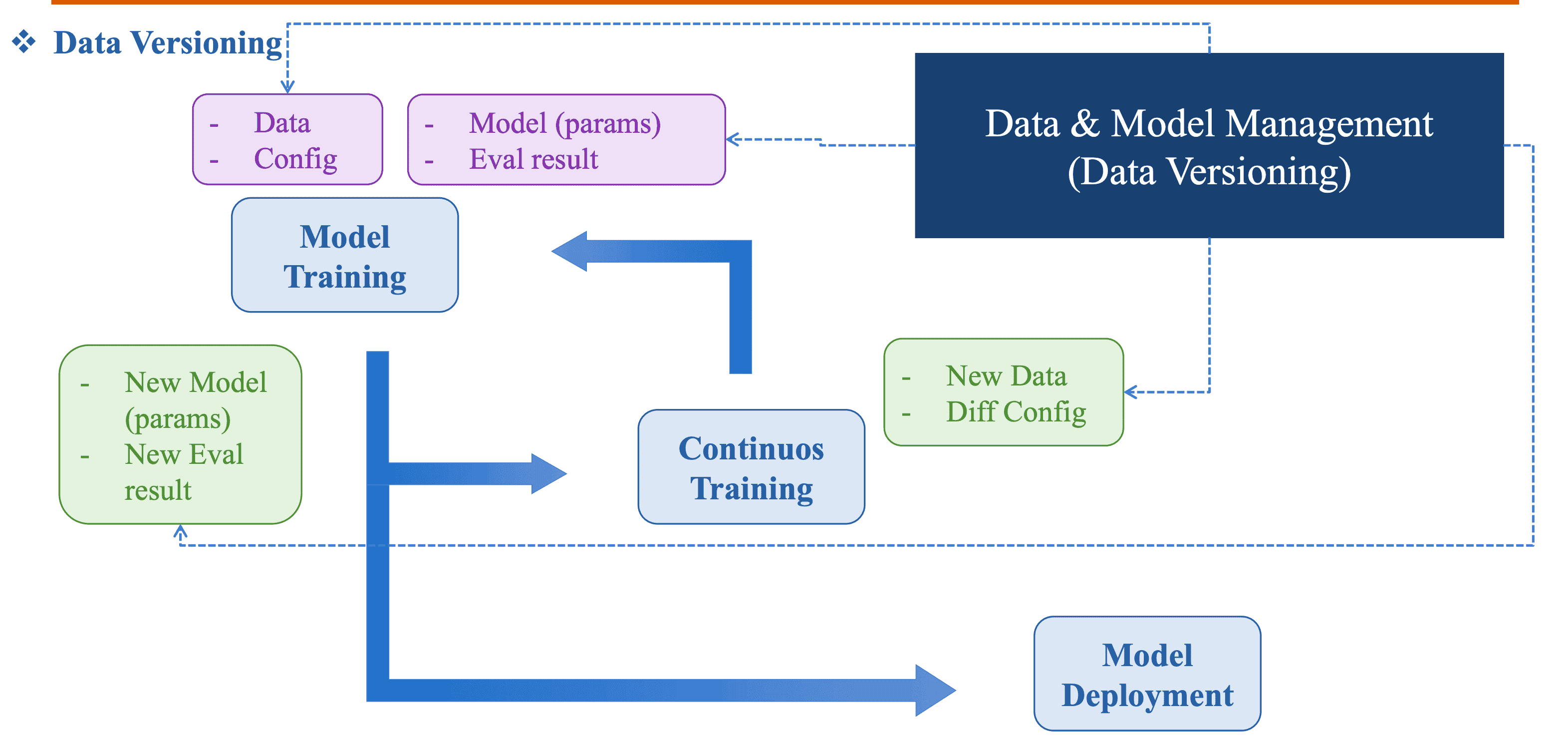
  Hình 3: Data Versioning trong MLOps pipeline [1]

3) DVC overview

Data Version Control (DVC) chính là git cho data, một công cụ mã nguồn mở giúp quản lý dữ liệu và mô hình trong quá trình phát triển các hệ thống học máy (Machine Learning – ML). Giống như Git giúp theo dõi mã nguồn, DVC giúp theo dõi và quản lý dữ liệu đầu vào, mô hình, và các kết quả trong các dự án học máy. Điều này đặc biệt quan trọng trong các dự án mà dữ liệu có kích thước lớn và có sự thay đổi liên tục, như trong phân loại và phân đoạn hình ảnh.

DVC không chỉ giúp theo dõi phiên bản dữ liệu mà còn cung cấp khả năng hợp tác giữa các nhóm, tăng cường sự tái sử dụng mô hình, và dễ dàng tái tạo lại kết quả từ các dữ liệu và mô hình trước đó.

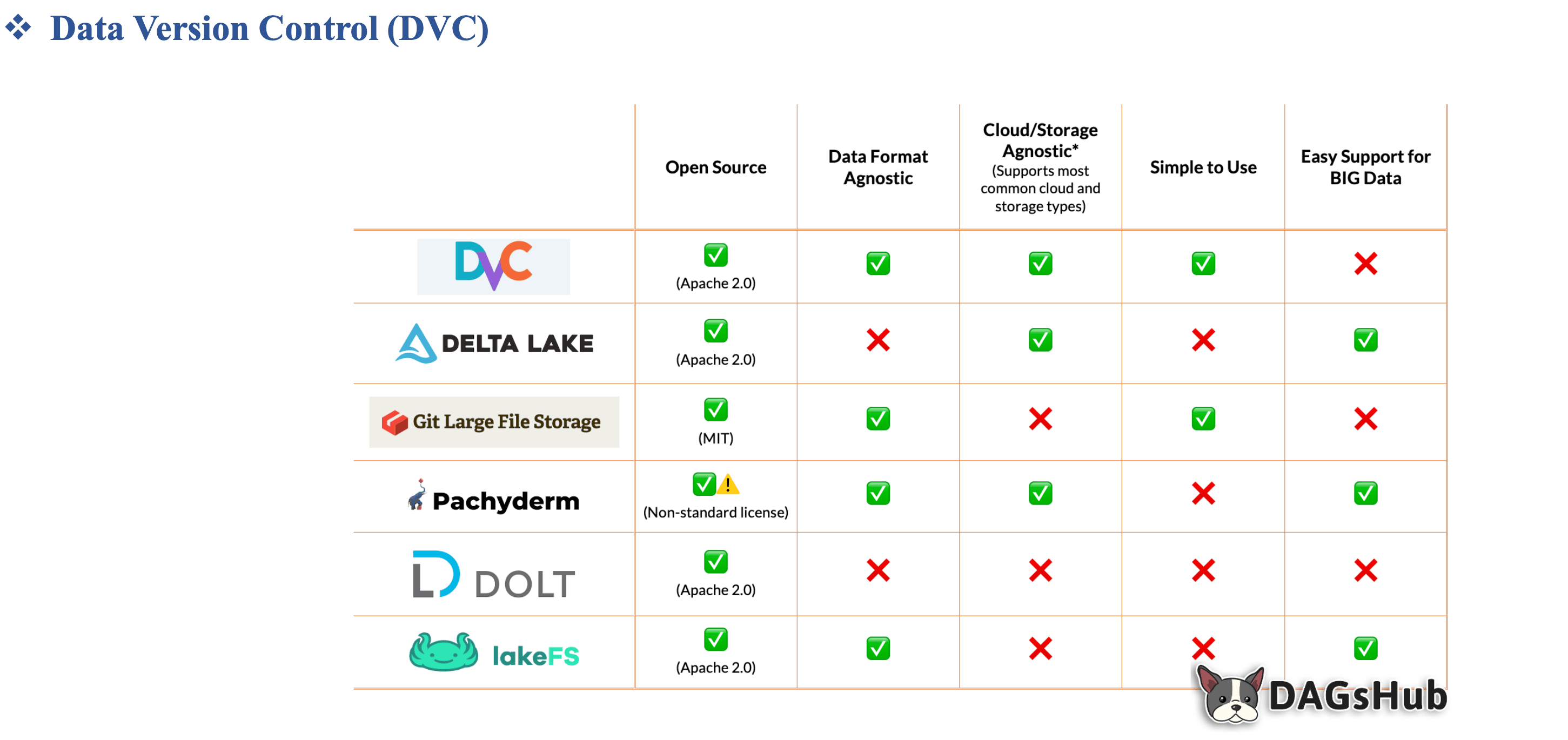
Hình 4: Bảng so sánh giữa các Data Versioning Platform [1]

3.1) Versioning Data và Models

Hình 5: Versioning Data và Models [1]

• DVC cho phép quản lý data, features (source code), model cùng nhau theo git commit.
• DVC cho phép chuyển đổi giữa các data version.
• Kết quả là chúng ta có 1 history hoàn chỉnh cho cả data, features và model.

Lợi ích:

• Nhẹ: DVC là một công cụ dòng lệnh miễn phí, mã nguồn mở, không yêu cầu cơ sở dữ liệu, máy chủ hay bất kỳ dịch vụ đặc biệt nào.

• Tính nhất quán: Giữ cho dự án của bạn dễ đọc với tên file ổn định — chúng không cần phải thay đổi chỉ vì dữ liệu thay đổi. Không cần các đường dẫn phức tạp như data/20190922/labels_v7_final hoặc phải liên tục chỉnh sửa chúng trong mã nguồn.

• Quản lý dữ liệu hiệu quả: Sử dụng giải pháp lưu trữ quen thuộc và tiết kiệm chi phí cho dữ liệu và mô hình (ví dụ SFTP, S3, HDFS, v.v.) — không bị ràng buộc bởi Git hosting. DVC tối ưu hóa quá trình lưu trữ và chuyển tải các file lớn.

• Giúp dễ dàng quá trình Collaboration: Dễ dàng phân phối phát triển dự án và chia sẻ dữ liệu của dự án cả nội bộ lẫn bên ngoài, hoặc tái sử dụng ở các nơi khác.

• Tuân thủ dữ liệu (Data compliance): Xem xét các lần chỉnh sửa dữ liệu như các pull request trên Git. Kiểm tra lịch sử bất biến của dự án để biết khi nào các bộ dữ liệu hoặc mô hình được chấp thuận, và lý do tại sao.

• GitOps: Kết nối dự án khoa học dữ liệu của bạn với hệ sinh thái Git. Quy trình làm việc với Git mở ra các công cụ CI/CD nâng cao (như CML), các mô hình chuyên biệt như data registry, và nhiều best practice khác.

3.2) CI/CD cho ML

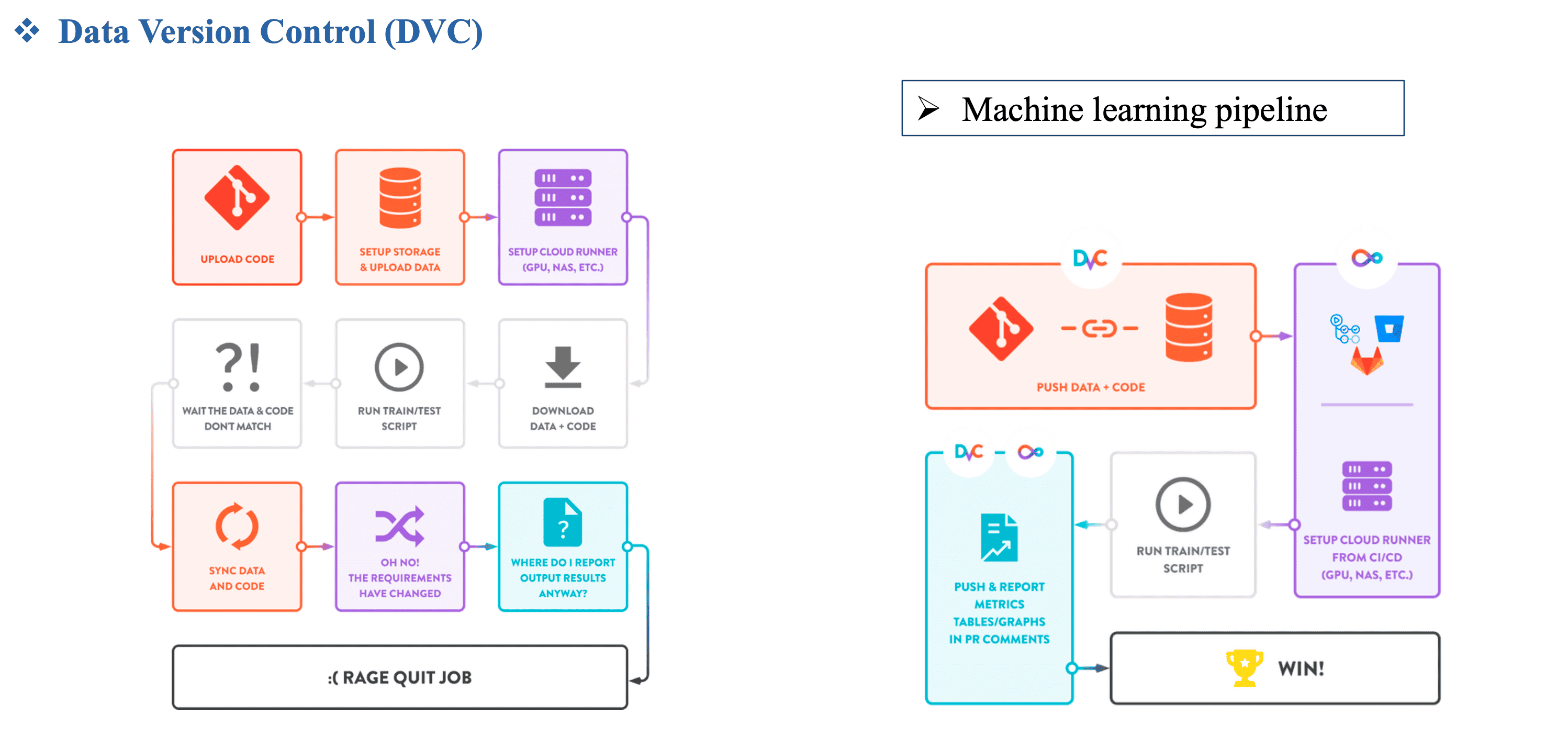
Hình 6: DVC trong CI/CD cho ML [1]

• DVC (kết hợp cùng CML) giúp việc setup,configure và maintain các CI/CD pipeline cho ML dễ dàng hơn nhiều.

3.3) Fast and Secure Data Caching Hub

• Các bộ dữ liệu được sử dụng trong khoa học dữ liệu thường vượt quá dung lượng lưu trữ và khả năng mạng thông thường. Nhu cầu lưu trữ tăng nhanh khi nhiều người cùng tải về dữ liệu, dẫn đến việc trùng lặp dữ liệu (làm tăng chi phí). Thời gian quý báu bị lãng phí khi phải chờ tải dữ liệu về ở từng môi trường khác nhau.

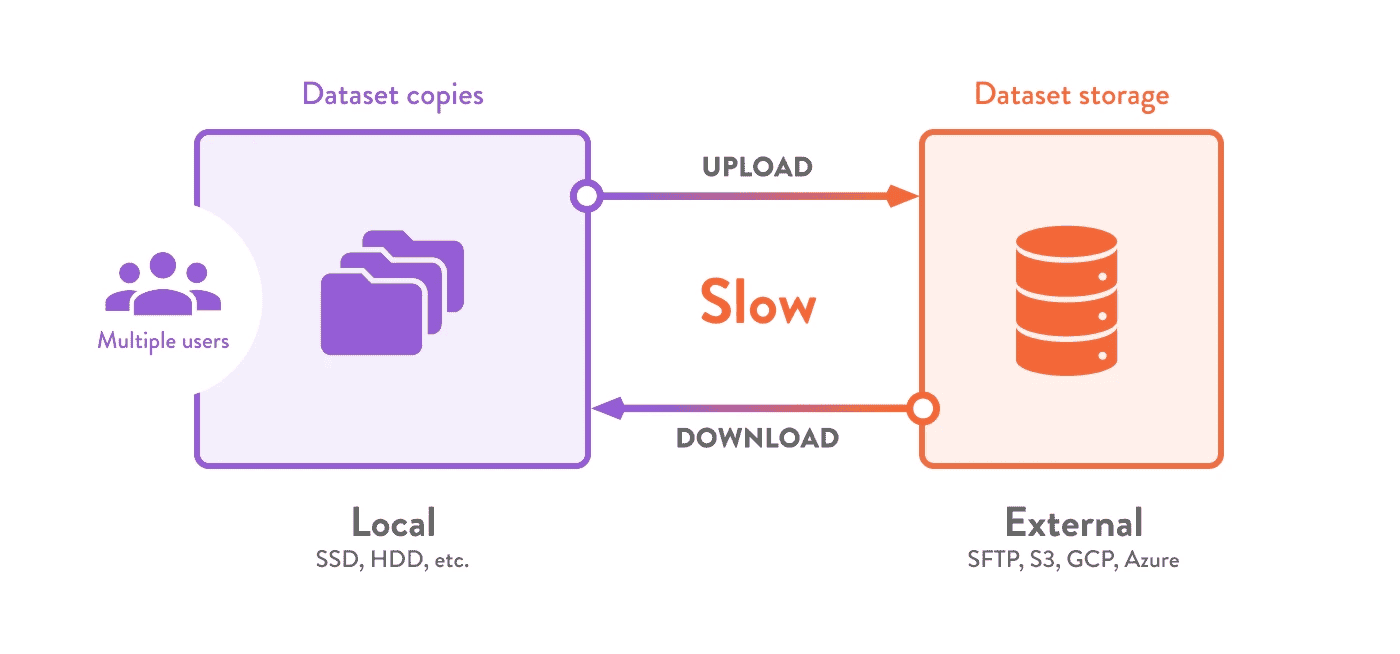
Hình 7: Người dùng chờ đợi các lần truyền tải lặp lại và tạo ra nhiều bản sao dữ liệu cục bộ[1]

• Chức năng caching dữ liệu tích hợp sẵn của DVC giúp bạn thiết lập một lớp lưu trữ hiệu quả cho toàn bộ nhóm, giải quyết các vấn đề:

• Tăng tốc độ truyền tải dữ liệu từ các kho lưu trữ dữ liệu lớn trên cloud, chia sẻ dữ liệu giữa nhiều máy mà không ảnh hưởng tới hiệu năng.

• Chỉ trả chi phí cho việc truy cập nhanh với dữ liệu được dùng thường xuyên (nâng cấp toàn bộ nền tảng lưu trữ là rất tốn kém).

• Tránh việc tải lại dữ liệu và trùng lặp file khi nhiều người cùng làm việc với dữ liệu giống nhau (như trên máy chủ phát triển chung).

• Chuyển đổi nhanh nguồn dữ liệu đầu vào (không phải tải lại) trên máy chủ dùng chung cho thí nghiệm máy học.
  
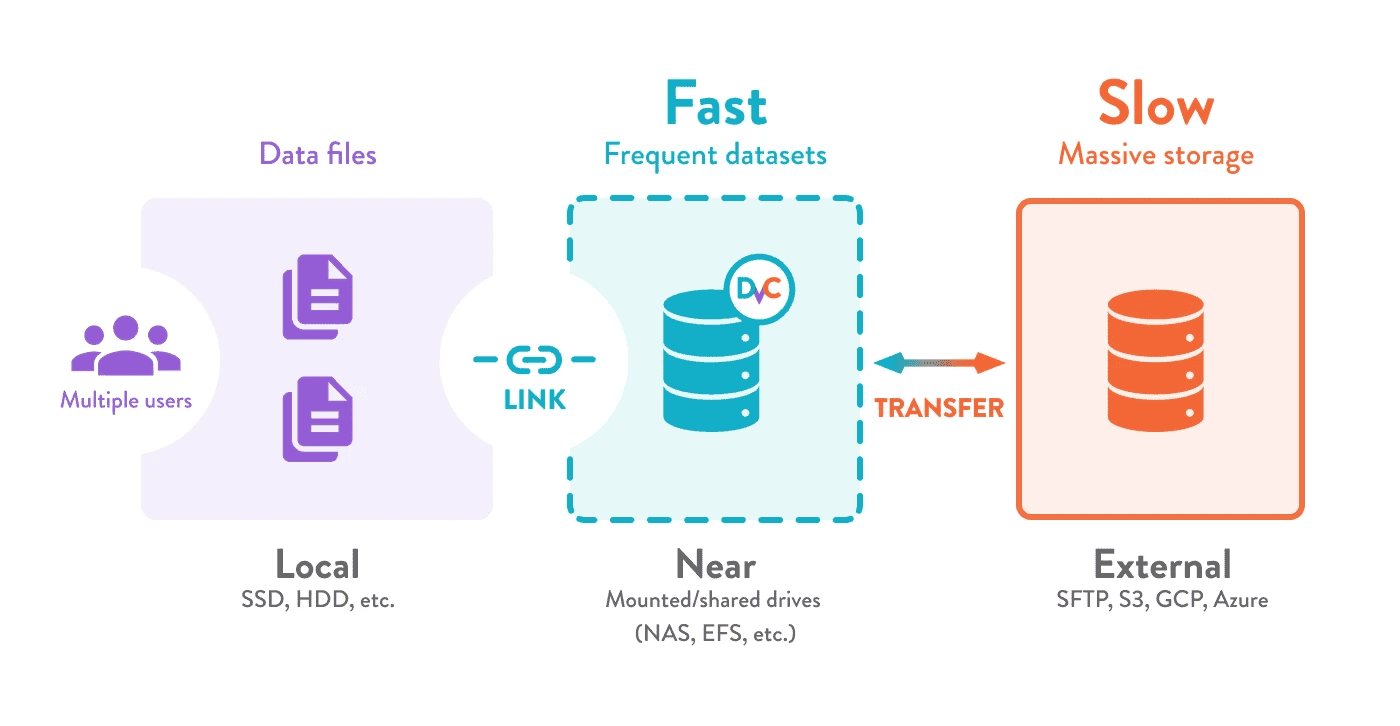
  Hình 7: Phần mềm trung gian lưu trữ dữ liệu cho nhiều dự án [1]

• Bạn có thể tổ chức một vùng lưu trữ duy nhất cho tất cả các dự án bằng cách thiết lập cache DVC dùng chung ở vị trí gần (mạng nội bộ, ổ đĩa ngoài…). Giải pháp này giúp loại bỏ file trùng lặp giữa các bộ dữ liệu, tránh truyền tải lặp lại qua việc liên kết file/directory. Chính sách bảo mật dữ liệu cũng được đảm bảo, vì dữ liệu không rời khỏi kho lưu trữ trung tâm. DVC còn giúp bạn sao lưu và chia sẻ dữ liệu & mô hình ML ở các vị trí ngoài/remote.

• Khi nhóm chia sẻ kho lưu trữ chính, nó có thể được quản lý độc lập như một phần của hạ tầng; được cấp phát tùy theo tốc độ truy cập dữ liệu và chi phí cần thiết. Bạn có thể linh hoạt chuyển đổi nhà cung cấp lưu trữ bất kỳ lúc nào mà không phải thay đổi cấu trúc dự án hay mã nguồn.

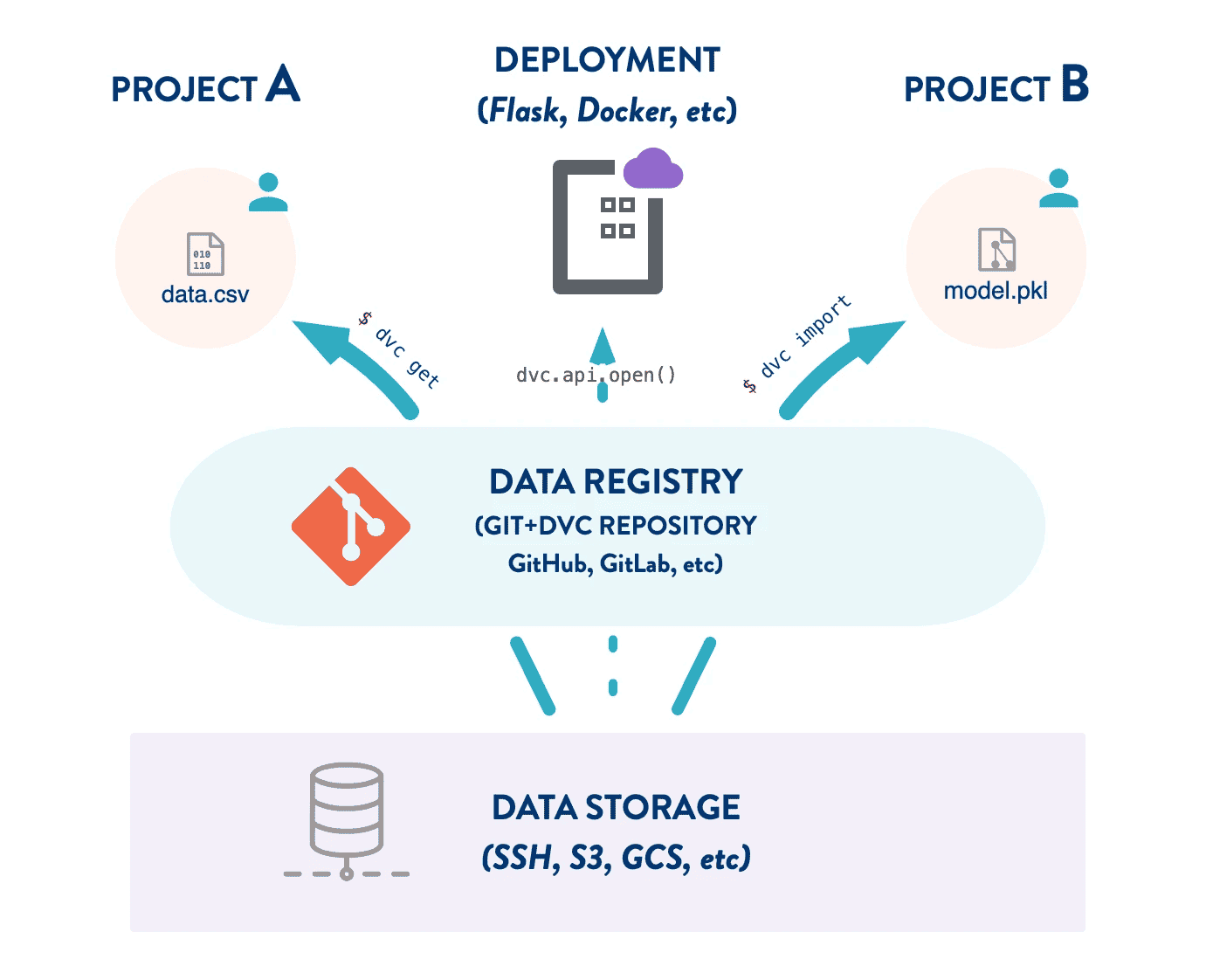
3.4) Data Registry

Hình 8: Phần mềm trung gian quản lý dữ liệu [1]

Bạn có thể tạo một dự án DVC riêng để quản lý phiên bản các tập dữ liệu (hoặc đặc trưng dữ liệu, mô hình ML, ...). Repository sẽ chứa metadata cần thiết và toàn bộ lịch sử thay đổi. Dữ liệu thực tế được lưu trữ ở các remote (điểm lưu trữ từ xa DVC). Đây chính là data registry — tầng trung gian quản lý dữ liệu giữa các dự án Machine Learning và cloud storage.

Ưu điểm

• Tái sử dụng: Tổ chức và truy xuất kho đặc trưng với câu lệnh CLI đơn giản (dvc get và dvc import), tương tự như quản lý gói phần mềm kiểu pip.

• Tính bền vững: Phân tách metadata và lưu trữ trên các nền tảng đáng tin cậy (Git, cloud), giúp dữ liệu của bạn bền vững hơn.

• Tối ưu hóa lưu trữ: Tập trung dữ liệu dùng chung cho nhiều dự án tại một nơi (hoặc các bản sao phân tán), đơn giản hóa quản lý và tiết kiệm dung lượng.

• Dữ liệu như mã nguồn: Tận dụng workflow của Git như lịch sử commit, tạo nhánh, pull request, review và cả CI/CD cho vòng đời dữ liệu và mô hình. Hãy tưởng tượng "Git dành cho cloud storage".

• Bảo mật: Remote storage được kiểm soát bởi DVC (ví dụ Amazon S3) có thể cấu hình giới hạn truy cập, ví dụ như endpoint chỉ đọc để ngăn xóa/ghi dữ liệu.

X. (MLOps) Serving Data using Feast

1) Giới thiệu

Các thách thức khi triển khai hệ thống ML từ thử nghiệm lên production:
Giai đoạn thử nghiệm

• Các nhà khoa học dữ liệu thử nghiệm trên Jupyter Notebook

• Xử lý dữ liệu, thiết kế features và huấn luyện mô hình đạt độ chính xác cao

• Ví dụ ứng dụng: hệ thống phát hiện gian lận thẻ tín dụng real-time

Thách thức khi triển khai

• Vấn đề chính: Không phải thuật toán mà là dữ liệu và features (các đặc trưng được tạo ra từ dữ liệu đó)

• Logic tính toán features đơn giản trong batch processing (offline) nhưng khó tái hiện trong real-time serving (online), vốn đòi hỏi độ trễ rất thấp.

• Feature mismatch: Sự không nhất quán giữa cách tính features ở môi trường thử nghiệm và production

Đây là vấn đề cốt lõi trong MLOps - đảm bảo feature processing đồng nhất giữa training và serving environment.

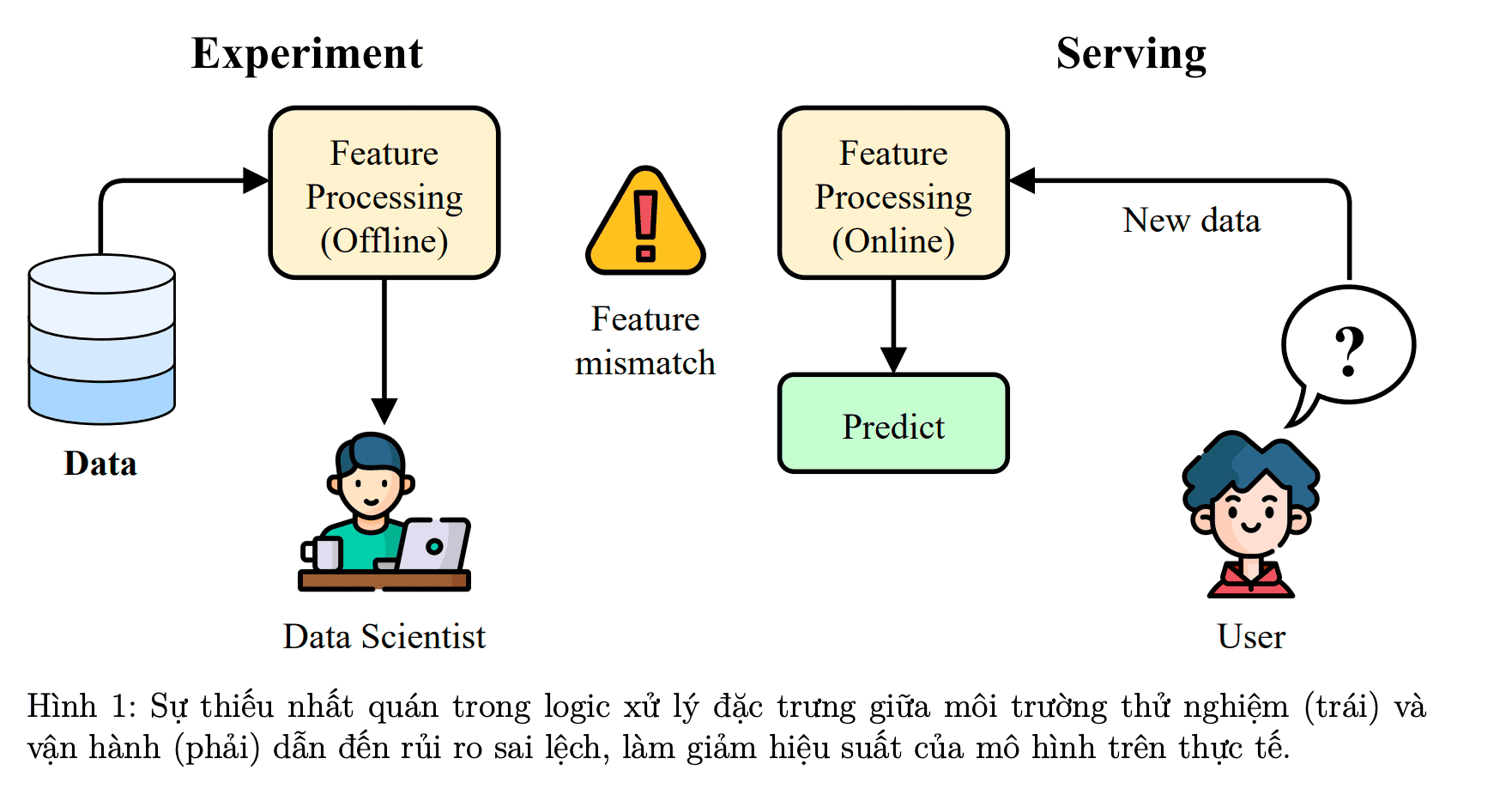
Hình 1: [1]

Để giải quyết những thách thức này và kết nối hiệu quả giữa giai đoạn nghiên cứu và giai đoạn vận hành, một thành phần hạ tầng chuyên biệt đã ra đời và trở thành phần cốt lõi trong các hệ thống MLOps (Machine Learning Operations) hiện đại: Feature Store.

Feature Store là 1 hệ thống trung tâm để quản lý, lưu trữ, và cung cấp các đặc trưng một cách nhất quán cho cả việc huấn luyện và dự đoán.

1.1) Từ ML đến MLOps

Trong môi trường học thuật hoặc thử nghiệm, quy trình Machine Learning thường nhằm tối ưu một mô hình trên một bộ dữ liệu tĩnh. Quy trình này thường diễn ra tuần tự qua các bước:

1. Thu thập và xử lý dữ liệu: Dữ liệu được thu thập và tiền xử lý một lần để chuẩn bị cho việc huấn luyện.
2. Xử lý đặc trưng: Các đặc trưng được tạo ra, lựa chọn và thử nghiệm thủ công.
3. Huấn luyện và đánh giá mô hình: Các nhà khoa học dữ liệu thử nghiệm nhiều thuật toán và tinh chỉnh siêu tham số để tìm ra mô hình tốt nhất.
4. Triển khai: Nếu có, bước này thường chỉ là một hoạt động riêng lẻ, ví dụ như xây dựng một API, giao diện đơn giản để demo.

Quy trình trên phù hợp cho việc nghiên cứu nhưng không đủ mạnh mẽ và linh hoạt để vận hành trong thế giới thực, nơi dữ liệu liên tục thay đổi và hệ thống đòi hỏi độ tin cậy, khả năng lặp lại kết quả và khả năng quan sát. Để giải quyết những thách thức này và xây dựng các hệ thống Machine Learning bền vững, ngành công nghiệp đã áp dụng một triết lý vận hành gọi là MLOps.

MLOps (Machine Learning Operations) chuyển trọng tâm từ việc tạo ra 1 mô hình đơn lẻ sang việc xây dựng 1 hệ thống tự động và tuần hoàn có khả năng liên tục cung cấp và duy trì các sản phẩm Machine Learning. MLOps kế thừa các nguyên tắc cốt lõi từ DevOps và điều chỉnh chúng cho phù hợp với vòng đời đặc thù của Machine Learning:

• CI (Continuous Integration): Không chỉ tích hợp mã nguồn, CI trong MLOps còn bao gồm cả việc kiểm thử cho cả dữ liệu và thành phần của model.
• CD (Continuous Delivery/Deployment): Tự động hóa quá trình đóng gói (containerize) và triển khai an toàn toàn bộ hệ thống (bao gồm mô hình, source code và cấu hình) ra môi trường sản phẩm.
• CT (Continuous Training): Một khái niệm đặc thù của MLOps, chỉ việc tự động huấn luyện lại mô hình khi có các yếu tố kích hoạt, ví dụ như có dữ liệu mới, hiệu suất mô hình suy giảm, hoặc theo lịch.

Một vòng đời MLOps đầy đủ bao gồm các giai đoạn được tích hợp chặt chẽ với nhau:

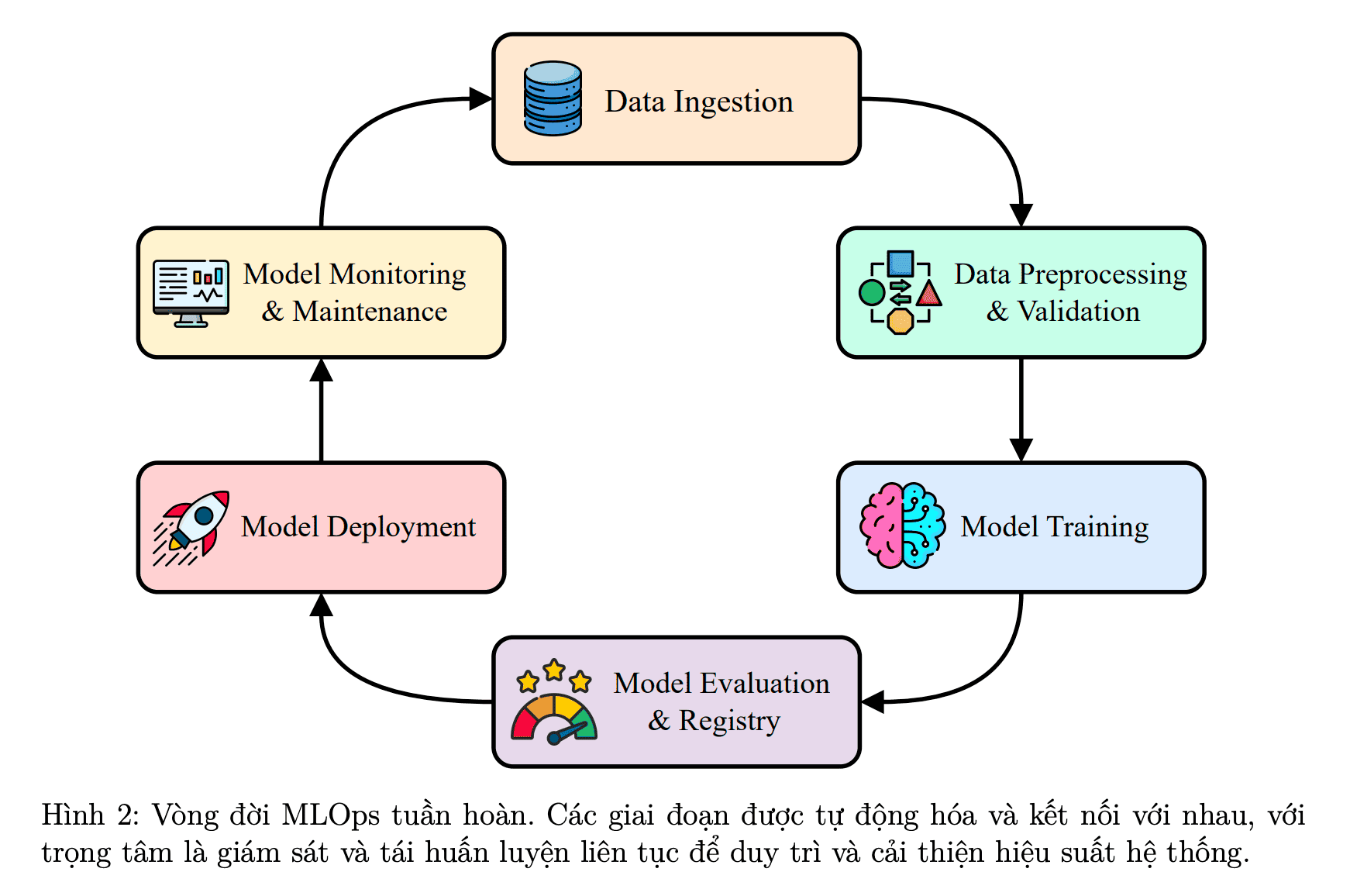
Hình 2: [1]

• Data Ingestion: Đây là một data pipeline tự động thu thập dữ liệu từ các nguồn khác nhau như streaming events, database hay data lakes.
• Data Preprocessing & Validation: Dữ liệu mới được tự động làm sạch và biến đổi. Quan trọng hơn, dữ liệu sẽ được xác thực để kiểm tra chất lượng, định dạng và tính hợp lệ, đảm bảo chỉ dữ liệu tốt mới được đưa vào huấn luyện.
• Model Training: Quá trình training được tự động hóa và kích hoạt theo lịch trình hoặc sự kiện. Các thông tin về thử nghiệm, tham số và chỉ số đánh giá được ghi nhận một cách có hệ thống bằng các công cụ theo dõi như MLflow, Wandb
• Model Evaluation & Registry: Mô hình mới được tự động đánh giá và so sánh với phiên bản đang chạy. Nếu tốt hơn, nó sẽ được đăng ký vào một Model Registry (ví dụ: cũng trong MLFlow) để quản lý phiên bản và chuẩn bị cho việc triển khai.
• Model Deployment: Mô hình được tự động đóng gói (ví dụ: Docker) và triển khai lên môi trường sản phẩm thông qua một quy trình CI/CD. Việc phục vụ mô hình ở quy mô lớn thường được quản lý bởi các nền tảng như Kubernetes hoặc các dịch vụ đám mây (AWS, GCP, Azure)
• Model Monitoring & Maintenance: Sau khi triển khai, mô hình được giám sát liên tục. Các hệ thống như Prometheus và Grafana được dùng để theo dõi các chỉ số vận hành và hiệu suất dự đoán. Khi phát hiện sự suy giảm chất lượng của mô hình, hệ thống sẽ gửi cảnh báo hoặc tự động kích hoạt lại vòng đời MLOps, bắt đầu bằng việc tái huấn luyện trên dữ liệu mới. Toàn bộ quy trình này được điều phối bởi các công cụ như Airflow.

Tóm lại, MLOps là một hệ sinh thái gồm nhiều thành phần quan trọng phối hợp nhịp nhàng. Trong đó, việc quản lý dữ liệu và đặc trưng một cách nhất quán cho cả môi trường huấn luyện và phục vụ là một thách thức nền tảng. Đây chính là lý do mà Feature Store ra đời và trở thành một trụ cột không thể thiếu trong các hệ thống MLOps hiện đại.

1.2) Những thách thức trong quản lý đặc trưng dữ liệu

Một vòng đời MLOps tự động hóa và hiệu quả như đã trình bày ở trên phụ thuộc rất nhiều vào chất lượng và tính nhất quán của input đầu vào: các đặc trưng. Việc thiếu một thành phần chuyên biệt cho nhiệm vụ này sẽ dẫn đến các vấn đề nghiêm trọng cả về mặt kỹ thuật lẫn quy trình vận hành trong tổ chức.

1.2.1) Đảm bảo tính nhất quán logic giữa các môi trường

Đây là rào cản kĩ thuật phức tạp và phổ biến nhất: Training-Serving Skew

• Bối cảnh: Trong MLOps, pipeline training (xử lý theo batch, offline) và pipeline serving (xử lý real-time, online) là 2 hệ thống hoàn toàn khác nhau. Chúng có thể được viết bằng các ngôn ngữ khác nhau, chạy trên hạ tầng khác nhau và có yêu cầu về độ trễ khác nhau.
• Vấn đề: Việc đảm bảo logic tính toán đặc trưng (ví dụ: cách xử lý giá trị null, làm tròn số, tổng hợp dữ liệu) giống hệt nhau 100% trên hai môi trường này là cực kỳ khó khăn và dễ phát sinh lỗi.
• Hệ quả: Chỉ một khác biệt nhỏ trong logic cũng đủ để làm hiệu suất của mô hình trên thực tế suy giảm nghiêm trọng so với kết quả đánh giá và gây ảnh hưởng trực tiếp đến giá trị kinh doanh

1.2.2) Tối ưu hóa việc phát triển và cộng tác

Khi một tổ chức mở rộng quy mô, việc thiếu một nền tảng quản lý đặc trưng chung sẽ tạo ra rào cản lớn về hiệu suất và sự hợp tác giữa các nhóm.

• Vấn đề: Mỗi nhóm/ dự án có xu hướng tự xây dựng lại các đặc trưng từ đầu. Vì thiếu hệ thống quản lý đặc trưng chung, các định nghĩa đặc trưng bị phân tán trong vô số notebook, tài liệu, source code, biến kiến thức này thành tài sản riêng của 1 vài cá nhân.
• Hệ quả:
• Lãng phí tài nguyên: Các nhóm tốn thời gian và công sức để thực hiện lại các công việc trùng lặp.
• Thiếu khả năng tái sử dụng và khám phá: Rất khó để một thành viên mới hoặc một nhóm khác biết được đặc trưng nào đã tồn tại để có thể tận dụng, làm giảm đáng kể tốc độ phát triển model mới.
• Định nghĩa không nhất quán: Cùng một khái niệm kinh doanh (ví dụ: “khách hàng thân thiết”) có thể có nhiều định nghĩa và cách tính toán khác nhau trong các dự án, dẫn đến sự thiếu nhất quán và khó so sánh kết quả.

Những thách thức trên cho thấy rõ, một hệ thống MLOps hoàn chỉnh không chỉ cần các pipeline tự động mà còn đòi hỏi một lớp hạ tầng chuyên biệt cho dữ liệu đặc trưng. Lớp hạ tầng này đảm bảo tính nhất quán, khả năng tái sử dụng và quản trị hiệu quả các đặc trưng. Đây chính là vai trò mà Feature Store đảm nhiệm trong kiến trúc MLOps hiện đại.

2) Tổng quan về Feature store

2.1) Vai trò và vị trí trong MLOps

Về bản chất, Feature Store hoạt động như một hệ thống trung tâm cho data và metadata của feature trong suốt vòng đời của 1 dự án. Nó phục vụ cho 2 nhu cầu hoàn toàn khác nhau: xử lý theo batch cho việc training và xử lý realtime cho serving.

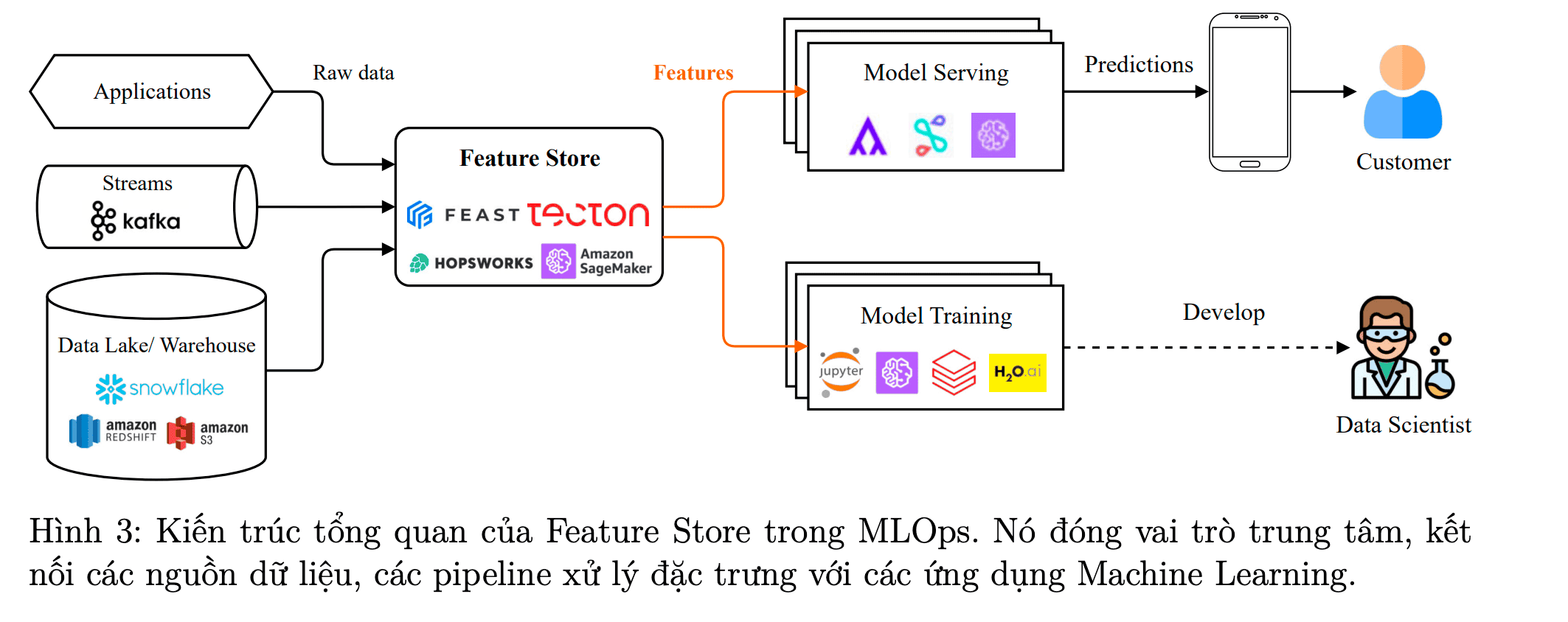
Hình 3: [1]

Như trong Hình 3, luồng dữ liệu và hoạt động của Feature Store có thể được tóm tắt như sau:

• Đầu vào: Các pipeline kỹ thuật đặc trưng đọc dữ liệu thô từ nhiều nguồn (Data Lake, Data Warehouse, Streaming Platforms) để tạo ra các giá trị đặc trưng.
• Data Ingestion: Các giá trị đặc trưng được nạp vào Feature Store và lưu trữ đồng thời ở hai nơi:
• Toàn bộ lịch sử giá trị được ghi vào Offline Store để huấn luyện mô hình.
• Giá trị mới nhất được ghi vào Online Store để dự đoán thời gian thực.
• Đầu ra:
• Các quy trình huấn luyện truy vấn Offline Store để lấy các bộ dữ liệu lịch sử lớn.
• Các dịch vụ dự đoán truy vấn Online Store để lấy vector đặc trưng mới nhất với độ trễ thấp.

2.2) Các thành phần cốt lõi

Một Feature Store hiện đại bao gồm 5 phần chính:

2.2.1) Serving

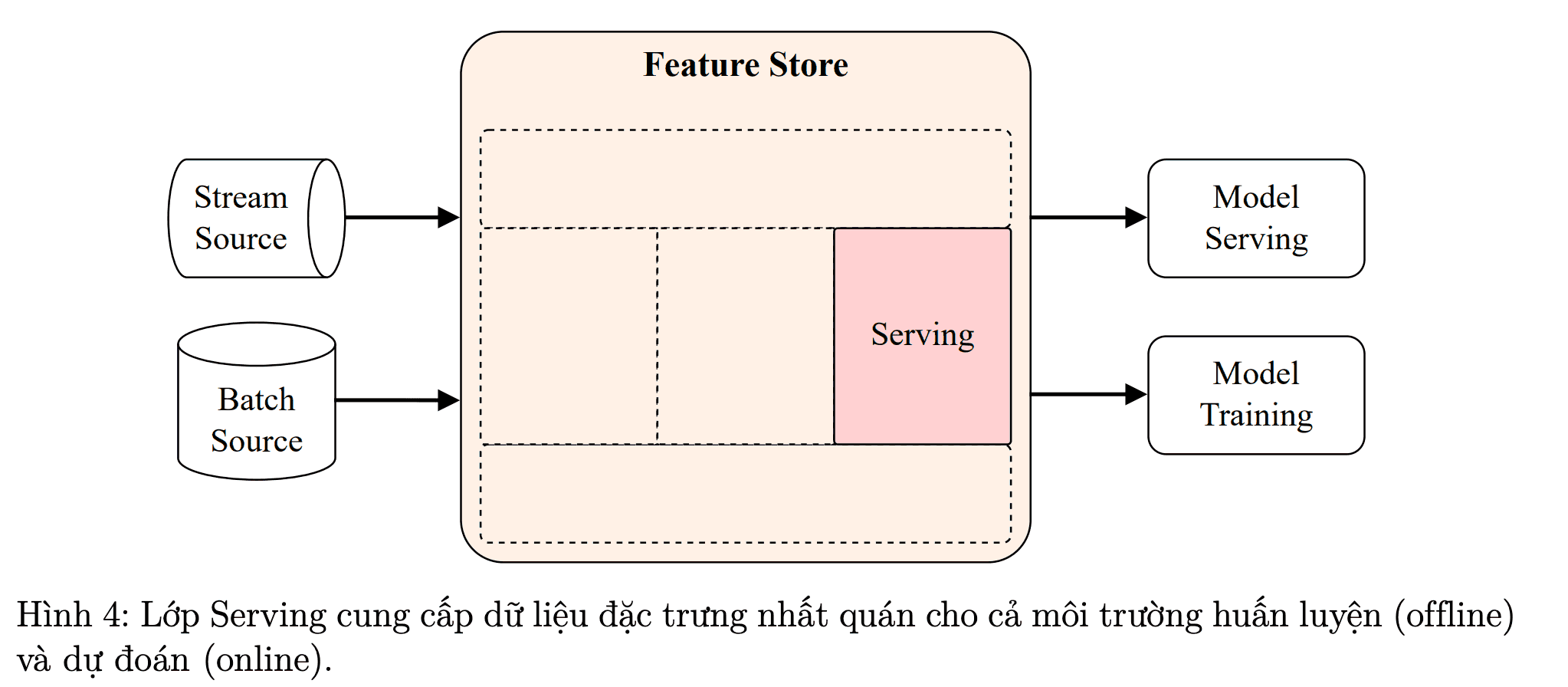
Hình 4: [1]

Đây là chức năng cưng cấp dữ liệu đặc trưng nhất quán cho các mô hình: Định nghĩa của đặc trưng được dùng để huấn luyện mô hình phải khớp chính xác 100% với đặc trưng được cung cấp khi dự đoán. Khi chúng không khớp, hiện tượng training-serving skew sẽ xảy ra, gây sụt giảm hiệu năng nghiêm trọng và rất khó để gỡ lỗi.

• Offline Serving: Cung cấp SDK để truy vấn các tập dữ liệu lịch sử lớn cho việc training. Chức năng này hỗ trợ các phép join point-in-time correct, cho phép “du hành thời gian” để lấy đúng giá trị của đặc trưng tại một thời điểm trong quá khứ, đảm bảo không bị rò rỉ dữ liệu.
• Online Serving: Cung cấp một API hiệu năng cao để lấy một vector đặc trưng (gồm các giá trị mới nhất) với độ trễ thấp. Các yêu cầu này được phục vụ bởi một cơ sở dữ liệu tốc độ cao.

2.2.2) Storage

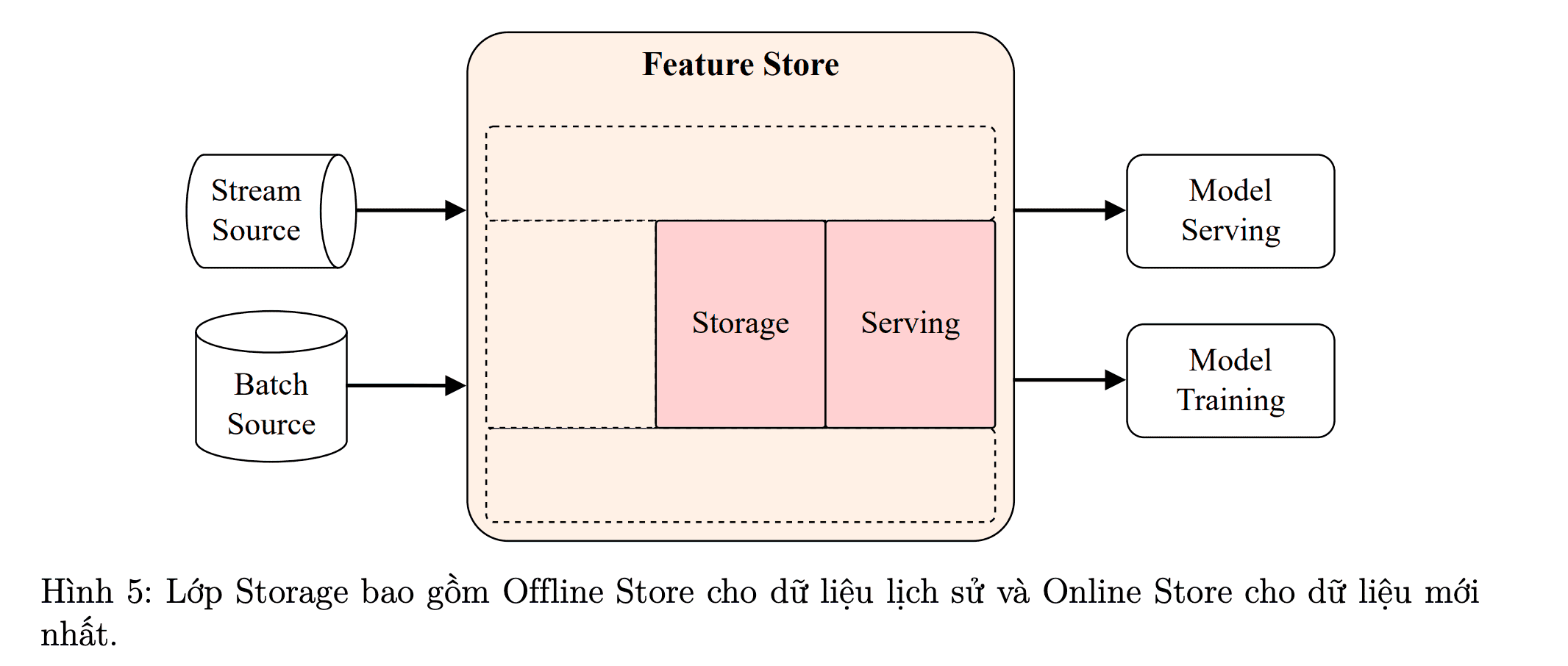
Hình 5: [1]

• Offline Store: Lưu trữ dữ liệu lịch sử của đặc trưng trong nhiều tháng hoặc nhiều năm để phục vụ việc training. Kho này thường được xây dựng trên các Data Warehouse (BigQuery, SnowFlake) hay các Data Lake (S3) có sẵn của tổ chức.
• Online Store: Chỉ lưu trữ giá trị mới nhất của đặc trưng cho mỗi thực thể để phục vụ truy vấn với độ trễ thấp khi dự đoán. Kho này thường được triển khai bằng các cơ sở dữ liệu Key-Value hiệu năng cao như Redis hoặc DynamoDB.

2.2.3) Transformation

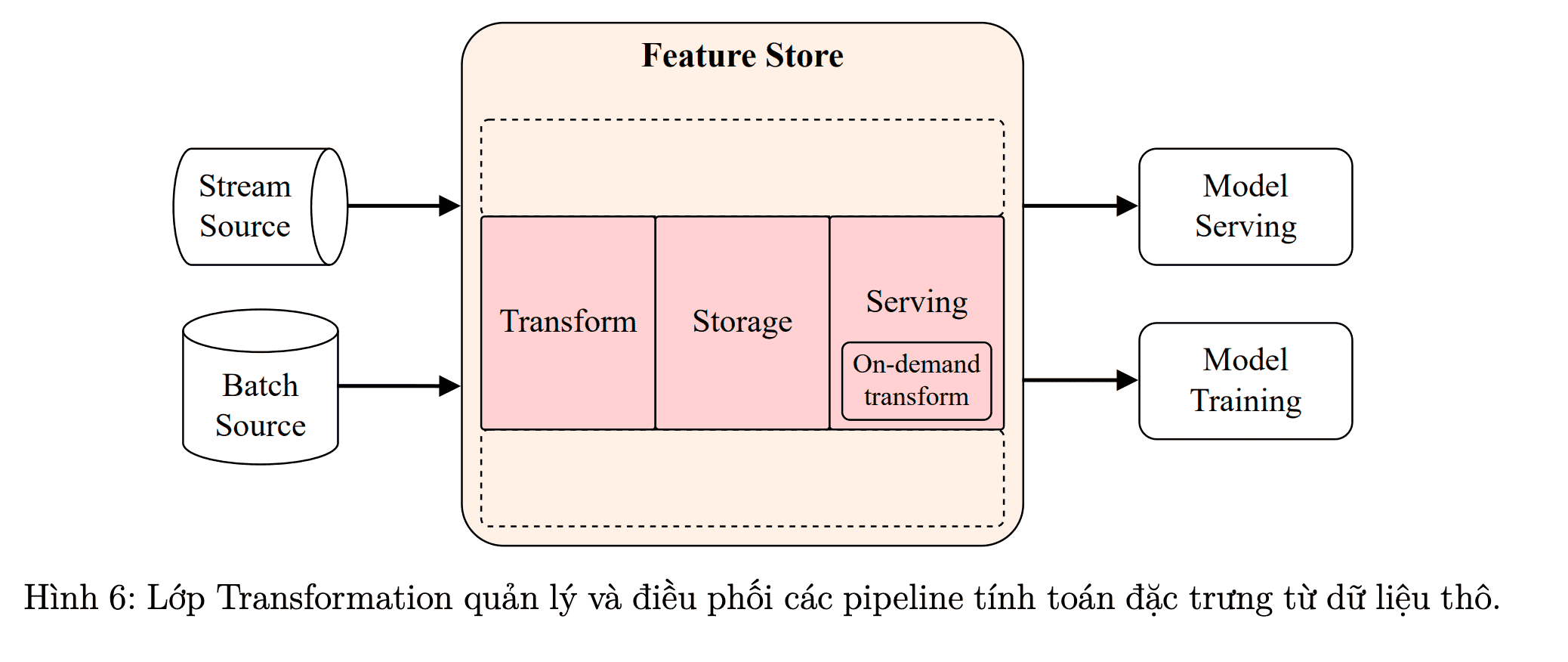
Hình 6: [1]
Feature Store quản lý và điều phối các pipeline tính toán đặc trưng từ dữ liệu thô. Việc tái sử dụng source code biến đổi đặc trưng giữa các môi trường là chìa khóa chính để giải quyết vấn đề Training-Serving Skew. Có 3 loại hình biến đổi chính:

• Batch Transformations: Áp dụng trên dữ liệu tĩnh (dữ liệu lịch sử) từ Data Warehouse hay Data Lake (Batch Source trong hình)
• Streaming Transformations: Áp dụng trên các nguồn dữ liệu streaming (như Kafka) để tính toán đặc trưng gần thời gian thực (Stream Source trong hình)
• On-demand Transformations: Tính toán đặc trưng “theo yêu cầu” tại thời điểm dự đoán, sử dụng những dữ liệu chỉ có sẵn tại lúc yêu cầu (ví dụ: vị trí hiện tại của người dùng).

2.2.4) Monitoring

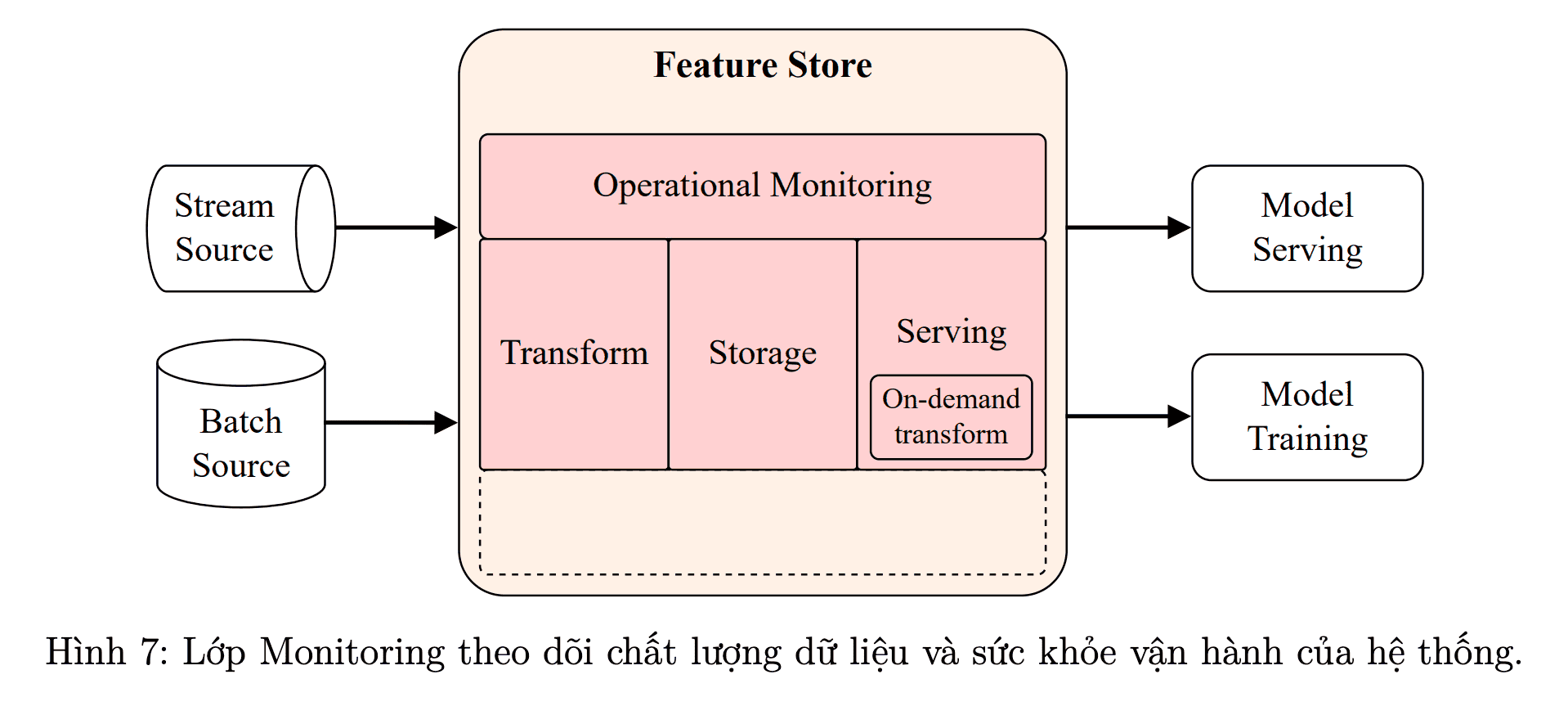
Hình 7: [1]

Khi xảy ra sự cố trong hệ thống Machine Learning, nguyên nhân thường đến từ dữ liệu. Feature Store có vị trí đặc biệt thuận lợi để phát hiện và cảnh báo những vấn đề này.

• Giám sát chất lượng dữ liệu: Theo dõi data drift và so sánh dữ liệu serving với dữ liệu training để phát hiện training-serving skew.
• Giám sát vận hành: Theo dõi các chỉ số hệ thống như latency, throughput, tỷ lệ lỗi của dịch vụ serving, hay độ mới của dữ liệu.

2.2.5) Registry

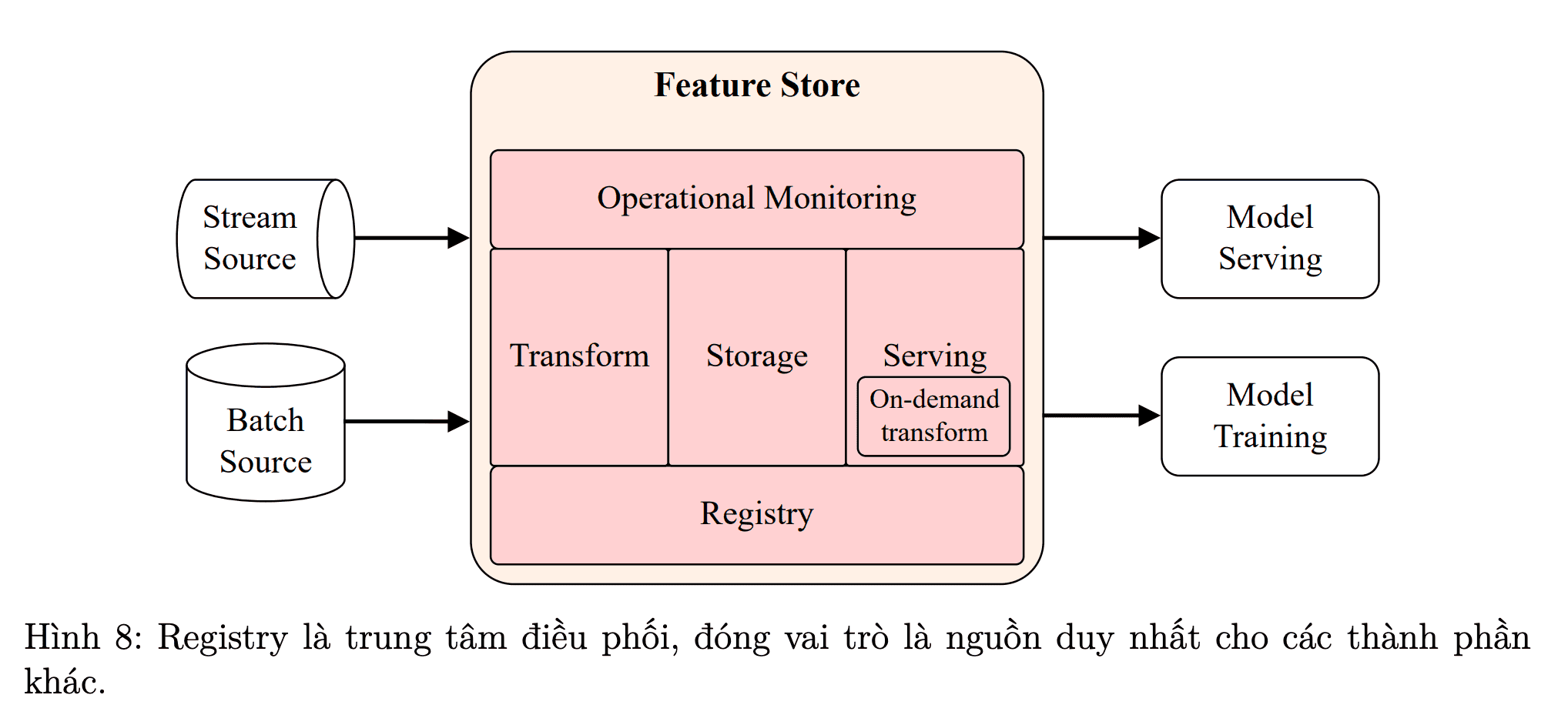
Hình 8: [1]

Registry là thành phần trung tâm, đóng vai trò là nguồn duy nhất cho mọi thông tin về đặc trưng trong hệ thống.

• Danh mục chung: Các nhóm sử dụng Registry như một data catalog để khám phá, cộng tác và chia sẻ các định nghĩa đặc trưng, tránh lãng phí công sức phát triển lại các đặc trưng đã có.
• Cấu hình hệ thống: Các định nghĩa trong Registry được các thành phần khác (Transformation, Storage, Serving) sử dụng để tự động hóa các tác vụ. Nó cũng lưu trữ thông tin về phiên bản và nguồn gốc để phục vụ việc gỡ lỗi và kiểm toán.

3) Feast

Feast (Feature Store for Machine Learning) là một opensource feature store, đã nhanh chóng trở thành một tiêu chuẩn mã nguồn mở hàng đầu. Điểm mạnh lớn nhất của Feast là tính linh hoạt và không bị ràng buộc vào nhà cung cấp. Nó không phải là một nền tảng “tất cả trong một” mà là một lớp điều phối mỏng, cho phép bạn tận dụng chính hạ tầng dữ liệu sẵn có của mình. Ví dụ như Snowflake, BigQuery cho offline store; Redis, DynamoDB cho online store.

3.1) Triết lý cốt lõi

Điểm khác biệt lớn nhất và cũng là điểm mạnh nhất của Feast là nó không phải là một nền tảng “tất cả trong một”. Thay vì xây dựng một hệ thống cồng kềnh với pipeline, cơ sở dữ liệu, và công cụ điều phối riêng, Feast được thiết kế như một lớp điều phối mỏng linh hoạt. Triết lý của Feast là kết nối và tái sử dụng chính hạ tầng dữ liệu mà tổ chức đã có sẵn.

• Nó không thay thế Data Warehouse (như BigQuery, Snowflake) mà sử dụng chúng làm Offline Store.
• Nó không thay thế cơ sở dữ liệu Key-Value (như Redis, DynamoDB) mà sử dụng chúng làm Online Store.
• Nó không thay thế công cụ điều phối (như Airflow) mà tích hợp với chúng để lên lịch cho các tác vụ data ingestion.
  Cách tiếp cận này giúp các đội MLOps có thể nhanh chóng triển khai một Feature Store mà không cần phải xây dựng lại toàn bộ hệ thống dữ liệu từ đầu.

3.2) Vai trò và phạm vi

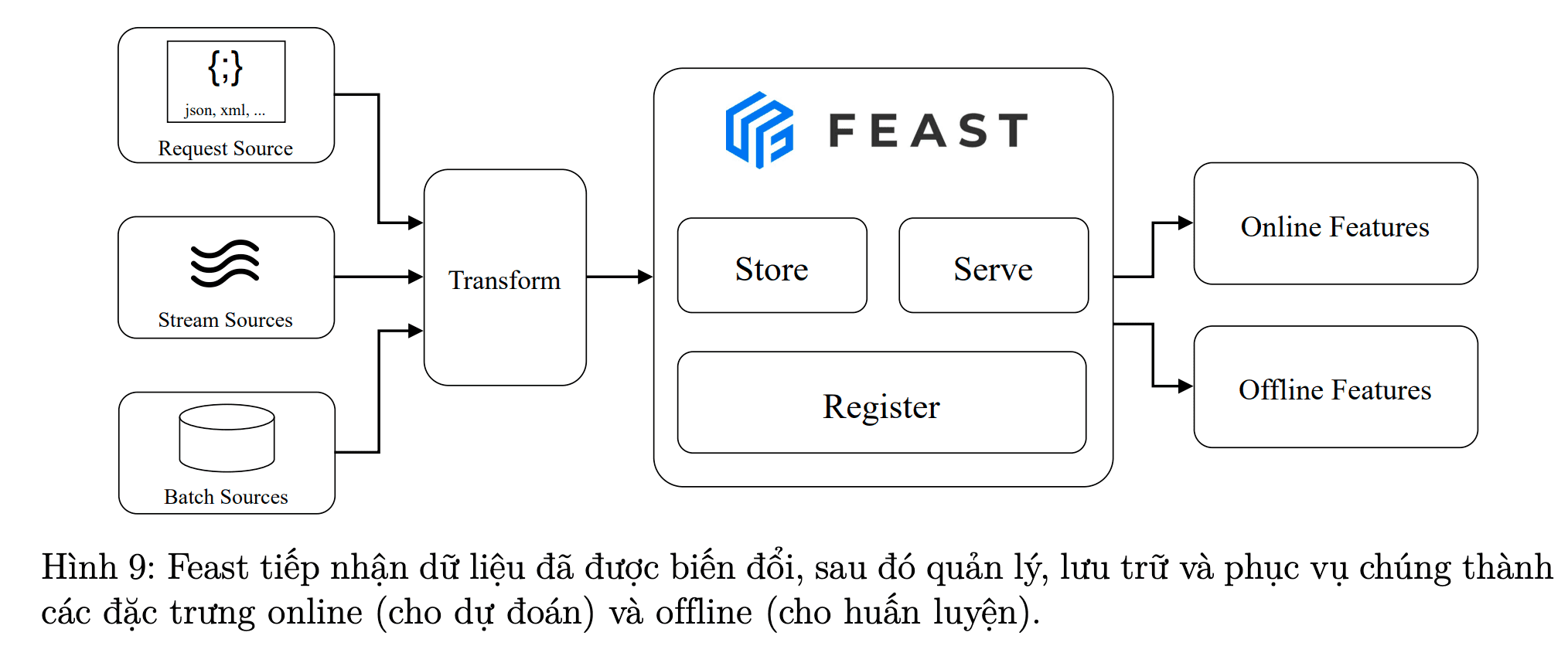
Hình 9: [1]

• Feast là một lớp truy cập dữ liệu thống nhất, giúp đảm bảo tính nhất quán giữa training và serving (với các phép join point-in-time correct) và hoạt động như một trung tâm registry để thúc đẩy việc cộng tác và tái sử dụng đặc trưng.
• Feast không phải là một hệ thống dữ liệu đa năng. Nó không thay thế các công cụ ETL (như dbt, Spark), công cụ điều phối (như Airflow), hay các hệ thống lưu trữ (như Data Warehouse, Database) mà được thiết kế để tích hợp và hoạt động bên trên chúng.

3.3) Cú pháp và cách sử dụng cơ bản

Tương tác với Feast chủ yếu diễn ra qua hai hình thức: khai báo các đối tượng bằng Python và sử dụng CLI/SDK để quản lý và truy vấn dữ liệu.

3.3.1) Các đối tượng định nghĩa chính

Đây là các khối xây dựng cơ bản mà bạn sẽ khai báo bằng Python trong một “Feature Repository:

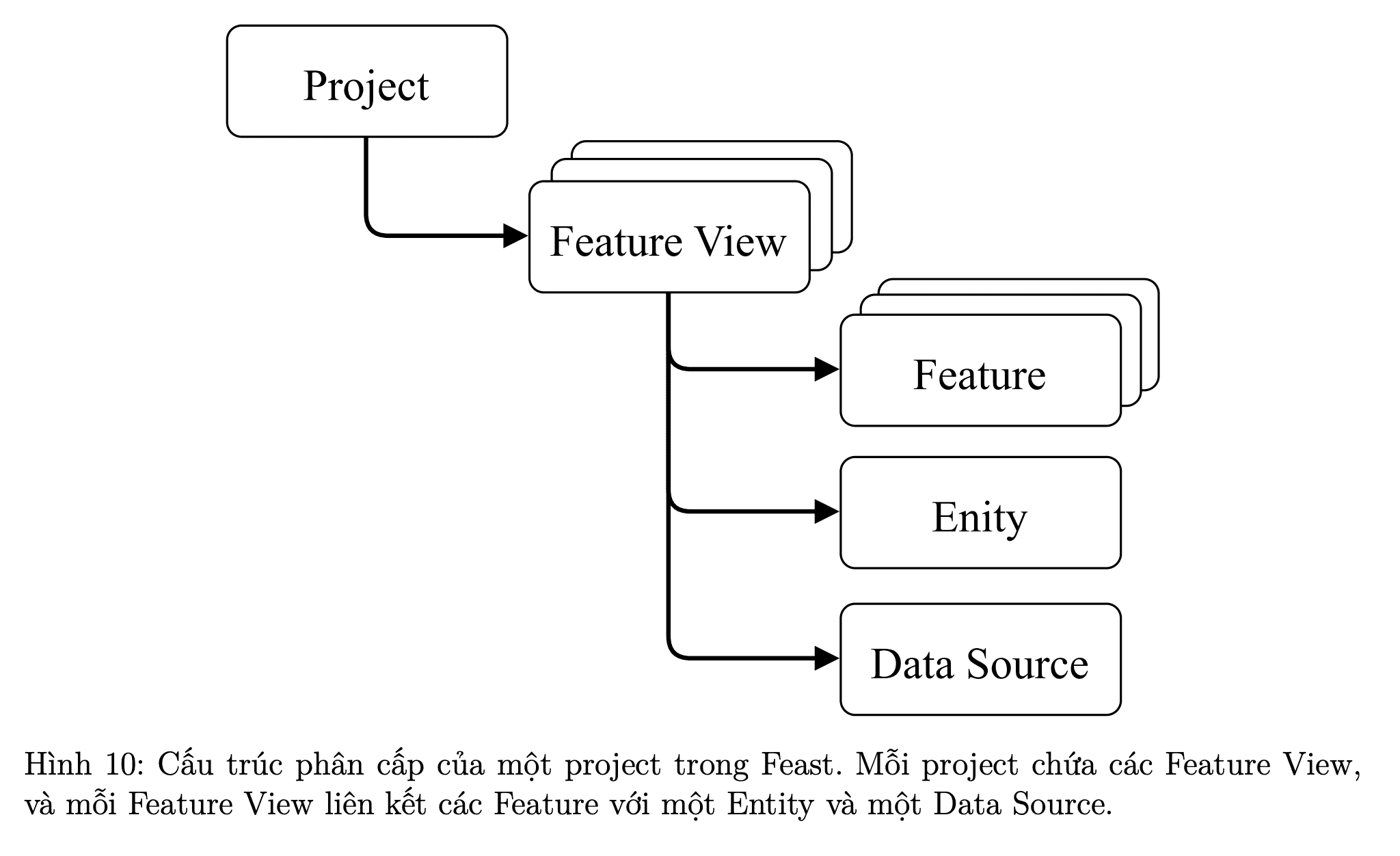
Hình 10: [1]

• Project: Là không gian tên (namespace) ở cấp cao nhất. Mỗi project là một dự án riêng biệt chứa các thực thể và đặc trưng, giúp cô lập hoàn toàn các môi trường khác nhau (ví dụ: dev, staging, production).
• FeatureView: Là thành phần trung tâm, định nghĩa một nhóm logic các đặc trưng. Một FeatureView sẽ:
• Chứa định nghĩa của một hoặc nhiều Features (tên, kiểu dữ liệu).
• Liên kết các features này với một hoặc nhiều Entity.
• Trỏ đến một DataSource để Feast biết nơi lấy dữ liệu.
• FeatureService: Dùng để nhóm các đặc trưng từ một hoặc nhiều FeatureView lại với nhau, phục vụ cho một phiên bản model hoặc một ứng dụng cụ thể. Đây là một cách thực hành tốt để quản lý vòng đời và các phụ thuộc dữ liệu của model.
• DataSource: Đối tượng chỉ định nguồn dữ liệu vật lý nơi các giá trị đặc trưng được lưu trữ. Đây có thể là một file Parquet, một bảng trong BigQuery, hay một topic Kafka.
• Entity: Đại diện cho đối tượng kinh doanh mà các đặc trưng mô tả (ví dụ: customer_id, product_id). Đây chính là khóa (join key) để liên kết và tra cứu đặc trưng.

3.3.2) Các lệnh CLI phổ biến

Đây là các lệnh bạn dùng trên terminal để quản lý vòng đời của Feature Store:

• feast init <tên_project>: Khởi tạo một cấu trúc thư mục project Feast mẫu (một Feature Repository).
• feast apply: Đọc các định nghĩa Python trong repo, đăng ký chúng vào registry, và cập nhật hạ tầng (ví dụ: tạo bảng trong Online Store).
• feast materialize <start_date> <end_date> : Nạp dữ liệu đặc trưng từ Offline Store vào Online Store trong một khoảng thời gian nhất định để chuẩn bị cho việc phục vụ online.
• feast ui: Khởi chạy một giao diện web để khám phá các đối tượng đã được đăng ký trong Feature Store.

3.3.3) Các hàm chính để truy vấn dữ liệu

Đây là các hàm Python bạn dùng trong code để lấy dữ liệu cho các tác vụ Machine Learning:

• store.get_historical_features(...): Dùng để lấy dữ liệu lịch sử từ Offline Store nhằm tạo ra bộ dữ liệu huấn luyện hoặc thực hiện dự đoán theo lô. Hàm này thực hiện các phép join point-in-time correct để chống rò rỉ dữ liệu.
• store.get_online_features(...): Dùng để lấy vector đặc trưng mới nhất từ Online Store với độ trễ thấp, phục vụ cho việc dự đoán thời gian thực

Reference

[1] Ảnh được lấy từ tài liệu khóa học AIO Module 05 Tuần 01 và 02.